Possible Early Generation of Physiological Helical Flow Could Benefit the Triflo Trileaflet Heart Valve Prosthesis Compared to Bileaflet Valves
Abstract
1. Introduction
- Angular momentum generated during the filling procedure of the left ventricle, which does not completely cease until the beginning of the systole—It is documented in previous research that a vortex ring or a tumble vortex [20] is generated in the filling phase. The flow in the ventricular outflow tract, therefore, has a non-axial component.
- The helical ventricle contraction—It is reasonable to assume that the left ventricle contraction re-orients the spin-vector of existing angular momentum into the ejection direction, causing a swirl component of the axial flow. This is supported eventually by the left ventricle torsional motion during contraction and the helical myofiber architecture of the LV wall [21,22].
- The bathtub vortex effect—Any weak swirl in the convergent outflow tract is strengthened when the flow accelerates towards the valve plane. This is due to conservation of angular momentum, similar to a bathtub vortex when draining through a small orifice. In their original paper, Kilner et al. [18] also mentioned that the existence of a possible helical flow in the ventricular outflow tract could not be excluded; a definite conclusion was not possible because of the limits of resolution power of MRI.
2. Materials and Methods
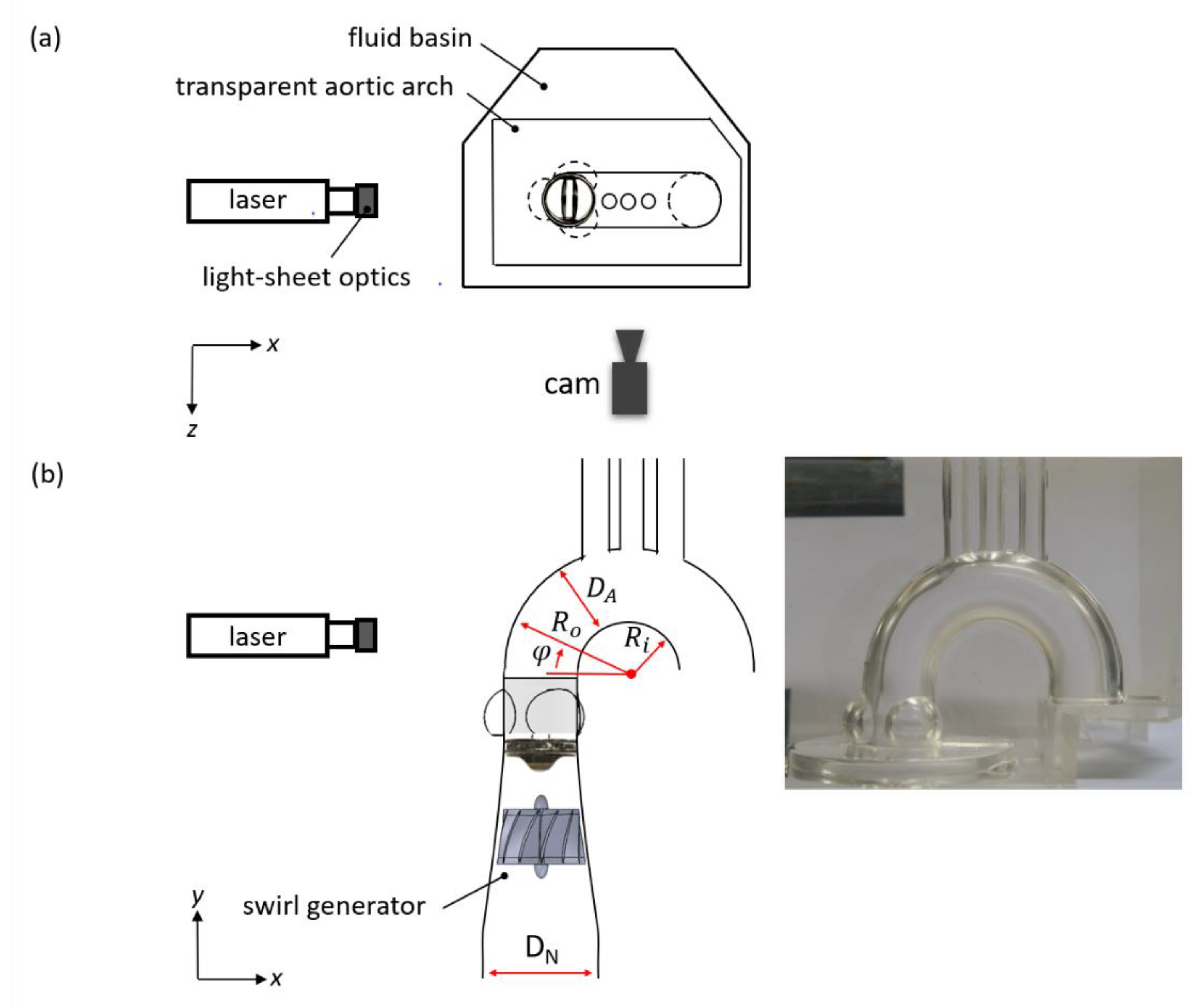
2.1. Pulse Duplicator
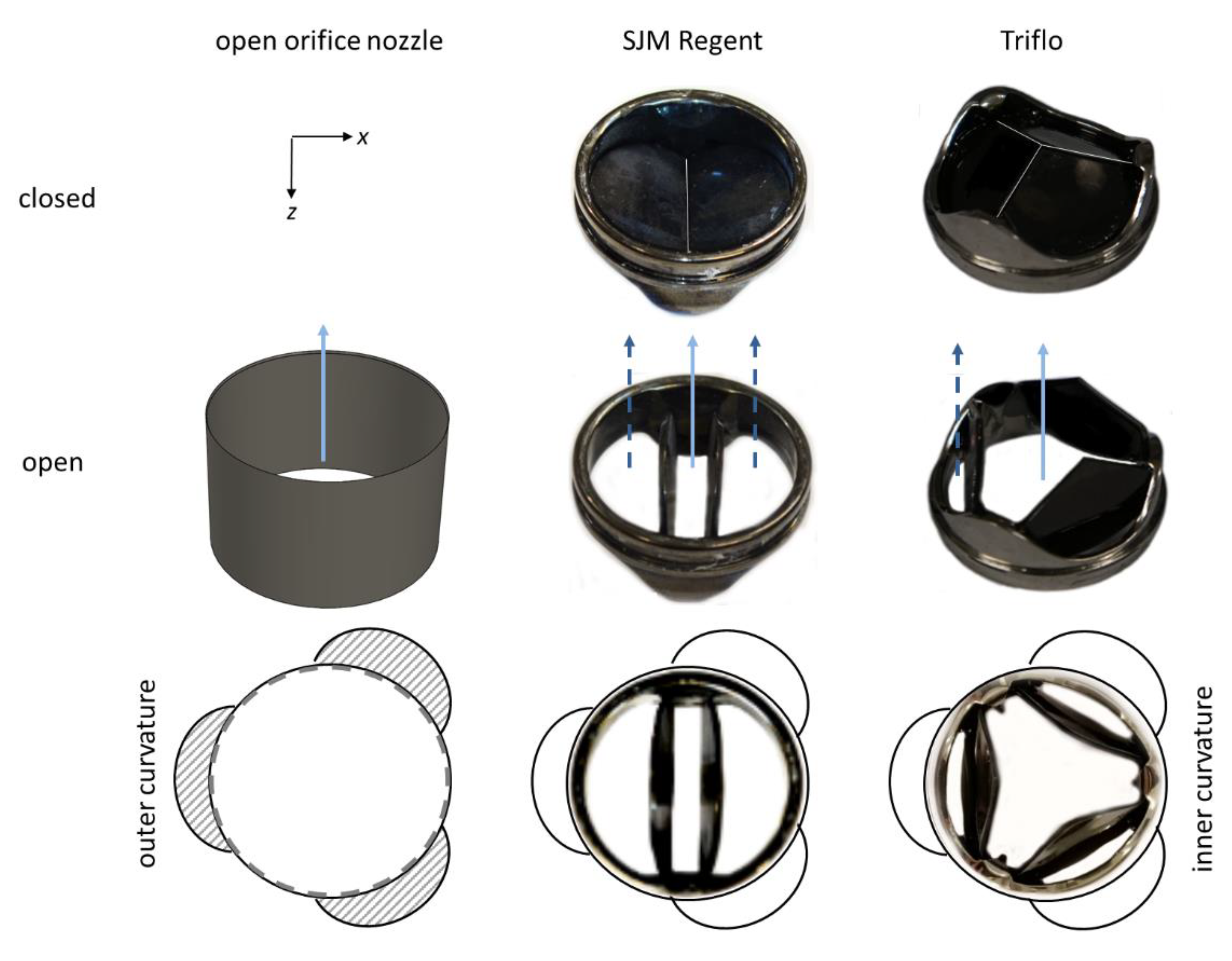
2.2. Heart Valve Prostheses
2.3. Optical Flow Mapping
2.4. High-Speed Particle Image Velocimetry
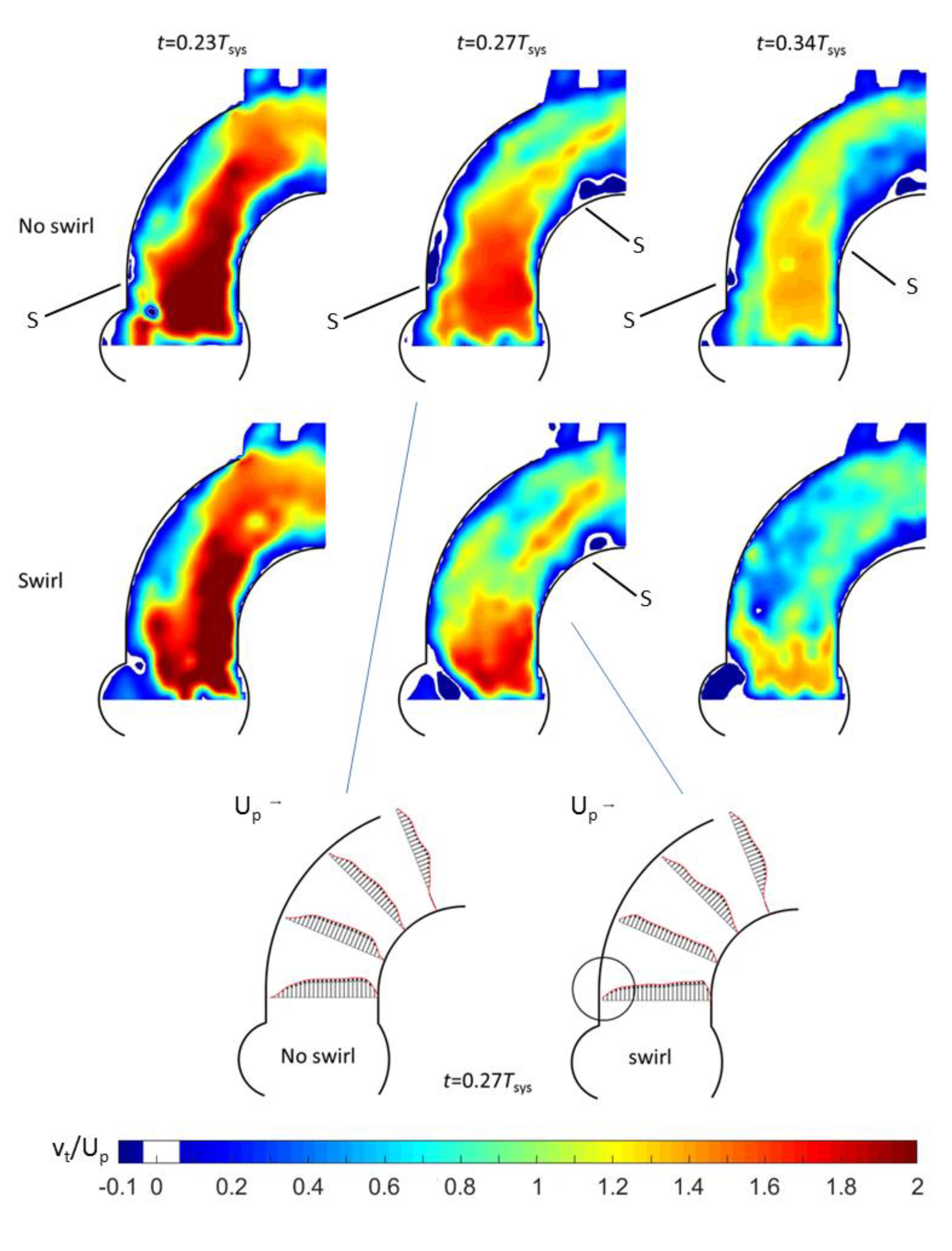
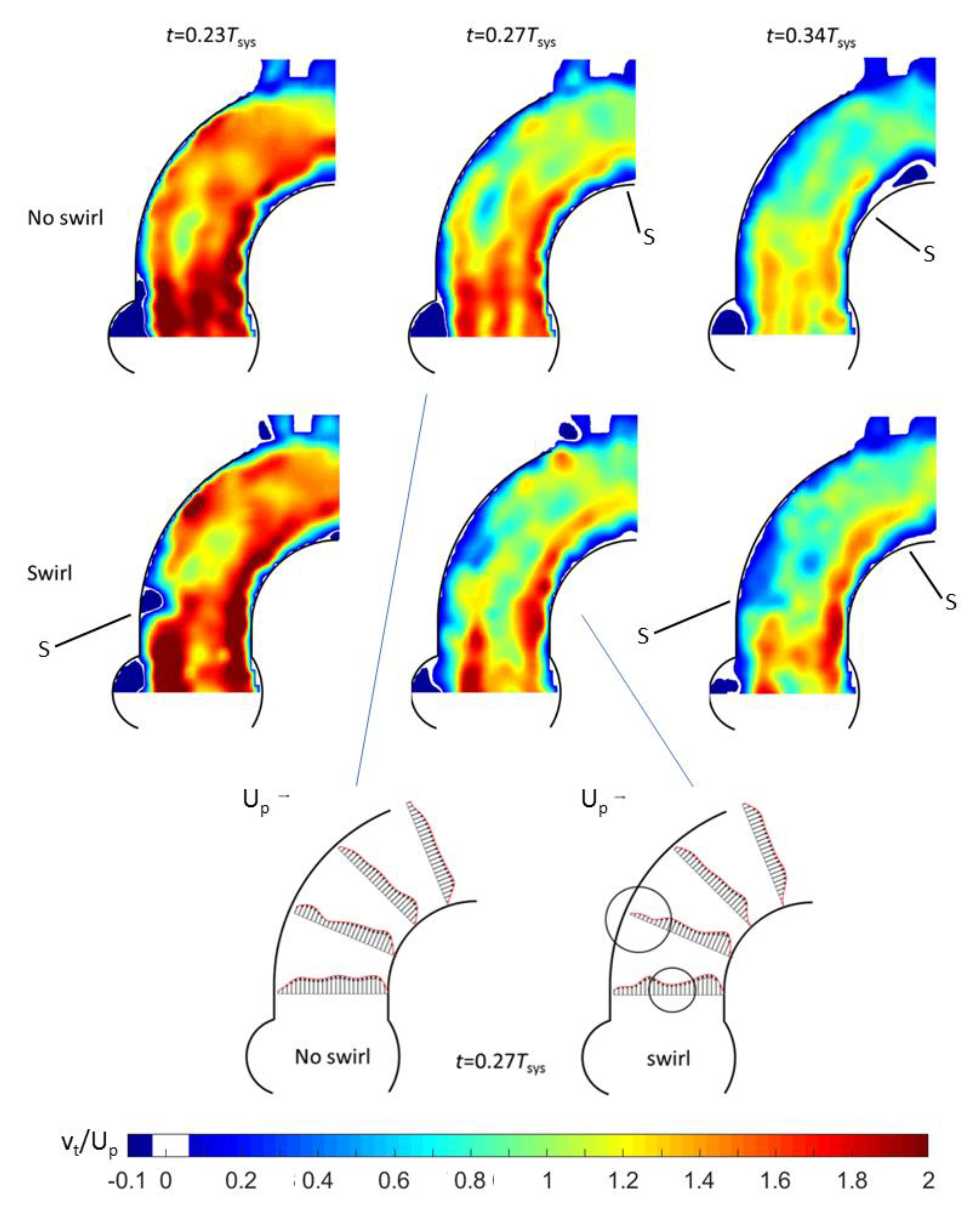
3. Results
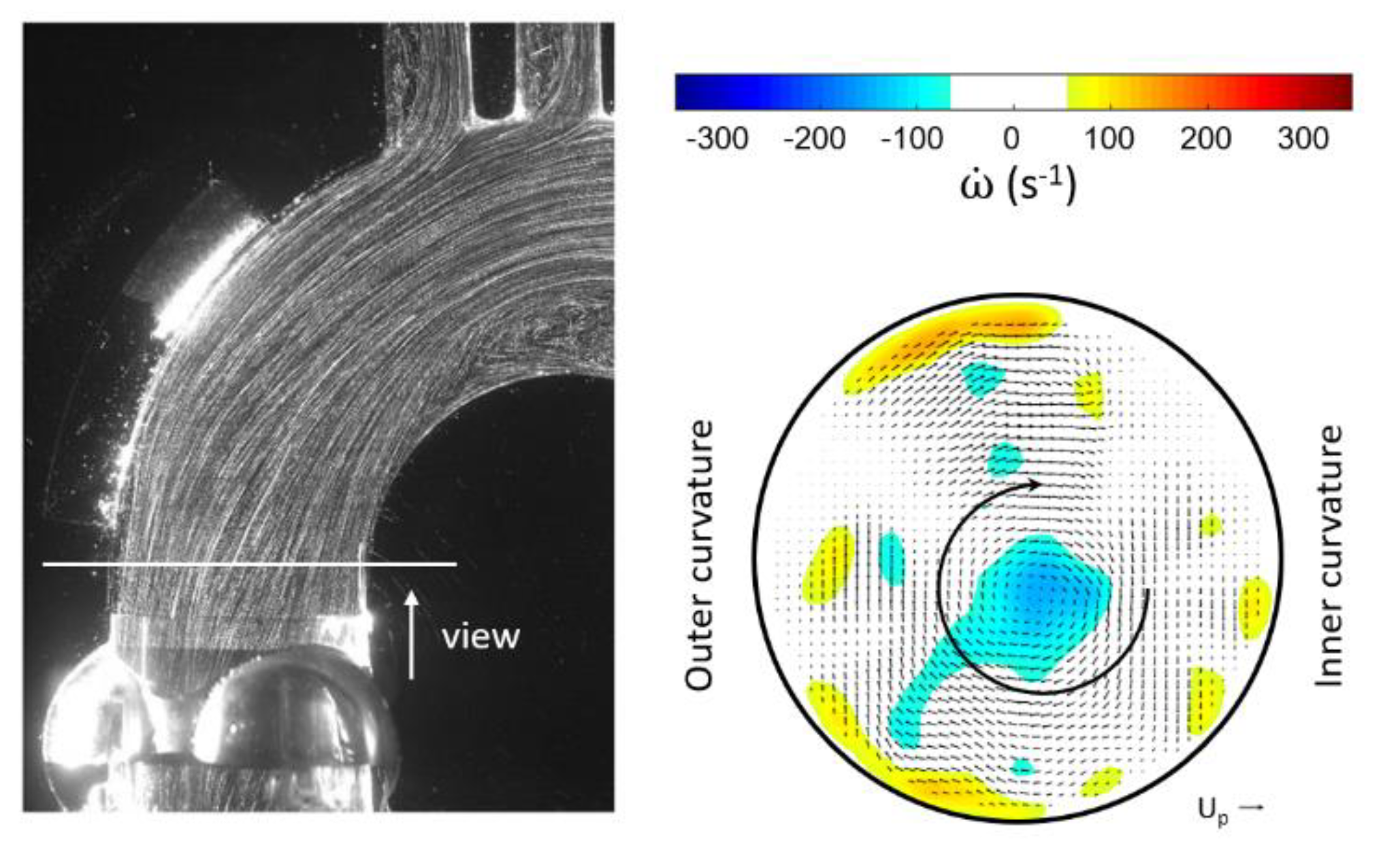
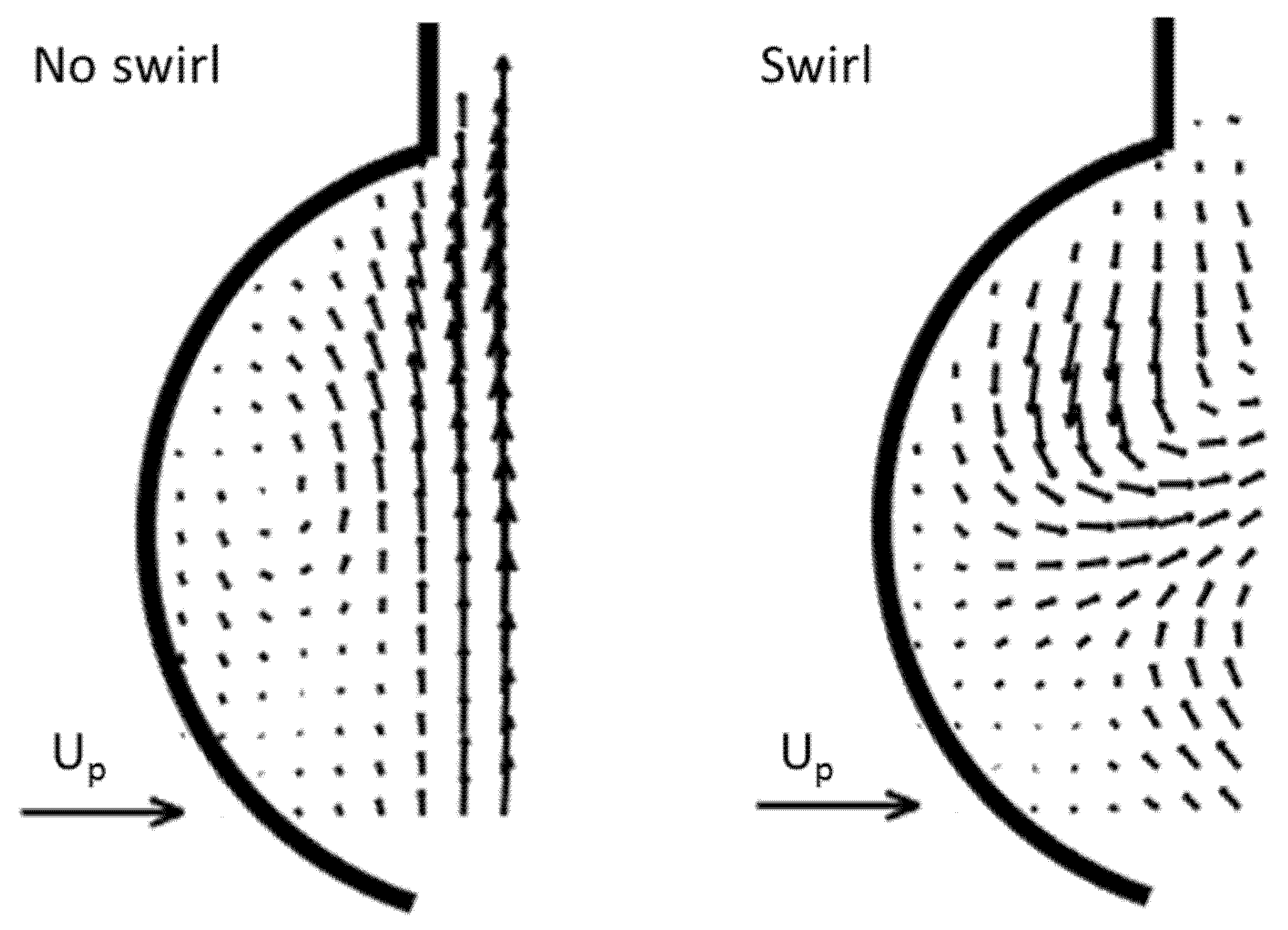
3.1. Outlet Flow with Swirl
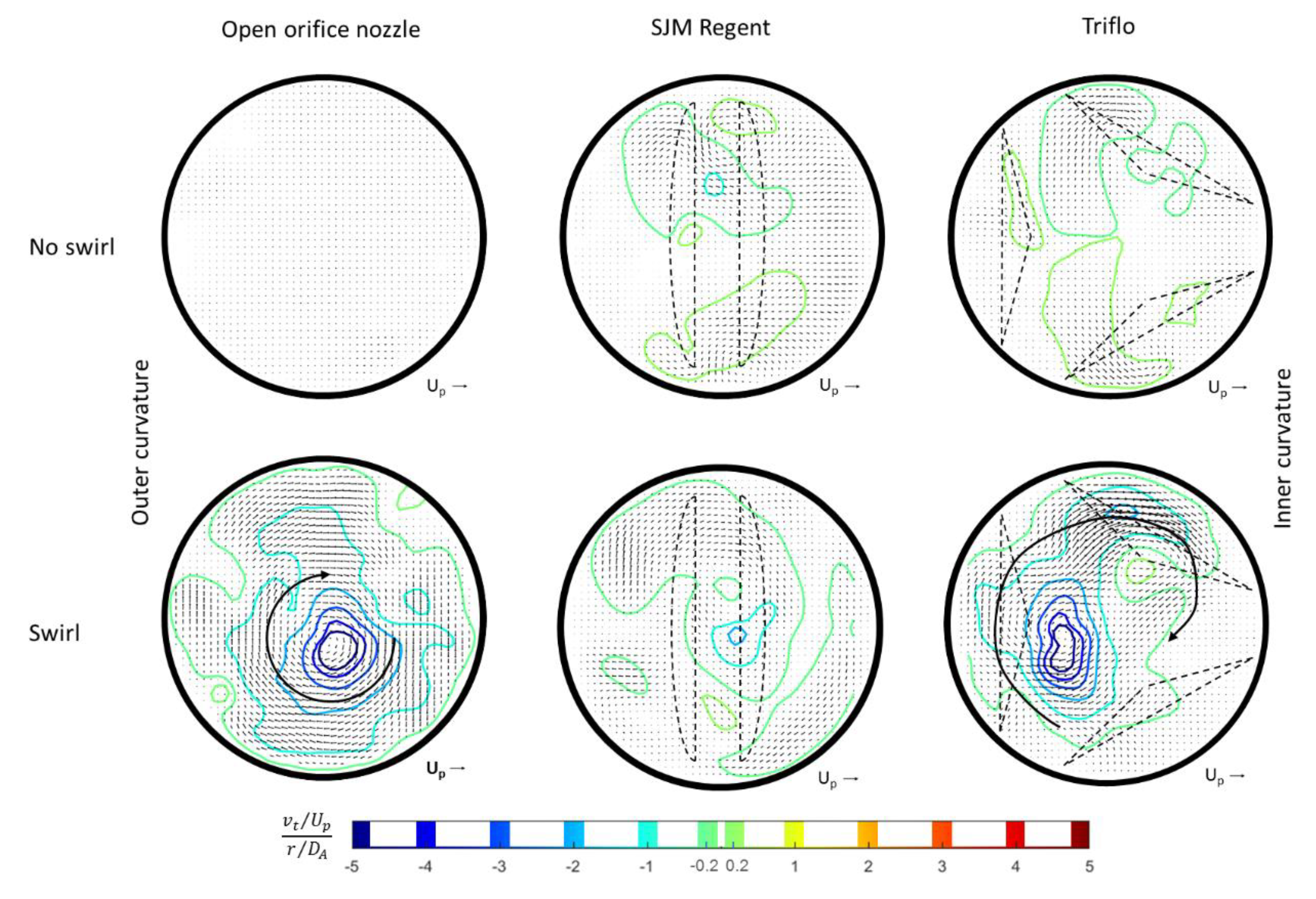
3.2. Helical Flow Interaction with MHVs
4. Discussion
5. Conclusions
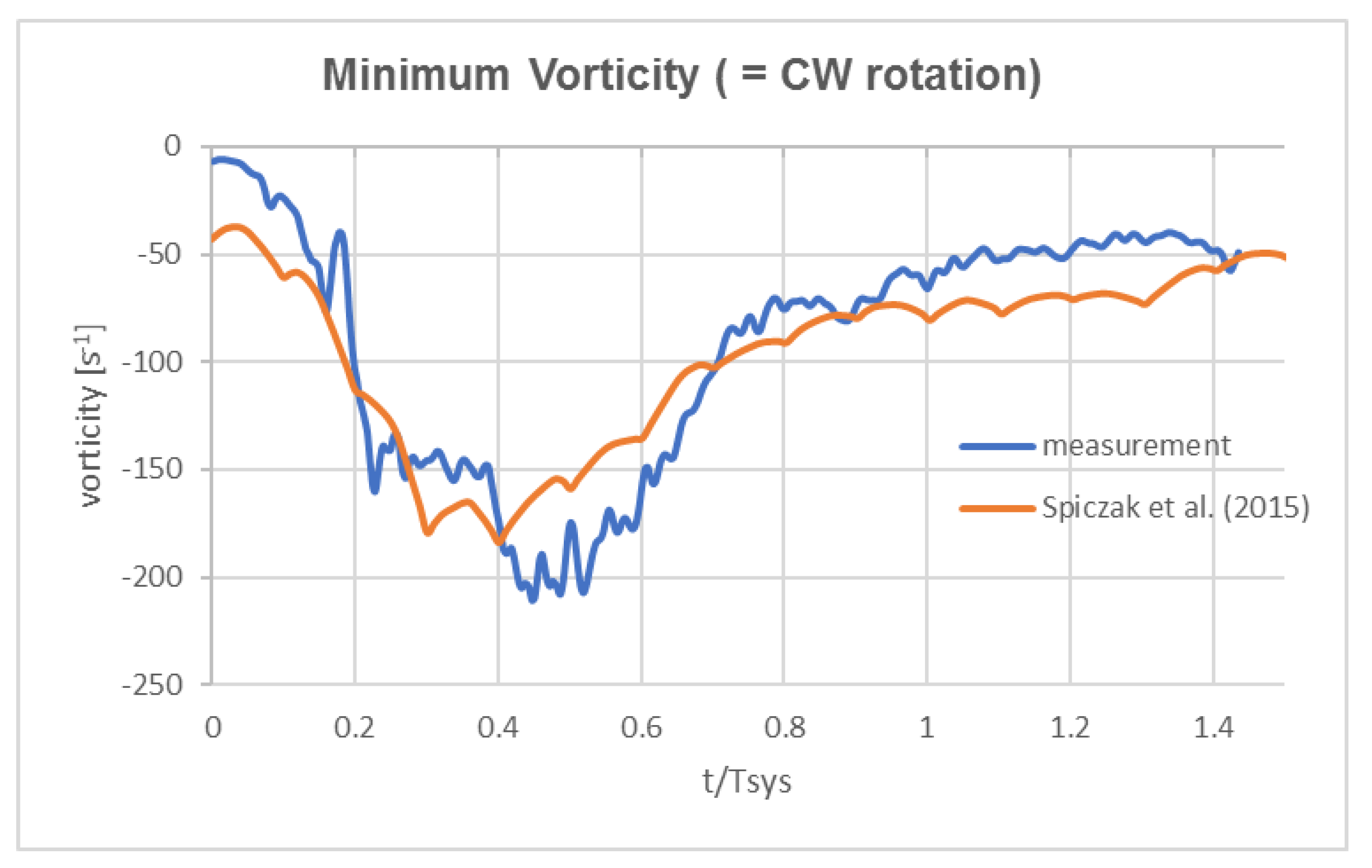
- Good agreement of the measured axial vortex in the valve plane of the aortic arch in the Pulse-Duplicator with recent published data of 4D MRI studies in the aortic arch of healthy volunteers.
- In the Pulse Duplicator, the axial vortex was generated with a swirl-generator inserted into the inlet tube upstream of the valve while in the MRI data, it was a result of the complex flow evolution during left ventricular ejection into the aortic arch. The near overlap of the magnitude and temporal evolution data between our experiment and the MRI suggest that early generation of helical flow in the valve plane indeed could originate from swirl in the ventricular outflow tract, which is convected into the arch.
- As mentioned already by Kilner et al. [18], the tortuous, S-shaped form of the vertebrate heart causes multidirectional intracardiac flow patterns, which may cause efficient directional exchange of energy between muscle and blood in the ejection. From reconstructions of path lines patterns alone, it is difficult to detect such a helical motion in the valve plane. Rather, quantifying the regions of concentrated axial vorticity in the cross-sectional planes of the ventricle and arch is necessary, similar to what has been done herein for the HS-PIV measurements and by von Spiczak et al. [14] in their MRI data.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- David, T. How to Decide Between a Bioprosthetic and Mechanical Valve. Can. J. Cardiol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Dasi, L.P.; Ge, L.; Simon, H.A.; Sotiropoulos, F.; Yoganathan, A.P. Vorticity dynamics of a bileaflet mechanical heart valve in an axisymmetric aorta. Phys. Fluids 2007, 19, 067105. [Google Scholar] [CrossRef]
- De Tullio, M.D.; Cristallo, A.; Balaras, E.; Verzicco, R. Direct numerical simulation of the pulsatile flow through an aortic bileaflet mechanical heart valve. J. Fluid Mech. 2009, 622, 259. [Google Scholar] [CrossRef]
- Barannyk, O.; Oshkai, P. The Influence of the Aortic Root Geometry on Flow Characteristics of a Prosthetic Heart Valve. J. Biomech. Eng. 2015, 137, 051005. [Google Scholar] [CrossRef]
- Borazjani, I.; Ge, L.; Sotiropoulos, F. High-Resolution Fluid–Structure Interaction Simulations of Flow Through a Bi-Leaflet Mechanical Heart Valve in an Anatomic Aorta. Ann. Biomed. Eng. 2010, 38, 326–344. [Google Scholar] [CrossRef]
- Li, Q.; Hegner, F.; Brücker, C. Comparative Study of Wall-Shear Stress at the Ascending Aorta for Different Mechanical Heart Valve Prostheses. J. Biomech. Eng. 2019, 142, 142. [Google Scholar] [CrossRef]
- Verma, S.; Siu, S.C. Aortic Dilatation in Patients with Bicuspid Aortic Valve. N. Engl. J. Med. 2014, 370, 1920–1929. [Google Scholar] [CrossRef]
- Walker, P.G.; Yoganathan, A.P. In vitro pulsatile flow hemodynamics of five mechanical aortic heart valve prostheses. Eur. J. Cardio Thorac. Surg. 1992, 6, S113–S123. [Google Scholar] [CrossRef]
- Marsden, A.L.; Bazilevs, Y.; Long, C.C.; Behr, M. Recent advances in computational methodology for simulation of mechanical circulatory assist devices. Wiley Interdiscip. Rev. Syst. Biol. Med. 2014, 6, 169–188. [Google Scholar] [CrossRef]
- Arzani, A.; Shadden, S.C. Wall shear stress fixed points in cardiovascular fluid mechanics. J. Biomech. 2018, 73, 145–152. [Google Scholar] [CrossRef]
- Guzzardi, D.G.; Barker, A.J.; Van Ooij, P.; Malaisrie, S.C.; Puthumana, J.J.; Belke, D.D.; Mewhort, H.E.; Svystonyuk, D.A.; Kang, S.; Verma, S. Valve-related hemodynamics mediate human bicuspid aortopathy: Insights from wall shear stress mapping. J. Am. Coll. Cardiol. 2015, 66, 892–900. [Google Scholar] [CrossRef] [PubMed]
- Baratchi, S.; Chen, Y.-C.; Peter, K. Helical flow: A means to identify unstable plaques and a new direction for the design of vascular grafts and stents. Atherosclerosis 2020, 300, 34–36. [Google Scholar] [CrossRef] [PubMed]
- De Nisco, G.; Kok, A.M.; Chiastra, C.; Gallo, D.; Hoogendoorn, A.; Migliavacca, F.; Wentzel, J.J.; Morbiducci, U. The Atheroprotective Nature of Helical Flow in Coronary Arteries. Ann. Biomed. Eng. 2018, 47, 425–438. [Google Scholar] [CrossRef] [PubMed]
- Von Spiczak, J.; Crelier, G.; Giese, D.; Kozerke, S.; Maintz, D.; Bunck, A.C. Quantitative Analysis of Vortical Blood Flow in the Thoracic Aorta Using 4D Phase Contrast MRI. PLoS ONE 2015, 10, e0139025. [Google Scholar] [CrossRef] [PubMed]
- Potters, W.V.; Marquering, H.A.; Van Bavel, E.; Nederveen, A.J. Measuring Wall Shear Stress Using Velocity-Encoded MRI. Curr. Cardiovasc. Imaging Rep. 2014, 7, 1–12. [Google Scholar] [CrossRef]
- Markl, M.; Wallis, W.; Harloff, A. Reproducibility of flow and wall shear stress analysis using flow-sensitive four-dimensional MRI. J. Magn. Reson. Imaging 2011, 33, 988–994. [Google Scholar] [CrossRef]
- Papathanasopoulou, P.; Zhao, S.; Köhler, U.; Robertson, M.B.; Long, Q.; Hoskins, P.; Xu, X.Y.; Marshall, I. MRI measurement of time-resolved wall shear stress vectors in a carotid bifurcation model, and comparison with CFD predictions. J. Magn. Reson. Imaging 2003, 17, 153–162. [Google Scholar] [CrossRef]
- Kilner, P.J.; Yang, G.Z.; Mohiaddin, R.H.; Firmin, D.N.; Longmore, D.B. Helical and retrograde secondary flow patterns in the aortic arch studied by three-directional magnetic resonance velocity mapping. Circulation 1993, 88, 2235–2247. [Google Scholar] [CrossRef]
- Ebel, S.; Dufke, J.; Köhler, B.; Preim, B.; Behrendt, B.; Riekena, B.; Jung, B.; Stehning, C.; Kropf, S.; Grothoff, M.; et al. Automated Quantitative Extraction and Analysis of 4D flow Patterns in the Ascending Aorta: An intraindividual comparison at 1.5 T and 3 T. Sci. Rep. 2020, 10, 2949–3013. [Google Scholar] [CrossRef]
- Dabiri, J.O.; Gharib, M. The role of optimal vortex formation in biological fluid transport. Proc. R. Soc. B Biol. Sci. 2005, 272, 1557–1560. [Google Scholar] [CrossRef]
- Corno, A.F.; Kocica, M.J.; Torrent-Guasp, F. The helical ventricular myocardial band of Torrent-Guasp: Potential implications in congenital heart defects. Eur. J. Cardio Thorac. Surg. 2006, 29, S61–S68. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nasiraei-Moghaddam, A.; Gharib, M. Evidence for the existence of a functional helical myocardial band. Am. J. Physiol. Circ. Physiol. 2009, 296, H127–H131. [Google Scholar] [CrossRef] [PubMed]
- Stalder, A.F.; Frydrychowicz, A.; Russe, M.F.; Korvink, J.G.; Hennig, J.; Li, K.; Markl, M. Assessment of flow instabilities in the healthy aorta using flow-sensitive MRI. J. Magn. Reson. Imaging 2011, 33, 839–846. [Google Scholar] [CrossRef]
- Vasava, P.; Jalali, P.; Dabagh, M.; Magjarevic, R. Computational Study of Pulstile Blood Flow in Aortic Arch: Effect of Blood Pressure. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; pp. 1198–1201. [Google Scholar]
- Shahcheraghi, N.; Dwyer, H.A.; Cheer, A.Y.; Barakat, A.I.; Rutaganira, T. Unsteady and Three-Dimensional Simulation of Blood Flow in the Human Aortic Arch. J. Biomech. Eng. 2002, 124, 378–387. [Google Scholar] [CrossRef] [PubMed]
- Linde, T.; Hamilton, K.F.; Navalon, E.C.; Schmitz-Rode, T.; Steinseifer, U. Aortic Root Compliance Influences Hemolysis in Mechanical Heart Valve Prostheses: AnIn-VitroStudy. Int. J. Artif. Organs 2012, 35, 495–502. [Google Scholar] [CrossRef] [PubMed]
- Vennemann, B.M.; Rösgen, T.; Carrel, T.P.; Obrist, D. Time-Resolved Micro PIV in the Pivoting Area of the Triflo Mechanical Heart Valve. Cardiovasc. Eng. Technol. 2016, 7, 210–222. [Google Scholar] [CrossRef] [PubMed]
- Bruecker, C.; Steinseifer, U.; Schröder, W.; Reul, H. Unsteady flow through a new mechanical heart valve prosthesis analysed by digital particle image velocimetry. Meas. Sci. Technol. 2002, 13, 1043–1049. [Google Scholar] [CrossRef]
- Gallegos, R.P.; Rivard, A.L.; Suwan, P.T.; Black, S.; Bertog, S.; Steinseifer, U.; Armien, A.; Lahti, M.; Bianco, R.W. In-vivo experience with the Triflo trileaflet mechanical heart valve. J. Heart Valve Dis. 2006, 15, 791–799. [Google Scholar]
- Christensen, K.T. Review of Particle Image Velocimetry: A Practical Guide, Second Edition. AIAA J. 2008, 46, 2974–2975. [Google Scholar] [CrossRef]
- Bruecker, C.; Althaus, W. Study of vortex breakdown by particle tracking velocimetry (PTV). Exp. Fluids 1992, 13, 339–349. [Google Scholar] [CrossRef]
- Althaus, W.; Bruecker, C.; Weimer, M. Breakdown of Slender Vortices. In Fluid Vortices; Springer: Berlin/Heidelberg, Germany, 1995; pp. 373–426. [Google Scholar]
- Milo, S.; Rambod, E.; Gutfinger, C.; Gharib, M. Mitral mechanical heart valves: In vitro studies of their closure, vortex and microbubble formation with possible medical implications. Eur. J. Cardio Thorac. Surg. 2003, 24, 364–370. [Google Scholar] [CrossRef][Green Version]
- Tagiltsev, I.I.; Shutov, A.V. Geometrically nonlinear modelling of pre-stressed viscoelastic fibre-reinforced composites with application to arteries. Biomech. Model. Mechanobiol. 2020, 1–15. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruecker, C.; Li, Q. Possible Early Generation of Physiological Helical Flow Could Benefit the Triflo Trileaflet Heart Valve Prosthesis Compared to Bileaflet Valves. Bioengineering 2020, 7, 158. https://doi.org/10.3390/bioengineering7040158
Bruecker C, Li Q. Possible Early Generation of Physiological Helical Flow Could Benefit the Triflo Trileaflet Heart Valve Prosthesis Compared to Bileaflet Valves. Bioengineering. 2020; 7(4):158. https://doi.org/10.3390/bioengineering7040158
Chicago/Turabian StyleBruecker, Ch., and Qianhui Li. 2020. "Possible Early Generation of Physiological Helical Flow Could Benefit the Triflo Trileaflet Heart Valve Prosthesis Compared to Bileaflet Valves" Bioengineering 7, no. 4: 158. https://doi.org/10.3390/bioengineering7040158
APA StyleBruecker, C., & Li, Q. (2020). Possible Early Generation of Physiological Helical Flow Could Benefit the Triflo Trileaflet Heart Valve Prosthesis Compared to Bileaflet Valves. Bioengineering, 7(4), 158. https://doi.org/10.3390/bioengineering7040158




