Abstract
The objective of the current research work is to study the differences between the predicted ablation volume in homogeneous and heterogeneous models of typical radiofrequency (RF) procedures for pain relief. A three-dimensional computational domain comprising of the realistic anatomy of the target tissue was considered in the present study. A comparative analysis was conducted for three different scenarios: (a) a completely homogeneous domain comprising of only muscle tissue, (b) a heterogeneous domain comprising of nerve and muscle tissues, and (c) a heterogeneous domain comprising of bone, nerve and muscle tissues. Finite-element-based simulations were performed to compute the temperature and electrical field distribution during conventional RF procedures for treating pain, and exemplified here for the continuous case. The predicted results reveal that the consideration of heterogeneity within the computational domain results in distorted electric field distribution and leads to a significant reduction in the attained ablation volume during the continuous RF application for pain relief. The findings of this study could provide first-hand quantitative information to clinical practitioners about the impact of such heterogeneities on the efficacy of RF procedures, thereby assisting them in developing standardized optimal protocols for different cases of interest.
Keywords:
radiofrequency therapies; pain relief; bioheat transfer; coupled thermo-electric analysis; multiscale models for biological tissues; feedback control systems; AI and machine learning algorithms; finite element method; coupled mathematical models; clinical applications of computational modeling 1. Introduction
Globally, pain management is an enormous challenge that places significant physical, social and economic burdens on society. In accordance with the International Association for the Study of Pain (IASP), pain is defined as “an unpleasant sensory and emotional experience associated with actual or potential tissue damage, or described in terms of such damage.” Furthermore, pain is always a highly subjective and integrative experience that is associated with biological, psychological, and social factors. This complex definition of pain continues to evolve with advancements in medical science and technology [1]. As per the current definition of pain, a plethora of pain and pain states exist, such as nociceptive pain, neuropathic pain, acute pain, chronic pain, etc. Developing an effective treatment option for tackling acute and chronic pain is the main focus of pain management therapists, owing to the significant effects they have on the quality of life of patients, including disability, mood swings, anxiety, and overuse of medicine, to name a few [2]. Notably, acute pain lasts for less than three days and tends to diminish afterward with the passage of time as healing occurs, whereas chronic pain is the extension of acute pain that can go well beyond the expected healing duration post-injury or surgery and typically lasts for more than three months, and in some cases may last indefinitely [1,2]. A multitude of drug-based and non-drug based options exists for the management of pain, which often utilizes multimodal and multidisciplinary approaches, viz., pharmaceutical, physical therapy, rehabilitation and surgery [1,2,3,4].
Chronic pain is one of the major public health problems affecting billions of people all around the world. In Canada, for example, chronic pain imposes a significant burden on healthcare resources, accounting for approximately $7.2 billion annually [5,6]. There has been widespread reliance on the usage of opioids as a pain medication for mitigating chronic pain, which can do more harm than good [7]. Several inexpensive alternative treatment options have also been explored in clinical practices for mitigating chronic pain and minimizing the usage of opioids. Among the available treatment modalities for chronic pain relief, minimally invasive radiofrequency ablation offers several advantages, such as it is precise, reproducible, cheap and highly effective [8,9]. The application of radiofrequency (RF) has been growing rapidly and increasing in popularity for treating different types of pain, such as in the management of low back pain, knee pain, hip pain, migraine, etc. [10,11,12,13,14,15,16,17]. Generally, the power delivery during such pain management procedures is done using either a continuous or a pulsed mode [14]. In the conventional continuous power delivery mode, RF currents applied between the electrode (accurately placed on the target nerve) and the dispersive ground electrode (placed on the patient’s skin) results in temperatures above 50 °C. The high temperature obtained during the continuous RF procedure results in coagulative necrosis of the neural tissue that further leads to protein denaturation and axon destruction, which ultimately stops the transmission of nociceptive signals from the periphery, thereby mitigating pain. In contrast to the continuous RF mode, which relies on the high temperature to cause neural ablation, the pulsed delivery mode utilizes the application of short pulses of RF current to the neural tissue from the RF generator that is followed by silent phases to allow time for heat dissemination [14,18,19]. The electric field generated due to these applied pulses disrupts the functioning of neuronal membrane, along with genetic changes that affect cytokine release [8]. Thus, the mechanism of action of both these modes is quite different. Importantly, the pulsed mode is a theoretically nonablative procedure, since the maximum temperature during such procedures is usually not allowed to exceed 42 °C, thus making it less destructive in comparison to the continuous RF. Although the exact explanation of the complete mechanisms of action involved during the pulsed RF procedure for treating chronic pain remains elusive, extensive research is being undertaken to quantify its associated effects [13,20]. Despite the increasing use of various radiofrequency therapies in clinical practices for treating pain, controversy still exists over their efficacy and treatment outcomes [6].
Computational modeling and simulations are vital tools for providing a quick, convenient and inexpensive evaluation of the treatment outcomes of such therapies, including the thermal ablative procedures. Computational modeling has been used in the past at different stages of thermal ablative procedures, which include the design and development of new protocols, as well as optimization and improvement of existing protocols of clinical systems [21,22,23,24,25,26]. Computational models also serve as a means of understanding the interaction between various physical phenomena and the effects of various intrinsic and extrinsic factors on the treatment outcomes of RF-based clinical techniques. The application of computational tools is widespread among different thermal ablative modalities, including those for treating tumors, but very few computational studies have been reported in the literature for treating pain [27,28,29]. Moreover, most of the computational studies reported to date have been conducted considering homogeneous tissues. The latter assumption means that although the ultimate goal of such works was to attain the ablation of the target nerve, in reality, its incorporation into the computational domain has been routinely neglected. Although the previously reported computational studies on the RF application for chronic pain management have addressed several important concerns and advanced this field of research by providing a quantitative prediction of the electrical field, the evaluation of the thermal field and ablation volume without accounting for heterogeneity within the computational domain, typically results in severe inaccuracies being introduced into the associated models.
Thus, the present study aims at quantifying the effects of heterogeneity in the computational domain of interest on the characteristics obtained during radiofrequency therapies for treating pain, exemplifying our main results for the ablation volume characteristics in the continuous RF procedure. The present paper has been originally initiated from a presentation of its part at the International Conference on Bioinformatics and Neurosciences (ICoBN 2019) held in Vancouver, Canada, August 26–28, 2019 [30]. As part of our comprehensive analysis that develops and extends the idea of [30], three different computational domains were considered: (a) a completely homogeneous domain comprised of muscle tissue alone, (b) a heterogeneous domain comprising of nerve embedded within the muscle tissue, and (c) a heterogeneous domain comprising of target bone, nerve and muscle tissues. Furthermore, a comparative study of continuous RF was conducted with and without utilizing a temperature-controller. This is an automated control loop proportional-integral-derivative (PID) controller within the computational domain that continuously modulates the applied voltage to keep the maximum temperature below the predefined value to avoid the occurrence of charring at the electrode tip.
2. Materials and Methods
This section provides the details of the computational domain, governing equations for the coupled thermo-electric model of the RF procedure, numerical setup and modeling details, along with the main material properties and thermo-electric characteristics considered in the present study. The details of the fidelity and integrity of the developed computational model are also provided in this section by comparing the predicted treatment outcomes from the present model and previously reported studies available in the literature.
2.1. Computational Domain
A schematic of a three-dimensional heterogeneous computational domain comprising of muscle, bone and nerve tissue [31], with an embedded 22-gauge monopolar RF electrode with a 5 mm active tip length [27] is shown in Figure 1. As mentioned earlier, the effect of heterogeneity on the efficacy of continuous RF procedure was quantified considering three different cases for the computational domain: (a) a complete homogeneous computational domain comprising of only muscle tissue, (b) a computational domain comprising of a 4 mm cylindrical nerve embedded within the muscle tissue, and (c) a completely heterogeneous computational domain comprising of bone, nerve and muscle tissues. Further possible advancements of the proposed model for case (c) are discussed later in the paper. The thermo-electric and biophysical properties considered in the present study are summarized in Table 1 [27,29,31,32]. In the present analysis, the thermo-electric characteristics of the bone presented in Table 1 correspond to the cortical bone (see Section 4.2 for additional details pertinent to this and other tissues considered here).
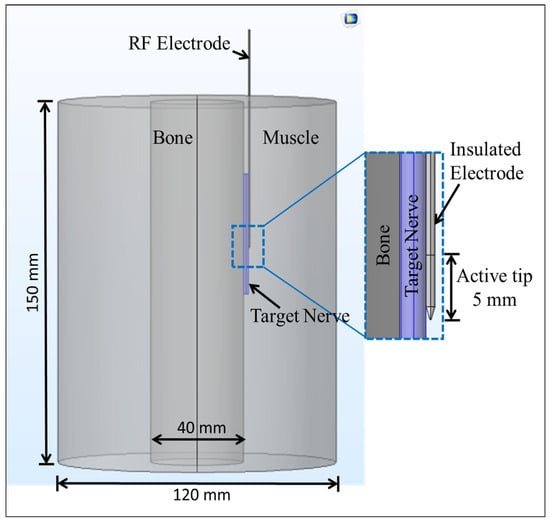
Figure 1.
Schematic of three-dimensional computational domain comprising of nerve, bone and muscle tissues with an inserted monopolar radiofrequency (RF) electrode.

Table 1.
Thermo-electric and biophysical properties of different materials considered in this study.
2.2. Governing Equations for Coupled Thermo-Electric Model
The RF procedure can be modeled as a coupled electro-thermal problem whereby electromagnetic energy is used to heat the biological tissue. In the lower frequency range of 500 kHz, as is generally used during RF procedures, a simplified version of Maxwell’s equations (known as the quasi-static approximation) can be used for computing the electric field distribution within the biological tissue without compromising accuracy. It is given by:
where σ is the temperature-dependent electrical conductivity (S/m), which has been modeled as a linear (+ 2% per °C) function of temperature in the present study [33,34,35], and V is the electric potential (V) that is related to the electric field “E” (V/m) by the standard potential field approximation given by:
Further, the current density “J” (A/m2) can be derived from the electrical conductivity and field as follows:
The volumetric heat generated, Qp (W/m3), within the biological tissue by electromagnetic field during the RF procedure is given by:
The Fourier-conduction-based Pennes bioheat transfer equation was used for computing the temperature distribution within the biological tissue during the continuous RF procedure for pain relief. It is given by:
where ρ is the density (kg/m3), c is the specific heat (J/(kg·K)), k is the thermal conductivity (W/(m·K)), ρb is the density of blood, cb is the specific heat capacity of the blood, ωb is the blood perfusion rate (1/s), Tb is the blood temperature (37 °C), and T is the unknown temperature within the biological tissue to be computed from Equation (5). The term accounts for the heat sink effect caused by small capillary vasculature, Qp is the volumetric heat source (W/m3) quantified using Equation (4), Qm is the metabolic heat generation (W/m3), which was neglected in the present study due to its insignificant contribution as compared to Qp [27], and t (s) is the duration of the continuous RF procedure.
Further, in the present computational study, the blood perfusion rate was modeled utilizing a temperature-dependent piecewise model. Accordingly, a constant predefined value of blood perfusion rate prevails below the tissue temperature of 50 °C and ceases beyond that owing to the collapse of microvasculature [31], and is given by:
where ωb,0 is the constant blood perfusion rate of the tissue domain given in Table 1 and T, as before, is the unknown temperature computed from Equation (5).
The ablation volume () was computed using the isotherm of 50 °C (i.e., the volume of tissue having a temperature ≥ 50 °C post-RF procedure) [31] within the computational domain, and it is given by:
The continuous RF procedure was modeled by applying a constant voltage (V) of 15 V with a reference impedance (Zref) of around 50 ohms, resulting in the constant power (P = V2/Zref) of 4.5 W [36]. Further, the temperature-controlled RF procedure was performed utilizing a closed-loop feedback PID controller that varies the applied input voltage to keep the target temperature below the pre-set temperature of 85 °C, and is given by:
where V(t) is the applied voltage (V) during the RF procedure for mitigating pain, e is the error, t is the treatment time (s) and Kp (= 0.02), Ki (= 0.01) and Kd (= 0.001) are the proportional, integral and derivative gains, respectively [33,37,38].
2.3. Numerical Setup and Modeling Details
The coupled thermo-electric models of continuous RF application for treating pain were solved by utilizing the finite element method (FEM), and implemented in the COMSOL Multiphysics 5.2 software [39] using an adaptive time-stepping scheme. The continuous RF procedures were performed by applying a constant voltage of 15 V at the active tip of the RF electrode. Further, the dispersive (ground) electrode was modeled by applying 0 V on the outer boundaries of the computational domain. The initial voltage and temperature prior to the application of the RF procedure within the entire computational domain were considered to be 0 V and 37 °C, respectively, and the thermal and electrical continuity boundary conditions were imposed at each interface. Additionally, the computational model for temperature-controlled RF was developed utilizing an automatic PID controller [33,34,35] to limit the maximum temperature to 85 °C and its treatment outcomes were compared to the model with a constant voltage source of 15 V. In its essence, we are dealing here with a feedback control system, and we used this controller to improve the system by combining its closed-loop control with the open-loop feedback control. This compensates for the difference (error) between the set-point and the system response to the feedback control. As a result, the system can, in principle, utilize artificial intelligence (AI) and machine learning algorithms [40,41,42,43,44]. In the present computational study, the treatment time of the continuous RF procedure was set to 60 s.
The discretization of the computational domain was done by utilizing the heterogeneous tetrahedral mesh elements constructed with COMSOL’s built-in mesh generator. An extra refinement close to the active tip of the electrode was applied, where the highest electrical and thermal gradients are expected. Further, a mesh convergence analysis was conducted to determine the optimal number of mesh elements that would result in a mesh-independent solution. Figure 2 presents the meshed computational domain of the heterogeneous model comprising of 174,486 elements and 476,384 degrees of freedom. All the numerical simulations were conducted on a Dell T7400 workstation with Quad-core 2.0 GHz Intel® Xeon® processors.
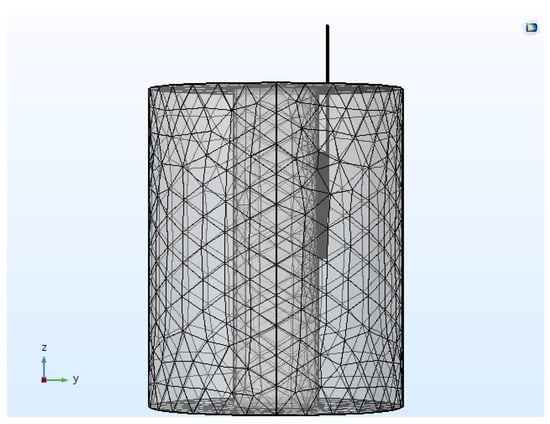
Figure 2.
Meshed computational domain of the continuous RF procedure comprising of 174,486 tetrahedral elements.
2.4. Model Validation
The developed computational model’s fidelity and integrity were evaluated by comparing the simulated results of the present model with that of previously reported experimental and numerical findings reported in [45]. All the material properties, dimensions, initial and boundary conditions were considered similar to those of [45]. Table 2 presents the comparative analysis of the rise in temperature (ΔT, i.e., the difference between the attained temperature after 120 s of RF procedure and the ambient temperature), that was simulated/computed from the present numerical study to that of the experimental and numerical findings of [45]. As presented in Table 2, the rise in temperature (ΔT) predicted by the present numerical study after 120 s of RF procedure for different considered cases was found to be in reasonable agreement with the experimental and numerical findings of [45]. Furthermore, Figure 3 presents the predicted temperature distribution from the current model after 60 s of RF procedure at the applied voltage of 13 V and the ambient temperature of 37 °C and utilizing the same material properties to those of [45]. The outer periphery of the temperature distribution presented in Figure 3 represents the ablation volume quantified using the 50 °C isotherm, and its shape agrees well with the existing knowledge about continuous RF procedure [45]. Importantly, the lateral (W = 4.4 mm) and longitudinal (L = 6.8 mm) dimensions predicted from the present model were found to be in good agreement with those of [45], which were reported to be around 4 mm and 7 mm, respectively. Additionally, the longitudinal extension of the ablation zone dimensions (corresponding to 50 °C isotherm) in the forward direction from the tip point of electrode and in backward direction from the insulation margin was found to be about 1 mm, analogous to that presented in [45].

Table 2.
Comparison of the rise in temperature (ΔT) reported by Cosman Jr. and Cosman Sr. [45] in terms of both numerical and experimental findings to that computed from the present model after 120 s of the continuous RF procedure.
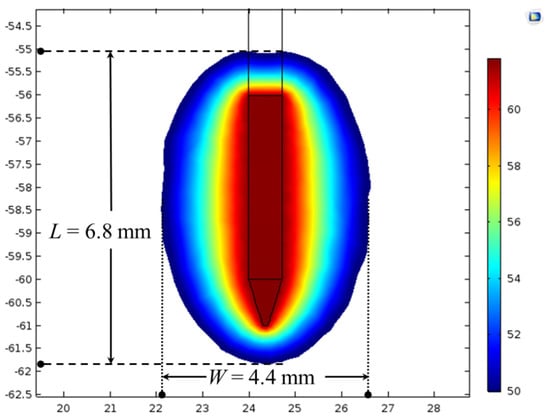
Figure 3.
Temperature distribution (in °C) along with lateral (W) and longitudinal (L) dimensions of the ablation zone obtained after 60 s of continuous RF procedure with the applied voltage of 13 V and an ambient temperature of 37 °C.
3. Results and Discussion
One of the key objectives of the present numerical study is to quantify the effect of heterogeneous surroundings in the computational domain on the efficacy of continuous RF procedure for pain relief. In pursuing this goal, the variations in temperature distribution and ablation volume were computed for the homogeneous domain (comprising of only muscle tissue) and the heterogeneous domain comprising of: (a) nerve and muscle tissues, and (b) bone, nerve and muscle tissues. Figure 4 and Figure 5 present the variation in the temperature distribution for different cases considered here obtained after 60 s of continuous RF procedure in a plane along the electrode axis (i.e., front view of Figure 1) and in a plane normal to the electrode axis (i.e., top view of Figure 1), respectively. As is evident from Figure 4 and Figure 5, the uniformity of the temperature distribution is ruined for the cases where nerve and bone are modeled within the muscular domain.
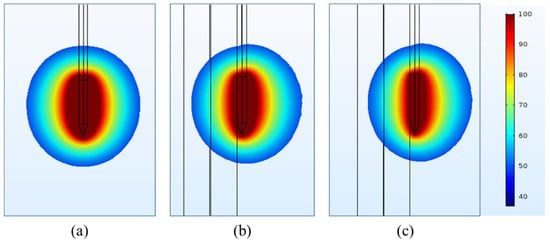
Figure 4.
Temperature distribution (in °C) obtained after 60 s of continuous RF procedure in a plane along the electrode axis for: (a) homogeneous domain comprising of muscle tissue alone, (b) heterogeneous domain comprising of the target nerve embedded in the muscle tissue and (c) heterogeneous domain comprising of target bone, nerve and muscle tissues.
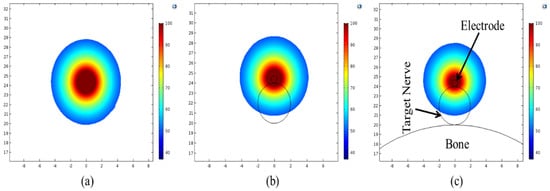
Figure 5.
Temperature distribution (in °C) obtained after 60 s of continuous RF procedure in a plane normal to the electrode axis for: (a) homogeneous domain comprising of muscle tissue alone, (b) heterogeneous domain comprising of the target nerve embedded in the muscle tissue and (c) heterogeneous domain comprising of target bone, nerve and muscle tissues.
Three points of interest (as shown in Figure 6a) were defined to analyze the thermal performance of the continuous RF application for treating pain. Importantly, point P1 lies 1 mm away from the tip of the electrode along the electrode axis, while P2 and P3 lie 1 mm away in a transversal plane in the opposite direction from the middle of the active part of the electrode. It is noteworthy that point P2 lies on the nerve and bone side of the computational domain of the heterogeneous model, whereas point P3 lies on the side surrounded by muscles alone. Figure 6b presents the variation in temperature with respect to time at point P1 for the considered cases. As is evident from Figure 6b, the introduction of heterogeneity within the computational domain results in a significant decrease in the predicted temperature at a particular instance. The predicted temperature at point P1 at the end of 60 s of the continuous RF procedure was found to be 75.70 °C, 70.73 °C and 67.03 °C for the homogeneous muscle domain, the heterogeneous muscle and nerve domain, and the heterogeneous muscle, nerve and bone domain, respectively. The variations in the temperature distribution with respect to time at P2 and P3 points are presented in Figure 6c,d, respectively. Again, a significant decrease in the predicted temperature with the introduction of heterogeneity in the computational domain can be clearly seen in these figures. This variation in the predicted temperature during the continuous RF procedure can be attributed to differences in the thermo-electric parameters of the muscle, nerve and bone tissues, as summarized in Table 1. The introduction of the nerve in the homogeneous muscle domain results in the lower electrical conductivity that leads to a distorted electrical field distribution. In turn, this results in lower volumetric heating as compared to the completely homogeneous computational domain comprising of muscles alone. Furthermore, the introduction of bone, which has lower electrical and thermal conductivities as compared to muscle tissue, does not allow efficient heat conduction from the electrode during the continuous RF procedure for treating pain.
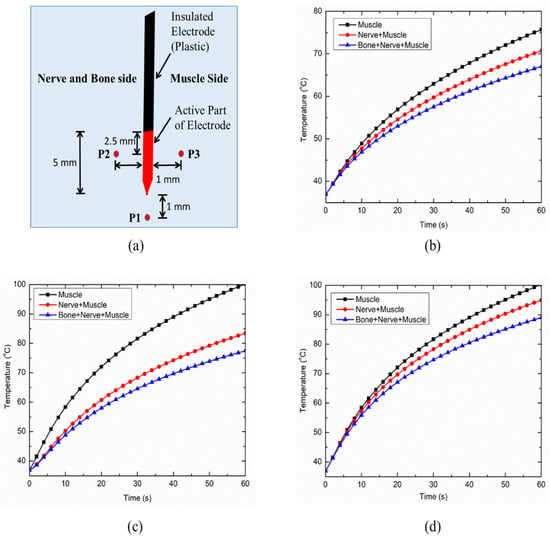
Figure 6.
(a) Schematic of three points (P1, P2 and P3) chosen for the evaluation of thermal performance during the continuous RF procedure. Variation in temperature distribution as a function of time at: (b) P1, (c) P2 and (d) P3, for different cases considered in the present study.
The inclusion of nerve and bone within the muscle tissue domain significantly hampers the thermal and electrical performances of the continuous RF procedure for pain relief. Figure 7a,b represent the temperature distribution at points P2 and P3 for the case of heterogeneous computational domains of the muscle, i.e., including both nerve and bone, and including only nerve, respectively. The inclusion of the nerve and/or bone within the homogeneous computational domain of the muscle (for simulating realistic anatomical situations) on one side of the RF electrode restricts the efficient conduction of the heat on that side owing to the lower thermal and electrical conductivities of bone and nerve in comparison to the muscle tissue. These variations result in asymmetric deviation in the temperature distribution on two equally spaced but oppositely placed points P2 and P3 on the transverse axis from the middle of the active part of the electrode, as shown in Figure 7a,b. Note that, for the homogeneous computational domain comprising of the muscle tissue, the temperature profiles at both points P2 and P3 are symmetric and completely coincide with each other. However, the decrements in temperature at points P2 and P3 after 60 s of continuous RF procedure were found to be 12.15% and 13.02% for the heterogeneous computational domain of muscle tissue embedded with only nerve, and embedded with both nerve and bone, respectively. Thus, consideration of the heterogeneous surroundings within the computational model significantly affects the thermal performance of continuous RF procedures for pain relief.
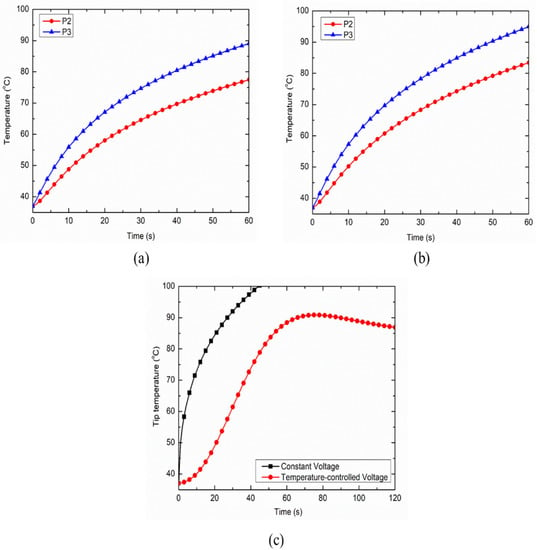
Figure 7.
Variation in temperature distribution as a function of time at points P2 and P3 for the heterogeneous computational domain comprising of: (a) nerve, bone and muscle tissues, and (b) nerve and muscle tissues. (c) Variation in the target tip temperature as a function of treatment time for constant voltage and temperature-controlled protocols of power delivery during the continuous RF procedure for pain relief.
Further, the comparison between the electrode tip temperature for the constant voltage and temperature-controlled protocols of power delivery during the continuous RF procedure are presented in Figure 7c. It is noteworthy that the temperature sensor for monitoring and maintaining the target tip temperature during the temperature-controlled RF procedure was located at a distance of 1 mm beneath the tip of the electrode, which was inspired by [27]. As evident in Figure 7c, the constant voltage source can result in the attainment of a 100 °C temperature close to the active tip of the electrode, which can then result in charring. This is a highly undesirable phenomenon during RF procedures that leads to an abrupt decline in the electrical and thermal conductivities of the biological tissues, limiting efficient conduction of thermal energy and thereby reducing the ablation size. Thus, the utilization of temperature-controlled power delivery protocol during continuous RF procedures in clinical practices can completely mitigate the chances of charring occurrence, whereby the applied voltage is varied between the electrodes to keep the maximum temperature at the tip of the electrode as 80–90 °C [28].
The variation in the total ablation volume obtained for different cases considered in the present study, viz., the homogeneous domain comprising of only muscle tissue and the heterogeneous domain comprising of: (a) nerve and muscle tissues and (b) bone, nerve and muscle tissues, is presented in Figure 8a. As seen from Figure 8a, the attained ablation volume significantly decreases as the heterogeneity in the surroundings is introduced within the computational domain during the continuous RF procedure for pain relief. The propagation of nerve damage with respect to time in the heterogeneous computational domain during the continuous RF procedure is presented in Figure 8b. The introduction of bone within the computational domain results in a 12.75% decrease in the nerve ablation volume after 60 s of continuous RF procedure. Thus, consideration of the heterogeneous surroundings to realistically replicate the anatomy becomes of utmost importance for accurately predicting the treatment outcomes of the continuous RF procedures for pain relief.
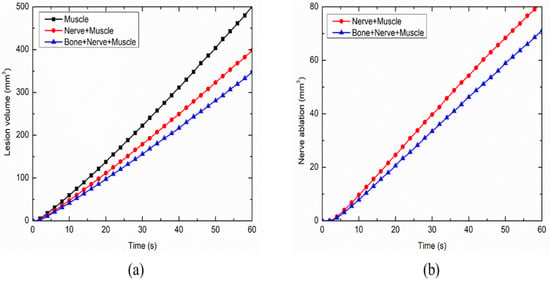
Figure 8.
Variations in (a) total ablation volume, and (b) nerve ablation, with respect to time during the continuous RF procedure for pain relief among different considered cases.
4. Clinical Applications, Future Outlook and Model Developments
In this section, we highlight the recent clinical studies related to the application of RF procedures in treating pain. Future research directions for the refinement of the proposed models by utilizing coupled multiscale and multiphysics models are also discussed.
4.1. Heterogeneous Surroundings and Clinical Trials
Radiofrequency ablation has been used for pain management since the mid-1970s [46] and has significantly evolved from a therapy that was mainly employed for mitigating neuropathic pain to one of the most promising and frequently applied techniques in clinical practices for alleviating axial spine and musculoskeletal pain [1,16]. Today, the application of RFA in treating pain has steadily expanded and accepted for the treatment of facet joint, sacroiliac joint dysfunction and osteoarthritis [8,9,10,11,12,13,15,16,17,18,19,20]. However, there are significant contradictions and inconsistencies in the reported clinical results on the efficacy of RF procedures. Most of the clinical studies available in the literature are retrospective studies or case studies limited to reporting high-quality randomized controlled trials [47,48,49,50,51,52,53,54,55]. Furthermore, inappropriate selection criteria and treatment parameters could result in poor treatment outcomes, whereas anatomical variations, which are still not well-established, could limit the accurate interpretation of the obtained results. Thus, additional large-scale clinical studies of RF application in pain management are needed with longer follow-up periods to demonstrate its efficacy along with quantification of associated long-term adverse effects.
There has been continuous development in RF delivery systems and protocols in the quest to increase the ablation volume, which will lead to enhanced efficacy of the RF procedure. Continuous RF is the conventional form of energy delivery, and it causes a decline in the transmission of pain signals by damaging both sensory and motor nerve fibers [1,19]. Three different types of electrodes are typically utilized for delivery of RF energy to the target neural tissue, viz., monopolar, bipolar and cooled RF electrodes (arranged in ascending order of ablation volume generation). Another mechanism of RF energy delivery to the target nerve is the pulsed RF procedure. As mentioned earlier, contrary to the continuous RF that causes tissue destruction by heat, the pulsed RF is virtually painless and does not lead to any neural coagulation and irreversible tissue damage. Instead, it leads to an alteration in the pain signal transduction of the nerve fibers [1,19]. Although the efficacy of pulsed RF has been well-documented, the exact mechanism of action in the mitigation of pain is not fully understood yet [14,18,54,56,57,58,59]. Pulsed RF has shown promise in treating neuropathic pain and certain other clinical conditions where continuous RF is potentially hazardous, such as radicular pain, headaches, chronic shoulder pain, knee and hip pain, axial low back pain, and peripheral nerve pain [18,56,57]. However, further clinical studies are required to quantify the exact mechanism responsible for pain mitigation and broaden the clinical utility of these interventional pain procedures.
4.2. Multiscale Models for Biological Tissues
In order to capture the nuances of the biological cells/tissues exposed to external forces, a multiscale modeling approach provides an efficient and cost-effective alternative for bridging the different scales during the computational analysis [60,61,62,63]. Thus, further refinements in the proposed pain management models can be attained by using multiscale modeling approaches, whereby the damage caused due to RF currents can be quantified at a cellular level. This can be accomplished by coupling predominant phenomena during RF procedures that occur at different scales. Such multiscale models would not only assist in a better understanding of the pre-existing bio-physical behavior during pain management therapy, but also help in predicting the mechanisms that remain elusive to date and in generating new hypotheses for quantifying small-scale effects. Furthermore, while dealing with the small-scale effects of biological cells exposed to RF currents, the development and usage of stochastic models is practically unavoidable [62,64,65]. Moreover, bones in general, and cortical bones in particular, are biological tissues considered as part of our computational domain in the present study. They may exhibit additional effects, based on coupled phenomena, that would be useful to incorporate in further developments of the presented model. Among these, piezoelectricity plays a special role (e.g., [66]). For example, for cortical bones, piezoelectric properties are often responsible for the coupling between macroscopic and micro/nanoscopic scales, which may provide additional insight into certain dysfunctions and diseases [66]. Such properties also provide a foundation for wider usage of these biomaterials in tissue engineering [67]. In describing piezoelectricity, we couple electrical and mechanical fields. The well-posedness of such models of coupled piezoelectricity, along with rigorous energy bounds, were derived by one of us in a series of earlier papers, e.g., [68]. This was done for the first time in a general, dynamic setting through the application of the Faedo–Galerkin procedure and generalized solution technique. Coupled electro-mechanical models have been developed and used in a wide range of applications [69,70,71,72,73,74,75,76,77].
Thermal field treatment requires special attention for problems like those considered in this study. Notably, the thermal effects in this study were quantified considering the classical Fourier’s law of heat conduction with the Pennes bioheat equation as presented in Equation (5), which assumes the infinite speed of heat propagation. However, in biological tissues that have non-homogenous inner structures, accounting for a finite speed of thermal disturbances becomes important, suggesting the existence of non-Fourier conduction with a delay ranging from 10 to 20 s [38,78]. Several studies have been reported providing a way to incorporate such non-Fourier heat transfer behaviors in their computational models, e.g., [23,38,79,80,81,82]. Moreover, the attainment of elevated temperatures during RF procedures can also result in thermo-elastic deformation, including thermal expansion and tissue shrinkage, which is interlinked with many complex small-scale effects, such as protein denaturation, collagen contraction and dehydration. Again, the exact mechanism of such associated effects at an elevated temperature within the biological tissue during thermal therapies are not completely elucidated yet, but significant recent developments have been devoted to this area of research utilizing both experimental and computational studies [23,78]. From a computational perspective, the coupling between thermal and mechanical fields, e.g., for elastic tissues such as muscles, etc., can be done by the development of coupled models of thermoelasticity, as well as efficient numerical methods for their solution, e.g., [83,84,85,86,87,88,89,90,91,92,93,94,95]. Moreover, the development of such models also includes complex nonlinear cases where numerous advances have been made in the improvement of numerical methodologies, e.g., [96,97,98,99]. The coupling of the thermoelasticity and piezoelectric model, as is the case for bone tissues, can be done by the development of piezothermoeleastic models [100,101,102]. This could lead to the development of fully coupled thermo-electro-mechanical models of thermal therapies [23]. Also, the development of such models is relevant to other areas of application, as well as in the development of new methods [103,104]. Furthermore, the proposed model of RF application for mitigating pain presented in this study assumed the quasi-static approximation of Maxwell’s equations (see Equation (1)), whereby the extent of variation of electric and magnetic fields is negligible. Consequently, the electromagnetic field is modeled only by considering the electric field component (neglecting the magnetic field effects) because the wavelength of the electromagnetic field at RF frequency of around 500 kHz is several orders of magnitude larger than the size of the active electrode. However, models exist in the literature that consistently include the magnetic field effects, e.g., [103]. The electrode-tissue and plastic-tissue interfaces (as presented in Figure 1) can be more rigorously modeled by incorporating electrode-tissue contact force [60,105,106,107,108,109], as well as other non-trivial effects, e.g., thermal degradation, spiking, etc., in polymeric materials [110,111,112].
Several studies have been reported in the literature for modeling blood perfusion within biological tissues, at both micro- and macro-vascular levels [78,113,114,115,116,117,118,119]. Notably, micro-vascular perfusion refers to the perfusion at a capillary (or small-scale) level while macro-vascular perfusion is associated with the heat-sink effect caused by large blood vessels [120]. The blood flow at a micro-vascular level within the biological tissue is typically modeled by utilizing the porous media theory, whereby the tissue is assumed to be comprised of two phases: the solid phase comprising of cells and the extracellular space, and the fluid phase comprising of capillary size blood vessels [94,95,118,119,121,122,123]. The blood flow within the large blood vessels ( 2 mm in diameter) is modeled by additional coupling of the fluid flow model with the proposed thermo-electric model presented in this study, whereby the geometry of the blood vessel within the computational domain can be incorporated either by including a cylinder or a vascular tree [113,114,115,116,117,124,125]. It is expected that further refinement of the model can be done by deriving the computational domain from actual patient-specific data, which will provide more rigorous analysis and would help medical practitioners to obtain more accurate and precise predictions of the treatment outcomes during the RF application in pain management. Thus, the coupled multiscale framework could assist us in quantifying the unknown biologically-relevant phenomena occurring at cellular and sub-cellular scales and lead to a better understanding of the associated intricacies of RF application in pain management.
4.3. Coupling Frameworks and Pain Relief Models
The application of machine learning has been growing rapidly in the biological, biomedical and behavioral sciences. Importantly, both machine learning and multiscale modeling complement each other in creating more robust predictive models in the current field of research [126,127]. Recently, several studies have been reported in the literature that have explored the application of AI and machine learning algorithms in the field of thermal therapies [40,128,129,130,131,132,133,134,135,136]. The integration of machine learning with the coupled models could play a vital role in decision-making processes and the treatment planning stage of such procedures, e.g., by providing a priori information about electrode placement for enhancing treatment efficacy or by the real-time monitoring of the damage to the target tissue and other critical structures. Furthermore, a general framework of incorporating human factors into mathematical models of complex systems with control has been provided in [137,138]. This can be useful in the context of AI and the machine learning algorithms mentioned earlier in Section 2. Moreover, there has been a surge in the development of neural tissue models for capturing the transduction, transmission, perception and modulation of pain at molecular, cellular and neuron networks levels [78,139,140,141,142,143]. The aforementioned coupled multiscale thermo-electro-mechanical model can be readily integrated with the Hodgkin–Huxley neural model for predicting the treatment outcomes in terms of decline in the actual pain signals that can be coupled with the damage model presented in Equation (7). Such coupling of the neuronal models with the proposed model would assist in our better understanding of the molecular changes affecting the neuronal behavior, such as in quantifying the exact damage to the axons during the application of RF procedures for treating pain. Future studies can be conducted by incorporating the actual physiological neuronal geometries and modeling of biophysical phenomena at sub-cellular scale, viz., accounting for changes in the concentrations of potassium, sodium, calcium and magnesium at the membrane layer [78,144,145,146,147,148]. Such multiscale, multiphysics and fully coupled models will provide a better understanding of the molecular changes affecting the neuronal behavior, along with quantification of the mitigation of actual pain signals during RF procedures.
5. Conclusions
This work quantified the effects of heterogeneities, such as nerve and bone tissues, on the efficacy of radiofrequency therapies, exemplifying main results on continuous RF procedures for pain relief. Based on the developed coupled mathematical models and their finite element implementations, a comparative analysis was conducted to evaluate the impact of different heterogeneities in the surrounding computational domain on the temperature distribution and the obtained ablation volume. Among other results, it was found that there was a decrease of 30.64% in the attained ablation volume considering a heterogeneous domain comprising of bone, nerve and muscle tissues, as compared to a homogeneous domain of muscle alone. Further, it was concluded that there is significant variation in the predicted temperature distribution among the different cases considered in the present study. Subsequently, this study emphasizes the importance of considering the effect of heterogeneous surroundings on the predicted treatment outcomes of continuous RF procedures for treating pain. It is expected that the results presented in this study will assist pain management clinicians and researchers to better tackle the issue of the variability in thermo-electric and biophysical properties. This can be achieved by proper treatment planning and consideration of the impact of each parameter on the treatment outcomes. The work also critically analyzed possible directions for further improvement of the developed models. This includes the incorporation of the neural model to replicate pain transmission and mitigation during RF procedures for pain relief. In addition, patient-specific models can be developed and integrated into the clinical workflow to quantify a priori estimates of the treatment outcomes and the risks involved during such minimally invasive treatment procedures.
Author Contributions
S.S. performed the simulations, validation, data analysis and drafted the manuscript. R.M. contributed to the conceptualization of the research idea, supervision of the study, and review and editing of the final manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Sciences and Engineering Research Council (NSERC) of Canada and Canada Research Chairs (CRC) Program.
Acknowledgments
R.M. also acknowledges the support of the BERC 2018-2021 program and Spanish Ministry of Science, Innovation and Universities through the Agencia Estatal de Investigacion (AEI) BCAM Severo Ochoa excellence accreditation SEV-2017-0718, and the Basque Government fund “AI in BCAM EXP. 2019/00432”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Deer, T.R.; Pope, J.E.; Lamer, T.J.; Provenzano, D. Deer’s Treatment of Pain: An Illustrated Guide for Practitioners; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Altilio, T.; Otis-Green, S.; Hedlund, S.; Fineberg, I.C. Pain management and palliative care. In Handbook of Health Social Work; John Wiley Sons, Inc.: Hoboken, NJ, USA, 2019; pp. 535–568. [Google Scholar]
- Eccleston, C.; Morley, S.; Williams, A.d.C. Psychological approaches to chronic pain management: Evidence and challenges. Br. J. Anaesth. 2013, 111, 59–63. [Google Scholar] [CrossRef]
- Gilron, I.; Carr, D.B.; Desjardins, P.J.; Kehlet, H. Current methods and challenges for acute pain clinical trials. Pain Rep. 2019, 4, e647. [Google Scholar] [CrossRef]
- Hogan, M.-E.; Taddio, A.; Katz, J.; Shah, V.; Krahn, M. Incremental health care costs for chronic pain in Ontario, Canada: A population-based matched cohort study of adolescents and adults using administrative data. Pain 2016, 157, 1626–1633. [Google Scholar] [CrossRef] [PubMed]
- Loh, E.; Reid, J.N.; Alibrahim, F.; Welk, B. Retrospective cohort study of healthcare utilization and opioid use following radiofrequency ablation for chronic axial spine pain in Ontario, Canada. Reg. Anesth. Pain Med. 2019, 44, 398–405. [Google Scholar] [CrossRef]
- Henningfield, J.E.; Ashworth, J.B.; Gerlach, K.K.; Simone, B.; Schnoll, S.H. The nexus of opioids, pain, and addiction: Challenges and solutions. Prev. Med. 2019, 128, 105852. [Google Scholar] [CrossRef] [PubMed]
- Orhurhu, V.; Urits, I.; Grandhi, R.; Abd-Elsayed, A. Systematic Review of Radiofrequency Ablation for Management of Knee Pain. Curr. Pain Headache Rep. 2019, 23, 55. [Google Scholar] [CrossRef]
- Soloman, M.; Mekhail, M.N.; Mekhail, N. Radiofrequency treatment in chronic pain. Expert Rev. Neurother. 2010, 10, 469–474. [Google Scholar] [CrossRef]
- Abd-Elsayed, A.; Kreuger, L.; Wheeler, S.; Robillard, J.; Seeger, S.; Dulli, D. Radiofrequency ablation of pericranial nerves for treating headache conditions: A promising option for patients. Ochsner J. 2018, 18, 59–62. [Google Scholar] [PubMed]
- Bhatia, A.; Hoydonckx, Y.; Peng, P.; Cohen, S.P. Radiofrequency procedures to relieve chronic hip pain: An evidence-based narrative review. Reg. Anesth. Pain Med. 2018, 43, 72–83. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, A.; Peng, P.; Cohen, S.P. Radiofrequency procedures to relieve chronic knee pain: An evidence-based narrative review. Reg. Anesth. Pain Med. 2016, 41, 501–510. [Google Scholar] [CrossRef]
- Calodney, A.; Rosenthal, R.; Gordon, A.; Wright, R.E. Targeted radiofrequency techniques. In Techniques of Neurolysis; Springer: Berlin/Heidelberg, Germany, 2016; pp. 33–73. [Google Scholar]
- Chua, N.H.; Vissers, K.C.; Sluijter, M.E. Pulsed radiofrequency treatment in interventional pain management: Mechanisms and potential indications—A review. Acta Neurochir. 2011, 153, 763–771. [Google Scholar] [CrossRef] [PubMed]
- Collighan, N.; Richardson, J. Radiofrequency lesioning techniques in the management of chronic pain. Anaesth. Intensive Care Med. 2008, 9, 61–64. [Google Scholar] [CrossRef]
- Jamison, D.E.; Cohen, S.P. Radiofrequency techniques to treat chronic knee pain: A comprehensive review of anatomy, effectiveness, treatment parameters, and patient selection. J. Pain Res. 2018, 11, 1879. [Google Scholar] [CrossRef] [PubMed]
- Leggett, L.E.; Soril, L.J.; Lorenzetti, D.L.; Noseworthy, T.; Steadman, R.; Tiwana, S.; Clement, F. Radiofrequency ablation for chronic low back pain: A systematic review of randomized controlled trials. Pain Res. Manag. 2014, 19, e146–e153. [Google Scholar] [CrossRef] [PubMed]
- Boudier-Revéret, M.; Thu, A.C.; Hsiao, M.Y.; Shyu, S.G.; Chang, M.C. The Effectiveness of Pulsed Radiofrequency on Joint Pain: A Narrative Review. Pain Pract. 2019. [Google Scholar] [CrossRef]
- Deniz, S.; Bakal, O.; Inangil, G. Application of Radiofrequency in Pain Management. In Pain Management; IntechOpen: London, UK, 2016; p. 95. [Google Scholar]
- Mendis, V.; Mottaleb, R.; Sethi, S. Radiofrequency techniques in pain management. Anaesth. Intensive Care Med. 2019, 20, 572–575. [Google Scholar] [CrossRef]
- Berjano, E.J. Theoretical modeling for radiofrequency ablation: State-of-the-art and challenges for the future. Biomed. Eng. Online 2006, 5, 24. [Google Scholar] [CrossRef]
- Chiang, J.; Wang, P.; Brace, C.L. Computational modelling of microwave tumour ablations. Int. J. Hyperth. 2013, 29, 308–317. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Coupled thermo-electro-mechanical models for thermal ablation of biological tissues and heat relaxation time effects. Phys. Med. Biol. 2019, 64, 245008. [Google Scholar] [CrossRef]
- Singh, S.; Repaka, R. Numerical study to establish relationship between coagulation volume and target tip temperature during temperature-controlled radiofrequency ablation. Electromagn. Biol. Med. 2018, 37, 13–22. [Google Scholar] [CrossRef]
- Singh, S.; Repaka, R.; Al-Jumaily, A. Sensitivity analysis of critical parameters affecting the efficacy of microwave ablation using Taguchi method. Int. J. RF Microw. Comput. Aided Eng. 2019, 29, e21581. [Google Scholar] [CrossRef]
- Zhang, B.; Moser, M.A.; Zhang, E.M.; Luo, Y.; Liu, C.; Zhang, W. A review of radiofrequency ablation: Large target tissue necrosis and mathematical modelling. Phys. Med. 2016, 32, 961–971. [Google Scholar] [CrossRef]
- Ewertowska, E.; Mercadal, B.; Muñoz, V.; Ivorra, A.; Trujillo, M.; Berjano, E. Effect of applied voltage, duration and repetition frequency of RF pulses for pain relief on temperature spikes and electrical field: A computer modelling study. Int. J. Hyperth. 2018, 34, 112–121. [Google Scholar] [CrossRef] [PubMed]
- Pérez, J.J.; Pérez-Cajaraville, J.J.; Muñoz, V.; Berjano, E. Computer modeling of electrical and thermal performance during bipolar pulsed radiofrequency for pain relief. Med Phys. 2014, 41, 071708. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Melnik, R. Computational analysis of pulsed radiofrequency ablation in treating chronic pain. In Computational Science–ICCS 2019, Proceedings of the ICCS 2019, Faro, Portugal, 12–14 June 2019; Lecture Notes in Computer, Science; Rodrigues, J.M.F., Cardoso, P.J.S., Monteiro, J., Lam, R., Krzhizhanovskaya, V.V., Lees, M.H., Dongarra, J.J., Sloot, P.M.A., Eds.; Springer: Cham, Switzerland, 2019; Volume 11539, pp. 436–450. [Google Scholar]
- Singh, S.; Melnik, R. Effects of heterogeneous surroundings on the efficacy of continuous radiofrequency for pain relief. Presented at the 2nd International Conference on Bioinformatics and Neurosciences (ICoBN 2019), Vancouver, BC, Canada, 26–28 August 2019; 5p. [Google Scholar]
- Singh, S.; Melnik, R. Radiofrequency ablation for treating chronic pain of bones: Effects of nerve locations. In Bioinformatics and Biomedical Engineering, Proceedings of the IWBBIO 2019, Granada, Spain, 8–10 May 2019; Lecture Notes in Computer Science; Rojas, I., Valenzuela, O., Rojas, F., Ortuño, F., Eds.; Springer: Cham, Switzerland, 2019; Volume 11466, pp. 418–429. [Google Scholar]
- Hasgall, P.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues, Version 4.0; 15 May 2018. Available online: https://itis.swiss/virtual-population/tissue-properties/database/ (accessed on 4 April 2020).
- Singh, S.; Repaka, R. Temperature-controlled radiofrequency ablation of different tissues using two-compartment models. Int. J. Hyperth. 2017, 33, 122–134. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Repaka, R. Effect of different breast density compositions on thermal damage of breast tumor during radiofrequency ablation. Appl. Therm. Eng. 2017, 125, 443–451. [Google Scholar] [CrossRef]
- Singh, S.; Repaka, R. Parametric sensitivity analysis of critical factors affecting the thermal damage during RFA of breast tumor. Int. J. Therm. Sci. 2018, 124, 366–374. [Google Scholar] [CrossRef]
- Singh, S.; Bhowmik, A.; Repaka, R. Thermal analysis of induced damage to the healthy cell during RFA of breast tumor. J. Therm. Boil. 2016, 58, 80–90. [Google Scholar] [CrossRef]
- Singh, S.; Repaka, R. Numerical investigation of convective cooling in minimizing skin burns during radiofrequency ablation of breast tumor. Sādhanā 2018, 43, 90. [Google Scholar] [CrossRef]
- Singh, S.; Repaka, R. Thermal characterization using fourier and non-fourier conduction during radiofrequency ablation of breast tumor. Multiph. Sci. Technol. 2018, 30, 207–219. [Google Scholar] [CrossRef]
- COMSOL Multiphysics v. 5.2; COMSOL AB: Stockholm, Sweden, 2016; Available online: www.comsol.com (accessed on 4 April 2020).
- Besler, E.; Curtis Wang, Y.; Chan, T.C.; Sahakian, A.V. Real-time monitoring radiofrequency ablation using tree-based ensemble learning models. Int. J. Hyperth. 2019, 36, 427–436. [Google Scholar] [CrossRef] [PubMed]
- Besler, E.; Wang, Y.C.; Chan, T.; Sahakian, A.V. Classifying Small Volumes of Tissue for Real-Time Monitoring Radiofrequency Ablation. In Proceedings of the Conference on Artificial Intelligence in Medicine in Europe, Poznan, Poland, 26–29 June 2019; pp. 205–215. [Google Scholar]
- Buchlak, Q.D.; Esmaili, N.; Leveque, J.-C.; Farrokhi, F.; Bennett, C.; Piccardi, M.; Sethi, R.K. Machine learning applications to clinical decision support in neurosurgery: An artificial intelligence augmented systematic review. Neurosurg. Rev. 2019, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Farrokhi, F.; Buchlak, Q.D.; Sikora, M.; Esmaili, N.; Marsans, M.; McLeod, P.; Mark, J.; Cox, E.; Bennett, C.; Carlson, J. Investigating risk factors and predicting complications in deep brain stimulation surgery with machine learning algorithms. World Neurosurg. 2020, 134, e325–e338. [Google Scholar] [CrossRef] [PubMed]
- Foreman, B. Neurocritical Care: Bench to Bedside (Eds. Claude Hemphill, Michael James) Integrating and Using Big Data in Neurocritical Care. Neurotherapeutics 2020, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Cosman, E.R., Jr.; Cosman, E.R., Sr. Electric and thermal field effects in tissue around radiofrequency electrodes. Pain Med. 2005, 6, 405–424. [Google Scholar] [CrossRef]
- Shealy, C.N. Percutaneous radiofrequency denervation of spinal facets: Treatment for chronic back pain and sciatica. J. Neurosurg. 1975, 43, 448–451. [Google Scholar] [CrossRef]
- Ajrawat, P.; Radomski, L.; Bhatia, A.; Peng, P.; Nath, N.; Gandhi, R. Radiofrequency Procedures for the Treatment of Symptomatic Knee Osteoarthritis: A Systematic Review. Pain Med. 2020, 21, 333–348. [Google Scholar] [CrossRef]
- Boesch, J.M.; Campoy, L.; Southard, T.; Dewey, C.; Erb, H.N.; Gleed, R.D.; Martin-Flores, M.; Sakai, D.M.; Sutton, J.; Williamson, B. Histological, electrophysiological and clinical effects of thermal radiofrequency therapy of the saphenous nerve and pulsed radiofrequency therapy of the sciatic nerve in dogs. Vet. Anaesth. Analg. 2019, 46, 689–698. [Google Scholar] [CrossRef]
- Filippiadis, D.; Charalampopoulos, G.; Mazioti, A.; Alexopoulou, E.; Vrachliotis, T.; Brountzos, E.; Kelekis, N.; Kelekis, A. Interventional radiology techniques for pain reduction and mobility improvement in patients with knee osteoarthritis. Diagn. Interv. Imaging 2019, 100, 391–400. [Google Scholar] [CrossRef]
- Filippiadis, D.; Velonakis, G.; Mazioti, A.; Konstantos, C.; Brountzos, E.; Kelekis, N.; Kelekis, A. Intra-articular application of pulsed radiofrequency combined with viscosupplementation for improvement of knee osteoarthritis symptoms: A single centre prospective study. Int. J. Hyperth. 2018, 34, 1265–1269. [Google Scholar] [CrossRef]
- Ho, K.W.D.; Przkora, R.; Kumar, S. Sphenopalatine ganglion: Block, radiofrequency ablation and neurostimulation-a systematic review. J. Headache Pain 2017, 18, 118. [Google Scholar] [CrossRef]
- Kwak, S.; Jeong, D.; Choo, Y.J.; Chang, M.C. Management of neuropathic pain induced by cubital tunnel syndrome using pulsed radiofrequency: Two case reports. Medicine 2019, 98, e15599. [Google Scholar] [CrossRef] [PubMed]
- Schneider, B.J.; Doan, L.; Maes, M.K.; Martinez, K.R.; Gonzalez Cota, A.; Bogduk, N. Systematic Review of the Effectiveness of Lumbar Medial Branch Thermal Radiofrequency Neurotomy, Stratified for Diagnostic Methods and Procedural Technique. Pain Med. 2020. [Google Scholar] [CrossRef] [PubMed]
- Sluijter, M.E.; Teixeira, A.; Serra, V.; Balogh, S.; Schianchi, P. Intra-articular application of pulsed radiofrequency for arthrogenic pain—Report of six cases. Pain Pract. 2008, 8, 57–61. [Google Scholar] [CrossRef] [PubMed]
- Xie, K.; Liu, S.; Huang, B.; Yao, M. Effects of Supraorbital Foramen Variations on the Treatment Efficacy of Radiofrequency Therapy for V1 Trigeminal Neuralgia: A Retrospective Study. Pain Res. Manag. 2020, 2020, 8142489. [Google Scholar] [CrossRef]
- Cohen, B.R.; Soriano, E.T. Pulsed Radiofrequency Neuromodulation in Interventional Pain Management—A Growing Technology. J. Radiol. Nurs. 2018, 37, 181–187. [Google Scholar] [CrossRef]
- Hata, J.; Perret-Karimi, D.; DeSilva, C.; Leung, D.; Betesh, N.; Luo, Z.D.; Dawodu, S.; Sinavsky, K.; Stokes, O.J.; English, S. Pulsed radiofrequency current in the treatment of pain. Crit. Rev.™ Phys. Rehabil. Med. 2011, 23. [Google Scholar] [CrossRef]
- Vallejo, R.; Benyamin, R.M.; Aliaga, L. Radiofrequency vs. pulse radiofrequency: The end of the controversy. Tech. Reg. Anesth. Pain Manag. 2010, 14, 128–132. [Google Scholar] [CrossRef]
- Vatansever, D.; Tekin, I.; Tuglu, I.; Erbuyun, K.; Ok, G. A comparison of the neuroablative effects of conventional and pulsed radiofrequency techniques. Clin. J. Pain 2008, 24, 717–724. [Google Scholar] [CrossRef] [PubMed]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A review of multiscale computational methods in polymeric materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef]
- Badu, S.; Prabhakar, S.; Melnik, R.; Singh, S. Atomistic to continuum model for studying mechanical properties of RNA nanotubes. Comput. Methods Biomech. Biomed. Eng. 2020, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Antoniouk, A.V.; Melnik, R. Mathematics and Life Sciences; De Gruyter: Berlin, Germany, 2013. [Google Scholar]
- Melnik, R.V.; Roberts, A.H. Computational models for multi-scale coupled dynamic problems. Future Gener. Comput. Syst. 2004, 20, 453–464. [Google Scholar] [CrossRef]
- Melnik, R.V.; Wei, X.; Moreno–Hagelsieb, G. Nonlinear dynamics of cell cycles with stochastic mathematical models. J. Biol. Syst. 2009, 17, 425–460. [Google Scholar] [CrossRef]
- Ortiz-Catalan, M. The stochastic entanglement and phantom motor execution hypotheses: A theoretical framework for the origin and treatment of phantom limb pain. Front. Neurol. 2018, 9, 748. [Google Scholar] [CrossRef]
- Stroe, M.; Crolet, J.; Racila, M. Mechanotransduction in cortical bone and the role of piezoelectricity: A numerical approach. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 119–129. [Google Scholar] [CrossRef]
- Jacob, J.; More, N.; Kalia, K.; Kapusetti, G. Piezoelectric smart biomaterials for bone and cartilage tissue engineering. Inflamm. Regen. 2018, 38, 2. [Google Scholar] [CrossRef]
- Melnik, R.V. Generalised solutions, discrete models and energy estimates for a 2D problem of coupled field theory. Appl. Math. Comput. 2000, 107, 27–55. [Google Scholar] [CrossRef]
- Mahapatra, D.R.; Melnik, R. Modelling and analysis of collagen piezoelectricity in human cornea. Dyn. Contin. Discret. Impulsive Syst. Ser. A Math. Anal. 2006, 13, 377–384. [Google Scholar]
- Melnik, R. Convergence of the operator-difference scheme to generalized solutions of a coupled field theory problem. J. Differ. Equ. Appl. 1998, 4, 185–212. [Google Scholar] [CrossRef]
- Melnik, R.; Mahapatra, R. Coupled effects in quantum dot nanostructures with nonlinear strain and bridging modelling scales. Comput. Struct. 2007, 85, 698–711. [Google Scholar] [CrossRef][Green Version]
- Melnik, R.; Melnik, K. A note on the class of weakly coupled problems of non-stationary piezoelectricity. Commun. Numer. Methods Eng. 1998, 14, 839–847. [Google Scholar] [CrossRef]
- Melnik, R.; Melnik, K. Modelling dynamics of piezoelectric solids in the two-dimensional case. Appl. Math. Model. 2000, 24, 147–163. [Google Scholar] [CrossRef]
- Melnik, R.V. Numerical analysis of dynamic characteristics of coupled piezoelectric systems in acoustic media. Math. Comput. Simul. 2003, 61, 497–507. [Google Scholar] [CrossRef]
- Melnik, R.V.N. The stability condition and energy estimate for nonstationary problems of coupled electroelasticity. Math. Mech. Solids 1997, 2, 153–180. [Google Scholar] [CrossRef]
- Patil, S.R.; Melnik, R.V. Coupled electromechanical effects in II–VI group finite length semiconductor nanowires. J. Phys. D Appl. Phys. 2009, 42, 145113. [Google Scholar] [CrossRef][Green Version]
- Prabhakar, S.; Melnik, R.V.; Neittaanmäki, P.; Tiihonen, T. Coupled electromechanical effects in wurtzite quantum dots with wetting layers in gate controlled electric fields: The multiband case. Phys. E Low Dimens. Syst. Nanostruct. 2012, 46, 97–104. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Thermal ablation of biological tissues in disease treatment: A review of computational models and future directions. Electromagn. Biol. Med. 2020. [Google Scholar] [CrossRef]
- Melnik, R.; Strunin, D.; Roberts, A. Nonlinear analysis of rubber-based polymeric materials with thermal relaxation models. Numer. Heat Transf. Part A Appl. 2005, 47, 549–569. [Google Scholar] [CrossRef]
- Strunin, D.; Melnik, R.; Roberts, A. Numerical modelling of thermoelastic processes using nonlinear theories with thermal relaxation time. ANZIAM J. 2000, 42, 1356–1378. [Google Scholar] [CrossRef][Green Version]
- Strunin, D.; Melnik, R.; Roberts, A. Coupled thermomechanical waves in hyperbolic thermoelasticity. J. Therm. Stresses 2001, 24, 121–140. [Google Scholar]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Modeling heat transfer in tumors: A review of thermal therapies. Ann. Biomed. Eng. 2019, 47, 676–693. [Google Scholar] [CrossRef] [PubMed]
- Melnik, R.; Roberts, A.; Thomas, K. Coupled thermomechanical dynamics of phase transitions in shape memory alloys and related hysteresis phenomena. Mech. Res. Commun. 2001, 28, 637–651. [Google Scholar] [CrossRef]
- Melnik, R.V. Discrete models of coupled dynamic thermoelasticity for stress–temperature formulations. Appl. Math. Comput. 2001, 122, 107–132. [Google Scholar] [CrossRef]
- Wang, L.-X.; Melnik, R.V. Differential-algebraic approach to coupled problems of dynamic thermoelasticity. Appl. Math. Mech. 2006, 27, 1185–1196. [Google Scholar] [CrossRef]
- Wang, L.X.; Melnik, R.V. Thermo-mechanical wave propagations in shape memory alloy rod with phase transformations. Mech. Adv. Mater. Struct. 2007, 14, 665–676. [Google Scholar] [CrossRef]
- Wang, L.X.; Melnik, R.V. Finite volume analysis of nonlinear thermo-mechanical dynamics of shape memory alloys. Heat Mass Transf. 2007, 43, 535–546. [Google Scholar] [CrossRef][Green Version]
- Dhote, R.; Melnik, R.; Zu, J. Dynamic thermo-mechanical coupling and size effects in finite shape memory alloy nanostructures. Comput. Mater. Sci. 2012, 63, 105–117. [Google Scholar] [CrossRef]
- Dhote, R.; Fabrizio, M.; Melnik, R.; Zu, J. Hysteresis phenomena in shape memory alloys by non-isothermal Ginzburg–Landau models. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2549–2561. [Google Scholar] [CrossRef]
- Dhote, R.; Melnik, R.; Zu, J. Dynamic multi-axial behavior of shape memory alloy nanowires with coupled thermo-mechanical phase-field models. Meccanica 2014, 49, 1561–1575. [Google Scholar] [CrossRef]
- Dhote, R.; Gomez, H.; Melnik, R.; Zu, J. 3D coupled thermo-mechanical phase-field modeling of shape memory alloy dynamics via isogeometric analysis. Comput. Struct. 2015, 154, 48–58. [Google Scholar] [CrossRef]
- Dhote, R.P.; Gomez, H.; Melnik, R.N.; Zu, J. Shape memory alloy nanostructures with coupled dynamic thermo-mechanical effects. Comput. Phys. Commun. 2015, 192, 48–53. [Google Scholar] [CrossRef]
- Dhote, R.; Gomez, H.; Melnik, R.; Zu, J. Effect of aspect ratio and boundary conditions in modeling shape memory alloy nanostructures with 3D coupled dynamic phase-field theories. Math. Probl. Eng. 2016, 2016, 3647470. [Google Scholar] [CrossRef]
- Andreozzi, A.; Iasiello, M.; Netti, P.A. A thermoporoelastic model for fluid transport in tumour tissues. J. R. Soc. Interface 2019, 16, 20190030. [Google Scholar] [CrossRef] [PubMed]
- Karaki, W.; Lopez, C.A.; Borca-Tasciuc, D.-A.; De, S. A continuum thermomechanical model of in vivo electrosurgical heating of hydrated soft biological tissues. Int. J. Heat Mass Transf. 2018, 127, 961–974. [Google Scholar] [CrossRef] [PubMed]
- Matus, P.; Melnik, R.V.; Wang, L.; Rybak, I. Applications of fully conservative schemes in nonlinear thermoelasticity: Modelling shape memory materials. Math. Comput. Simul. 2004, 65, 489–509. [Google Scholar] [CrossRef]
- Melnik, R.V.; Roberts, A. Modelling nonlinear dynamics of shape-memory-alloys with approximate models of coupled thermoelasticity. ZAMM J. Appl. Math. Mech 2003, 83, 93–104. [Google Scholar] [CrossRef]
- Dhote, R.; Fabrizio, M.; Melnik, R.; Zu, J. A three-dimensional non-isothermal Ginzburg–Landau phase-field model for shape memory alloys. Model. Simul. Mater. Sci. Eng. 2014, 22, 085011. [Google Scholar] [CrossRef]
- Dhote, R.; Gomez, H.; Melnik, R.; Zu, J. Isogeometric analysis of a dynamic thermo-mechanical phase-field model applied to shape memory alloys. Comput. Mech. 2014, 53, 1235–1250. [Google Scholar] [CrossRef]
- Melnik, R.V. Computational analysis of coupled physical fields in piezothermoelastic media. Comput. Phys. Commun. 2001, 142, 231–237. [Google Scholar] [CrossRef]
- Melnik, R. Modelling coupled dynamics: Piezoelectric elements under changing temperature conditions. Int. Commun. Heat Mass Transf. 2003, 30, 83–92. [Google Scholar] [CrossRef]
- Patil, S.R.; Melnik, R. Thermopiezoelectric effects on optoelectronic properties of CdTe/ZnTe quantum wires. Phys. Status Solidi A 2009, 206, 960–964. [Google Scholar] [CrossRef]
- Prabhakar, S.; Melnik, R.V.; Neittaanmäki, P.; Tiihonen, T. Coupled magneto-thermo-electromechanical effects and electronic properties of quantum dots. J. Comput. Theor. Nanosci. 2013, 10, 534–547. [Google Scholar] [CrossRef]
- Wang, D.; Du, H.; Wang, L.; Melnik, R. A phase field approach for the fully coupled thermo-electro-mechanical dynamics of nanoscale ferroelectric actuators. Smart Mater. Struct. 2018, 27, 055012. [Google Scholar] [CrossRef]
- Melnik, R.; Uhlherr, A.; Hodgkin, J.; De Hoog, F. Distance geometry algorithms in molecular modelling of polymer and composite systems. Comput. Math. Appl. 2003, 45, 515–534. [Google Scholar] [CrossRef][Green Version]
- Petras, A.; Leoni, M.; Guerra, J.M.; Jansson, J.; Gerardo-Giorda, L. A computational model of open-irrigated radiofrequency catheter ablation accounting for mechanical properties of the cardiac tissue. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3232. [Google Scholar] [CrossRef] [PubMed]
- Woeppel, K.; Yang, Q.; Cui, X.T. Recent advances in neural electrode–tissue interfaces. Curr. Opin. Biomed. Eng. 2017, 4, 21–31. [Google Scholar] [CrossRef]
- Won, S.M.; Song, E.; Zhao, J.; Li, J.; Rivnay, J.; Rogers, J.A. Recent advances in materials, devices, and systems for neural interfaces. Adv. Mater. 2018, 30, 1800534. [Google Scholar] [CrossRef]
- Yan, S.; Gu, K.; Wu, X.; Wang, W. Computer simulation study on the effect of electrode–tissue contact force on thermal lesion size in cardiac radiofrequency ablation. Int. J. Hyperth. 2020, 37, 37–48. [Google Scholar] [CrossRef]
- Melnik, R.V. Computationally efficient algorithms for modelling thermal degradation and spiking phenomena in polymeric materials. Comput. Chem. Eng. 2003, 27, 1473–1484. [Google Scholar] [CrossRef]
- Melnik, R. Mathematical and Computer Modelling of Coupled Reaction Kinetics and Heat Transfer in Processing Polymeric Materials. Model. Simul. Mater. Sci. Eng. 2002, 10, 341–358. [Google Scholar] [CrossRef][Green Version]
- Gupta, R.; Noraziah, A.; Gupta, A.; Fauzi, A.A.C. Challenges in Predicting Wood Plastic Composites (WPCs). Adv. Sci. Lett. 2017, 23, 11035–11039. [Google Scholar] [CrossRef]
- Audigier, C.; Mansi, T.; Delingette, H.; Rapaka, S.; Passerini, T.; Mihalef, V.; Jolly, M.-P.; Pop, R.; Diana, M.; Soler, L. Comprehensive preclinical evaluation of a multi-physics model of liver tumor radiofrequency ablation. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 1543–1559. [Google Scholar] [CrossRef] [PubMed]
- Chaichanyut, M.; Tungjitkusolmun, S. Microwave ablation using four-tine antenna: Effects of blood flow velocity, vessel location, and total displacement on porous hepatic cancer tissue. Comput. Math. Methods Med. 2016, 2016, 4846738. [Google Scholar] [CrossRef] [PubMed]
- Paul, A.; Paul, A. Thermomechanical analysis of a triple layered skin structure in presence of nanoparticle embedding multi-level blood vessels. Int. J. Heat Mass Transf. 2020, 148, 119076. [Google Scholar] [CrossRef]
- Salimpour, M.R.; Shirani, E. Heat transfer analysis of skin during thermal therapy using thermal wave equation. J. Therm. Biol. 2017, 64, 7–18. [Google Scholar]
- Shao, Y.; Arjun, B.; Leo, H.; Chua, K. A computational theoretical model for radiofrequency ablation of tumor with complex vascularization. Comput. Biol. Med. 2017, 89, 282–292. [Google Scholar] [CrossRef]
- Keangin, P.; Rattanadecho, P. A numerical investigation of microwave ablation on porous liver tissue. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Heat transfer through a porous medium. In Convection in Porous Media; Springer: Berlin/Heidelberg, Germany, 2013; pp. 31–46. [Google Scholar]
- Schutt, D.J.; Haemmerich, D. Effects of variation in perfusion rates and of perfusion models in computational models of radio frequency tumor ablation. Med. Phys. 2008, 35, 3462–3470. [Google Scholar] [CrossRef]
- Yang, X.-D.; Melnik, R.V. Effect of internal viscosity on Brownian dynamics of DNA molecules in shear flow. Comput. Boil. Chem. 2007, 31, 110–114. [Google Scholar] [CrossRef][Green Version]
- Yang, X.-D.; Melnik, R.V. Accounting for the effect of internal viscosity in dumbbell models for polymeric fluids and relaxation of DNA. Discret. Contin. Dyn. Syst. 2007, 1052–1060. Available online: scholars.wlu.ca/cgi/viewcontent.cgi?article=1031context=math_faculty (accessed on 4 April 2020).
- Yang, X.-D.; Melnik, R.V. Effect of internal viscosity of polymeric fluids under strong extensional flows. Chin. J. Polym. Sci. 2009, 27, 189–193. [Google Scholar] [CrossRef]
- Kamath, H.; Willatzen, M.; Melnik, R.V. Vibration of piezoelectric elements surrounded by fluid media. Ultrasonics 2006, 44, 64–72. [Google Scholar] [CrossRef] [PubMed]
- Liang, F.; Yang, X.; Zhang, W.; Qian, Y.; Melnik, R. Parametric Vibration Analysis of Pipes Conveying Fluid by Nonlinear Normal Modes and a Numerical Iterative Approach. Adv. Appl. Math. Mech. 2019, 11, 38–52. [Google Scholar] [CrossRef]
- Alber, M.; Tepole, A.B.; Cannon, W.R.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; Petzold, L. Integrating machine learning and multiscale modeling—Perspectives, challenges, and opportunities in the biological, biomedical, and behavioral sciences. NPJ Digit. Med. 2019, 2, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Peng, G.C.; Alber, M.; Tepole, A.B.; Cannon, W.R.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P. Multiscale Modeling Meets Machine Learning: What Can We Learn? Arch. Comput. Methods Eng. 2020, 1–21. [Google Scholar] [CrossRef]
- Negro, R.; Rucco, M.; Creanza, A.; Mormile, A.; Limone, P.P.; Garberoglio, R.; Spiezia, S.; Monti, S.; Cugini, C.; El Dalati, G. Machine Learning Prediction of Radiofrequency Thermal Ablation Efficacy: A New Option to Optimize Thyroid Nodule Selection. Eur. Thyroid J. 2019, 1–8. [Google Scholar] [CrossRef]
- Hajimolahoseini, H.; Hashemi, J.; Gazor, S.; Redfearn, D. Inflection point analysis: A machine learning approach for extraction of IEGM active intervals during atrial fibrillation. Artif. Intell. Med. 2018, 85, 7–15. [Google Scholar] [CrossRef]
- Lötsch, J.; Ultsch, A. Machine learning in pain research. Pain 2018, 159, 623. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chan, T.C.-H.; Sahakian, A.V. Real-time estimation of lesion depth and control of radiofrequency ablation within ex vivo animal tissues using a neural network. Int. J. Hyperth. 2018, 34, 1104–1113. [Google Scholar] [CrossRef]
- Besler, E.; Wang, Y.C.; Sahakian, A.V. Early and Late Fusion Machine Learning on Multi-Frequency Electrical Impedance Data to Improve Radiofrequency Ablation Monitoring. IEEE J. Biomed. Health Inform. 2019. [Google Scholar] [CrossRef]
- Li, K.; Vakharia, V.N.; Sparks, R.; França, L.G.; Granados, A.; McEvoy, A.W.; Miserocchi, A.; Wang, M.; Ourselin, S.; Duncan, J.S. Optimizing trajectories for cranial laser interstitial thermal therapy using computer-assisted planning: A machine learning approach. Neurotherapeutics 2019, 16, 182–191. [Google Scholar] [CrossRef] [PubMed]
- Yildiz, F.; Özdemir, A.T. Prediction of laser-induced thermal damage with artificial neural networks. Laser Phys. 2019, 29, 075205. [Google Scholar] [CrossRef]
- Zhang, J.; Chauhan, S. Neural network methodology for real-time modelling of bio-heat transfer during thermo-therapeutic applications. Artif. Intell. Med. 2019, 101, 101728. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhong, Y.; Gu, C. Neural network modelling of soft tissue deformation for surgical simulation. Artif. Intell. Med. 2019, 97, 61–70. [Google Scholar] [CrossRef]
- Melnik, R.V. Coupling control and human factors in mathematical models of complex systems. Eng. Appl. Artif. Intell. 2009, 22, 351–362. [Google Scholar] [CrossRef]
- Melnik, R.V. Markov chain network training and conservation law approximations: Linking microscopic and macroscopic models for evolution. Appl. Math. Comput. 2008, 199, 315–333. [Google Scholar] [CrossRef]
- Moayedi, M.; Davis, K.D. Theories of pain: From specificity to gate control. J. Neurophysiol. 2013, 109, 5–12. [Google Scholar] [CrossRef]
- Argüello, E.J.; Silva, R.J.; Huerta, M.K.; Avila, R.S. Computational modeling of peripheral pain: A commentary. Biomed. Eng. Online 2015, 14, 56. [Google Scholar] [CrossRef]
- Kucyi, A.; Davis, K.D. The dynamic pain connectome. Trends Neurosci. 2015, 38, 86–95. [Google Scholar] [CrossRef]
- Seth, B.; de Gray, L. Genesis of chronic pain. Anaesth. Intensive Care Med. 2016, 17, 431–435. [Google Scholar] [CrossRef]
- Tiemann, L.; Hohn, V.D.; Dinh, S.T.; May, E.S.; Nickel, M.M.; Gross, J.; Ploner, M. Distinct patterns of brain activity mediate perceptual and motor and autonomic responses to noxious stimuli. Nat. Commun. 2018, 9, 1–12. [Google Scholar] [CrossRef]
- Li, Y.; Yue, J.; Yang, C. Unraveling the role of Mg++ in osteoarthritis. Life Sci. 2016, 147, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Srebro, D.; Vuckovic, S.; Milovanovic, A.; Kosutic, J.; Savic Vujovic, K.; Prostran, M. Magnesium in pain research: State of the art. Curr. Med. Chem. 2017, 24, 424–434. [Google Scholar]
- Mercadal, B.; Vicente, R.; Ivorra, A. Pulsed Radiofrequency for Chronic Pain: An Electroporation Mediated Calcium Signaling Process? Biophys. J. 2018, 114, 287a. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Y.; Pang, X.; Tang, B. Potential Therapeutic Effects of Mg/HCOOH Metal Organic Framework on Relieving Osteoarthritis. ChemMedChem 2019, 15, 13–16. [Google Scholar] [CrossRef] [PubMed]
- Kosik-Bogacka, D.I.; Lanocha-Arendarczyk, N.; Kot, K.; Zietek, P.; Karaczun, M.; Prokopowicz, A.; Kupnicka, P.; Ciosek, Z. Calcium, magnesium, zinc and lead concentrations in the structures forming knee joint in patients with osteoarthritis. J. Trace Elem. Med. Biol. 2018, 50, 409–414. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).