Biomechanical Role and Motion Contribution of Ligaments and Bony Constraints in the Elbow Stability: A Preliminary Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Instruments
- 1 self-contained and pre-calibrated Optitrack Bar V120 Trio for 3D motion capture (120 Hz) and markers registration;
- 1 visible light camera for video recording;
- 2 rigid clusters of 4 markers (Ø 12 mm) applied to the humerus and ulna;
- Generic medical instrumentations for specimen preparation.
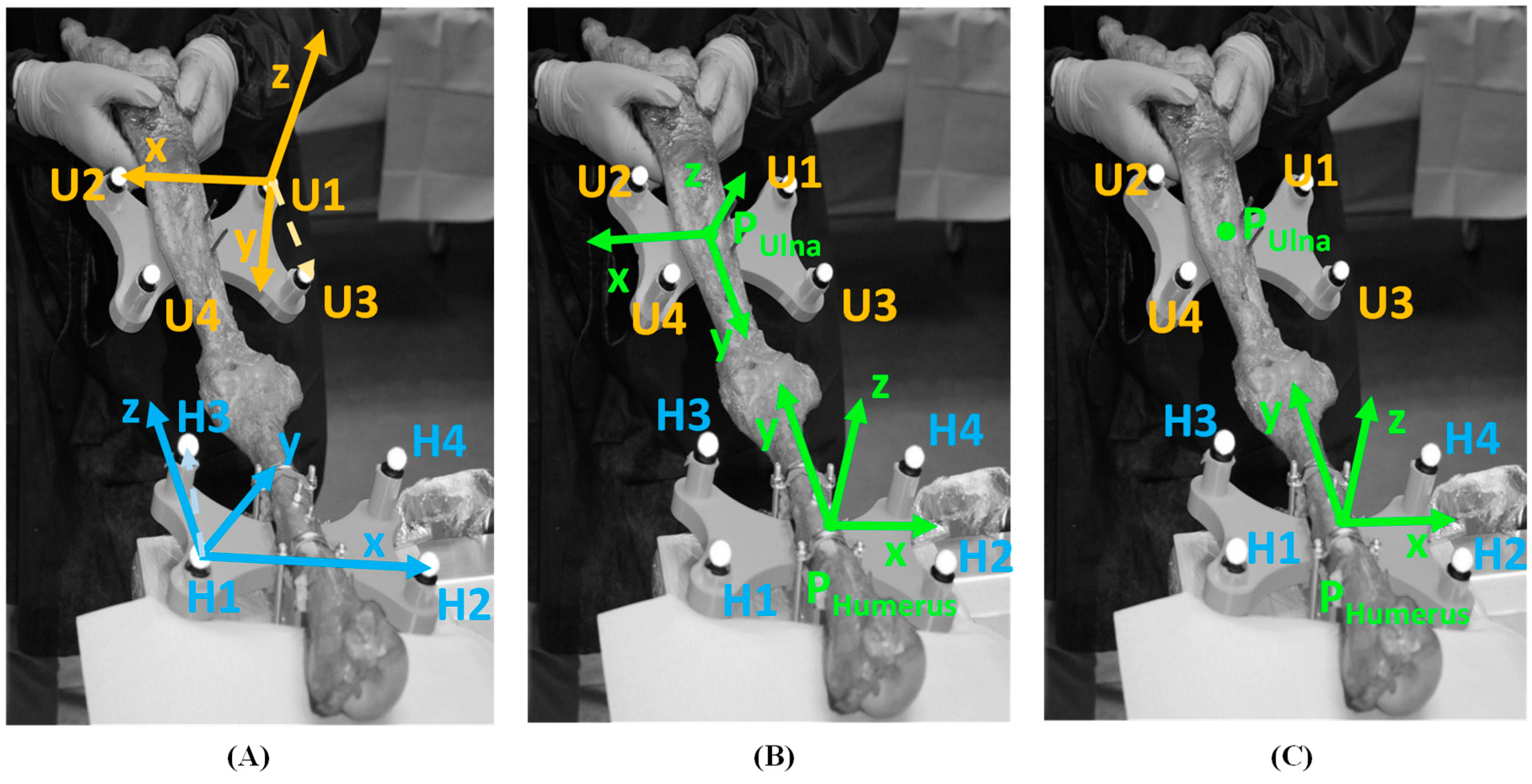
2.2. Specimen Preparation and Surgical Maneuver
2.3. Data Analysis
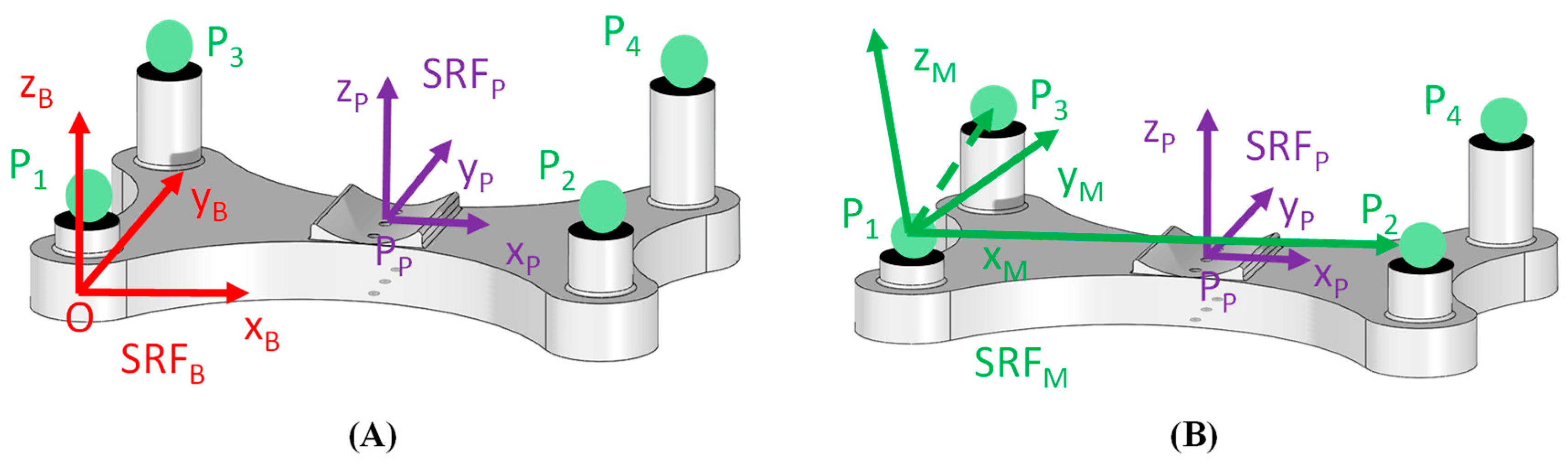
2.3.1. Local Reference System Definition
2.3.2. Baseline Condition
2.3.3. Maneuver Analysis
3. Results
4. Discussion
4.1. Intact Condition
4.2. First Section Condition (pMUCL)
4.3. First Section Condition (Coronoid)
4.4. Coronoid + pMUCL Section Condition
Author Contributions
Funding
Conflicts of Interest
References
- Bryce, C.D.; Armstrong, A.D. Anatomy and Biomechanics of the Elbow. Orthop. Clin. North Am. 2008, 39, 141–154. [Google Scholar] [CrossRef] [PubMed]
- Karbach, L.E.; Elfar, J. Elbow Instability: Anatomy, Biomechanics, Diagnostic Maneuvers, and Testing. J. Hand Surg. Am. 2017, 42, 118–126. [Google Scholar] [CrossRef] [PubMed]
- Tarassoli, P.; McCann, P.; Amirfeyz, R. Complex instability of the elbow. Injury 2017, 48, 568–577. [Google Scholar] [CrossRef] [PubMed]
- de Haan, J.; Schep, N.W.L.; Eygendaal, D.; Kleinrensink, G.J.; Tuinebreijer, W.E.; den Hartog, D. Stability of the elbow joint: Relevant anatomy and clinical implications of in vitro biomechanical studies. Open Orthop. J. 2011, 5, 168–176. [Google Scholar] [CrossRef] [PubMed]
- Wells, J.; Ablove, R.H. Coronoid fractures of the elbow. Clin. Med. Res. 2008, 6, 40–44. [Google Scholar] [CrossRef] [PubMed]
- Morrey, B.F.; An, K.N. Functional anatomy of the ligaments of the elbow. Clin. Orthop. Relat. Res. 1985, 201, 84–90. [Google Scholar] [CrossRef]
- Sard, A.; Dutto, E.; Rotini, R.; Vanni, S.; Pastorelli, S.; Battiston, B. The posterior bundle of the elbow medial collateral ligament: Biomechanical study and proposal for a new reconstruction surgical technique. Musculoskelet. Surg. 2017, 101, 181–186. [Google Scholar] [CrossRef]
- Jackson, T.J.; Jarrell, S.E.; Adamson, G.J.; Chung, K.C.; Lee, T.Q. Biomechanical differences of the anterior and posterior bands of the ulnar collateral ligament of the elbow. Knee Surg. Sports Traumatol. Arthrosc. 2016, 24, 2319–2323. [Google Scholar] [CrossRef]
- Driscoll, S.W.O.; Jupiter, J.B.; King, G.J.W.; Hotchkiss, R.N.; Morrey, B.F.; Surgery, J. The Unstable Elbow. J. Bone Jt. Surg. Am. 2000, 82, 724–738. [Google Scholar] [CrossRef]
- McKee, M.D.; Pugh, D.M.; Wild, L.M.; Schemitsch, E.H.; King, G.J. Standard surgical protocol to treat elbow dislocations with radial head and coronoid fractures. J. Bone Jt. Surg. Ser. A 2005, 87, 22–32. [Google Scholar] [CrossRef]
- Sanchez-Sotelo, J.; Morrey, B.F.; O’Driscoll, S.W. Ligamentous repair and reconstruction for posterolateral rotatory instability of the elbow. J. Bone Joint Surg. Br. 2005, 87, 54–61. [Google Scholar] [CrossRef]
- Kim, J.W.; Lee, S.H.; Kim, S.J.; Park, J.S. Surgical Technique for Arthroscopic Lateral Collateral Ligament Repair. JBJS Essent. Surg. Technol. 2016, 6, e33. [Google Scholar] [CrossRef]
- Agostini, V.; Rosati, S.; Balestra, G.; Trucco, M.; Visconti, L.; Knaflitz, M. Estimation of joint position error. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2017, 2017, 2474–2477. [Google Scholar]
- Zanetti, E.M.; Bignardi, C.; Terzini, M.; Putame, G.; Audenino, A.L. A multibody model for the optimization of hip arthroplasty in relation to range of movement. AMJ 2018, 11, 486–491. [Google Scholar] [CrossRef]
- Terzini, M.; Zanetti, E.M.; Audenino, A.L.; Putame, G.; Gastaldi, L.; Pastorelli, S.; Panero, E.; Sard, A.; Bignardi, C. Multibody modelling of ligamentous and bony stabilizers in the human elbow. Muscles. Ligaments Tendons J. 2017, 7, 493–502. [Google Scholar] [CrossRef]
- Zanetti, E.; Terzini, M.; Mossa, L.; Bignardi, C.; Costa, P.; Audenino, A.; Vezzoni, A. A structural numerical model for the optimization of double pelvic osteotomy in the early treatment of canine hip dysplasia. Vet. Comp. Orthop. Traumatol. 2017, 30, 256–264. [Google Scholar] [PubMed]
- Callaway, G.H.; Field, L.D.; Deng, X.H.; Torzilli, P.A.; O’Brien, S.J.; Altchek, D.W.; Warren, R.F. Biomechanical evaluation of the medial collateral ligament of the elbow. J. Bone Joint Surg. Am. 1997, 79, 1223–1231. [Google Scholar] [CrossRef]
- Pollock, J.W.; Brownhill, J.; Ferreira, L.M.; McDonald, C.P.; Johnson, J.A.; King, G.J. Effect of the Posterior Bundle of the Medial Collateral Ligament on Elbow Stability. J. Hand Surg. Am. 2009, 34, 116–123. [Google Scholar] [CrossRef] [PubMed]
- Gluck, M.J.; Beck, C.M.; Golan, E.J.; Nasser, P.; Shukla, D.R.; Hausman, M.R. Varus posteromedial rotatory instability: A biomechanical analysis of posterior bundle of the medial ulnar collateral ligament reconstruction. J. Shoulder Elb. Surg. 2018, 27, 1317–1325. [Google Scholar] [CrossRef]
- Gluck, M.; Beck, C.; Golan, E.; Nasser, P.; Shukla, D.; Hausman, M. Pmucl Reconstruction Recovers Elbow Stability in the Presence of Posteromedial Rotatory Instability a cadaveric study. In Proceedings of the ORS 2017 Annual Meeting, Rosemont, IL, USA, 19–22 March 2017. [Google Scholar]
- Golan, E.J.; Shukla, D.R.; Nasser, P.; Hausman, M. Isolated ligamentous injury can cause posteromedial elbow instability: A cadaveric study. J. Shoulder Elb. Surg. 2016, 25, 2019–2024. [Google Scholar] [CrossRef]
- Shukla, D.R.; Golan, E.; Nasser, P.; Culbertson, M.; Hausman, M. Importance of the posterior bundle of the medial ulnar collateral ligament. J. Shoulder Elb. Surg. 2016, 25, 1868–1873. [Google Scholar] [CrossRef] [PubMed]
- Shukla, D.R.; Golan, E.; Weiser, M.C.; Nasser, P.; Choueka, J.; Hausman, M. The Posterior Bundle’s Effect on Posteromedial Elbow Instability After a Transverse Coronoid Fracture: A Biomechanical Study. J. Hand Surg. Am. 2018, 43, 381.e1–381.e8. [Google Scholar] [CrossRef] [PubMed]
- Borzelli, D.; Gastaldi, L.; Bignardi, C.; Audenino, A.; Terzini, M.; Sard, A.; Pastorelli, S. Method for Measuring the Displacement of Cadaveric Elbow After the Section of Medial Collateral Ligament Anterior and Posterior Bundles; Springer: Cham, Switzerland, 2018; pp. 972–979. [Google Scholar]
- Gastaldi, L.; Lisco, G.; Pastorelli, S. Evaluation of functional methods for human movement modelling. Acta Bioeng. Biomech. 2015, 17, 32–38. [Google Scholar] [PubMed]
- Lisco, G.; Pastorelli, S.; Gastaldi, L. Application of a functional method for subject and motion specific joints kinematics during walking. Int. J. Appl. Eng. Res. 2016, 11, 7588–7591. [Google Scholar]
- Galetto, M.; Gastaldi, L.; Lisco, G.; Mastrogiacomo, L.; Pastorelli, S. Accuracy evaluation of a new stereophotogrammetry-based functional method for joint kinematic analysis in biomechanics. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2014, 228, 1183–1192. [Google Scholar] [CrossRef]
- Miana, A.N.; Prudêncio, M.V.; Barros, R.M.L. Comparison of Protocols for Walking and Running Kinematics Based on Skin Surface Markers and Rigid Clusters of Markers. Int. J. Sports Med. 2009, 30, 827–833. [Google Scholar] [CrossRef][Green Version]
- Vladimir, M.; Zatsiorsky, V.M.Z. Kinematics of Human Motion; Human Kinetics: Champaign, IL, USA, 1998. [Google Scholar]



| Surgical Sections Sequence | ||
|---|---|---|
| Test | Elbow_1 | Elbow_2 |
| Test 1 | Intact | Intact |
| Test 2 | pMUCL | Coronoid |
| Test 3 | pMUCL + Coronoid | Coronoid + pMUCL |
| PULNA Distance to Reference Regression Plane | |||||||
|---|---|---|---|---|---|---|---|
| Elbow_1 | Elbow_2 | ||||||
| Elbow section | Intact | pMUCL | pMUCL + Coronoid | Intact | Coronoid | Coronoid + pMUCL | |
| Flexion angle | 30° | ||||||
| Elbow deflection | Mean [mm] | −9.55 | −5.09 | −18.54 | 7.84 | 4.64 | 34.4 |
| STD [mm] | 2.89 | 3.36 | 14.89 | 7.40 | 6.44 | 9.10 | |
| Flexion angle | 60° | ||||||
| Elbow deflection | Mean [mm] | −12.04 | −5.42 | −21.66 | 18.52 | 26.05 | 45.41 |
| STD [mm] | 6.11 | 6.26 | 16.2 | 6.22 | 6.79 | 18.47 | |
| Flexion angle | 90° | ||||||
| Elbow deflection | Mean [mm] | −4.50 | −1.81 | −15.63 | 1.83 | 11.49 | 52.16 |
| STD [mm] | 1.79 | 1.63 | 13.25 | 6.27 | 17.39 | 21.92 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panero, E.; Gastaldi, L.; Terzini, M.; Bignardi, C.; Sard, A.; Pastorelli, S. Biomechanical Role and Motion Contribution of Ligaments and Bony Constraints in the Elbow Stability: A Preliminary Study. Bioengineering 2019, 6, 68. https://doi.org/10.3390/bioengineering6030068
Panero E, Gastaldi L, Terzini M, Bignardi C, Sard A, Pastorelli S. Biomechanical Role and Motion Contribution of Ligaments and Bony Constraints in the Elbow Stability: A Preliminary Study. Bioengineering. 2019; 6(3):68. https://doi.org/10.3390/bioengineering6030068
Chicago/Turabian StylePanero, Elisa, Laura Gastaldi, Mara Terzini, Cristina Bignardi, Arman Sard, and Stefano Pastorelli. 2019. "Biomechanical Role and Motion Contribution of Ligaments and Bony Constraints in the Elbow Stability: A Preliminary Study" Bioengineering 6, no. 3: 68. https://doi.org/10.3390/bioengineering6030068
APA StylePanero, E., Gastaldi, L., Terzini, M., Bignardi, C., Sard, A., & Pastorelli, S. (2019). Biomechanical Role and Motion Contribution of Ligaments and Bony Constraints in the Elbow Stability: A Preliminary Study. Bioengineering, 6(3), 68. https://doi.org/10.3390/bioengineering6030068





