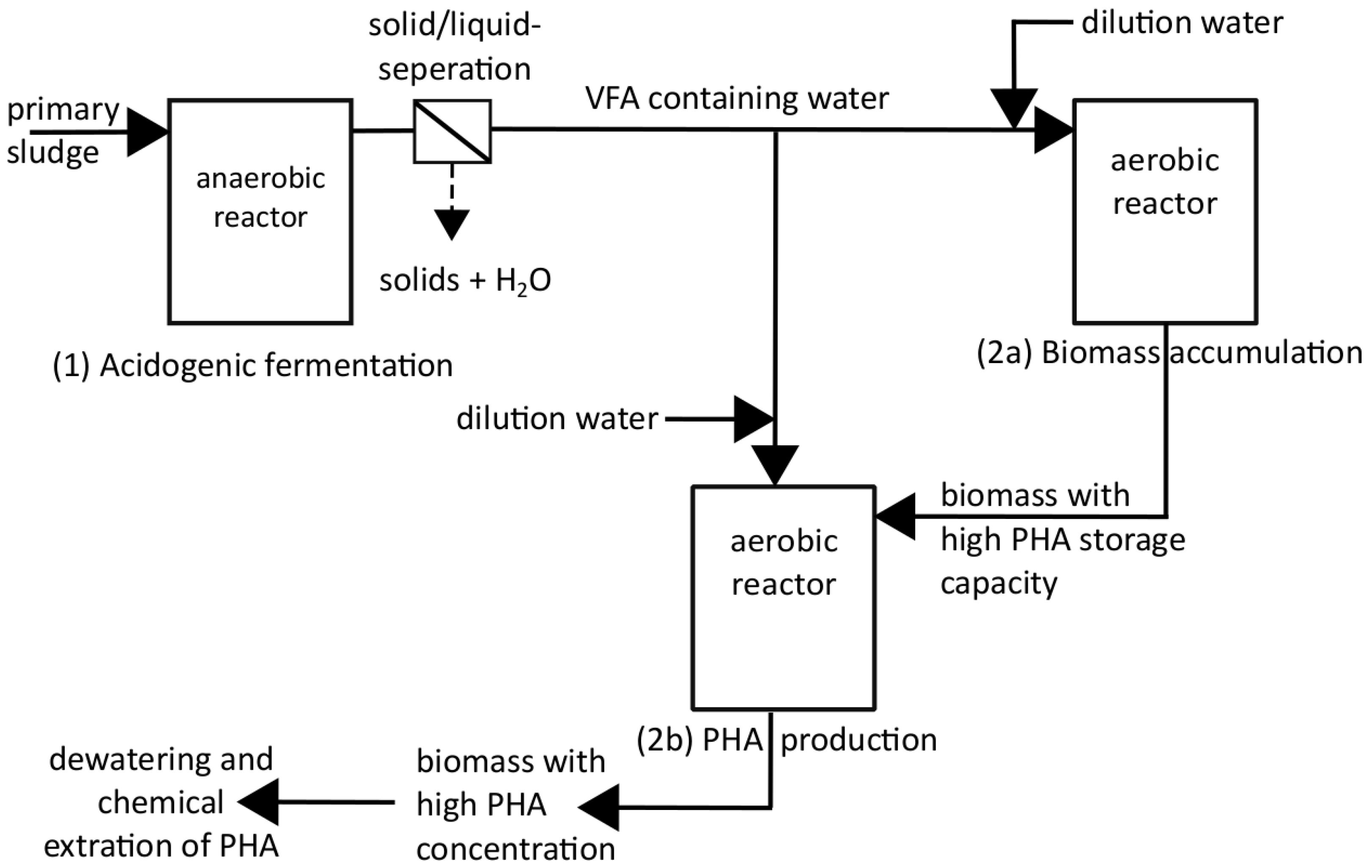
3.3.1. Calculation for German Waste Water Treatment Plants
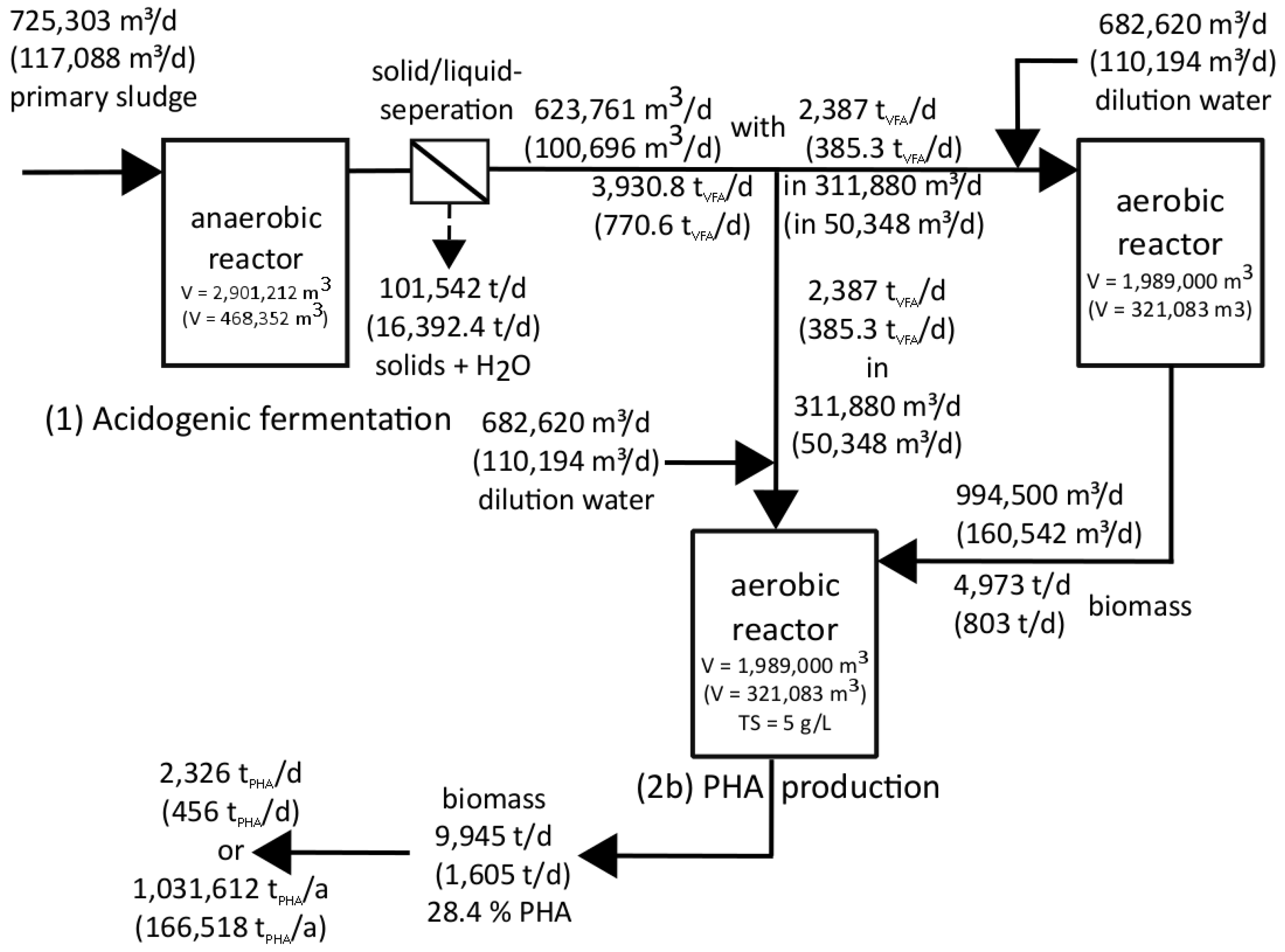
Figure 8 shows the results for possible biopolymer production on German WWTPs. All material streams and reactor volumes in this figure are theoretical values showing the size of the flows, if the best substrate for acidification [
34] of all German WWTPs with preliminary sedimentation potential (PSP = more than 10,000 PE) would be used for PHA production.
First of all, the calculation for the amount of primary sludge in Germany regarding the PEs (
Table 1) connected to German WWTPs is shown in Equation (6).
Around 92% of PEs are coming from WWTPs with preliminary sedimentation potential (
Table 1), on which a primary clarifier is installed or the construction of a primary clarifier would be preferable. Thus, the actual amount of primary sludge is calculated as follows:
Using these data and the results of own experiments [
34,
42] and of Chapter 3.1 and 3.2 a calculation of the possible PHA production through various steps can be performed.
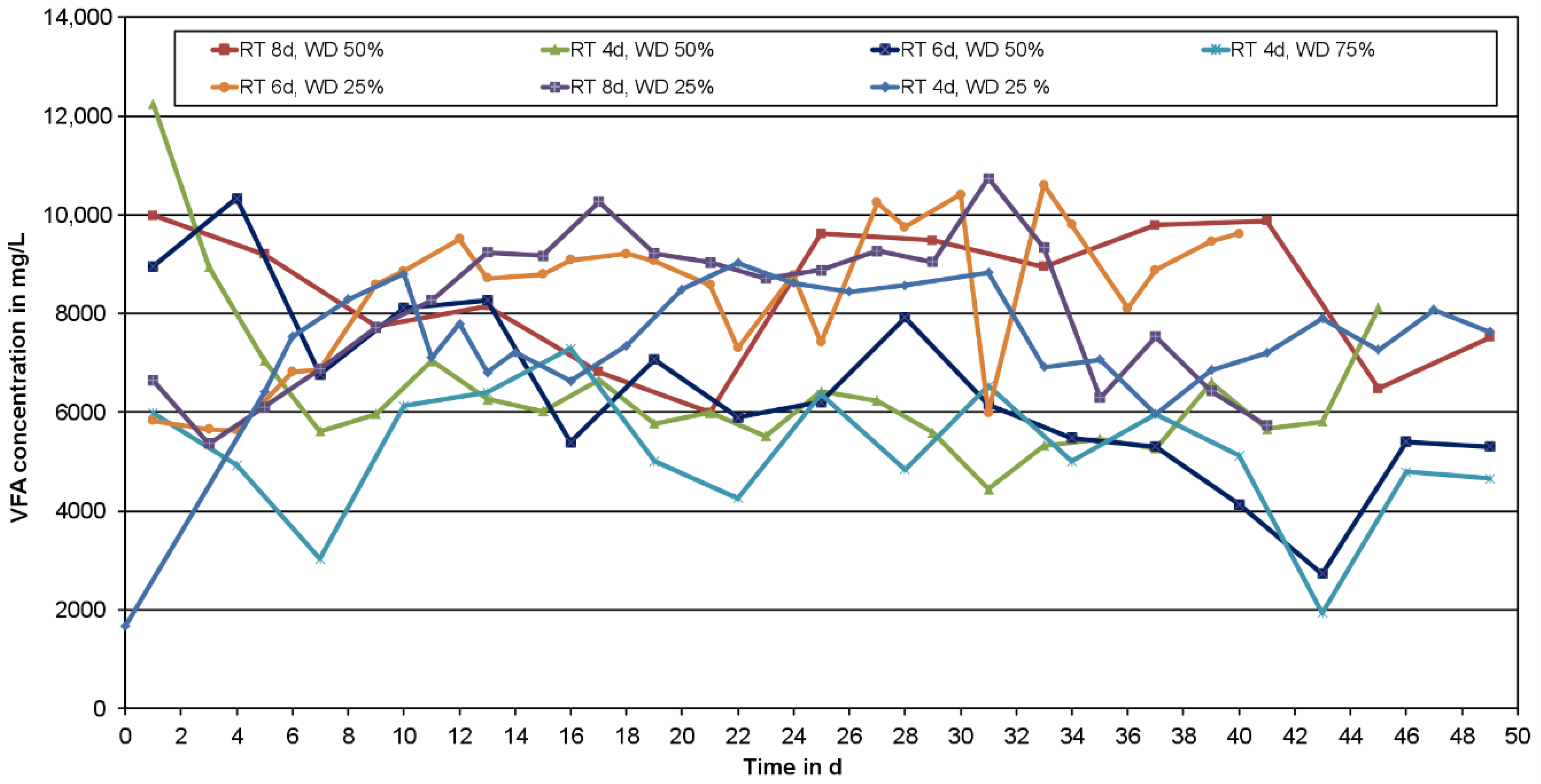
Implementing the best reactor operation method, using a retention time of 4 days and a daily withdrawal of 25% (
Table 1) 117,088.4
acidified material could be used for PHA production every day (Equation (8)).
The total solid (TS) concentration of the acidified material of 35
(
Table 1) and the assumed residual moisture after de-watering via centrifuge of 75% leads to a daily acidified liquid production of 100,696
(Equations (9)–(11)).
The assumed residual moisture of 75% means that the calculated 4098.1
biomass is 25% of the total mass separated by the centrifuge. Accordingly, 75% of the separated total mass is water. Assuming that the solid phase is completely separated it follows:
With an assumed average density of 1
the amount of
of acidified liquid is available for the PHA production step.
Regarding the average VFA concentration of 7653
(
Table 1) the amount of VFA in the acidified water can be calculated (Equation (12)).
The substrate is divided into equal parts to both reactors (2a and 2b) of the second production step so that each reactor is supplied with 50,348
of acidified liquid (Equation (13)), containing 385.3
(Equation (14)).
In order to achieve the required loading rate of 1.2
in both reactors of the second production step, the volume of Reactor 2a (sum over Germany) and 2b (sum over Germany) should be 321,083 m
3 each (Equation (15)).
Reactor 2a is operated with a retention time of 2 days, a daily withdrawal of 50% of the reactors volume and a total solid concentration of TS = 5
(
Table 1). Due to the fact that there is no biomass sedimentation before the removal of the material, the withdrawn material can be considered as fully mixed. Therefore, the amount of bacteria must double every cycle to achieve a constant concentration of total solids. During the own experiments it was shown that this necessary condition was fulfilled [
42].
The removal of 50% of the reactor volume leads to the amount of substrate, which has to be filled in the Reactor 2b every day (Equation (16)).
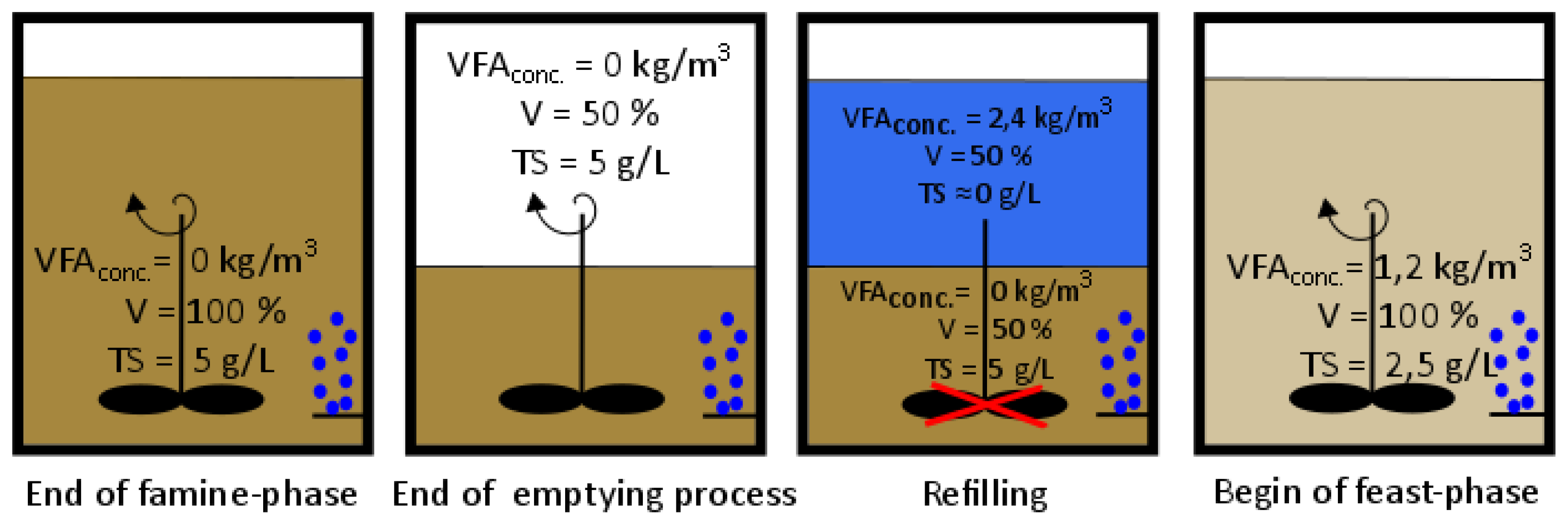
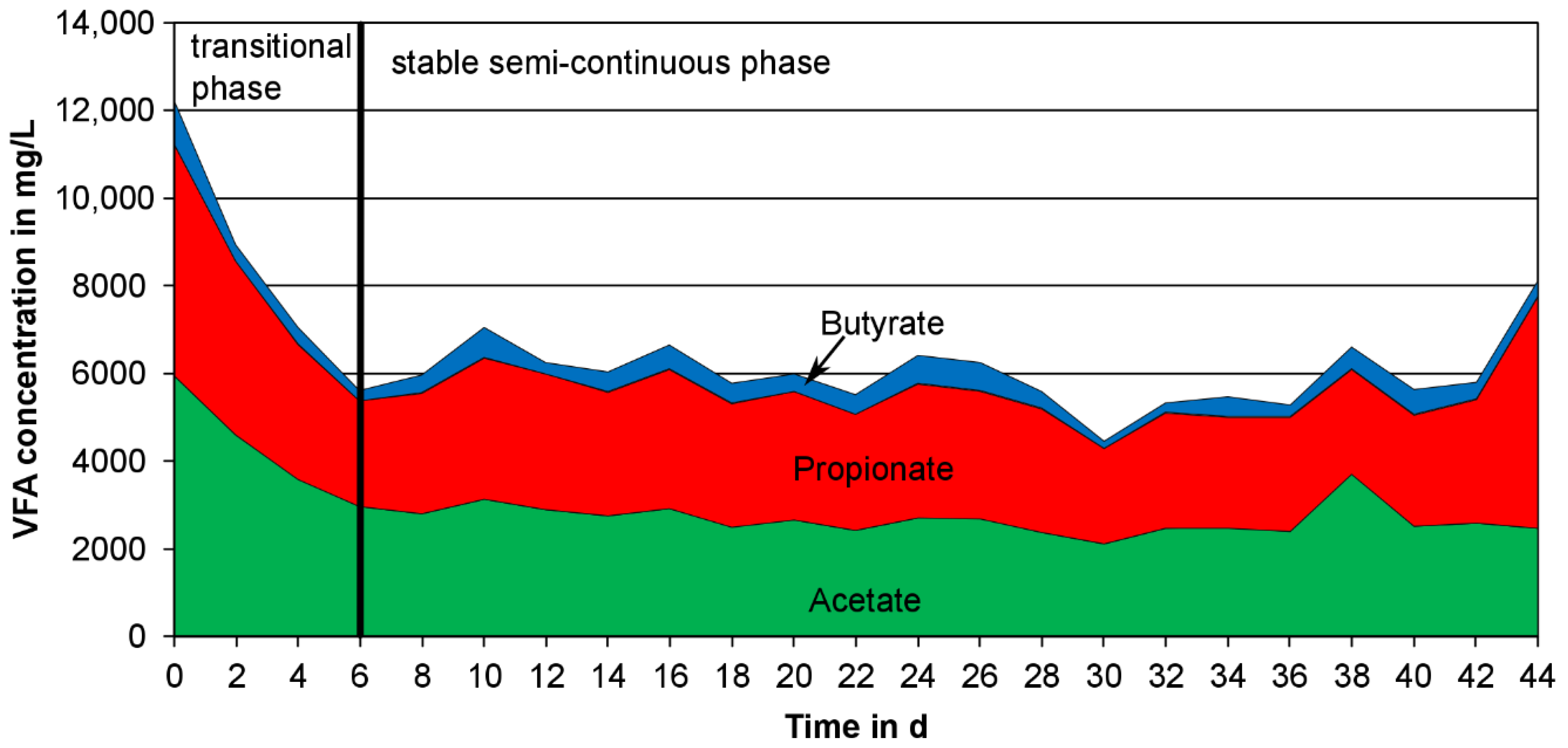
The emptying and refilling process at the beginning of every cycle is represented in
Figure 3. In order to reach a VFA concentration of 1.2
and regarding to the fact that the VFA concentration at the end of a cycle is zero, a substrate with a VFA concentration of 2.4
is needed if half of the reactors volume is exchanged.
Equation (16) shows the required amount of substrate for one day for one reactor regarding the needed VFA concentration. Hence the amount of VFA rich liquid of 50,348
(Equation (13)) has to be diluted with 110,193.7
fresh water (Equation (17)).
When calculating the amount of dilution water it should be noted that the large amount of water is due to the reactors comparatively low total solid concentration of TS = 5
, which was installed during the experiments in [
42]. This concentration is used for the potential analysis as well, to keep the calculation as close as possible to the operation conditions of the carried out experiments. Of course, a much higher solid concentration could be installed, leading to significantly smaller reactor volumes as well as less dilution water. As the amount of dilution water does not affect the result of the potential analysis it was kept.
As described, the biomass concentration in Reactor 2a was 5
at the end of a cycle. Regarding the withdrawal of 50% of the reactor’s volume a total of
biomass is transferred into Reactor 2b. This reactor also had a dry matter content of 5
after the PHA production step (
Table 1). Considering a cycle time of one day and the volume of 321,083 m
3, the amount of biomass in Reactor 2b sums up to (Equation (19)):
With the reached PHA concentration of 28.4% of the cell dry weight (CDW) [
42] the daily amount of biopolymer is calculated in Equation (20).
Finally, the possible annual amount of PHA production on German waste water treatment plants can be calculated in Equation (21).
Dividing the reactor volume (sum of all production stages) of 1,110,518 m
3 by the people’s equivalent with preliminary sedimentation potential of 106.56 Mio. PE (
Table 1) results in a reactor volume (sum of all production stages) per capita of around 10.4 L/PE. Each PE can contribute to the production of 1.6 kg
PHA/(PE×a). Keeping in mind that the aeration tank volume on a WWTP with 100,000 PE sums up to 10,000 m
3–15,000 m
3 an additional reactor volume of approximately 1050 m
3 would be needed for the biopolymer production, only. Thus, the extra volume would not be disproportional.
3.3.2. Estimation for European Waste Water Treatment Plants
The Biopolymer potential for European WWTPs are calculated similar to
Section 3.3.1 and also shown in
Figure 8.
As there are missing data about the amount of connected persons (PEs) for many EU member states as well as about the amount of municipal waste water, it is impossible to calculate the EU-wide production of primary sludge analogous to Equations (6) and (7). However, there are data for all 28 EU member states regarding the production of sewage sludge. These data show the dry weight of sewage sludge in
(
Table 1) and hence their unit must be transferred into
(Equation (22)) to compare them with the data used for German WWTP in Equation (6). Therefore, an average total solid concentration of 15
or 66.67
for European sewage sludge (primary and secondary) is assumed.
On the assumption that the proportion of primary sludge in the amount of sewage sludge is more or less constant in all member states, the percentage can be calculated (Equation (25)) using the theoretical yearly amount of primary sludge produced in Germany (Equations (6) and (23)) and the yearly amount of German sewage sludge (
Table 1) (Equation (24)).
Assuming that not all European waste water treatment plants are equipped with a primary clarifier, the proportion of primary sludge is rounded off to 30%, so that the yearly amount of European primary sludge sums up to 265 Mio.
(Equation (26)) or 725,303
(Equation (27)).
By now, the European biopolymer potential can be calculated analogous to Equations (8)–(21).
The amount of acidified material is:
Using Equations (9)–(11) the amount of acidified liquid can be calculated (Equation (31)):
With an average density of 1
of acidified liquid can be used within the second PHA production step. This leads to the amount of VFAs in the acidified water (Equation (32)):
Analogous to Equations (13) and (14) both reactors of the second production step are supplied with 311,880
(Equation (33)) of acidified liquid containing 2386.8
(Equation (34)).
The reactor volumes (Equation (35)) can be calculated analogous to Equation (15):
The daily substrate amount for one reactor is (Equation (36)):
Analogous to Equation (17) the amount of dilution water can be calculated (Equation (37)):
With a withdrawal of 50% a biomass transfer to Reactor 2b of 4094.58
is necessary (Equation (38)).
With the described total solid concentration of 5
after the PHA production the amount of biomass in Reactor 2b is (Equation (39)):
With a cycle time of one day and the reached PHA concentration of 28.4% CDW (
Table 1) the daily amount of PHA sums up to (Equation (40)):
Finally, the possible annual amount of PHA production on European waste water treatment plants can be calculated in Equation (41).
3.3.3. Summary of the Results and Optimization Potential
The market for biopolymers is predicted to grow continuously [
43]. In 2016, a worldwide biopolymer production of 4.16 Mio.
, of which 861,120
or 20.7% [
43] suit the criteria of the stringent definition for biopolymers, introduced in Chapter 1, were achieved. Taking Equation (21) into account approximately 4.0% of the worldwide biopolymer production (bio- and non-biodegradable) could be produced just by using primary sludge from German WWTPs. Around 19.3% of the worldwide biopolymers could be produced on WWTPs in Germany considering the stringent definition, only.
For the biopolymer production on European WWTPs (Equation (41)) approximately 24.7% of 2016’s worldwide biopolymer production (bio- and non-biodegradable) or around 119.8% of 2016’s worldwide biopolymer production due to the stringent definition could be produced.
Assuming an improved PHA production with an achievable PHA concentration of 0.5
[
44] or even around 60% CDW [
45,
46] a total amount of 2,179,446.8
(Equation (42)) could be produced on European WWTPs by using primary sludge, only.
Thus, approximately 52.4% of 2016’s worldwide biopolymer production (bio- and non-biodegradable) or 253.1% of 2016’s worldwide biopolymer production due to the stringent definition could be produced in an improved production on WWTPs in the EU.
A large proportion of polymers (biopolymers and those from synthetic production) is used for packing materials. The PHAs feature similar characteristics like polypropylene (PP), which is the mostly sold plastic in the EU with 18.8% (around 8.6 Mio.
) market share in 2012 [
47]. The potential analysis for Germany equates to approximately 1.9% of the EUs PP production. Using the calculation for the EU for PHA production from primary sludge around 12.0% of the conventional PP sold in the EU could be substituted which is a significant potential.