Macroscopic Dynamic Modeling of Sequential Batch Cultures of Hybridoma Cells: An Experimental Validation
Abstract
:1. Introduction
- A simple dynamic model of cultures of hybridoma cells in SBR is developed and validated with experimental data. Confidence intervals for the parameters and the estimated trajectories are provided.
- A systematic model identification procedure, based on rigorous yet simple to use tools—MLPCA to determine the stoichiometry, nonlinear least squares to identify the parameters of the kinetic laws, sensitivity analysis and Monte Carlo analysis to infer the confidence intervals—is assessed in a real case study, showing good performance and promise for future applications.
- The simple dynamic model is further exploited to optimize the medium renewal strategy in the sequential batches.
2. Dynamic Modeling of Hybridoma Cultures
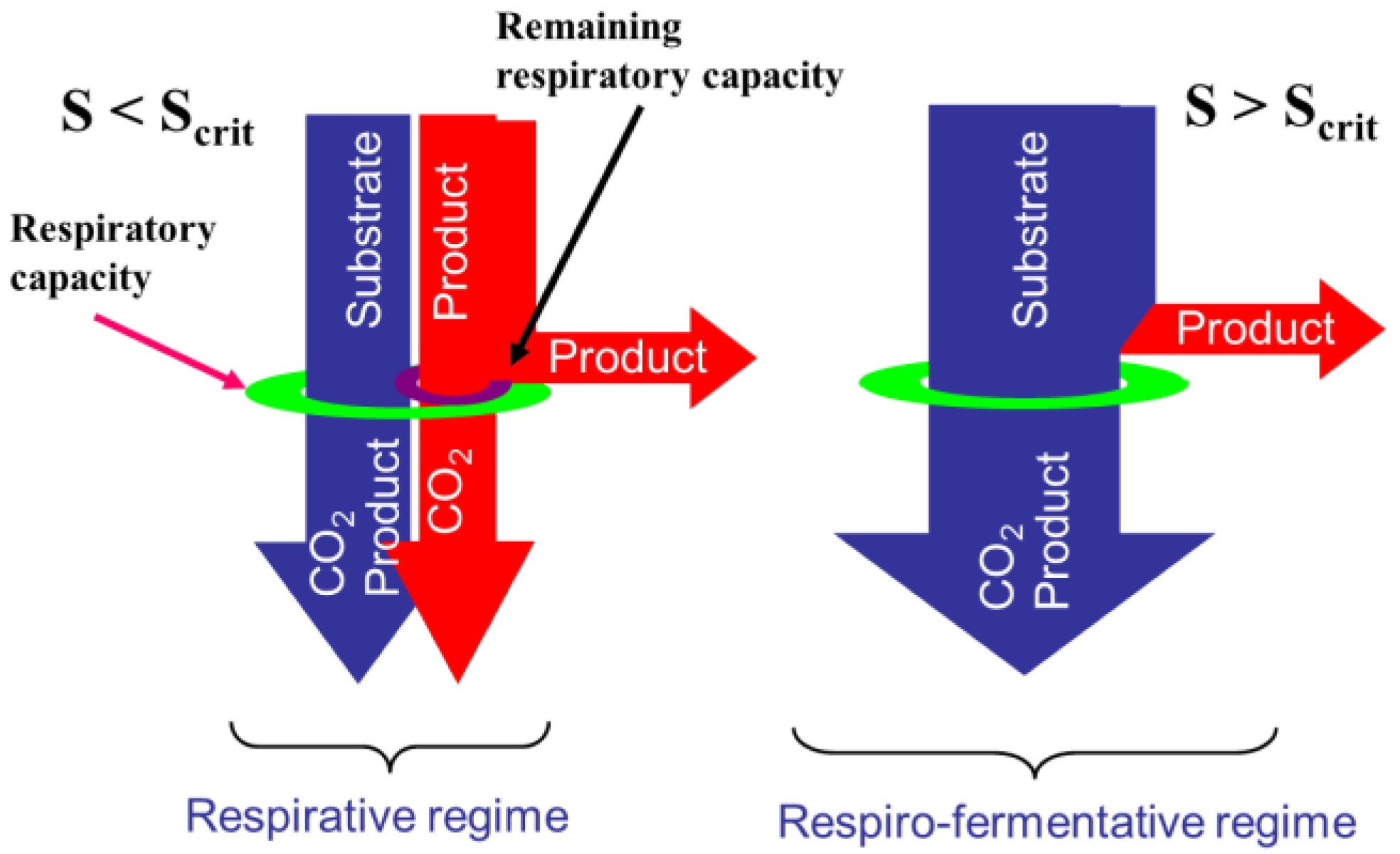
2.1. Overflow Metabolism
- The glycolysis which is a series of degradation reactions of glucose (the main substrate) taking place in the cytoplasm and leading to a final product, i.e., pyruvate.
- The Krebs cycle, also called the tricarboxylic acids (TCA) cycle or citric acids cycle, which takes place inside the mitochondrions and uses pyruvate to product the cells energy units (Adenosine triphosphate or ATP) and reduced cofactors (typically NADH and FADH).
- The electron transport, still taking place in mitochondrions and producing ATP from the reduced cofactors.
- The fermentative pathway which, in oxygen limitation, produces typical products like lactate from pyruvate in the cytoplasm.
2.2. Systematic Modeling Procedure
3. Experimental Case Study—Materials and Methods
3.1. Operating Conditions
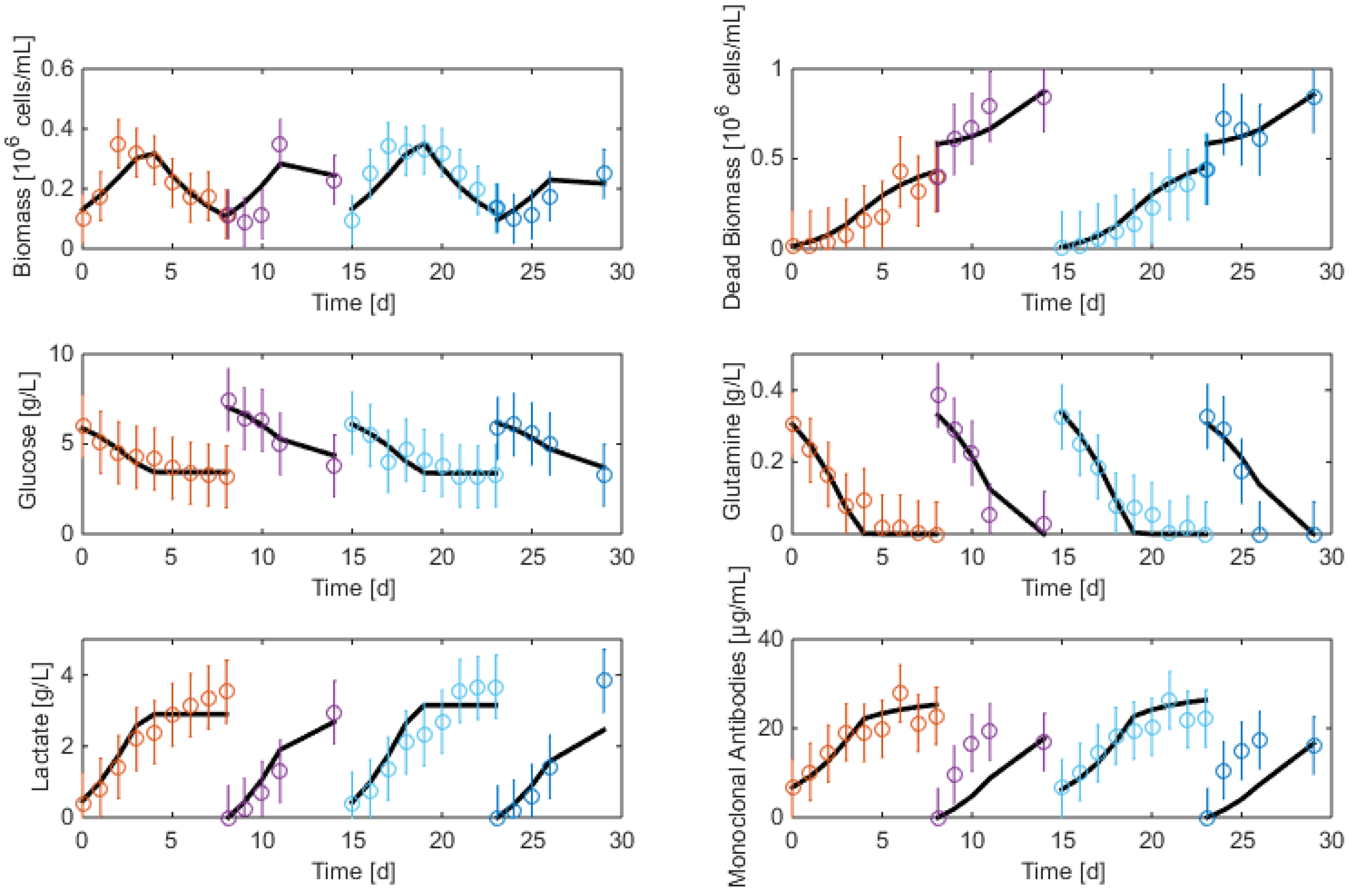
3.2. Measurements and Data Sets
- Biomass: Living and dead biomasses are measured by cell-counting using Trypan blue and a Neubauer chamber.
- Glucose concentration is measured by using a Roche glycemic analytical device called Accu-Chek allowing a fast calculus of the glucose concentration within a few seconds.
- Lactate concentration is also measured using a Roche device called Accutrend delivering fast concentration measurements using dipsticks.
- A “Mega-Calc” enzymatic kit from Megazyme is used to obtain the glutamine and ammonium concentrations. This method is based on absorbance measurements.
- Antibody concentration is obtained using an ELISA dosage of murine IgG designed by the CER group from Aye (Belgium) based on reactants from Bethyl Laboratories (ref A90-131A for coatage antibodies and A90-131P for revelation).
4. Data-Driven Model Derivation
4.1. Data Processing
4.2. MLPCA-Based Systematic Procedure
- (a)
- The existence of a glycolysis pathway where biomass grows on substrates, producing no lactate and without mortality (, , );
- (b)
- A sole glucose overflow pathway, according to the absence of ammonium (i.e., of glutamine overflow), where no dead biomass nor antibody is produced (, , );
- (c)
- A biomass death pathway (, ) theoretically with no substrate or metabolite concentration variations. The latter would represent too many constraints with respect to the available degree of freedom and arbitrarily, only the lactate coefficient is set to zero (). Indeed, due to the size of G, which is a 3 by 3 matrix, only 3 constraints can be expressed per reaction.
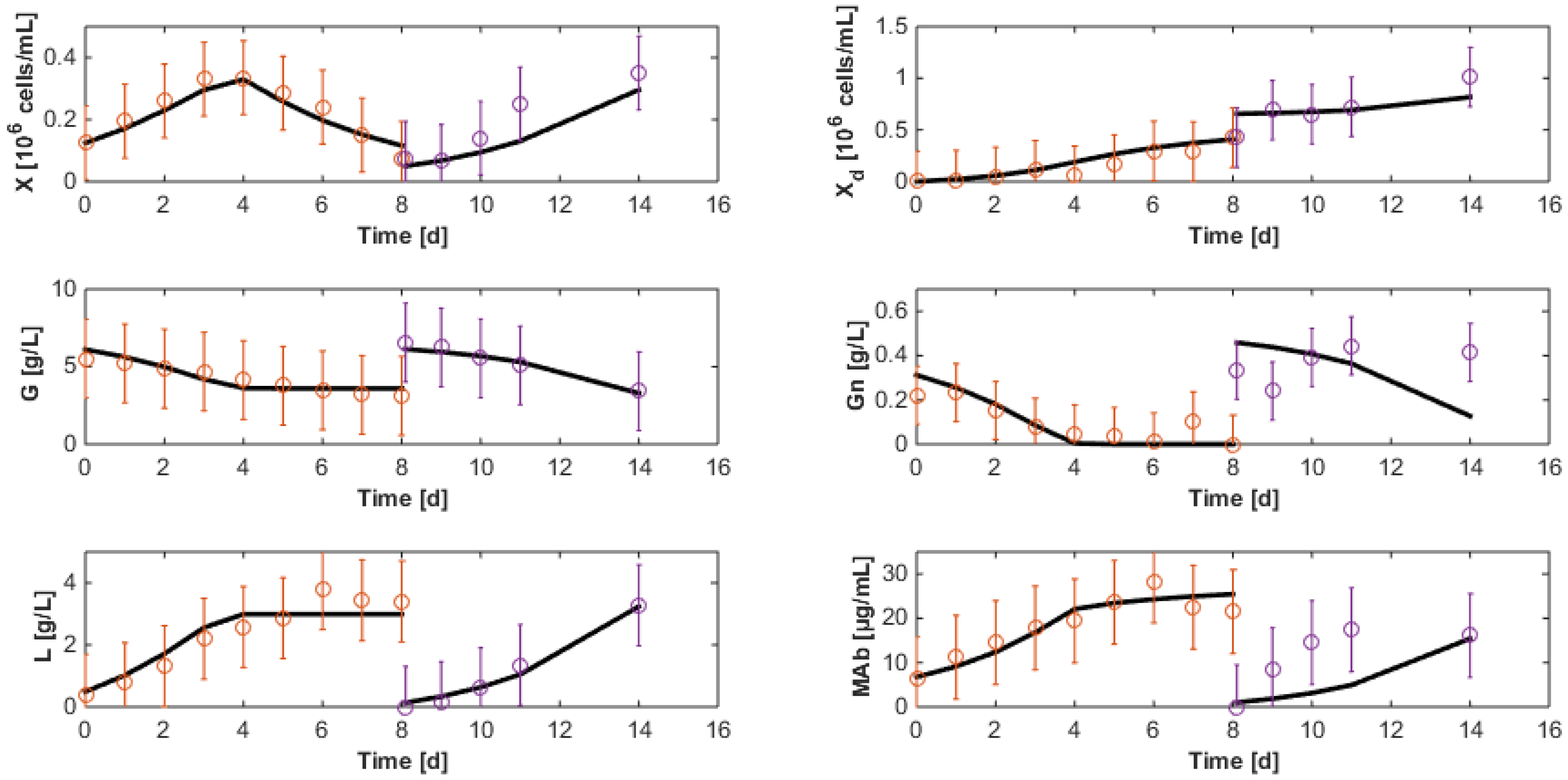
5. Parameter Identification
5.1. Reaction Rates
5.2. Initial Conditions and Identification Criterion
5.3. Minimization and Multi-Start Strategy
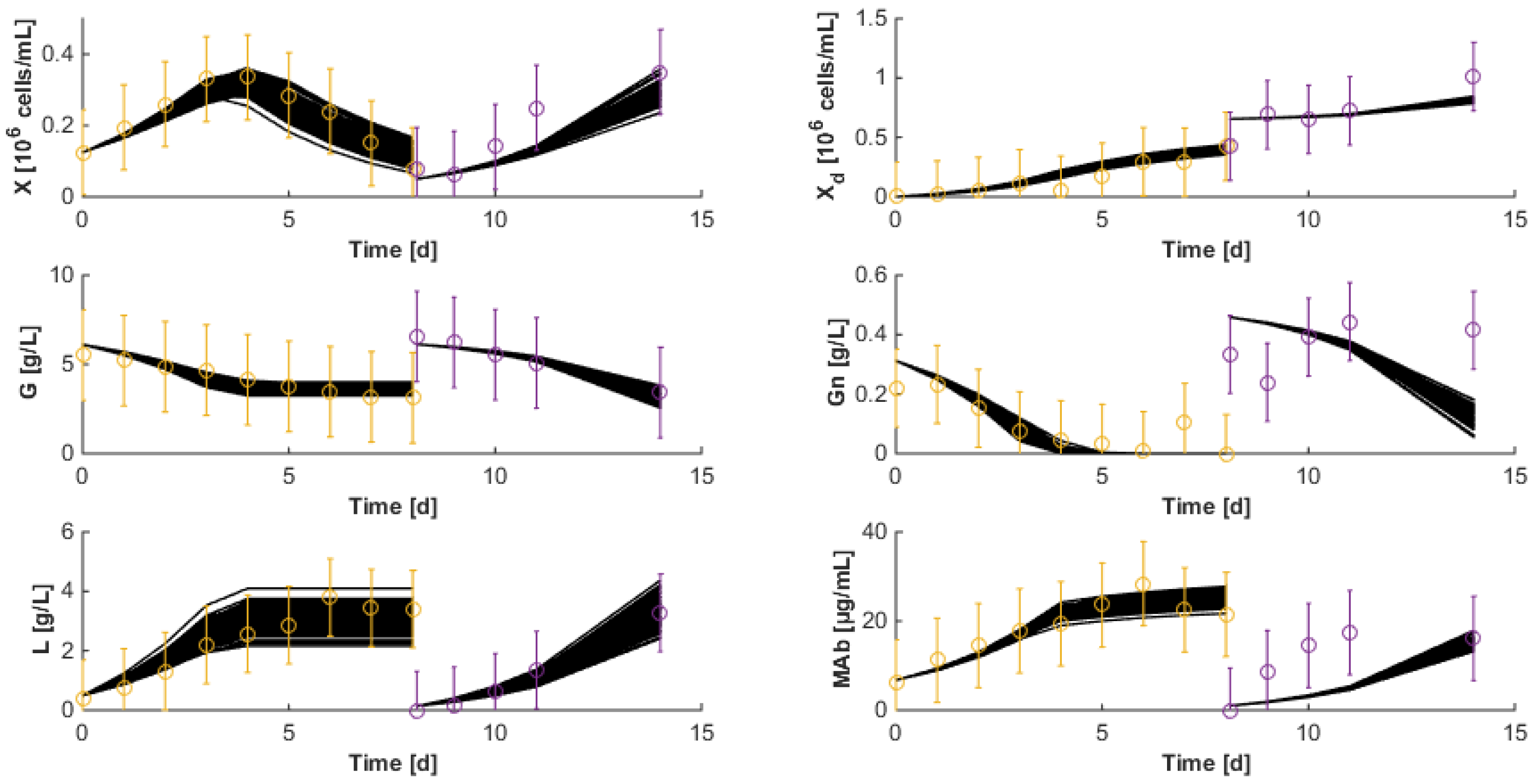
6. Parametric Sensitivity Analysis
6.1. Parameter Error Covariance
6.2. Application to the Case Study
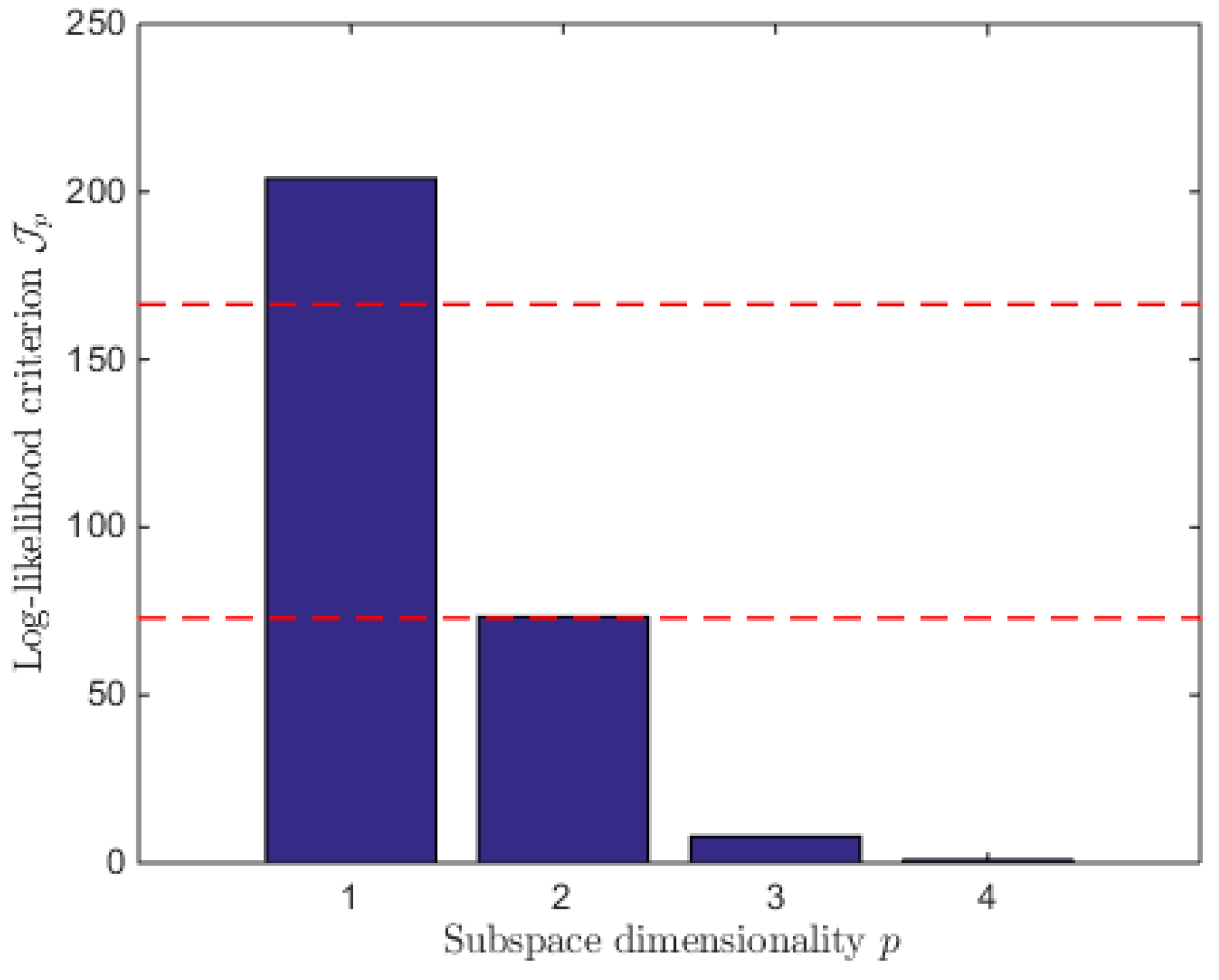
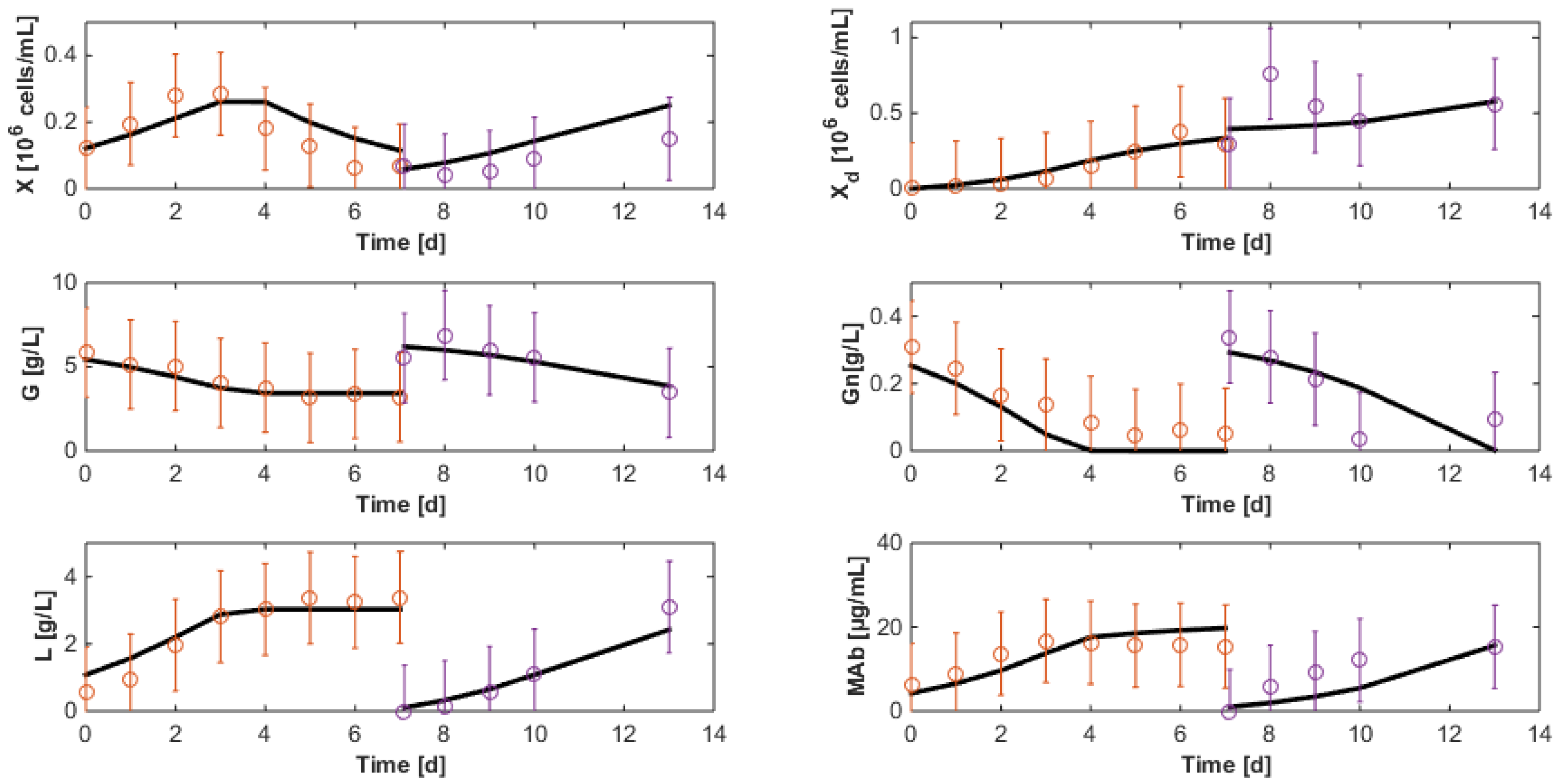
7. Reduced Model Identification
7.1. Model Reduction
7.2. Re-Identification
7.3. Reduced Model Cross-Validation
7.4. Robustness to Parameter Uncertainty
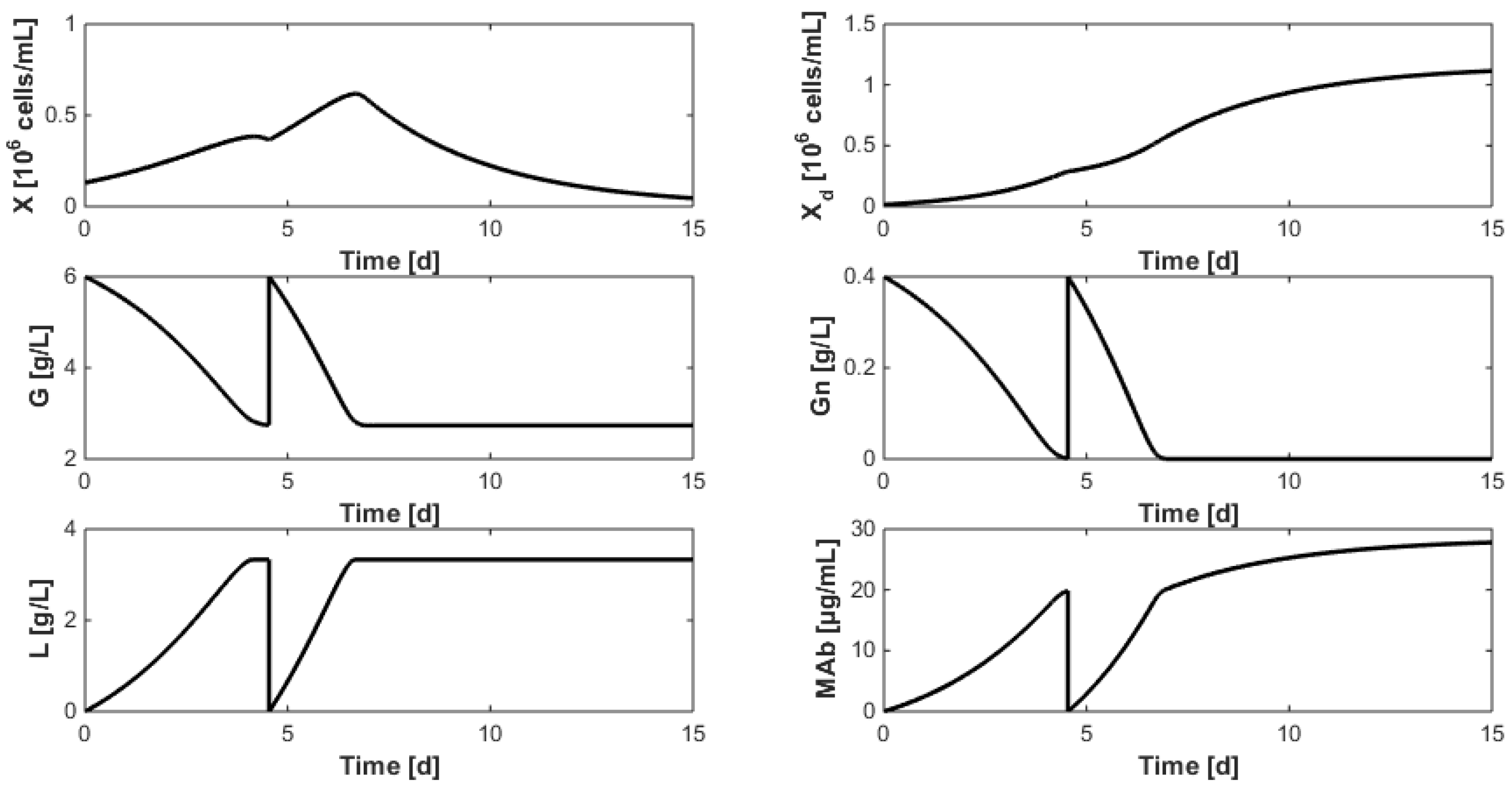
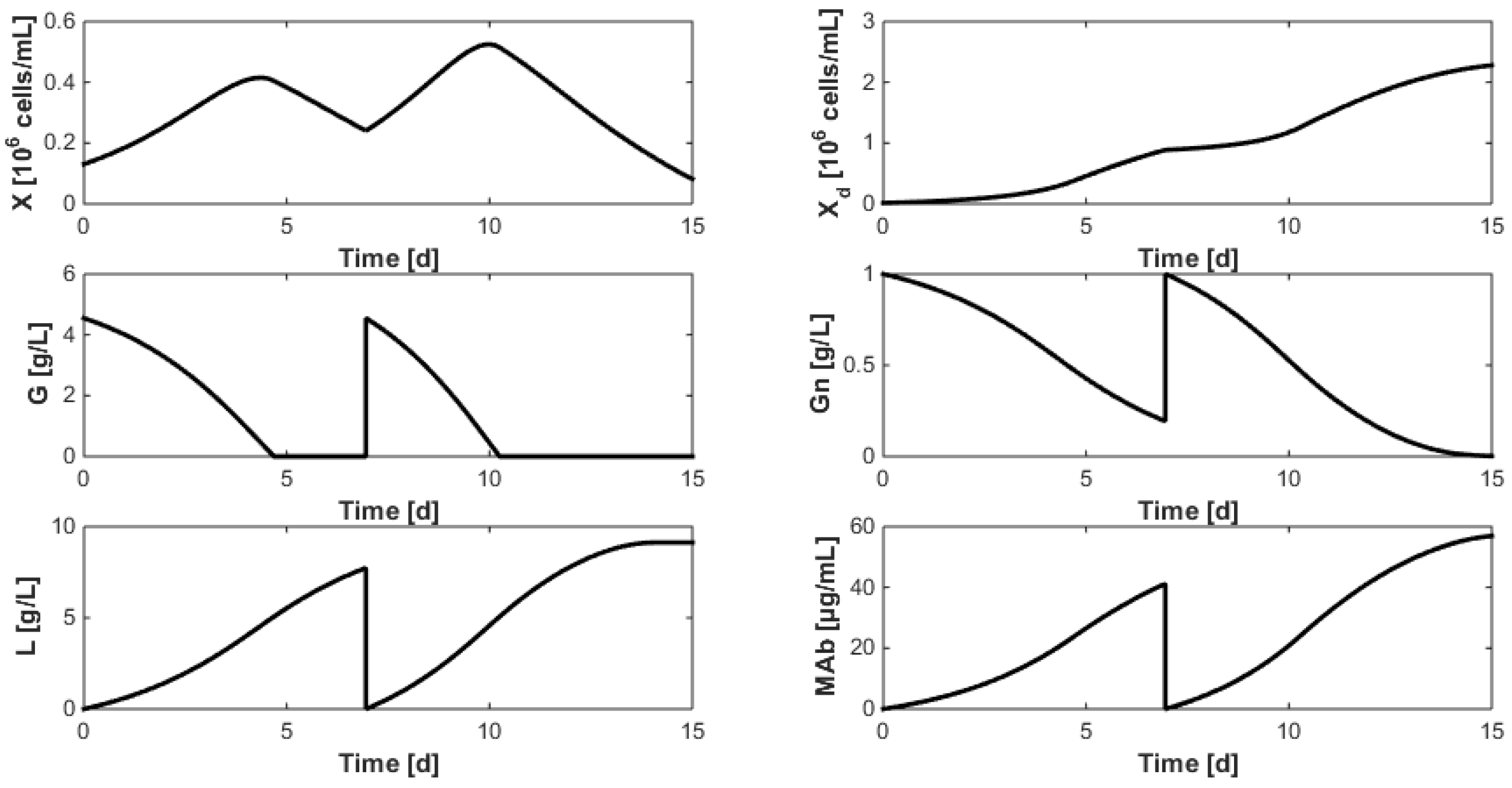
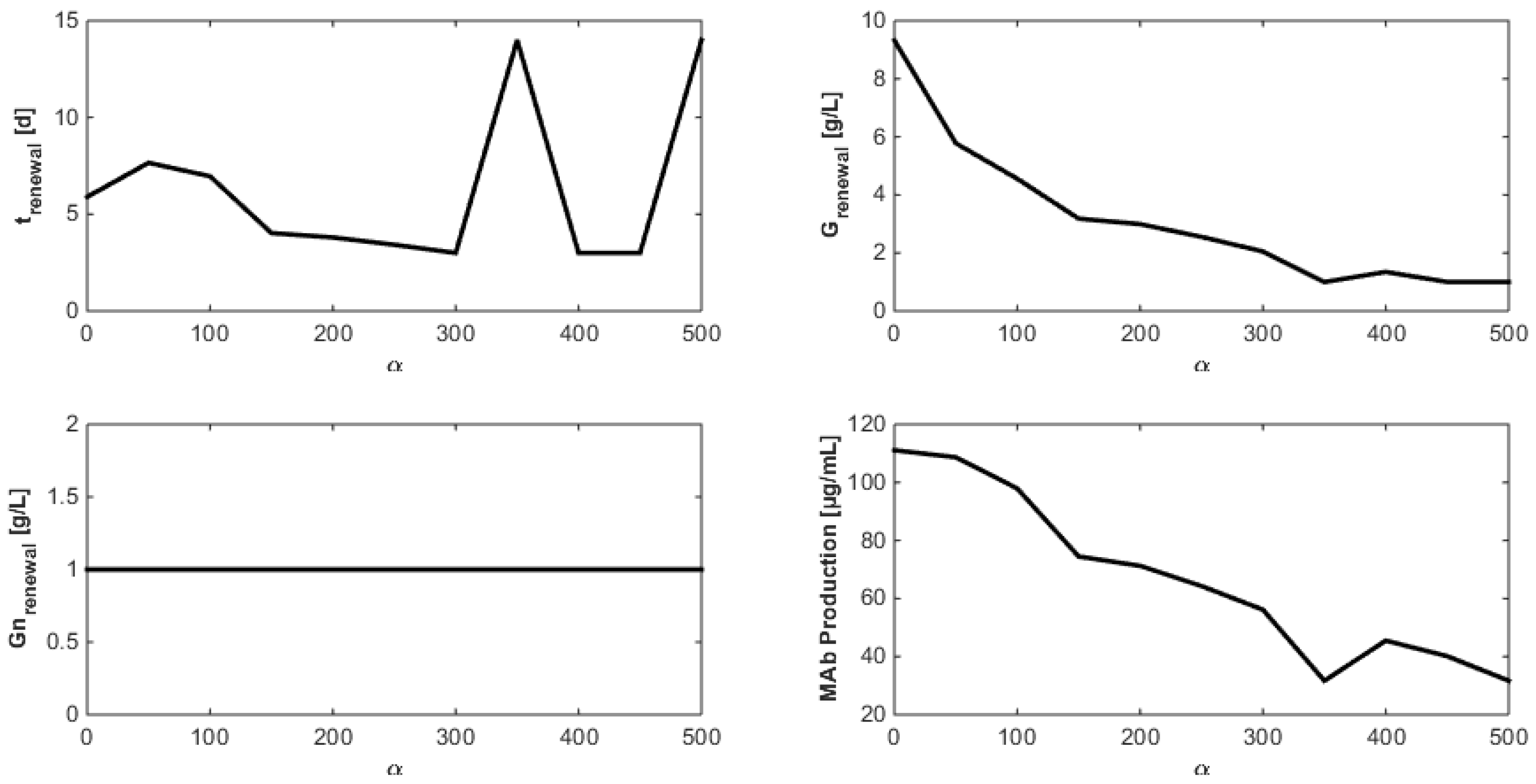
8. Optimization of the Monoclonal Antibody Production
- Even when considering substrate savings, the upper bound of Gnrefresh is reached. Indeed, when G is depleted, Gn still limits biomass decay and therefore maintains an efficient MAb production rate. However, since ammonium production (byproduct formed by glutamine overflow) is not considered in the model obtained in Section 7, higher values of Gnrefresh are not recommended.
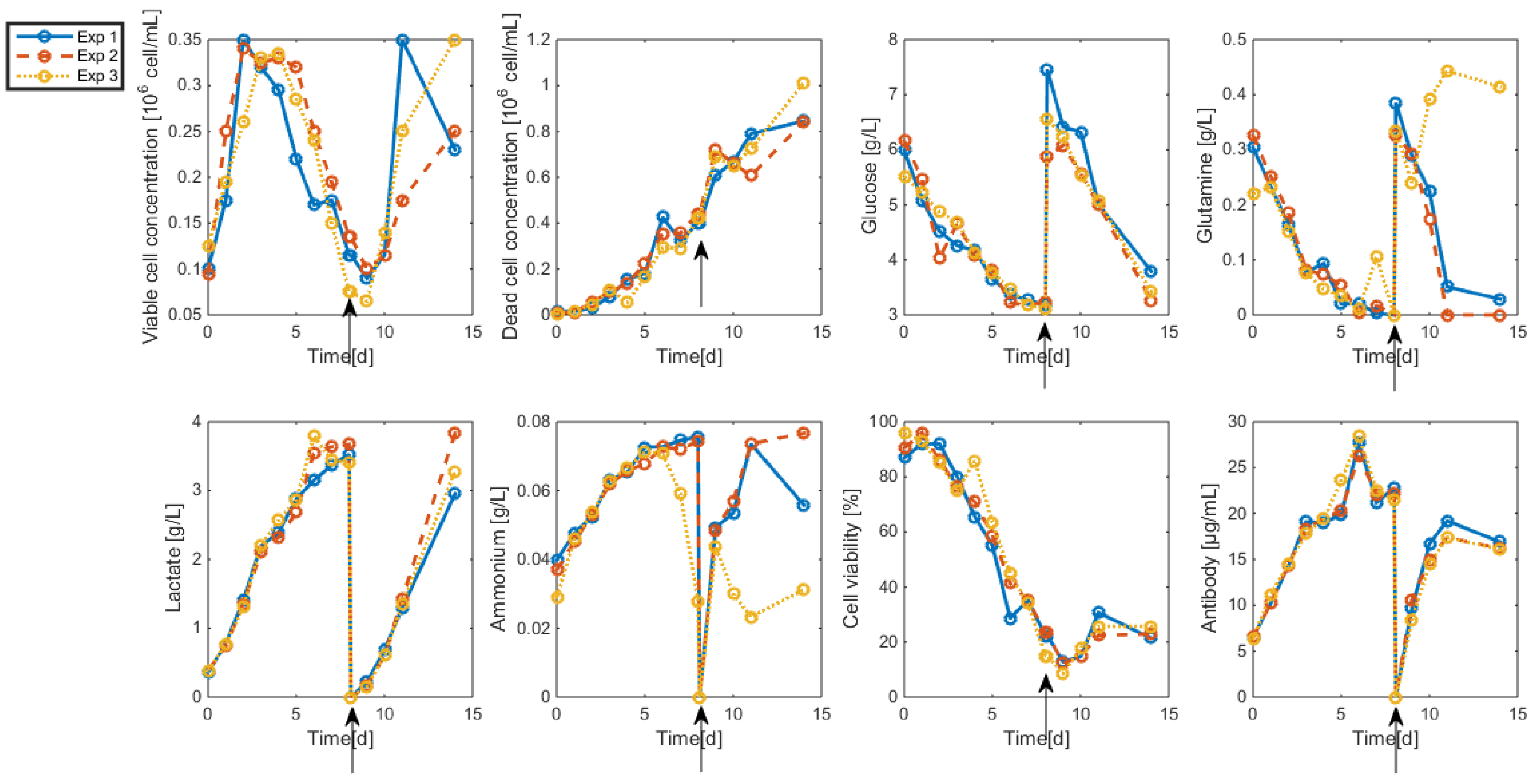
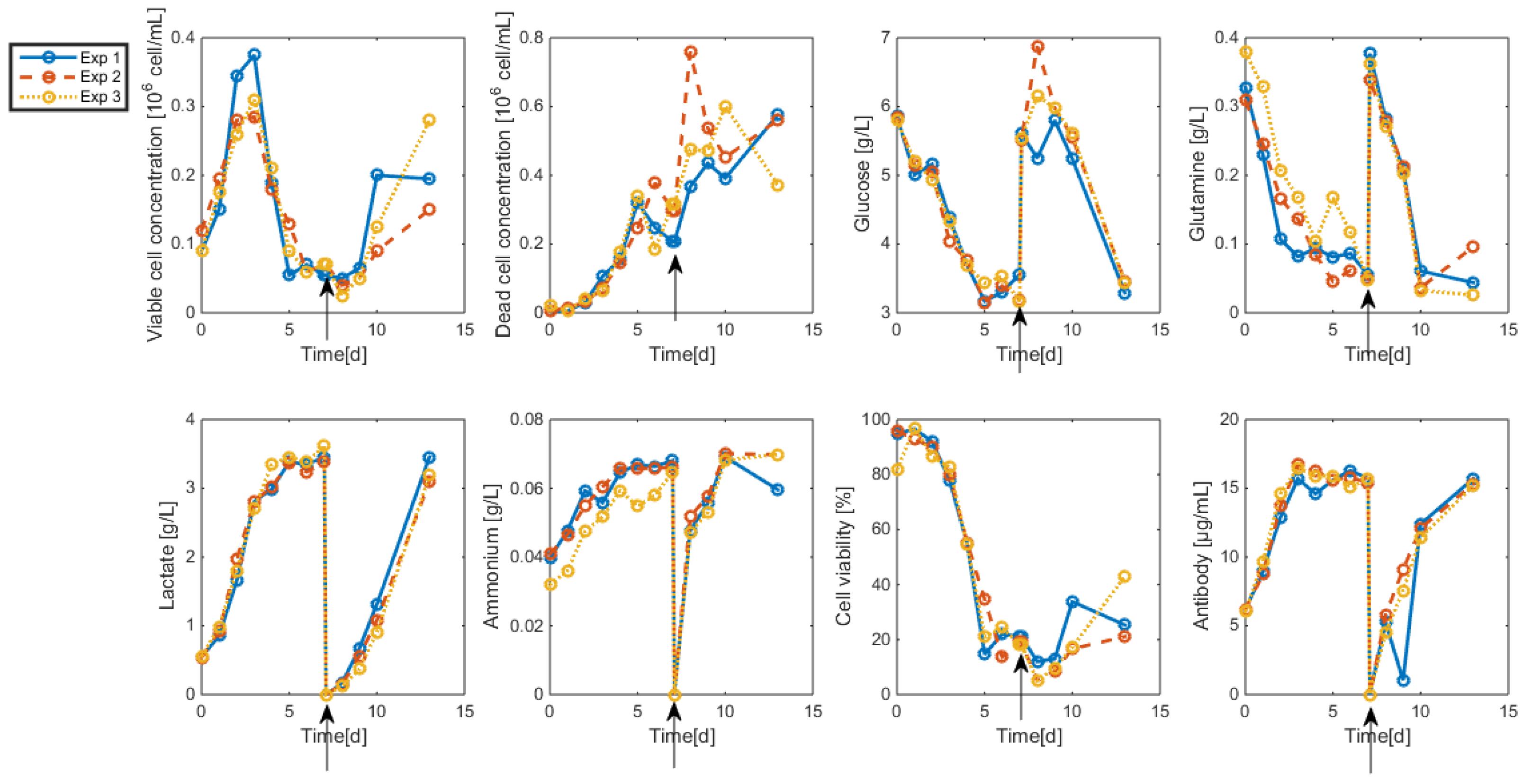
- Interestingly, approximately the same renewal time as in Figure 2 is obtained, which means that these experiments could be “economically” optimized only by revising the medium composition.
9. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| 0.5559 | 0.1410 | 0.1456 | 0.0224 | 2.1895 | 0.1922 | 0.7028 | 2.4175 | 6.0250 | 1.2867 | 0.5061 | 10.6769 | 119.7005 | 7.6599 |
| 0.5880 | 0.2670 | 0.0451 | 0.0162 | 1.9315 | 1.1321 | 0.7073 | 2.3867 | 6.6606 | 0.7739 | 0.6705 | 14.6022 | 68.0054 | 7.7126 |
| 0.5547 | 0.1500 | 0.0115 | 0.0094 | 1.2845 | 1.2627 | 0.9401 | 4.2541 | 4.4612 | 0.4948 | 0.8604 | 9.6828 | 114.3043 | 9.5609 |
| 0.5473 | 0.1429 | 0.0280 | 0.0145 | 1.9152 | 0.3041 | 0.7235 | 2.8453 | 6.0009 | 0.7705 | 0.7854 | 10.3002 | 122.0962 | 10.2667 |
| 0.6058 | 0.0611 | 0.0526 | 0.0413 | 0.8423 | 0.9630 | 1.2922 | 4.2558 | 5.7751 | 2.0796 | 0.5338 | 8.1830 | 234.9037 | 14.3253 |
| 0.5626 | 0.1100 | 0.0521 | 0.0286 | 0.9322 | 0.3854 | 1.2512 | 3.2340 | 5.6626 | 1.5257 | 0.4498 | 9.6220 | 161.7081 | 4.3626 |
| 0.5887 | 0.2774 | 0.0273 | 0.0170 | 2.3108 | 1.7476 | 0.6160 | 2.7446 | 8.1550 | 0.8308 | 0.5936 | 15.0889 | 62.0973 | 10.5890 |
| 0.6303 | 0.1737 | 0.0988 | 0.0229 | 2.0640 | 2.0451 | 0.6517 | 2.7454 | 6.1184 | 1.0883 | 0.5328 | 10.1684 | 94.7350 | 13.3752 |
| 0.6139 | 0.2062 | 0.1491 | 0.0195 | 1.0761 | 1.6163 | 1.0645 | 2.8275 | 6.4991 | 0.9660 | 0.5718 | 11.4731 | 78.7716 | 13.9319 |
| 0.5195 | 0.2916 | 0.0223 | 0.0061 | 2.5413 | 0.3398 | 0.6242 | 3.9897 | 5.4858 | 0.3507 | 1.5180 | 18.3348 | 65.0805 | 5.7034 |
| 0.2676 | 0.5515 | 0.0170 | 0.0123 | 1.8476 | 1.9618 | 0.1667 | 3.5684 | 13.6956 | 1.4072 | 1.3057 | 15.4667 | 107.3452 | 17.9771 |
| 0.6048 | 0.1698 | 0.0305 | 0.0232 | 2.0572 | 0.7868 | 0.6622 | 3.5670 | 5.3198 | 1.1648 | 0.5179 | 10.4758 | 104.5675 | 9.7748 |
| 0.5868 | 0.1808 | 0.0329 | 0.0219 | 2.4127 | 1.7841 | 0.6059 | 3.3243 | 5.3469 | 1.0981 | 0.4273 | 10.7470 | 94.6231 | 7.8496 |
| 0.5865 | 0.1951 | 0.0285 | 0.0185 | 1.1563 | 0.6525 | 1.0732 | 2.5100 | 4.3891 | 0.8773 | 0.6274 | 11.3024 | 98.2351 | 3.4642 |
| 0.5287 | 0.2558 | 0.0744 | 0.0099 | 2.4822 | 2.1080 | 0.6520 | 5.1365 | 4.3431 | 0.6706 | 0.8310 | 16.4441 | 59.0160 | 12.3303 |
| 0.9859 | 0.6572 | 0.0100 | 0.1800 | 5.7454 | 2.3415 | 0.3338 | 7.0345 | 0.2045 | 0.8892 | 0.0953 | 0.0064 | 50.4414 | 0.0511 |
| 0.5609 | 0.2443 | 0.0260 | 0.0116 | 0.8086 | 0.6322 | 1.3976 | 2.7069 | 6.8815 | 0.5485 | 0.9639 | 13.8020 | 76.5734 | 6.3556 |
| 0.6099 | 0.0984 | 0.1118 | 0.0176 | 2.1902 | 1.6137 | 0.6266 | 2.4999 | 5.1055 | 0.8327 | 0.7344 | 8.4616 | 146.6756 | 18.1001 |
| 0.6311 | 0.1634 | 0.0090 | 0.0452 | 1.2904 | 1.3282 | 0.8407 | 0.5745 | 9.7854 | 1.9713 | 0.1358 | 10.8829 | 126.9890 | 0.2194 |
| 0.5854 | 0.1725 | 0.1799 | 0.0251 | 1.7937 | 0.2995 | 0.7516 | 2.8422 | 6.3408 | 1.2724 | 0.4102 | 11.3594 | 101.7783 | 8.0611 |
| 0.3523 | 0.1682 | 0.2644 | 0.0147 | 0.2683 | 0.2306 | 0.3314 | 3.5112 | 17.5043 | 0.9900 | 1.5072 | 27.5654 | 98.4703 | 16.7248 |
| 0.5577 | 0.3183 | 0.0328 | 0.0073 | 1.6475 | 1.3849 | 0.8834 | 2.8735 | 5.5942 | 0.4435 | 1.1310 | 17.5563 | 6.7974 | 47.0452 |
| 0.6057 | 0.2115 | 0.0757 | 0.0163 | 1.5704 | 1.5814 | 0.8071 | 2.4129 | 5.6236 | 0.7583 | 0.6688 | 11.0633 | 87.1816 | 7.4376 |
| 0.5954 | 0.1964 | 0.0197 | 0.0171 | 1.2385 | 0.7389 | 0.9992 | 2.3813 | 5.4283 | 0.7576 | 0.7362 | 11.0359 | 100.4704 | 3.6202 |
| 0.5482 | 0.2715 | 0.0400 | 0.0182 | 1.5790 | 0.2627 | 0.8576 | 6.9704 | 1.5800 | 1.0154 | 0.3502 | 17.0623 | 67.7835 | 6.2548 |
| 3.6662 | 22.6437 | 130.2128 | 17.8640 | 49.5212 | 13.2501 | 31.2599 | 120.2970 | 24.7702 | 21.8237 | 16.9119 | 10.8063 | 22.3173 | 22.0970 |
| 3.1545 | 11.4168 | 361.2676 | 18.2503 | 55.3056 | 40.4276 | 36.8463 | 57.3265 | 26.6477 | 11.5497 | 15.0769 | 12.9871 | 11.3732 | 22.5188 |
| 2.7529 | 27.1667 | 1181.2541 | 23.8344 | 46.7243 | 43.2328 | 34.3950 | 73.5869 | 32.0299 | 30.7479 | 11.1012 | 12.1905 | 27.1262 | 20.1369 |
| 3.6238 | 24.3889 | 720.1689 | 20.7425 | 59.3874 | 18.0344 | 39.2357 | 103.7392 | 24.0107 | 24.4068 | 11.3759 | 11.0635 | 24.1557 | 17.9644 |
| 5.1282 | 46.0975 | 628.3497 | 18.5780 | 114.7653 | 46.7917 | 93.0397 | 126.2801 | 16.7504 | 42.9210 | 10.6211 | 8.0060 | 45.4639 | 15.6957 |
| 3.6607 | 27.9484 | 379.5510 | 17.5197 | 73.0553 | 20.8103 | 57.9583 | 107.1231 | 22.6208 | 26.9998 | 16.0283 | 9.7616 | 27.6345 | 44.1384 |
| 3.0754 | 11.0214 | 574.9346 | 18.7735 | 51.3645 | 61.7058 | 31.3976 | 48.8369 | 23.7644 | 10.9953 | 17.3372 | 13.4790 | 10.9730 | 16.2965 |
| 3.7369 | 19.7116 | 211.5824 | 17.6190 | 54.5606 | 71.9202 | 34.9982 | 83.7420 | 21.9111 | 18.2301 | 14.1168 | 10.5920 | 19.4313 | 13.2615 |
| 3.8635 | 16.5377 | 145.3122 | 18.6602 | 84.8642 | 60.1199 | 65.9035 | 69.0624 | 23.7561 | 15.6449 | 15.0802 | 11.7848 | 16.3232 | 12.8728 |
| 2.5121 | 10.8171 | 546.0726 | 24.6565 | 49.0097 | 18.0168 | 29.2449 | 32.5452 | 39.8743 | 17.6116 | 15.2724 | 16.7534 | 10.9220 | 30.5888 |
| 3.5450 | 19.6658 | 640.1403 | 17.3780 | 54.9197 | 32.1188 | 35.3471 | 67.2044 | 25.6640 | 18.4603 | 15.0928 | 10.6327 | 19.3963 | 17.6762 |
| 3.9618 | 18.6565 | 667.0940 | 18.3143 | 57.4314 | 68.1850 | 34.5779 | 65.4403 | 26.6676 | 17.9300 | 18.1388 | 11.5034 | 18.5005 | 24.8874 |
| 3.4707 | 16.9881 | 644.5080 | 17.9580 | 71.5894 | 26.5994 | 55.1697 | 79.9299 | 32.5613 | 16.7107 | 13.7367 | 11.4200 | 16.8977 | 52.9654 |
| 4.2695 | 14.5552 | 280.6340 | 24.0336 | 59.1986 | 67.5103 | 36.0739 | 34.9784 | 50.1691 | 15.7086 | 18.0133 | 17.5370 | 14.6961 | 16.8627 |
| 3.0381 | 13.3080 | 609.3884 | 20.3656 | 87.6372 | 27.4640 | 72.0226 | 57.3727 | 25.6625 | 15.4098 | 12.4396 | 13.1777 | 13.3089 | 27.3362 |
| 3.7332 | 36.3680 | 186.6357 | 20.3580 | 49.4555 | 58.1809 | 31.1673 | 159.1482 | 21.3178 | 32.7821 | 9.1231 | 9.4398 | 35.9587 | 11.4881 |
| 3.3887 | 16.9274 | 1933.8346 | 15.1813 | 69.0932 | 49.6417 | 50.7343 | 401.5180 | 14.7875 | 16.6962 | 52.5206 | 9.3112 | 16.6627 | 722.5528 |
| 3.5640 | 17.3184 | 110.6870 | 17.5278 | 61.0394 | 17.2553 | 41.0509 | 77.7436 | 23.3178 | 16.9096 | 19.8023 | 10.6291 | 17.0292 | 21.2591 |
| 3.2513 | 12.6435 | 484.7580 | 27.1346 | 58.2372 | 46.5384 | 40.9441 | 46.2395 | 44.1952 | 15.8306 | 17.7920 | 20.7195 | 25.5029 | 4.2209 |
| 3.4716 | 16.2920 | 247.1369 | 18.5861 | 60.9806 | 55.8643 | 43.1792 | 76.6727 | 26.1026 | 16.0291 | 12.9251 | 11.8084 | 16.2252 | 24.4574 |
| 3.2776 | 16.8715 | 871.4772 | 17.9683 | 61.5156 | 28.8860 | 46.3341 | 82.1495 | 25.7187 | 16.8224 | 11.7135 | 11.0761 | 16.8066 | 49.3217 |
| 3.0620 | 10.1596 | 397.7225 | 18.8584 | 77.1272 | 16.8420 | 54.2770 | 20.9435 | 121.3063 | 10.1811 | 31.2955 | 13.8143 | 9.9632 | 24.4122 |
References
- De Tremblay, M.; Perrier, M.; Chavarie, C.; Archambault, J. Optimization of fed-batch culture of hybridoma cells using dynamic programming: Single and multi-feed cases. Bioprocess. Biosyst. Eng. 1992, 7, 229–234. [Google Scholar] [CrossRef]
- Dhir, S.; Morrow, K.J., Jr.; Rhinehart, R.R.; Wiesne, T. Dynamic optimization of hybridoma growth in a fed-batch bioreactor. Biotechnol. Bioeng. 2000, 67, 197–205. [Google Scholar] [CrossRef]
- Amribt, Z.; Niu, H.; Bogaerts, P. Macroscopic modelling of over_ow metabolism and model based optimization of hybridoma cell fed-batch cultures. Biochem. Eng. J. 2013, 70, 196–209. [Google Scholar] [CrossRef]
- Crabtree, H. Observations on the carbohydrate metabolism of tumors. Biochem. J. 1929, 23, 536–545. [Google Scholar] [CrossRef] [PubMed]
- Bernard, O.; Bastin, G. On the estimation of the pseudo stoichiometric matrix for macroscopic mass balance modelling of biotechnological processes. Math. Biosci. 2005, 193, 51–77. [Google Scholar] [CrossRef] [PubMed]
- Mailier, J.; Remy, M.; Vande Wouwer, A. Stoichiometric identi_cation with maximum likelihood principal component analysis. J. Math. Biol. 2013, 67, 739–765. [Google Scholar] [CrossRef] [PubMed]
- Deken, R.H.D. The crabtree effect: A regulatory system in yeast. J. Gen. Microbiol. 1966, 44, 149–156. [Google Scholar] [CrossRef] [PubMed]
- Rocha, I. Model-Based Strategies for Computer-Aided Operation of Recombinant E. coli Fermentation. Ph.D. Thesis, Universidade do Minho, Braga, Portugal, 2003. [Google Scholar]
- Vemuri, G.N.; Altman, E.; Sangurdekar, D.P.; Khodursky, A.B.; Eiteman, M.A. Overflow metabolism in escherichia coli during steady-state growth: Transcriptional regulation and effect of the redox ratio. Appl. Environ. Microbiol. 2006, 72, 3653–3661. [Google Scholar] [CrossRef] [PubMed]
- Vemuri, G.N.; Eiteman, M.A.; McEwen, J.E.; Olsson, L.; Nielsen, J. Increasing nadh oxidation reduces overflow metabolism in saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA 2007, 104, 2402–2407. [Google Scholar] [CrossRef] [PubMed]
- Cappuyns, A.M.; Bernaerts, K.; Vanderleyden, J.; Impe, J.F.V. A dynamicmodel for diauxic growth, overflowmetabolism, and al-2-mediated cell-cell communication of salmonella typhimurium based on systems biology concepts. Biotechnol. Bioeng. 2009, 102, 280–293. [Google Scholar] [CrossRef] [PubMed]
- Sonnleitner, B.; Käppeli, O. Growth of Saccharomyces cerevisiae is controlled by its limited respiratory capacity: Formulation and verification of a hypothesis. Biotechnol. Bioeng. 1986, 28, 927–937. [Google Scholar] [CrossRef] [PubMed]
- Valentinotti, S.; Srinivasan, B.; Holmberg, U.; Bonvin, D.; Cannizzaro, C.; Rhiel, M.; von Stockar, U. Optimal operation of fed-batch fermentations via adaptive control of overflow metabolite. Control Eng. Pract. 2003, 11, 665–674. [Google Scholar] [CrossRef]
- Renard, F.; Vande Wouwer, A.; Valentinotti, S.; Dumur, D. A practical robust control scheme for yeast fed-batch cultures—An experimental validation. J. Process Control 2006, 16, 855–864. [Google Scholar] [CrossRef]
- Dewasme, L.; Richelle, A.; Dehottay, P.; Georges, P.; Remy, M.; Bogaerts, Ph.; Vande Wouwer, A. Linear robust control of S. cerevisiae fed-batch cultures at differentscales. Biochem. Eng. J. 2010, 53, 26–37. [Google Scholar] [CrossRef]
- Veloso, A.C.A.; Rocha, I.; Ferreira, E.C. Monitoring of fed-batch E. coli fermentations with software sensors. Bioprocess Biosyst. Eng. 2009, 32, 381–388. [Google Scholar] [CrossRef] [PubMed]
- Dewasme, L.; Goffaux, G.; Hantson, A.-L.; Vande Wouwer, A. Experimental validation of an extended Kalman filter estimating acetate concentration in E. coli cultures. J. Process Control 2013, 23, 148–157. [Google Scholar] [CrossRef]
- Bastin, G.; Dochain, D. On-Line Estimation and Adaptive Control of Bioreactors, Volume 1 of Process Measurement and Control; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Mahalanobis, P.C. On the generalized distance in statistics. Proc. Natl. Inst. Sci. India 1936, 2, 49–55. [Google Scholar]
- Rao, C.R. Information and the Accuracy Attainable in the Estimation of Statistical Parameters; Bulletin of the Calcutta Mathematical Society: Kolkata, India, 1945; Volume 37, pp. 81–89. [Google Scholar]

| Kinetic Parameters/Min–Max Values | Minimum Initial Value | Maximum Initial Value |
|---|---|---|
| 0.1 h−1 | 1 h−1 | |
| 0.1 h−1 | 1 h−1 | |
| 0.01 g/L | 1 g/L | |
| 0.01 g/L | 1 g/L | |
| 0.1 g/L | 10 g/L | |
| 0.1 g/L | 10 g/L | |
| 0.1 h−1 | 1 h−1 |
| Parameter | Relative Error Standard Deviation | |
|---|---|---|
| 0.4849 | 1.7652 | |
| 0.3198 | 8.1283 | |
| 0.0089 | 23.2540 | |
| 1.5899 | 15.4666 | |
| 1.3359 | 49.2893 | |
| 0.8667 | 66.5216 | |
| 3.1207 | 34.1265 | |
| 15.2090 | 26.3604 | |
| 0.6245 | 9.5667 | |
| 1.2221 | 19.2377 | |
| 23.9586 | 20.3273 | |
| 43.5907 | 8.3527 | |
| 14.2221 | 10.9999 |
| Runs | Min J | Max J | J Mean | J Std Deviation |
|---|---|---|---|---|
| 100 | 1.3412 | 1.6225 | 1.4050 | 0.0576 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dewasme, L.; Côte, F.; Filee, P.; Hantson, A.-L.; Vande Wouwer, A. Macroscopic Dynamic Modeling of Sequential Batch Cultures of Hybridoma Cells: An Experimental Validation. Bioengineering 2017, 4, 17. https://doi.org/10.3390/bioengineering4010017
Dewasme L, Côte F, Filee P, Hantson A-L, Vande Wouwer A. Macroscopic Dynamic Modeling of Sequential Batch Cultures of Hybridoma Cells: An Experimental Validation. Bioengineering. 2017; 4(1):17. https://doi.org/10.3390/bioengineering4010017
Chicago/Turabian StyleDewasme, Laurent, François Côte, Patrice Filee, Anne-Lise Hantson, and Alain Vande Wouwer. 2017. "Macroscopic Dynamic Modeling of Sequential Batch Cultures of Hybridoma Cells: An Experimental Validation" Bioengineering 4, no. 1: 17. https://doi.org/10.3390/bioengineering4010017
APA StyleDewasme, L., Côte, F., Filee, P., Hantson, A.-L., & Vande Wouwer, A. (2017). Macroscopic Dynamic Modeling of Sequential Batch Cultures of Hybridoma Cells: An Experimental Validation. Bioengineering, 4(1), 17. https://doi.org/10.3390/bioengineering4010017









