Experimental Validation of Time-Explicit Ultrasound Propagation Models with Sound Diffusivity or Viscous Attenuation in Biological Tissues Using COMSOL Multiphysics
Abstract
1. Introduction
2. Theoretical Background
3. Materials and Methods
3.1. Experimental Characterization
3.2. Simulation Setup (COMSOL Multiphysics)
3.3. Post-Processing
4. Results and Discussion
4.1. Experimental Results
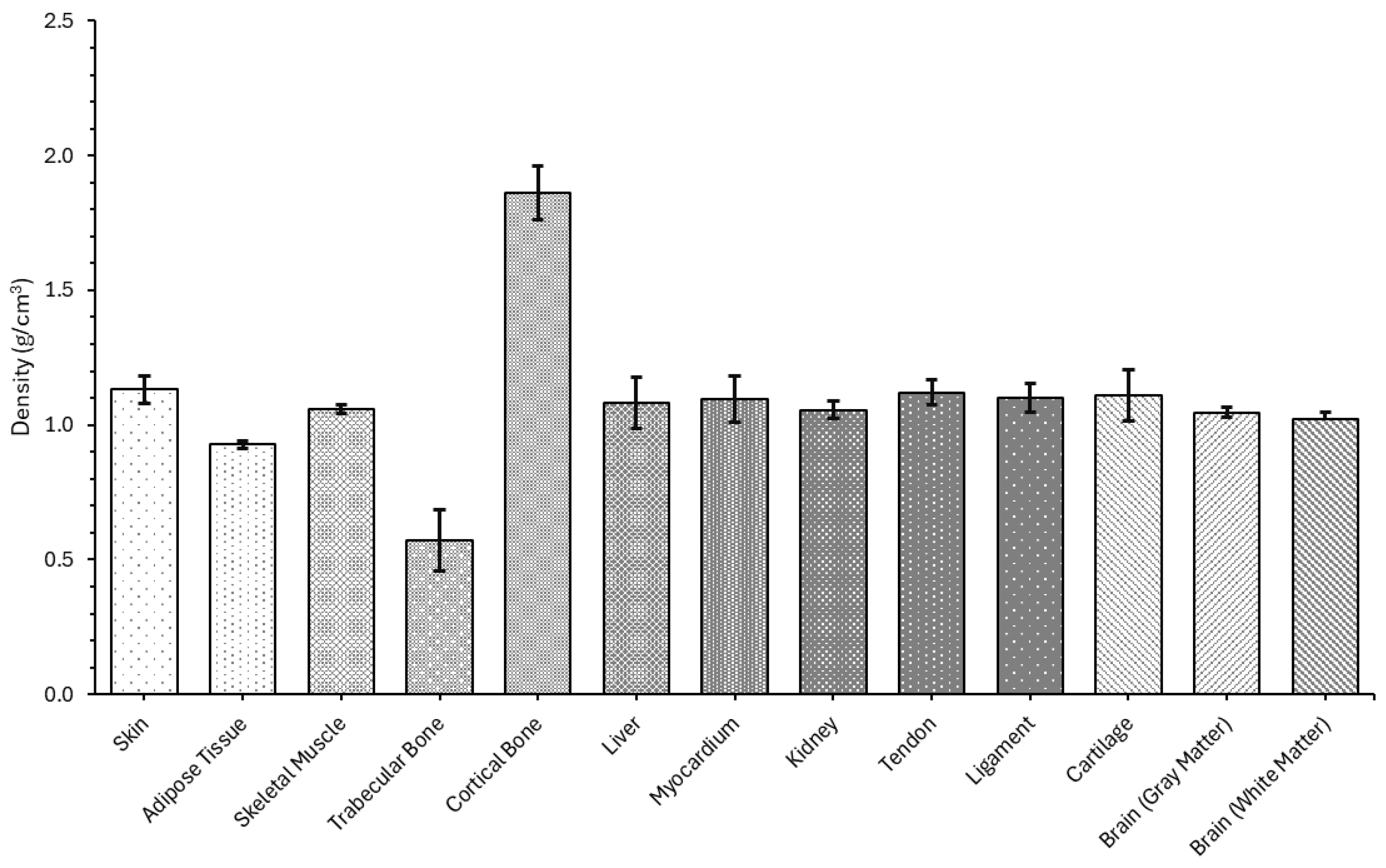
4.1.1. Density
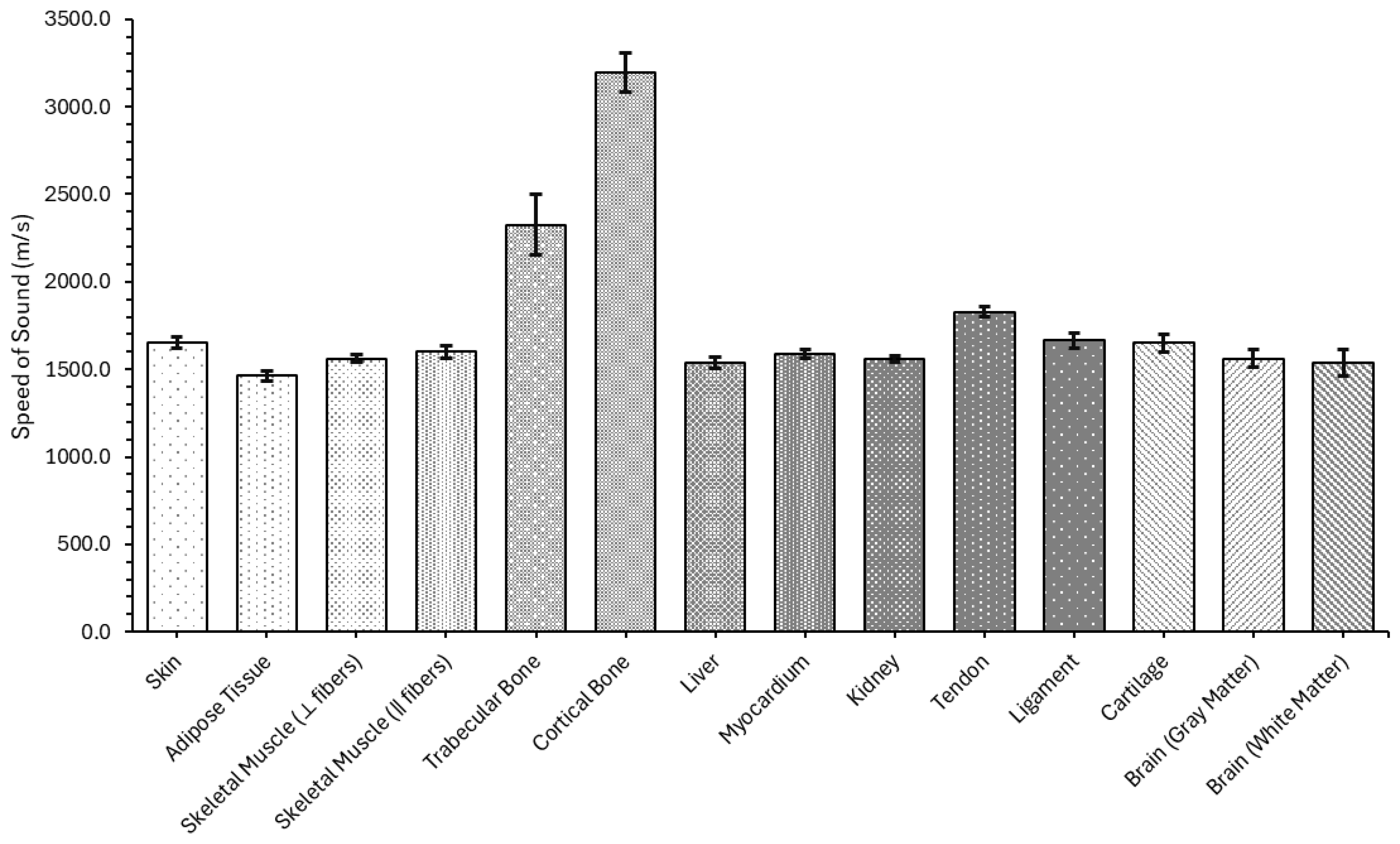
4.1.2. Speed of Sound
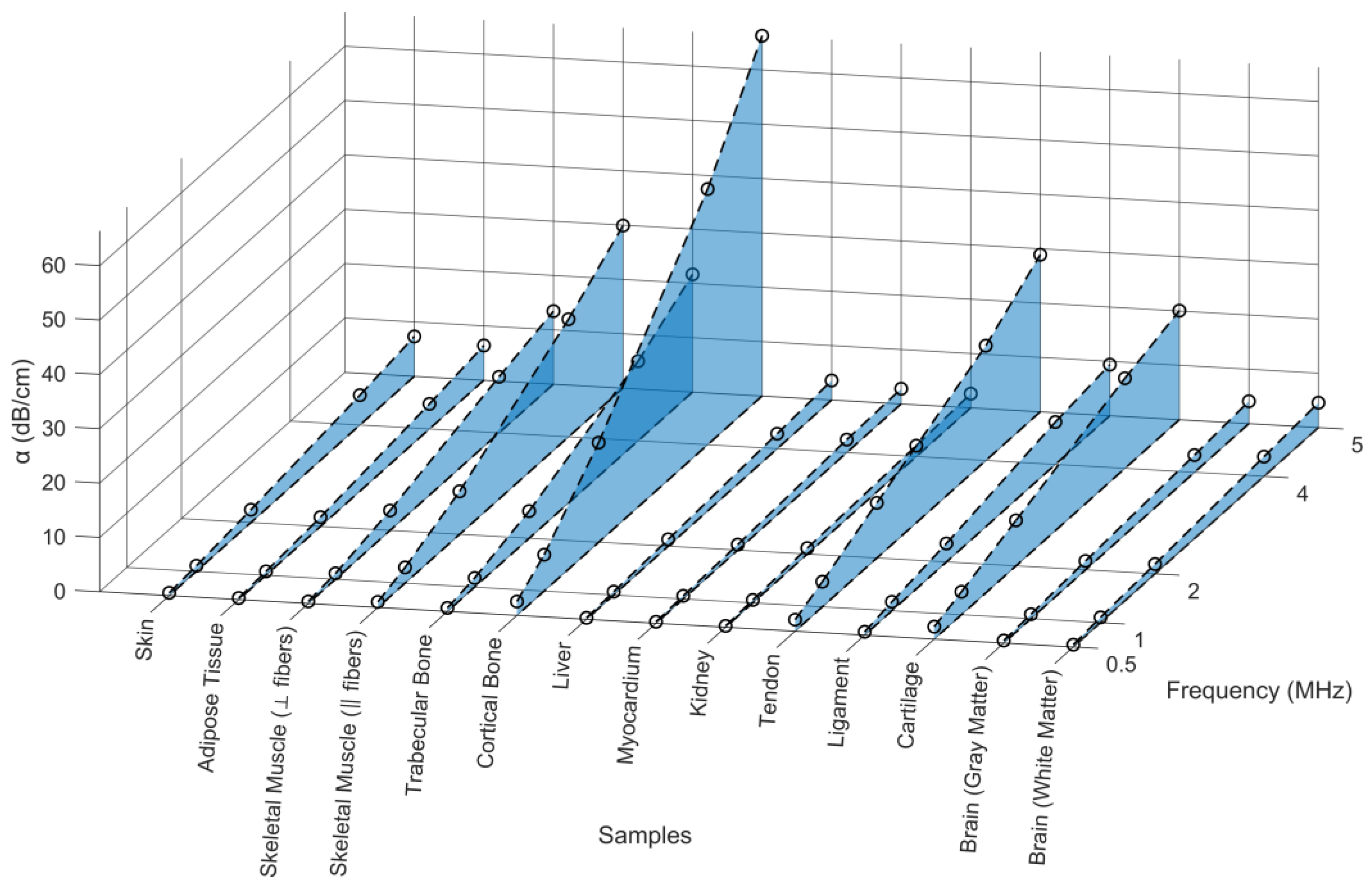
4.1.3. Acoustic Attenuation Coefficient
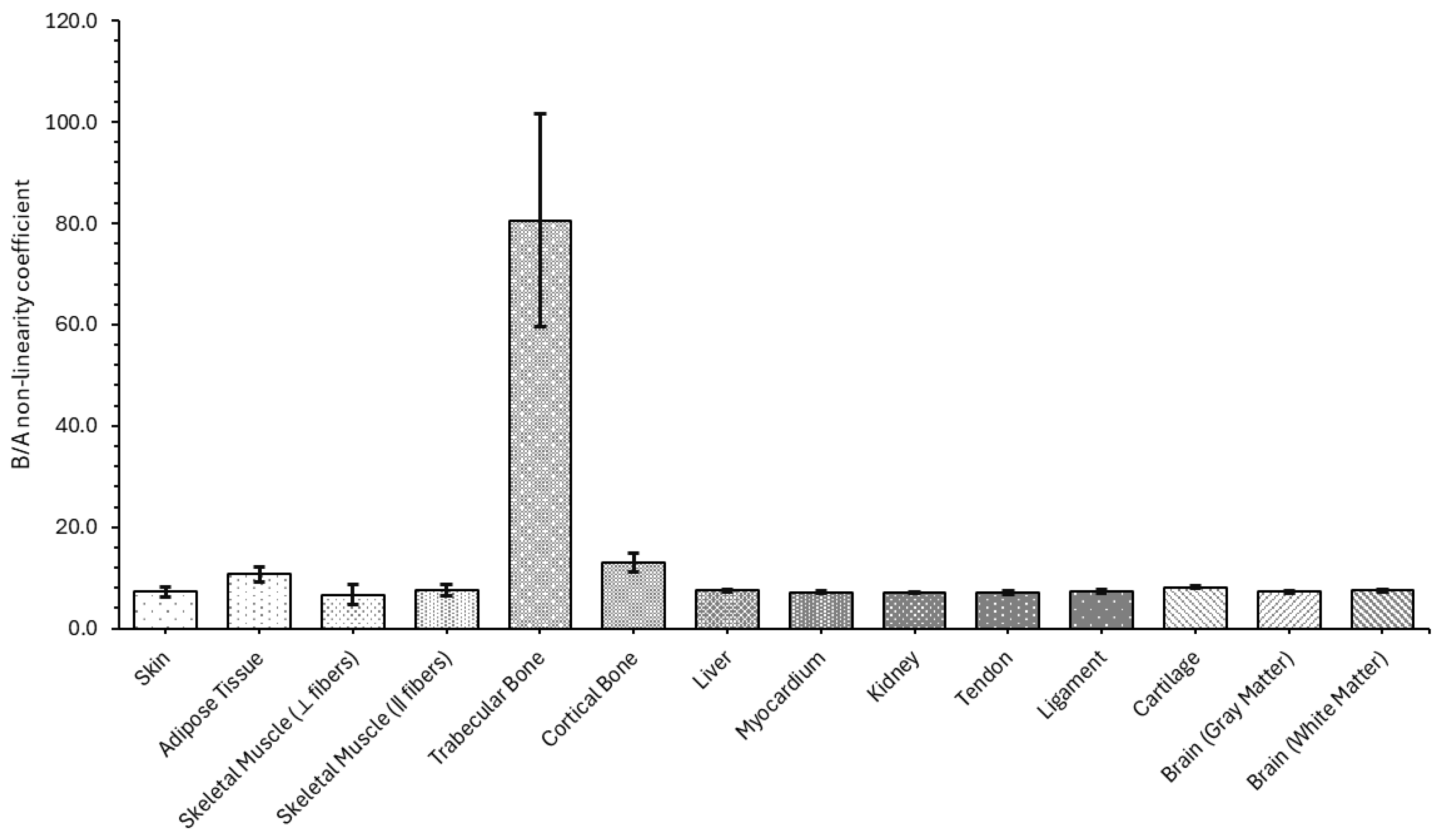
4.1.4. B/A Nonlinearity Coefficient
4.2. Computational Results
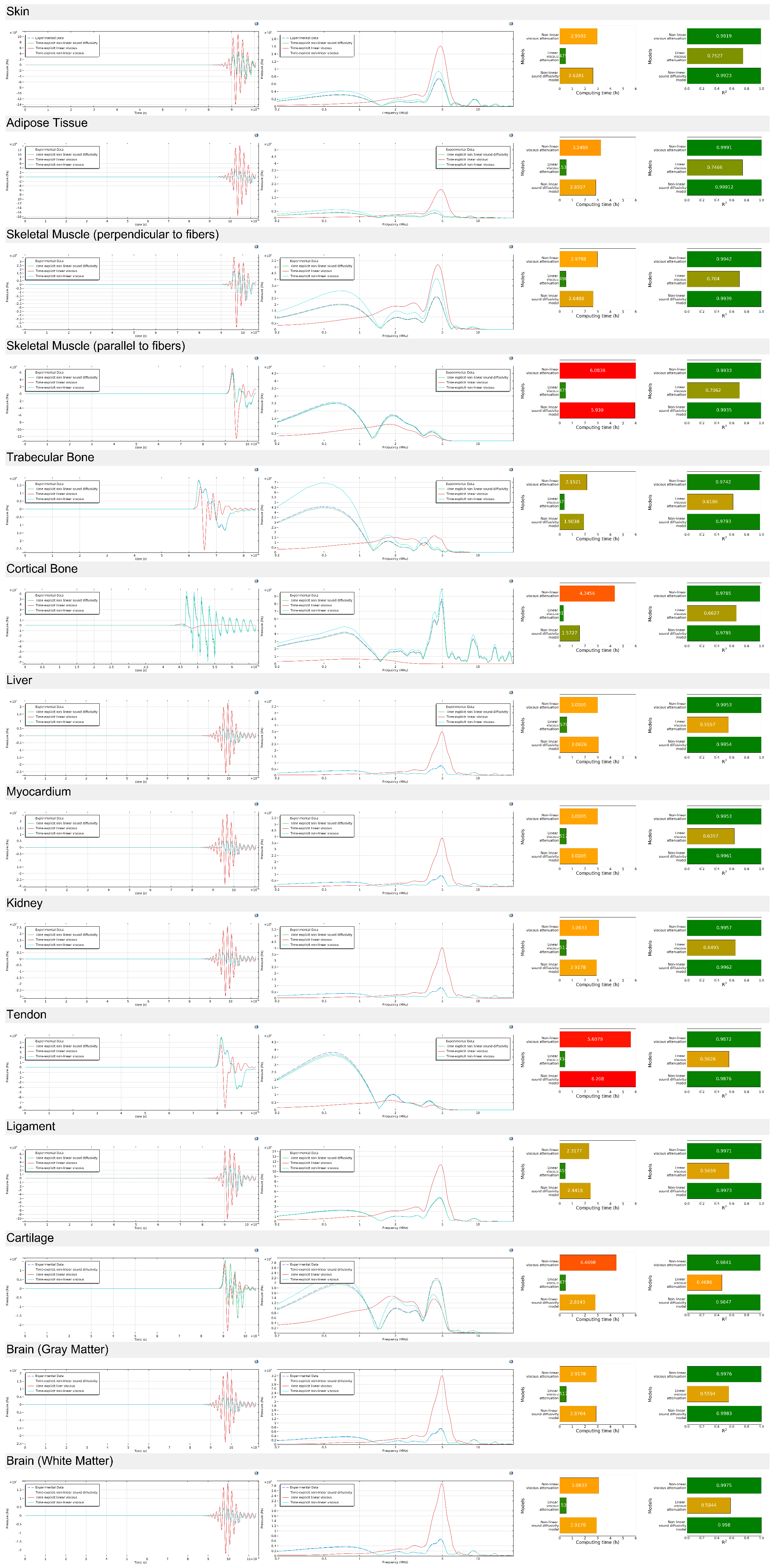
4.2.1. Acoustic Wave Propagation (0.5 Megahertz)
4.2.2. Acoustic Wave Propagation (5 Megahertz)
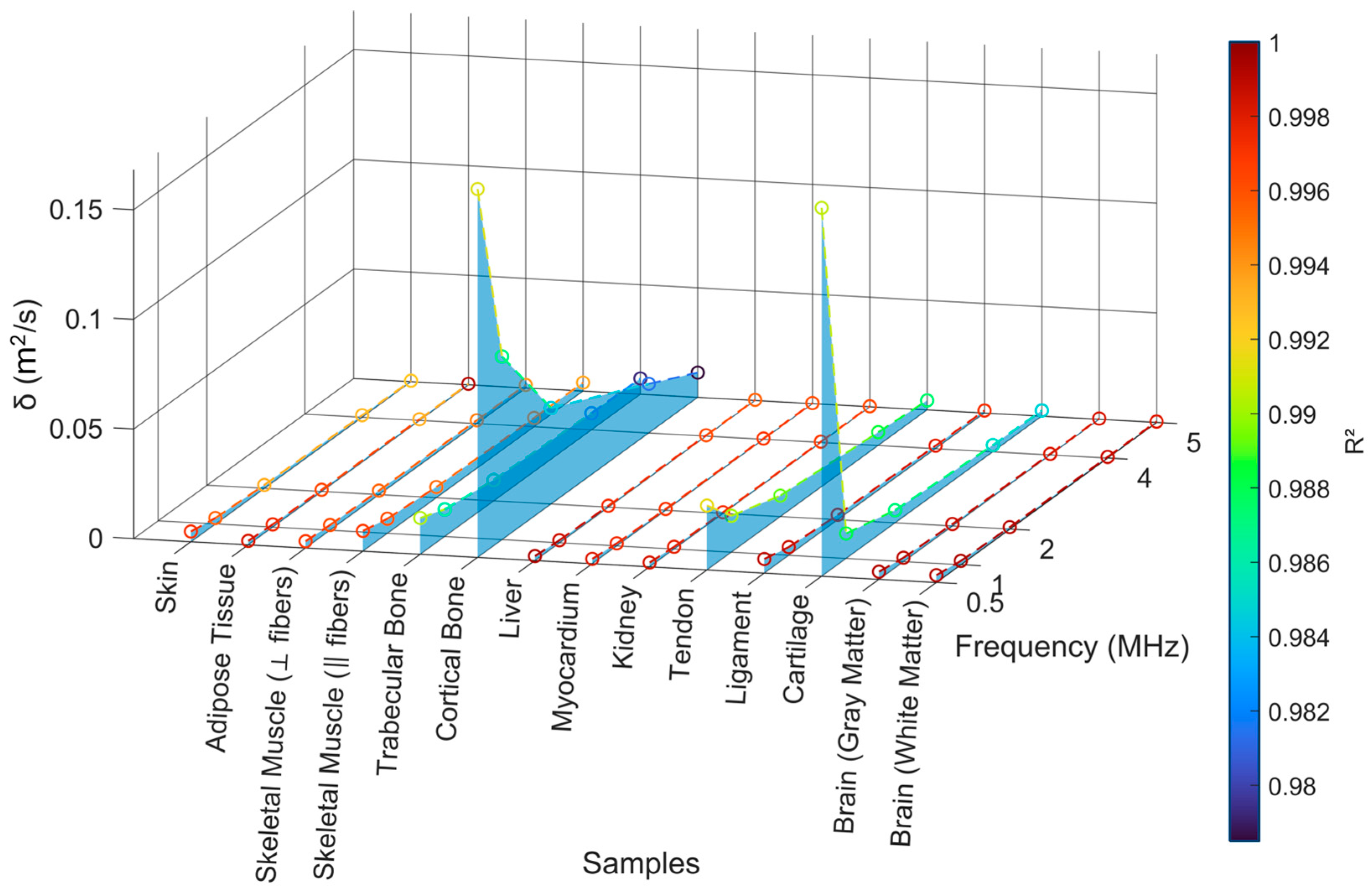
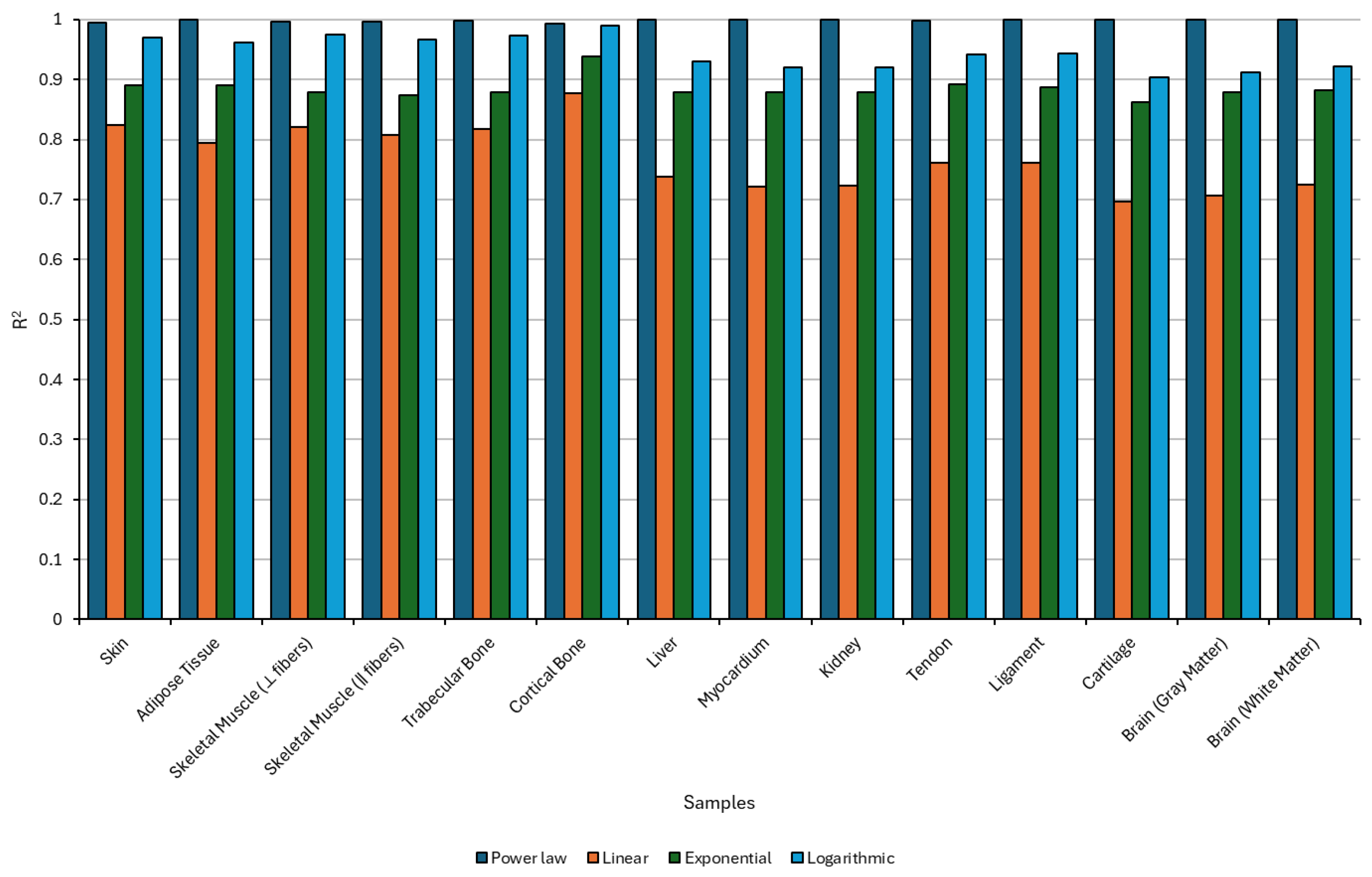
4.2.3. Sound Diffusivity Regression
4.2.4. Viscous Attenuation Regression
4.3. General Discusion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HIFU | High-Intensity Focused Ultrasound |
| LIPUS | Low-Intensity Pulsed Ultrasound |
| SoS | Speed of Sound |
| B/A | Non-Linearity Parameter |
Appendix A
Appendix A.1
| Sample | Density (g/cm3) |
|---|---|
| Skin | 1.13124 ± 0.05183 |
| Adipose Tissue | 0.927091 ± 0.01549 |
| Skeletal Muscle | 1.05775 ± 0.01573 |
| Trabecular Bone | 0.571999 ± 0.115192 |
| Cortical Bone | 1.86170 ± 0.10130 |
| Liver | 1.08368 ± 0.09560 |
| Myocardium | 1.09702 ± 0.08479 |
| Kidney | 1.05648 ± 0.03172 |
| Tendon | 1.12106 ± 0.04536 |
| Ligament | 1.10088 ± 0.05362 |
| Cartilage | 1.03345 ± 0.04336 |
| Brain (gray matter) | 1.04692 ± 0.01831 |
| Brain (white matter) | 1.02378 ± 0.02289 |
Appendix A.2
| Sample | Speed of Sound (m/s) |
|---|---|
| Skin | 1654.93 ± 32.82 |
| Adipose Tissue | 1461.77 ± 26.11 |
| Skeletal Muscle (⟂ fibers) | 1562.18 ± 20.76 |
| Skeletal Muscle (‖ fibers) | 1598.68 ± 34.34 |
| Trabecular Bone | 2325.38 ± 172.80 |
| Cortical Bone | 3193.95 ± 113.28 |
| Liver | 1539.69 ± 33.06 |
| Myocardium | 1585.83 ± 24.16 |
| Kidney | 1556.87 ± 17.38 |
| Tendon | 1827.43 ± 29.43 |
| Ligament | 1663.68 ± 42.29 |
| Cartilage | 1650.80 ± 51.95 |
| Brain (gray matter) | 1562.09 ± 53.55 |
| Brain (white matter) | 1538.46 ± 76.33 |
Appendix A.3
| Sample | (dB/cm) | ||||
|---|---|---|---|---|---|
| Skin | 0.521 ± 0.113 | 1.029 ± 0.217 | 2.356 ± 0.572 | 5.491 ± 1.118 | 7.323± 1.443 |
| Adipose Tissue | 0.301 ± 0.043 | 0.708 ± 0.161 | 1.721 ± 0.227 | 4.609 ± 0.814 | 6.391 ± 1.131 |
| Skeletal Muscle (⟂ fibers) | 0.397 ± 0.084 | 1.070 ± 0.264 | 3.663 ± 0.497 | 10.312 ± 1.650 | 13.432 ± 2.478 |
| Skeletal Muscle (‖ fibers) | 1.037 ± 0.181 | 2.894 ± 0.368 | 7.911 ± 0.802 | 21.647 ± 1.526 | 29.899 ± 1.970 |
| Trabecular Bone | 0.654 ± 0.105 | 1.679 ± 0.168 | 5.009 ± 0.457 | 14.641 ± 1.522 | 21.650 ± 2.652 |
| Cortical Bone | 2.562 ± 0.190 | 6.684 ± 0.844 | 18.335 ± 1.982 | 47.043 ± 6.160 | 66.284 ± 8.267 |
| Liver | 0.271 ± 0.007 | 0.604 ± 0.007 | 1.267 ± 0.020 | 2.754 ± 0.066 | 3.576 ± 0.074 |
| Myocardium | 0.273 ± 0.028 | 0.566 ± 0.116 | 1.021 ± 0.150 | 2.395 ± 0.303 | 2.785 ± 0.320 |
| Kidney | 0.242 ± 0.028 | 0.527 ± 0.109 | 1.104 ± 0.309 | 2.007 ± 0.591 | 2.600 ± 0.604 |
| Tendon | 2.119 ± 0.187 | 4.615 ± 0.464 | 10.161 ± 1.254 | 21.127 ± 2.563 | 28.890 ± 2.981 |
| Ligament | 0.608 ± 0.118 | 1.652 ± 0.357 | 3.405 ± 0.522 | 7.814 ± 0.838 | 9.405 ± 1.268 |
| Cartilage | 2.280 ± 0.536 | 4.214 ± 0.964 | 8.383 ± 2.327 | 16.593 ± 4.270 | 20.057 ± 5.292 |
| Brain (gray matter) | 0.454 ± 0.052 | 0.813 ± 0.095 | 1.643 ± 0.177 | 3.177 ± 0.338 | 4.119 ± 0.635 |
| Brain (white matter) | 0.412 ± 0.026 | 0.962 ± 0.099 | 1.801 ± 0.163 | 3.626 ± 0.352 | 4.567 ± 0.629 |
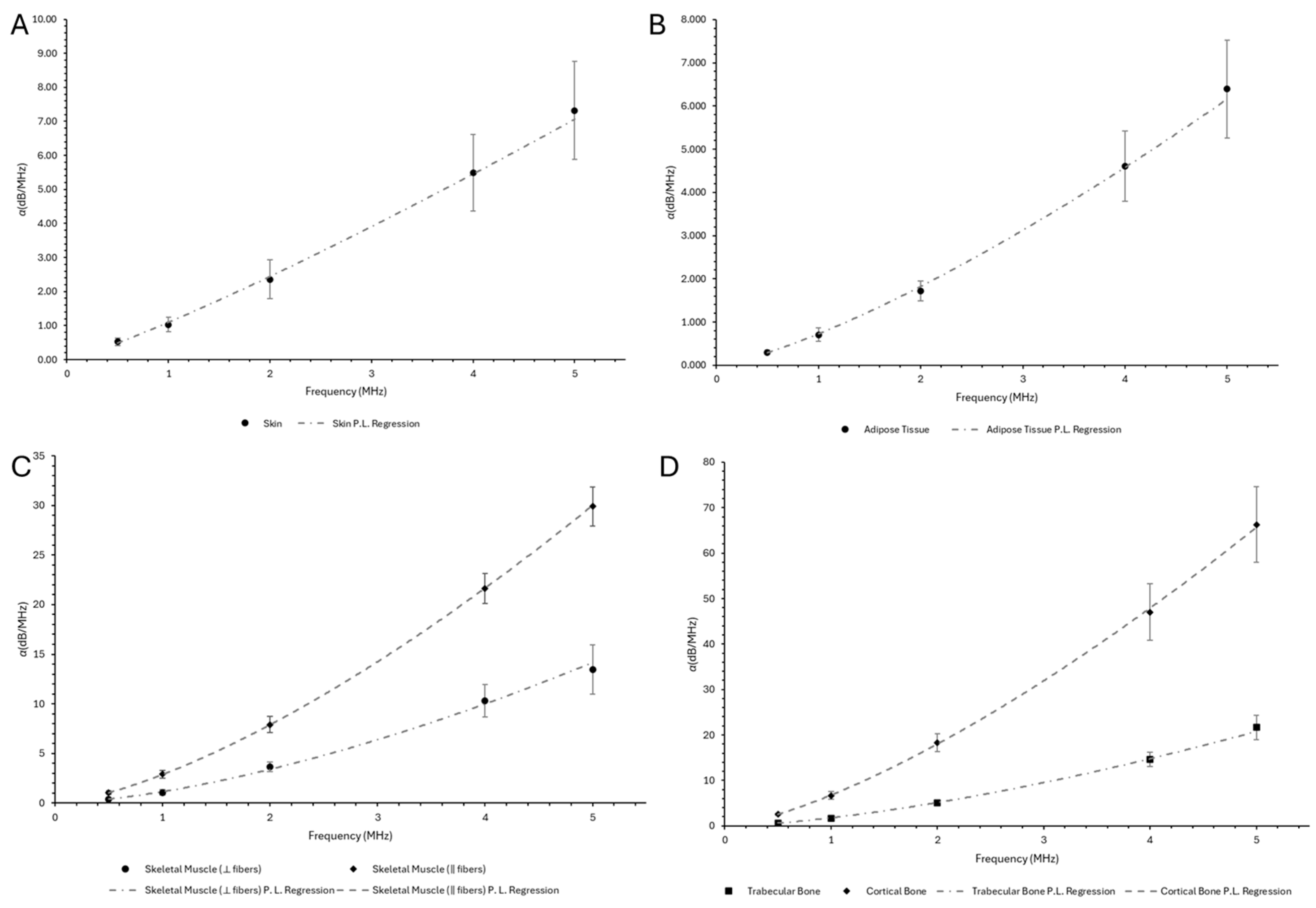


Appendix A.4
| Sample | B/A Nonlinearity Parameter |
|---|---|
| Skin | 7.237 ± 0.948 |
| Adipose Tissue | 10.754 ± 1.457 |
| Skeletal Muscle (⟂ fibers) | 6.632 ± 2.023 |
| Skeletal Muscle (‖ fibers) | 7.611 ± 1.099 |
| Trabecular Bone | 80.582 ± 21.027 |
| Cortical Bone | 12.948 ± 1.900 |
| Liver | 7.465 ± 0.197 |
| Myocardium | 7.188 ± 0.343 |
| Kidney | 7.045 ± 0.197 |
| Tendon | 7.047 ± 0.337 |
| Ligament | 7.206 ± 0.375 |
| Cartilage | 8.118 ± 0.227 |
| Brain (gray matter) | 7.216 ± 0.345 |
| Brain (white matter) | 7.476 ± 0.272 |
Appendix B
Appendix B.1
| Sample | (m2/s) | ||||
|---|---|---|---|---|---|
| Skin | 0.0046541 | 0.0026709 | 0.001542 | 0.000897 | 0.000446 |
| Adipose Tissue | 0.0018071 | 0.0011943 | 0.0007797 | 0.0005127 | 0.0004460 |
| Skeletal Muscle (⟂ fibers) | 0.0030714 | 0.0023591 | 0.0018314 | 0.0014533 | 0.0013849 |
| Skeletal Muscle (‖ fibers) | 0.0092088 | 0.0066373 | 0.0048843 | 0.0039815 | 0.0038835 |
| Trabecular Bone | 0.0165340 | 0.0123610 | 0.0094581 | 0.0075485 | 0.0071822 |
| Cortical Bone | 0.1680300 | 0.0835210 | 0.0438240 | 0.0223810 | 0.0112840 |
| Liver | 0.0020157 | 0.0011208 | 0.0006263 | 0.0003505 | 0.0002887 |
| Myocardium | 0.0021628 | 0.0011345 | 0.0005941 | 0.0003109 | 0.0002501 |
| Kidney | 0.0019224 | 0.0009979 | 0.0005220 | 0.0002731 | 0.0002189 |
| Tendon | 0.0293460 | 0.0165710 | 0.0095488 | 0.0060492 | 0.0043049 |
| Ligament | 0.0063957 | 0.0037370 | 0.0022007 | 0.0013106 | 0.0011161 |
| Cartilage | 0.1680300 | 0.0113610 | 0.0057624 | 0.0030086 | 0.0025893 |
| Brain (gray matter) | 0.0034649 | 0.0017210 | 0.0008619 | 0.0004319 | 0.0003438 |
| Brain (white matter) | 0.0032856 | 0.0017142 | 0.0008997 | 0.0004729 | 0.0003833 |
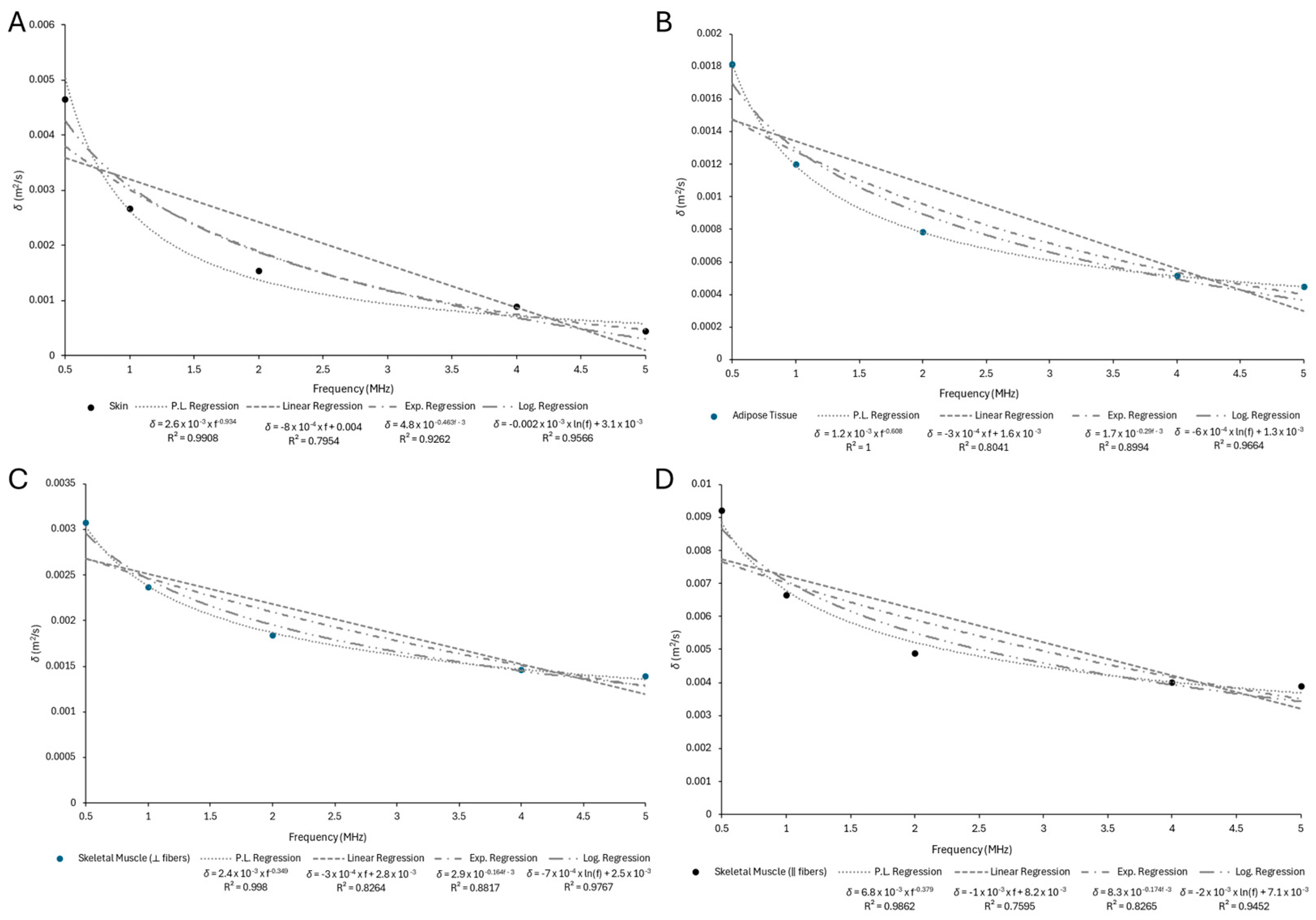
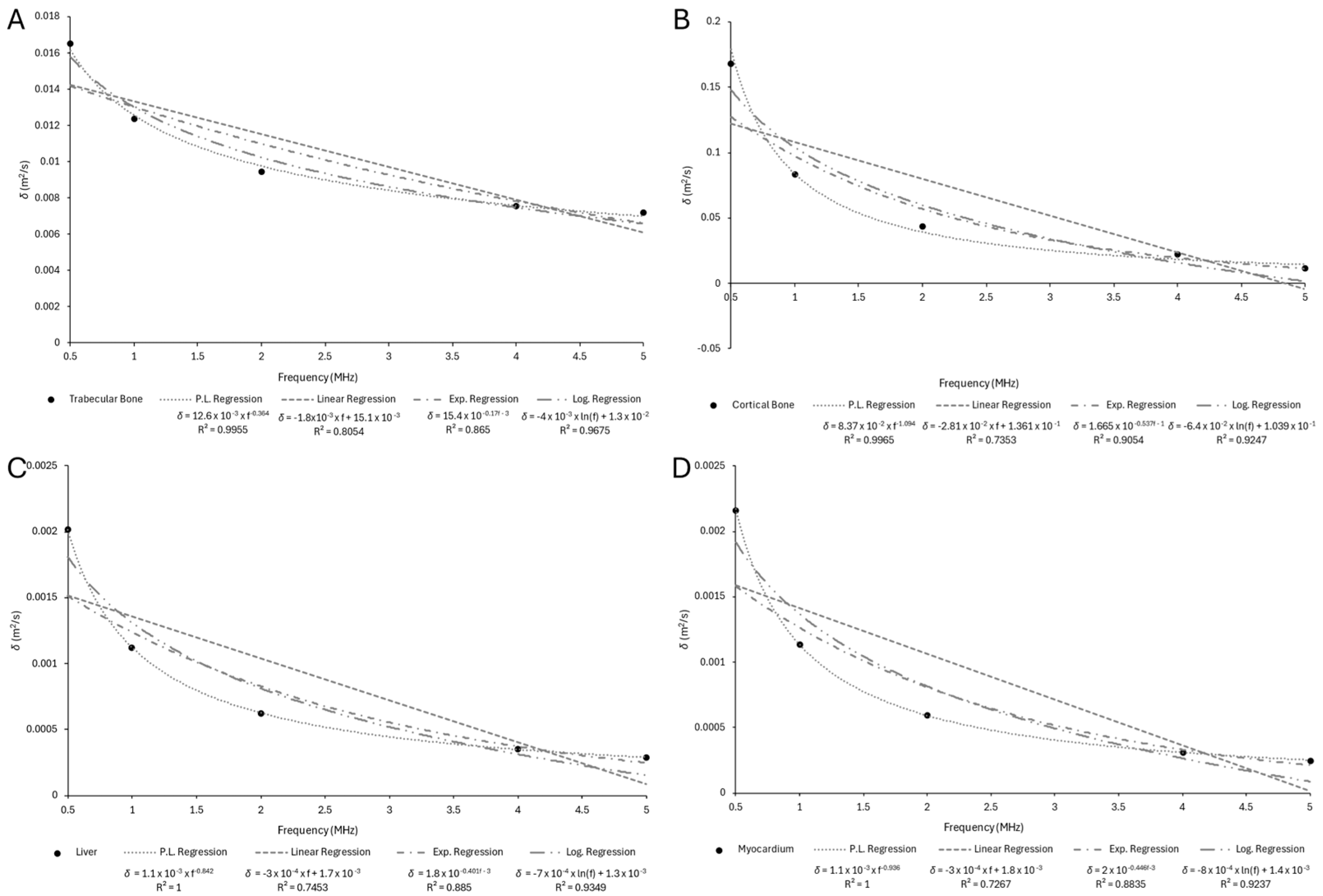
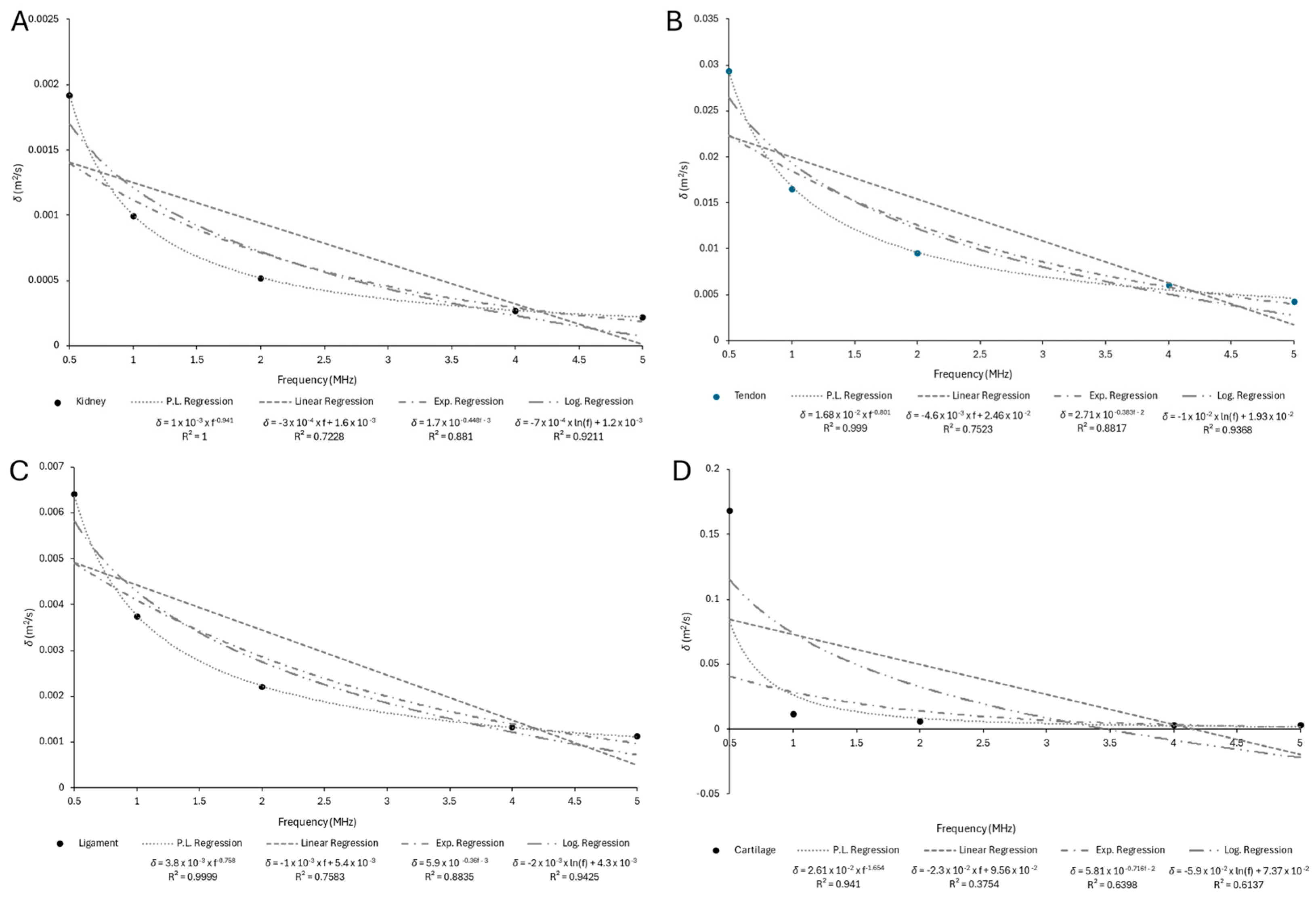

Appendix B.2
| Sample | (Pa·s) | ||||
|---|---|---|---|---|---|
| Skin | 0.018412 | 0.012715 | 0.010061 | 0.006913 | 0.006419 |
| Adipose Tissue | 0.035102 | 0.019314 | 0.010292 | 0.004623 | 0.005383 |
| Skeletal Muscle (⟂ fibers) | 0.016341 | 0.008656 | 0.002010 | 0.002483 | 0.000513 |
| Skeletal Muscle (‖ fibers) | 0.000194 | 0.001422 | 0.012017 | 0.052651 | 0.088172 |
| Trabecular Bone | 0.001883 | 0.005150 | 0.016389 | 0.038733 | 0.054621 |
| Cortical Bone | 0.129760 | 0.256180 | 0.380000 | 0.634210 | 0.714860 |
| Liver | 0.051783 | 0.020033 | 0.009566 | 0.004825 | 0.003678 |
| Myocardium | 0.017032 | 0.007693 | 0.003072 | 0.002192 | 0.001219 |
| Kidney | 0.006987 | 0.002228 | 0.000401 | 0.000297 | 0.000177 |
| Tendon | 0.001285 | 0.000902 | 0.000601 | 0.000419 | 0.000314 |
| Ligament | 0.021614 | 0.010881 | 0.007587 | 0.005932 | 0.002239 |
| Cartilage | 0.125650 | 0.051580 | 0.021970 | 0.009730 | 0.007340 |
| Brain (gray matter) | 0.014205 | 0.010266 | 0.006119 | 0.005506 | 0.004277 |
| Brain (white matter) | 0.016707 | 0.009774 | 0.006200 | 0.005904 | 0.004753 |


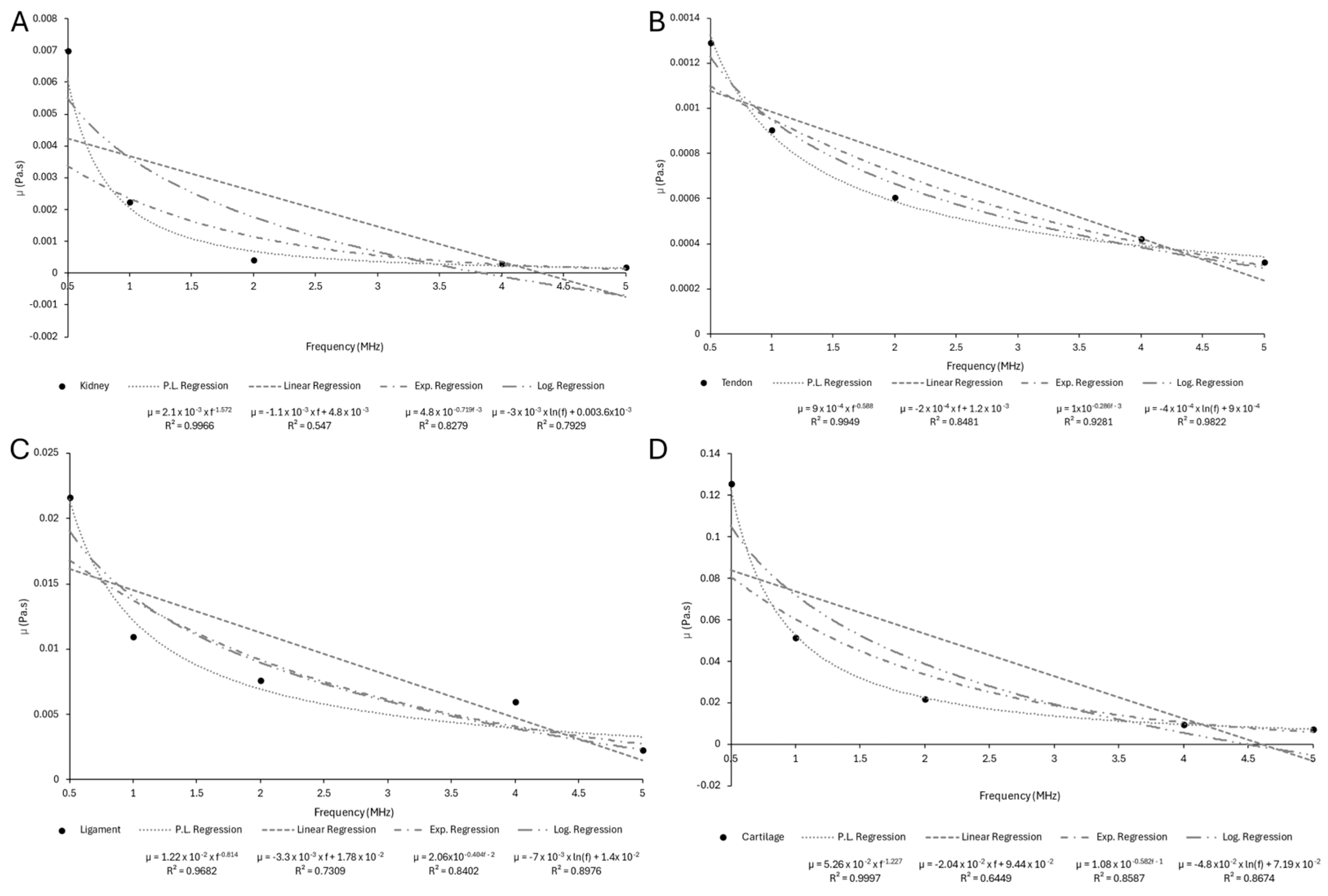
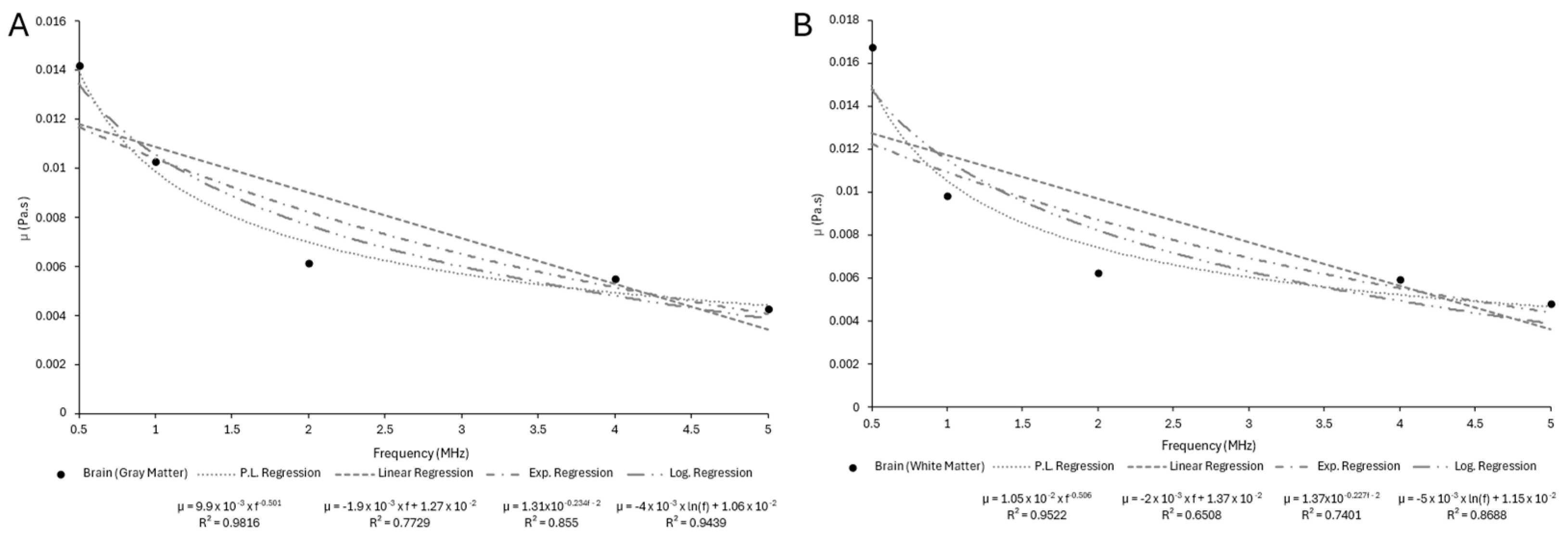
Appendix B.3
| Sample | (Pa·s) | ||||
|---|---|---|---|---|---|
| Skin | 5.247600 | 3.009100 | 1.722100 | 0.999730 | 0.845820 |
| Adipose Tissue | 1.668400 | 1.081400 | 0.709090 | 0.469090 | 0.407280 |
| Skeletal Muscle (⟂ fibers) | 3.261500 | 2.510400 | 1.931000 | 1.520400 | 1.480200 |
| Skeletal Muscle (‖ fibers) | 9.652800 | 6.910400 | 5.059100 | 4.033700 | 3.479900 |
| Trabecular Bone | 9.387300 | 7.118600 | 5.338900 | 4.135800 | 4.009300 |
| Cortical Bone | 329.040000 | 237.920000 | 180.340000 | 121.760000 | 99.465000 |
| Liver | 2.172700 | 1.187800 | 0.665870 | 0.373130 | 0.307230 |
| Myocardium | 2.356300 | 1.218700 | 0.645840 | 0.336810 | 0.273560 |
| Kidney | 1.979800 | 1.021700 | 0.551040 | 0.288260 | 0.229860 |
| Tendon | 32.594000 | 18.582000 | 10.578000 | 6.627900 | 4.496100 |
| Ligament | 7.002000 | 4.087400 | 2.419700 | 1.372100 | 1.218700 |
| Cartilage | 25.209000 | 12.351000 | 6.366900 | 3.334700 | 2.772700 |
| Brain (gray matter) | 3.608400 | 1.788100 | 0.893780 | 0.444900 | 0.353820 |
| Brain (white matter) | 3.340600 | 1.741900 | 0.912760 | 0.477130 | 0.385620 |
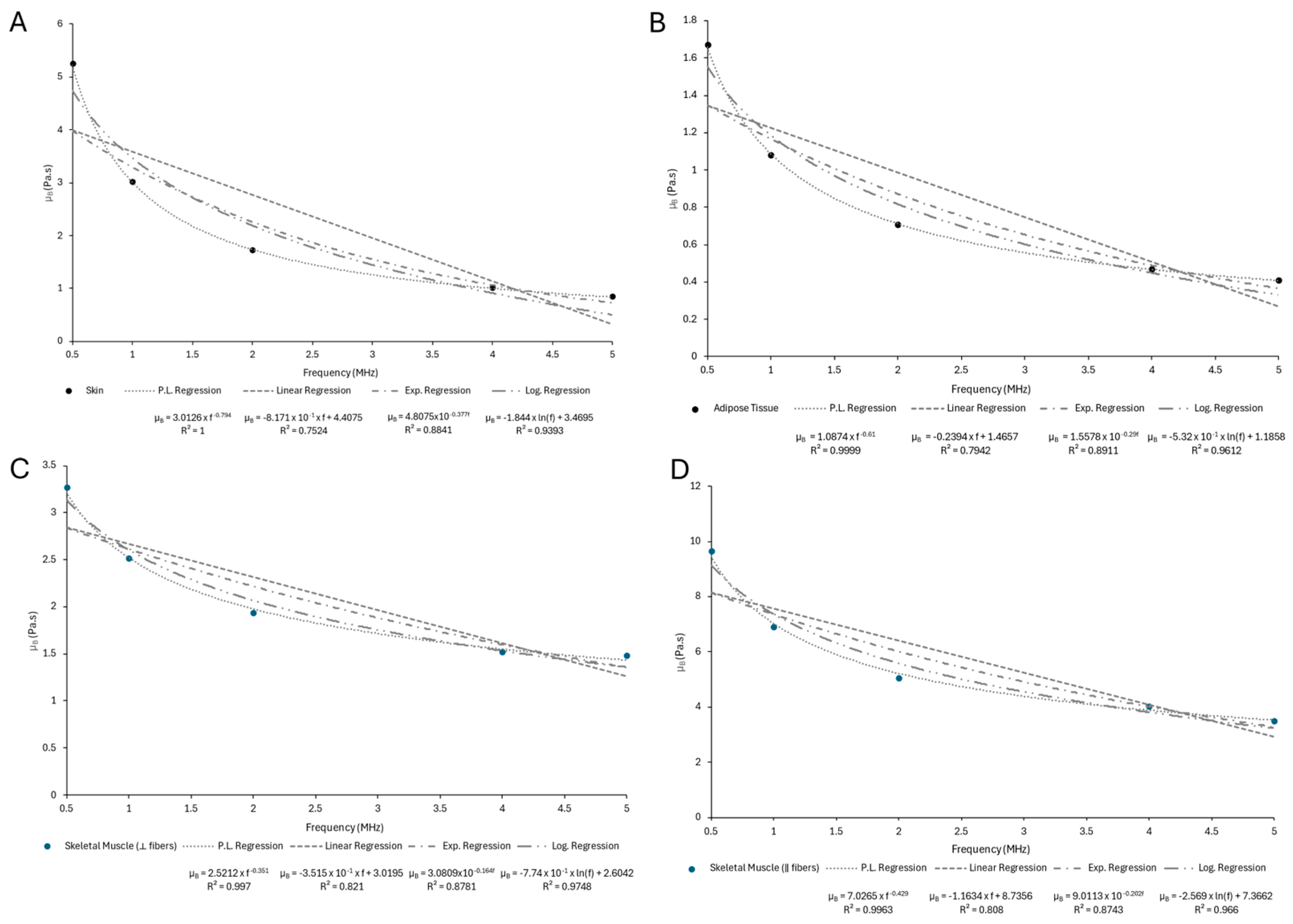
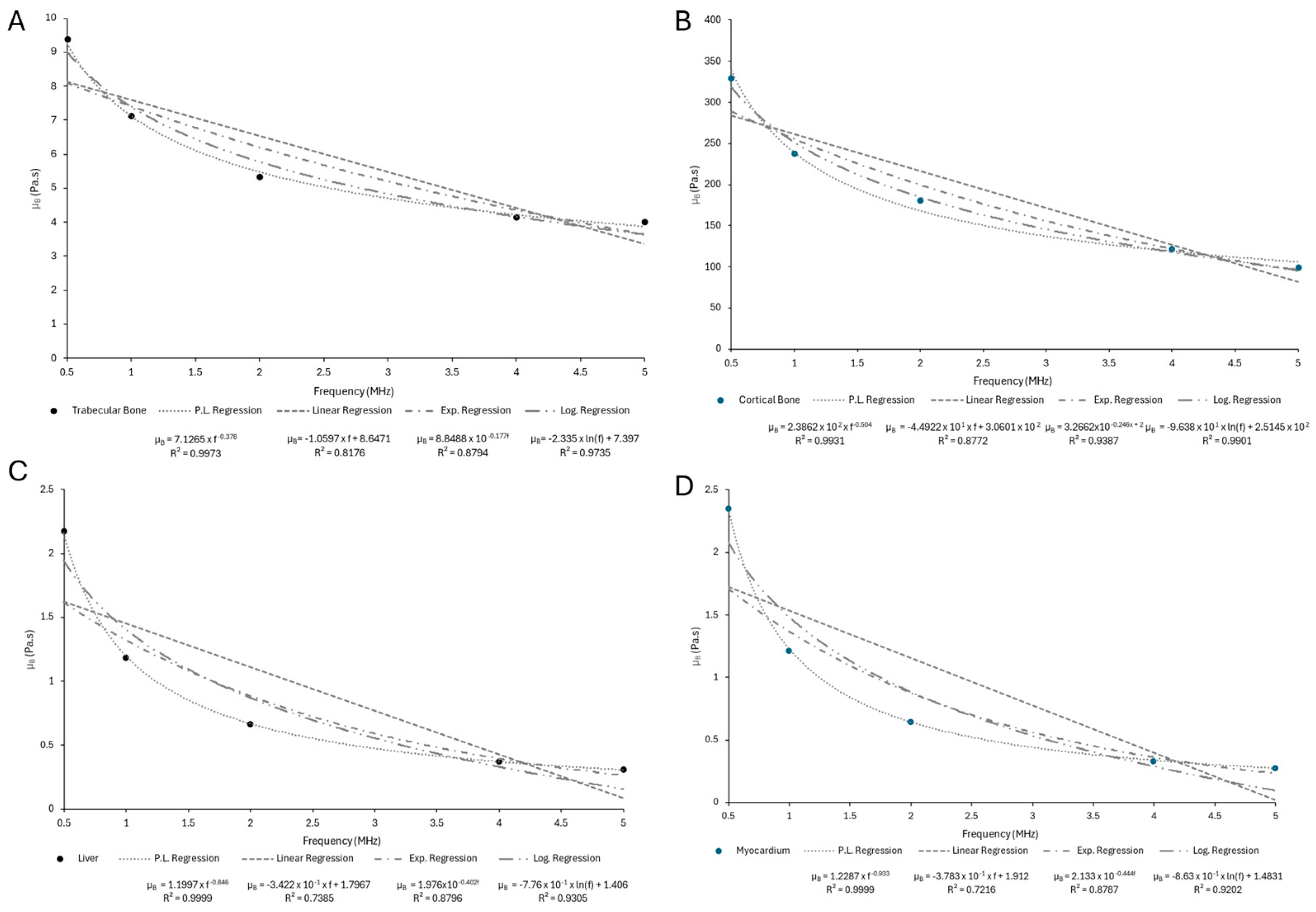


Appendix C
Appendix C.1
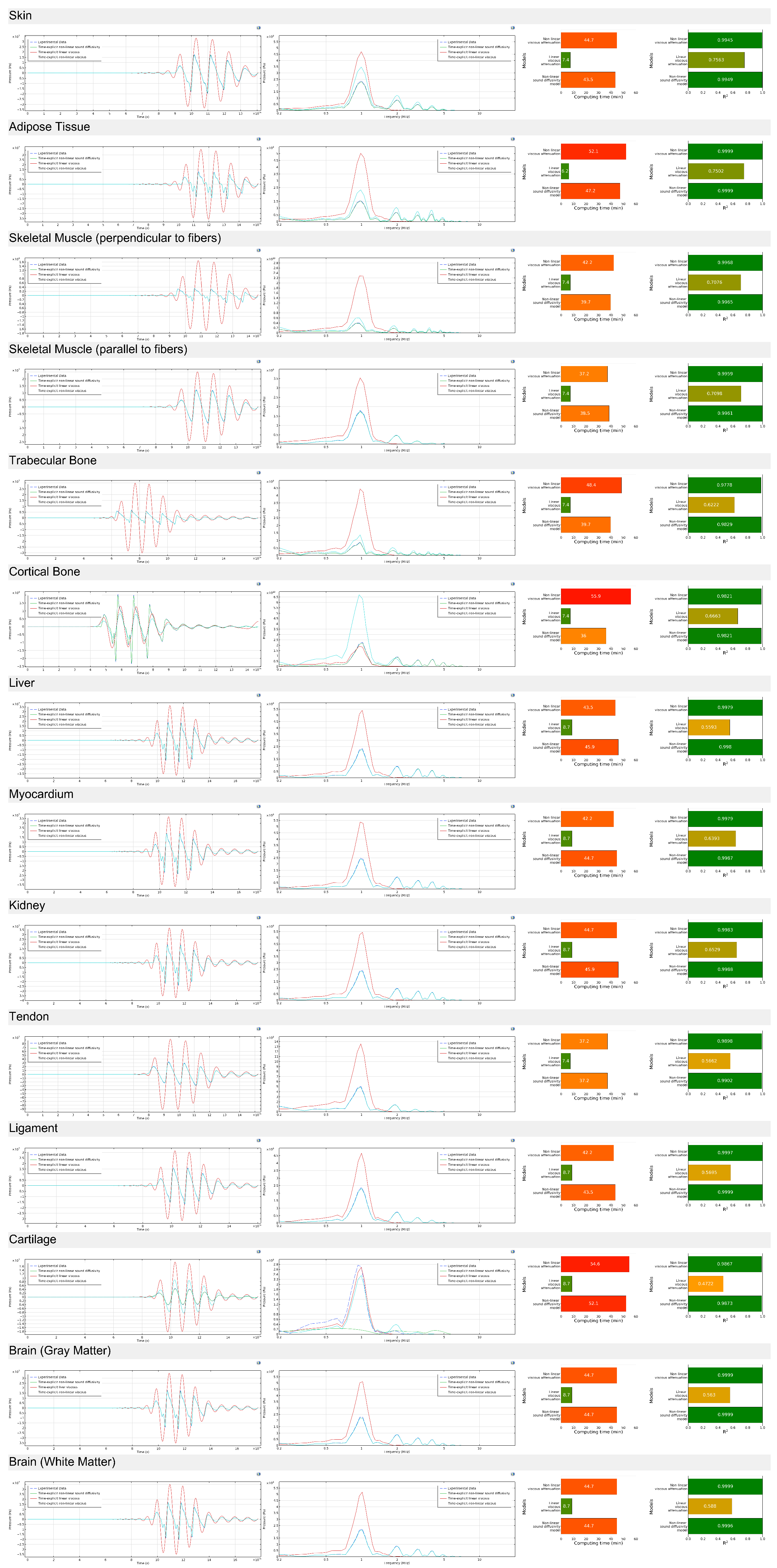
Appendix C.2

Appendix C.3

References
- Miller, D.L.; Abo, A.; Abramowicz, J.S.; Bigelow, T.A.; Dalecki, D.; Dickman, E.; Donlon, J.; Harris, G.; Nomura, J. Diagnostic Ultrasound Safety Review for Point-of-Care Ultrasound Practitioners. J. Ultrasound Med. 2020, 39, 1069–1084. [Google Scholar] [CrossRef]
- Phillips, R.A.; Stratmeyer, M.E.; Harris, G.R. Safety and U.S. Regulatory Considerations in the Nonclinical Use of Medical Ultrasound Devices. Ultrasound Med. Biol. 2010, 36, 1224–1228. [Google Scholar] [CrossRef]
- Ungur, R.A.; Ciortea, V.M.; Irsay, L.; Ciubean, A.D.; Năsui, B.A.; Codea, R.A.; Singurean, V.E.; Groza, O.B.; Căinap, S.; Martiș, G.S.; et al. Can Ultrasound Therapy Be an Environmental-Friendly Alternative to Non-Steroidal Anti-Inflammatory Drugs in Knee Osteoarthritis Treatment? Materials 2021, 14, 2715. [Google Scholar] [CrossRef]
- Li, X.; Lin, Y.; He, P.; Wang, Q. Efficacy and Safety of Low-Intensity Ultrasound Therapy for Myofascial Pain Syndrome: A Systematic Review and Meta-Analysis. BMC Musculoskelet. Disord. 2024, 25, 1059. [Google Scholar] [CrossRef]
- Papadacci, C.; Bunting, E.A.; Konofagou, E.E. 3D Quasi-Static Ultrasound Elastography With Plane Wave In Vivo. IEEE Trans. Med. Imaging 2017, 36, 357–365. [Google Scholar] [CrossRef] [PubMed]
- Qin, H.; Du, L.; Luo, Z.; He, Z.; Wang, Q.; Chen, S.; Zhu, Y.-L. The Therapeutic Effects of Low-Intensity Pulsed Ultrasound in Musculoskeletal Soft Tissue Injuries: Focusing on the Molecular Mechanism. Front. Bioeng. Biotechnol. 2022, 10, 1080430. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Hou, C. Progresses and Clinical Application of Super-Resolution Ultrasound Imaging: A Narrative Review. Ultrasound J. 2025, 17, 29. [Google Scholar] [CrossRef]
- Seddiki, R.; Mirault, T.; Sitruk, J.; Mohamedi, N.; Messas, E.; Pernot, M.; Baranger, J.; Goudot, G. Advancements in Noncontrast Ultrasound Imaging for Low-Velocity Flow: A Technical Review and Clinical Applications in Vascular Medicine. Ultrasound Med. Biol. 2025, 51, 1035–1042. [Google Scholar] [CrossRef]
- Mushtaq, G.; Veningston, K. A Comprehensive Review on Fetal Health Surveillance Using Ultrasound Imagery. Discov. Appl. Sci. 2025, 7, 478. [Google Scholar] [CrossRef]
- Boumeridja, H.; Ammar, M.; Alzubaidi, M.; Mahmoudi, S.; Benamer, L.N.; Agus, M.; Househ, M.; Lekadir, K.; El Habib Daho, M. Enhancing Fetal Ultrasound Image Quality and Anatomical Plane Recognition in Low-Resource Settings Using Super-Resolution Models. Sci. Rep. 2025, 15, 8376. [Google Scholar] [CrossRef]
- Sidhu, P.S.; Ewertsen, C.; Piskunowicz, M.; Secil, M.; Ricci, P.; Fischer, T.; Gaitini, D.; Mitkov, V.; Lim, A.K.P.; Lu, Q.; et al. Diversity of Current Ultrasound Practice within and Outside Radiology Departments with a Vision for 20 Years into the Future: A Position Paper of the ESR Ultrasound Subcommittee. Insights Imaging 2023, 14, 202. [Google Scholar] [CrossRef]
- O’Reilly, M.A. Exploiting the Mechanical Effects of Ultrasound for Noninvasive Therapy. Science 2024, 385, eadp7206. [Google Scholar] [CrossRef]
- Singh, A.; Reynolds, J.N.J. Therapeutic Ultrasound: An Innovative Approach for Targeting Neurological Disorders Affecting the Basal Ganglia. Front. Neuroanat. 2024, 18, 1469250. [Google Scholar] [CrossRef]
- Lin, Z.; Gao, L.; Hou, N.; Zhi, X.; Zhang, Y.; Che, Z.; Deng, A. Application of Low-Intensity Pulsed Ultrasound on Tissue Resident Stem Cells: Potential for Ophthalmic Diseases. Front. Endocrinol. 2023, 14, 1153793. [Google Scholar] [CrossRef]
- Fernandes, N.A.T.C.; Arieira, A.; Hinckel, B.; Silva, F.S.; Carvalho, Ó.; Leal, A. Unlocking the Secrets of Knee Joint Unloading: A Systematic Review and Biomechanical Study of the Invasive and Non-Invasive Methods and Their Influence on Knee Joint Loading. Rheumato 2025, 5, 8. [Google Scholar] [CrossRef]
- Fernandes, N.; Silva, F.S.; Carvalho, Ó.; Leal, A. The Effect That Lower Limb Orthoses Have on Cartilage on Patients with Knee Osteoarthritis: A Narrative Review. Prosthet. Orthot. Int. 2022, 46, 466–476. [Google Scholar] [CrossRef]
- Oliveira, S.; Andrade, R.; Silva, F.S.; Espregueira-Mendes, J.; Hinckel, B.B.; Leal, A.; Carvalho, Ó. Effects and Mechanotransduction Pathways of Therapeutic Ultrasound on Healthy and Osteoarthritic Chondrocytes: A Systematic Review of in Vitro Studies. Osteoarthr. Cartil. 2023, 31, 317–339. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, S.; Andrade, R.; Valente, C.; Espregueira-Mendes, J.; Silva, F.; Hinckel, B.B.; Carvalho, Ó.; Leal, A. Mechanical-Based Therapies May Reduce Pain and Disability in Some Patients with Knee Osteoarthritis: A Systematic Review with Meta-Analysis. Knee 2022, 37, 28–46. [Google Scholar] [CrossRef] [PubMed]
- Beeckmans, M.; Huycke, P.; Verguts, T.; Verbeke, P. How Much Data Do We Need to Estimate Computational Models of Decision-Making? The COMPASS Toolbox. Behav. Res. 2023, 56, 2537–2548. [Google Scholar] [CrossRef]
- Arifin, A.-A.; S M, B.B.; Asif Ashrafi, K.M. Development of Less Computational Costly Ultrasound Imaging Using the Finite Element Method. IJETT 2024, 72, 299–312. [Google Scholar] [CrossRef]
- Winslow, R.L.; Trayanova, N.; Geman, D.; Miller, M.I. Computational Medicine: Translating Models to Clinical Care. Sci. Transl. Med. 2012, 4, 158rv11. [Google Scholar] [CrossRef]
- Luqmani, R.; Lee, E.; Singh, S. The Role of Ultrasound Compared to Biopsy of Temporal Arteries in the Diagnosis and Treatment of Giant Cell Arteritis (TABUL): A Diagnostic Accuracy and Cost-Effectiveness Study. In Cost-Effectiveness Analysis; NIHR Journals Library: Southampton, UK, 2016; Chapter 7. [Google Scholar]
- Chintada, B.R.; Rau, R.; Goksel, O. Nonlinear Characterization of Tissue Viscoelasticity with Acoustoelastic Attenuation of Shear-Waves. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2022, 69, 38–53. [Google Scholar] [CrossRef]
- Jiménez, N.; Camarena, F.; Redondo, J.; Sánchez-Morcillo, V.; Hou, Y.; Konofagou, E.E. Time-Domain Simulation of Ultrasound Propagation in a Tissue-like Medium Based on the Resolution of the Nonlinear Acoustic Constitutive Relations. Acta Acust. United Acust. 2016, 102, 876–892. [Google Scholar] [CrossRef]
- Acosta, S.; Chan, J.; Johnson, R.; Palacios, B. Pseudodifferential Models for Ultrasound Waves with Fractional Attenuation. SIAM J. Appl. Math. 2023, 84, 1609–1630. [Google Scholar] [CrossRef]
- Meral, F.C.; Royston, T.J.; Magin, R.L. Fractional Order Models for Viscoelasticity of Soft Biological Tissues. In Proceedings of the Volume 2: Biomedical and Biotechnology Engineering, Seattle, WA, USA, 11–15 November 2007; ASMEDC: Boston, MA, USA, 2008; pp. 721–722. [Google Scholar]
- Gomez, A.; Rus, G.; Saffari, N. Wave Propagation in a Fractional Viscoelastic Tissue Model: Application to Transluminal Procedures. Sensors 2021, 21, 2778. [Google Scholar] [CrossRef]
- Gomez, A.; Callejas, A.; Rus, G.; Saffari, N. Experimental Evidence of Shear Waves in Fractional Viscoelastic Rheological Models. Sci. Rep. 2022, 12, 7448. [Google Scholar] [CrossRef]
- Holm, S.; Näsholm, S.P. Comparison of Fractional Wave Equations for Power Law Attenuation in Ultrasound and Elastography. Ultrasound Med. Biol. 2014, 40, 695–703. [Google Scholar] [CrossRef]
- Meral, F.C.; Royston, T.J.; Magin, R. Fractional Calculus in Viscoelasticity: An Experimental Study. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 939–945. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Okamura, N.; Tsukune, M.; Fujie, M.G.; Tanaka, M. Non-Minimum Phase Viscoelastic Properties of Soft Biological Tissues. J. Mech. Behav. Biomed. Mater. 2018, 110, 103795. [Google Scholar] [CrossRef]
- Qiang, B.; Brigham, J.C.; Aristizabal, S.; Greenleaf, J.F.; Zhang, X.; Urban, M.W. Modeling Transversely Isotropic, Viscoelastic, Incompressible Tissue-like Materials with Application in Ultrasound Shear Wave Elastography. Phys. Med. Biol. 2015, 60, 1289–1306. [Google Scholar] [CrossRef][Green Version]
- Levinson, S.F. Ultrasound Propagation in Anisotropic Soft Tissues: The Application of Linear Elastic Theory. J. Biomech. 1987, 20, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Parker, K.J. Power Laws Prevail in Medical Ultrasound. Phys. Med. Biol. 2022, 67, 09TR02. [Google Scholar] [CrossRef]
- Valdez, M.; Balachandran, B. Longitudinal Nonlinear Wave Propagation through Soft Tissue. J. Mech. Behav. Biomed. Mater. 2013, 20, 192–208. [Google Scholar] [CrossRef]
- Shishlenin, M.; Kozelkov, A.; Novikov, N. Nonlinear Medical Ultrasound Tomography: 3D Modeling of Sound Wave Propagation in Human Tissues. Mathematics 2024, 12, 212. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Turco, S.; Van Sloun, R.J.G.; Mischi, M. Ultrasound Viscoelastography by Acoustic Radiation Force: A State-of-the-Art Review. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2024, 71, 536–557. [Google Scholar] [CrossRef]
- Chintada, B.R.; Rau, R.; Goksel, O. Spectral Ultrasound Imaging of Speed-of-Sound and Attenuation Using an Acoustic Mirror. Front. Phys. 2022, 10, 860725. [Google Scholar] [CrossRef]
- Moghimnezhad, M. Multiphysics Analysis of Ultrasonic Shock Wave Lithotripsy and Side Effects on Surrounding Tissues. J. Biomed. Phys. Eng. 2021, 11, 701–712. [Google Scholar] [CrossRef]
- Gharehnazifam, Z.; Dolatabadi, R.; Baniassadi, M.; Shahsavari, H.; Kajbafzadeh, A.-M.; Abrinia, K.; Gharehnazifam, K.; Baghani, M. Multiphysics Modeling and Experiments on Ultrasound-Triggered Drug Delivery from Silk Fibroin Hydrogel for Wilms Tumor. Int. J. Pharm. 2022, 621, 121787. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Qi, P.; Peng, D.; Zhang, X.; Zhu, L. Propagation of Ultrasound-Modulated Scattered Light in Biological Tissue by Using COMSOL Multiphysics. In Proceedings of the Advanced Optical Imaging Technologies II, Hangzhou, China, 21–23 October 2019; Carney, P.S., Yuan, X.-C., Shi, K., Somekh, M.G., Eds.; SPIE: Hangzhou, China, 2019; p. 37. [Google Scholar]
- Nikolić, V.; Said-Houari, B. The Westervelt-Pennes Model of Nonlinear Thermoacoustics: Global Solvability and Asymptotic Behavior. J. Differ. Equ. 2022, 336, 628–653. [Google Scholar] [CrossRef]
- El-Brawany, M.A.; Nassiri, D.K.; Terhaar, G.; Shaw, A.; Rivens, I.; Lozhken, K. Measurement of Thermal and Ultrasonic Properties of Some Biological Tissues. J. Med. Eng. Technol. 2009, 33, 249–256. [Google Scholar] [CrossRef]
- Benjamin, A.; Zubajlo, R.E.; Dhyani, M.; Samir, A.E.; Thomenius, K.E.; Grajo, J.R.; Anthony, B.W. Surgery for Obesity and Related Diseases: I. A Novel Approach to the Quantification of the Longitudinal Speed of Sound and Its Potential for Tissue Characterization. Ultrasound Med. Biol. 2018, 44, 2739–2748. [Google Scholar] [CrossRef]
- Panfilova, A.; Van Sloun, R.J.G.; Wijkstra, H.; Sapozhnikov, O.A.; Mischi, M. A Review on B/A Measurement Methods with a Clinical Perspective. J. Acoust. Soc. Am. 2021, 149, 2200–2237. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, M.F.; Blackstock, D.T. (Eds.) Nonlinear Acoustics; Springer Nature: Cham, Switzerland, 2024; ISBN 978-3-031-58962-1. [Google Scholar]
- Njeh, C.F.; Langton, C.M. The Effect of Cortical Endplates on Ultrasound Velocity through the Calcaneus: An in Vitro Study. Br. J. Radiol. 1997, 70, 504–510. [Google Scholar] [CrossRef]
- Eskner, M.; Sandström, R. Mechanical Property Evaluation Using the Small Punch Test. J. Test. Eval. 2004, 32, 282–289. [Google Scholar] [CrossRef]
- Lannin, T.B.; Kelly, M.P.; James, T.P. Reciprocating Bone Saw: Effect of Blade Speed on Cutting Rate. In Proceedings of the Volume 3: Design and Manufacturing, Denver, CO, USA, 11–17 November 2011; ASMEDC: Denver, CO, USA, 2011; pp. 767–771. [Google Scholar]
- Shakouri, E.; Ghorbani, P.; Pourheidari, P.; Fotuhi, S. Resection of Bone by Sagittal Saw: Investigation of Effects of Blade Speed, Feed Rate, and Irrigation on Temperature Rise. Proc. Inst. Mech. Eng. H 2021, 235, 625–635. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, N.A.T.C.; Alves, D.I.; Ferreira, D.P.; Monteiro, M.; Arieira, A.; Silva, F.; Hinckel, B.; Leal, A.; Carvalho, Ó. Sustainable Tunable Anisotropic Ultrasound Medical Phantoms for Skin, Skeletal Muscle, and Other Fibrous Biological Tissues Using Natural Fibers and a Bio-Elastomeric Matrix. J. Compos. Sci. 2025, 9, 370. [Google Scholar] [CrossRef]
- Blackstock, D.T. Fundamentals of Physical Acoustics; A Wiley-Interscience publication; Wiley: New York, NY, USA, 2000; ISBN 978-0-471-31979-5. [Google Scholar]
- White, F.E. Elements of Acoustics, by Samuel Temkin. J. Acoust. Soc. Am. 1982, 71, 522. [Google Scholar] [CrossRef]
- Tadano, S.; Giri, B. X-Ray Diffraction as a Promising Tool to Characterize Bone Nanocomposites. Sci. Technol. Adv. Mater. 2011, 12, 064708. [Google Scholar] [CrossRef]
- Musthafa, H.-S.N.; Walker, J. Design of Trabecular Bone Mimicking Voronoi Lattice-Based Scaffolds and CFD Modelling of Non-Newtonian Power Law Blood Flow Behaviour. Computation 2024, 12, 241. [Google Scholar] [CrossRef]
- Seltzer, S. Stopping-Powers and Range Tables for Electrons, Protons, and Helium Ions, NIST Standard Reference Database 124; NIST: Boulder, CO, USA, 1993.
- Harrington, T.A.M.; Thomas, E.L.; Frost, G.; Modi, N.; Bell, J.D. Distribution of Adipose Tissue in the Newborn. Pediatr. Res. 2004, 55, 437–441. [Google Scholar] [CrossRef]
- Leonard, K.C.; Worden, N.; Boettcher, M.L.; Dickinson, E.; Omstead, K.M.; Burrows, A.M.; Hartstone-Rose, A. Anatomical and Ontogenetic Influences on Muscle Density. Sci. Rep. 2021, 11, 2114. [Google Scholar] [CrossRef] [PubMed]
- Ward, S.R.; Lieber, R.L. Density and Hydration of Fresh and Fixed Human Skeletal Muscle. J. Biomech. 2005, 38, 2317–2320. [Google Scholar] [CrossRef]
- Morgan, E.F.; Unnikrisnan, G.U.; Hussein, A.I. Bone Mechanical Properties in Healthy and Diseased States. Annu. Rev. Biomed. Eng. 2018, 20, 119–143. [Google Scholar] [CrossRef]
- Öhman-Mägi, C.; Holub, O.; Wu, D.; Hall, R.M.; Persson, C. Density and Mechanical Properties of Vertebral Trabecular Bone—A Review. JOR Spine 2021, 4, e1176. [Google Scholar] [CrossRef]
- Niehues, S.; Unger, J.; Malinowski, M.; Neymeyer, J.; Hamm, B.; Stockmann, M. Liver Volume Measurement: Reason of the Difference between In Vivo CT-Volumetry and Intraoperative Ex Vivo Determination and How to Cope It. Eur. J. Med. Res. 2010, 15, 345. [Google Scholar] [CrossRef]
- Hudsmith†, L.; Petersen†, S.; Francis, J.; Robson, M.; Neubauer, S. Normal Human Left and Right Ventricular and Left Atrial Dimensions Using Steady State Free Precession Magnetic Resonance Imaging. J. Cardiovasc. Magn. Reson. 2005, 7, 775–782. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, B.; Xi, D.; Chen, R.; Xiao, P.; Xie, Q. Feasibility Study of YSO/SiPM Based Detectors for Virtual Monochromatic Image Synthesis. J. X-Ray Sci. Technol. 2024, 32, 1363–1383. [Google Scholar] [CrossRef]
- Staanum, P.F.; Frellsen, A.F.; Olesen, M.L.; Iversen, P.; Arveschoug, A.K. Practical Kidney Dosimetry in Peptide Receptor Radionuclide Therapy Using [177Lu]Lu-DOTATOC and [177Lu]Lu-DOTATATE with Focus on Uncertainty Estimates. EJNMMI Phys. 2021, 8, 78. [Google Scholar] [CrossRef]
- Snelling, E.P.; Biewener, A.A.; Hu, Q.; Taggart, D.A.; Fuller, A.; Mitchell, D.; Maloney, S.K.; Seymour, R.S. Scaling of the Ankle Extensor Muscle-tendon Units and the Biomechanical Implications for Bipedal Hopping Locomotion in the Post-pouch Kangaroo Macropus fuliginosus. J. Anat. 2017, 231, 921–930. [Google Scholar] [CrossRef] [PubMed]
- Kar, S.; Smith, D.W.; Gardiner, B.S.; Grodzinsky, A.J. Systems Based Study of the Therapeutic Potential of Small Charged Molecules for the Inhibition of IL-1 Mediated Cartilage Degradation. PLoS ONE 2016, 11, e0168047. [Google Scholar] [CrossRef] [PubMed]
- Barber, T.W.; Brockway, J.A.; Higgins, L.S. The Density of Tissues in and About the Head. Acta Neurol. Scand. 1970, 46, 85–92. [Google Scholar] [CrossRef]
- Moran, C.M.; Bush, N.L.; Bamber, J.C. Ultrasonic Propagation Properties of Excised Human Skin. Ultrasound Med. Biol. 1995, 21, 1177–1190. [Google Scholar] [CrossRef]
- Korta Martiartu, N.; Nakhostin, D.; Ruby, L.; Frauenfelder, T.; Rominger, M.B.; Sanabria, S.J. Speed of Sound and Shear Wave Speed for Calf Soft Tissue Composition and Nonlinearity Assessment. Quant. Imaging Med. Surg. 2021, 11, 4149–4161. [Google Scholar] [CrossRef]
- Wearing, S.C.; Hooper, S.L.; Langton, C.M.; Keiner, M.; Horstmann, T.; Crevier-Denoix, N.; Pourcelot, P. The Biomechanics of Musculoskeletal Tissues during Activities of Daily Living: Dynamic Assessment Using Quantitative Transmission-Mode Ultrasound Techniques. Healthcare 2024, 12, 1254. [Google Scholar] [CrossRef]
- Gatos, I.; Drazinos, P.; Loupas, T.; Yarmenitis, S.; Koskinas, J.; Zoumpoulis, P.S. Speed of Sound Index for Liver Steatosis Estimation: A Reliability Study in Normal Subjects. Diagn. Interv. Radiol. 2022, 28, 418–427. [Google Scholar] [CrossRef] [PubMed]
- Alves, N.; Kim, A.; Tan, J.; Hwang, G.; Javed, T.; Neagu, B.; Courtney, B.K. Cardiac Tissue-Mimicking Ballistic Gel Phantom for Ultrasound Imaging in Clinical and Research Applications. Ultrasound Med. Biol. 2020, 46, 2057–2069. [Google Scholar] [CrossRef]
- Töyräs, J.; Laasanen, M.S.; Saarakkala, S.; Lammi, M.J.; Rieppo, J.; Kurkijärvi, J.; Lappalainen, R.; Jurvelin, J.S. Speed of Sound in Normal and Degenerated Bovine Articular Cartilage. Ultrasound Med. Biol. 2003, 29, 447–454. [Google Scholar] [CrossRef] [PubMed]
- Dahis, D.; Azhari, H. Speed of Sound and Attenuation Temperature Dependence of Bovine Brain: Ex Vivo Study. J. Ultrasound Med. 2020, 39, 1175–1186. [Google Scholar] [CrossRef] [PubMed]
- Oftadeh, R.; Perez-Viloria, M.; Villa-Camacho, J.C.; Vaziri, A.; Nazarian, A. Biomechanics and Mechanobiology of Trabecular Bone: A Review. J. Biomech. Eng. 2015, 137, 010802. [Google Scholar] [CrossRef] [PubMed]
- Neuroanatomy, Gray Matter. Available online: https://www.ncbi.nlm.nih.gov/books/NBK553239/ (accessed on 18 July 2025).
- Hysi, E.; Baek, J.; Koven, A.; He, X.; Ulloa Severino, L.; Wu, Y.; Kek, K.; Huang, S.; Krizova, A.; Farcas, M.; et al. A First-in-Human Study of Quantitative Ultrasound to Assess Transplant Kidney Fibrosis. Nat. Med. 2025, 31, 970–978. [Google Scholar] [CrossRef]
- Baldwin, S.L.; Marutyan, K.R.; Yang, M.; Wallace, K.D.; Holland, M.R.; Miller, J.G. Estimating Myocardial Attenuation from M-Mode Ultrasonic Backscatter. Ultrasound Med. Biol. 2005, 31, 477–484. [Google Scholar] [CrossRef] [PubMed]
- Nassiri, D.K.; Nicholas, D.; Hill, C.R. Attenuation of Ultrasound in Skeletal Muscle. Ultrasonics 1979, 17, 230–232. [Google Scholar] [CrossRef]
- Sagar, K.B.; Agemura, D.H.; D O’Brien, W.; Pelc, L.R.; Rhyne, T.L.; Wann, L.S.; Komorowski, R.A.; Warltier, D.C. Quantitative Ultrasonic Assessment of Normal and Ischaemic Myocardium with an Acoustic Microscope: Relationship to Integrated Backscatter. Cardiovasc. Res. 1990, 24, 447–455. [Google Scholar] [CrossRef] [PubMed]
- Strowitzki, M.; Brand, S.; Jenderka, K.-V. Ultrasonic Radio-Frequency Spectrum Analysis of Normal Brain Tissue. Ultrasound Med. Biol. 2007, 33, 522–529. [Google Scholar] [CrossRef]
- Buckley, M.R.; Evans, E.B.; Matuszewski, P.E.; Chen, Y.-L.; Satchel, L.N.; Elliott, D.M.; Soslowsky, L.J.; Dodge, G.R. Distributions of Types I, II and III Collagen by Region in the Human Supraspinatus Tendon. Connect. Tissue Res. 2013, 54, 374–379. [Google Scholar] [CrossRef]
- Nieminen, H.J.; Saarakkala, S.; Laasanen, M.S.; Hirvonen, J.; Jurvelin, J.S.; Töyräs, J. Ultrasound Attenuation in Normal and Spontaneously Degenerated Articular Cartilage. Ultrasound Med. Biol. 2004, 30, 493–500. [Google Scholar] [CrossRef]
- Han, S.; Rho, J.; Medige, J.; Ziv1, I. Ultrasound Velocity and Broadband Attenuation over a Wide Range of Bone Mineral Density. Osteoporos. Int. 1996, 6, 291–296. [Google Scholar] [CrossRef]
- U.S. Department of Health and Human Services. Marketing Clearance of Diagnostic Ultrasound Systems and Transducers; FDA-2017-D-5372; U.S. Department of Health and Human Services: Washington, DC, USA, 2023.
- Sehgal, C.M.; Brown, G.M.; Bahn, R.C.; Greenleaf, J.F. Measurement and Use of Acoustic Nonlinearity and Sound Speed to Estimate Composition of Excised Livers. Ultrasound Med. Biol. 1986, 12, 865–874. [Google Scholar] [CrossRef]
- Law, W.K.; Frizzell, L.A.; Dunn, F. Determination of the Nonlinearity Parameter B/A of Biological Media. Ultrasound Med. Biol. 1985, 11, 307–318. [Google Scholar] [CrossRef]
- Fernandes, N.A.; Schmitt, S.; Martynenko, O.V. Modelling and Validation of the 3D Muscle-Tendon Unit with Solid Finite Elements in LS-DYNA for Active Human Body Model Applications. In Proceedings of the S1-8: Computer Modelling/Human Body Models, Florence, Italy, 11–13 September 2019. [Google Scholar]
- Hunt, K.D.; O’Loughlin, V.D.; Fitting, D.W.; Adler, L. Ultrasonic Determination of the Elastic Modulus of Human Cortical Bone. Med. Biol. Eng. Comput. 1998, 36, 51–56. [Google Scholar] [CrossRef] [PubMed]
- McCarty, W.J.; Pallante, A.L.; Rone, R.J.; Bugbee, W.D.; Sah, R.L. The Proteoglycan Metabolism of Articular Cartilage in Joint-Scale Culture. Tissue Eng. Part A 2010, 16, 1717–1727. [Google Scholar] [CrossRef]
- Hudson, D.M.; Archer, M.; Rai, J.; Weis, M.; Fernandes, R.J.; Eyre, D.R. Age-Related Type I Collagen Modifications Reveal Tissue-Defining Differences between Ligament and Tendon. Matrix Biol. Plus 2021, 12, 100070. [Google Scholar] [CrossRef] [PubMed]
- Rumian, A.P.; Wallace, A.L.; Birch, H.L. Tendons and Ligaments Are Anatomically Distinct but Overlap in Molecular and Morphological Features—A Comparative Study in an Ovine Model. J. Orthop. Res. 2007, 25, 458–464. [Google Scholar] [CrossRef]
- Zavolskova, M.; Senko, D.; Osetrova, M.; Efimova, O.; Stekolshchikova, E.; Vladimirov, G.; Nikolaev, E.; Khaitovich, P. Lipid Composition Diversity of the Human Brain White Matter Tracts. J. Neurochem. 2025, 169, e70042. [Google Scholar] [CrossRef]
- O’Brien, J.S.; Sampson, E.L. Lipid Composition of the Normal Human Brain: Gray Matter, White Matter, and Myelin. J. Lipid Res. 1965, 6, 537–544. [Google Scholar] [CrossRef]
- Shah, H.; Guddati, M.N. Towards Linking Histological Changes to Liver Viscoelasticity: A Hybrid Analytical-Computational Micromechanics Approach. Phys. Med. Biol. 2025, 70, 045005. [Google Scholar] [CrossRef] [PubMed]
- Nordsletten, D.; Capilnasiu, A.; Zhang, W.; Wittgenstein, A.; Hadjicharalambous, M.; Sommer, G.; Sinkus, R.; Holzapfel, G.A. A Viscoelastic Model for Human Myocardium. Acta Biomater. 2021, 135, 441–457. [Google Scholar] [CrossRef]
- Karimi, A.; Shojaei, A. Measurement of the Mechanical Properties of the Human Kidney. IRBM 2017, 38, 292–297. [Google Scholar] [CrossRef]
- Cederlund, A.A.; Aspden, R.M. Walking on Water: Revisiting the Role of Water in Articular Cartilage Biomechanics in Relation to Tissue Engineering and Regenerative Medicine. J. R. Soc. Interface. 2022, 19, 20220364. [Google Scholar] [CrossRef]
- Streitbürger, D.-P.; Möller, H.E.; Tittgemeyer, M.; Hund-Georgiadis, M.; Schroeter, M.L.; Mueller, K. Investigating Structural Brain Changes of Dehydration Using Voxel-Based Morphometry. PLoS ONE 2012, 7, e44195. [Google Scholar] [CrossRef] [PubMed]
- Huh, H.K.; Ha, H.; Lee, S.J. Effect of Non-Newtonian Viscosity on the Fluid-Dynamic Characteristics in Stenotic Vessels. Exp. Fluids 2015, 56, 167. [Google Scholar] [CrossRef]
- Weizel, A.; Distler, T.; Schneidereit, D.; Friedrich, O.; Bräuer, L.; Paulsen, F.; Detsch, R.; Boccaccini, A.R.; Budday, S.; Seitz, H. Complex Mechanical Behavior of Human Articular Cartilage and Hydrogels for Cartilage Repair. Acta Biomater. 2020, 118, 113–128. [Google Scholar] [CrossRef] [PubMed]
- Lamsfuss, J.; Bargmann, S. Skeletal Muscle: Modeling the Mechanical Behavior by Taking the Hierarchical Microstructure into Account. J. Mech. Behav. Biomed. Mater. 2021, 122, 104670. [Google Scholar] [CrossRef] [PubMed]
- Raghunathan, S.; Evans, D.; Sparks, J.L. Poroviscoelastic Modeling of Liver Biomechanical Response in Unconfined Compression. Ann. Biomed. Eng. 2010, 38, 1789–1800. [Google Scholar] [CrossRef]
- Feng, Y.; Okamoto, R.J.; Namani, R.; Genin, G.M.; Bayly, P.V. Measurements of Mechanical Anisotropy in Brain Tissue and Implications for Transversely Isotropic Material Models of White Matter. J. Mech. Behav. Biomed. Mater. 2013, 23, 117–132. [Google Scholar] [CrossRef]
- Cloutier, G.; Destrempes, F.; Yu, F.; Tang, A. Quantitative Ultrasound Imaging of Soft Biological Tissues: A Primer for Radiologists and Medical Physicists. Insights Imaging 2021, 12, 127. [Google Scholar] [CrossRef]
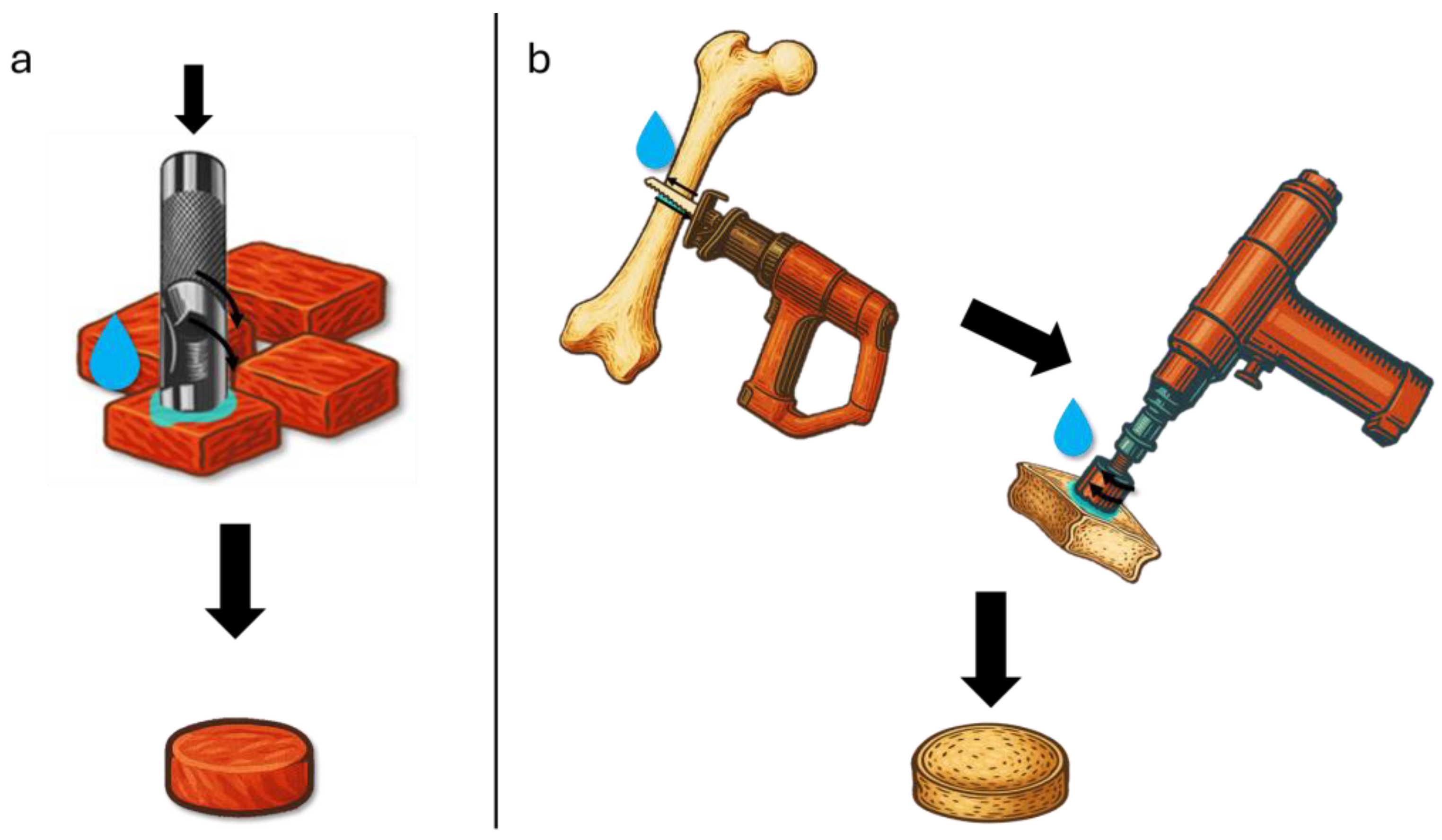







| Biological Tissue | Origin | Number of Samples |
|---|---|---|
| Skin (thigh) | Porcine | 5 |
| Adipose Tissue (thigh) | Porcine | 5 |
| Skeletal Muscle (biceps femoris) | Porcine | 10 |
| Trabecular Bone (femur) | Bovine | 5 |
| Cortical Bone (femur) | Bovine | 5 |
| Liver | Bovine | 7 |
| Myocardium | Porcine | 11 |
| Kidney | Bovine | 9 |
| Tendon (flexor digitorum medialis) | Bovine | 5 |
| Ligament (anterior cruciate ligament) | Bovine | 5 |
| Cartilage (femorotibial joint) | Bovine | 5 |
| Brain (gray matter) | Porcine | 7 |
| Brain (white matter) | Porcine | 7 |
| Sample | Number of Domain Elements | ||||
|---|---|---|---|---|---|
| Skin | 4484 | 17,668 | 70,188 | 286,734 | 454,478 |
| Adipose Tissue | 3410 | 13,436 | 53,188 | 211,874 | 336,434 |
| Skeletal Muscle (⟂ fibers) | 4746 | 18,524 | 73,650 | 302,692 | 478,522 |
| Skeletal Muscle (‖ fibers) | 7502 | 29,298 | 117,240 | 500,168 | 782,262 |
| Trabecular Bone | 8484 | 33,556 | 133,310 | 567,116 | 904,214 |
| Cortical Bone | 4560 | 17,746 | 70,728 | 291,248 | 462,560 |
| Liver | 6412 | 25,404 | 101,128 | 427,390 | 681,504 |
| Myocardium | 4594 | 17,998 | 71,446 | 295,510 | 471,958 |
| Kidney | 4444 | 17,376 | 69,188 | 285,316 | 453,792 |
| Tendon | 3658 | 14,500 | 57,632 | 235,336 | 375,674 |
| Ligament | 2500 | 9766 | 39,208 | 155,366 | 243,538 |
| Cartilage | 1720 | 6786 | 26,426 | 104,988 | 165,692 |
| Brain (gray matter) | 5992 | 23,450 | 93,336 | 394,520 | 601,568 |
| Brain (white matter) | 5838 | 22,892 | 90,890 | 380,628 | 608,176 |
| Parameters | Initial Value | Scale | Lower Bound | Upper Bound |
|---|---|---|---|---|
| Sound Diffusivity (m2/s) | 0 | 1 × 10−3 | 0 | 0.2 |
| Dynamic Viscosity (Pa·s) | 0 | 1 × 10−3 | 0 | 0.2 |
| Bulk Viscosity (Pa·s) | 0 | 0.1 | 0 | 100 |
| Sample | n | ||
|---|---|---|---|
| Skin | 1.096 | 1.157 | 0.9979 |
| Adipose Tissue | 0.7264 | 1.328 | 0.9989 |
| Skeletal Muscle (⟂ fibers) | 1.150 | 1.560 | 0.9983 |
| Skeletal Muscle (‖ fibers) | 2.870 | 1.458 | 0.9930 |
| Trabecular Bone | 1.784 | 1.525 | 0.9989 |
| Cortical Bone | 6.779 | 1.410 | 0.9999 |
| Liver | 0.5918 | 1.114 | 0.9998 |
| Myocardium | 0.5486 | 1.018 | 0.9968 |
| Kidney | 0.5115 | 1.016 | 0.9977 |
| Tendon | 4.617 | 1.123 | 0.9995 |
| Ligament | 1.489 | 1.180 | 0.9960 |
| Cartilage | 4.336 | 0.9553 | 0.9995 |
| Brain (gray matter) | 0.8513 | 0.9600 | 0.9986 |
| Brain (white matter) | 0.8862 | 1.026 | 0.9974 |
| Sample | n | ||
|---|---|---|---|
| Skin | 0.0026 | −0.934 | 0.9908 |
| Adipose Tissue | 0.0012 | −0.608 | 1 |
| Skeletal Muscle (⟂ fibers) | 0.0024 | −0.349 | 0.9980 |
| Skeletal Muscle (‖ fibers) | 0.0068 | −0.379 | 0.9862 |
| Trabecular Bone | 0.0126 | −0.364 | 0.9955 |
| Cortical Bone | 0.0837 | −1.094 | 0.9965 |
| Liver | 0.0011 | −0.842 | 1 |
| Myocardium | 0.0011 | −0.936 | 1 |
| Kidney | 0.0010 | −0.941 | 1 |
| Tendon | 0.0168 | −0.801 | 0.999 |
| Ligament | 0.0038 | −0.758 | 0.999 |
| Cartilage | 0.0261 | −1.654 | 0.941 |
| Brain (gray matter) | 0.0017 | −1.002 | 1 |
| Brain (white matter) | 0.0017 | −0.932 | 1 |
| Sample | n | ||
|---|---|---|---|
| Skin | 0.132 | −0.454 | 0.9946 |
| Adipose Tissue | 0.019 | −0.883 | 0.9975 |
| Skeletal Muscle (⟂ fibers) | 0.0071 | −1.304 | 0.9685 |
| Skeletal Muscle (‖ fibers) | 0.0014 | 2.6616 | 0.9966 |
| Trabecular Bone | 0.0053 | 1.4635 | 0.998 |
| Cortical Bone | 0.2306 | 0.7249 | 0.9956 |
| Liver | 0.0219 | −1.123 | 0.9938 |
| Myocardium | 0.0077 | −1.077 | 0.9958 |
| Kidney | 0.0021 | −1.572 | 0.9966 |
| Tendon | 0.0009 | −0.588 | 0.9949 |
| Ligament | 0.0122 | −0.814 | 0.9682 |
| Cartilage | 0.0526 | −1.227 | 0.9997 |
| Brain (gray matter) | 0.0099 | −0.501 | 0.9816 |
| Brain (white matter) | 0.0105 | −0.506 | 0.9522 |
| Sample | n | ||
|---|---|---|---|
| Skin | 3.0126 | −0.794 | 1 |
| Adipose Tissue | 1.0874 | −0.61 | 0.9999 |
| Skeletal Muscle (⟂ fibers) | 2.5212 | −0.351 | 0.997 |
| Skeletal Muscle (‖ fibers) | 7.0265 | −0.429 | 0.9963 |
| Trabecular Bone | 7.1265 | −0.378 | 0.9973 |
| Cortical Bone | 238.62 | −0.504 | 0.9931 |
| Liver | 1.1997 | −0.846 | 0.9999 |
| Myocardium | 1.2287 | −0.933 | 0.9999 |
| Kidney | 1.036 | −0.929 | 0.9998 |
| Tendon | 18.626 | −0.822 | 0.9987 |
| Ligament | 4.0994 | −0.769 | 0.9999 |
| Cartilage | 12.646 | −0.958 | 0.9992 |
| Brain (gray matter) | 1.7933 | −1.007 | 1 |
| Brain (white matter) | 1.7447 | −0.937 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandes, N.A.T.C.; Sharma, S.; Arieira, A.; Hinckel, B.; Silva, F.; Leal, A.; Carvalho, Ó. Experimental Validation of Time-Explicit Ultrasound Propagation Models with Sound Diffusivity or Viscous Attenuation in Biological Tissues Using COMSOL Multiphysics. Bioengineering 2025, 12, 946. https://doi.org/10.3390/bioengineering12090946
Fernandes NATC, Sharma S, Arieira A, Hinckel B, Silva F, Leal A, Carvalho Ó. Experimental Validation of Time-Explicit Ultrasound Propagation Models with Sound Diffusivity or Viscous Attenuation in Biological Tissues Using COMSOL Multiphysics. Bioengineering. 2025; 12(9):946. https://doi.org/10.3390/bioengineering12090946
Chicago/Turabian StyleFernandes, Nuno A. T. C., Shivam Sharma, Ana Arieira, Betina Hinckel, Filipe Silva, Ana Leal, and Óscar Carvalho. 2025. "Experimental Validation of Time-Explicit Ultrasound Propagation Models with Sound Diffusivity or Viscous Attenuation in Biological Tissues Using COMSOL Multiphysics" Bioengineering 12, no. 9: 946. https://doi.org/10.3390/bioengineering12090946
APA StyleFernandes, N. A. T. C., Sharma, S., Arieira, A., Hinckel, B., Silva, F., Leal, A., & Carvalho, Ó. (2025). Experimental Validation of Time-Explicit Ultrasound Propagation Models with Sound Diffusivity or Viscous Attenuation in Biological Tissues Using COMSOL Multiphysics. Bioengineering, 12(9), 946. https://doi.org/10.3390/bioengineering12090946










