Ultrasonic Surgical Aspirator in Intramedullary Spinal Cord Tumours Treatment: A Simulation Study of Vibration and Temperature Field
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Construction
2.2. Finite Element Analysis (FEA)
2.3. Model Boundary and Initial Conditions
3. Results
3.1. Strain Fields
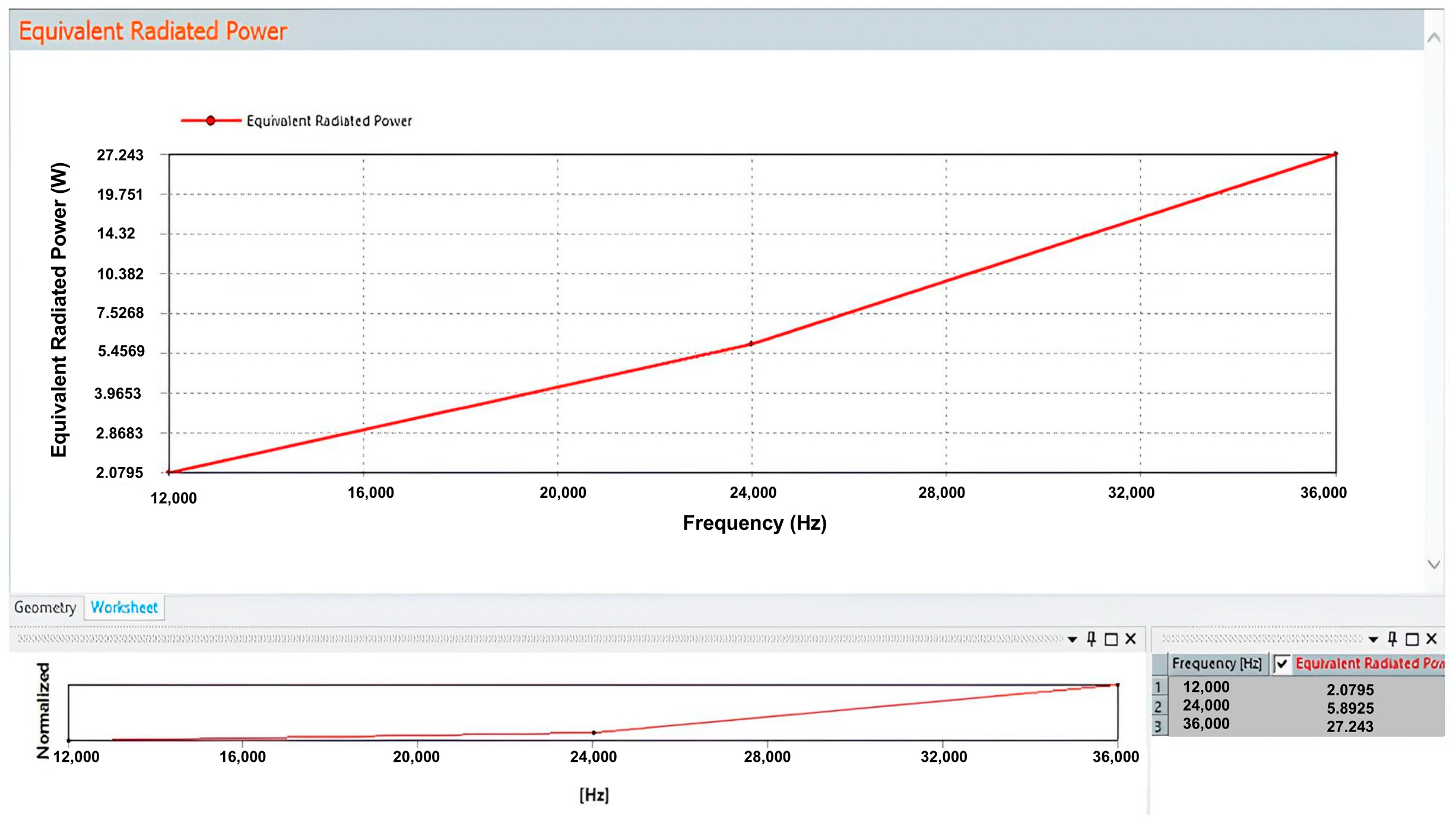
3.2. Heat Generation Estimation
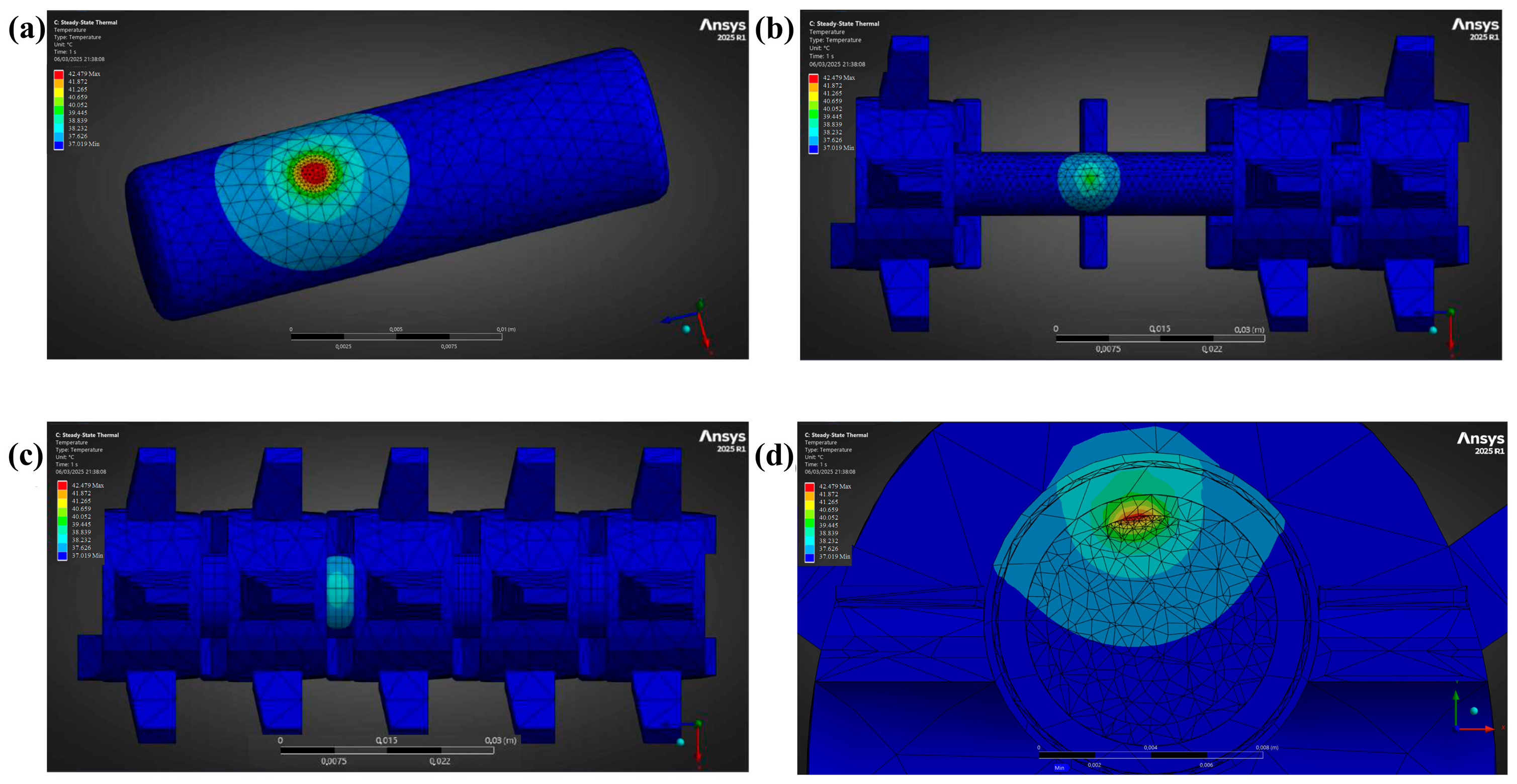
3.3. Temperature Fields
4. Discussions and Model Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Samartzis, D.; Gillis, C.C.; Shih, P.; O’Toole, J.E.; Fessler, R.G. Intramedullary Spinal Cord Tumors: Part I—Epidemiology, Pathophysiology, and Diagnosis. Glob. Spine J. 2015, 5, 425–435. [Google Scholar] [CrossRef]
- Houten, J.K.; Weiner, H.L. Pediatric Intramedullary Spinal Cord Tumors: Special Considerations. J. Neurooncol. 2000, 47, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Hongo, H.; Takai, K.; Komori, T.; Taniguchi, M. Intramedullary Spinal Cord Ependymoma and Astrocytoma: Intraoperative Frozen-Section Diagnosis, Extent of Resection, and Outcomes. J. Neurosurg. Spine 2019, 30, 133–139. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; Kim, J.H.; Choi, S.H.; Sohn, C.H.; Yun, T.J.; Kim, C.H.; Chang, K.H. Differentiation between Intramedullary Spinal Ependymoma and Astrocytoma: Comparative MRI Analysis. Clin. Radiol. 2014, 69, 29–35. [Google Scholar] [CrossRef]
- Berhouma, M.; Bahri, K.; Houissa, S.; Zemmel, I.; Khouja, N.; Aouidj, L.; Jemel, H.; Khaldi, M. Management of Intramedullary Spinal Cord Tumors: Surgical Considerations and Results in 45 Cases. Neurochirurgie 2009, 55, 293–302. [Google Scholar] [CrossRef] [PubMed]
- Barzilai, O.; Lidar, Z.; Constantini, S.; Salame, K.; Bitan-Talmor, Y.; Korn, A. Continuous Mapping of the Corticospinal Tracts in Intramedullary Spinal Cord Tumor Surgery Using an Electrified Ultrasonic Aspirator. J. Neurosurg. Spine 2017, 27, 161–168. [Google Scholar] [CrossRef]
- Pio, L.; Guérin, F.; Martucci, C.; Martelli, H.; Gauthier, F.; Branchereau, S. The Use of Cavitron Ultrasonic Surgical Aspirator for High-Risk Neuroblastoma with Image-Defined Risk Factors in Children. Children 2023, 10, 89. [Google Scholar] [CrossRef]
- Wang, Y.H.; Tsai, S.C.S.; Lin, F.C.F. Reduction of Blood Loss by Means of the Cavitron Ultrasonic Surgical Aspirator for Thoracoscopic Salvage Anatomic Lung Resections. Cancers 2023, 15, 4069. [Google Scholar] [CrossRef]
- Jallo, G.I. CUSA EXcel Ultrasonic Aspiration System. Neurosurgery 2001, 48, 695–697. [Google Scholar] [CrossRef]
- Sharma, A.; Chauhan, S.S.; Sinha, A.; Sharma, S.; Gupta, V.; Singh, G.; Agrawal, R. Cusa (Cavitron Ultrasonic Surgical Aspirator) “The New Armour of Periodontal Therapy”. Int. J. Innov. Sci. Res. Technol. 2022, 7, 1529–1531. [Google Scholar]
- Zhang, Y.; Luo, X.; Wu, W.; Zhang, Q.; Xiong, S.; Lin, S.; Zhou, P.; Xu, Y.; Hu, M.; Zhou, Z. Identification of Key Performance Metrics for Different Ultrasonic Surgical Devices. Proc. J. Phys. Conf. Ser. Inst. Phys. 2024, 2822, 012006. [Google Scholar] [CrossRef]
- Suetsuna, F.; Harata, S.; Yoshimura, N. Influence of the Ultrasonic Surgical Aspirator on the Dura and Spinal Cord: An Electrohistologic Study. Spine 1991, 16, 503–509. [Google Scholar] [CrossRef]
- Young, W.; Cohen, A.R.; Hunt, C.D.; Ransohoff, J. Acute Physiological Effects of Ultrasonic Vibrations on Nervous Tissue. Neurosurgery 1981, 8, 689–694. [Google Scholar] [CrossRef]
- Davidson, C.L.; Das, J.M.; Mesfin, F.B. Intramedullary Spinal Cord Tumors; StatPearls Publishing: Treasure Island, FL, USA, 2025. [Google Scholar]
- Kane, P.J.; El-Mahdy, W.; Singh, A.; Powell, M.P.; Crockard, H.A. Spinal Intradural Tumours: Part II—Intramedullary. Br. J. Neurosurg. 1999, 13, 558–563. [Google Scholar] [CrossRef]
- Wu, C.Y.; Yeh, W.C.; Chang, S.M.; Hsu, C.W.; Lin, Z.J. The Application of Deep Learning to Accurately Identify the Dimensions of Spinal Canal and Intervertebral Foramen as Evaluated by the IoU Index. Bioengineering 2024, 11, 981. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chen, X.; Liu, B.; Hai, J.; Qiao, K.; Yuan, Z.; Yang, L.; Yan, B.; Su, Z.; Lu, H. Deep-Learning-Based Computer-Aided Grading of Cervical Spinal Stenosis from MR Images: Accuracy and Clinical Alignment. Bioengineering 2025, 12, 604. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, L.; Cavarzan, F.; Ciampitti, L.; Cremonesi, M.; Grilli, F.; Saccomandi, P. Thermophysical and mechanical properties of biological tissues as a function of temperature: A systematic literature review. Int. J. Hyperth. 2022, 39, 297–340. [Google Scholar] [CrossRef] [PubMed]
- Scott, S.J.; Salgaonkar, V.; Prakash, P.; Burdette, E.C.; Diederich, C.J. Interstitial Ultrasound Ablation of Vertebral and Paraspinal Tumours: Parametric and Patient-Specific Simulations. Int. J. Hyperth. 2014, 30, 228–244. [Google Scholar] [CrossRef]
- Tschirhart, C.E.; Nagpurkar, A.; Whyne, C.M. Effects of Tumor Location, Shape and Surface Serration on Burst Fracture Risk in the Metastatic Spine. J. Biomech. 2004, 37, 653–660. [Google Scholar] [CrossRef]
- Falcinelli, C.; Di Martino, A.; Gizzi, A.; Vairo, G.; Denaro, V. Mechanical Behavior of Metastatic Femurs through Patient-Specific Computational Models Accounting for Bone-Metastasis Interaction. J. Mech. Behav. Biomed. Mater. 2019, 93, 9–22. [Google Scholar] [CrossRef]
- Zannou, A.L.; Khadka, N.; FallahRad, M.; Truong, D.Q.; Kopell, B.H.; Bikson, M. Tissue Temperature Increases by a 10 KHz Spinal Cord Stimulation System: Phantom and Bioheat Model. Neuromodulation 2021, 24, 1327–1335. [Google Scholar] [CrossRef]
- Zannou, A.L.; Khadka, N.; Truong, D.Q.; Zhang, T.; Esteller, R.; Hershey, B.; Bikson, M. Temperature Increases by Kilohertz Frequency Spinal Cord Stimulation. Brain Stimul. 2019, 12, 62–72. [Google Scholar] [CrossRef]
- Pisu, S.; Cosentino, M.; Apa, L.; Musarò, A.; Rizzuto, E.; Prete, Z.D. Measuring the Maximum Power of an Ex Vivo Engineered Muscle Tissue with Isovelocity Shortening Technique. IEEE Trans. Instrum. Meas. 2019, 68, 2404–2411. [Google Scholar] [CrossRef]
- Katsamba, I.; Evangelidis, P.; Voutouri, C.; Tsamis, A.; Vavourakis, V.; Stylianopoulos, T. Biomechanical Modelling of Spinal Tumour Anisotropic Growth. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190364. [Google Scholar] [CrossRef]
- Cardillo, G.; Camporeale, C. Modeling Fluid–Structure Interactions between Cerebro-Spinal Fluid and the Spinal Cord. J. Fluids Struct. 2021, 102, 103251. [Google Scholar] [CrossRef]
- Hipp, J.A.; Rosenberg, A.E.; Hayes, W.C. Mechanical Properties of Trabecular Bone within and Adjacent to Osseous Metastases. J. Bone Miner. Res. 1992, 7, 1165–1171. [Google Scholar] [CrossRef]
- Feldmann, A.; Wili, P.; Maquer, G.; Zysset, P. The Thermal Conductivity of Cortical and Cancellous Bone. Eur. Cell Mater. 2018, 35, 25–33. [Google Scholar] [CrossRef]
- Xu, X.; Rioux, T.P.; Castellani, M.P. The Specific Heat of the Human Body Is Lower than Previously Believed: The Journal Temperature Toolbox. Temperature 2023, 10, 235–239. [Google Scholar] [CrossRef] [PubMed]
- Comley, K.; Fleck, N.A. A Micromechanical Model for the Young’s Modulus of Adipose Tissue. Int. J. Solids Struct. 2010, 47, 2982–2990. [Google Scholar] [CrossRef]
- Nedergaard, J.; Cannon, B. Brown Adipose Tissue as a Heat-Producing Thermoeffector. In Handbook of Clinical Neurology; Elsevier: Amsterdam, The Netherlands, 2018; Volume 156. [Google Scholar]
- De Kegel, D.; Vastmans, J.; Fehervary, H.; Depreitere, B.; Vander Sloten, J.; Famaey, N. Biomechanical Characterization of Human Dura Mater. J. Mech. Behav. Biomed. Mater. 2018, 79, 122–134. [Google Scholar] [CrossRef]
- Nagel, S.J.; Reddy, C.G.; Frizon, L.A.; Chardon, M.K.; Holland, M.; Machado, A.G.; Gillies, G.T.; Howard, M.A.; Wilson, S. Spinal Dura Mater: Biophysical Characteristics Relevant to Medical Device Development. J. Med. Eng. Technol. 2018, 42, 128–139. [Google Scholar] [CrossRef] [PubMed]
- Eslaminejad, A.; Sarvghad-Moghaddam, H.; Rezaei, A.; Ziejewski, M.; Karami, G. Comparison of Brain Tissue Material Finite Element Models Based on Threshold for Traumatic Brain Injury. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Proceedings (IMECE), Phoenix, AZ, USA, 11–17 November 2016; Volume 3. [Google Scholar]
- Karimi, A.; Shojaei, A.; Tehrani, P. Mechanical Properties of the Human Spinal Cord under the Compressive Loading. J. Chem. Neuroanat. 2017, 86, 15–18. [Google Scholar] [CrossRef]
- Bhargav, A.G.; Domino, J.S.; Chamoun, R.; Thomas, S.M. Mechanical Properties in the Glioma Microenvironment: Emerging Insights and Theranostic Opportunities. Front. Oncol. 2022, 11, 805628. [Google Scholar] [CrossRef]
- Yacoob, S.M.; Hassan, N.S. FDTD Analysis of a Noninvasive Hyperthermia System for Brain Tumors. Biomed. Eng. Online 2012, 11, 47. [Google Scholar] [CrossRef]
- Popiel, C.O. Free Convection Heat Transfer from Vertical Slender Cylinders: A Review. Heat Transf. Eng. 2008, 29, 521–536. [Google Scholar] [CrossRef]
- Peeters, H.; van Zwol, E.M.; Brancato, L.; da Cunha, M.G.M.C.; Bogers, J. Systematic Review of the Registered Clinical Trials for Oncological Hyperthermia Treatment. Int. J. Hyperth. 2022, 39, 806–812. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, S.; Yashiro, K.; Takahashi, H.; Homma, T. An Experimental Study of Spinal Cord Evoked Potentials and Histologic Changes Following Spinal Cord Heating. Spine 1989, 14, 1215–1219. [Google Scholar] [CrossRef] [PubMed]
- Yamane, T.; Tateishi, A.; Cho, S.; Manabe, S.; Yamanashi, M.; Dezawa, A.; Yasukouchi, H.; Ishioka, K. The Effects of Hyperthermia on the Spinal Cord. Spine 1992, 17, 1386–1391. [Google Scholar] [CrossRef]
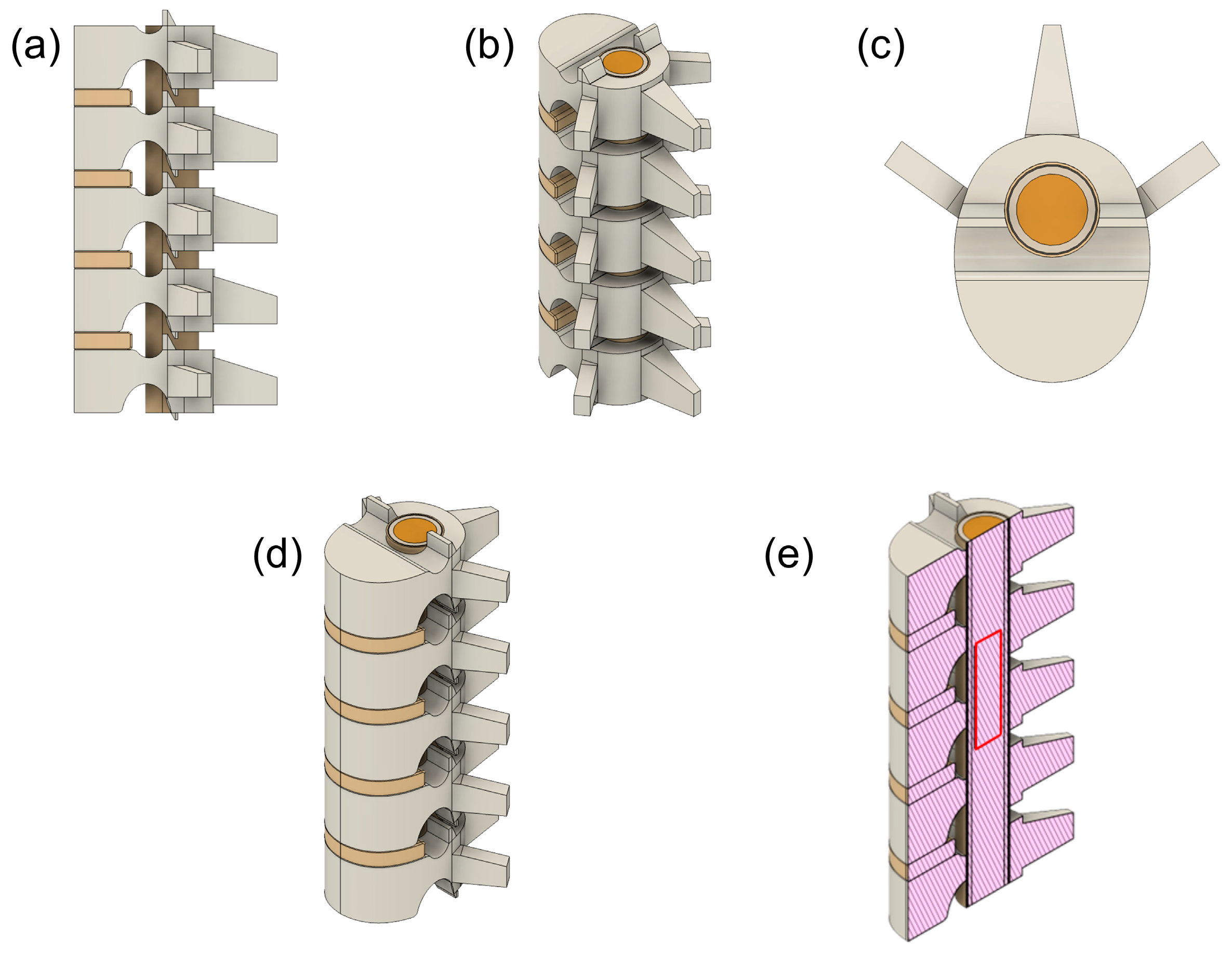






| Element | Measurement | Dimension (mm) |
|---|---|---|
| Overall Cervical C3–C7 | total height | 90 |
| body height | 14 | |
| Vertebra | mediolateral width | 24.5 |
| anteroposterior width | 14 | |
| cavity diameter | 12 | |
| Intervertebral Disc | height | 4 |
| Epidural Fat | diameter | 12 |
| thickness | 0.3 | |
| Dura Mater | diameter | 11.4 |
| thickness | 0.2 | |
| CSF | diameter | 11 |
| thickness | 1 | |
| Spinal Cord | diameter | 9 |
| Tumour | diameter | 7 |
| body height | 25 |
| Tissue | Density (g/cm3) | Young’s Modulus (MPa) | Poisson’s Ratio | Thermal Conductivity (W/m °C) | Heat Capacity (J/kg °C) |
|---|---|---|---|---|---|
| Bone | 0.131 [27] | 7600 [25] | 0.3 [25] | 0.68 [28] | 1313 [29] |
| Intervertebral Disc | 1.1 [18] | 500 [25] | 0.3 [25] | 0.49 [18] | 3568 [18] |
| Epidural Fat | 0.911 [18] | 3 [30] | 0.49 [23] | 0.2 [31] | 2348 [29] |
| Dura Mater | 1.174 [18] | 31.5 [32] | 0.3 [32] | 0.44 [33] | 3364 [33] |
| CSF | 1 [26] | 10−3 [26] | 0.4887 [34] | 0.57 [18] | 4096 [18] |
| Spinal Cord | 1.075 [18] | 40.12 × 10−3 [35] | 0.49 [25] | 0.51 [18] | 3630 [18] |
| Tumour (glioma) | 1.075 [18] | 1.8 × 10−3 [36] | 0.3 [36] | 0.5 [37] | 3621 [37] |
| Element | Temperature (°C) | |
|---|---|---|
| 70 μm Displacement | 213 μm Displacement | |
| Tumour | 37.59 | 42.48 |
| Bone | 37.07 | 37.62 |
| Intervertebral Disc | 37.02 | 37.02 |
| Epidural Fat | 37.18 | 38.75 |
| Dura Mater | 37.19 | 38.83 |
| CSF | 37.27 | 39.45 |
| Spinal Cord | 37.57 | 41.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apa, L.; Palmieri, M.; Familiari, P.; Rizzuto, E.; Del Prete, Z. Ultrasonic Surgical Aspirator in Intramedullary Spinal Cord Tumours Treatment: A Simulation Study of Vibration and Temperature Field. Bioengineering 2025, 12, 842. https://doi.org/10.3390/bioengineering12080842
Apa L, Palmieri M, Familiari P, Rizzuto E, Del Prete Z. Ultrasonic Surgical Aspirator in Intramedullary Spinal Cord Tumours Treatment: A Simulation Study of Vibration and Temperature Field. Bioengineering. 2025; 12(8):842. https://doi.org/10.3390/bioengineering12080842
Chicago/Turabian StyleApa, Ludovica, Mauro Palmieri, Pietro Familiari, Emanuele Rizzuto, and Zaccaria Del Prete. 2025. "Ultrasonic Surgical Aspirator in Intramedullary Spinal Cord Tumours Treatment: A Simulation Study of Vibration and Temperature Field" Bioengineering 12, no. 8: 842. https://doi.org/10.3390/bioengineering12080842
APA StyleApa, L., Palmieri, M., Familiari, P., Rizzuto, E., & Del Prete, Z. (2025). Ultrasonic Surgical Aspirator in Intramedullary Spinal Cord Tumours Treatment: A Simulation Study of Vibration and Temperature Field. Bioengineering, 12(8), 842. https://doi.org/10.3390/bioengineering12080842









