Finite Element Analysis of Biomechanical Assessment: Traditional Bilateral Pedicle Screw System vs. Novel Reverse Transdiscal Screw System for Lumbar Degenerative Disc Disease
Abstract
1. Introduction
2. Materials and Methods
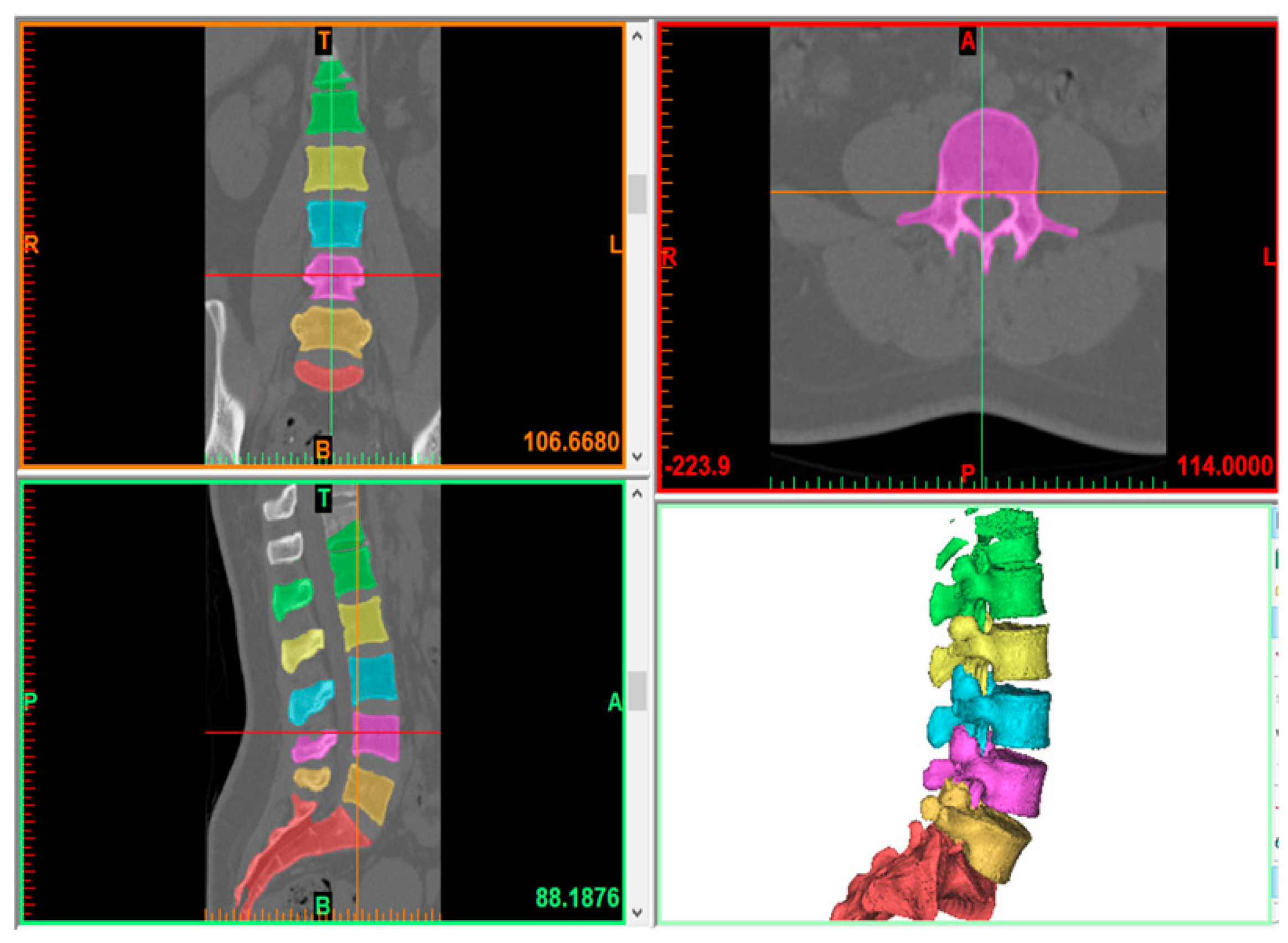
2.1. Model Creation
2.2. Finite Element Model
2.3. Contact, Loading, and Boundary Conditions
| Component | Young Modulus (Mpa) | Poisson Ratio | Element Type |
|---|---|---|---|
| Cortical [23] | 12,000 | 0.3 | Tetrahedral element |
| Cancellous [23,24] | 100 | 0.2 | Tetrahedral element |
| Endplate [25] | 500 | 0.45 | Tetrahedral element |
| Annulus ground [23] | 4.2 | 0.45 | Hexahedral element |
| Annulus fiber [17,26,27,28] | 360–450 | Cross-sectional area (0.15 mm2) | Link element |
| Ligament [23,28,29,30] | Calibrated force–deflection curve | Spring element | |
| Nucleus [29] | 1 | 0.4 | Tetrahedral element |
| Titanium [30] | 110,000 | 0.3 | Tetrahedral element |
3. Results
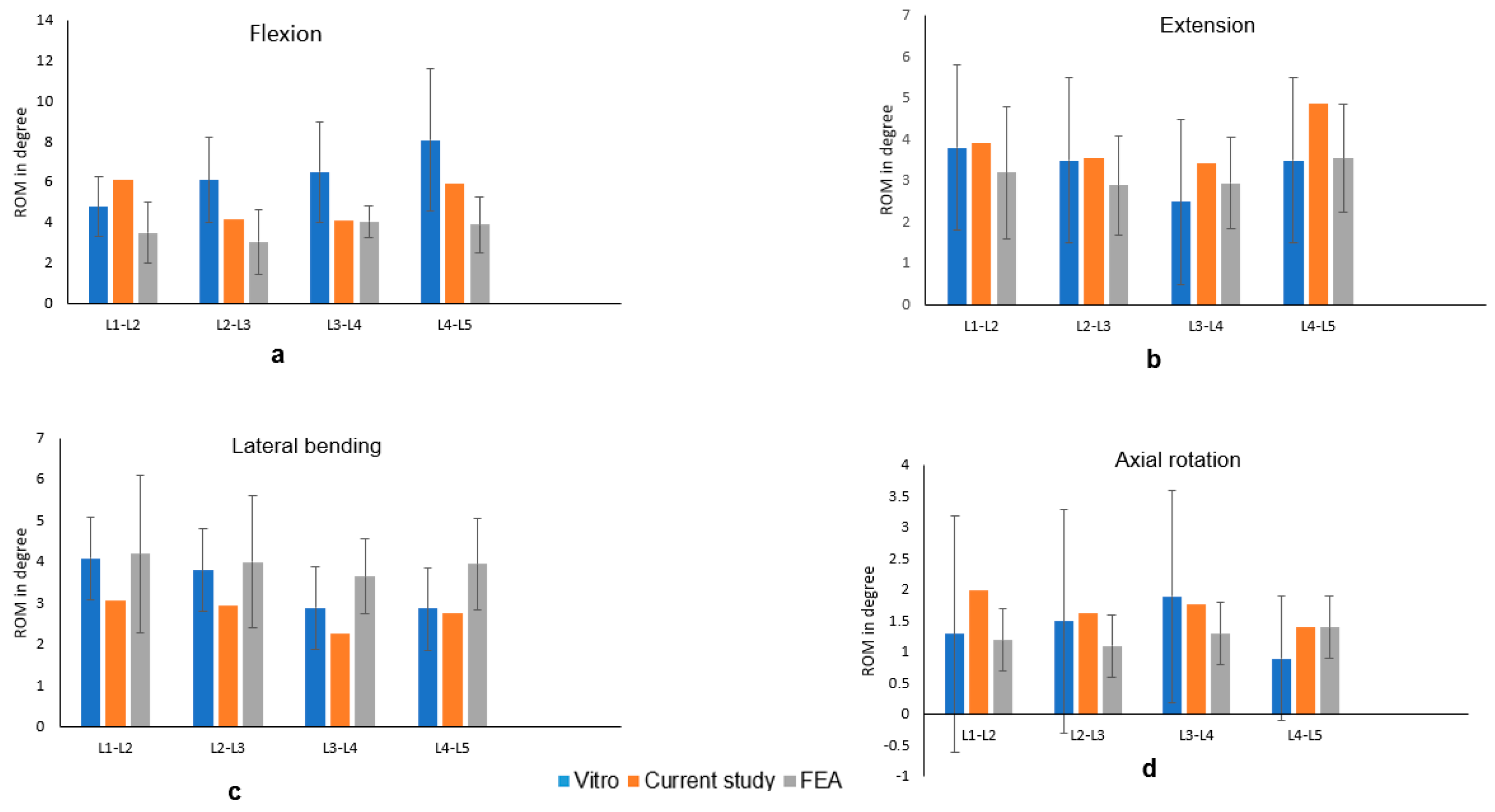
3.1. FE Model Validation
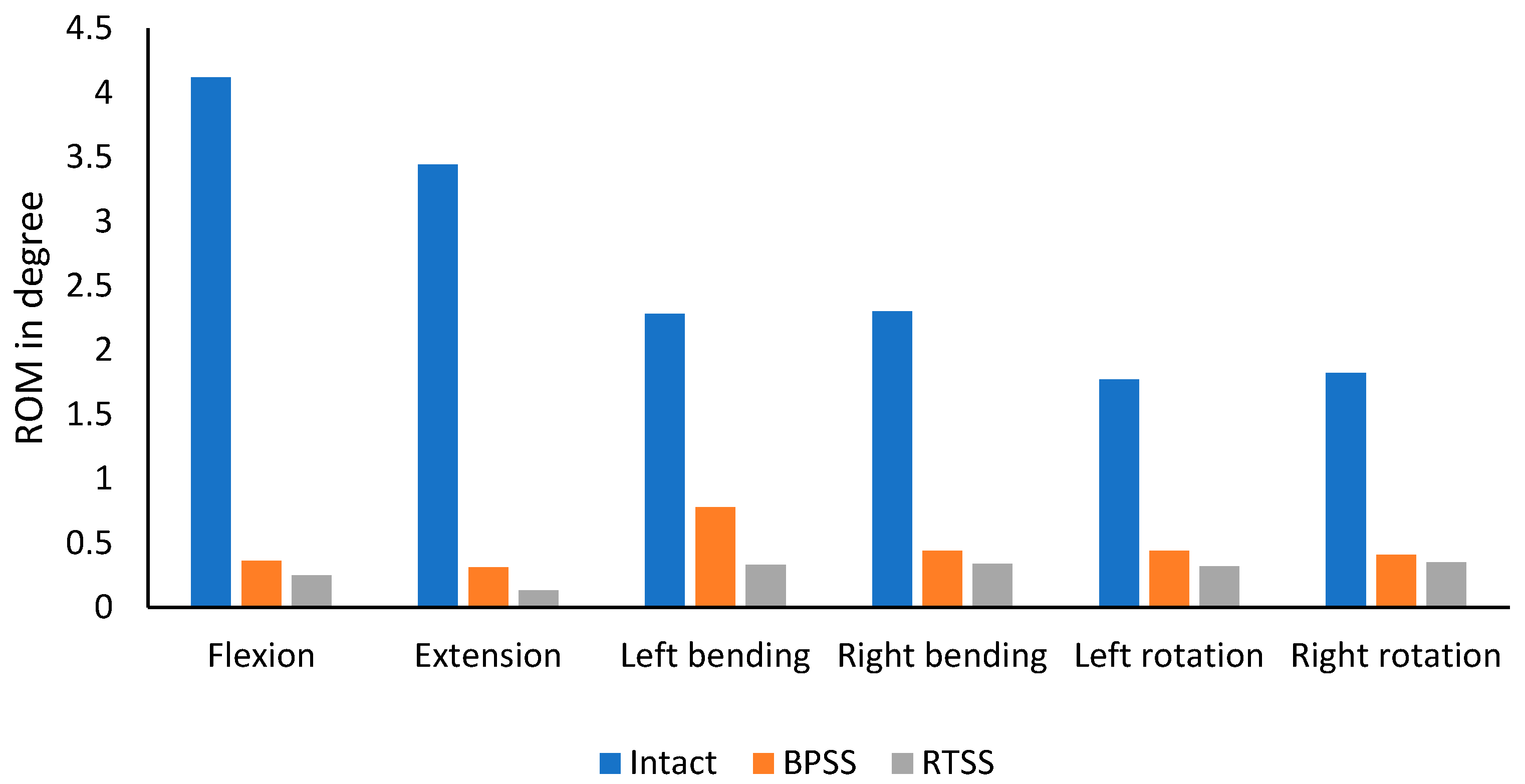
3.2. ROM
3.3. Cage von Mises Stress
3.4. Screw von Mises Stress
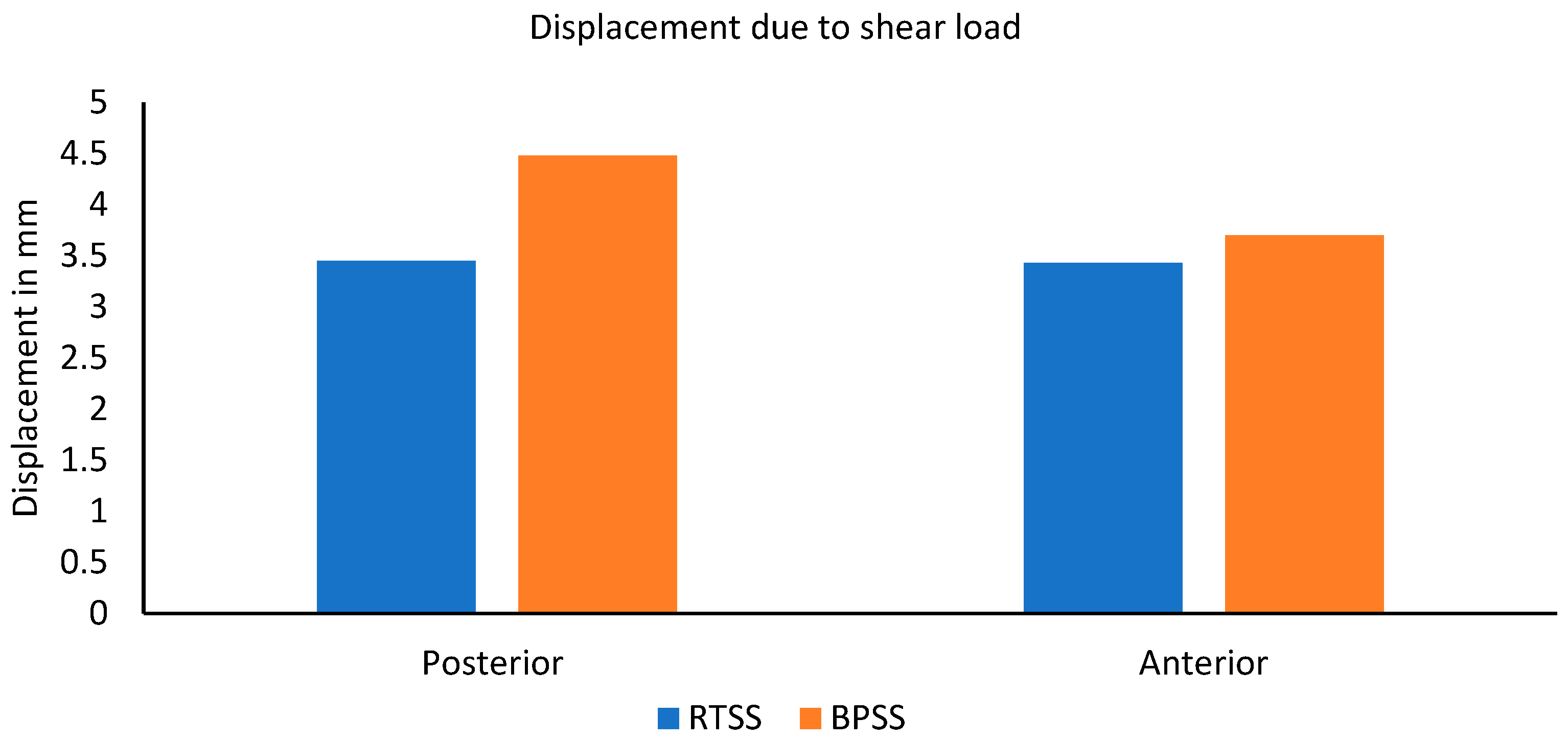
3.5. Resistance to Shear Load
4. Discussion
5. Conclusions
6. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, Y.C.; Zotti, M.G.T.; Osti, O.L. Operative Management of Lumbar Degenerative Disc Disease. Asian Spine J. 2016, 10, 801–819. [Google Scholar] [CrossRef] [PubMed]
- Mok, J.M.; Forsthoefel, C.; Diaz, R.L.; Lin, Y.; Amirouche, F. Biomechanical Comparison of Unilateral and Bilateral Pedicle Screw Fixation after Multilevel Lumbar Lateral Interbody Fusion. Glob. Spine J. 2022, 14, 1524–1531. [Google Scholar] [CrossRef]
- Dhar, U.K.; Sultan, H.; Aghayev, K.; Tsai, C.-T.; Vrionis, F.D. Biomechanical assessment of anterior plate system, bilateral pedicle screw and transdiscal screw system for high-grade spondylolisthesis: A finite element study. Front. Bioeng. Biotechnol. 2024, 12, 1491420. [Google Scholar] [CrossRef]
- Aghayev, K.; Dhar, U.K.; Tsai, C.-T.; Ahmedov, M.; Vrionis, F.D. Sacrolumbar Interbody Fusion (SLIF): Feasibility, Technical Nuances, Biomechanical Assessment, and Clinical Outcomes. Spine Surg. Relat. Res. 2024, 8, 448–457. [Google Scholar] [CrossRef]
- Pietrantonio, A.; Trungu, S.; Famà, I.; Forcato, S.; Miscusi, M.; Raco, A. Long-term clinical outcomes after bilateral laminotomy or total laminectomy for lumbar spinal stenosis: A single-institution experience. Neurosurg. Focus 2019, 46, E2. [Google Scholar] [CrossRef] [PubMed]
- Natarajan, R.N.; Garretson, R.B.; Biyani, A.; Lim, T.H.; Andersson, G.B.J.; An, H.S. Effects of slip severity and loading directions on the stability of isthmic spondylolisthesis: A finite element model study. Spine 2003, 28, 1103–1112. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Mo, Z.; Li, D.; Yang, B.; Huang, S.; Tang, S. Biomechanical Comparison of Lumbar Fixed-Point Oblique Pulling Manipulation and Traditional Oblique Pulling Manipulation in Treating Lumbar Intervertebral Disk Protrusion. J. Manip. Physiol. Ther. 2020, 43, 446–456. [Google Scholar] [CrossRef]
- Obeidallah, M.; Hamad, M.K.; Holland, R.; Mammis, A. The Use of a Transforaminal Lumbar Interbody Fusion (TLIF) Cage Following Inadequate Access to the Disc Space During an Anterior Lumbar Interbody Fusion Procedure. Cureus 2022, 14, e22792. [Google Scholar] [CrossRef]
- Gum, J.L.; Reddy, D.; Glassman, S. Transforaminal Lumbar Interbody Fusion (TLIF). JBJS Essent. Surg. Tech. 2016, 6, e22. [Google Scholar] [CrossRef]
- Cai, X.; Sun, M.; Huang, Y.; Liu, Z.; Liu, C.; Du, C.; Yang, Q. Biomechanical Effect of L4–L5 Intervertebral Disc Degeneration on the Lower Lumbar Spine: A Finite Element Study. Orthop. Surg. 2020, 12, 917–930. [Google Scholar] [CrossRef]
- Li, Q.Y.; Kim, H.-J.; Son, J.; Kang, K.-T.; Chang, B.-S.; Lee, C.-K.; Seok, H.S.; Yeom, J.S. Biomechanical analysis of lumbar decompression surgery in relation to degenerative changes in the lumbar spine—Validated finite element analysis. Comput. Biol. Med. 2017, 89, 512–519. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, K.; Shah, A.; Kelkar, A.; Parajuli, D.; Sudershan, S.; Goel, V.K.; Sairyo, K. Biomechanical evaluation of a novel decompression surgery: Transforaminal full-endoscopic lateral recess decompression (TE-LRD). N. Am. Spine Soc. J. 2021, 5, 100045. [Google Scholar] [CrossRef]
- Kang, S.; Park, C.-H.; Jung, H.; Lee, S.; Min, Y.-S.; Kim, C.-H.; Cho, M.; Jung, G.-H.; Kim, D.-H.; Kim, K.-T.; et al. Analysis of the physiological load on lumbar vertebrae in patients with osteoporosis: A finite-element study. Sci. Rep. 2022, 12, 11001. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Niu, W.-X.; Zeng, Z.-L.; Tong, J.-H.; Zhen, Z.-W.; Zhou, S.; Yu, Y.; Cheng, L.-M. The effects of muscle weakness on degenerative spondylolisthesis: A finite element study. Clin. Biomech. 2017, 41, 34–38. [Google Scholar] [CrossRef]
- Lin, M.; Paul, R.; Dhar, U.K.; Doulgeris, J.; O’cOnnor, T.E.; Tsai, C.-T.; Vrionis, F.D. A Review of Finite Element Modeling for Anterior Cervical Discectomy and Fusion. Asian Spine J. 2023, 17, 949–963. [Google Scholar] [CrossRef]
- Xu, Z.; Zheng, Q.; Zhang, L.; Chen, R.; Li, Z.; Xu, W. Biomechanical evaluation of different oblique lumbar interbody fusion constructs: A finite element analysis. BMC Musculoskelet. Disord. 2024, 25, 97. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.S.; Lee, K.; Kim, D. Biomechanical study of lumbar spine with dynamic stabilization device using finite element method. Comput. Des. 2007, 39, 559–567. [Google Scholar] [CrossRef]
- Spina, N.T.; Moreno, G.S.; Brodke, D.S.; Finley, S.M.; Ellis, B.J. Biomechanical effects of laminectomies in the human lumbar spine: A finite element study. Spine J. 2021, 21, 150–159. [Google Scholar] [CrossRef]
- Ahuja, S.; Moideen, A.N.; Dudhniwala, A.G.; Karatsis, E.; Papadakis, L.; Varitis, E. Lumbar stability following graded unilateral and bilateral facetectomy: A finite element model study. Clin. Biomech. 2020, 75, 105011. [Google Scholar] [CrossRef]
- Edwards, W.T.; Zheng, Y.; Ferrara, L.A.; Yuan, H.A. Structural features and thickness of the vertebral cortex in the thoracolumbar spine. Spine 2001, 26, 218–225. [Google Scholar] [CrossRef]
- Nachemson, A.L.; Schultz, A.B.; Berkson, M.H. Mechanical properties of human lumbar spine motion segments. Influence of age, sex, disc level, and degeneration. Spine 1979, 4, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Panjabi, M.M.; Krag, M.H.; Chung, T.Q. Effects of Disc Injury on Mechanical Behavior of the Human Spine. Spine 1984, 9, 707–713. [Google Scholar] [CrossRef] [PubMed]
- Shirazi-Adl, S.A.; Shrivastava, S.C.; Ahmed, A.M. Stress analysis of the lumbar disc-body unit in compression. A three-dimensional nonlinear finite element study. Spine 1984, 9, 120–134. [Google Scholar] [CrossRef] [PubMed]
- Carter, D.R.; Caler, W.E.; Spengler, D.M.; Frankel, V.H. Fatigue behavior of adult cortical bone: The influence of mean strain and strain range. Acta Orthop. 1981, 52, 481–490. [Google Scholar] [CrossRef]
- Panjabi, M.M.; Crisco, J.J.; Vasavada, A.; Oda, T.; Cholewicki, J.; Nibu, K.; Shin, E. Mechanical properties of the human cervical spine as shown by three-dimensional load–displacement curves. Spine 2001, 26, 2692–2700. [Google Scholar] [CrossRef]
- Bereczki, F.; Turbucz, M.; Kiss, R.; Eltes, P.E.; Lazary, A. Stability Evaluation of Different Oblique Lumbar Interbody Fusion Constructs in Normal and Osteoporotic Condition–A Finite Element Based Study. Front. Bioeng. Biotechnol. 2021, 9, 749914. [Google Scholar] [CrossRef] [PubMed]
- Eberlein, R.; Holzapfel, G.A.; Fröhlich, M. Multi-segment FEA of the human lumbar spine including the heterogeneity of the annulus fibrosus. Comput. Mech. 2004, 34, 147–163. [Google Scholar] [CrossRef]
- Wang, Q.-D.; Guo, L.-X. Biomechanical role of cement augmentation in the vibration characteristics of the osteoporotic lumbar spine after lumbar interbody fusion. J. Mater. Sci. Mater. Med. 2022, 33, 52. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Z.; Lu, C.; Zhao, L.; Feng, C.; Wang, Y.; Zhang, Y. Oblique lateral interbody fusion combined with different internal fixations for the treatment of degenerative lumbar spine disease: A finite element analysis. BMC Musculoskelet. Disord. 2022, 23, 206. [Google Scholar] [CrossRef]
- Lv, Q.-B.; Gao, X.; Pan, X.-X.; Jin, H.-M.; Lou, X.-T.; Li, S.-M.; Yan, Y.-Z.; Wu, C.-C.; Lin, Y.; Ni, W.-F.; et al. Biomechanical properties of novel transpedicular transdiscal screw fixation with interbody arthrodesis technique in lumbar spine: A finite element study. J. Orthop. Transl. 2018, 15, 50–58. [Google Scholar] [CrossRef]
- Dreischarf, M.; Zander, T.; Shirazi-Adl, A.; Puttlitz, C.; Adam, C.; Chen, C.; Goel, V.; Kiapour, A.; Kim, Y.; Labus, K.; et al. Comparison of eight published static finite element models of the intact lumbar spine: Predictive power of models improves when combined together. J. Biomech. 2014, 47, 1757–1766. [Google Scholar] [CrossRef] [PubMed]
- Panjabi, M.M.; Oxland, T.R.; Yamamoto, I.; Crisco, J.J. Mechanical behavior of the human lumbar and lumbosacral spine as shown by three-dimensional load-displacement curves. J. Bone Jt. Surg. 1994, 76, 413–424. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.; Teo, E. Effects of laminectomy and facetectomy on the stability of the lumbar motion segment. Med. Eng. Phys. 2004, 26, 183–192. [Google Scholar] [CrossRef]
- Dhar, U.K.; Menzer, E.L.; Lin, M.; Hagerty, V.; O’cOnnor, T.; Tsai, C.-T.; Vrionis, F.D. Factors influencing cage subsidence in anterior cervical corpectomy and discectomy: A systematic review. Eur. Spine J. 2023, 32, 957–968. [Google Scholar] [CrossRef] [PubMed]
- Lonstein, J.E.; Denis, F.; Perra, J.H.; Pinto, M.R.; Smith, M.D.; Winter, R.B. Complications associated with pedicle screws. J. Bone Jt. Surg. 1999, 81, 1519–1528. [Google Scholar] [CrossRef]
- Gallagher, S.; Marras, W.S. Tolerance of the lumbar spine to shear: A review and recommended exposure limits. Clin. Biomech. 2012, 27, 973–978. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhar, U.K.; Aghayev, K.; Sultan, H.; Rajendran, S.; Tsai, C.-T.; Vrionis, F.D. Finite Element Analysis of Biomechanical Assessment: Traditional Bilateral Pedicle Screw System vs. Novel Reverse Transdiscal Screw System for Lumbar Degenerative Disc Disease. Bioengineering 2025, 12, 671. https://doi.org/10.3390/bioengineering12060671
Dhar UK, Aghayev K, Sultan H, Rajendran S, Tsai C-T, Vrionis FD. Finite Element Analysis of Biomechanical Assessment: Traditional Bilateral Pedicle Screw System vs. Novel Reverse Transdiscal Screw System for Lumbar Degenerative Disc Disease. Bioengineering. 2025; 12(6):671. https://doi.org/10.3390/bioengineering12060671
Chicago/Turabian StyleDhar, Utpal K., Kamran Aghayev, Hadi Sultan, Saahas Rajendran, Chi-Tay Tsai, and Frank D. Vrionis. 2025. "Finite Element Analysis of Biomechanical Assessment: Traditional Bilateral Pedicle Screw System vs. Novel Reverse Transdiscal Screw System for Lumbar Degenerative Disc Disease" Bioengineering 12, no. 6: 671. https://doi.org/10.3390/bioengineering12060671
APA StyleDhar, U. K., Aghayev, K., Sultan, H., Rajendran, S., Tsai, C.-T., & Vrionis, F. D. (2025). Finite Element Analysis of Biomechanical Assessment: Traditional Bilateral Pedicle Screw System vs. Novel Reverse Transdiscal Screw System for Lumbar Degenerative Disc Disease. Bioengineering, 12(6), 671. https://doi.org/10.3390/bioengineering12060671






