Breast Cancer Detection Using Infrared Thermography: A Survey of Texture Analysis and Machine Learning Approaches
Abstract
1. Introduction
- A comprehensive review of recent advancements in texture analysis techniques and machine learning approaches specifically applied to breast cancer detection using infrared thermography, filling a gap in previous reviews that did not adequately emphasize texture analysis, and showing that this approach achieves top performance.
- A systematic analysis of the complete infrared thermography processing pipeline, including image preprocessing techniques, feature extraction methods, feature reduction techniques, classification approaches, and performance assessment metrics used in thermographic breast cancer detection, rather than focusing on isolated components of the workflow.
- A critical analysis of the current limitations in infrared thermography research, particularly noting the over-reliance on limited thermal image datasets (primarily from the DMR-IR database). This study also notes that some reported results may be unreliable due to potential leakage caused by splitting patient images between training and test sets which could contribute to model overfitting.
- The identification of promising research directions, highlighting how automated analysis through texture analysis and machine learning can address practical implementation challenges, such as the shortage of specialized radiologists and differing interpretation standards, bridging technical advances and clinical application. Numerous approaches achieved very high performance; therefore, this review advo-cates investing in research focused on developing tools that improve radiologists’ comprehension of medical images and the rationale behind CAD system recommendations.
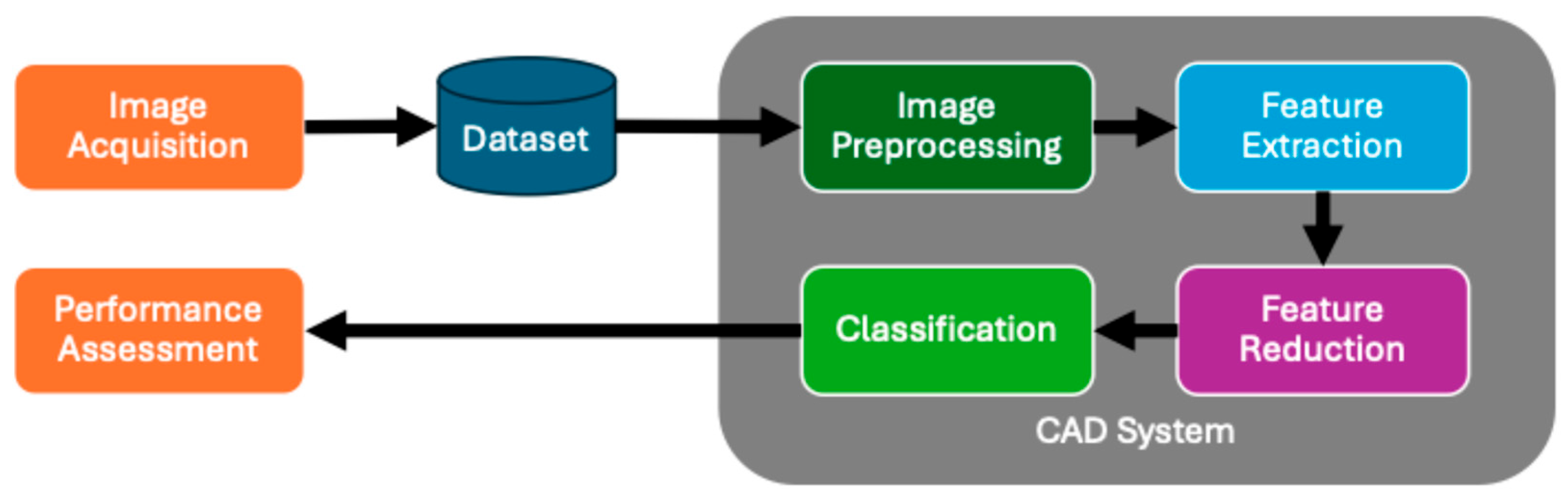
2. Computer-Aided Diagnosis System Architecture
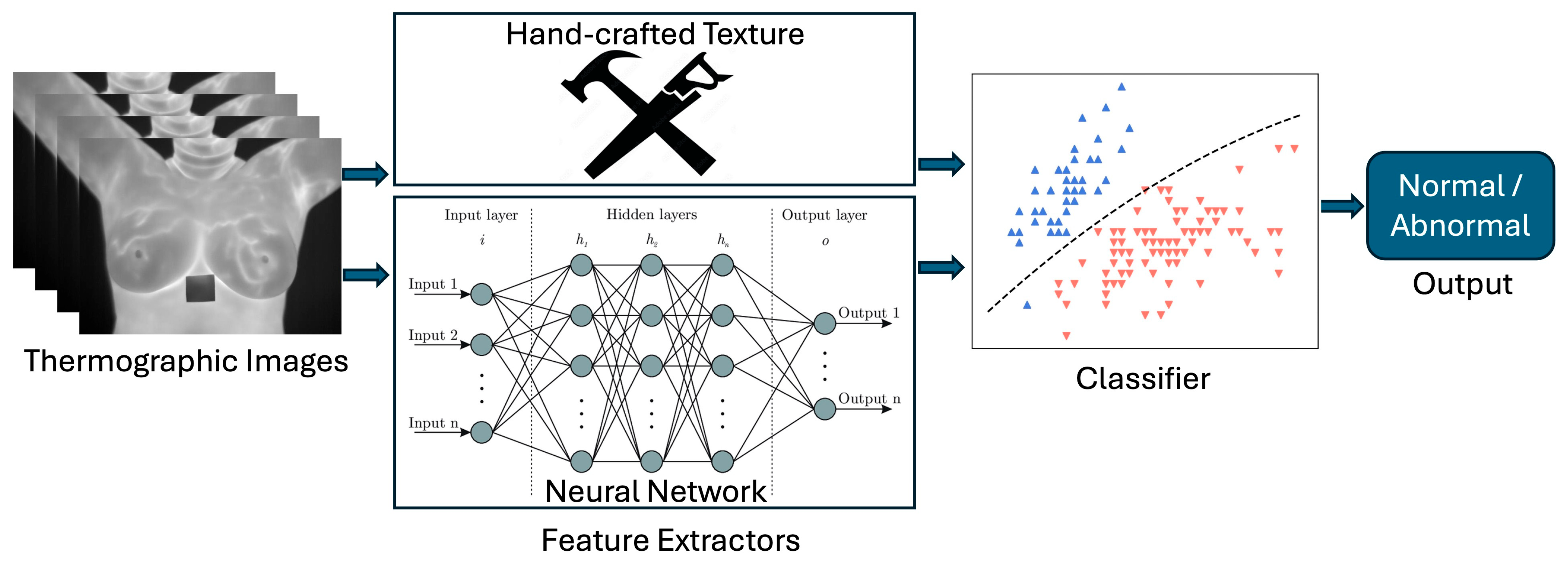
3. Computer-Aided Diagnosis for Breast Cancer Detection
3.1. Image Acquisition
Datasets
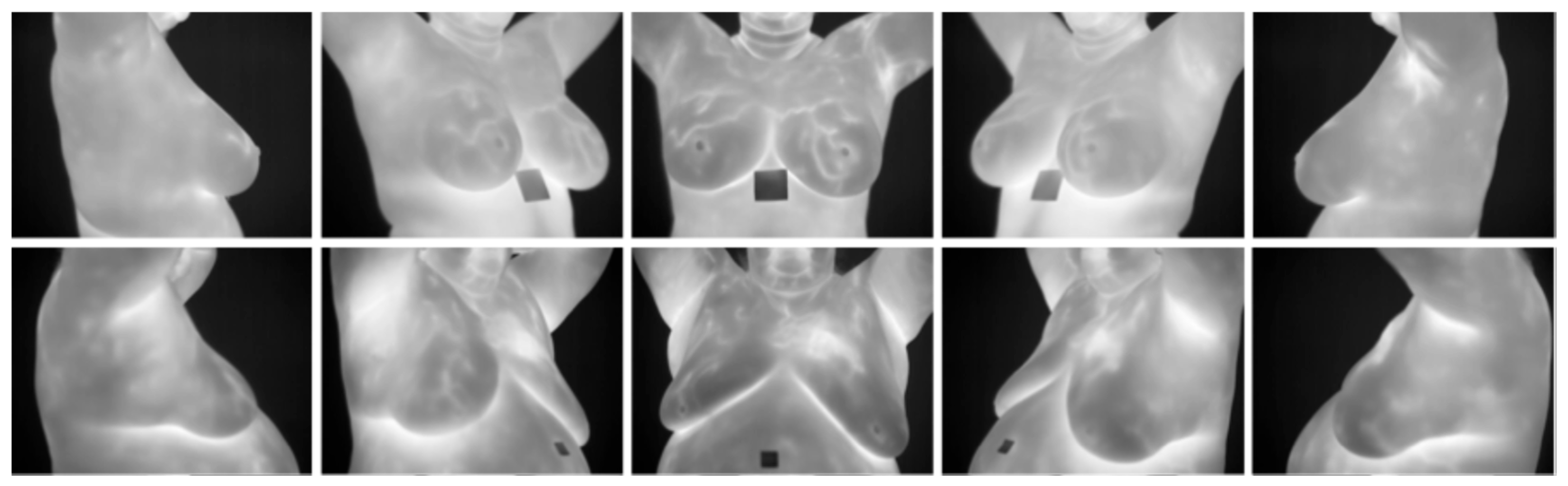
- DMR-IR Dataset: The Database for Mastology Research Infrared (DMR-IR) dataset [39] is the most widely used database in research studies. Of the 26 studies covered in this review, 20, 77%, used this dataset. The DMR-IR dataset includes infrared (IR) images, several digitized mammograms, several ROI masks, and clinical data for 293 patients captured at the Hospital Universitario Antonio Pedro (HUAP) of the Federal University Fluminense. The use of this dataset was approved by the Ethical Committee of the HUAP and registered with the Brazilian Ministry of Health under number CAAE: 01042812.0.0000.5243 and is publicly available at http://visual.ic.uff.br/dmi/, accessed on 6 April 2025. Infrared images are captured using Static Image Thermography (SIT) and Dynamic Image Thermography (DIT) described in [19]. The database also includes segmented images for 56 patients (37 sick and 19 normal). Figure 4 shows sample images from this dataset.
3.2. Image Preprocessing
3.3. Feature Extraction
3.3.1. Statistical Methods
- First Order Statistics (FOS): This depends on individual pixel values and not on their interaction with other pixels. Captured statistics include entropy, energy, maximum, minimum, inter-quantile range, mean, standard deviation, mean absolute deviation, variance, range, root mean square, skewness, uniformity, and kurtosis [74,79]. Entropy measures the average level of information in an image, and therefore, breasts without cancer should have a lower entropy due to their homogenous temperature distribution, while a cancerous breast would have a higher entropy due to vascularization. Skewness measures distribution asymmetry, and therefore, a breast with cancer should show a higher skewness due to greater temperature values. See Table A1 in Appendix A for the first-order statistic equations.
- Tamura: These are features that globally quantify six texture characteristics: coarseness, contrast, directionality, line-likeness, roughness, and regularity [80]. The equations for calculating these six features are in Table A2 in Appendix A.
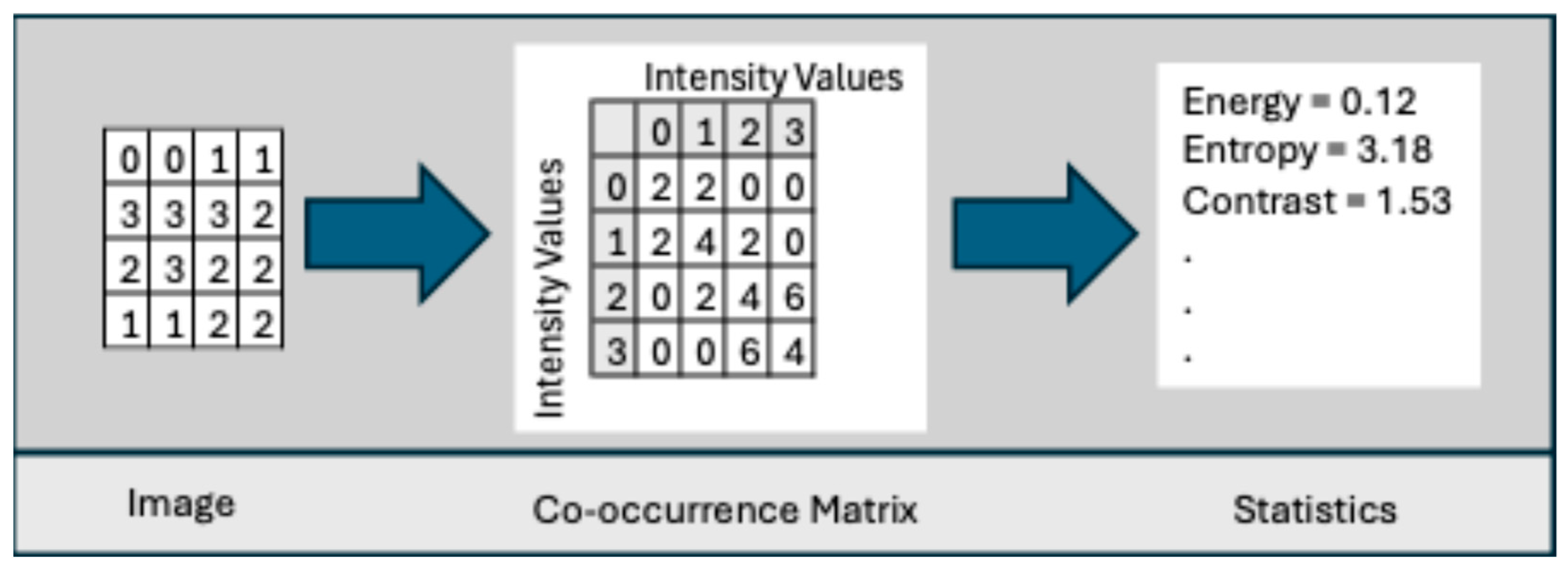
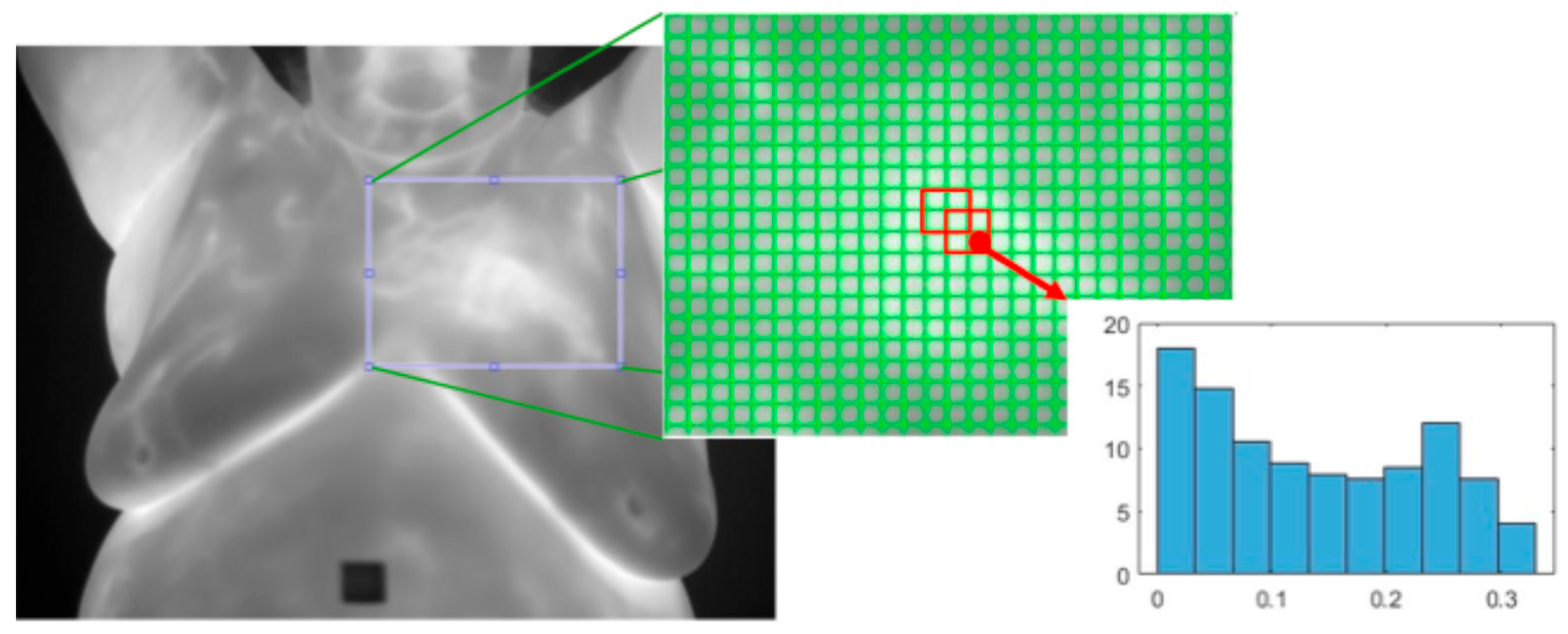
- Co-occurrence Matrix: This was developed by Haralick et al. [78] to codify textural information by calculating second-order statistics on the spatial relationships of gray tones in an image. This spatial relationship is captured in a matrix, called a Gray-level co-occurrence matrix (GLCM) of size . Let g(a,b) represent an entry in the matrix that records the number of pixel pairs in image I that are separated by a specified angle and distance, where one pixel has a gray level of a and the other has a gray level of b. Figure 6 shows the neighboring pixels for all angles of distance 1.
- Non-parametric local transforms: rely on the relative ordering of local pixels, not on their intensity value. It includes Census Transform (CT) [86], Local Ternary Pattern (LTP) [76], Local Directional Number Pattern (LDN) [89], and local binary pattern (LBP) [87], which encode the local textural and structural properties of an image as binary codes.
3.3.2. Model-Based Methods
| Citation | Method | Features | Advantages | Limitations |
|---|---|---|---|---|
| [41,47,50,52] | Fractal [106] | Captures texture self-similarity patterns in the image. Includes fractal dimensions [91,107], Hurst exponent [92], and lacunarity [108]. | Blood vessel growth is fractal [109]. Captures self-similar natural patterns. Invariant to rotation. Robust to illumination variations. | Inability to detect non-fractal patterns. Interpretability challenges. Sensitive to scale and noise. |
| [47,49,51] | Vascular Network | Models blood vessel development as a network. | Captures blood vessel network. | Accuracy of model. May require manual tuning. |
- Fractal: This represents texture as a self-similar pattern under varying degrees of magnification [110]. It was introduced into image processing by Pentland [106] and has been widely applied across image analysis, especially in medical image analysis [111]. Furthermore, many natural phenomena are fractal, including blood vessel growth and flow [109]. Therefore, fractal textures may prove effective in detecting cancer lesions in thermographic images.
- Vascular Network: Several studies developed models to capture the vasodilation and angiogenesis of blood vessels. During preprocessing, Pramanik et al. [51] applied a breast blood profusion model based on breast thermal physiology which they developed and published in [26]. Chebbah et al. [49] applied thresholding and morphological operations (medial axis transformation) and a skeletonization algorithm called homotopic thinning to yield features representing blood vessels. Abdel-Nasser et al. [47] applied lacunarity analysis of Vascular Networks [120], but HOG outperformed it.
3.3.3. Signal Processing Methods
| Citation | Method | Features | Advantages | Limitations |
|---|---|---|---|---|
| [46,122] | Spatial Domain Filters [74] | Obtain pixel value by applying operation to pixel neighbor. Used for edge detection and feature extraction. Includes Sobel [123], Canny [124] and HED [125]. | Capture fine textures and edges. | Sensitive to noise. Does not capture course details. |
| [46] | Gabor Filter [126] | Captures spatial frequency texture information. Multi-scale and multi-orientation. | Capture course and fine detail. Spatial localization. Robust to illumination variations. | Sensitive to noise. Requires parameter tuning. Not rotational invariant. High dimensional vector. |
| [31,32,48,127] | Wavelet Analysis [90] | Represent textures spatially and frequency at multiple scales. | Capture course and fine detail. Spatial localization. Robust to illumination variations and noise. | Requires parameter tuning. Not rotational invariant. High dimensional vector. |
| [48] | Curvelet Transform [128] | Decomposes images into small, elongated wave-like shapes that capture details at different scales and orientations. | Identify vascular structures. Multi-scale and multi-orientation. Detection of curved edges. | Not in standard libraries. Not rotational invariant. |
| [29,44,45,46,47,127] | HOG [33] | Splits image into cells, calculates gradient/pixel and builds histograms of gradients/cells. Normalizes gradient in region of cells. Cells retain spatial detail. | Cells capture spatial detail. Identify shapes with distinct edges. Robust to illumination and geometric changes. Robust to noise and cluttered background. Detects abnormal structures in medical images. | Reliant on strong edge features. Dependent on manual choice of parameters. Output is a high-dimensional feature vector. |
- Spatial Domain Filters: Edge detection was employed by a few studies. Dihmani et al. [46] tested and compared the Canny edge detector [124] against HOG, LBP, and Gabor filters, but HOG achieved the best result. Youssef et al. [29] enhanced a thermographic with edges generated by the Canny and Holistically nested edge detector (HED) [125]. The HED is an end-to-end edge and boundary detector based on CNN.
- Gabor Filter: This is a linear filter that identifies frequencies in a point’s localized area in a specified direction and is represented as a 2D Gaussian kernel modulated by a sinusoidal function [74]. The formula for the Gabor filter is as follows:
- Wavelet Analysis: Wavelets [90] are filters that decompose a signal in both space and time across a scale hierarchy. de Santana et al. [31] extract features using the Deep-Wavelet Neural Network (DWNN) based on the Haar Discrete Transform of Wavelets. They used 336 frontal images from the HC-UFPE dataset, which classifies an image as cyst, benign lesion, malignant lesion, or no lesion. The images were converted to grayscale and fed into DWNN and then classified with various classifiers. The best result was obtained with an SVM classifier with a linear kernel achieving an accuracy of 99.17%, macro sensitivity of 99.17%, and macro specificity of 93.45%. De Freitas Barbosa et al. [32] extended this work by adding a random forest feature selector, but they classified an image as normal (no lesion) or abnormal (cyst, benign lesion, or malignant lesion). They showed that DWNN outperformed InceptionV3 [130], MobileNet [131], ResNet-50 [65], VGG16 [132], VGG19 [132], and Xception [133] in the tasks of lesion detection and classification. The best result was obtained with an SVM classifier with a linear kernel achieving 99% accuracy, 100% sensitivity, and 98% specificity for lesion detection and 97.3% accuracy, 100% sensitivity, and 97% specificity for the lesion classification task.
- Curvelet transform: This [128] decomposes an image into small, elongated wave-like shapes that capture details at different scales and orientations, particularly along curved edges. This technique may be particularly helpful in identifying the vascular structures associated with cancer. Karthiga and Narasimhan [48] applied a curvelet transform [128] to segment 60 thermographic frontal images (30 normal and 30 abnormal) from the DMR-IR dataset before extracting GLCM features. They also extracted first-order statistics, geometrical, and intensity features from the original images. Feature selection was performed using hypothesis testing and several machine learning models were subsequently compared. The best results were achieved with an accuracy of 93.3% and AUC of 94%. They also noted that the GLCM features extracted from the curvet domain increased accuracy by 10% points.
- Histogram of Oriented Gradients (HOG): This [33] is a texture feature extractor that is also applied to the detection of objects in images. An image is split into non-overlapping cells of a predefined size. Regions are defined as a fixed number of cells and may overlap. The gradient is calculated for each pixel and the histogram of all the gradients within each cell is calculated. All the cell histograms of gradients within a region are normalized and concatenated into a single vector and then all the region vectors are concatenated into one vector. See Figure 11.
3.4. Feature Reduction
3.4.1. Feature Selection
3.4.2. Dimension Reduction
3.4.3. Embedded
3.4.4. Bio-Inspired
3.5. Classification
3.6. Performance Assessment
3.7. Key Studies Included in This Review
4. Future Directions
4.1. Benchmark
4.2. Robust Clinical Trials
4.3. Improving Explainability for Radiologists
4.4. Increasing Coverage
4.5. Multi-Modal Methods
4.6. Advances in Artificial Intelligence/Machine Learning
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acc. | Accuracy |
| ACR | American College of Radiology |
| AUC | Area Under Curve |
| BI-RADS | Breast Imaging Reporting and Data System |
| CAD | Computer-aided diagnostic |
| CBE | Clinical breast exam |
| CSLBP | Center-Symmetric Local Binary Pattern |
| CT | Census Transform |
| DIT | Dynamic Image Thermography |
| DMR-IR | Database for Mastology Research Infrared |
| DWNN | Deep-Wavelet Neural Network |
| DWT | Discrete Wavelet Transform |
| ELM | Extreme Learning Machine |
| FD | Fractal Dimension |
| FDA | Food and Drug Administration |
| FOS | First-Order Statistics |
| GA | Genetic Algorithm |
| GAN | Generational Adversarial Networks |
| GLCM | Gray-Level Co-occurrence Matrix |
| GLDM | Gray-Level Dependence Matrix |
| GLRLM | Gray-Level Run Length Matrix |
| GLSZM | Gray-Level Size Zone Matrix |
| HE | Hurst Exponent |
| HED | Holistically nested Edge Detector |
| HH | Higher High |
| HOG | Histogram of Oriented Gradient |
| KAN | Kolmogorov–Arnold Network |
| KELM | Kernel Extreme Learning Machine |
| KNN | K-Nearest Neighbor |
| LASSO | Least absolute Shrinkage and Selection Operator |
| LBP | Local Binary Pattern |
| LDN | Local Directional Number Pattern |
| LINPE | Local instance-and-center-symmetric neighbor-based pattern |
| LINPE-BL | LINPE Broad Learner |
| LR | Logistic Regression |
| LSSVM | Least Square Support Vector Machine |
| LTP | Local Ternary Pattern |
| LTriDP | Local Tridirectional Pattern |
| MLP | Multilayer Perceptron |
| MRI | Magnetic Resonance Imaging |
| NCA | Neighborhood Component Analysis |
| NGTDM | Neighborhood Grey Tone Different Matrix |
| PCA | Principal Component Analysis |
| RBF | Radial Basis Function |
| ROI | Region of Interest |
| SBBC | Synchronous Bilateral Breast Cancer |
| SBE | Self-Breast Exam |
| Sens. | Sensitivity |
| SFTA | Segmentation Fractal Texture Analysis |
| SHAP | Shaplet Additive exPlanations |
| SIT | Static Image Thermography |
| Spec. | Specificity |
| SSM | Structured State-Space Model |
| SVM | Support Vector Machine |
| UBC | Unilateral Breast Cancer |
| ViT | Vision Transformer |
| WHO | World Health Organization |
| WLD | Web Local Descriptor |
Appendix A
| Citation | Description | Equation | Citation | Description | Equation |
|---|---|---|---|---|---|
| [79] | Energy 1 | [49,61,79] | Mean () | ||
| [45,47,48,79] | Min | [49] | Smoothness [190] | ||
| [48,79] | Max | [79] | Interquartile Range | ||
| [45,61,79] | Entropy | [79] | Mean Absolute Deviation | ||
| [45,49,79] | Standard Deviation | [45,48,49,79] | Kurtosis | ||
| [79] | Range | [45,48,49,61,79] | Skewness | ||
| [79] | Root Mean Square | [49,61,79] | Variance ( |
| Citation | Description | Equation |
|---|---|---|
| [79,80] | Coarseness () | k = {1,2…h: h is a given positive integer} |
| [79,80] | Contrast () | |
| [79,80] | Directionality 1 () | |
| [80] | Line-Likeness () | |
| [80] | Regularity 2 | |
| [80] | Roughness |
| Citation | Description | Equation |
|---|---|---|
| [5,44,47,48,49,61,68,75,76,79] | Angular Second Momentum 1 | |
| [5,44,47,48,49,68,75,76,79] | Contrast | |
| [5,44,47,48,49,68,75,76,79] | Correlation | |
| [47,49,75,76,79] | Sum of Squares: Variance 2 | |
| [49,75,76,79] | Inverse Difference Moment | |
| [47,68,75,76,79] | Sum Average () | |
| [47,68,75,76,79] | Sum Variance | |
| [47,68,75,76,79] | Sum Entropy | |
| [47,49,68,75,76,79] | Entropy (H) | |
| [47,68,75,76,79] | Difference Variance | |
| [47,68,75,76,79] | Difference Entropy | |
| [47,68,75,76,79] | Information Measures of Correlation | |
| [79] | Maximal Correlation Coefficient |
| Citation | Description | Equation |
|---|---|---|
| [47,68,75,76,79] | Autocorrelation | |
| [61] | Contrast | |
| [47,61] | Correlation | |
| [47,68,75,76,79] | Cluster Prominence | |
| [47,68,75,76,79] | Cluster Shade | |
| [79] | Cluster Tendency | |
| [79] | Difference Average | |
| [5,44,47,75,76] | Dissimilarity | |
| [5,44,47,48,61,75,76] | Homogeneity I and II | |
| [79] | Inverse Difference | |
| [79] | Inverse Difference Normalized | |
| [79] | Inverse Variance | |
| [79] | Joint Average | |
| [47,68,75,76,79] | Maximum Probability | |
| [47,68,75,76] | Inverse Difference Normalized | |
| [47,68,79] | Inverse Difference Moment Normalized |
| Citation | Description | Equation | Citation | Description | Equation |
|---|---|---|---|---|---|
| [68,75,76,79] | Short Run Emphasis (SRE) | [68,75,76,79] | High Gray-Level Run Emphasis | ||
| [68,75,76,79] | Long Run Emphasis (LRE) | [68,79] | Short Run Low Gray-Level Emphasis | ||
| [68,75,76,79] | Gray-Level Nonuniformity (GLN) | [68,79] | Short Run High Gray-Level Emphasis | ||
| [68,75,76,79] | Run Length Nonuniformity (RLN) | [68,79] | Long Run Low Gray-Level Emphasis | ||
| [68,75,76,79] | Run Percentage | [68,79] | Long Run High Gray-Level Emphasis | ||
| [68,75,76,79] | Low Gray-Level Run Emphasis |
| Citation | Description | Equation | Citation | Description | Equation |
|---|---|---|---|---|---|
| [79] | Gray-Level Nonuniformity Normalized | [79] | Run Variance | ||
| [79] | Run Length Nonuniformity Normalized | [79] | Run Entropy | ||
| [79] | Gray Level Variance |
| Citation | Description | Equation |
|---|---|---|
| [68,79] | Coarseness | |
| [68,79] | Contrast | |
| [68,79] | Busyness | |
| [68,79] | Complexity | |
| [68,79] | Strength |
| Citation | Description | Equation | Citation | Description | Equation |
|---|---|---|---|---|---|
| [79] | Small Dependence Emphasis | [79] | Dependence Entropy | ||
| [79] | Large Dependence Emphasis | [79] | Low Gray Level Emphasis | ||
| [79] | Gray-Level Nonuniformity | [79] | High Gray Level Emphasis | ||
| [79] | Dependence Nonuniformity | [79] | Small Dependence Low Gray Level Emphasis | ||
| [79] | Dependence Nonuniformity Normalized | [79] | Small Dependence High Gray Level Emphasis | ||
| [79] | Gray-Level Variance | [79] | Large Dependence Low Gray Level Emphasis | ||
| [79] | Dependence Variance | [79] | Large Dependence High Gray Level Emphasis |
References
- Bray, F.; Laversanne, M.; Sung, H.; Ferlay, J.; Siegel, R.L.; Soerjomataram, I.; Jemal, A. Global Cancer Statistics 2022: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA Cancer J. Clin. 2024, 74, 229–263. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, L.; Gathani, T. Understanding Breast Cancer as a Global Health Concern. Br. J. Radiol. 2022, 95, 20211033. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Harper, A.; McCormack, V.; Sung, H.; Houssami, N.; Morgan, E.; Mutebi, M.; Garvey, G.; Soerjomataram, I.; Fidler-Benaoudia, M.M. Global Patterns and Trends in Breast Cancer Incidence and Mortality across 185 Countries. Nat. Med. 2025, 31, 1154–1162. [Google Scholar] [CrossRef]
- FDA Breast Cancer Screening: Thermogram No Substitute for Mammogram. Available online: https://www.fda.gov/consumers/consumer-updates/breast-cancer-screening-thermogram-no-substitute-mammogram (accessed on 16 January 2024).
- Resmini, R.; Faria Da Silva, L.; Medeiros, P.R.T.; Araujo, A.S.; Muchaluat-Saade, D.C.; Conci, A. A Hybrid Methodology for Breast Screening and Cancer Diagnosis Using Thermography. Comput. Biol. Med. 2021, 135, 104553. [Google Scholar] [CrossRef]
- Kakileti, S.T.; Manjunath, G.; Madhu, H.; Ramprakash, H.V. Advances in Breast Thermography. In New Perspectives in Breast Imaging; IntechOpen: London, UK, 2017; ISBN 978-953-51-3558-6. [Google Scholar]
- Heywang-Köbrunner, S.H.; Hacker, A.; Sedlacek, S. Advantages and Disadvantages of Mammography Screening. Breast Care 2011, 6, 199–207. [Google Scholar] [CrossRef]
- Mann, R.M.; Cho, N.; Moy, L. Breast MRI: State of the Art. Radiology 2019, 292, 520–536. [Google Scholar] [CrossRef]
- Hooley, R.J.; Scoutt, L.M.; Philpotts, L.E. Breast Ultrasonography: State of the Art. Radiology 2013, 268, 642–659. [Google Scholar] [CrossRef]
- Prasad, S.N.; Houserkova, D. The Role of Various Modalities in Breast Imaging. Biomed. Pap. Med. Fac. Univ. Palacky. Olomouc Czech Repub. 2007, 151, 209–218. [Google Scholar] [CrossRef] [PubMed]
- ACR Breast Imaging Reporting & Data System (BI-RADS). Available online: https://www.acr.org/Clinical-Resources/Clinical-Tools-and-Reference/Reporting-and-Data-Systems/BI-RADS (accessed on 10 February 2025).
- Periyasamy, S.; Prakasarao, A.; Menaka, M.; Venkatraman, B.; Jayashree, M. Thermal Grading Scale for Classification of Breast Thermograms. IEEE Sens. J. 2021, 21, 13996–14002. [Google Scholar] [CrossRef]
- Corrales, V.V.; Shyyab, I.M.Y.A.; Gowda, N.S.; Alaawad, M.; Mohamed, M.Y.H.; Almistarihi, O.J.S.; Gopala, A.H.; Jayaprakash, N.; Yadav, P.; Jakka, J.; et al. Advancing Early Breast Cancer Detection with Artificial Intelligence in Low-Resource Healthcare Systems: A Narrative Review. Int. J. Community Med. Public Health 2025, 12, 1571–1577. [Google Scholar] [CrossRef]
- Resmini, R.; Silva, L.; Araujo, A.S.; Medeiros, P.; Muchaluat-Saade, D.; Conci, A. Combining Genetic Algorithms and SVM for Breast Cancer Diagnosis Using Infrared Thermography. Sensons 2021, 21, 4802. [Google Scholar] [CrossRef] [PubMed]
- de Freitas Oliveira Baffa, M.; Grassano Lattari, L. Convolutional Neural Networks for Static and Dynamic Breast Infrared Imaging Classification. In Proceedings of the 2018 31st SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Paraná, Brazil, 29 October–1 November 2018; pp. 174–181. [Google Scholar]
- Galukande, M.; Kiguli-Malwadde, E. Rethinking Breast Cancer Screening Strategies in Resource-Limited Settings. Afr. Health Sci. 2010, 10, 89–92. [Google Scholar]
- Aggarwal, A.K.; Alpana; Pandey, M. Deep Learning Based Breast Cancer Classification on Thermogram. In Proceedings of the 2022 International Conference on Computing, Communication, and Intelligent Systems (ICCCIS), Greater Noida, India, 4–5 November 2022; pp. 769–774. [Google Scholar]
- Humphrey, L.L.; Helfand, M.; Chan, B.K.S.; Woolf, S.H. Breast Cancer Screening: A Summary of the Evidence for the U.S. Preventive Services Task Force. Ann. Intern. Med. 2002, 137, 347–360. [Google Scholar] [CrossRef] [PubMed]
- Captura de Imagens Térmicas No HUAP. Available online: http://visual.ic.uff.br/dmi/prontuario/protocolo.pdf (accessed on 12 January 2024).
- Rakhunde, M.B.; Gotarkar, S.; Choudhari, S.G. Thermography as a Breast Cancer Screening Technique: A Review Article. Cureus 2022, 14, e31251. [Google Scholar] [CrossRef]
- Rodriguez-Guerrero, S.; Loaiza Correa, H.; Restrepo-Girón, A.-D.; Reyes, L.A.; Olave, L.A.; Diaz, S.; Pacheco, R. Breast Thermography. Mendeley Data 2024, V3. [Google Scholar] [CrossRef]
- McDonald, R.J.; Schwartz, K.M.; Eckel, L.J.; Diehn, F.E.; Hunt, C.H.; Bartholmai, B.J.; Erickson, B.J.; Kallmes, D.F. The Effects of Changes in Utilization and Technological Advancements of Cross-Sectional Imaging on Radiologist Workload. Acad. Radiol. 2015, 22, 1191–1198. [Google Scholar] [CrossRef]
- Sonka, M.; Hlavac, V.; Boyle, R. Image Processing, Analysis and Machine Vision; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-1-4899-3216-7. [Google Scholar]
- Ghalati, M.K.; Nunes, A.; Ferreira, H.; Serranho, P.; Bernardes, R. Texture Analysis and Its Applications in Biomedical Imaging: A Survey. IEEE Rev. Biomed. Eng. 2022, 15, 222–246. [Google Scholar] [CrossRef]
- Zuluaga-Gomez, J.; Zerhouni, N.; Al Masry, Z.; Devalland, C.; Varnier, C. A Survey of Breast Cancer Screening Techniques: Thermography and Electrical Impedance Tomography. J. Med. Eng. Technol. 2019, 43, 305–322. [Google Scholar] [CrossRef]
- Mashekova, A.; Zhao, Y.; Ng, E.Y.K.; Zarikas, V.; Fok, S.C.; Mukhmetov, O. Early Detection of the Breast Cancer Using Infrared Technology—A Comprehensive Review. Therm. Sci. Eng. Progress. 2022, 27, 101142. [Google Scholar] [CrossRef]
- Iyadurai, J.; Chandrasekharan, M.; Muthusamy, S.; Panchal, H. An Extensive Review on Emerging Advancements in Thermography and Convolutional Neural Networks for Breast Cancer Detection. Wirel. Pers. Commun. 2024, 137, 1797–1821. [Google Scholar] [CrossRef]
- Tsietso, D.; Yahya, A.; Samikannu, R. A Review on Thermal Imaging-Based Breast Cancer Detection Using Deep Learning. Mob. Inf. Syst. 2022, 2022, 8952849. [Google Scholar] [CrossRef]
- Youssef, D.; Atef, H.; Gamal, S.; El-Azab, J.; Ismail, T. Early Breast Cancer Prediction Using Thermal Images and Hybrid Feature Extraction-Based System. IEEE Access 2025, 13, 29327–29339. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000; ISBN 978-1-4757-3264-1. [Google Scholar]
- De Santana, M.A.; De Freitas Barbosa, V.A.; De Cássia Fernandes De Lima, R.; Dos Santos, W.P. Combining Deep-Wavelet Neural Networks and Support-Vector Machines to Classify Breast Lesions in Thermography Images. Health Technol. 2022, 12, 1183–1195. [Google Scholar] [CrossRef]
- De Freitas Barbosa, V.A.; Félix Da Silva, A.; De Santana, M.A.; Rabelo De Azevedo, R.; Fernandes De Lima, R.D.C.; Dos Santos, W.P. Deep-Wavelets and Convolutional Neural Networks to Support Breast Cancer Diagnosis on Thermography Images. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2023, 11, 895–913. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Goñi-Arana, A.; Pérez-Martín, J.; Díez, F.J. Breast Thermography: A Systematic Review and Meta-Analysis. Syst. Rev. 2024, 13, 295. [Google Scholar] [CrossRef]
- Bandalakunta Gururajarao, S.; Venkatappa, U.; Shivaram, J.M.; Sikkandar, M.Y.; Al Amoudi, A. Chapter 4—Infrared Thermography and Soft Computing for Diabetic Foot Assessment. In Machine Learning in Bio-Signal Analysis and Diagnostic Imaging; Dey, N., Borra, S., Ashour, A.S., Shi, F., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 73–97. ISBN 978-0-12-816086-2. [Google Scholar]
- Keyserlingk, J.R.; Ahlgren, P.D.; Yu, E.; Belliveau, N. Infrared Imaging of the Breast: Initial Reappraisal Using High-Resolution Digital Technology in 100 Successive Cases of Stage I and II Breast Cancer. Breast J. 1998, 4, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, R.G.; Kane, R.; Pittman, J.; Crawford, J.; Tokman, A.; Brioschi, M.; Manjunath, G.; Ehle, E.; Gershenson, J. The American Academy of Thermology Guidelines for Breast Thermology; The American Academy of Thermology: Greenville, SC, USA, 2024. [Google Scholar]
- International Association of Certified Thermographers. Clinical Thermography Standards & Guidelines; International Association of Certified Thermographers: Foster City, CA, USA, 2015. [Google Scholar]
- Silva, L.F.; Saade, D.C.M.; Sequeiros, G.O.; Silva, A.C.; Paiva, A.C.; Bravo, R.S.; Conci, A. A New Database for Breast Research with Infrared Image. J. Med. Imaging Health Inform. 2014, 4, 92–100. [Google Scholar] [CrossRef]
- Gonzalez-Hernandez, J.-L.; Recinella, A.N.; Kandlikar, S.G.; Dabydeen, D.; Medeiros, L.; Phatak, P. Technology, Application and Potential of Dynamic Breast Thermography for the Detection of Breast Cancer. Int. J. Heat. Mass. Transf. 2019, 131, 558–573. [Google Scholar] [CrossRef]
- Dey, A.; Ali, E.; Rajan, S. Bilateral Symmetry-Based Abnormality Detection in Breast Thermograms Using Textural Features of Hot Regions. IEEE Open J. Instrum. Meas. 2023, 2, 1–14. [Google Scholar] [CrossRef]
- Dey, A.; Rajan, S.; Lambadaris, I. Detection of Abnormality in Deterministic Compressive Sensed Breast Thermograms Using Bilateral Asymmetry. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Dey, A.; Rajan, S. Unsupervised Learning for Breast Abnormality Detection Using Thermograms. In Proceedings of the 2024 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 20–23 May 2024; pp. 1–6. [Google Scholar]
- Garia, L.; Muthusamy, H. Dual-Tree Complex Wavelet Pooling and Attention-Based Modified U-Net Architecture for Automated Breast Thermogram Segmentation and Classification. J. Digit. Imaging Inform. Med. 2024, 38, 887–901. [Google Scholar] [CrossRef]
- Gonzalez-Leal, R.; Kurban, M.; López-Sánchez, L.D.; Gonzalez, F.J. Automatic Breast Cancer Detection on Breast Thermograms. In Proceedings of the 2020 International Conference on Quantitative InfraRed Thermography, Porto, Portugal, 6–10 July 2020. [Google Scholar]
- Dihmani, H.; Bousselham, A.; Bouattane, O. A New Computer-Aided Diagnosis System for Breast Cancer Detection from Thermograms Using Metaheuristic Algorithms and Explainable AI. Algorithms 2024, 17, 462. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Moreno, A.; Puig, D. Breast Cancer Detection in Thermal Infrared Images Using Representation Learning and Texture Analysis Methods. Electronics 2019, 8, 100. [Google Scholar] [CrossRef]
- Karthiga, R.; Narasimhan, K. Medical Imaging Technique Using Curvelet Transform and Machine Learning for the Automated Diagnosis of Breast Cancer from Thermal Image. Pattern Anal. Applic 2021, 24, 981–991. [Google Scholar] [CrossRef]
- Chebbah, N.K.; Ouslim, M.; Benabid, S. New Computer Aided Diagnostic System Using Deep Neural Network and SVM to Detect Breast Cancer in Thermography. Quant. InfraRed Thermogr. J. 2023, 20, 62–77. [Google Scholar] [CrossRef]
- Moradi, M.; Rezai, A. High-Performance Breast Cancer Diagnosis Method Using Hybrid Feature Selection Method. Biomed. Eng. Biomed. Tech. 2024, 70, 2. [Google Scholar] [CrossRef] [PubMed]
- Pramanik, S.; Bhattacharjee, D.; Nasipuri, M.; Krejcar, O. LINPE-BL: A Local Descriptor and Broad Learning for Identification of Abnormal Breast Thermograms. IEEE Trans. Med. Imaging 2021, 40, 3919–3931. [Google Scholar] [CrossRef]
- Hakim, A.; Awale, R.N. Identification of Breast Abnormality from Thermograms Based on Fractal Geometry Features. In Proceedings of the IOT with Smart Systems; Senjyu, T., Mahalle, P., Perumal, T., Joshi, A., Eds.; Springer Nature: Ahmedabad, India, 2022; Volume 251, pp. 393–401. [Google Scholar]
- Jalloul, R.; Krishnappa, C.H.; Agughasi, V.I.; Alkhatib, R. Enhancing Early Breast Cancer Detection with Infrared Thermography: A Comparative Evaluation of Deep Learning and Machine Learning Models. Technologies 2025, 13, 7. [Google Scholar] [CrossRef]
- Dey, A.; Rajan, S.; Dansereau, R. Improved Detection of Abnormality in Grayscale Breast Thermal Images Using Binary Encoding. In Proceedings of the 2024 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Eindhoven, The Netherlands, 26–28 June 2024; pp. 1–5. [Google Scholar]
- Images of Breast Screening by Digital Infrared Thermal Imaging. Available online: https://aathermography.com/breast/breasthtml/breasthtml.html (accessed on 12 February 2025).
- Rodrigues Da Silva, A.L.; Araújo De Santana, M.; Lins De Lima, C.; Silva De Andrade, J.F.; Silva De Souza, T.K.; Jacinto De Almeida, M.B.; Azevedo Da Silva, W.W.; Fernandes De Lima, R.D.C.; Pinheiro Dos Santos, W. Features Selection Study for Breast Cancer Diagnosis Using Thermographic Images, Genetic Algorithms, and Particle Swarm Optimization. Int. J. Artif. Intell. Mach. Learn. 2021, 11, 1–18. [Google Scholar] [CrossRef]
- Pereira, J.M.S.; Santana, M.A.; Gomes, J.C.; de Freitas Barbosa, V.A.; Valença, M.J.S.; de Lima, S.M.L.; dos Santos, W.P. Feature Selection Based on Dialectics to Support Breast Cancer Diagnosis Using Thermographic Images. Res. Biomed. Eng. 2021, 37, 485–506. [Google Scholar] [CrossRef]
- Amalu, W. Breast Thermography Case Studies. Available online: http://breastthermography.com/wp-content/uploads/2020/03/Breast-Thermography-Case-Studies.pdf (accessed on 16 February 2025).
- Bhowmik, M.K.; Gogoi, U.R.; Majumdar, G.; Bhattacharjee, D.; Datta, D.; Ghosh, A.K. Designing of Ground-Truth-Annotated DBT-TU-JU Breast Thermogram Database Toward Early Abnormality Prediction. IEEE J. Biomed. Health Inform. 2018, 22, 1238–1249. [Google Scholar] [CrossRef] [PubMed]
- Bhowmik, M.K. DBT-TU-JU Breast Thermogram Dataset. Available online: https://www.mkbhowmik.in/dbtTu.aspx (accessed on 16 February 2025).
- Josephine, J.; Ulaganathan, M.; Shenbagavalli, A.; Venkatraman, B.; Menaka, M. Statistical Analysis on Breast Thermograms Using Logistic Regression for Image Classification. In Proceedings of the 2021 IEEE Bombay Section Signature Conference (IBSSC), Gwalior, India, 18–20 November 2021; pp. 1–6. [Google Scholar]
- Siu, A.L. Screening for Breast Cancer: U.S. Preventive Services Task Force Recommendation Statement. Ann. Intern. Med. 2016, 164, 279–296. [Google Scholar] [CrossRef] [PubMed]
- Lahiri, B.B.; Bagavathiappan, S.; Jayakumar, T.; Philip, J. Medical Applications of Infrared Thermography: A Review. Infrared Phys. Technol. 2012, 55, 221–235. [Google Scholar] [CrossRef]
- Rodriguez-Guerrero, S.; Loaiza-Correa, H.; Restrepo-Girón, A.-D.; Reyes, L.A.; Olave, L.A.; Diaz, S.; Pacheco, R. Dataset of Breast Thermography Images for the Detection of Benign and Malignant Masses. Data Brief. 2024, 110503. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- FLIR SC620. Available online: https://p.globalsources.com/IMAGES/PDT/SPEC/305/K1034869305.pdf (accessed on 12 January 2024).
- Madhavi, V.; Thomas, C.B. Multi-View Breast Thermogram Analysis by Fusing Texture Features. Quant. InfraRed Thermogr. J. 2019, 16, 111–128. [Google Scholar] [CrossRef]
- Mitiche, A.; Ayed, I.B. Variational and Level Set Methods in Image Segmentation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-15352-5. [Google Scholar]
- Apache MXNet. Available online: https://mxnet.apache.org/versions/1.9.1/ (accessed on 10 February 2025).
- Ma, J.; He, Y.; Li, F.; Han, L.; You, C.; Wang, B. Segment Anything in Medical Images. Nat. Commun. 2024, 15, 654. [Google Scholar] [CrossRef] [PubMed]
- Trongtirakul, T.; Agaian, S.; Oulefki, A. Automated Tumor Segmentation in Thermographic Breast Images. MBE 2023, 20, 16786–16806. [Google Scholar] [CrossRef]
- Trongtirakul, T.; Oulefki, A.; Agaian, S.; Chiracharit, W. Enhancement and Segmentation of Breast Thermograms. In Proceedings of the Mobile Multimedia/Image Processing, Security, and Applications 2020, Baltimore, MD, USA, 21 April 2020; Volume 11399, pp. 96–107. [Google Scholar]
- Tuceryan, M.; Jain, A.K. Texture Analysis. In Handbook of Pattern Recognition and Computer Vision; World Scientific: Singapore, 1993; pp. 235–276. ISBN 978-981-02-1136-3. [Google Scholar]
- Mishra, V.; Rath, S.K. Detection of Breast Cancer Thermograms Based on Asymmetry Analysis Using Texture Features. In Proceedings of the 2019 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kanpur, India, 6–8 July 2019; pp. 1–5. [Google Scholar]
- Mishra, V.; Rath, S.K. Detection of Breast Cancer Tumours Based on Feature Reduction and Classification of Thermograms. Quant. InfraRed Thermogr. J. 2021, 18, 300–313. [Google Scholar] [CrossRef]
- Mejdahl, M.K.; Wohlfahrt, J.; Holm, M.; Balslev, E.; Knoop, A.S.; Tjønneland, A.; Melbye, M.; Kroman, N. Breast Cancer Mortality in Synchronous Bilateral Breast Cancer Patients. Br. J. Cancer 2019, 120, 761–767. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst.Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Mishra, V.; Rath, S.K.; Mohapatra, D.P. Thermograms-Based Detection of Cancerous Tumors in Breasts Applying Texture Features. Quant. InfraRed Thermogr. J. 2024, 21, 191–216. [Google Scholar] [CrossRef]
- Tamura, H.; Mori, S.; Yamawaki, T. Textural Features Corresponding to Visual Perception. IEEE Trans. Syst. Man Cybern. 1978, 8, 460–473. [Google Scholar] [CrossRef]
- Galloway, M.M. Texture Analysis Using Gray Level Run Lengths. Comput. Graph. Image Process. 1975, 4, 172–179. [Google Scholar] [CrossRef]
- Tang, X. Texture Information in Run-Length Matrices. IEEE Trans. Image Process. 1998, 7, 1602–1609. [Google Scholar] [CrossRef]
- Amadasun, M.; King, R. Textural Features Corresponding to Textural Properties. IEEE Trans. Syst. Man Cybern. 1989, 19, 1264–1274. [Google Scholar] [CrossRef]
- Weszka, J.S.; Dyer, C.R.; Rosenfeld, A. A Comparative Study of Texture Measures for Terrain Classification. IEEE Trans. Syst. Man Cybern. 1976, SMC-6, 269–285. [Google Scholar] [CrossRef]
- Thibault, G.; Fertil, B.; Navarro, C.; Pereira, S.; Cau, P.; Levy, N.; Sequeira, J.; Mari, J.-L. Texture Indexes and Gray Level Size Zone Matrix Application to Cell Nuclei Classification. In Proceedings of the Pattern Recognition and Information Processing, Belarusian State University Publishing Center, Minsk, Balarus, 19 May 2009. [Google Scholar]
- Zabih, R.; Woodfill, J. Non-Parametric Local Transforms for Computing Visual Correspondence. In Proceedings of the Computer Vision—ECCV ’94; Eklundh, J.-O., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 151–158. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Tan, X.; Triggs, B. Enhanced Local Texture Feature Sets for Face Recognition Under Difficult Lighting Conditions. IEEE Trans. Image Process. 2010, 19, 1635–1650. [Google Scholar] [CrossRef]
- Ramirez Rivera, A.; Rojas Castillo, J.; Oksam Chae, O. Local Directional Number Pattern for Face Analysis: Face and Expression Recognition. IEEE Trans. Image Process. 2013, 22, 1740–1752. [Google Scholar] [CrossRef]
- Burrus, C.; Gopinath, R.; Guo, H. Introduction to Wavelets and Wavelet Transforms: A Primer, 1st ed.; Pearson: Upper Saddle River, NJ, USA, 1997; ISBN 978-0-13-489600-7. [Google Scholar]
- Sarkar, N.; Chaudhuri, B.B. An Efficient Differential Box-Counting Approach to Compute Fractal Dimension of Image. IEEE Trans. Syst. Man Cybern. 1994, 24, 115–120. [Google Scholar] [CrossRef]
- Dlask, M.; Kukal, J. Hurst Exponent Estimation of Fractional Surfaces for Mammogram Images Analysis. Phys. A Stat. Mech. Its Appl. 2022, 585, 126424. [Google Scholar] [CrossRef]
- Siedlecki, W.; Sklansky, J. A Note on Genetic Algorithms for Large-Scale Feature Selection. Pattern Recognit. Lett. 1989, 10, 335–347. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Khotanzad, A.; Hong, Y.H. Invariant Image Recognition by Zernike Moments. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 489–497. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective, Illustrated ed.; The MIT Press: Cambridge, MA, USA, 2012; ISBN 978-0-262-01802-9. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Ding, S.; Zhao, H.; Zhang, Y.; Xu, X.; Nie, R. Extreme Learning Machine: Algorithm, Theory and Applications. Artif. Intell. Rev. 2015, 44, 103–115. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; ISBN 978-0-387-31073-2. [Google Scholar]
- Thibault, G.; Fertil, B.; Navarro, C.; Pereira, S.; Cau, P.; Levy, N.; Sequeira, J.; Mari, J.-L. Shape and Texture Indexes Application to Cell Nuclei Classification. Int. J. Patt. Recogn. Artif. Intell. 2013, 27, 1357002. [Google Scholar] [CrossRef]
- Heikkilä, M.; Pietikäinen, M.; Schmid, C. Description of Interest Regions with Local Binary Patterns. Pattern Recognit. 2009, 42, 425–436. [Google Scholar] [CrossRef]
- Verma, M.; Raman, B. Local Tri-Directional Patterns: A New Texture Feature Descriptor for Image Retrieval. Digit. Signal Process. 2016, 51, 62–72. [Google Scholar] [CrossRef]
- Chen, J.; Shan, S.; He, C.; Zhao, G.; Pietikäinen, M.; Chen, X.; Gao, W. WLD: A Robust Local Image Descriptor. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1705–1720. [Google Scholar] [CrossRef]
- Liao, S.; Zhu, X.; Lei, Z.; Zhang, L.; Li, S.Z. Learning Multi-Scale Block Local Binary Patterns for Face Recognition. In Proceedings of the Advances in Biometrics; Lee, S.-W., Li, S.Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 828–837. [Google Scholar]
- Zhao, S.; Gao, Y.; Zhang, B. Sobel-LBP. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 2144–2147. [Google Scholar]
- Pentland, A.P. Fractal-Based Description of Natural Scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 661–674. [Google Scholar] [CrossRef] [PubMed]
- Ranganath, A.; Senapati, M.R.; Sahu, P.K. Estimating the Fractal Dimension of Images Using Pixel Range Calculation Technique. Vis. Comput. 2021, 37, 635–650. [Google Scholar] [CrossRef]
- de Melo, R.H.C.; de A. Vieira, E.; Conci, A. Characterizing the Lacunarity of Objects and Image Sets and Its Use as a Technique for the Analysis of Textural Patterns. In Proceedings of the Advanced Concepts for Intelligent Vision Systems; Blanc-Talon, J., Philips, W., Popescu, D., Scheunders, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 208–219. [Google Scholar]
- Jayalalitha, G.; Shanthoshini Deviha, V.; Uthayakumar, R. Fractal Model for Blood Flow in Cardiovascular System. Comput. Biol. Med. 2008, 38, 684–693. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature, 2nd prt. ed.; Times Books: New York, NY, USA, 1982; ISBN 978-0-7167-1186-5. [Google Scholar]
- Lopes, R.; Betrouni, N. Fractal and Multifractal Analysis: A Review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an Irregular Time Series on the Basis of the Fractal Theory. Phys. D Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Petrosian, A. Kolmogorov Complexity of Finite Sequences and Recognition of Different Preictal EEG Patterns. In Proceedings of the Eighth IEEE Symposium on Computer-Based Medical Systems, Lubbock, TX, USA, 9–10 June 1995; pp. 212–217. [Google Scholar]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Perona, P.; Malik, J. Scale-Space and Edge Detection Using Anisotropic Diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; ter Haar Romeny, B.; Zimmerman, J.B.; Zuiderveld, K. Adaptive Histogram Equalization and Its Variations. Comput. Vis. Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Costa, A.F.; Humpire-Mamani, G.; Traina, A.J.M. An Efficient Algorithm for Fractal Analysis of Textures. In Proceedings of the 2012 25th SIBGRAPI Conference on Graphics, Patterns and Images, Ouro Preto, Brazil, 22–25 August 2012; pp. 39–46. [Google Scholar]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. In Proceedings of the Stochastic Algorithms: Foundations and Applications; Watanabe, O., Zeugmann, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Hu, P.; Pan, J.-S.; Chu, S.-C. Improved Binary Grey Wolf Optimizer and Its Application for Feature Selection. Knowl.-Based Syst. 2020, 195, 105746. [Google Scholar] [CrossRef]
- Saniei, E.; Setayeshi, S.; Akbari, M.E.; Navid, M. A Vascular Network Matching in Dynamic Thermography for Breast Cancer Detection. Quant. InfraRed Thermogr. J. 2015, 12, 24–36. [Google Scholar] [CrossRef]
- Serrano, R.C.; Ulysses, J.; Ribeiro, S.; Conci, A.; Lima, R. Using Hurst Coefficient and Lacunarity to Diagnosis Early Breast Diseases. In Proceedings of the IWSSIP 2010—17th International Conference on Systems, Signals and Image Processing, Rio de Janeiro, Brazil, 17–19 June 2010. [Google Scholar]
- Gamal, S.; Atef, H.; Youssef, D.; Ismail, T.; El-Azab, J. Early Breast Cancer Screening from Thermography via Deep Pre-Trained Edge Detection with Extreme Gradient Boosting. In Proceedings of the 2023 Intelligent Methods, Systems, and Applications (IMSA), Giza, Egypt, 15–16 July 2023; pp. 430–433. [Google Scholar] [CrossRef]
- Sobel, I. Camera Models and Machine Perception; Stanford University: Palo Algo, CA, USA, 1970. [Google Scholar]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Xie, S.; Tu, Z. Holistically-Nested Edge Detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Granlund, G.H. In Search of a General Picture Processing Operator. Comput. Graph. Image Process. 1978, 8, 155–173. [Google Scholar] [CrossRef]
- Al-Rababah, K.; Mustaffa, M.R.; Doraisamy, S.C.; Khalid, F. Hybrid Discrete Wavelet Transform and Histogram of Oriented Gradients for Feature Extraction and Classification of Breast Dynamic Thermogram Sequences. In Proceedings of the 2021 Fifth International Conference on Information Retrieval and Knowledge Management (CAMP), Virtual, 15–16 June 2021; pp. 31–35. [Google Scholar]
- Hammouche, A.; El-Bakry, H.; Mostafa, R. Image Contrast Enhancement Using Fast Discrete Curvelet Transform via Wrapping (FDCT-Wrap). UJARCST 2017, 5, 51830780. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, New York, NY, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper With Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Chollet, F. Xception: Deep Learning With Depthwise Separable Convolutions. arXiv 2017, arXiv:1610.02357. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Shapley, L.S. A Value for n-Person Games. In Contributions to the Theory of Games, Volume II; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; pp. 307–318. ISBN 978-1-4008-8197-0. [Google Scholar]
- Huang, G.-B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, E.L.; Romano, J.P. Testing Statistical Hypotheses; Springer Texts in Statistics; Springer International Publishing: Cham, Switzerland, 2022; ISBN 978-3-030-70577-0. [Google Scholar]
- Hapfelmeier, A.; Ulm, K. Variable Selection by Random Forests Using Data with Missing Values. Comput. Stat. Data Anal. 2014, 80, 129–139. [Google Scholar] [CrossRef]
- Goldberger, J.; Hinton, G.E.; Roweis, S.; Salakhutdinov, R.R. Neighbourhood Components Analysis. In Proceedings of the Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2004; Volume 17. [Google Scholar]
- Liu, H.; Motoda, H. Computational Methods of Feature Selection; CRC Press: Boca Raton, FL, USA, 2007; ISBN 978-1-58488-879-6. [Google Scholar]
- Santos, W.P.; Assis, F.M.; Souza, R.E.; Santos Filho, P.B.; Lima Neto, F.B. Dialectical Multispectral Classification of Diffusion-Weighted Magnetic Resonance Images as an Alternative to Apparent Diffusion Coefficients Maps to Perform Anatomical Analysis. Comput. Med. Imaging Graph. 2009, 33, 442–460. [Google Scholar] [CrossRef]
- Shlens, J. A Tutorial on Independent Component Analysis. arXiv 2014, arXiv:1404.2986. [Google Scholar]
- He, X.; Niyogi, P. Locality Preserving Projections. In Proceedings of the Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2003; Volume 16. [Google Scholar]
- Chen, S.-B.; Zhang, Y.-M.; Ding, C.H.Q.; Zhang, J.; Luo, B. Extended Adaptive Lasso for Multi-Class and Multi-Label Feature Selection. Knowl.-Based Syst. 2019, 173, 28–36. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Bansal, J.C.; Sharma, H.; Jadon, S.S.; Clerc, M. Spider Monkey Optimization Algorithm for Numerical Optimization. Memetic Comp. 2014, 6, 31–47. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G. Ant Colony Optimization: A New Meta-Heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 2, pp. 1470–1477. [Google Scholar]
- Karaboga, D.; Basturk, B. A Powerful and Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony (ABC) Algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Tilahun, S.L.; Ong, H.C. Modified Firefly Algorithm. J. Appl. Math. 2012, 2012, 467631. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A Discrete Binary Version of the Particle Swarm Algorithm. In Proceedings of the Computational Cybernetics and Simulation 1997 IEEE International Conference on Systems, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar]
- Singh, U.; Salgotra, R.; Rattan, M. A Novel Binary Spider Monkey Optimization Algorithm for Thinning of Concentric Circular Antenna Arrays. IETE J. Res. 2016, 62, 736–744. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Suykens, J.a.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Chen, C.L.P.; Liu, Z. Broad Learning System: An Effective and Efficient Incremental Learning System Without the Need for Deep Architecture. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhou, Z.-H. Improve Computer-Aided Diagnosis With Machine Learning Techniques Using Undiagnosed Samples. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2007, 37, 1088–1098. [Google Scholar] [CrossRef]
- Yi, X.; Walia, E.; Babyn, P. Generative Adversarial Network in Medical Imaging: A Review. Med. Image Anal. 2019, 58, 101552. [Google Scholar] [CrossRef]
- Kim, E.; Cho, H.; Ko, E.; Park, H. Generative Adversarial Network with Local Discriminator for Synthesizing Breast Contrast-Enhanced MRI. In Proceedings of the 2021 IEEE EMBS International Conference on Biomedical and Health Informatics (BHI), Virtual, 27–30 July 2021; pp. 1–4. [Google Scholar]
- Luo, L.; Wang, X.; Lin, Y.; Ma, X.; Tan, A.; Chan, R.; Vardhanabhuti, V.; Chu, W.C.; Cheng, K.-T.; Chen, H. Deep Learning in Breast Cancer Imaging: A Decade of Progress and Future Directions. IEEE Rev. Biomed. Eng. 2025, 18, 130–151. [Google Scholar] [CrossRef] [PubMed]
- Breast Cancer Pre-Screening, AI, Thermal Imaging, Predictive Medicine | Thermaiscan.Com. Available online: https://www.thermaiscan.com/ (accessed on 22 February 2025).
- Niramai—A Novel Breast Cancer Screening Solution. Available online: https://www.niramai.com/ (accessed on 22 February 2025).
- Adapa, K.; Gupta, A.; Singh, S.; Kaur, H.; Trikha, A.; Sharma, A.; Rahul, K. A Real World Evaluation of an Innovative Artificial Intelligence Tool for Population-Level Breast Cancer Screening. npj Digit. Med. 2025, 8, 1–11. [Google Scholar] [CrossRef]
- Ginsburg, G.S.; Picard, R.W.; Friend, S.H. Key Issues as Wearable Digital Health Technologies Enter Clinical Care. N. Engl. J. Med. 2024, 390, 1118–1127. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Amin, O.; Shihada, B. Intelligent Wearable Systems: Opportunities and Challenges in Health and Sports. ACM Comput. Surv. 2024, 56, 1–42. [Google Scholar] [CrossRef]
- Elouerghi, A.; Bellarbi, L.; Errachid, A.; Yaakoubi, N. An IoMT-Based Wearable Thermography System for Early Breast Cancer Detection. IEEE Trans. Instrum. Meas. 2024, 73, 1–17. [Google Scholar] [CrossRef]
- Francis, S.V.; Sasikala, M.; Bhavani Bharathi, G.; Jaipurkar, S.D. Breast Cancer Detection in Rotational Thermography Images Using Texture Features. Infrared Phys. Technol. 2014, 67, 490–496. [Google Scholar] [CrossRef]
- James, A.P.; Dasarathy, B.V. Medical Image Fusion: A Survey of the State of the Art. Inf. Fusion. 2014, 19, 4–19. [Google Scholar] [CrossRef]
- Huang, R.; Lin, Z.; Dou, H.; Wang, J.; Miao, J.; Zhou, G.; Jia, X.; Xu, W.; Mei, Z.; Dong, Y.; et al. AW3M: An Auto-Weighting and Recovery Framework for Breast Cancer Diagnosis Using Multi-Modal Ultrasound. Med. Image Anal. 2021, 72, 102137. [Google Scholar] [CrossRef]
- Liu, T.; Huang, J.; Liao, T.; Pu, R.; Liu, S.; Peng, Y. A Hybrid Deep Learning Model for Predicting Molecular Subtypes of Human Breast Cancer Using Multimodal Data. IRBM 2022, 43, 62–74. [Google Scholar] [CrossRef]
- Vanguri, R.S.; Luo, J.; Aukerman, A.T.; Egger, J.V.; Fong, C.J.; Horvat, N.; Pagano, A.; Araujo-Filho, J.d.A.B.; Geneslaw, L.; Rizvi, H.; et al. Multimodal Integration of Radiology, Pathology and Genomics for Prediction of Response to PD-(L)1 Blockade in Patients with Non-Small Cell Lung Cancer. Nat. Cancer 2022, 3, 1151–1164. [Google Scholar] [CrossRef]
- Arena, F.; DiCicco, T.; Anand, A. Multimodality Data Fusion Aids Early Detection of Breast Cancer Using Conventional Technology and Advanced Digital Infrared Imaging. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; Volume 1, pp. 1170–1173. [Google Scholar]
- Minavathi; Murali, S.; Dinesh, M.S. Information Fusion from Mammogram and Ultrasound Images for Better Classification of Breast Mass. In Proceedings of International Conference on Advances in Computing; Springer: New Delhi, India, 2013; pp. 943–953. ISBN 978-81-322-0740-5. [Google Scholar]
- Li, C.; Wong, C.; Zhang, S.; Usuyama, N.; Liu, H.; Yang, J.; Naumann, T.; Poon, H.; Gao, J. LLaVA-Med: Training a Large Language-and-Vision Assistant for Biomedicine in One Day. Adv. Neural Inf. Process. Syst. 2023, 36, 28541–28564. [Google Scholar]
- Bommasani, R.; Hudson, D.A.; Adeli, E.; Altman, R.; Arora, S.; von Arx, S.; Bernstein, M.S.; Bohg, J.; Bosselut, A.; Brunskill, E.; et al. On the Opportunities and Risks of Foundation Models. Available online: https://crfm.stanford.edu/report.html (accessed on 16 April 2025).
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Shamshad, F.; Khan, S.; Zamir, S.W.; Khan, M.H.; Hayat, M.; Khan, F.S.; Fu, H. Transformers in Medical Imaging: A Survey. Med. Image Anal. 2023, 88, 102802. [Google Scholar] [CrossRef]
- Haq, M.U.; Sethi, M.A.J.; Rehman, A.U. Capsule Network with Its Limitation, Modification, and Applications—A Survey. Mach. Learn. Knowl. Extr. 2023, 5, 891–921. [Google Scholar] [CrossRef]
- Srinivasan, M.N.; Sikkandar, M.Y.; Alhashim, M.; Chinnadurai, M. Capsule Network Approach for Monkeypox (CAPSMON) Detection and Subclassification in Medical Imaging System. Sci. Rep. 2025, 15, 3296. [Google Scholar] [CrossRef]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model. In Proceedings of the 41st International Conference on Machine Learning, Vienna, Austria, 8 July 2024; pp. 62429–62442. [Google Scholar]
- Yue, Y.; Li, Z. MedMamba: Vision Mamba for Medical Image Classification. arXiv 2024, arXiv:2403.03849. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2025, arXiv:2404.19756. [Google Scholar]
- Wang, G.; Zhu, Q.; Song, C.; Wei, B.; Li, S. MedKAFormer: When Kolmogorov-Arnold Theorem Meets Vision Transformer for Medical Image Representation. IEEE J. Biomed. Health Inform. 2025, 1–11. [Google Scholar] [CrossRef]
- Kumar, S.; Rastogi, U. A Comprehensive Review on the Advancement of High-Dimensional Neural Networks in Quaternionic Domain with Relevant Applications. Arch. Comput. Methods Eng. 2023, 30, 3941–3968. [Google Scholar] [CrossRef]
- Parcollet, T.; Morchid, M.; Linarès, G. A Survey of Quaternion Neural Networks. Artif. Intell. Rev. 2020, 53, 2957–2982. [Google Scholar] [CrossRef]
- Greenblatt, A.; Mosquera-Lopez, C.; Agaian, S. Quaternion Neural Networks Applied to Prostate Cancer Gleason Grading. In Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics, Manchester, UK, 13–16 October 2013; pp. 1144–1149. [Google Scholar]
- Singh, S.; Kumar, M.; Kumar, A.; Verma, B.K.; Shitharth, S. Pneumonia Detection with QCSA Network on Chest X-Ray. Sci. Rep. 2023, 13, 9025. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Tripathi, B.K.; Rawat, S.S. Deep Quaternion Convolutional Neural Networks for Breast Cancer Classification. Multimed. Tools Appl. 2023, 82, 31285–31308. [Google Scholar] [CrossRef]
- Soulard, R.; Carré, P. Quaternionic Wavelets for Texture Classification. Pattern Recognit. Lett. 2011, 32, 1669–1678. [Google Scholar] [CrossRef]
- Lawson, R. Implications of Surface Temperatures in the Diagnosis of Breast Cancer. Can. Med. Assoc. J. 1956, 75, 309–310. [Google Scholar]
- Wilson, A.N.; Gupta, K.A.; Koduru, B.H.; Kumar, A.; Jha, A.; Cenkeramaddi, L.R. Recent Advances in Thermal Imaging and Its Applications Using Machine Learning: A Review. IEEE Sens. J. 2023, 23, 3395–3407. [Google Scholar] [CrossRef]
- Gonzalez, R.; Woods, R. Digital Image Processing, 4th ed.; Pearson: New York, NY, USA, 2017; ISBN 978-0-13-335672-4. [Google Scholar]




| Modality | Description | Advantages | Limitations |
|---|---|---|---|
| Mammography | Uses low-dose X-rays on compressed breasts to identify abnormal growths such as tumors, cysts, or calcifications. | FDA approved as the primary modality. Appropriate for screening and diagnosis. Quick and non-invasive. Well-defined standard [11]. | Less sensitive to women with dense breasts, especially in young women. Radiation exposure. Uncomfortable for women. Cannot use on pregnant women. Costly and less available in developing countries. |
| MRI | Uses a magnetic field and radio waves to create a detailed image of the breast after injecting the patient with IV contrast dye. | Detecting suspicious masses. Well-defined standard [11]. Greater sensitivity than mammography. | FDA approved as an adjunct modality. Expensive and less available in developing countries. |
| Ultrasound | Uses high-frequency sound waves to detect changes in the breasts. Used as an adjunct to mammography to detect and help classify abnormalities and guide biopsy. | East of use. Real-time imaging. Differentiates cysts from solid masses. Well-defined standard [11]. Sensitive to women with dense breasts. Can diagnose benign palpable masses. Can be used with breast implants. Radiation free. Painless and no discomfort. Can use on pregnant and lactating women. | FDA approved as an adjunct modality. Poor visibility to deep lesions. |
| Thermography | Uses thermal radiation emitted from breasts to detect differences. | Mobile and ease of use. Real-time imaging. Sensitive to women with dense breasts. Can be used with breast implants. Radiation free. Contactless and painless. Cost-effective for developing countries. | FDA approved as an adjunct modality. Multiple standards [12]. Patient temperature differences due to hormones, exercising, pregnancy, and menopausal cycle impact results. Requires temperature and humidity-controlled environment. Limited trials. |
| Symbol | Description |
|---|---|
| I | Symbol representing an image. |
| L | Number of intensity levels in image I. |
| Intensity level of pixel in image I at horizontal location and vertical location . | |
| Number of rows and columns in image I. | |
| The intensity levels for an L-level digital image, where . | |
| Number of pixels in image f with intensity level . | |
| is the histogram of intensity values in f. | |
| is the normalized histogram of intensity values in f. |
| Modified Ville Marie [36] | Thermobiological Grading System [37] | Twenty Point Thermobiological [38] | |||
|---|---|---|---|---|---|
| Grade | Description | Grade | Description | Grade | Description |
| IR1 | Absence of any vascular pattern to mild vascular symmetry | TH1 | Symmetrical, bilateral, and nonvascular (non-suspicious, normal study) | TH1 | Normal Symmetrical Non-Vascular |
| IR2 | Significant buy symmetrical vascular pattern to moderate vascular asymmetry, particularly if stable | TH2 | Symmetrical, bilateral, and vascular (non-suspicious, normal study) | TH2 | Normal Symmetrical Vascular |
| IR3 | One abnormal sign | TH3 | Equivocal (low index of suspicious) | TH3 | Questionable |
| IR4 | Two abnormal signs | TH4 | Abnormal (moderate index of suspicion) | TH4 | Abnormal |
| IR5 | Three abnormal signs | TH5 | Highly abnormal (high index of suspicion) | TH5 | Very Abnormal |
| Citations | Designer | Public | Classes | Protocol | Camera |
|---|---|---|---|---|---|
| [5,29,41,42,43,44,45,46,47,48,49,50,51,52,53] | DMR-IR [39] | Yes | Normal: 184, Sick: 105, Unknown:4 | DIT, SIT | FLIR SC620 |
| [41,42,43,54] | Ann-Arbor [55] | Yes | Normal: 4, Sick: 11, 15 images | SIT | Not specified |
| [31,32,56,57] | HC-UFPE [31,57] | No | Benign Lesion: 121, Malignant Lesion: 76, Cyst: 72, No Lesion: 66; 1052 images | SIT | FLIR S45 |
| [53] | Mendeley [21] | Yes | Normal: 0, Benign: 84, Malignant: 35 | SIT | FLIR A300 |
| None known | Unnamed [58] | Yes | Normal: 6, High Risk: 2, Malignant: 11 | SIT | Not specified |
| [51] | DBT-TU-JU [59,60] | No | Normal 45, Benign: 36, Malignant: 13, Unknown: 6 | SIT | FLIR T650sc |
| [61] | Unnamed [61] | No | Normal: 30, Abnormal: 20 | SIT | FLIR 74 |
| Citation | Method | Features | Advantages | Limitations |
|---|---|---|---|---|
| [45,48,49,61,79] | First-Order Statistics [74,79] | Estimate properties of individual pixels (mean, energy, entropy, kurtosis, etc.) | Statistical summary of intensity information. Computational efficient. Works well for homogenous images. | No spatial and local information. Ineffective for multi-texture images. Cannot identify lesion location. |
| [79] | Tamura [80] | Globally quantify coarseness, contract, directionality, likeness, roughness, and regularity. | Mimic human perception. Classifies texture. Scale invariant. Works well for homogenous images. | May not distinguish fine texture details. Ineffective for multi-texture images. Cannot identify lesion location. |
| [5,44,45,48,49,56,57,61,68,79] | Co-occurrence Matrix [78] | Capture frequencies of co-located values and calculate 2nd-order statistics (energy, entropy, contrast, homogeneity, etc.). Includes GLCM [78], GLRLM [81,82], NGTDM [83], GLDM [84], GLSZM [85], and GLDM [79,84]. | Describes spatial relationships between pixels. Identifies surface pattern. Invariance to gray-level transformation. | Does not detect textures based on large primitives. Sensitive to scale and rotation. Restricted to a single direction. Dependent on manual choice of parameters |
| [44,45,46,51] | Non- parametric local transform [86] | Encodes local pixel intensity relationships. Includes LBP [87], CT [86], LTP [5,88], and LDN [89] texture features. | No probability distribution requirement. Robust to varying illumination. Captures local texture. Computational simplicity. | Noise sensitive. Limited global context. High dimensional vectors. |
| Method | Cite | Type | Description |
|---|---|---|---|
| Feature Selection | [49,68] | t-test [137] | Select features with significant differences in class means. |
| [32] | Random Forest [138] | Select features that maximally reduce impurity. | |
| [44] | Neighborhood Component Analysis [139] | Select features by maximizing an objective function. | |
| [57] | Forward Selection [97] | Add features until the target objective does not improve. | |
| [57] | Correlation Method [140] | Retain uncorrelated features. | |
| [57] | Objective Dialectical Method [141] | Select features that optimally balance relevance and redundancy. | |
| Dimension Reduction | [45,57,68] | Principal Component Analysis (PCA) [99] | Reduce dimensions by mapping signals to orthogonal components and select those with the highest variance. |
| [45] | Independent Component Analysis [142] | Map features to fewer statistically independent components. | |
| [45] | Locality Preserving Projections [143] | Preserves local structure in lower dimensional space. | |
| Embedded | [79] | Adaptive LASSO Regression [144] | Select features by applying L1 regression penalizing absolute values of coefficients. |
| Bio- inspired | [57] | Genetic Algorithm [93] | Select feature subset evolved from feature population that maximizes fitness function. |
| [46,57] | Particle Swarm Optimization [145] | Select features by simulating the collective movement of particles. | |
| [46] | Spider Monkey Optimization [146] | Select features by simulating the foraging behavior of monkeys. | |
| [57] | Ant Colony Search [147] | Select features by simulating the foraging behavior of ants. | |
| [57] | Bee Colony Search [148] | Select features by simulating the foraging behavior of bees. | |
| [50] | Binary Grey Wolf Optimizer [119] | Select features by simulating the behavior of grey wolves. | |
| [50] | Firefly Algorithm [149] | Select features by simulating the behavior of fireflies. |
| Classifier Method | Description |
|---|---|
| Support Vector Machine (SVM) [30] | Find a hyperplane that maximizes class separation. |
| Logistic Regression (LR) [96] | Maximum likelihood estimator of sigmoid function. |
| Decision Tree [96] | Recursive partition feature space to identify class. |
| Random Forest [97] | Train multiple trees on different feature and data subsets. |
| Multilayer Perceptron (MLP) [96] | A multilayered feedforward neural network with a non-linear activation function. |
| Naïve Bayes [96] | Identify class by maximum posterior probability. |
| AdaBoost [152] | Reduce misclassified instances by cascading multiple weak classifiers. |
| Least Square Support Vector Machine (LSSVM) [153] | Least square SVM that solves a set of linear equations instead of classical SVM technique. |
| Extreme Learning Machine (ELM) [98] | Single-layer feedforward neural network updating weights using Moore–Penrose pseudo-inverse. |
| Extreme Gradient Boosting (EGB) [129] | Reduce residual error by cascading weak decision trees. |
| Description | Equation | Advantages | Limitations |
|---|---|---|---|
| Accuracy | Simple to understand and compute. Useful as a baseline metric. | Misleading for imbalanced datasets. Does not distinguish the type of error. | |
| Sensitivity (Recall) | Works for imbalanced datasets. Good metric for high-risk use cases. Compliments Precision and Specificity. | Ignores false positives, therefore may lead to high noise. Not complete alone. | |
| Specificity | Works for imbalanced datasets. Good metric for avoiding false alarms. Compliments Sensitivity. | Ignores false negatives, therefore may lead to high undetected positives. Not complete alone. | |
| Precision | Works for imbalanced datasets. Useful when positive is costly. Complements recall. | Ignores false negatives, therefore may lead to high undetected positives. May lead to under detection. Not complete alone. | |
| F-Score | Works better for imbalanced datasets than accuracy. One metric that balances precision and recall. Widely adopted and understood. | Ignores true negatives. Hides precision and recall metrics. |
| Author(s) | Dataset | Leaked | Feature Extraction | Feature Reduction | Classifier | Performance |
|---|---|---|---|---|---|---|
| Madhavi and Thomas [68] | DMR-IR (63 patients) | No | GLCM, GLRLM, GLSZM, and NGTDM | t-test into Kernel PCA | LSSVM | Acc: 96% Sens: 100% Spec: 92% |
| Rodrigues da Silva et al. [56] | HC-UFPE (336 patients) | ? | GLCM and Zernike moments | None | ELM | Acc: 94.00% ± 2.8 Kappa: 93.23% ± 3.1 |
| Resmini et al. [5] | DMR-IR (80 patients) | GLCM | GA | SVM | Acc: 94.61% Sens: 94.61% Spec: 94.87% | |
| Pereira et al. [57] | HC-UFPE (336 patients) | ? | GLCM and Zernike moments | None | SVM | Acc: 91.42% ± 2.93 Macro Sens: 91.12% Macro Spec: 91.36% |
| Josephine et al. [61] | Private (50 images) | ? | FOS and GLCM | None | AdaBoost | Acc: 91% F1-Score: 89% |
| Pramanik et al. [51] | DMR-IR (226 patients) | ? | LINPE [51] | Training-based | LINPE-BL [51] | Acc: 96.9% Sens: 95.7% Spec: 97.2% |
| Chebbah et al. [49] | DMR-IR (90 images) | ? | FOS, GLCM, and blood vessels | t-test | SVM | Acc: 92.2% Sens: 86.7% Spec: 98.3% |
| Mishra and Rath [79] | DMR-IR (56 patients) | ? | FOS, GLCM, GLRCM, NGTDM, GLSZM, GLDM, and Tamura | Adaptive LASSO | SVM | Acc: 96.79% Precision: 98.77% Recall: 93.02% F1-Score: 95.81% |
| Author(s) | Dataset | Leaked | Feature Extraction | Feature Reduction | Classifier | Performance |
|---|---|---|---|---|---|---|
| Hakim and Awale [52] | DMR-IR (255 images) | ? | HE, FD, and lacunarity | None | Naïve Bayes | Acc: 94.53% Sens: 86.25% Spec: 97.75% |
| Dey et al. [41] | DMR-IR (85 patients) Ann Arbor (16 patients) | No | HE and FD | None | Ensemble | Acc: 96.08% ± 3.87 Sens: 100% ± 0 Spec: 93.57% ± 7.29 |
| Moradi and Rezai [50] | DMR-IR (200 images) | ? | SFTA [117] | Firefly Algorithm to Binary Grey Wolf Optimizer | Decision Tree | Acc: 97% Sens: 98% Spec: 96% |
| Author(s) | Dataset | Leaked | Feature Extraction | Feature Reduction | Classifier | Performance |
|---|---|---|---|---|---|---|
| Abdel-Nasser et al. [47] | DMR-IR (56 patients) | No | HOG | None | MLP | Acc: 95.8% Precision: 94.6% Recall: 97.1% F1-Score: 95.4% |
| Gonzalez-Leal et al. [45] | DMR-IR and others (1793 patients) | No | FOS, GLCM, LBP, and HOG | Kernel PCA | LR | AUC: 78.5% |
| Al-Rababah et al. [127] | DMR-IR (47 patients) | ? | DWT into HOG | None | SVM | Acc: 98.0% Sens: 97.7% Spec: 98.7% |
| Karthiga and Narasimhan [48] | DMR-IR (60 patients) | ? | FOS, GLCM, and curvelet transform to GLCM | Hypothesis testing | SVM | Acc: 93.3% AUC: 94% |
| de Santana et al. [31] | HC-UFPE (336 images) | ? | DWNN | None | SVM | Acc: 99.17% Macro Sens: 99.17% Macro Spec: 93.45% |
| De Freitas Barbosa et al. [32] | HC-UFPE (336 images) | ? | DWNN | Random Forest | SVM | Acc: 99% Sens: 100% Spec: 98% |
| Gama et al. [122] | DMR-IR (80 patients) | ? | Canny edge and HED | None | EGB | Acc: 97.4% Precision: 95% Recall: 100% F1-Score: 97% |
| Garia and Muthusamy [44] | DMR-IR (1000 images) | No | HOG | NCA | Random Forest | Acc: 98.00% Precision: 97.05% Recall: 99:00% F1-Score: 98.01% |
| Dihmani et al. [46] | DMR-IR (56 patients) | No | HOG, LBP, Gabor filter, and Canny Edge | Hybrid Spider Monkey Optimization | SVM | Acc: 98.27% F1-Score: 98.15% |
| Youssef et al. [29] | DMR-IR (90 patients) | ? | Image enhanced with Gabor filter, Canny edge, and HED to HOG fused with Resnet-50 + MobileNet | PCA | EGB | Acc: 96.22% Sens: 97.19% Spec: 95.23% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryan, L.; Agaian, S. Breast Cancer Detection Using Infrared Thermography: A Survey of Texture Analysis and Machine Learning Approaches. Bioengineering 2025, 12, 639. https://doi.org/10.3390/bioengineering12060639
Ryan L, Agaian S. Breast Cancer Detection Using Infrared Thermography: A Survey of Texture Analysis and Machine Learning Approaches. Bioengineering. 2025; 12(6):639. https://doi.org/10.3390/bioengineering12060639
Chicago/Turabian StyleRyan, Larry, and Sos Agaian. 2025. "Breast Cancer Detection Using Infrared Thermography: A Survey of Texture Analysis and Machine Learning Approaches" Bioengineering 12, no. 6: 639. https://doi.org/10.3390/bioengineering12060639
APA StyleRyan, L., & Agaian, S. (2025). Breast Cancer Detection Using Infrared Thermography: A Survey of Texture Analysis and Machine Learning Approaches. Bioengineering, 12(6), 639. https://doi.org/10.3390/bioengineering12060639







