Development, Validation, and Deployment of a Time-Dependent Machine Learning Model for Predicting One-Year Mortality Risk in Critically Ill Patients with Heart Failure
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Problem and Objectives
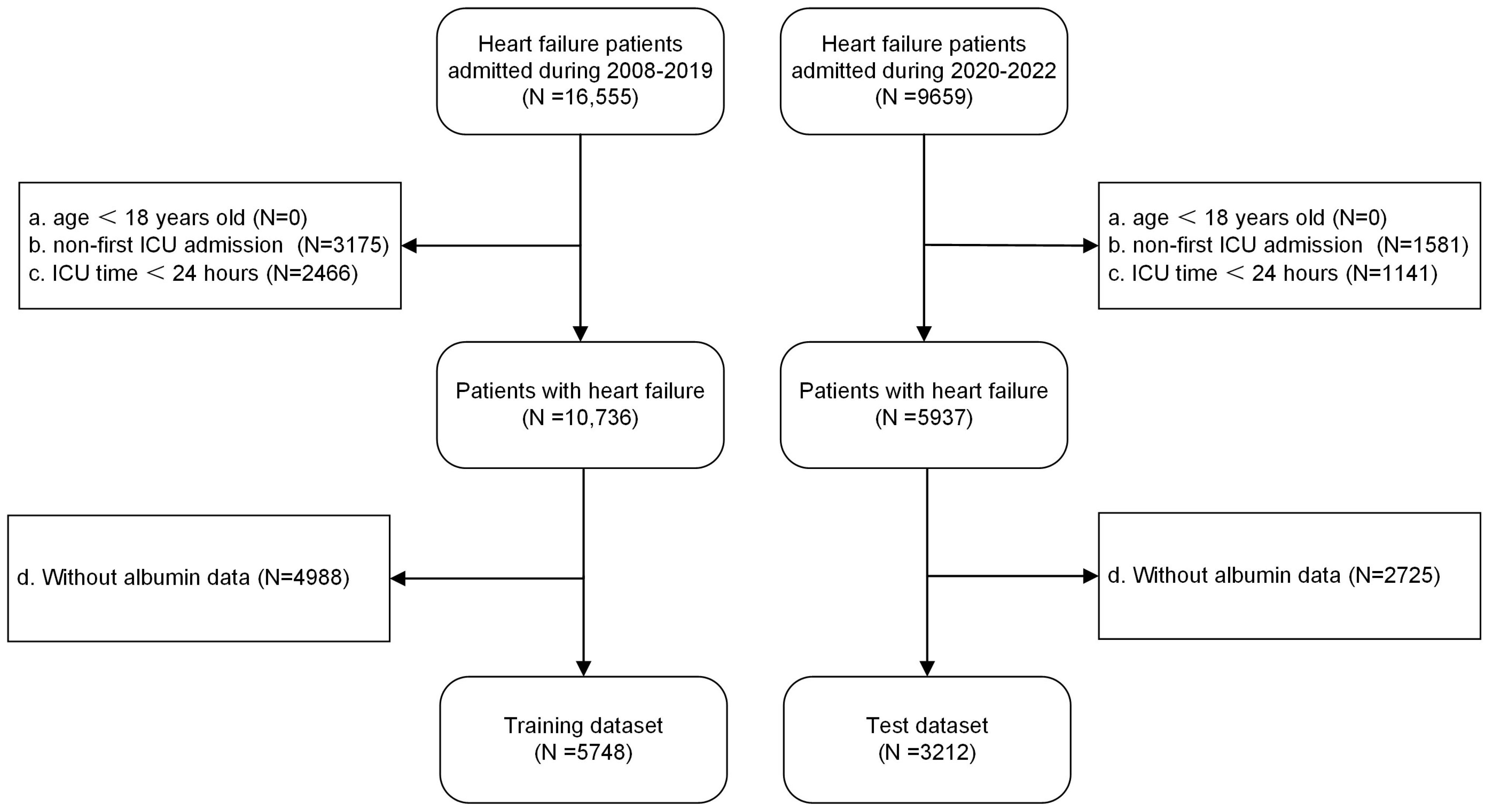
2.2. Sample Size and Study Population
2.3. Data Collection and Outcome Definition
2.4. Statistical Analysis
2.4.1. Data Preprocessing
2.4.2. Model Development and Evaluation
2.4.3. Model Interpretation
2.4.4. Model Deployment
3. Results
3.1. Sample Size and Baseline Characteristics
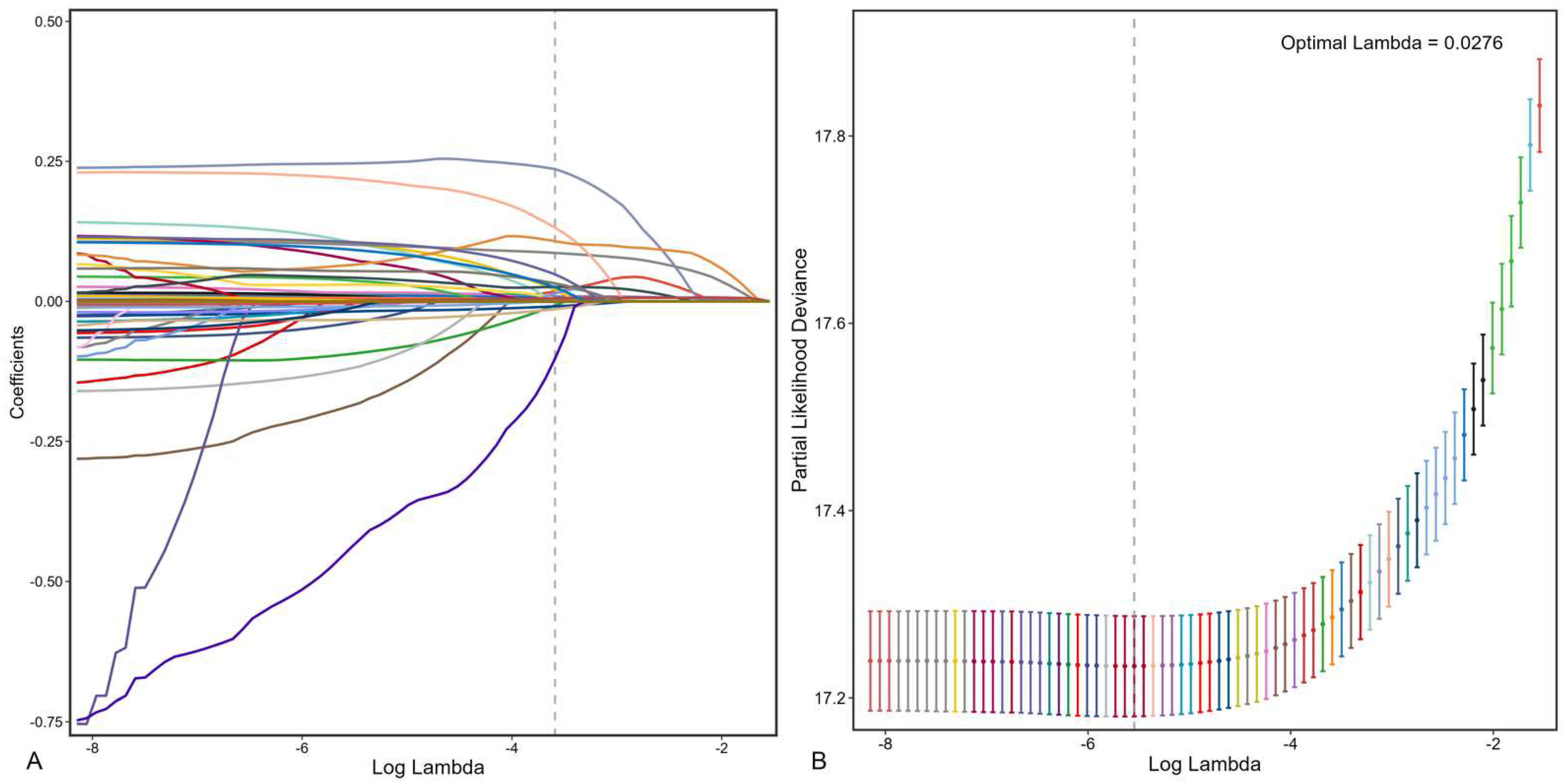
3.2. Feature Selection and Model Development
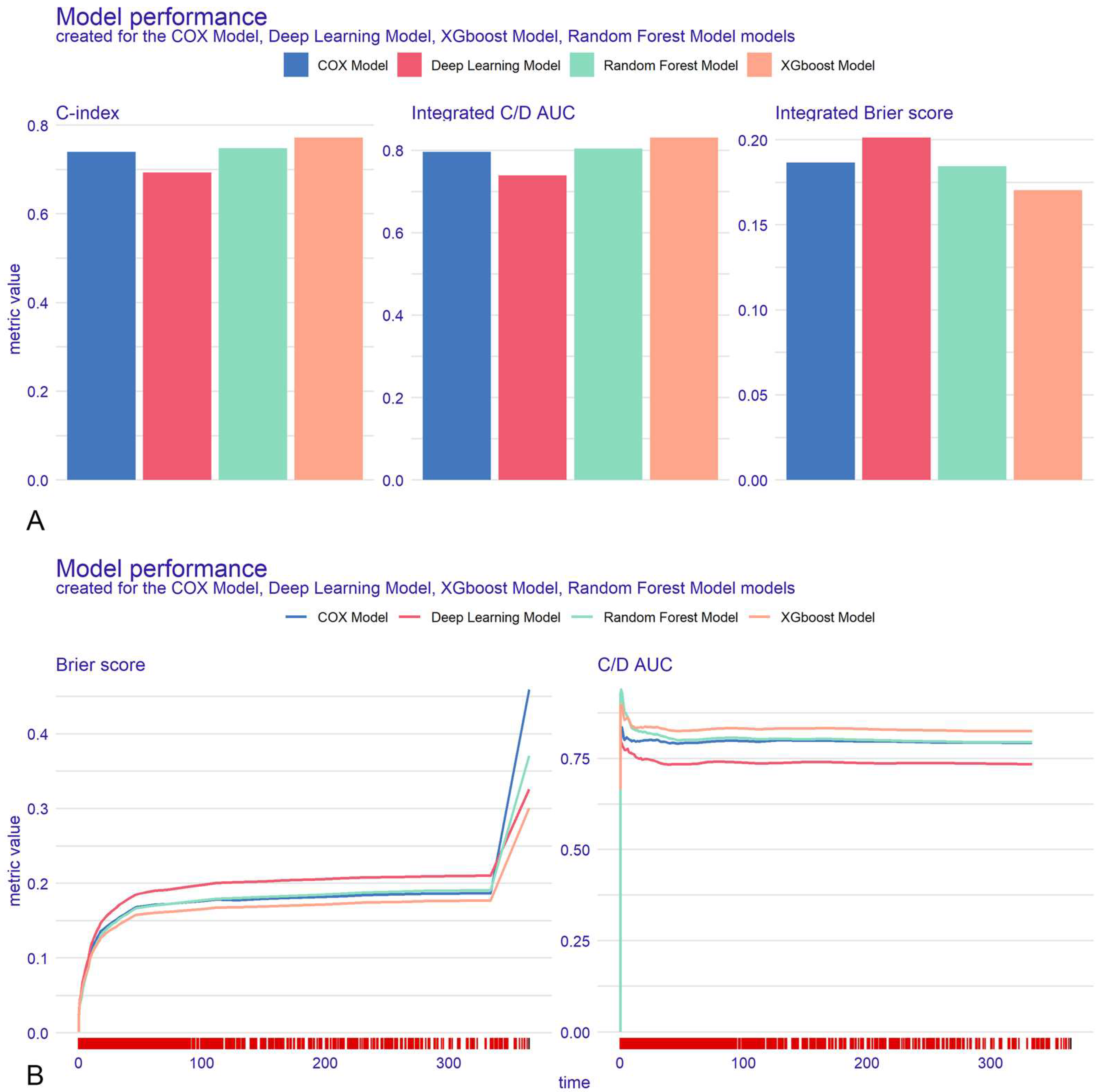
3.3. Model Evaluation
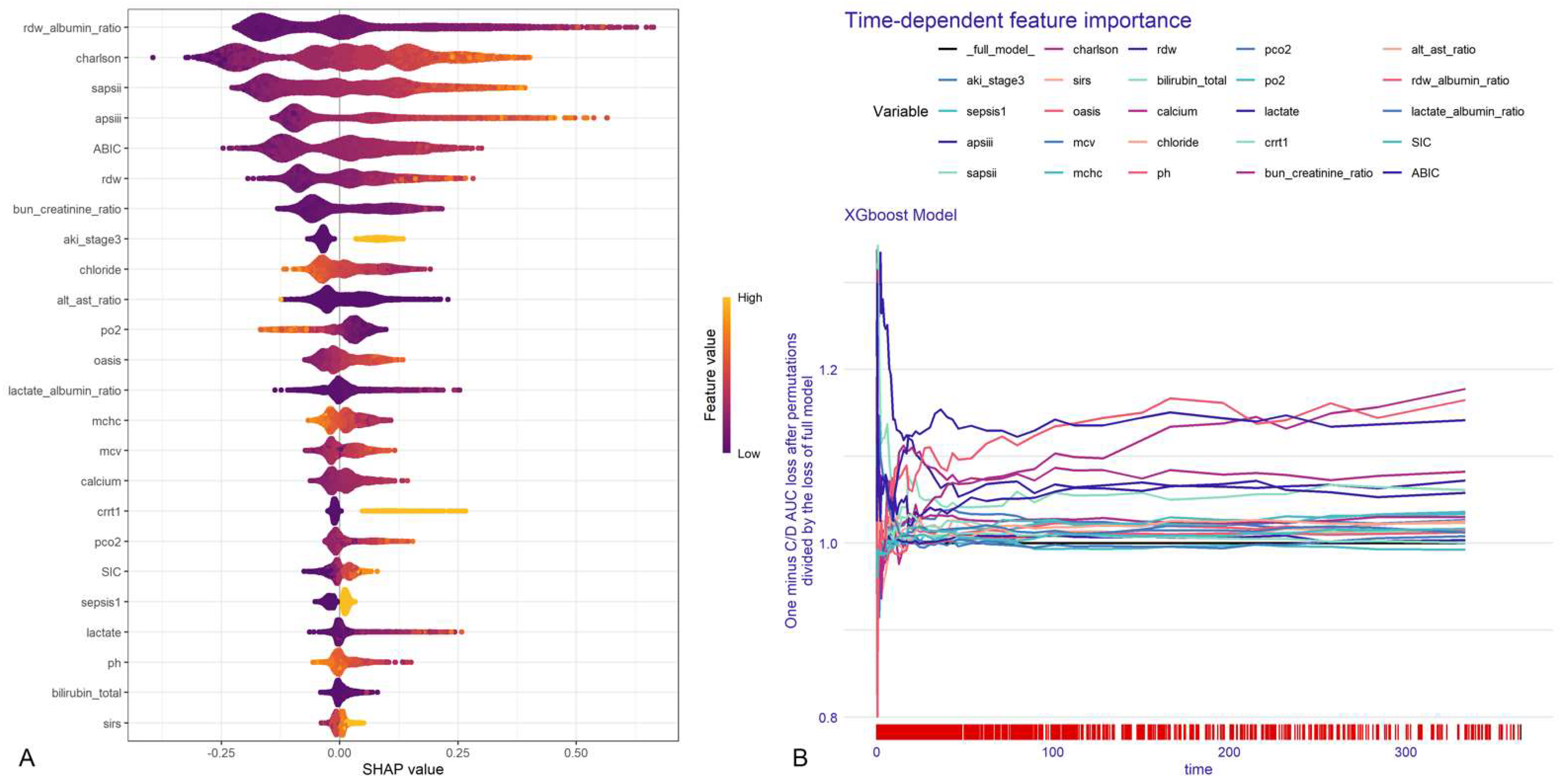
3.4. Model Interpretation and Online Deployment
3.4.1. Global Explanations
3.4.2. Local Explanations
3.4.3. Model Deployment
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roger, V.L. Epidemiology of Heart Failure: A Contemporary Perspective. Circ. Res. 2021, 128, 1421–1434. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, Z.; Li, X.; Yan, Y.; Liu, J.; Wang, J.; Guan, J.; Xin, A.; Zhang, F.; Ouyang, W.; et al. Global trends in heart failure from 1990 to 2019: An age-period-cohort analysis from the Global Burden of Disease study. ESC Heart Fail. 2024, 11, 3264–3278. [Google Scholar] [CrossRef]
- Zannad, F.; Mebazaa, A.; Juillière, Y.; Cohen-Solal, A.; Guize, L.; Alla, F.; Rougé, P.; Blin, P.; Barlet, M.; Paolozzi, L.; et al. Clinical profile, contemporary management and one-year mortality in patients with severe acute heart failure syndromes: The EFICA study. Eur. J. Heart Fail. 2006, 8, 697–705. [Google Scholar] [CrossRef]
- Bray, F.; Laversanne, M.; Sung, H.; Ferlay, J.; Siegel, R.L.; Soerjomataram, I.; Jemal, A. Global cancer statistics 2022: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2024, 74, 229–263. [Google Scholar] [CrossRef]
- Levy, W.C.; Mozaffarian, D.; Linker, D.T.; Sutradhar, S.C.; Anker, S.D.; Cropp, A.B.; Anand, I.; Maggioni, A.; Burton, P.; Sullivan, M.D.; et al. The Seattle Heart Failure Model: Prediction of survival in heart failure. Circulation 2006, 113, 1424–1433. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, S.; Yoshihisa, A.; Sato, Y.; Kanno, Y.; Watanabe, S.; Abe, S.; Sato, T.; Oikawa, M.; Kobayashi, A.; Yamaki, T.; et al. Clinical Significance of Get With the Guidelines-Heart Failure Risk Score in Patients With Chronic Heart Failure After Hospitalization. J. Am. Heart Assoc. 2018, 7, e008316. [Google Scholar] [CrossRef] [PubMed]
- Spinar, J.; Jarkovsky, J.; Spinarova, L.; Mebazaa, A.; Gayat, E.; Vitovec, J.; Linhart, A.; Widimsky, P.; Miklik, R.; Zeman, K.; et al. AHEAD score--Long-term risk classification in acute heart failure. Int. J. Cardiol. 2016, 202, 21–26. [Google Scholar] [CrossRef]
- Jing, L.; Ulloa Cerna, A.E.; Good, C.W.; Sauers, N.M.; Schneider, G.; Hartzel, D.N.; Leader, J.B.; Kirchner, H.L.; Hu, Y.; Riviello, D.M.; et al. A Machine Learning Approach to Management of Heart Failure Populations. JACC. Heart Fail. 2020, 8, 578–587. [Google Scholar] [CrossRef]
- Diprose, W.K.; Buist, N.; Hua, N.; Thurier, Q.; Shand, G.; Robinson, R. Physician understanding, explainability, and trust in a hypothetical machine learning risk calculator. J. Am. Med. Inform. Assoc. 2020, 27, 592–600. [Google Scholar] [CrossRef]
- Park, J.; Hwang, I.C.; Yoon, Y.E.; Park, J.B.; Park, J.H.; Cho, G.Y. Predicting Long-Term Mortality in Patients With Acute Heart Failure by Using Machine Learning. J. Card. Fail. 2022, 28, 1078–1087. [Google Scholar] [CrossRef]
- Segar, M.W.; Jaeger, B.C.; Patel, K.V.; Nambi, V.; Ndumele, C.E.; Correa, A.; Butler, J.; Chandra, A.; Ayers, C.; Rao, S.; et al. Development and Validation of Machine Learning-Based Race-Specific Models to Predict 10-Year Risk of Heart Failure: A Multicohort Analysis. Circulation 2021, 143, 2370–2383. [Google Scholar] [CrossRef] [PubMed]
- Tian, P.; Liang, L.; Zhao, X.; Huang, B.; Feng, J.; Huang, L.; Huang, Y.; Zhai, M.; Zhou, Q.; Zhang, J.; et al. Machine Learning for Mortality Prediction in Patients With Heart Failure With Mildly Reduced Ejection Fraction. J. Am. Heart Assoc. 2023, 12, e029124. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Li, J.; Wang, K. Independent prognostic importance of the albumin-corrected anion gap in critically ill patients with congestive heart failure: A retrospective study from MIMIC-IV database. BMC Cardiovasc. Disord. 2024, 24, 735. [Google Scholar] [CrossRef]
- Matsue, Y.; Kagiyama, N.; Yamaguchi, T.; Kuroda, S.; Okumura, T.; Kida, K.; Mizuno, A.; Oishi, S.; Inuzuka, Y.; Akiyama, E.; et al. Clinical and Prognostic Values of ALBI Score in Patients With Acute Heart Failure. Heart Lung Circ. 2020, 29, 1328–1337. [Google Scholar] [CrossRef]
- Li, N.; Li, J.; Wang, K. Association between red cell distribution width—Albumin ratio and all-cause mortality in intensive care unit patients with heart failure. Front. Cardiovasc. Med. 2025, 12, 1410339. [Google Scholar] [CrossRef]
- Johnson, A.E.W.; Bulgarelli, L.; Shen, L.; Gayles, A.; Shammout, A.; Horng, S.; Pollard, T.J.; Hao, S.; Moody, B.; Gow, B.; et al. MIMIC-IV, a freely accessible electronic health record dataset. Sci. Data 2023, 10, 1, Erratum in Sci. Data 2023, 10, 219. [Google Scholar] [CrossRef]
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Riley, R.D.; Ensor, J.; Snell, K.I.E.; Harrell, F.E., Jr.; Martin, G.P.; Reitsma, J.B.; Moons, K.G.M.; Collins, G.; van Smeden, M. Calculating the sample size required for developing a clinical prediction model. BMJ (Clin. Res. Ed.) 2020, 368, m441. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Li, T.; Guo, S.; Zeng, D.; Wang, K. Machine learning-based in-hospital mortality risk prediction tool for intensive care unit patients with heart failure. Front. Cardiovasc. Med. 2023, 10, 1119699. [Google Scholar] [CrossRef]
- Adler, E.D.; Voors, A.A.; Klein, L.; Macheret, F.; Braun, O.O.; Urey, M.A.; Zhu, W.; Sama, I.; Tadel, M.; Campagnari, C.; et al. Improving risk prediction in heart failure using machine learning. Eur. J. Heart Fail. 2020, 22, 139–147, Erratum in Eur. J. Heart Fail. 2020, 22, 2399. [Google Scholar] [CrossRef]
- Shin, S.; Austin, P.C.; Ross, H.J.; Abdel-Qadir, H.; Freitas, C.; Tomlinson, G.; Chicco, D.; Mahendiran, M.; Lawler, P.R.; Billia, F.; et al. Machine learning vs. conventional statistical models for predicting heart failure readmission and mortality. ESC Heart Fail. 2021, 8, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Tong, R.; Zhu, Z.; Ling, J. Comparison of linear and non-linear machine learning models for time-dependent readmission or mortality prediction among hospitalized heart failure patients. Heliyon 2023, 9, e16068. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liu, S.; Hu, Y.; Zhu, L.; Mao, Y.; Liu, J. Predicting Mortality in Intensive Care Unit Patients With Heart Failure Using an Interpretable Machine Learning Model: Retrospective Cohort Study. J. Med. Internet Res. 2022, 24, e38082. [Google Scholar] [CrossRef]
- Hao, M.; Jiang, S.; Tang, J.; Li, X.; Wang, S.; Li, Y.; Wu, J.; Hu, Z.; Zhang, H. Ratio of Red Blood Cell Distribution Width to Albumin Level and Risk of Mortality. JAMA Netw. Open 2024, 7, e2413213. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.T.; Pan, Y.; Zheng, Y.Y.; Yang, Y.; Hou, X.G.; Deng, C.J.; Ma, Y.T.; Xie, X. Age-Bilirubin-International Normalized Ratio (INR)-Creatinine (ABIC) Score, a Potential Prognostic Model for Long-Term Mortality of CAD Patients After PCI. J. Inflamm. Res. 2023, 16, 333–341. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Feng, G.; Wang, K. Association between albumin corrected anion gap (ACAG) and all-cause mortality in intensive care unit heart failure patients treated with inotropes and vasopressors. Signa Vitae 2025, 21, 51–59. [Google Scholar] [CrossRef]
- Wang, J.; Wang, K.; Feng, G.; Tian, X. Association Between the Albumin-Bilirubin (ALBI) Score and All-cause Mortality Risk in Intensive Care Unit Patients with Heart Failure. Glob. Heart 2024, 19, 97. [Google Scholar] [CrossRef]
- Wang, J.; Li, N.; Mu, Y.; Wang, K.; Feng, G. Association between serum albumin creatinine ratio and all-cause mortality in intensive care unit patients with heart failure. Front. Cardiovasc. Med. 2024, 11, 1406294. [Google Scholar] [CrossRef]
- Krzyziński, M.; Spytek, M.; Baniecki, H.; Biecek, P. SurvSHAP(t): Time-dependent explanations of machine learning survival models. Knowl.-Based Syst. 2023, 262, 110234. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]

| Models | Optimal Parameters | |
|---|---|---|
| XGBoost | nrounds = 368, nthread = 1 | subsample = 0.5488236 |
| eta = 0.004817722 | colsample_bytree = 0.5026403 | |
| max_depth = 8 | lambda = 0.1330041 | |
| min_child_weight = 4.4415141 | alpha = 2.646525 | |
| RSF | num.trees = 264, mtry = 2 | num.threads = 1 |
| min.node.size = 5 | max.depth = 10 | |
| DeepSur | num_nodes = 246 | batch_norm = TRUE |
| learning_rate = 0.00111408 | activation = “sigmoid” | |
| dropout = 0.3304397 | optimizer = “adamax” | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Kang, Q.; Tian, S.; Zhang, S.; Wang, K.; Feng, G. Development, Validation, and Deployment of a Time-Dependent Machine Learning Model for Predicting One-Year Mortality Risk in Critically Ill Patients with Heart Failure. Bioengineering 2025, 12, 511. https://doi.org/10.3390/bioengineering12050511
Wang J, Kang Q, Tian S, Zhang S, Wang K, Feng G. Development, Validation, and Deployment of a Time-Dependent Machine Learning Model for Predicting One-Year Mortality Risk in Critically Ill Patients with Heart Failure. Bioengineering. 2025; 12(5):511. https://doi.org/10.3390/bioengineering12050511
Chicago/Turabian StyleWang, Jiuyi, Qingxia Kang, Shiqi Tian, Shunli Zhang, Kai Wang, and Guibo Feng. 2025. "Development, Validation, and Deployment of a Time-Dependent Machine Learning Model for Predicting One-Year Mortality Risk in Critically Ill Patients with Heart Failure" Bioengineering 12, no. 5: 511. https://doi.org/10.3390/bioengineering12050511
APA StyleWang, J., Kang, Q., Tian, S., Zhang, S., Wang, K., & Feng, G. (2025). Development, Validation, and Deployment of a Time-Dependent Machine Learning Model for Predicting One-Year Mortality Risk in Critically Ill Patients with Heart Failure. Bioengineering, 12(5), 511. https://doi.org/10.3390/bioengineering12050511








