Simulation-Based Design and Machine Learning Optimization of a Novel Liquid Cooling System for Radio Frequency Coils in Magnetic Hyperthermia
Abstract
1. Introduction
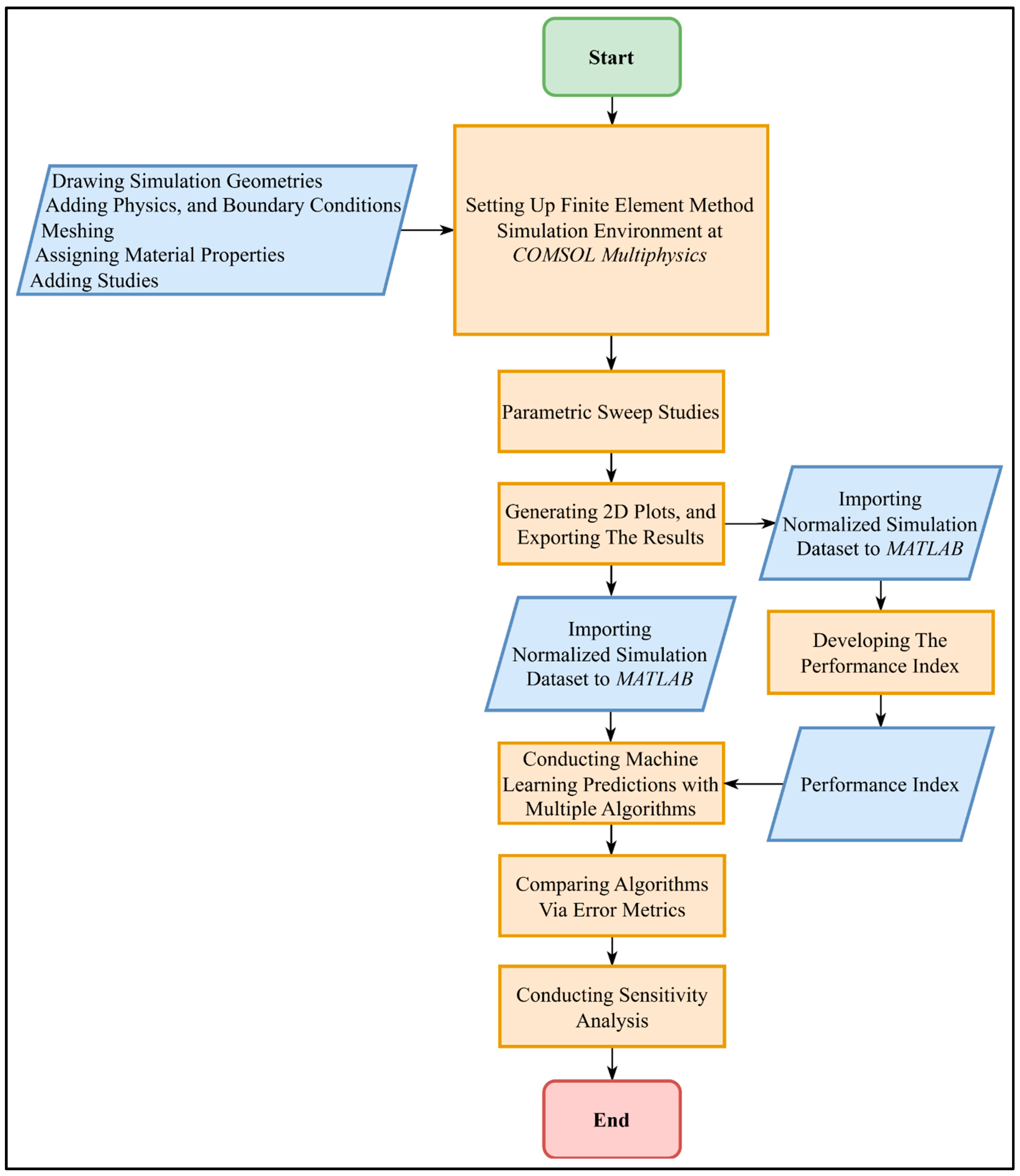
2. Materials and Methods
2.1. Simulations
2.2. Performance Index
2.3. Machine Learning Predictions
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Perigo, E.A.; Hemery, G.; Sandre, O.; Ortega, D.; Garaio, E.; Plazaola, F.; Teran, F.J. Fundamentals and advances in magnetic hyperthermia. Appl. Phys. Rev. 2015, 2, 041302. [Google Scholar] [CrossRef]
- Kafrouni, L.; Savadogo, O. Recent Progress on Magnetic Nanoparticles for Magnetic Hyperthermia. Prog Biomater. 2016, 5, 147–160. [Google Scholar] [CrossRef] [PubMed]
- Rubia-Rodríguez, I.; Santana-Otero, A.; Spassov, S.; Tombácz, E.; Johansson, C.; De La Presa, P.; Teran, F.J.; Del Puerto Morales, M.; Veintemillas-Verdaguer, S.; Thanh, N.T.K.; et al. Whither Magnetic Hyperthermia? A Tentative Roadmap. Materials 2021, 14, 706. [Google Scholar] [CrossRef] [PubMed]
- Usov, N.A. Low Frequency Hysteresis Loops of Superparamagnetic Nanoparticles with Uniaxial Anisotropy. J. Appl. Phys. 2010, 107, 123909. [Google Scholar] [CrossRef]
- Tishin, A.M.; Shtil, A.A.; Pyatakov, A.P.; Zverev, V.I. Developing Antitumor Magnetic Hyperthermia: Principles, Materials and Devices. Recent Pat. Anti-Cancer Drug Discov. 2016, 11, 360–375. [Google Scholar] [CrossRef]
- Rodriguez, B.; Rivera, D.; Zhang, J.Y.; Brown, C.; Young, T.; Williams, T.; Huq, S.; Mattioli, M.; Bouras, A.; Hadjpanayis, C.G. Magnetic Hyperthermia Therapy for High-Grade Glioma: A State-of-the-Art Review. Pharmaceuticals 2024, 17, 300. [Google Scholar] [CrossRef]
- Manescu, V.; Antoniac, I.; Paltanea, G.; Nemoianu, V.; Mohan, A.G.; Antoniac, A.; Rau, J.V.; Laptoiu, S.A.; Mihai, P.; Gavrila, H.; et al. Magnetic Hyperthermia in Glioblastoma Multiforme Treatment. Int. J. Mol. Sci. 2024, 25, 10065. [Google Scholar] [CrossRef]
- Sebastian, A.R.; Ryu, S.H.; Ko, H.M.; Kim, S.H. Design and Control of Field-Free Region Using Two Permanent Magnets for Selective Magnetic Hyperthermia. IEEE Access 2019, 7, 96094–96104. [Google Scholar] [CrossRef]
- Küçükdermenci, S. Analysis of Field-Free Region Formed by Parametric Positioning of a Magnet Pair for Targeted Magnetic Hyperthermia. Kuwait J. Sci. 2022, 49, 63–72. [Google Scholar] [CrossRef]
- Zeinoun, M.; Domingo-Diez, J.; Rodriguez-Garcia, M.; Garcia, O.; Vasic, M.; Ramos, M.; Olmedo, J.J.S. Enhancing Magnetic Hyperthermia Nanoparticle Heating Efficiency with Non-Sinusoidal Alternating Magnetic Field Waveforms. Nanomaterials 2021, 11, 3240. [Google Scholar] [CrossRef]
- Vilas-Boas, V.; Espiña, B.; Kolen’ko, Y.V.; Bañobre-López, M.; Brito, M.; Martins, V.; Duarte, J.A.; Petrovykh, D.Y.; Freitas, P.; Carvalho, F. Effectiveness and Safety of a Nontargeted Boost for a CXCR4-Targeted Magnetic Hyperthermia Treatment of Cancer Cells. ACS Omega 2019, 4, 1931–1940. [Google Scholar] [CrossRef]
- Park, Y.; Demessie, A.A.; Luo, A.; Taratula, O.R.; Moses, A.S.; Do, P.; Campos, L.; Jahangiri, Y.; Wyatt, C.R.; Albarqi, H.A.; et al. Targeted Nanoparticles with High Heating Efficiency for the Treatment of Endometriosis with Systemically Delivered Magnetic Hyperthermia. Small 2022, 18, e2107808. [Google Scholar] [CrossRef] [PubMed]
- Nica, V.; Marino, A.; Pucci, C.; Şen, O.z.; Emanet, M.; Pasquale, D.D.; Carmignani, A.; Petretto, A.; Bartolucci, M.; Lauciello, S.; et al. Cell-Membrane-Coated and Cell-Penetrating Peptide-Conjugated Trimagnetic Nanoparticles for Targeted Magnetic Hyperthermia of Prostate Cancer Cells. ACS Appl. Mater. Interfaces 2023, 15, 30008–30028. [Google Scholar] [CrossRef] [PubMed]
- Tan, M.; Reyes-Ortega, F.; Schneider-Futschik, E.K. Successes and Challenges: Inhaled Treatment Approaches Using Magnetic Nanoparticles in Cystic Fibrosis. Magnetochemistry 2020, 6, 25. [Google Scholar] [CrossRef]
- Deist, T.M.; Patti, A.; Wang, Z.; Krane, D.; Sorenson, T.; Craft, D. Simulation-Assisted Machine Learning. Bioinformatics 2019, 35, 4072–4080. [Google Scholar] [CrossRef] [PubMed]
- Ullah, A.; Asami, K.; Holtz, L.; Röver, T.; Azher, K.; Bartsch, K.; Emmelmann, C. A Machine Learning Approach for Mechanical Component Design Based on Topology Optimization Considering the Restrictions of Additive Manufacturing. J. Manuf. Mater. Process. 2024, 8, 220. [Google Scholar] [CrossRef]
- Comsol AB. Comsol Multiphysics® Software; Version 5; Comsol AB: Burlington, MA, USA, 2023. [Google Scholar]
- Abidin, M.N.Z.; Misro, Y. Numerical Simulation of Heat Transfer using Finite Element Method. J. Adv. Res. Fluid Mech. Therm. Sci. 2022, 92, 104–115. [Google Scholar] [CrossRef]
- Kuczmann, M.; Iványi, A. The Finite Element Method in Magnetics; Akademiai Kiado: Budapest, Hungary, 2008. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to The Finite Element Method, 3rd ed.; McGraw Hill: New York, NY, USA, 2006. [Google Scholar]
- Lei, J.; Shen, L.; Bi, Y.; Chen, J. A Design of Cooling Water Jacket Structure and an Analysis of Its Coolant Flow Characteristics for a Horizontal Diesel Engine. SAE Technol. Pap. 2011, 21. [Google Scholar] [CrossRef]
- Thulukkanam, K. Heat Exchanger Design Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Total Materia Database. In Altair Engineering; Total Materia Database: Zürich, Switzerland, 2023.
- Mathworks Inc. Matlab® R2022a, version 9.12.0; Mathworks Inc.: Natick, MA, USA, 2022. [Google Scholar]
- Atkinson, W.J.; Brezovich, I.A.; Chakraborty, P. Usable Frequencies in Hyperthermia with Thermal Seeds. IEEE Trans. Biomed. Eng. 1984, 31, 70–75. [Google Scholar] [CrossRef]
- Parte, B.H.d.l.; Rodrigo, I.; Gutiérrez-Basoa, J.; Correcher, S.I.; Medina, C.M.; Echevarría-Uraga, J.J.; Garcia, J.A.; Plazaola, F.; García-Alonso, I. Proposal of New Safety Limits for In Vivo Experiments of Magnetic Hyperthermia Antitumor Therapy. Cancers 2022, 14, 3084. [Google Scholar] [CrossRef]
- Sharma, A.; Jangam, A.; Shen, J.L.Y.; Ahmad, A.; Arepally, N.; Rodriguez, B.; Borrello, J.; Bouras, A.; Kleinberg, L.; Ding, K.; et al. Validation of a Temperature-Feedback Controlled Automated Magnetic Hyperthermia Therapy Device. Cancers 2023, 15, 327. [Google Scholar] [CrossRef] [PubMed]
- Vilas-Boas, V.; Carvalho, F.; Espiña, B. Magnetic Hyperthermia for Cancer Treatment: Main Parameters Affecting the Outcome of In Vitro and In Vivo Studies. Molecules 2020, 25, 2874. [Google Scholar] [CrossRef]
- Baldick, R. Applied Optimization: Formulation and Algorithms for Engineering Systems. IEEE Control. Syst. Mag. 2008, 28, 85. [Google Scholar]
- Rao, S.S. Engineering Optimization Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python: A Guide For Data Scientists; O’Reilly Media: Sebastopol, CA, USA, 2016. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Kira, K.; Rendell, L.A. The Feature Selection Problem: Traditional Methods and a New Algorithm. In Proceedings of the AAAI 10th Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992. [Google Scholar]
- Robnik-Sikonja, M.; Kononenko, I. Theoretical and Empirical Analysis of ReliefF and RReliefF. Mach. Learn. J. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K. High-Frequency Magnetic Components, 2nd ed.; Wliey: Hoboken, NJ, USA, 2014. [Google Scholar]
- Welsby, V.G. The Theory and Design of Inductance Coils; Macdonald and Co. Ltd.: London, UK, 1950. [Google Scholar]
- Nemala, H.; Thakur, J.S.; Naik, V.M.; Vaishnava, P.P.; Lawes, G.; Naik, R. Investigation of Magnetic Properties of Fe3O4 Nanoparticles Using Temperature Dependent Magnetic Hyperthermia in Ferrofluids. J. Appl. Phys. 2014, 116, 034309. [Google Scholar] [CrossRef]
- Patade, S.R.; Andhare, D.D.; Somvanshi, S.B.; Jadhav, S.A.; Khedkar, M.V.; Jadhav, K.M. Self-Heating Evaluation of Superparamagnetic MnFe2O4 Nanoparticles for Magnetic Fluid Hyperthermia Application Towards Cancer Treatment. Ceram. Int. 2020, 46, 25576–25583. [Google Scholar] [CrossRef]
- Bognar, G.; Takacs, G.; Szabo, P.G. A Novel Approach for Cooling Chiplets in Heterogeneously Integrated 2.5-D Packages Applying Microchannel Heatsink Embedded in the Interposer. IEEE Trans. Compon. Packag. Manuf. Technol. 2023, 13, 1155–1163. [Google Scholar] [CrossRef]
- Yoner, S.I.; Ozcan, A. Design of a Novel Liquid Cooling System in Simulation Environment for Radio Frequency Coils Used in Magnetic Hyperthermia Systems. In Proceedings of the 12th International Conference on Biomedical Engineering Systems, Barcelona, Spain, 19–21 August 2024. [Google Scholar]
- Haridas, D.; Tharkar, A.D.; Nimbalkar, U. Precision Cooling: Microchannel Heat Exchangers in Modern Engineering; Parab Publications: Uttar Pradesh, India, 2024. [Google Scholar]
- Ray, D.R.; Das, D.K. Simulations of Flows via CFD in Microchannels for Characterizing Entrance Region and Developing New Correlations for Hydrodynamic Entrance Length. Micromachines 2023, 14, 1418. [Google Scholar] [CrossRef]
- Christov, I.C.; Cognet, V.; Shidhore, T.C.; Stone, H.A. Flow Rate–Pressure Drop Relation for Deformable Shallow Microfluidic Channels. J. Fluid Mech. 2018, 841, 267–286. [Google Scholar] [CrossRef]
- Bhatkar, O.; Kudav, P.; Pendhari, S.; Bhojane, A.; Shitap, S. Study and Design of Engine Cooling System with Distilled Water as a Coolant for FSAE Car. Int. Res. J. Eng. Technol. 2017, 4, 585–587. [Google Scholar]
- Abdulmunem, A.R. Experimental Comparison Between Conventional Coolants and (TiO2/Water) Nano fluid to Select the Best Coolant for Automobiles in Iraq’s Summer Season. Eng. Technol. J. 2016, 34, 15. [Google Scholar] [CrossRef]
- Lorrain, P.; Corson, D.R.; Lorrain, F. Electromagnetic Fields and Waves, 3rd ed.; W.H. Freeman & Co.: New York, NY, USA, 1987. [Google Scholar]
- Kleinstreuer, C. Microfluidics and Nanofluidics: Theory and Selected Applications; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Tang, Y.; Ding, Y.; Jin, T.; Flesch, R.C.C. Improvement for Magnetic Field Uniformity of Helmholtz Coils and Its Influence on Magnetic Hyperthermia. IEEE Trans. Instrum. Meas. 2023, 72, 3325860. [Google Scholar] [CrossRef]
- Schölkopf, B. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond, 1st ed.; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning, 1st ed.; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Kleijnen, J.P.C. Sensitivity Analysis and Related Analyses: A Review of Some Statistical Techniques. J. Stat. Comput. Simul. 1997, 57, 111–142. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw Hill: New York, NY, USA, 2005. [Google Scholar]

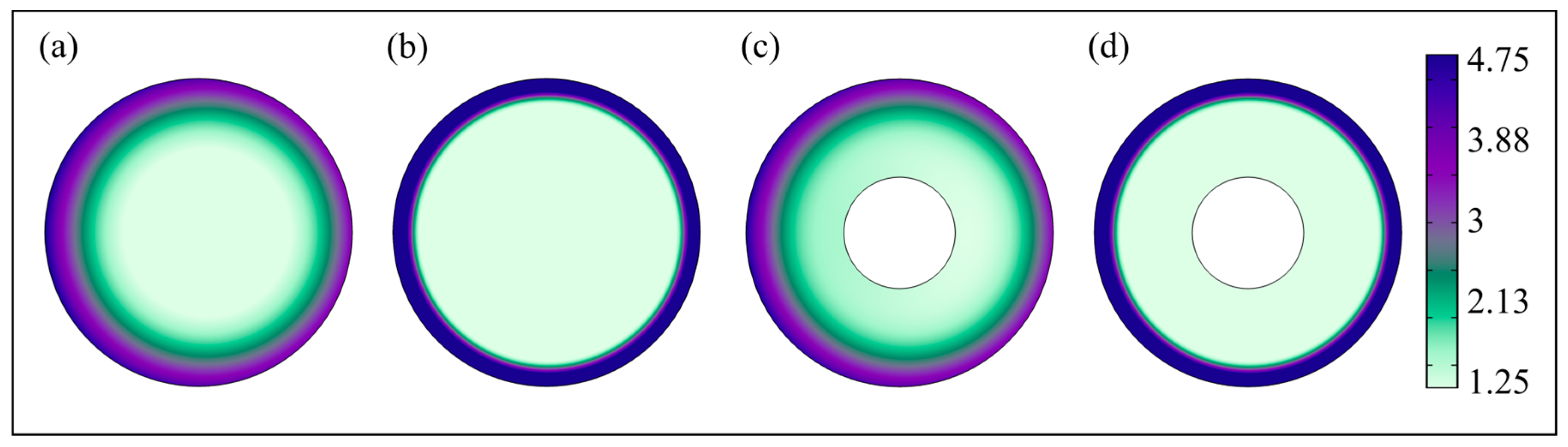

| Applied Frequency (MHz) | Cooling Systems | Water Flow Rate (m/s) | |
|---|---|---|---|
| 0.1 | 0.5 | ||
| 0.1 | Conventional Liquid | 24.964 | 23.172 |
| Novel Liquid with 0.25 mm Microchannel Radius | 21.590 | 20.773 | |
| Novel Liquid with 0.30 mm Microchannel Radius | 21.376 | 20.667 | |
| Novel Liquid with 0.35 mm Microchannel Radius | 21.275 | 20.618 | |
| 2.9 | Conventional Liquid | 52.050 | 40.816 |
| Novel Liquid with 0.25 mm Microchannel Radius | 30.948 | 25.374 | |
| Novel Liquid with 0.30 mm Microchannel Radius | 29.319 | 24.550 | |
| Novel Liquid with 0.35 mm Microchannel Radius | 28.134 | 23.960 | |
| Applied Frequency (MHz) | Water Flow Rate (m/s) | ||||
|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 0.1 | 0.879 | 0.736 | 0.627 | 0.544 | 0.480 |
| 0.3 | 0.839 | 0.727 | 0.631 | 0.555 | 0.493 |
| 0.5 | 0.831 | 0.736 | 0.646 | 0.572 | 0.511 |
| 0.7 | 0.834 | 0.750 | 0.664 | 0.591 | 0.531 |
| 0.9 | 0.843 | 0.767 | 0.684 | 0.611 | 0.551 |
| 1.1 | 0.855 | 0.785 | 0.704 | 0.632 | 0.572 |
| 1.3 | 0.868 | 0.805 | 0.725 | 0.654 | 0.592 |
| 1.5 | 0.883 | 0.824 | 0.747 | 0.675 | 0.613 |
| 1.7 | 0.899 | 0.845 | 0.768 | 0.697 | 0.634 |
| 1.9 | 0.915 | 0.865 | 0.790 | 0.718 | 0.655 |
| 2.1 | 0.932 | 0.886 | 0.811 | 0.739 | 0.675 |
| 2.3 | 0.949 | 0.906 | 0.833 | 0.761 | 0.696 |
| 2.5 | 0.966 | 0.927 | 0.854 | 0.782 | 0.716 |
| 2.7 | 0.983 | 0.947 | 0.875 | 0.803 | 0.737 |
| 2.9 | 1.000 | 0.968 | 0.896 | 0.824 | 0.757 |
| Applied Frequency (MHz) | Water Flow Rate (m/s) | ||||
|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 0.1 | 0.970 | 0.789 | 0.662 | 0.569 | 0.499 |
| 0.3 | 0.992 | 0.822 | 0.695 | 0.601 | 0.528 |
| 0.5 | 1.026 | 0.860 | 0.731 | 0.634 | 0.559 |
| 0.7 | 1.063 | 0.900 | 0.769 | 0.668 | 0.590 |
| 0.9 | 1.103 | 0.940 | 0.806 | 0.702 | 0.621 |
| 1.1 | 1.143 | 0.981 | 0.844 | 0.737 | 0.652 |
| 1.3 | 1.183 | 1.022 | 0.882 | 0.771 | 0.683 |
| 1.5 | 1.224 | 1.063 | 0.919 | 0.805 | 0.714 |
| 1.7 | 1.264 | 1.103 | 0.957 | 0.839 | 0.745 |
| 1.9 | 1.305 | 1.144 | 0.994 | 0.873 | 0.776 |
| 2.1 | 1.345 | 1.184 | 1.032 | 0.907 | 0.807 |
| 2.3 | 1.386 | 1.224 | 1.069 | 0.941 | 0.838 |
| 2.5 | 1.426 | 1.264 | 1.106 | 0.975 | 0.868 |
| 2.7 | 1.466 | 1.304 | 1.143 | 1.008 | 0.899 |
| 2.9 | 1.505 | 1.344 | 1.179 | 1.042 | 0.930 |
| Applied Frequency (MHz) | Water Flow Rate (m/s) | ||||
|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 0.1 | 0.976 | 0.792 | 0.664 | 0.570 | 0.500 |
| 0.3 | 1.007 | 0.829 | 0.699 | 0.603 | 0.530 |
| 0.5 | 1.044 | 0.870 | 0.737 | 0.638 | 0.561 |
| 0.7 | 1.086 | 0.912 | 0.776 | 0.673 | 0.593 |
| 0.9 | 1.129 | 0.955 | 0.815 | 0.708 | 0.625 |
| 1.1 | 1.173 | 0.998 | 0.854 | 0.743 | 0.657 |
| 1.3 | 1.217 | 1.041 | 0.893 | 0.779 | 0.689 |
| 1.5 | 1.261 | 1.084 | 0.932 | 0.814 | 0.720 |
| 1.7 | 1.306 | 1.126 | 0.971 | 0.849 | 0.752 |
| 1.9 | 1.350 | 1.169 | 1.010 | 0.884 | 0.784 |
| 2.1 | 1.393 | 1.212 | 1.049 | 0.919 | 0.815 |
| 2.3 | 1.437 | 1.254 | 1.088 | 0.954 | 0.847 |
| 2.5 | 1.480 | 1.296 | 1.126 | 0.989 | 0.878 |
| 2.7 | 1.523 | 1.338 | 1.165 | 1.023 | 0.910 |
| 2.9 | 1.566 | 1.380 | 1.203 | 1.058 | 0.941 |
| Applied Frequency (MHz) | Water Flow Rate (m/s) | ||||
|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| 0.1 | 0.980 | 0.794 | 0.664 | 0.571 | 0.500 |
| 0.3 | 1.019 | 0.835 | 0.703 | 0.606 | 0.532 |
| 0.5 | 1.059 | 0.877 | 0.742 | 0.641 | 0.563 |
| 0.7 | 1.103 | 0.921 | 0.781 | 0.677 | 0.596 |
| 0.9 | 1.150 | 0.965 | 0.822 | 0.712 | 0.628 |
| 1.1 | 1.196 | 1.010 | 0.862 | 0.749 | 0.660 |
| 1.3 | 1.243 | 1.055 | 0.902 | 0.784 | 0.693 |
| 1.5 | 1.290 | 1.099 | 0.942 | 0.820 | 0.725 |
| 1.7 | 1.337 | 1.144 | 0.982 | 0.856 | 0.757 |
| 1.9 | 1.384 | 1.188 | 1.022 | 0.892 | 0.790 |
| 2.1 | 1.430 | 1.232 | 1.062 | 0.928 | 0.822 |
| 2.3 | 1.477 | 1.276 | 1.102 | 0.963 | 0.854 |
| 2.5 | 1.523 | 1.320 | 1.141 | 0.999 | 0.886 |
| 2.7 | 1.569 | 1.364 | 1.181 | 1.034 | 0.918 |
| 2.9 | 1.614 | 1.407 | 1.220 | 1.070 | 0.950 |
| Cooling Systems | SVR | GPR (95% Confidence Level) |
|---|---|---|
| Conventional Liquid | 0.9777 | 0.9999 |
| Novel Liquid with 0.25 mm Microchannel Radius | 0.9705 | 0.9999 |
| Novel Liquid with 0.30 mm Microchannel Radius | 0.9695 | 0.9999 |
| Novel Liquid with 0.35 mm Microchannel Radius | 0.9687 | 0.9999 |
| Cooling Systems | Parameter | GPR | |
|---|---|---|---|
| Sensitivity Analysis | RelifF Feature Weights | ||
| Conventional Liquid | Applied Frequency | 0.0161 | 2 |
| Water Flow Rate | 0.0197 | 1 | |
| Novel Liquid with 0.25 mm Microchannel Radius | Applied Frequency | 0.0291 | 1 |
| Water Flow Rate | 0.0319 | 2 | |
| Novel Liquid with 0.30 mm Microchannel Radius | Applied Frequency | 0.0308 | 1 |
| Water Flow Rate | 0.0335 | 2 | |
| Novel Liquid with 0.35 mm Microchannel Radius | Applied Frequency | 0.0322 | 1 |
| Water Flow Rate | 0.0348 | 2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yöner, S.I.; Özcan, A. Simulation-Based Design and Machine Learning Optimization of a Novel Liquid Cooling System for Radio Frequency Coils in Magnetic Hyperthermia. Bioengineering 2025, 12, 490. https://doi.org/10.3390/bioengineering12050490
Yöner SI, Özcan A. Simulation-Based Design and Machine Learning Optimization of a Novel Liquid Cooling System for Radio Frequency Coils in Magnetic Hyperthermia. Bioengineering. 2025; 12(5):490. https://doi.org/10.3390/bioengineering12050490
Chicago/Turabian StyleYöner, Serhat Ilgaz, and Alpay Özcan. 2025. "Simulation-Based Design and Machine Learning Optimization of a Novel Liquid Cooling System for Radio Frequency Coils in Magnetic Hyperthermia" Bioengineering 12, no. 5: 490. https://doi.org/10.3390/bioengineering12050490
APA StyleYöner, S. I., & Özcan, A. (2025). Simulation-Based Design and Machine Learning Optimization of a Novel Liquid Cooling System for Radio Frequency Coils in Magnetic Hyperthermia. Bioengineering, 12(5), 490. https://doi.org/10.3390/bioengineering12050490







