Optimization-Incorporated Deep Learning Strategy to Automate L3 Slice Detection and Abdominal Segmentation in Computed Tomography
Abstract
1. Introduction
- To address the imbalance of target classes, an optimization process is proposed in which the augmentation ratio and class weight adjustments are considered as correction design variables (CDVs), and the objective function is defined based on the performance of the training models.
- The proposed optimization-integrated deep learning strategy is validated using various state-of-the-art deep learning techniques.
- The proposed strategy is applied to human CT images to extract the L3 slice and segment abdominal tissues.
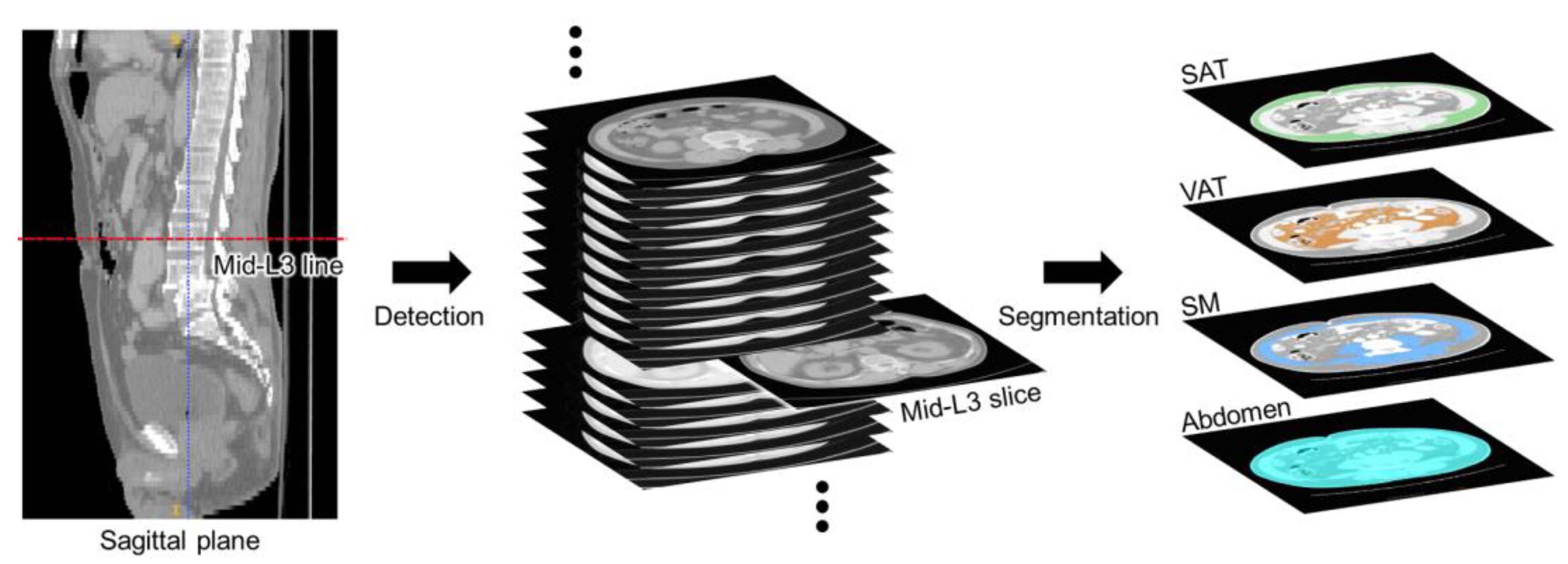
2. L3 Slice Detection and Abdominal Segmentation Strategy
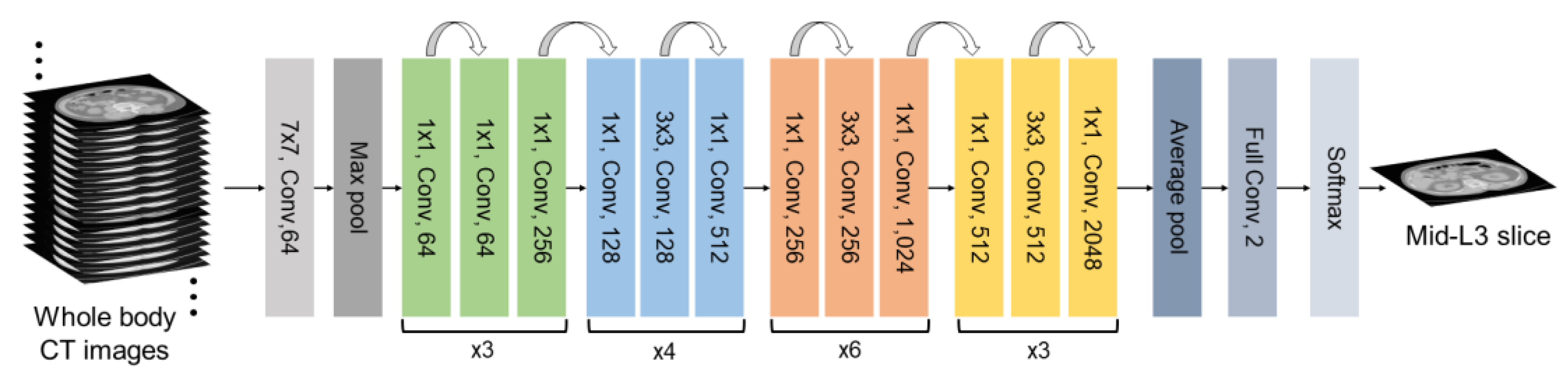
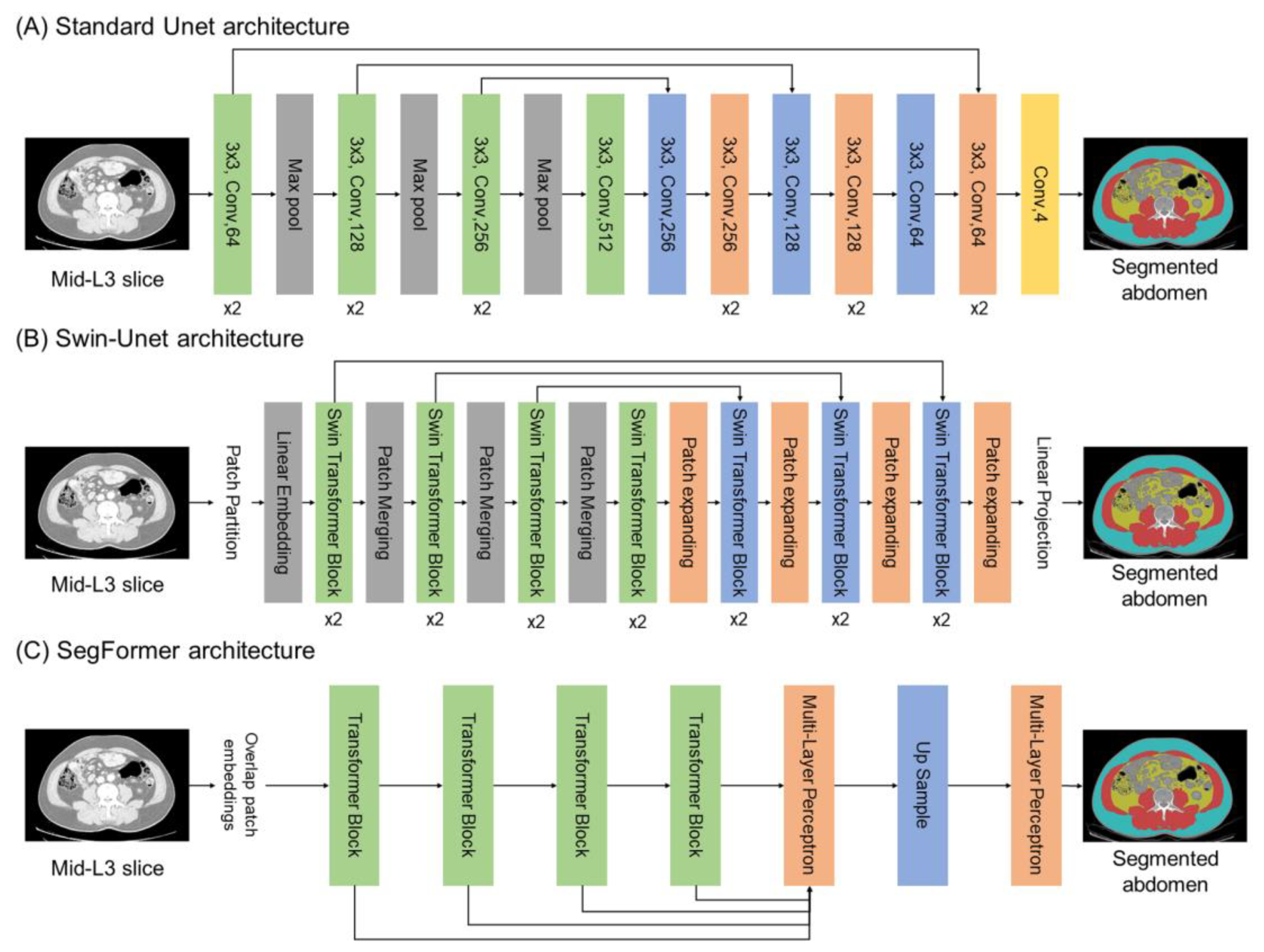
2.1. Deep Learning Architectures
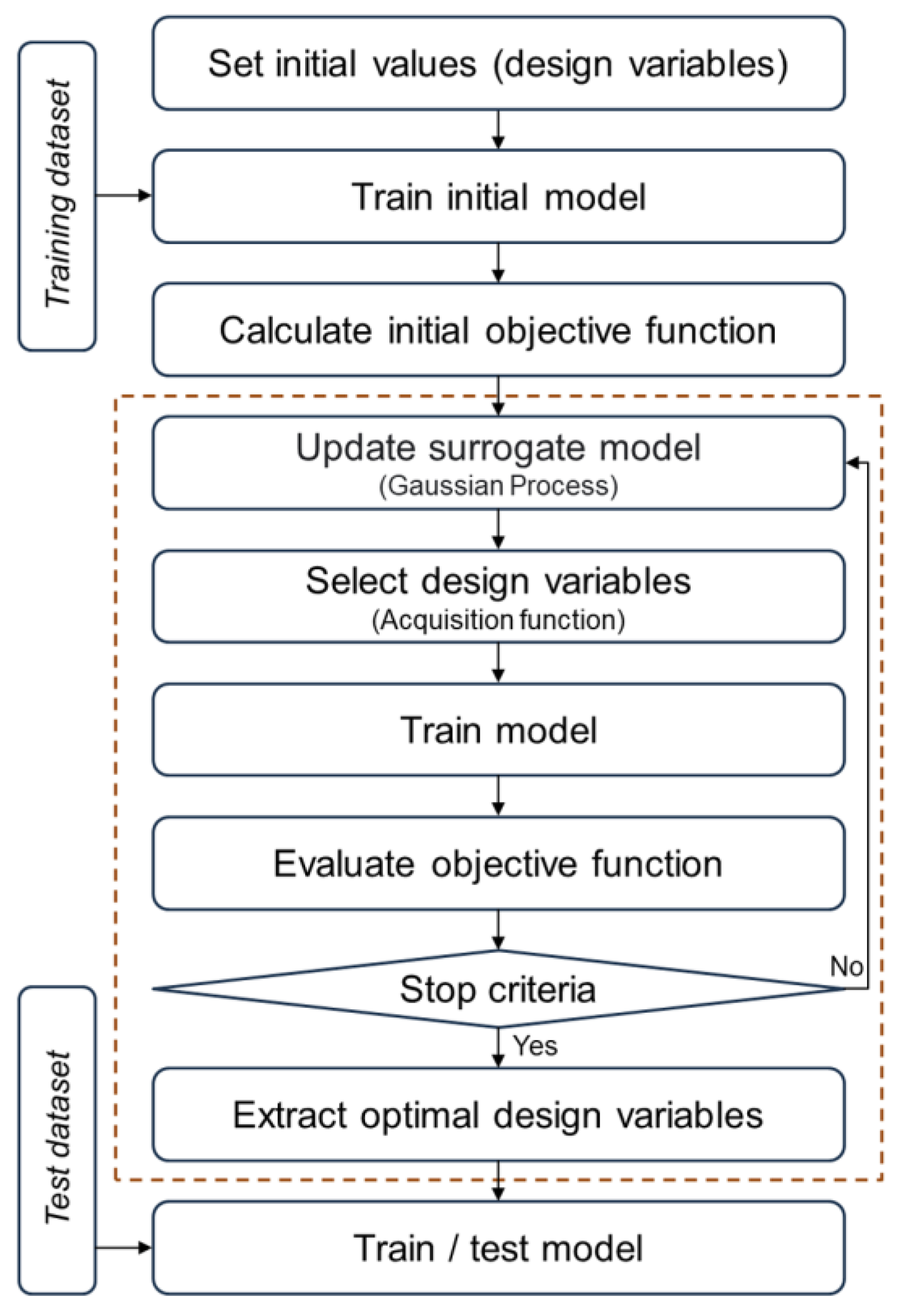
2.2. Optimization Approach
3. Dataset
4. Model Implementation
4.1. Preprocessing
4.2. Implementation of L3 Slice Detection Model with Optimization
4.3. Implementation of Abdominal Segmentation Model with Optimization
5. Performance Evaluation
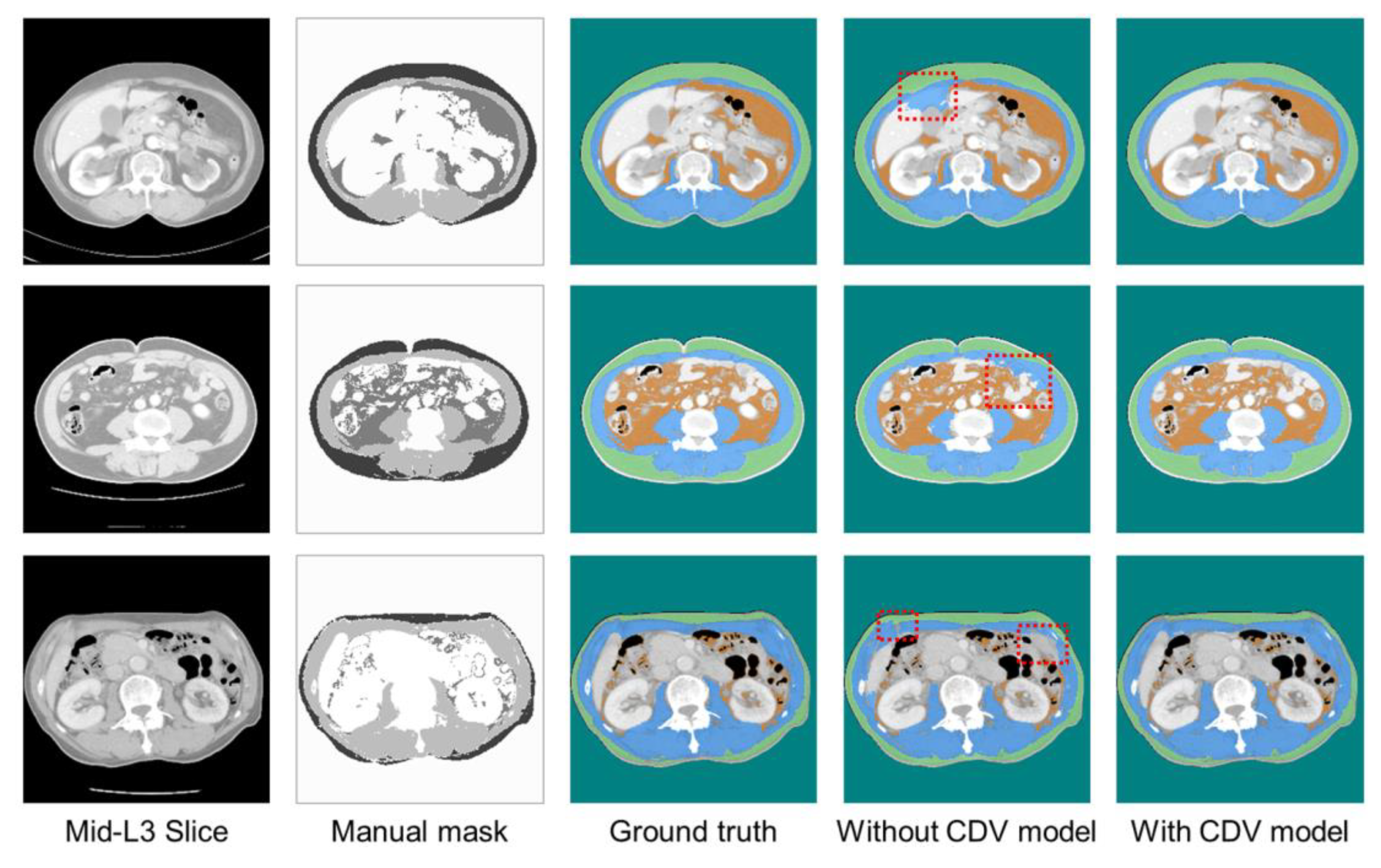
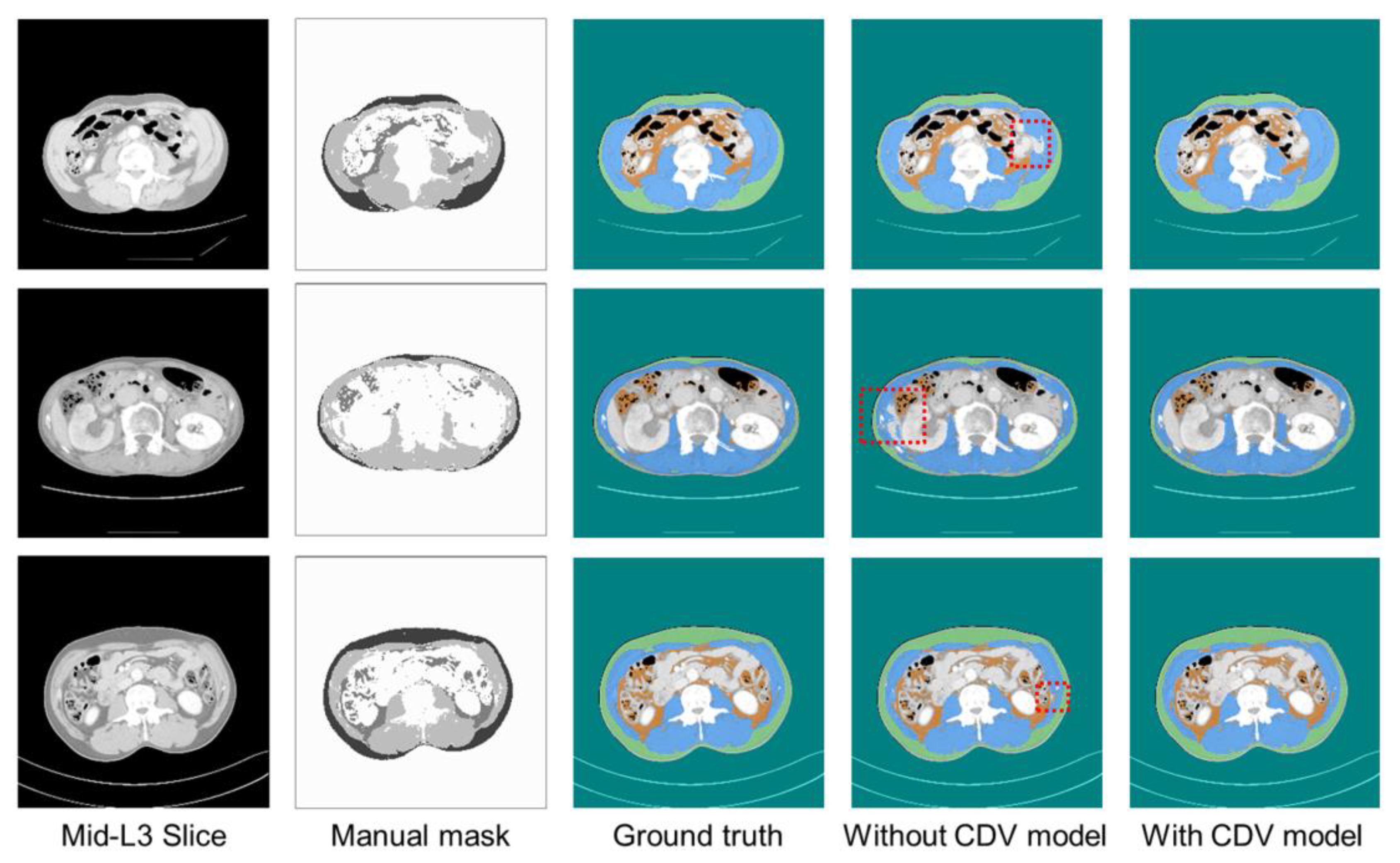
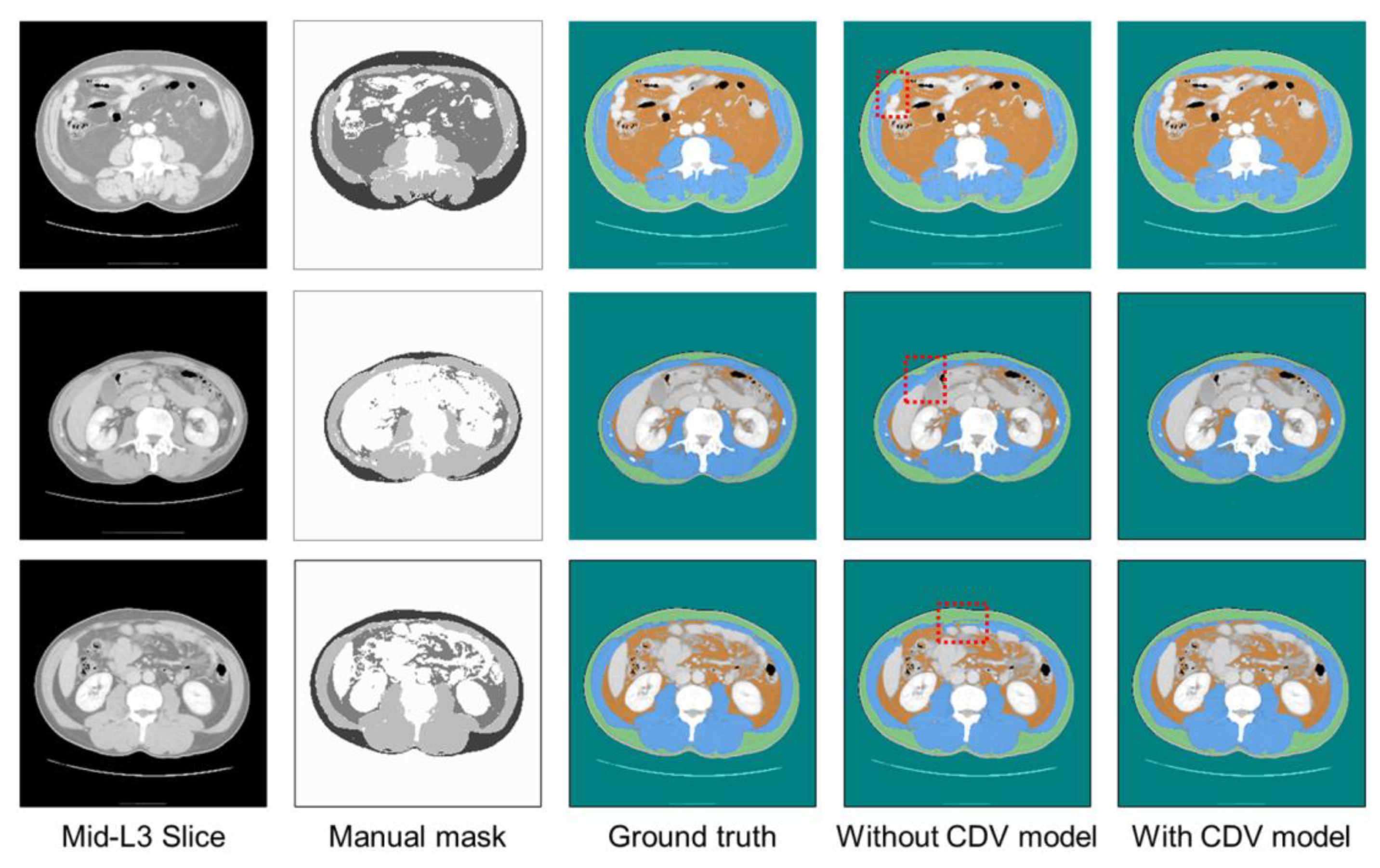
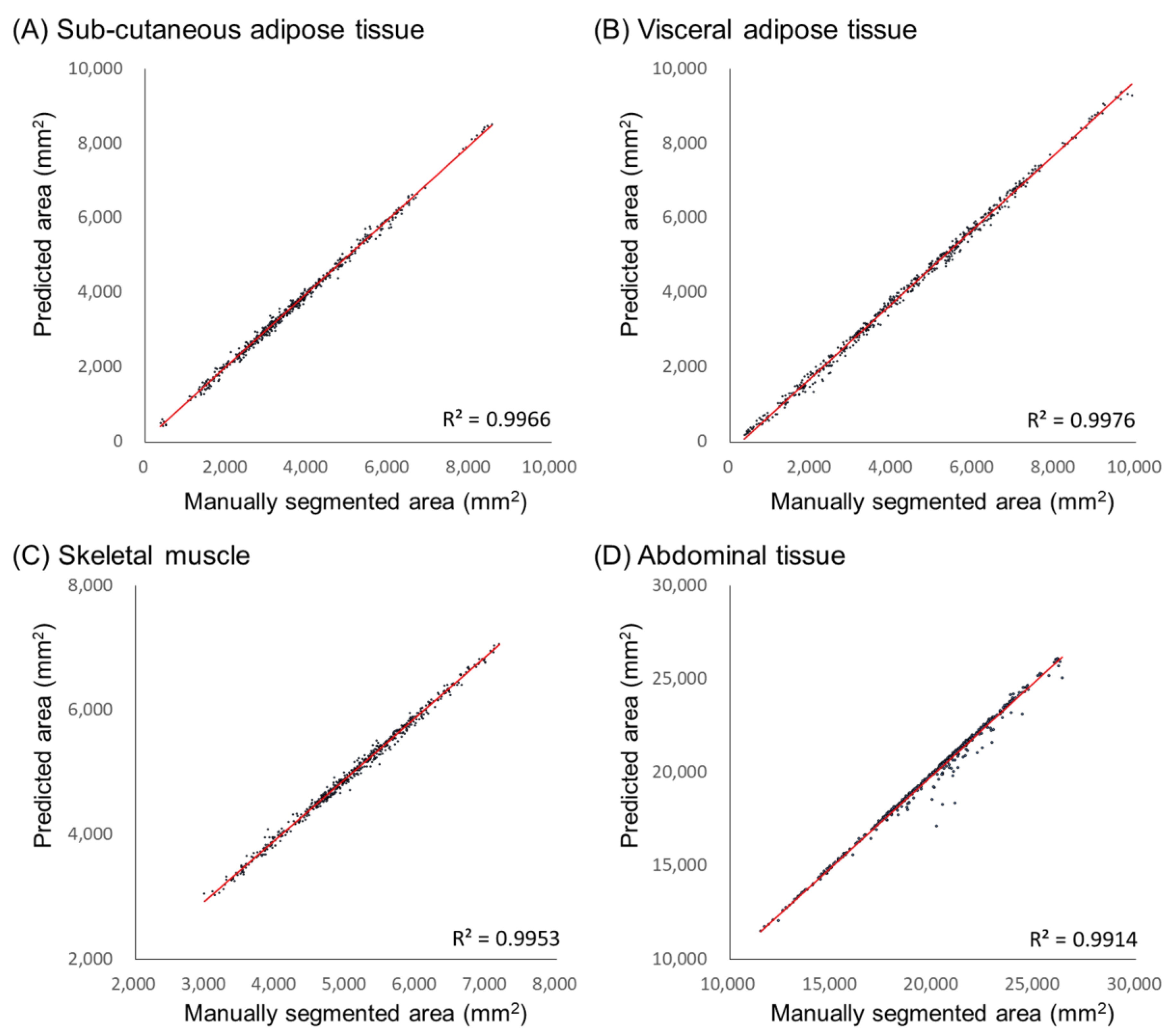
6. Results
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Bray, F.; Ferlay, J.; Soerjomataram, I.; Siegel, R.L.; Torre, L.A.; Jemal, A. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2018, 68, 394–424. [Google Scholar] [CrossRef] [PubMed]
- Siegel, R.L.; Miller, K.D.; Fuchs, H.E. Cancer statistics, 2022. CA Cancer J. Clin. 2022, 72, 7–33. [Google Scholar] [CrossRef] [PubMed]
- Valastyan, S.; Weinberg, R.A. Tumor metastasis: Molecular insights and evolving paradigms. Cell 2011, 147, 275–292. [Google Scholar] [CrossRef]
- Garrett, W.S. Cancer and the microbiota. Science 2015, 348, 80–86. [Google Scholar] [CrossRef]
- Zitvogel, L.; Ma, Y.; Raoult, D.; Kroemer, G.; Gajewski, T.F. The microbiome in cancer immunotherapy: Diagnostic tools and therapeutic strategies. Science 2018, 359, 1366–1370. [Google Scholar] [CrossRef]
- Kim, S.J.; Park, M.; Choi, A.; Yoo, S. Microbiome and prostate cancer: Emerging diagnostic and therapeutic opportunities. Pharmaceuticals 2024, 17, 112. [Google Scholar] [CrossRef]
- Song, M.; Chan, A.T.; Sun, J. Influence of the gut microbiome, diet, and environment on risk of colorectal cancer. Gastroenterology 2020, 158, 322–340. [Google Scholar] [CrossRef]
- Helmink, B.A.; Khan, M.A.W.; Hermann, A.; Gopalakrishnan, V.; Wargo, J.A. The microbiome, cancer, and cancer therapy. Nat. Med. 2019, 25, 377–388. [Google Scholar] [CrossRef]
- Bradshaw, P.T. Body composition and cancer survival: A narrative review. Br. J. Cancer 2024, 130, 176–183. [Google Scholar] [CrossRef]
- Lopez, P.; Newton, R.U.; Taaffe, D.R.; Singh, F.; Buffart, L.M.; Spry, N.; Tang, C.; Saad, F.; Galvão, D.A. Associations of fat and muscle mass with overall survival in men with prostate cancer: A systematic review with meta-analysis. Prostate Cancer Prostatic Dis. 2022, 25, 615–626. [Google Scholar] [CrossRef] [PubMed]
- Ridaura, V.K.; Faith, J.J.; Rey, F.E.; Cheng, J.; Duncan, A.E.; Kau, A.L.; Griffin, N.W.; Lombard, V.; Henrissat, B.; Bain, J.R.; et al. Gut microbiota from twins discordant for obesity modulate metabolism in mice. Science 2013, 341, 1241214. [Google Scholar] [CrossRef]
- Halpenny, D.F.; Goncalves, M.; Schwitzer, E.; Golia Pernicka, J.; Jackson, J.; Gandelman, S.; Plodkowski, A.J. Computed tomography-derived assessments of regional muscle volume: Validating their use as predictors of whole-body muscle volume in cancer patients. Br. J. Radiol. 2018, 91, 20180451. [Google Scholar] [CrossRef]
- Guerri, S.; Mercatelli, D.; Gómez, M.P.A.; Napoli, A.; Battista, G.; Guglielmi, G.; Bazzocchi, A. Quantitative imaging techniques for the assessment of osteoporosis and sarcopenia. Quant. Imaging Med. Surg. 2018, 8, 60. [Google Scholar] [CrossRef]
- Borga, M.; West, J.; Bell, J.D.; Harvey, N.C.; Romu, T.; Heymsfield, S.B.; Dahlqvist Leinhard, O. Advanced body composition assessment: From body mass index to body composition profiling. J. Investig. Med. 2018, 66, 1–9. [Google Scholar] [CrossRef]
- Shen, W.; Punyanitya, M.; Wang, Z.; Gallagher, D.; St Onge, M.P.; Albu, J.; Pierson, R.N.; Heymsfield, S.B. Total body skeletal muscle and adipose tissue volumes: Estimation from a single abdominal cross-sectional image. J. Appl. Physiol. 2004, 97, 2333–2338. [Google Scholar] [CrossRef]
- Kazemi-Bajestani, S.M.R.; Mazurak, V.C.; Baracos, V.E. Computed tomography-defined muscle and fat wasting are associated with cancer clinical outcomes. Semin. Cell Dev. Biol. 2016, 54, 2–10. [Google Scholar] [CrossRef]
- Islam, M.; Blum, R.; Waqas, M.; Moorthy, R.K.; Shuang, J. Fully automated deep-learning section-based muscle segmentation from CT images for sarcopenia assessment. Clin. Radiol. 2022, 77, e363–e371. [Google Scholar] [CrossRef]
- Belharbi, S.; Frouin, F.; Richard, C. Spotting L3 slice in CT scans using deep convolutional network and transfer learning. Comput. Biol. Med. 2017, 87, 95–103. [Google Scholar] [CrossRef]
- Dabiri, R.; Emami, H.; Kazeminasab, M.; Shayan, A. Muscle segmentation in axial computed tomography (CT) images at the lumbar (L3) and thoracic (T4) levels for body composition analysis. Comput. Med. Imaging Graph. 2019, 75, 47–55. [Google Scholar] [CrossRef]
- Shen, L.; Gao, F.; Wu, Y.; Li, Q.; Zhang, Z. A deep learning model based on the attention mechanism for automatic segmentation of abdominal muscle and fat for body composition assessment. Quant. Imaging Med. Surg. 2023, 13, 1384–1398. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, J.; Yang, Z.; Yan, J.; Zhang, L.; Gong, L.B. The development of an attention mechanism enhanced deep learning model and its application for body composition assessment with L3 CT images. Sci. Rep. 2024, 14, 28953. [Google Scholar] [CrossRef]
- Dabiri, R.; Emami, H.; Kazeminasab, M. Deep learning method for localization and segmentation of abdominal CT. Comput. Med. Imaging Graph. 2020, 85, 101776. [Google Scholar] [CrossRef]
- Tanha, J.; Abdi, Y.; Samadi, N.; Razzaghi, N.; Asadpour, M. Boosting methods for multi-class imbalanced data classification: An experimental review. J. Big Data 2020, 7, 70. [Google Scholar] [CrossRef]
- Thabtah, F.; Hammoud, S.; Kamalov, F.; Gonsalves, A. Data imbalance in classification: Experimental evaluation. Inf. Sci. 2020, 513, 429–441. [Google Scholar] [CrossRef]
- Chen, X.W.; Wasikowski, M. FAST: A ROC-based feature selection metric for small samples and imbalanced data classification problems. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 124–132. [Google Scholar] [CrossRef]
- Abdi, L.; Hashemi, S. To combat multi-class imbalanced problems by means of over-sampling and boosting techniques. Soft Comput. 2015, 19, 3369–3385. [Google Scholar] [CrossRef]
- Tao, X.; Li, Q.; Guo, W.; Ren, C.; Li, C.; Liu, R.; Zou, J. Self-adaptive cost weights-based support vector machine cost-sensitive ensemble for imbalanced data classification. Inf. Sci. 2019, 487, 31–56. [Google Scholar] [CrossRef]
- Lemley, J.; Bazrafkan, S.; Corcoran, P. Smart augmentation learning an optimal data augmentation strategy. IEEE Access 2017, 5, 5858–5869. [Google Scholar] [CrossRef]
- Fernando, K.R.M.; Tsokos, C.P. Dynamically weighted balanced loss: Class imbalanced learning and confidence calibration of deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 2940–2951. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision. and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III. Springer International Publishing: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-Unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the European Conference on Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Springer Nature: Cham, Switzerland, 2022; pp. 205–218. [Google Scholar] [CrossRef]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. Adv. Neural. Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar]
- Herath, S.; Harandi, M.; Fernando, B.; Nock, R. Min-Max Statistical Alignment for Transfer Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9288–9297. [Google Scholar] [CrossRef]
- Choi, A.; Park, E.; Kim, T.H.; Im, G.J.; Mun, J.H. A novel optimization-based convolution neural network to estimate the contribution of sensory inputs to postural stability during quiet standing. IEEE J. Biomed. Health Inform. 2022, 26, 4414–4425. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Liu, W.D.; Gu, J. Predictive model for water absorption in sublayers using a Joint Distribution Adaption based XGBoost transfer learning method. J. Pet. Sci. Eng. 2020, 188, 106937. [Google Scholar] [CrossRef]
- Prado, C.M.; Lieffers, J.R.; McCargar, L.J.; Reiman, T.; Sawyer, M.B.; Martin, L.; Baracos, V.E. Prevalence and clinical implications of sarcopenic obesity in patients with solid tumors of the respiratory and gastrointestinal tracts: A population-based study. Lancet Oncol. 2008, 9, 629–635. [Google Scholar] [CrossRef]
- Shahedi, M.; Ma, L.; Halicek, M.; Guo, R.; Zhang, G.; Schuster, D.M.; Nieh, P.; Master, V.; Fei, B. A semiautomatic algorithm for three-dimensional segmentation of the prostate on CT images using shape and local texture characteristics. In Proceedings of the Medical Imaging 2018: Image-Guided Procedures, Robotic Interventions, and Modeling, SPIE, Houston, TX, USA, 10–15 February 2018; Volume 10576, pp. 280–287. [Google Scholar] [CrossRef]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. Adv. Neural Inf. Process Syst. 2013, 26, 3111–3119. [Google Scholar] [CrossRef]
- Mahajan, D.; Girshick, R.; Ramanathan, V.; He, K.; Paluri, M.; Li, Y.; Bharambe, A.; van der Maaten, L. Exploring the limits of weakly supervised pretraining. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar] [CrossRef]
- Machann, J.; Stefan, N.; Schick, F. Magnetic resonance imaging of skeletal muscle and adipose tissue at the molecular level. Best Pract. Res. Clin. Endocrinol. Metab. 2013, 27, 261–277. [Google Scholar] [CrossRef]
- Vergara-Fernandez, O.; Trejo-Avila, M.; Salgado-Nesme, N. Sarcopenia in patients with colorectal cancer: A comprehensive review. World J. Clin. Cases 2020, 8, 1188–1203. [Google Scholar] [CrossRef]
- Cruz-Jentoft, A.J.; Baeyens, J.P.; Bauer, J.M.; Boirie, Y.; Cederholm, T.; Landi, F.; Martin, F.C.; Michel, J.P.; Rolland, Y.; Schneider, S.M.; et al. Sarcopenia: European consensus on definition and diagnosis: Report of the European Working Group on Sarcopenia in Older People. Age Ageing 2010, 39, 412–423. [Google Scholar] [CrossRef]
- Shachar, S.S.; Williams, G.R.; Muss, H.B.; Nishijima, T.F. Prognostic value of sarcopenia in adults with solid tumors: A meta-analysis and systematic review. Eur. J. Cancer 2017, 57, 58–67. [Google Scholar] [CrossRef]
- Fehrenbach, U.; Yalman, D.; Ozmen, S.; Ozcelik, S. CT body composition of sarcopenia and sarcopenic obesity: Predictors of postoperative complications and survival in patients with locally advanced esophageal adenocarcinoma. Cancers 2021, 13, 2921. [Google Scholar] [CrossRef]
- Gouerant, S.; Leheurteur, M.; Chaker, M.; Modzelewski, R.; Rigal, O.; Veyret, C.; Lauridant, G.; Clatot, F. A higher body mass index and fat mass are factors predictive of docetaxel dose intensity. Anticancer Res. 2013, 33, 5655–5662. [Google Scholar]
- Yoo, H.; Choi, A.; Mun, J.H. Acquisition of point cloud in CT image space to improve accuracy of surface registration: Application to neurosurgical navigation system. J. Mech. Sci. Technol. 2020, 34, 2667–2677. [Google Scholar] [CrossRef]
- Choi, A.; Yun, T.S.; Suh, S.W.; Yang, J.H.; Park, H.; Lee, S.; Roh, M.S.; Kang, T.G.; Mun, J.H. Determination of input variables for the development of a gait asymmetry expert system in patients with idiopathic scoliosis. Int. J. Precis. Eng. Manuf. 2013, 14, 811–818. [Google Scholar] [CrossRef]
- Li, C.; Huang, Y.; Wang, H.; Tao, X.; Guo, W.; Ren, C.; Liu, R.; Zou, J. Application of imaging methods and the latest progress in sarcopenia. Chin. J. Acad. Radiol. 2024, 7, 15–27. [Google Scholar] [CrossRef]
- Kanavati, F.; Islam, S.; Aboagye, E.O.; Rockall, A.G. Automatic L3 slice detection in 3D CT images using fully-convolutional networks. arXiv 2018, arXiv:1811.09244. [Google Scholar] [CrossRef]
- Burns, J.E.; Yao, J.; Chalhoub, D.; Ghosh, S.; Raghavan, M.L.; Aspelund, G. A machine learning algorithm to estimate sarcopenia on abdominal CT. Acad. Radiol. 2020, 27, 311–320. [Google Scholar] [CrossRef]
- Lee, H.; Troschel, F.M.; Tajmir, S.; Alvarez-Jimenez, J.R.; Henderson, W.; Brink, J.A. Pixel-level deep segmentation: Artificial intelligence quantifies muscle on computed tomography for body morphometric analysis. J. Digit. Imaging 2017, 30, 487–498. [Google Scholar] [CrossRef]
- Weston, A.D.; Korfiatis, P.; Kline, T.L.; Philbrick, K.A.; Kostandy, P.; Sakinis, T.; Erickson, B.J. Automated abdominal segmentation of CT scans for body composition analysis using deep learning. Radiology 2019, 290, 669–679. [Google Scholar] [CrossRef]
- Cui, Y.; Jia, M.; Lin, T.Y.; Song, Y.; Belongie, S. Class-balanced loss based on effective number of samples. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9268–9277. [Google Scholar] [CrossRef]
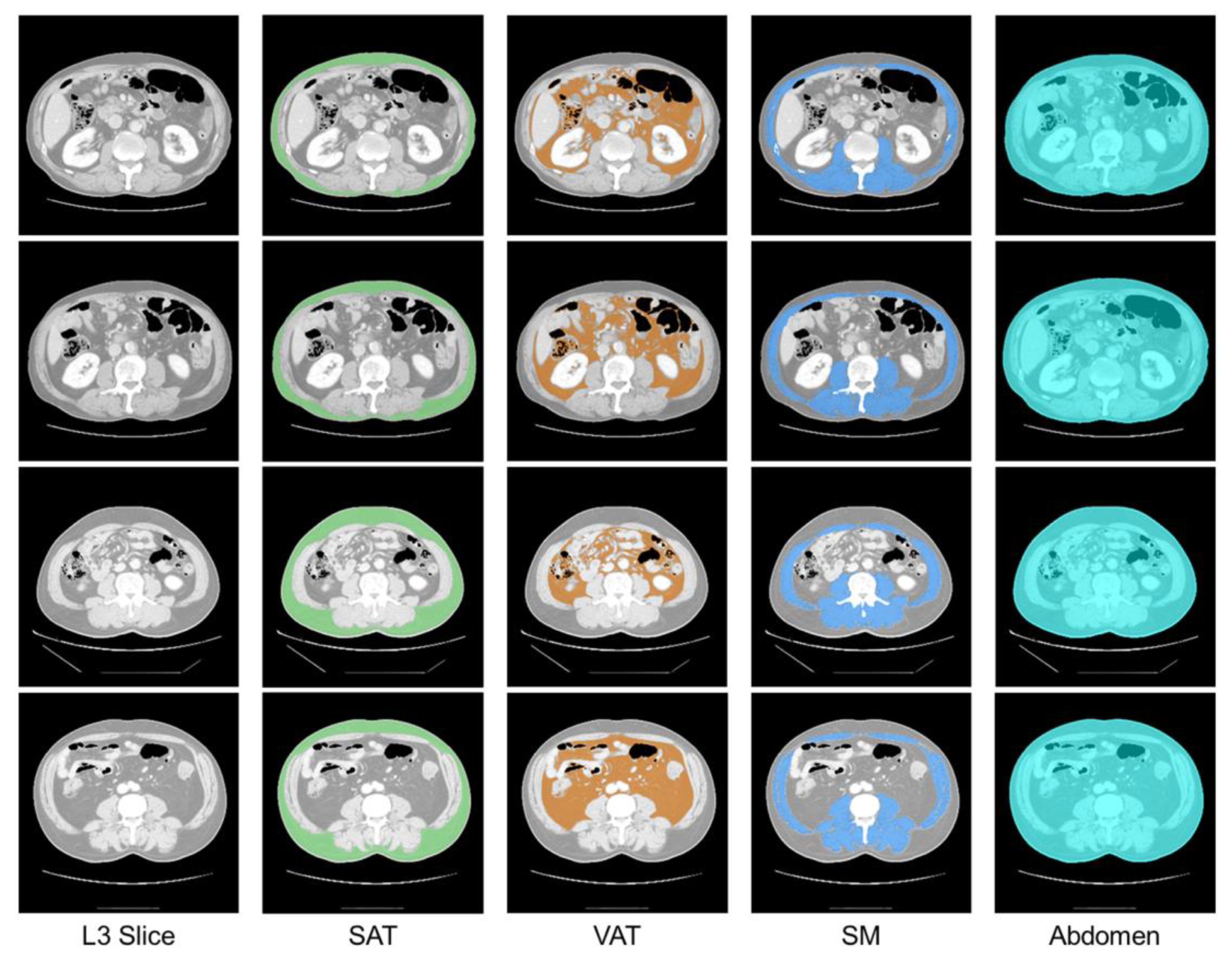
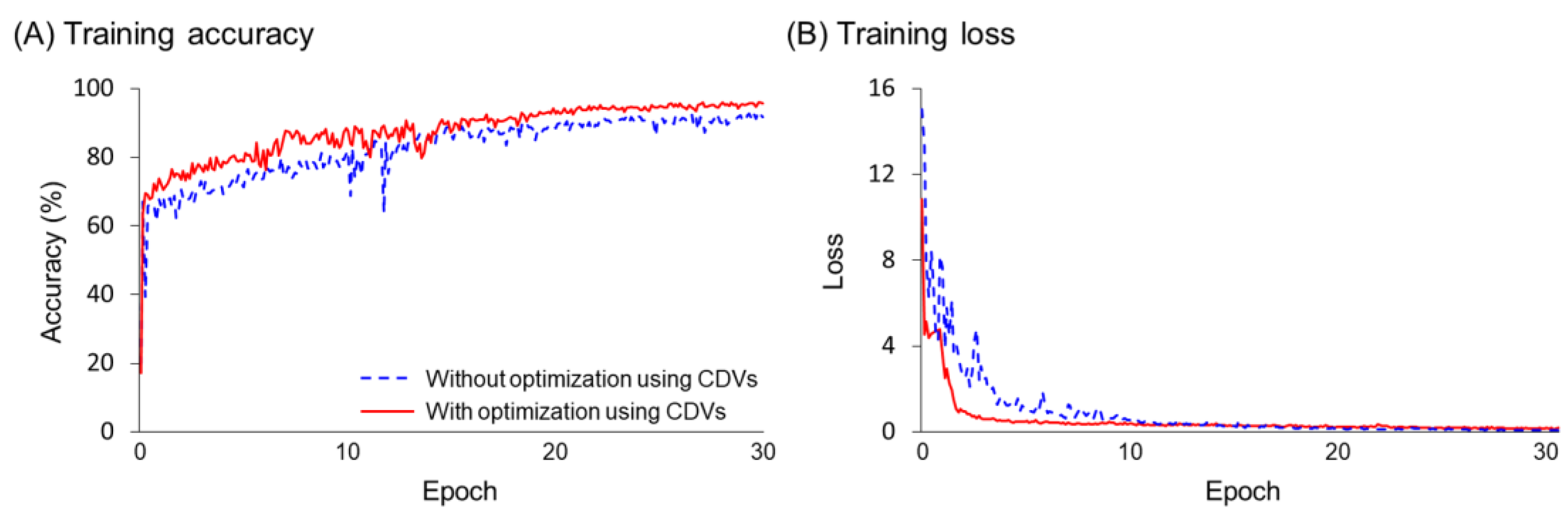
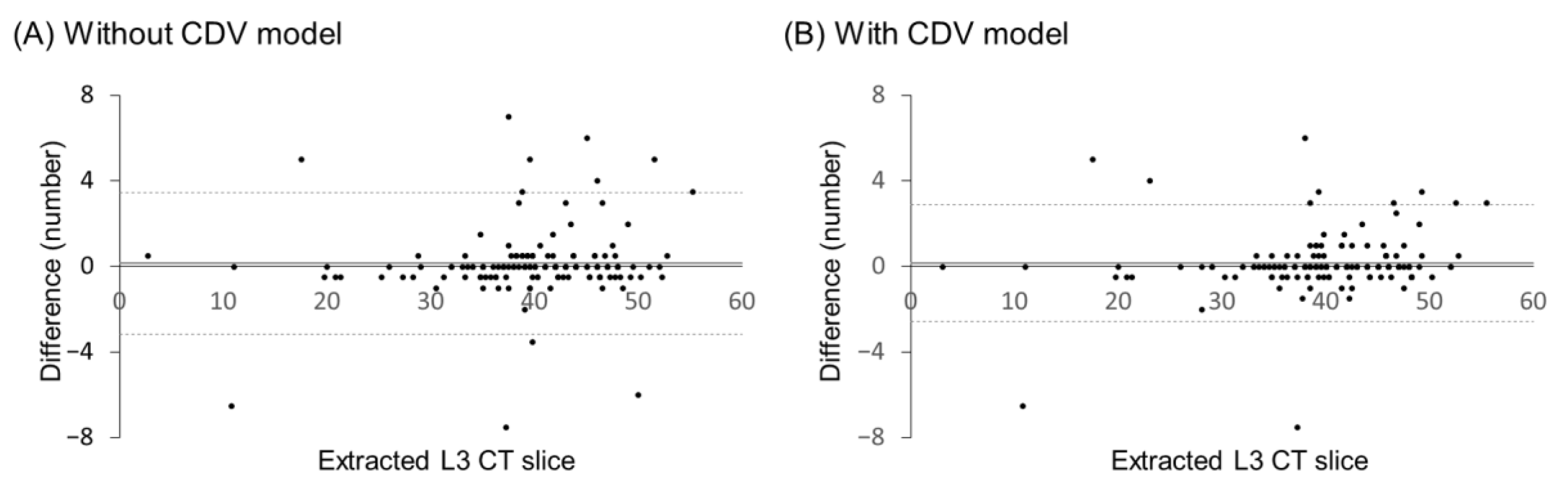
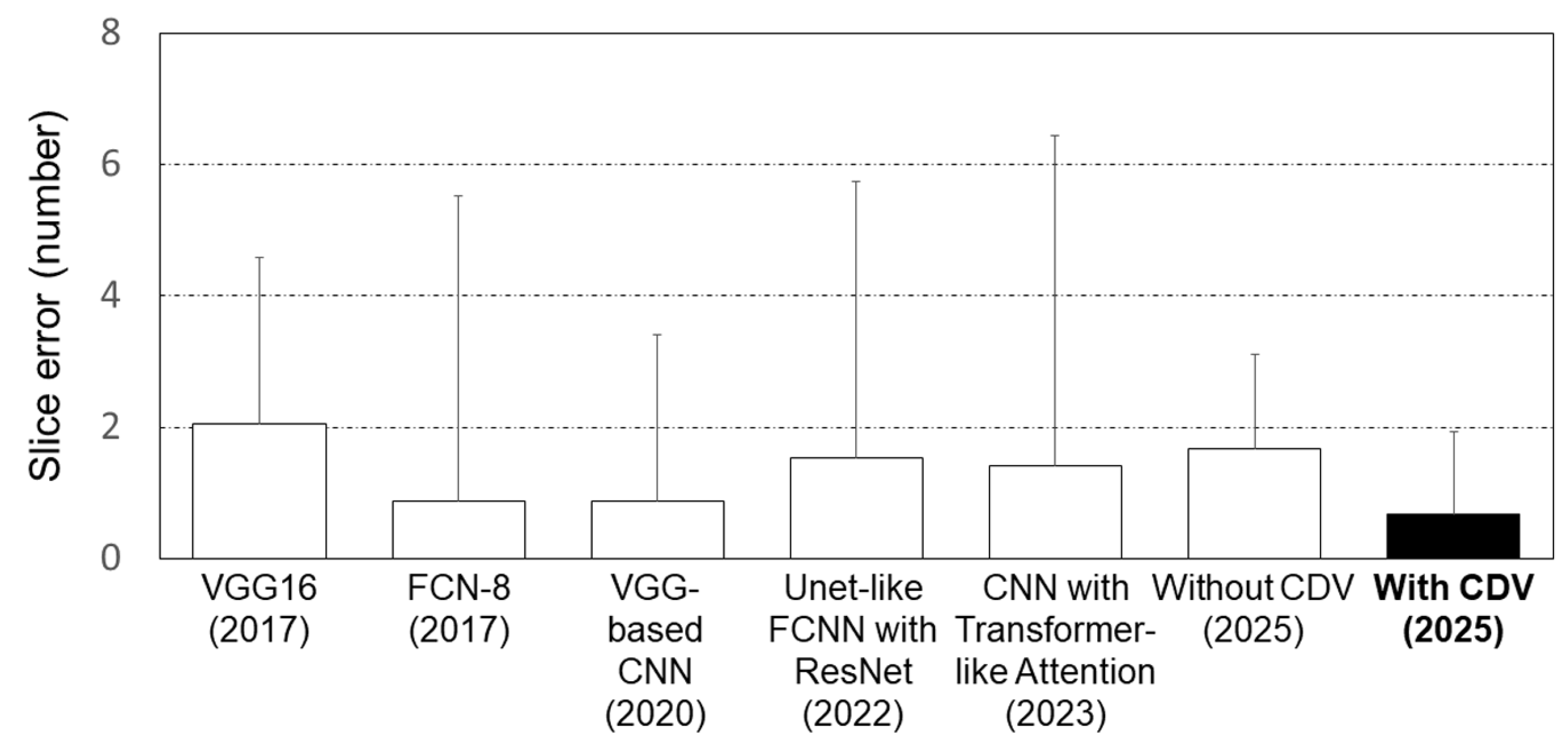
| Parameters | Type | Range |
|---|---|---|
| L2Regularization | Logarithmic (continuous) | [0.0001, 0.01] |
| InitialLearningRate | Logarithmic (continuous) | [0.0001, 0.01] |
| Batchsize | Integer (discrete) | [10, 32] |
| GradientThreshold | Integer (discrete) | [1, 6] |
| Epoch | Integer (discrete) | [5, 20] |
| Momentum | Real (continuous) | [0.7, 0.99] |
| All Patients (n = 150) | ||
|---|---|---|
| Disease | Prostate cancer, n (%) Bladder cancer, n (%) | 104 (69.3) 46 (30.7) |
| Sex | Male, n (%), female, n (%) | 142 (94.7), 8 (5.3) |
| Age | Median age, yr (IQR) | 67.5 (62.2–73.0) |
| BMI | Median BMI, kg/m2 (IQR) | 24.5 (22.6–26.2) |
| Height | Median height, cm (IQR) | 165.0 (161.1–168.7) |
| Weight | Median weight, kg (IQR) | 66.4 (60.1–72.3) |
| DM | n (%) | 37 (24.7) |
| HTN | n (%) | 67 (44.7) |
| Tissue | Jaccard Score | Dice Coefficient | Sensitivity | Specificity | MSD | ||
|---|---|---|---|---|---|---|---|
| Standard Unet | Without CDVs | SM | 0.908 ± 0.006 | 0.950 ± 0.004 | 0.944 ± 0.003 | 0.994 ± 0.001 | 1.027 ± 0.210 |
| VAT | 0.871 ± 0.005 | 0.906 ± 0.004 | 0.936 ± 0.011 | 0.989 ± 0.002 | 1.721 ± 0.261 | ||
| SAT | 0.912 ± 0.004 | 0.945 ± 0.003 | 0.965 ± 0.009 | 0.995 ± 0.001 | 0.812 ± 0.188 | ||
| Abdomen | 0.963 ± 0.001 | 0.981 ± 0.001 | 0.976 ± 0.004 | 0.957 ± 0.006 | 0.310 ± 0.121 | ||
| With CDVs | SM | 0.945 ± 0.001 | 0.971 ± 0.001 | 0.981 ± 0.003 | 0.996 ± 0.001 | 0.618 ± 0.234 | |
| VAT | 0.898 ± 0.003 | 0.924 ± 0.002 | 0.963 ± 0.007 | 0.996 ± 0.001 | 1.287 ± 0.168 | ||
| SAT | 0.960 ± 0.001 | 0.976 ± 0.001 | 0.980 ± 0.004 | 0.998 ± 0.001 | 0.354 ± 0.153 | ||
| Abdomen | 0.974 ± 0.001 | 0.987 ± 0.001 | 0.988 ± 0.001 | 0.976 ± 0.002 | 0.312 ± 0.134 | ||
| Swin-Unet | Without CDVs | SM | 0.936 ± 0.005 | 0.967 ± 0.003 | 0.969 ± 0.003 | 0.992 ± 0.001 | 0.754 ± 0.093 |
| VAT | 0.875 ± 0.012 | 0.933 ± 0.007 | 0.922 ± 0.006 | 0.994 ± 0.001 | 0.692 ± 0.188 | ||
| SAT | 0.899 ± 0.008 | 0.947 ± 0.004 | 0.953 ± 0.006 | 0.994 ± 0.001 | 0.582 ± 0.177 | ||
| Abdomen | 0.964 ± 0.002 | 0.981 ± 0.001 | 0.982 ± 0.001 | 0.951 ± 0.004 | 0.375 ± 0.133 | ||
| With CDVs | SM | 0.952 ± 0.004 | 0.975 ± 0.002 | 0.981 ± 0.003 | 0.977 ± 0.001 | 0.588 ± 0.080 | |
| VAT | 0.903 ± 0.012 | 0.949 ± 0.006 | 0.973 ± 0.002 | 0.995 ± 0.001 | 0.442 ± 0.145 | ||
| SAT | 0.962 ± 0.005 | 0.975 ± 0.003 | 0.974 ± 0.003 | 0.992 ± 0.001 | 0.404 ± 0.126 | ||
| Abdomen | 0.982 ± 0.001 | 0.986 ± 0.001 | 0.981 ± 0.001 | 0.997 ± 0.001 | 0.279 ± 0.113 | ||
| SegFormer | Without CDVs | SM | 0.942 ± 0.007 | 0.970 ± 0.004 | 0.984 ± 0.001 | 0.996 ± 0.001 | 0.325 ± 0.115 |
| VAT | 0.821 ± 0.018 | 0.901 ± 0.011 | 0.930 ± 0.008 | 0.986 ± 0.001 | 0.847 ± 0.171 | ||
| SAT | 0.914 ± 0.006 | 0.955 ± 0.003 | 0.975 ± 0.002 | 0.992 ± 0.001 | 0.585 ± 0.138 | ||
| Abdomen | 0.960 ± 0.002 | 0.979 ± 0.001 | 0.971 ± 0.001 | 0.970 ± 0.003 | 0.385 ± 0.143 | ||
| With CDVs | SM | 0.957 ± 0.002 | 0.978 ± 0.001 | 0.989 ± 0.003 | 0.987 ± 0.001 | 0.548 ± 0.193 | |
| VAT | 0.907 ± 0.008 | 0.951 ± 0.002 | 0.975 ± 0.001 | 0.992 ± 0.001 | 0.967 ± 0.316 | ||
| SAT | 0.969 ± 0.002 | 0.975 ± 0.001 | 0.975 ± 0.001 | 0.985 ± 0.001 | 0.416 ± 0.228 | ||
| Abdomen | 0.986 ± 0.001 | 0.987 ± 0.001 | 0.992 ± 0.001 | 0.994 ± 0.001 | 0.376 ± 0.141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chae, S.; Chae, S.; Kang, T.G.; Kim, S.J.; Choi, A. Optimization-Incorporated Deep Learning Strategy to Automate L3 Slice Detection and Abdominal Segmentation in Computed Tomography. Bioengineering 2025, 12, 367. https://doi.org/10.3390/bioengineering12040367
Chae S, Chae S, Kang TG, Kim SJ, Choi A. Optimization-Incorporated Deep Learning Strategy to Automate L3 Slice Detection and Abdominal Segmentation in Computed Tomography. Bioengineering. 2025; 12(4):367. https://doi.org/10.3390/bioengineering12040367
Chicago/Turabian StyleChae, Seungheon, Seongwon Chae, Tae Geon Kang, Sung Jin Kim, and Ahnryul Choi. 2025. "Optimization-Incorporated Deep Learning Strategy to Automate L3 Slice Detection and Abdominal Segmentation in Computed Tomography" Bioengineering 12, no. 4: 367. https://doi.org/10.3390/bioengineering12040367
APA StyleChae, S., Chae, S., Kang, T. G., Kim, S. J., & Choi, A. (2025). Optimization-Incorporated Deep Learning Strategy to Automate L3 Slice Detection and Abdominal Segmentation in Computed Tomography. Bioengineering, 12(4), 367. https://doi.org/10.3390/bioengineering12040367







