Vortex Dynamics in the Sinus of Valsalva
Abstract
1. Introduction
2. Material and Methods
2.1. Governing Equations and Numerical Method
2.2. Two-Dimensional Parametrized Aortic Model
3. Results
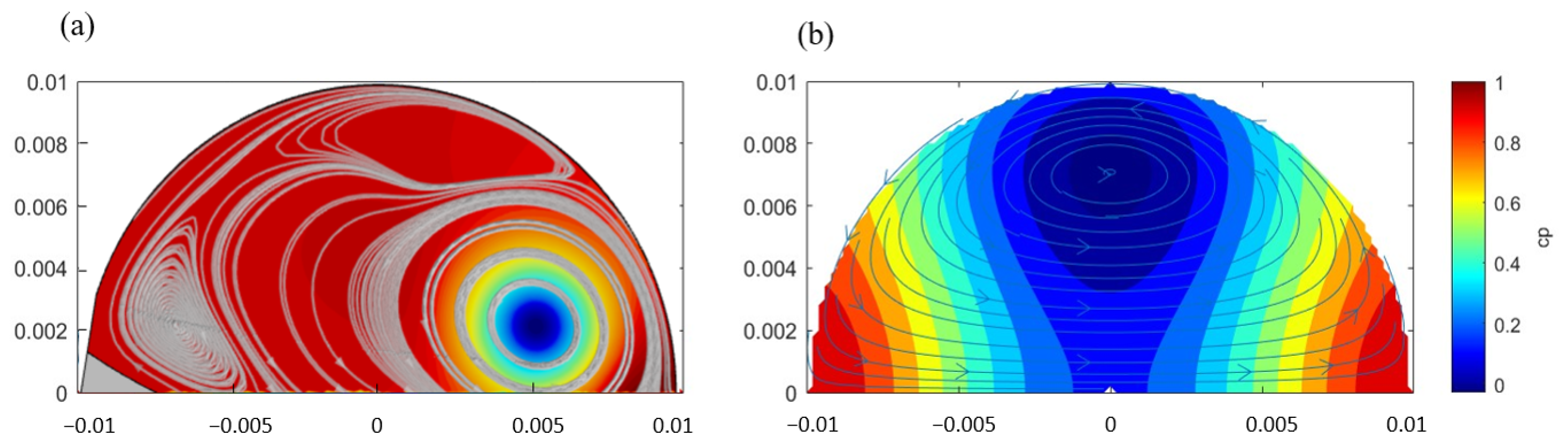
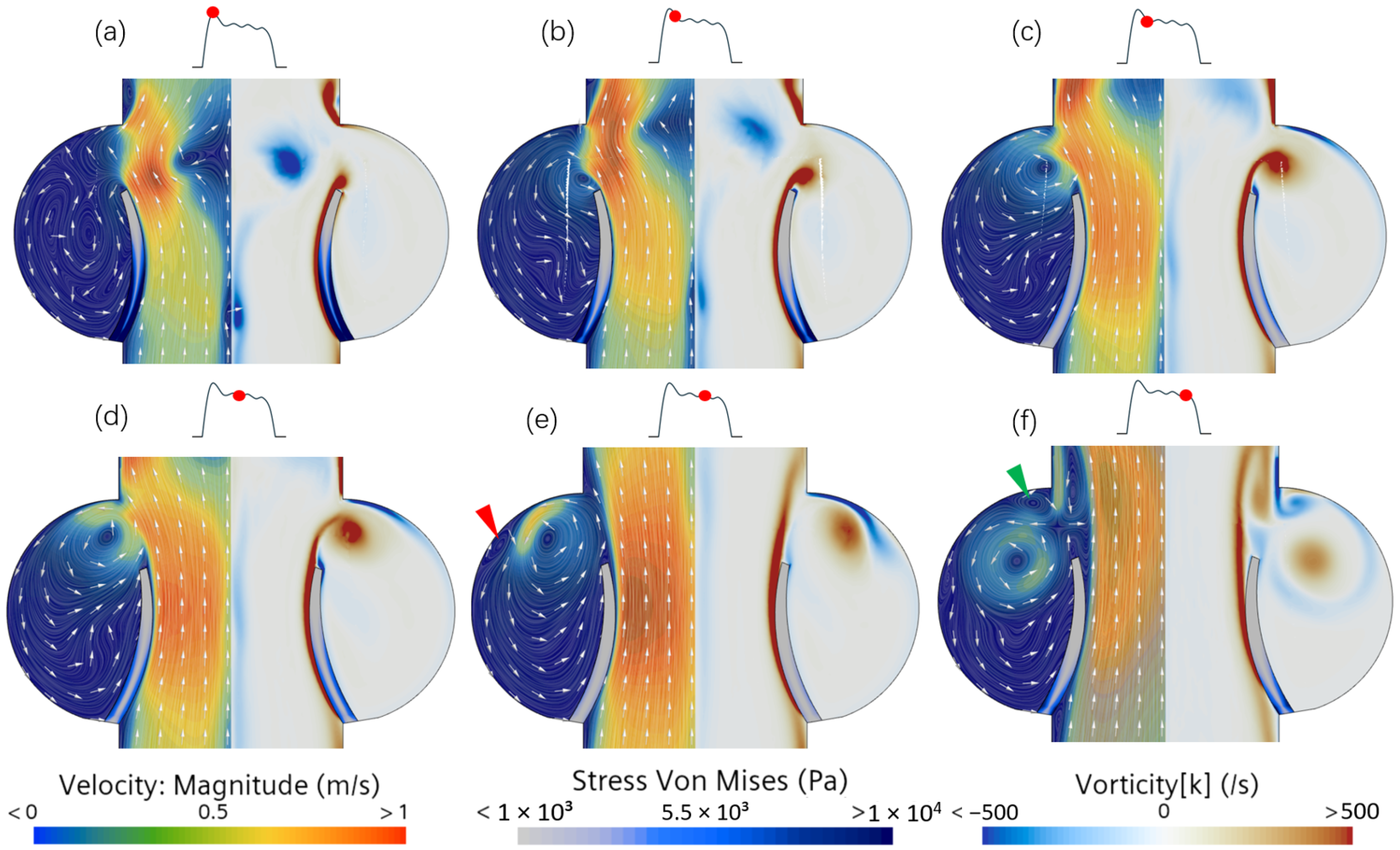
3.1. Vortex Behavior in Steady Flow
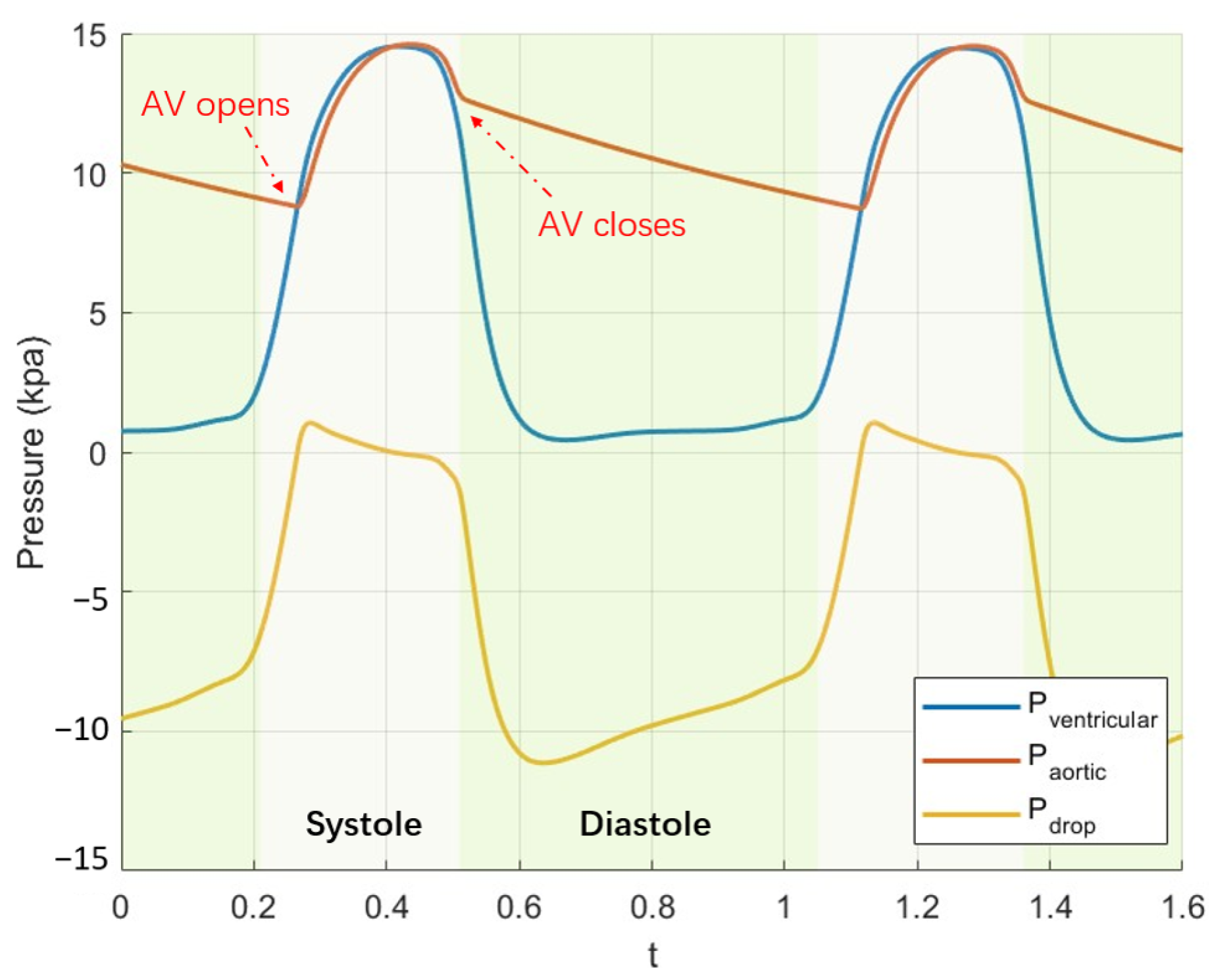
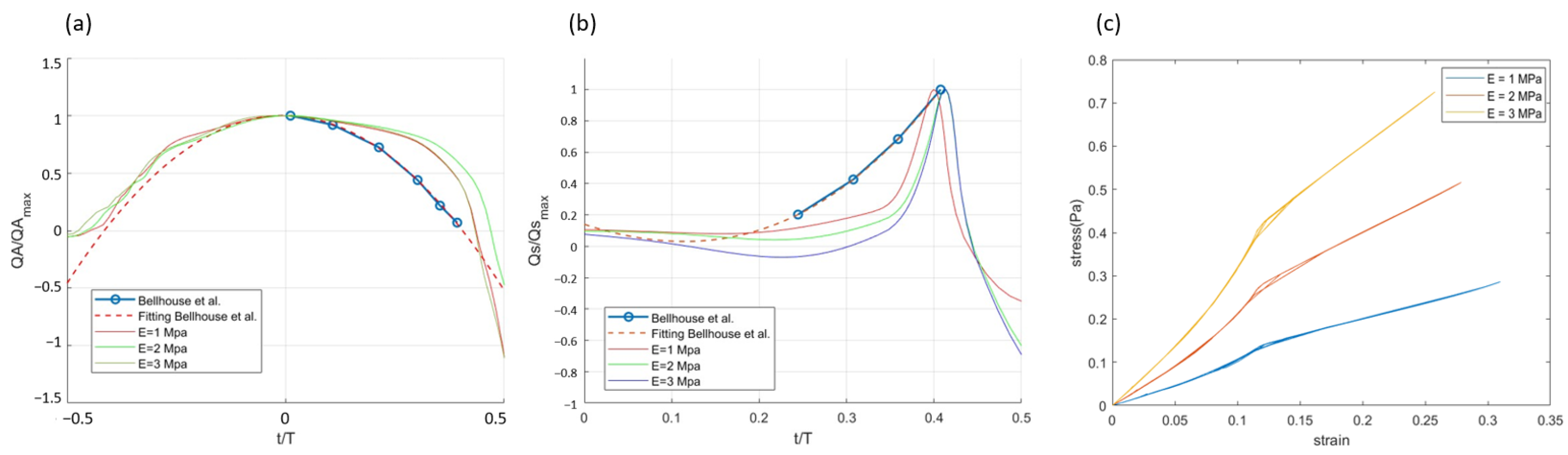
3.2. Effect of Leaflet Stiffness in Pulsatile Flow
3.3. Unsteady Vortex Solution
3.4. Pressure Coefficient
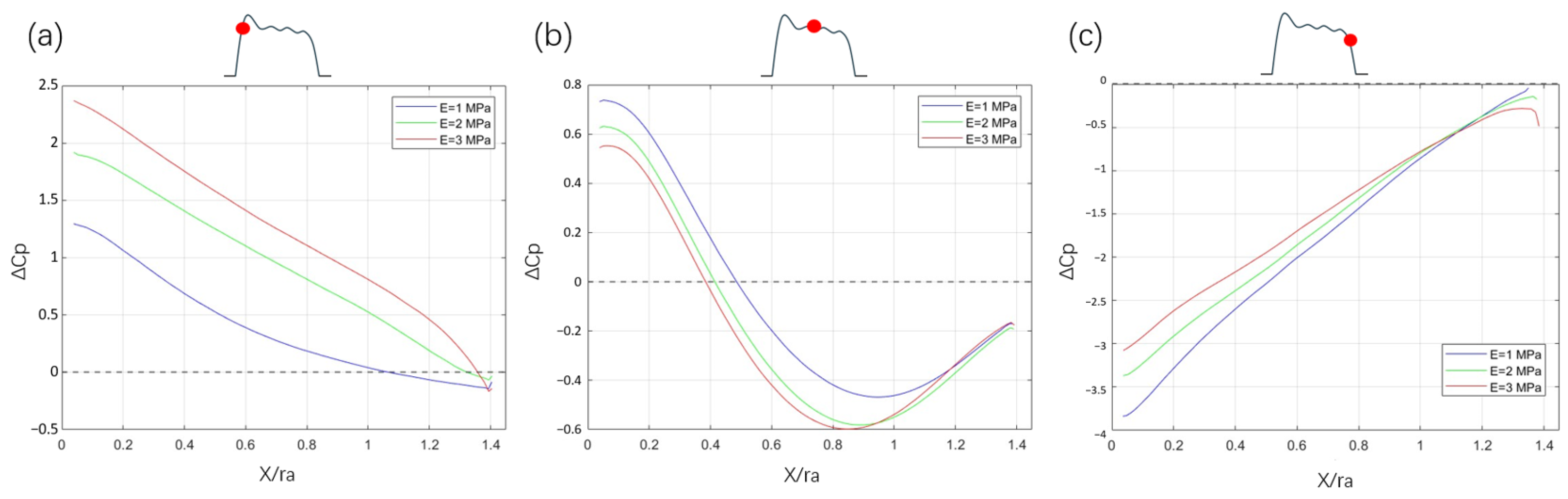
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Mesh Sensitivity Analysis
| Description | Coarse | Medium | Fine |
|---|---|---|---|
| Solid domain: | |||
| Number of elements | 80 | 160 | 320 |
| Approximate element size [mm] | 0.7 | 0.35 | 0.175 |
| Fluid domain: | |||
| Number of elements | 16,671 | 35,005 | 41,513 |
| Approximate element size [mm] | 0.2 | 0.1 | 0.05 |

References
- Leo, H.L.; Simon, H.; Carberry, J.; Lee, S.C.; Yoganathan, A.P. A comparison of flow field structures of two tri-leaflet polymeric heart valves. Ann. Biomed. Eng. 2005, 33, 429–443. [Google Scholar] [CrossRef]
- Forouhar, A.S.; Liebling, M.; Hickerson, A.; Nasiraei-Moghaddam, A.; Tsai, H.J.; Hove, J.R.; Fraser, S.E.; Dickinson, M.E.; Gharib, M. The Embryonic Vertebrate Heart Tube Is a Dynamic Suction Pump. Science 2006, 312, 751–753. [Google Scholar] [CrossRef] [PubMed]
- Sotiropoulos, F.; Le, T.B.; Gilmanov, A. Fluid Mechanics of Heart Valves and Their Replacements. Annu. Rev. Fluid Mech. 2016, 48, 259–283. [Google Scholar] [CrossRef]
- da Vinci, L. Quaderni d’Anatomica II; Royal Library, Royal Collection Trust: Windsor, UK, 1513; p. 9. [Google Scholar]
- Bellhouse, B.J.; Talbot, L. The fluid mechanics of the aortic valve. J. Fluid Mech. 1969, 35, 721–735. [Google Scholar] [CrossRef]
- Peacock, J.A. An in vitro study of the onset of turbulence in the sinus of Valsalva. Circ. Res. 1990, 67, 448–455. [Google Scholar] [CrossRef]
- Toninato, R.; Salmon, J.; Susin, F.M.; Ducci, A.; Burriesci, G. Physiological vortices in the sinuses of Valsalva: An in vitro approach for bio-prosthetic valves. J. Biomech. 2016, 49, 2635–2643. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, H. A computational study of the three-dimensional fluid–structure interaction of aortic valve. J. Fluids Struct. 2018, 80, 332–349. [Google Scholar] [CrossRef]
- Moore, B.; Dasi, L.P. Spatiotemporal complexity of the aortic sinus vortex. Exp. Fluids 2014, 55, 1770. [Google Scholar] [CrossRef] [PubMed]
- Sundström, E.; Jonnagiri, R.; Gutmark-Little, I.; Gutmark, E.; Critser, P.; Taylor, M.D.; Tretter, J.T. Effects of normal variation in the rotational position of the aortic root on hemodynamics and tissue biomechanics of the thoracic aorta. Cardiovasc. Eng. Technol. 2020, 11, 47–58. [Google Scholar] [CrossRef]
- Sundström, E.; Jiang, M.; Najm, H.K.; Tretter, J.T. Blood Speckle Imaging: An Emerging Method for Perioperative Evaluation of Subaortic and Aortic Valvar Repair. Bioengineering 2023, 10, 1183. [Google Scholar] [CrossRef]
- Fukui, T.; Orinishi, K. Influence of vortices in the sinus of Valsalva on local wall shear stress distribution. Int. J. Life Sci. Med. Res. 2013, 3, 94–102. [Google Scholar] [CrossRef]
- Bornemann, K.M.; Obrist, D. Instability mechanisms initiating laminar–turbulent transition past bioprosthetic aortic valves. J. Fluid Mech. 2024, 985, A41. [Google Scholar] [CrossRef]
- Hose, D.R.; Narracott, A.J.; Penrose, J.M.; Baguley, D.; Jones, I.P.; Lawford, P.V. Fundamental mechanics of aortic heart valve closure. J. Biomech. 2006, 39, 958–967. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, E.J.; Shahmirzadi, D.; Mofrad, M.R.K. On the multiscale modeling of heart valve biomechanics in health and disease. Biomech. Model. Mechanobiol. 2010, 9, 373–387. [Google Scholar] [CrossRef]
- Luraghi, G.; Migliavacca, F.; Matas, J.F.R. Study on the Accuracy of Structural and FSI Heart Valves Simulations. Cardiovasc. Eng. Technol. 2018, 9, 723–738. [Google Scholar] [CrossRef]
- Sundström, E.; Tretter, J.T. Impact of Variation in Commissural Angle between Fused Leaflets in the Functionally Bicuspid Aortic Valve on Hemodynamics and Tissue Biomechanics. Bioengineering 2023, 10, 1219. [Google Scholar] [CrossRef]
- Tai, C.; Liew, K.; Zhao, Y. Numerical simulation of 3D fluid–structure interaction flow using an immersed object method with overlapping grids. Comput. Struct. 2007, 85, 749–762. [Google Scholar] [CrossRef]
- Hart, J.D.; Peters, G.; Schreurs, P.; Baaijens, F. A two-dimensional fluid–structure interaction model of the aortic valve. J. Biomech. 2000, 33, 1079–1088. [Google Scholar] [CrossRef]
- Donea, J.; Giuliani, S.; Halleux, J. An arbitrary lagrangian-eulerian finite element method for transient dynamic fluid-structure interactions. Comput. Methods Appl. Mech. Eng. 1982, 33, 689–723. [Google Scholar] [CrossRef]
- Miller, S.T.; Campbell, R.L.; Elsworth, C.W.; Pitt, J.S.; Boger, D.A. An Overset Grid Method for Fluid-Structure Interaction. World J. Mech. 2014, 4, 48290. [Google Scholar] [CrossRef]
- Baaijens, F.P.T. A fictitious domain/mortar element method for fluid–structure interaction. Int. J. Numer. Methods Fluids 2001, 35, 743–761. [Google Scholar] [CrossRef]
- Swim, E.; Seshaiyer, P. A nonconforming finite element method for fluid–structure interaction problems. Comput. Methods Appl. Mech. Eng. 2006, 195, 2088–2099. [Google Scholar] [CrossRef]
- Peskin, C.; McQueen, D. A general method for the computer simulation of biological systems interacting with fluids. Symp. Soc. Exp. Biol. 1995, 49, 265–276. [Google Scholar]
- Wang, H.; Chessa, J.; Liu, W.K.; Belytschko, T. The immersed/fictitious element method for fluid–structure interaction: Volumetric consistency, compressibility and thin members. Int. J. Numer. Methods Eng. 2008, 74, 32–55. [Google Scholar] [CrossRef]
- Hua, M.; Peskin, C.S. An analysis of the numerical stability of the immersed boundary method. J. Comput. Phys. 2022, 467, 111435. [Google Scholar] [CrossRef]
- Nowak, M.; Adamczyk, W.; Melka, B.; Ostrowski, Z.; Bialecki, R. Numerical Model of the Aortic Valve Implanted Within Real Human Aorta. In Information Technology in Biomedicine; Pitka, E., Badura, P., Kawa, J., Wiecek, W., Eds.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2021; Volume 1186, pp. 265–275. [Google Scholar] [CrossRef]
- Bornoff, J.; Gill, H.; Najar, A.; Perkins, I.; Cookson, A.; Fraser, K. Overset meshing in combination with novel blended weak-strong fluid-structure interactions for simulations of a translating valve in series with a second valve. Comput. Methods Biomech. Biomed. Eng. 2024, 27, 736–750. [Google Scholar] [CrossRef]
- Ge, L.; Jones, S.C.; Sotiropoulos, F.; Healy, T.M. Numerical Simulation of Flow in Mechanical Heart Valves: Grid Resolution and the Assumption of Flow Symmetry. J. Biomech. Eng. 2003, 125, 709–718. [Google Scholar] [CrossRef]
- Lincoln, J.; Garg, V. Etiology of Valvular Heart Disease–Genetic and Developmental Origins–. Circ. J. 2014, 78, 1801–1807. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Chandra, S.; Sucosky, P. Ex vivo evidence for the contribution of hemodynamic shear stress abnormalities to the early pathogenesis of calcific bicuspid aortic valve disease. PLoS ONE 2012, 7, e48843. [Google Scholar] [CrossRef]
- Hatoum, H.; Dasi, L.P. Spatiotemporal complexity of the aortic sinus vortex as a function of leaflet calcification. Ann. Biomed. Eng. 2019, 47, 1116–1128. [Google Scholar] [CrossRef]
- Lee, S.; Wolberg, G.; Shin, S.Y. Scattered data interpolation with multilevel b-splines. IEEE Trans. Vis. Comput. Graph. 1997, 3, 228–244. [Google Scholar] [CrossRef]
- Prather, R.O.; Kassab, A.; Ni, M.W.; Divo, E.; Argueta-Morales, R.; DeCampli, W.M. Multi-scale pulsatile CFD modeling of thrombus transport in a patient-specific LVAD implantation. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 1022–1039. [Google Scholar] [CrossRef]
- Lumens, J.; Delhaas, T.; Kirn, B.; Arts, T. Three-wall segment (TriSeg) model describing mechanics and hemodynamics of ventricular interaction. Ann. Biomed. Eng. 2009, 37, 2234–2255. [Google Scholar] [CrossRef] [PubMed]
- Brown, J.A.; Lee, J.H.; Smith, M.A.; Wells, D.R.; Barrett, A.; Puelz, C.; Vavalle, J.P.; Griffith, B.E. Patient–specific immersed finite element–difference model of transcatheter aortic valve replacement. Ann. Biomed. Eng. 2023, 51, 103–116. [Google Scholar] [CrossRef]
- Pfensig, S.; Kaule, S.; Stiehm, M.; Sämann, M. Assessment of heart valve performance by finite-element design studies of polymeric leaflet-structures. Curr. Dir. Biomed. Eng. 2017, 3, 631–634. [Google Scholar] [CrossRef][Green Version]
- Kovarovic, B.; Helbock, R.; Baylous, K.; Rotman, O.M. Visions of TAVR Future: Development and Optimization of a Second Generation Novel Polymeric TAVR. J. Biomech. Eng. 2022, 144, 061008. [Google Scholar] [CrossRef] [PubMed]
- Kvitting, J.P.E.; Ebbers, T.; Wigström, L.; Engvall, J.; Olin, C.L.; Bolger, A.F. Flow patterns in the aortic root and the aorta studied with time-resolved, 3-dimensional, phase-contrast magnetic resonance imaging: Implications for aortic valve-sparing surgery. J. Thorac. Cardiovasc. Surg. 2004, 127, 1602–1607. [Google Scholar] [CrossRef]
- Rosakis, A.; Gharib, M. The Influence of Valve Leaflet Stiffness Variability on Aortic Wall Shear Stress. Ann. Biomed. Eng. 2022, 50, 29–38. [Google Scholar] [CrossRef]
- Sundström, E.; Laudato, M. Machine learning-based segmentation of the thoracic aorta with congenital valve disease using MRI. Bioengineering 2023, 10, 1216. [Google Scholar] [CrossRef]
- Hsu, M.C.; Kamensky, D.; Bazilevs, Y.; Sacks, M.S.; Hughes, T.J. Fluid–structure interaction analysis of bioprosthetic heart valves: Significance of arterial wall deformation. Comput. Mech. 2014, 54, 1055–1071. [Google Scholar] [CrossRef]
- Mao, W.; Li, W.; S, W. Fluid–Structure Interaction Study of Transcatheter Aortic Valve Dynamics Using Smoothed Particle Hydrodynamics. Cardiovasc. Eng. Technol. 2016, 7, 374–388. [Google Scholar] [CrossRef]
- De Tullio, M.D.; Cristallo, A.; Balaras, E.; Verzicco, R. Direct numerical simulation of the pulsatile flow through an aortic bileaflet mechanical heart valve. J. Fluid Mech. 2009, 622, 259–290. [Google Scholar] [CrossRef]
- Nitti, A.; De Cillis, G.; De Tullio, M.D. Numerical investigation of turbulent features past different mechanical aortic valves. J. Fluid Mech. 2022, 940, A43. [Google Scholar] [CrossRef]
- Hedayat, M.; Borazjani, I. Comparison of platelet activation through hinge vs bulk flow in bileaflet mechanical heart valves. J. Biomech. 2019, 83, 280–290. [Google Scholar] [CrossRef]
- Borazjani, I.; Ge, L.; Sotiropoulos, F. High-resolution fluid-structure interaction simulations of flow through a bi-leaflet mechanical heart valve in an anatomic aorta. Ann. Biomed. Eng. 2010, 38, 326–344. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, N.; Sharma, S.D.; Chakraborty, S.; Roy, S. A comparative study of Newtonian and non-Newtonian blood flow through Bi-Leaflet Mechanical Heart Valve. Comput. Fluids 2024, 279, 106337. [Google Scholar] [CrossRef]
- Pawlikowski, M.; Nieroda, A. Comparative analyses of blood flow through mechanical trileaflet and bileaflet aortic valves. Acta Bioeng. Biomech. 2022, 24, 141–152. [Google Scholar] [CrossRef]
- De Vita, F.; De Tullio, M.D.; Verzicco, R. Numerical simulation of the non-Newtonian blood flow through a mechanical aortic valve: Non-Newtonian blood flow in the aortic root. Theor. Comput. Fluid Dyn. 2015, 30, 129–138. [Google Scholar] [CrossRef]
- Yeh, H.H.; Barannyk, O.; Grecov, D.; Oshkai, P. The influence of hematocrit on the hemodynamics of artificial heart valve using fluid-structure interaction analysis. Comput. Biol. Med. 2019, 110, 79–92. [Google Scholar] [CrossRef]
- Chauhan, A.; Sasmal, C. The influence of non-Newtonian behaviors of blood on the hemodynamics past a bileaflet mechanical heart valve. Physics of Fluids 2024, 36, 10. [Google Scholar] [CrossRef]
- Jadidi, M.; Habibnezhad, M.; Anttila, E.; Maleckis, K.; Desyatova, A.; MacTaggart, J.; Kamenskiy, A. Mechanical and structural changes in human thoracic aortas with age. Acta Biomater. 2020, 103, 172–188. [Google Scholar] [CrossRef] [PubMed]
- Liogky, A.; Karavaikin, P.; Salamatova, V. Impact of Material Stiffness and Anisotropy on Coaptation Characteristics for Aortic Valve Cusps Reconstructed from Pericardium. Mathematics 2021, 9, 2193. [Google Scholar] [CrossRef]
- Li, J.; Luo, X.; Kuang, Z. A nonlinear anisotropic model for porcine aortic heart valves. J. Biomech. 2001, 34, 1279–1289. [Google Scholar] [CrossRef] [PubMed]
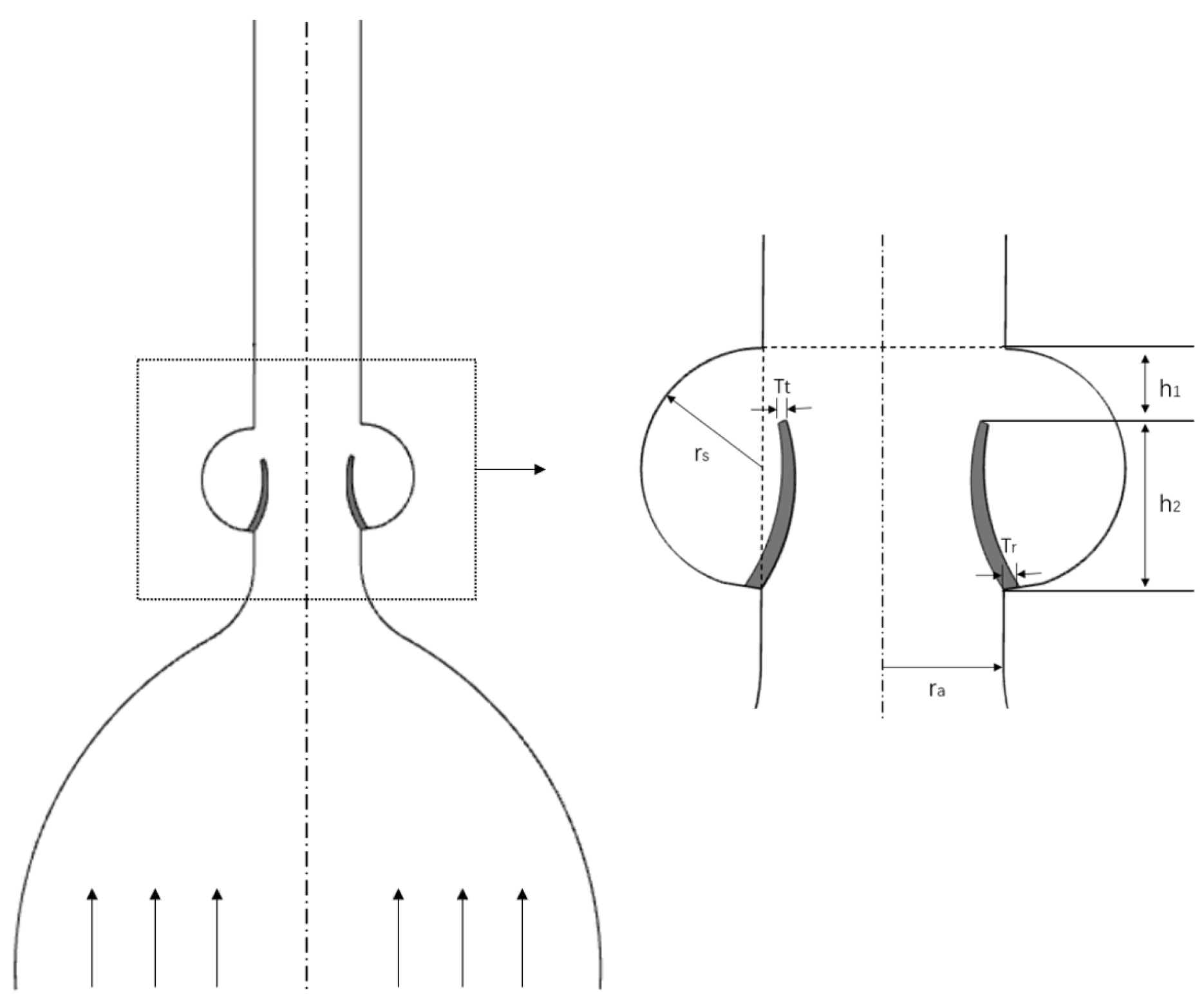


| Parameter | Notation | Value |
|---|---|---|
| Annular radius | 0.01 m | |
| Sinus radius | 0.01 m | |
| Upper sinus height | 0.015 m | |
| Lower sinus height | 0.005 m | |
| Leaflet tip thickness | 0.0007 m | |
| Leaflet root thickness | 0.002 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Sundström, E. Vortex Dynamics in the Sinus of Valsalva. Bioengineering 2025, 12, 279. https://doi.org/10.3390/bioengineering12030279
Fan J, Sundström E. Vortex Dynamics in the Sinus of Valsalva. Bioengineering. 2025; 12(3):279. https://doi.org/10.3390/bioengineering12030279
Chicago/Turabian StyleFan, Jiaxuan, and Elias Sundström. 2025. "Vortex Dynamics in the Sinus of Valsalva" Bioengineering 12, no. 3: 279. https://doi.org/10.3390/bioengineering12030279
APA StyleFan, J., & Sundström, E. (2025). Vortex Dynamics in the Sinus of Valsalva. Bioengineering, 12(3), 279. https://doi.org/10.3390/bioengineering12030279





