Comparing Growth Models Dependent on Irradiation and Nutrient Consumption on Closed Outdoor Cultivations of Nannochloropsis sp.
Abstract
1. Introduction
2. Materials and Methods
2.1. Bioreactor Configurations and Assays
- Having the same number of assays in each group;
- Having a balance of the number of multilayer and unilayer assays in each group.
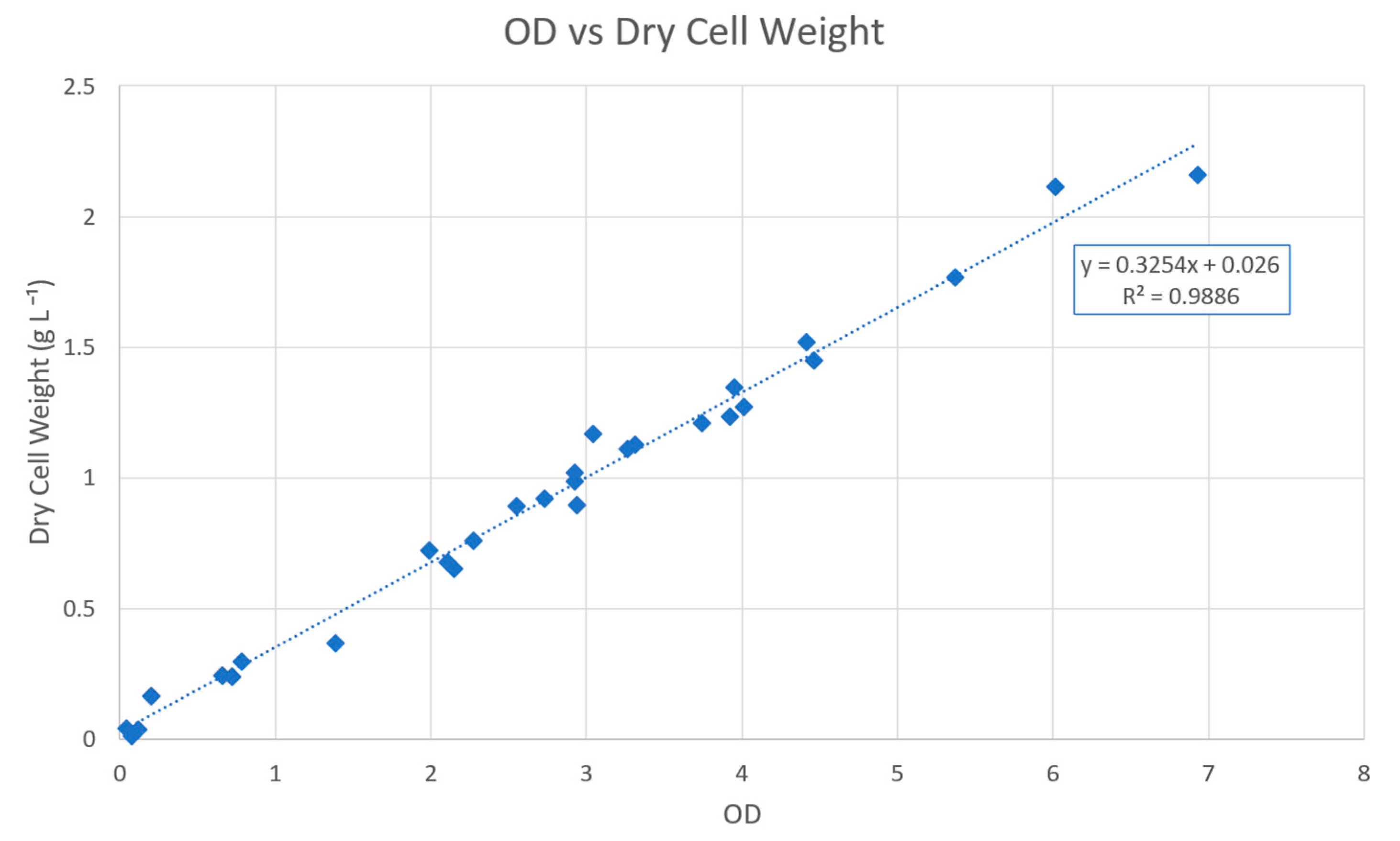
2.2. Measurements and Process Data
2.3. Data Processing and Model Construction
2.4. Models Tested
2.4.1. Model M
2.4.2. Model E
2.4.3. Model H
2.4.4. Model D
2.5. Comparison Metrics
2.5.1. Root Mean Squared Error (RMSE)
2.5.2. Akaike Information Criterion
2.6. Bootstrapping
3. Results & Discussion
3.1. Model Parameter Analysis
- Model M: μmax = 0.041 h−1; KS = 13.3 MJ m−2 day−1; and α = 1.645 m3 kg−1;
- Model H: μmax = 0.032 h−1; Iopt = 41.4 MJ m−2 day−1; γ = 1.070; and α = 1.337 m3 kg−1;
- Model E: μmax = 0.033 h−1; λ2 = 9.933 MJ m−2 day−1; and α = 1.515 m3 kg−1;
- Model D: μmax = 0.082 h−1; KS = 63.3 MJ m−2 day−1; α = 1.003 m3 kg−1; Qmin = 0.0025 gN gC−1; Qmax = 8 × 10−6 gN gC−1 h−1; Ksub = 0 gN gC−1; and QI = 3.98 gN gC−1.
3.1.1. Maximum Growth Rate
3.1.2. Half-Saturation Constant for Light
- Model M: 61.6 μmol m−2 s−1;
- Model D: 293 μmol m−2 s−1.
3.1.3. Beer–Lambert-like Constant
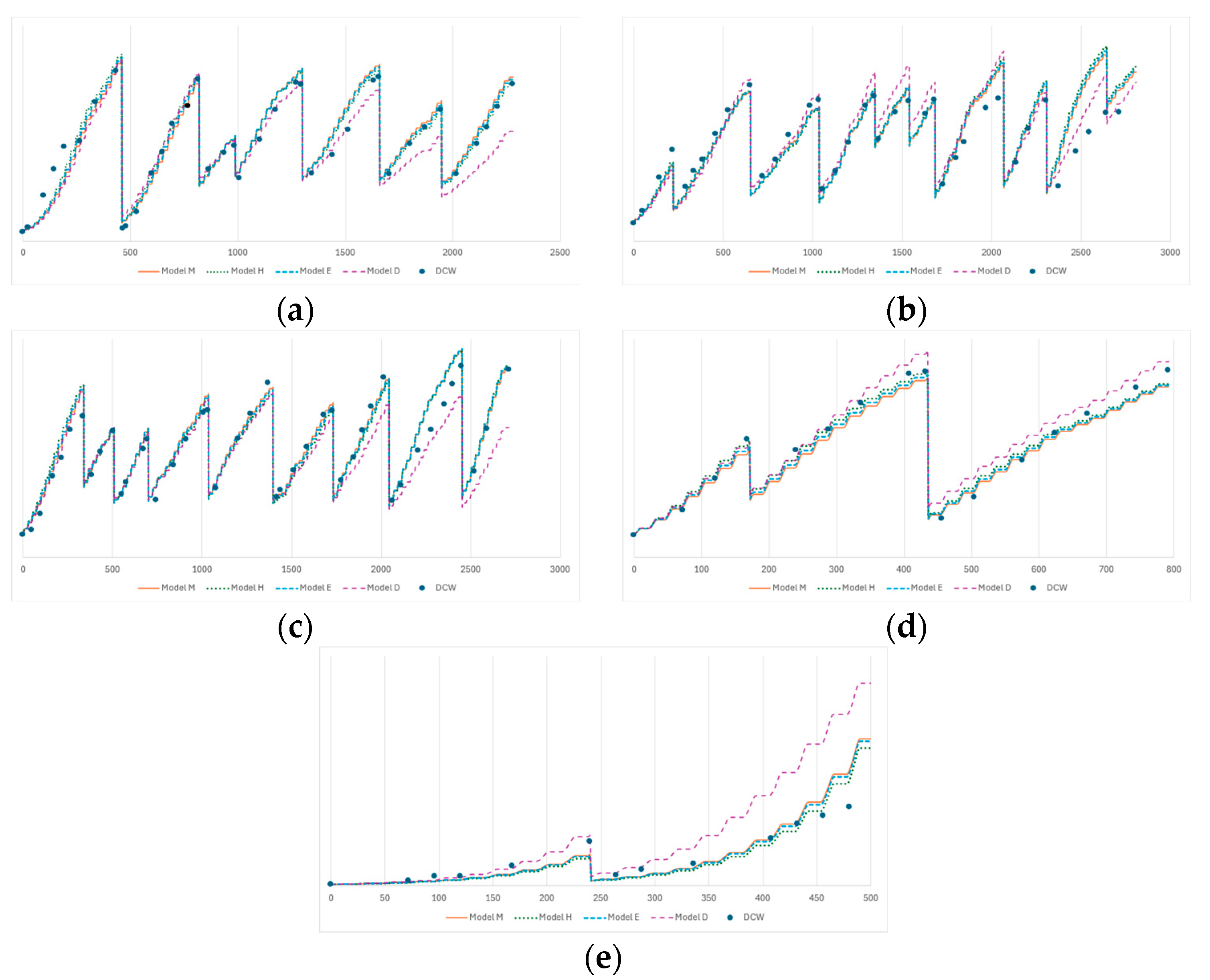
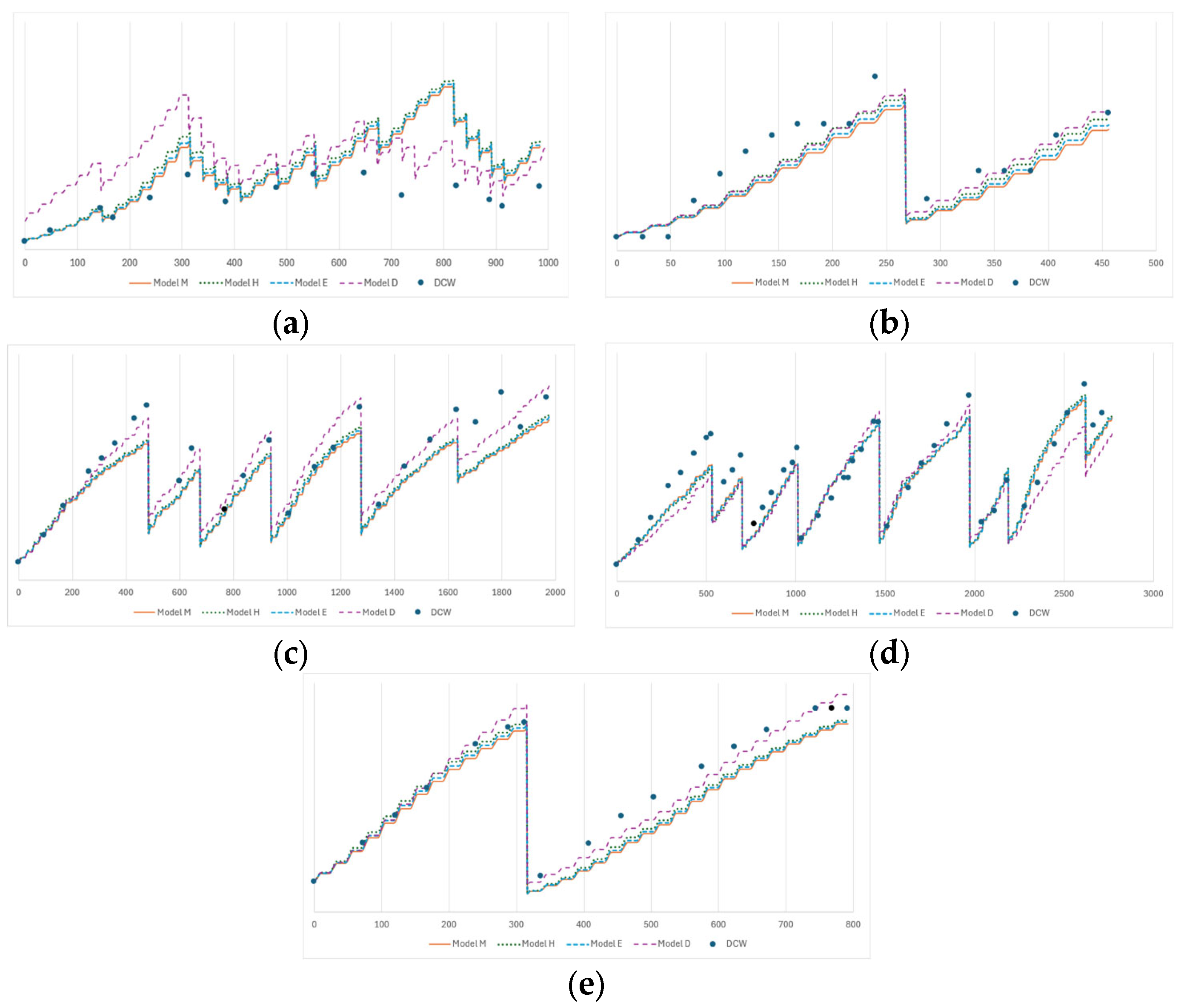
3.2. Model Fitting Analysis
3.3. Calculation of the Akaike Information Criterion (AIC)
- Model M: −694;
- Model H: −717;
- Model E: −707;
- Model D: −505.
3.4. Comparative Analysis of the Models
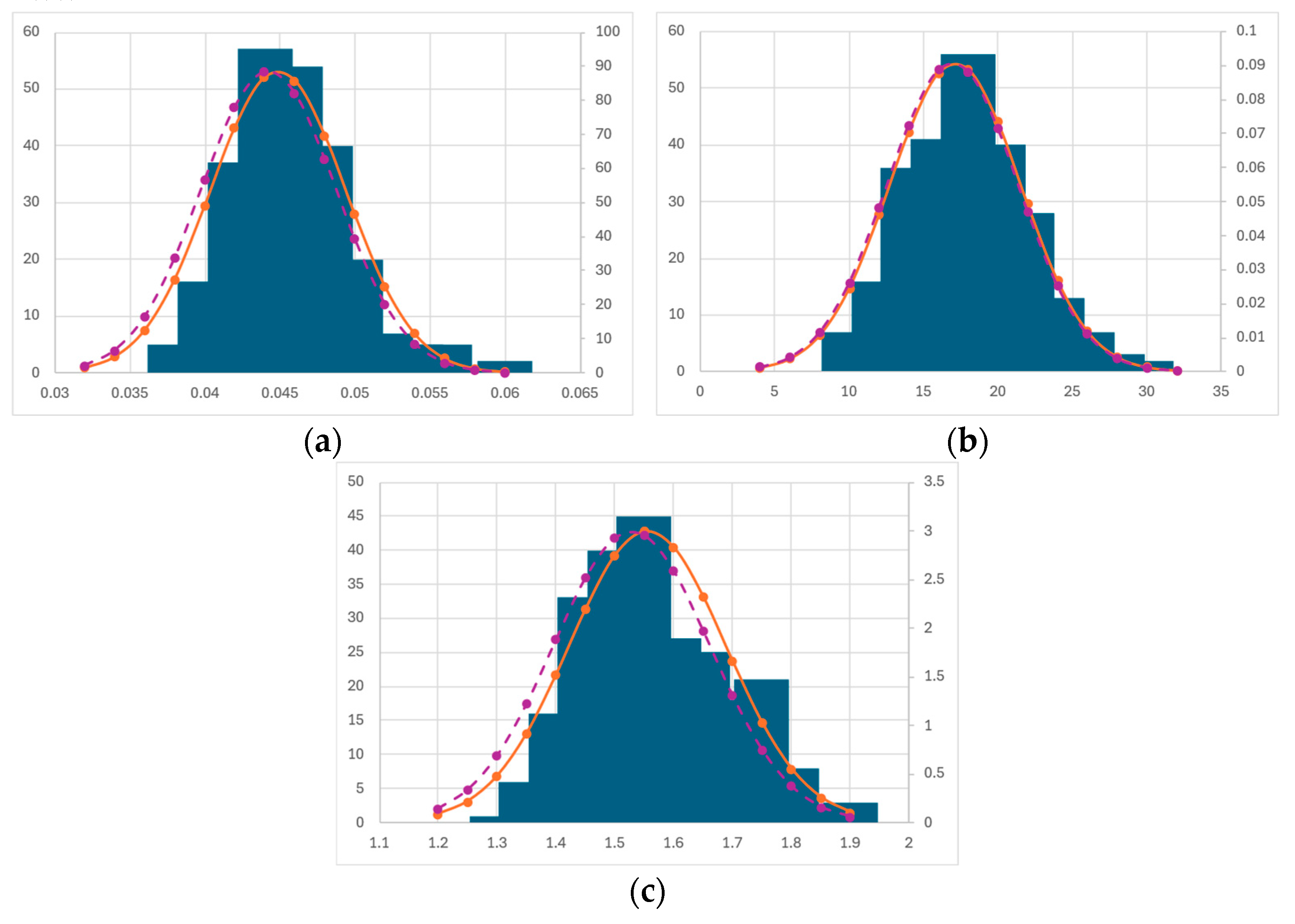
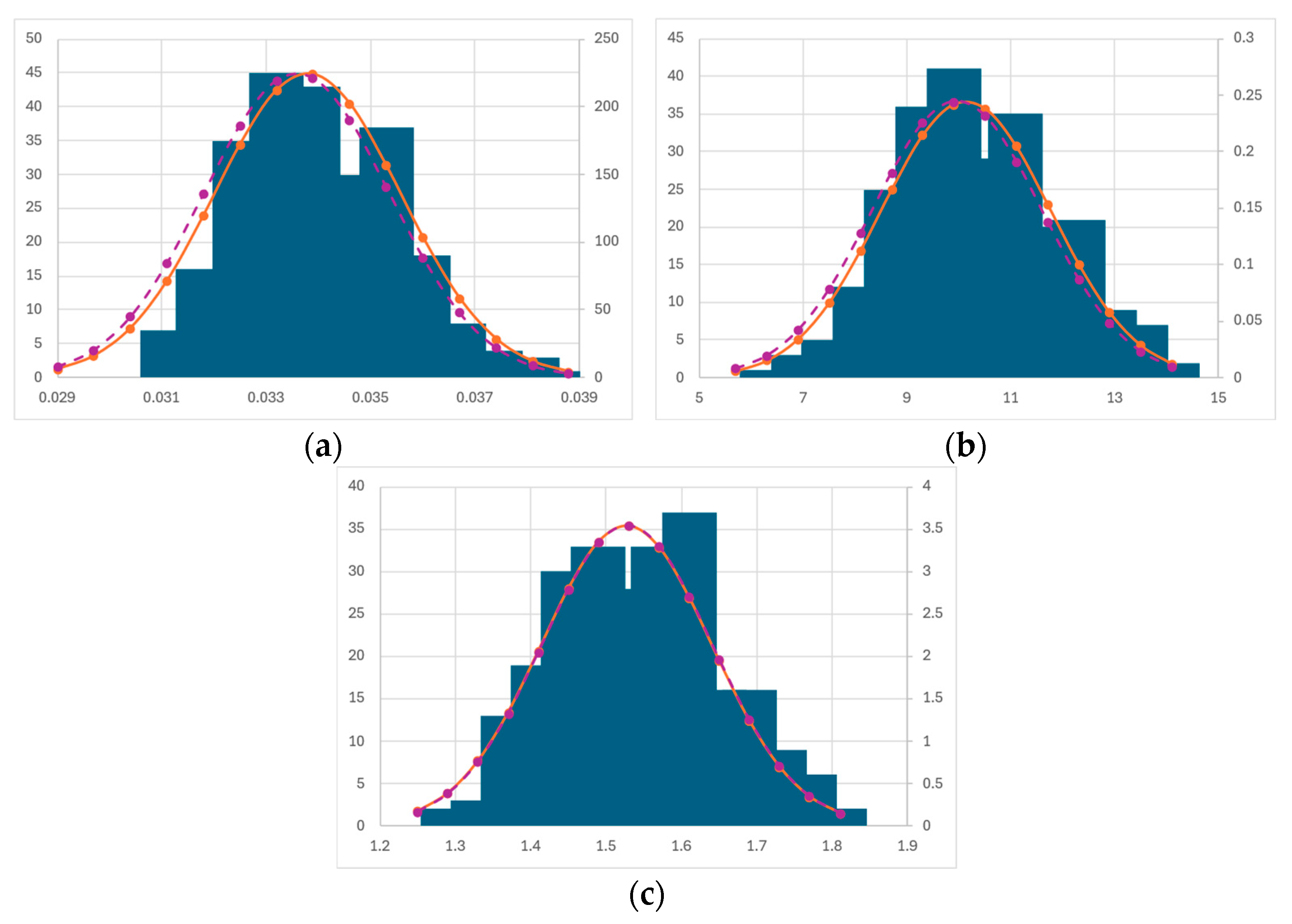
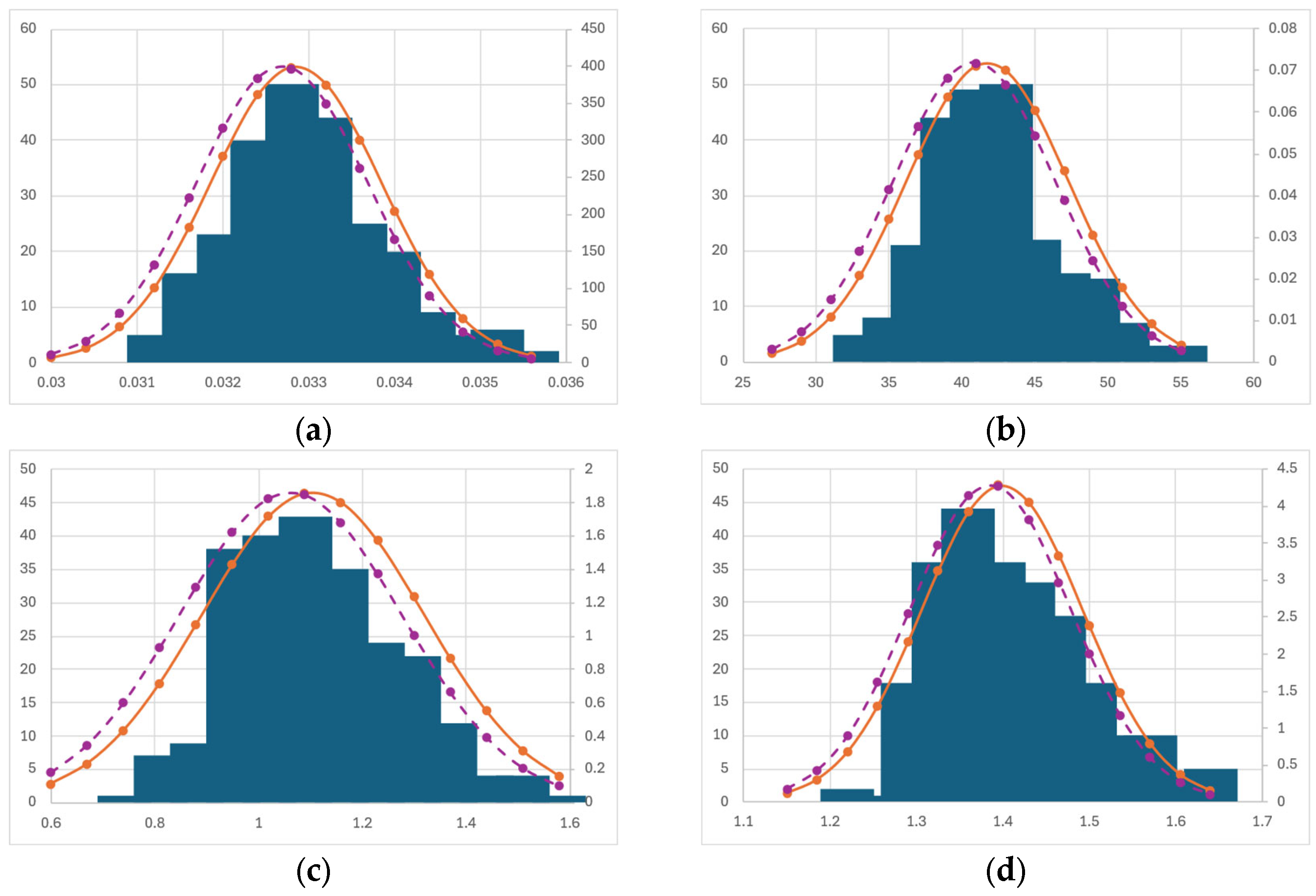
3.5. Bootstrapping Statistics
Bootstrapping Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C

Appendix D

References
- Richmond, A. Handbook of Microalgal Culture: Biotechnology and Applied Phycology; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lara-Gil, J.A.; Carolina, S.G.; Pacheco, A. Cement flue gas as a potential source of nutrients during CO2 mitigation by microalgae. Algal Res. 2016, 17, 285–292. [Google Scholar] [CrossRef]
- Cheah, W.Y.; Jo-Shu, C.; Chuan, T.L.; Show, P.L.; Juan, J.C. Biosequestration of atmospheric CO2 and flue gas-containing CO2 by microalgae. Bioresour. Technol. 2015, 184, 190–201. [Google Scholar] [CrossRef] [PubMed]
- Béchet, Q.; Shilton, A.; Guieysse, B. Modelling the effects of light and temperature on algae growth: Stat of the art and critical cassessment for productivity prediction during outdoor cultivation. Biotechnol. Adv. 2013, 31, 1648–1663. [Google Scholar] [CrossRef] [PubMed]
- Fernández, F.G.A.; Camacho, F.G.; Pérez, J.S.; Sevilla, J.F.; Grima, E.M. Modeling of biomass productivity in tubular photobioreactors for microalgal cultures: Effects of dilution rate, tube diameter, and solar irradiance. Biotechnol. Bioeng. 1998, 58, 605–616. [Google Scholar] [CrossRef]
- Fernández, I.A.; Fernández, F.G.; Magán, J.J.; Guzmán, J.L.; Berenguel, M. Dynamic model of microalgal production in tubular photobioreactors. Bioresour. Technol. 2012, 126, 172–181. [Google Scholar] [CrossRef]
- Ippoliti, D.; Gómez, C.; Morales-Amaral, M.D.M.; Pistocchi, R.; Fernández-Sevilla, J.M.; Acién, F.G. Modeling of photosynthesis and respiration rate for Isochrysis galbana (T-Iso) and its influence on the production of this strain. Bioresour. Technol. 2016, 203, 71–79. [Google Scholar] [CrossRef]
- Boussiba, S.; Cohen, V.A.Z.; Avissar, Y.; Richmond, A. Lipid and biomass production by the halotolerant microalga Nannochloropsis salina. Biomass 1987, 12, 37–47. [Google Scholar] [CrossRef]
- American Public Health Association; American Water Works Association; Water Environment Federation. 4500 NO3-B. In Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2017. [Google Scholar]
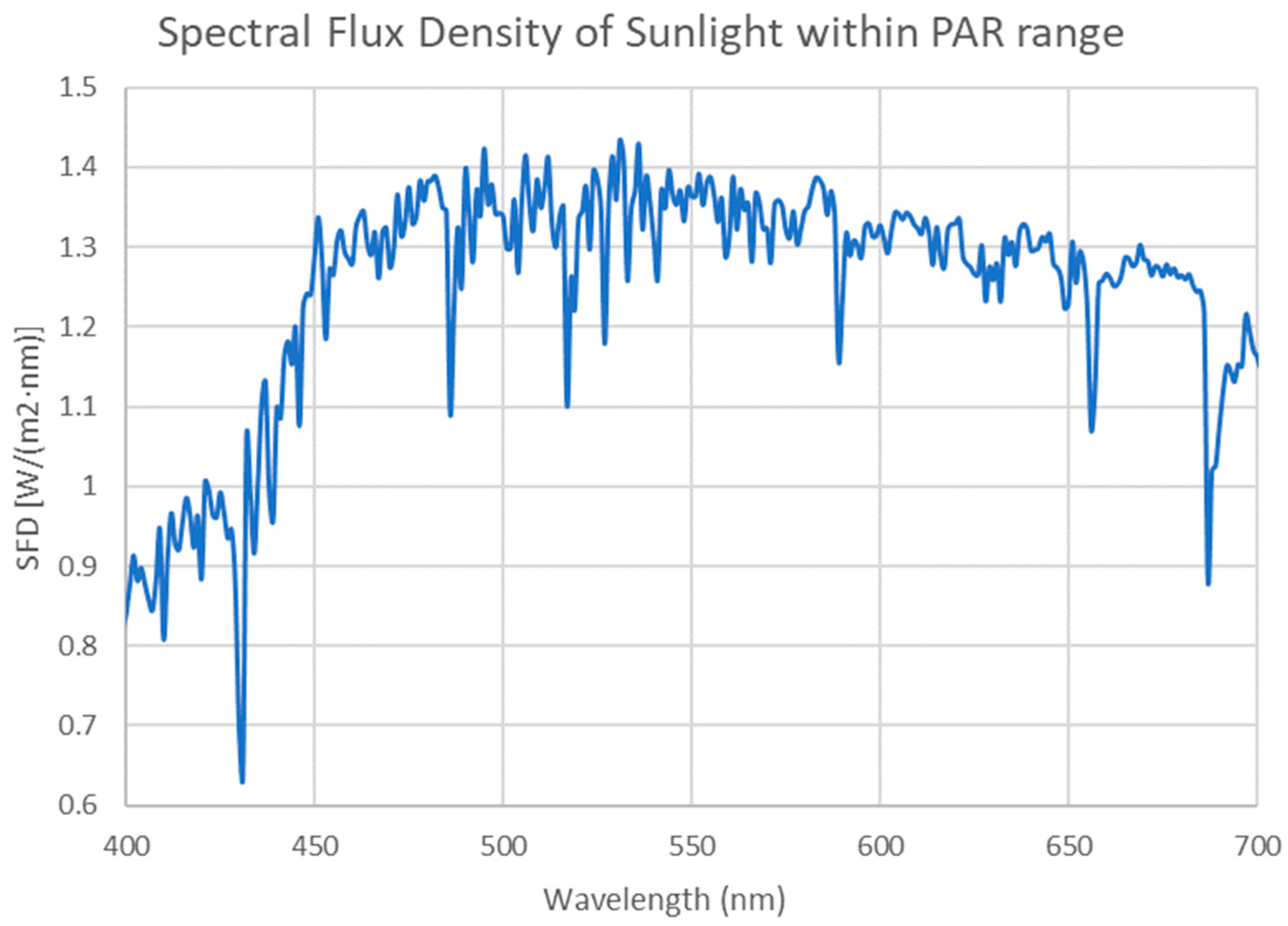
- European Comission, Photovoltaic Geographical Information System. [Online]. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/#api_5.2 (accessed on 22 December 2023).
- Darvehei, P.; Bahri, P.A.; Moheimani, N.R. Model development for the growth of microalgae: A review. Renew. Sustain. Energy Rev. 2018, 97, 233–258. [Google Scholar] [CrossRef]
- Yun, Y.S.; Park, J.M. Kinetic modeling of the light-dependent photosynthetic activity of the green microalga Chlorella vulgaris. Biotechnol. Bioeng. 2003, 83, 303–311. [Google Scholar] [CrossRef]
- Carli, B. Basics About Radiative Transfer. [Online]. Available online: https://earth.esa.int/dragon/D2_L2_Carli.pdf (accessed on 2 March 2022).
- Van Wagenen, J.; Miller, T.W.; Hobbs, S.; Hook, P.; Crowe, B.; Huesemann, M. Effects of light and temperature on fatty acid production in Nannochloropsis salina. Energies 2012, 5, 731–740. [Google Scholar] [CrossRef]
- Tamiya, H.; Hase, E.; Shibata, K.; Mituya, A.; Iwamura, T. Kinetics of growth of Chlorella, with special refer-ence to its dependence on quantity of available light and on temperature. In Algal Culture from Laboratory to Pilot Plant; Carnegie Institution of Washington: Washington, DC, USA, 1953; pp. 204–232. [Google Scholar]
- Lee, H.Y.; Erickson, L.E.; Yang, S.S. Kinetics and bioenergetics of light-limited photoautotrophic growth of Spirulina platensis. Biotechnol. Bioeng. 1987, 29, 832–843. [Google Scholar] [CrossRef] [PubMed]
- Franz, A.; Lehr, F.; Posten, C.; Schaub, G. Modeling microalgae cultivation productivities in different geo-graphic locations–estimation method for idealized photobioreactors. Biotechnol. J. 2012, 7, 546–557. [Google Scholar] [CrossRef] [PubMed]
- Molina, G.E.; Sevilla, M.F.; Sánchez, J. A study on simultaneous photolimitation and photoinhibition in dense microalgal cultures taking into account incident and averaged irradiances. J. Biotechnol. 1996, 45, 59–69. [Google Scholar]
- van Oorschot, J.L.P. Conversion of Light Energy in Algal Culture; Veenman: Wageningen, The Netherlands, 1955. [Google Scholar]
- Meseck, S.L.; Alix, J.H.; Wikfors, G.H. Photoperiod and light intensity effects on growth and utilization of nutrients by the aquaculture feed microalga, Tetraselmis chui (PLY429). Aquaculture 2005, 246, 393–404. [Google Scholar] [CrossRef]
- Haldane, J. Enzymes; Longmans Green: London, UK, 1930. [Google Scholar]
- Eilers, P.H.C.; Peeters, J.C.H. A model for the relationship between light intensity and the rate of photosyn-thesis in phytoplankton. Ecol. Model. 1988, 42, 199–215. [Google Scholar] [CrossRef]
- Bernard, O.; Rémond, B. Validation of a simple model accounting for light and temperature effect on micro-algal growth. Bioresour. Technol. 2012, 123, 520–527. [Google Scholar] [CrossRef]
- Megard, R.O.; Tonkyn, D.W.; Senft, W.H. Kinetics of oxygenic photosynthesis in planktonic algae. J. Plankton Res. 1984, 6, 325–337. [Google Scholar] [CrossRef]
- Fouchard, S.; Pruvost, J.; Degrenne, B.; Titica, M.; Legrand, J. Kinetic modeling of light limitation and sulfur deprivation effects in the induction of hydrogen production with Chlamydomonas reinhardtii: Part I. Model development and parameter identification. Biotechnol. Bioeng. 2009, 102, 232–245. [Google Scholar] [CrossRef]
- Concas, A.; Pisu, M.; Giacomo, C. A novel mathematical model to simulate the size-structured growth of mi-croalgae strains dividing by multiple fission. Chem. Eng. J. 2016, 287, 252–268. [Google Scholar] [CrossRef]
- Mirzaie, M.; Kalbasi, M.; Ghobadian, B.; Mousavi, S.M. Kinetic modeling of mixotrophic growth of Chlorella vulgaris as a new feedstock for biolubricant. J. Appl. Phycol. 2016, 28, 2707–2717. [Google Scholar] [CrossRef]
- Dauta, A.; Devaux, J.; Piquemal, F.; Boumnich, L. Growth rate of four freshwater algae in relation to light and temperature. Hydrobiologia 1990, 207, 221–226. [Google Scholar] [CrossRef]
- Pessi, B.A.; Pruvost, E.; Talec, A.; Sciandra, A.; Bernard, O. Does temperature shift justify microalgae pro-duction under greenhouse? Algal Res. 2021, 61, 102579. [Google Scholar] [CrossRef]
- Nikolaou, A.; Hartmann, P.; Sciand, A.; Chachuat, B.; Bernard, O. Dynamic coupling of photoacclimation and photoinhibition in a model of microalgae growth. J. Theor. Biol. 2016, 390, 61–72. [Google Scholar] [CrossRef] [PubMed]
- Droop, M.R. Vitamin B12 and marine ecology. IV. The kinetics of uptake, growth and inhibition in Monochrysis lutheri. J. Mar. Biol. Assoc. United Kingd. 1968, 48, 689–733. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA, 1998; pp. 75–117. [Google Scholar]
- Manly, B.F. Randomization, Bootstrap and Monte Carlo Methods in Biology; CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Huesemann, M.H.; Van Wagenen, J.; Miller, T.; Cha, A. A Screening Model to Predict Microalgae Biomass Growth in Photobioreactors and Raceway Ponds. Biotechnol. Bioeng. 2013, 110, 1583–1594. [Google Scholar] [CrossRef]
- ASTM International. Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispheri-cal on 37° Tilted Surface. 14 7 2020. [Online]. Available online: https://www.astm.org/g0173-03r12.html (accessed on 30 January 2022).
- French, A.; Taylor, E. An Introduction to Quantum Physics; Van Nostrand Reinhold: London, UK, 1978. [Google Scholar]

| Assay Code | Duration (Days) | Number of Data Points | Assay Type |
|---|---|---|---|
| M1-1 | 41 | 15 | Validation |
| M1-2 | 95 | 38 | Training |
| M1-3 | 19 | 17 | Validation |
| M1-4 | 117 | 38 | Training |
| U1-1 | 113 | 44 | Training |
| U1-2 | 33 | 16 | Training |
| U1-3 | 82 | 25 | Validation |
| U2-1 | 113 | 42 | Validation |
| U2-2 | 20 | 14 | Training |
| U2-3 | 33 | 17 | Validation |
| RMSE | ||||
|---|---|---|---|---|
| Assay | Model M | Model H | Model E | Model D |
| M1-2 | 0.070 | 0.079 | 0.102 | 0.170 |
| M1-4 | 0.107 | 0.091 | 0.082 | 0.217 |
| U1-1 | 0.104 | 0.106 | 0.098 | 0.161 |
| U1-2 | 0.121 | 0.080 | 0.097 | 0.120 |
| U2-2 | 0.073 | 0.048 | 0.054 | 0.130 |
| Global | 0.098 | 0.090 | 0.093 | 0.173 |
| RMSE | ||||
|---|---|---|---|---|
| Assay | Model M | Model H | Model E | Model D |
| M1-1 | 0.295 | 0.240 | 0.380 | 0.951 |
| M1-3 | 0.360 | 0.407 | 0.273 | 0.236 |
| U1-3 | 0.428 | 0.383 | 0.405 | 0.235 |
| U2-1 | 0.206 | 0.220 | 0.211 | 0.292 |
| U2-3 | 0.245 | 0.206 | 0.227 | 0.131 |
| Global | 0.309 | 0.296 | 0.302 | 0.413 |
| Parameter | Mean | Median | St. Dev. | Confidence Interval | Full Dataset Fitting |
|---|---|---|---|---|---|
| µmax (h−1) | 0.045 | 0.044 | 0.005 | ±0.01 | 0.041 |
| KS (MJ m−2 day−1) | 17.13 | 16.95 | 4.404 | ±8.8 | 13.3 |
| α (m3 kg−1) | 1.555 | 1.528 | 0.133 | ±0.26 | 1.645 |
| Parameter | Mean | Median | St. Dev. | Confidence Interval | Full Dataset Fitting |
|---|---|---|---|---|---|
| µmax (h−1) | 0.033 | 0.033 | 0.001 | ±0.001 | 0.032 |
| Iopt (MJ m−2 day−1) | 41.74 | 40.84 | 5.549 | ±11.1 | 41.4 |
| γ | 1.106 | 1.063 | 0.214 | ±0.428 | 1.070 |
| α (m3 kg−1) | 1.399 | 1.385 | 0.093 | ±0.186 | 1.337 |
| Parameter | Mean | Median | St. Dev. | Confidence Interval | Full Dataset Fitting |
|---|---|---|---|---|---|
| µmax (h−1) | 0.034 | 0.034 | 0.002 | ±0.004 | 0.033 |
| λ2 (MJ m−2 day−1) | 10.13 | 9.957 | 1.631 | ±3.26 | 9.933 |
| α (m3 kg−1) | 1.527 | 1.528 | 0.113 | ±0.22 | 1.515 |
| Parameter | Mean | Median | St. Dev. | Confidence Interval | Full Dataset Fitting |
|---|---|---|---|---|---|
| μmax (h−1) | 0.094 | 0.084 | 0.028 | ±0.056 | 0.082 |
| KS (MJ m−2 day−1) | 72.86 | 64.74 | 25.02 | ±50 | 63.3 |
| Qmin (gN gC−1) | 0.026 | 0.006 | 0.037 | ±0.074 | 0.0025 |
| ρmax (gN gC−1 h−1) | 3 × 10−4 | 4 × 10−5 | 5 × 10−4 | ±1 × 10−3 | 8 × 10−6 |
| Ksub (gN gC−1) | 0.055 | 0 | 0.189 | ±0.378 | 0 |
| QI (gN gC−1) | 16334 | 14.84 | 49772 | ±99544 | 3.98 |
| α (m3 kg−1) | 0.994 | 0.997 | 0.014 | ±0.28 | 1.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taborda, T.; Pires, J.C.M.; Badenes, S.M.; Lemos, F. Comparing Growth Models Dependent on Irradiation and Nutrient Consumption on Closed Outdoor Cultivations of Nannochloropsis sp. Bioengineering 2025, 12, 272. https://doi.org/10.3390/bioengineering12030272
Taborda T, Pires JCM, Badenes SM, Lemos F. Comparing Growth Models Dependent on Irradiation and Nutrient Consumption on Closed Outdoor Cultivations of Nannochloropsis sp. Bioengineering. 2025; 12(3):272. https://doi.org/10.3390/bioengineering12030272
Chicago/Turabian StyleTaborda, Tiago, José C. M. Pires, Sara M. Badenes, and Francisco Lemos. 2025. "Comparing Growth Models Dependent on Irradiation and Nutrient Consumption on Closed Outdoor Cultivations of Nannochloropsis sp." Bioengineering 12, no. 3: 272. https://doi.org/10.3390/bioengineering12030272
APA StyleTaborda, T., Pires, J. C. M., Badenes, S. M., & Lemos, F. (2025). Comparing Growth Models Dependent on Irradiation and Nutrient Consumption on Closed Outdoor Cultivations of Nannochloropsis sp. Bioengineering, 12(3), 272. https://doi.org/10.3390/bioengineering12030272







