Optimization of the Parameters of a Minimal Coagulation Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Detailed Coagulation Model by Hockin
2.2. Reduced Wagenvoord Model
2.3. Optimization
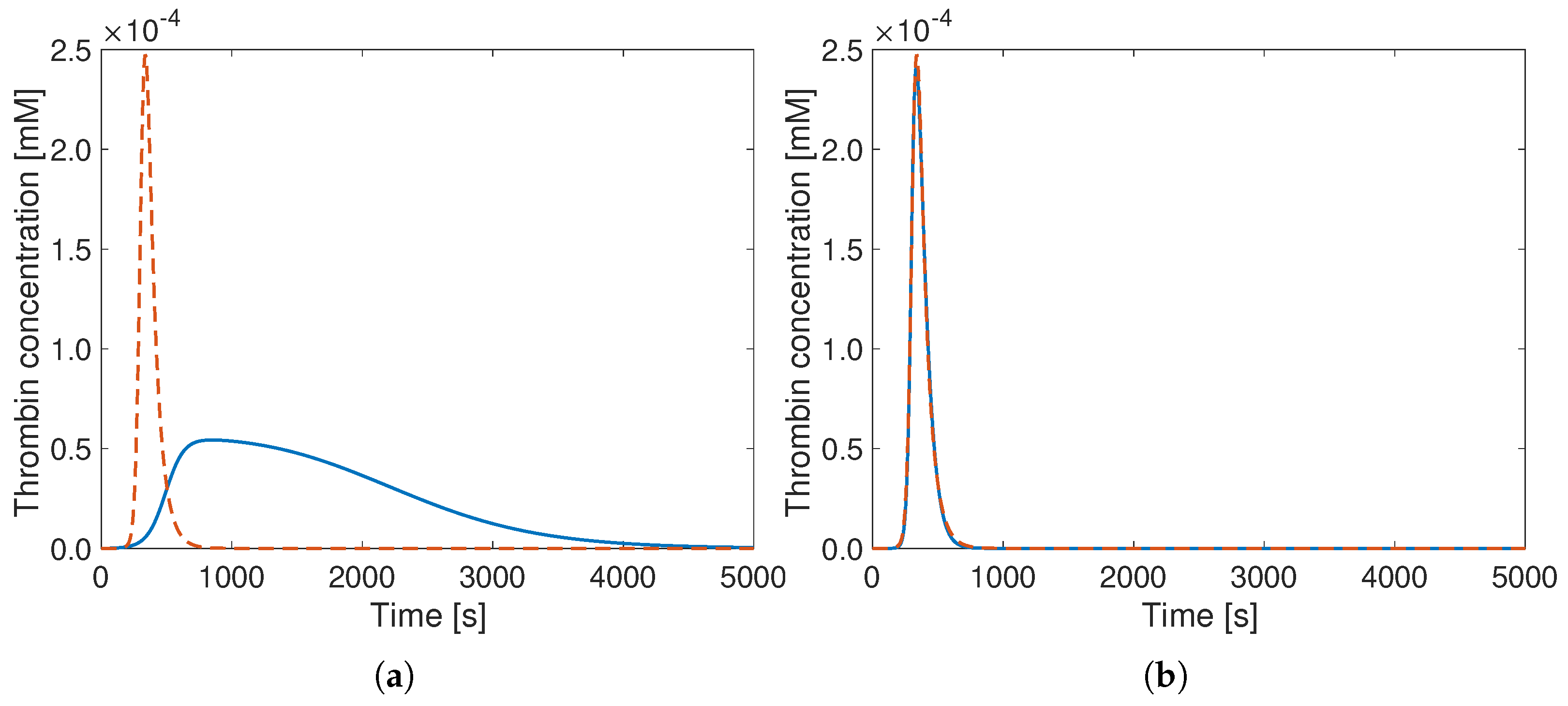
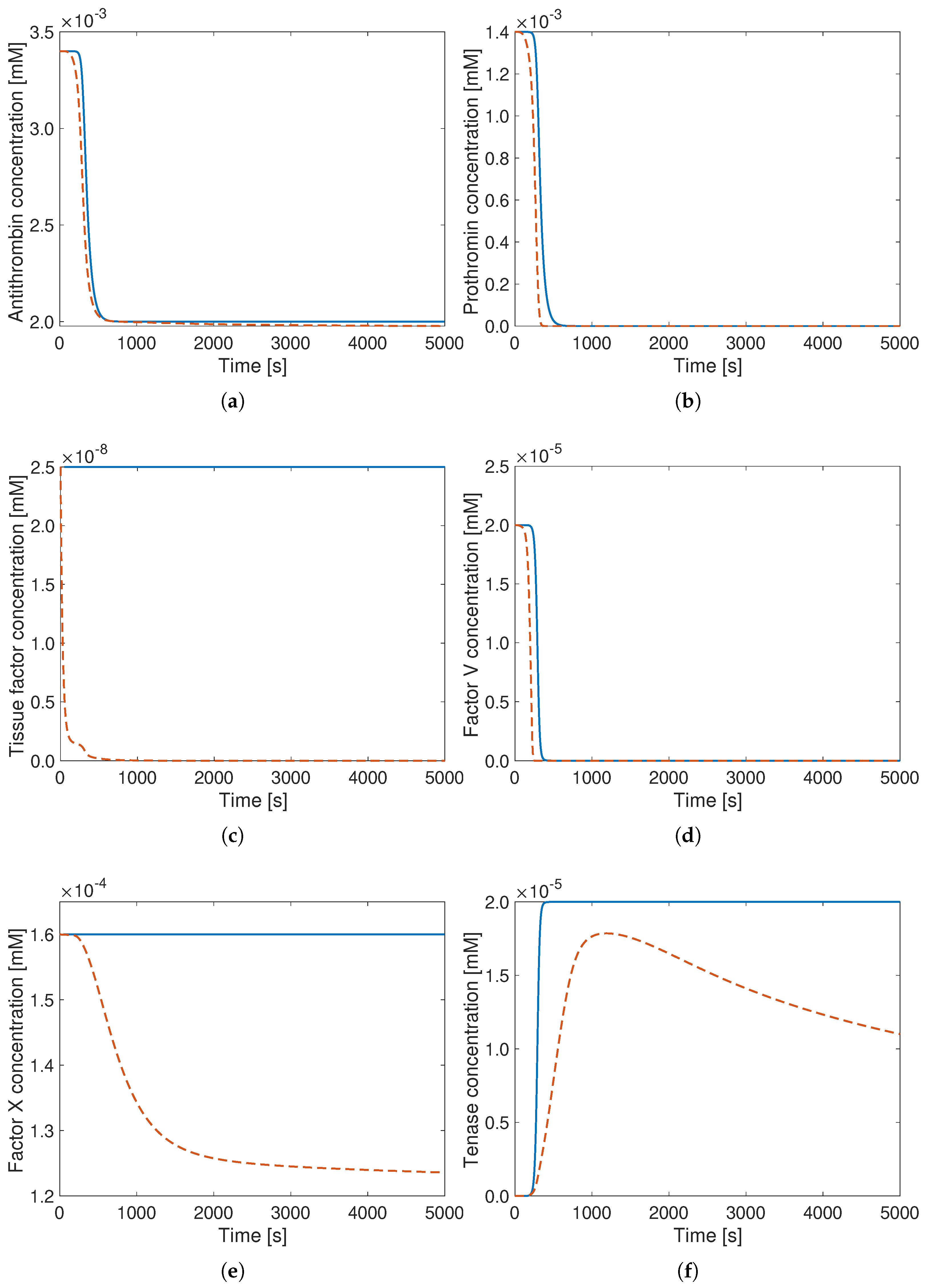
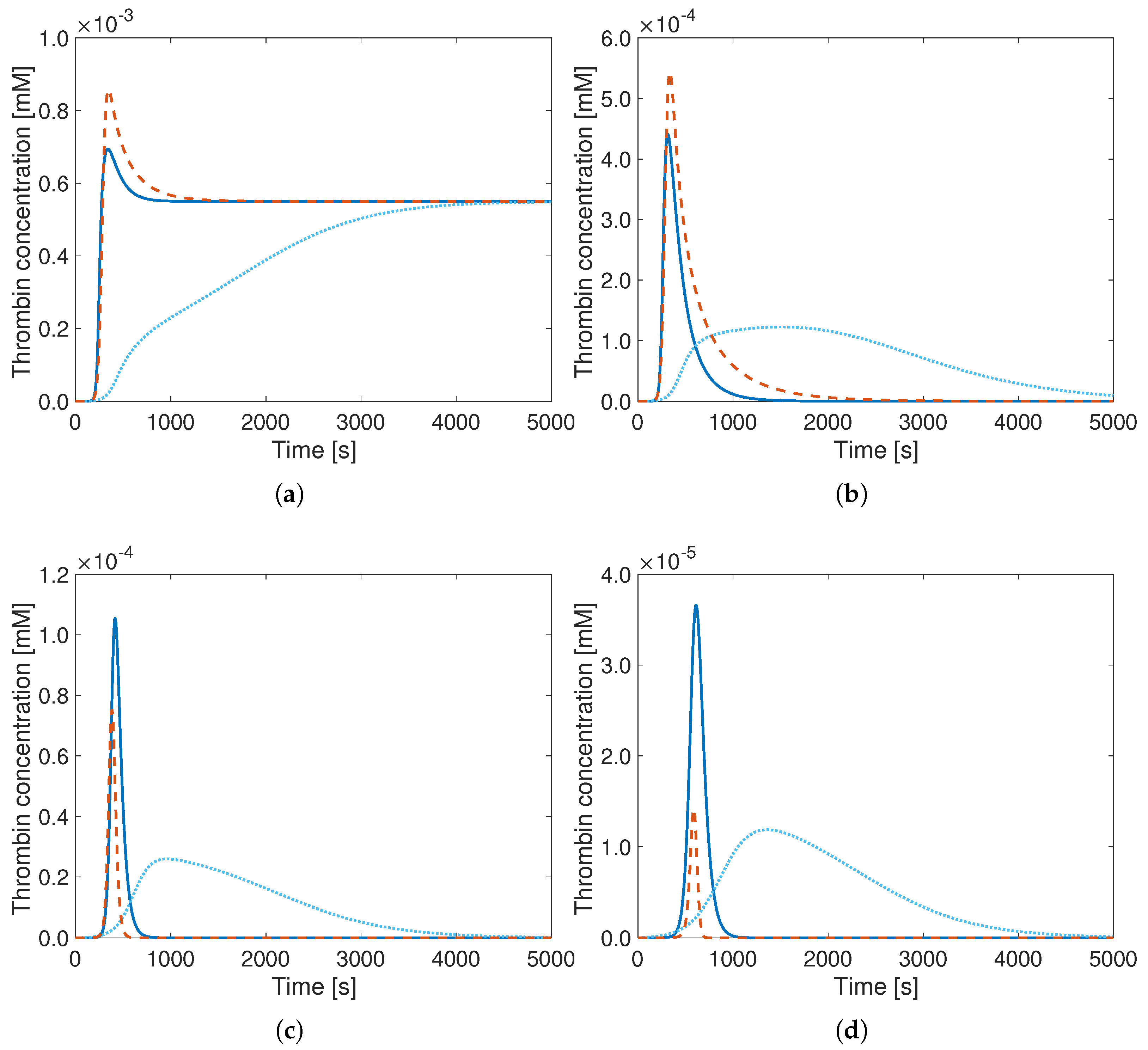
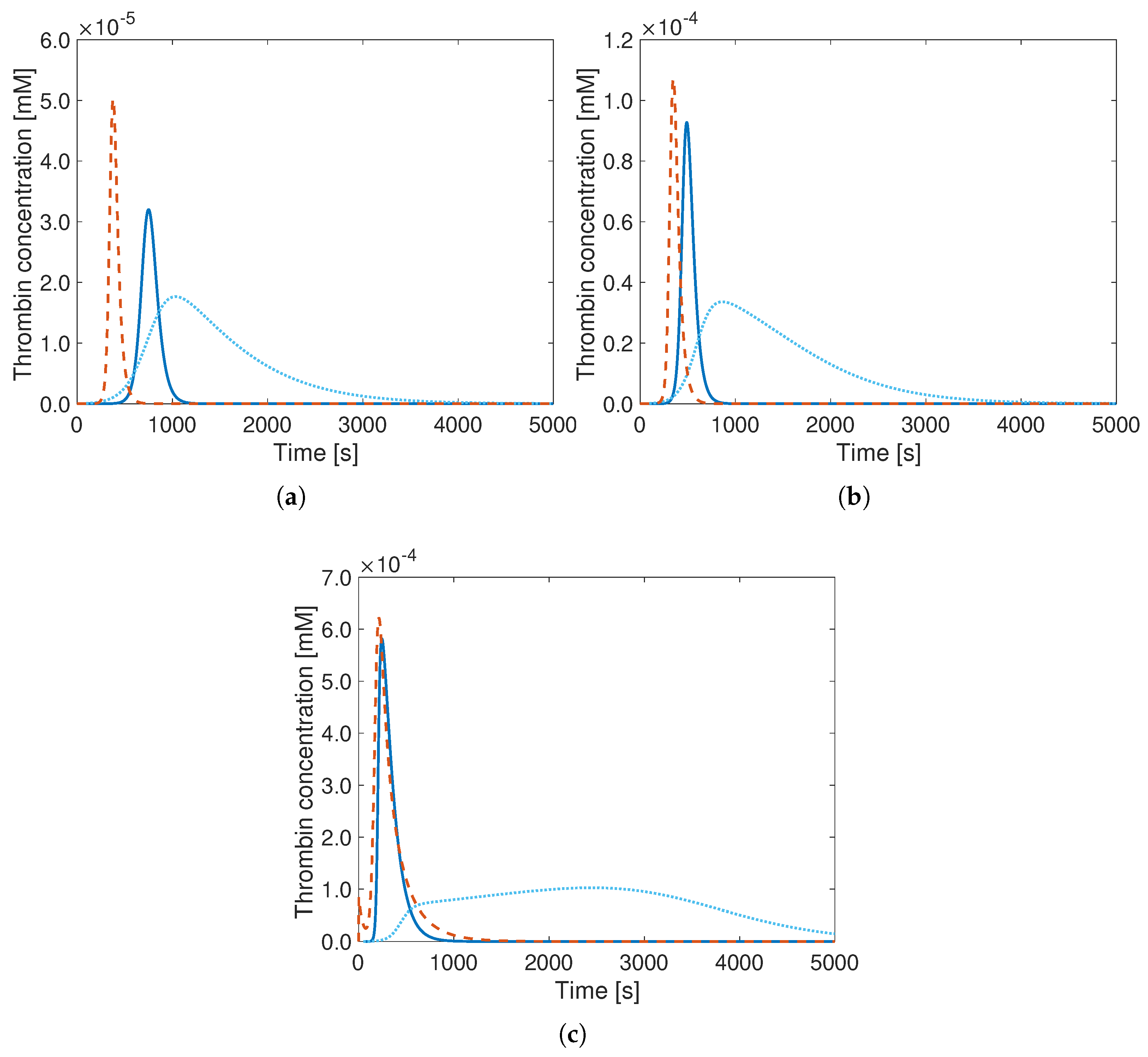
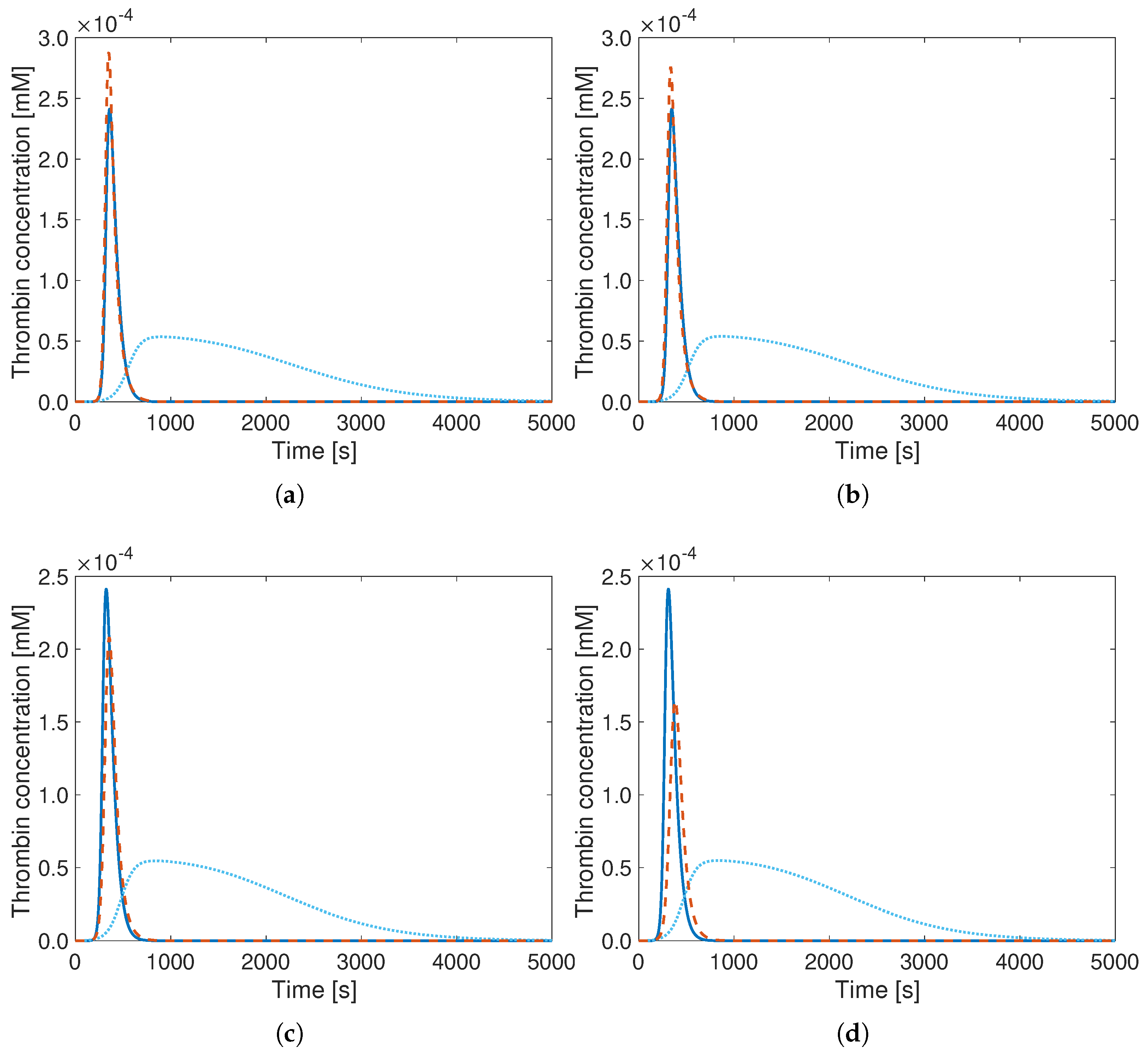
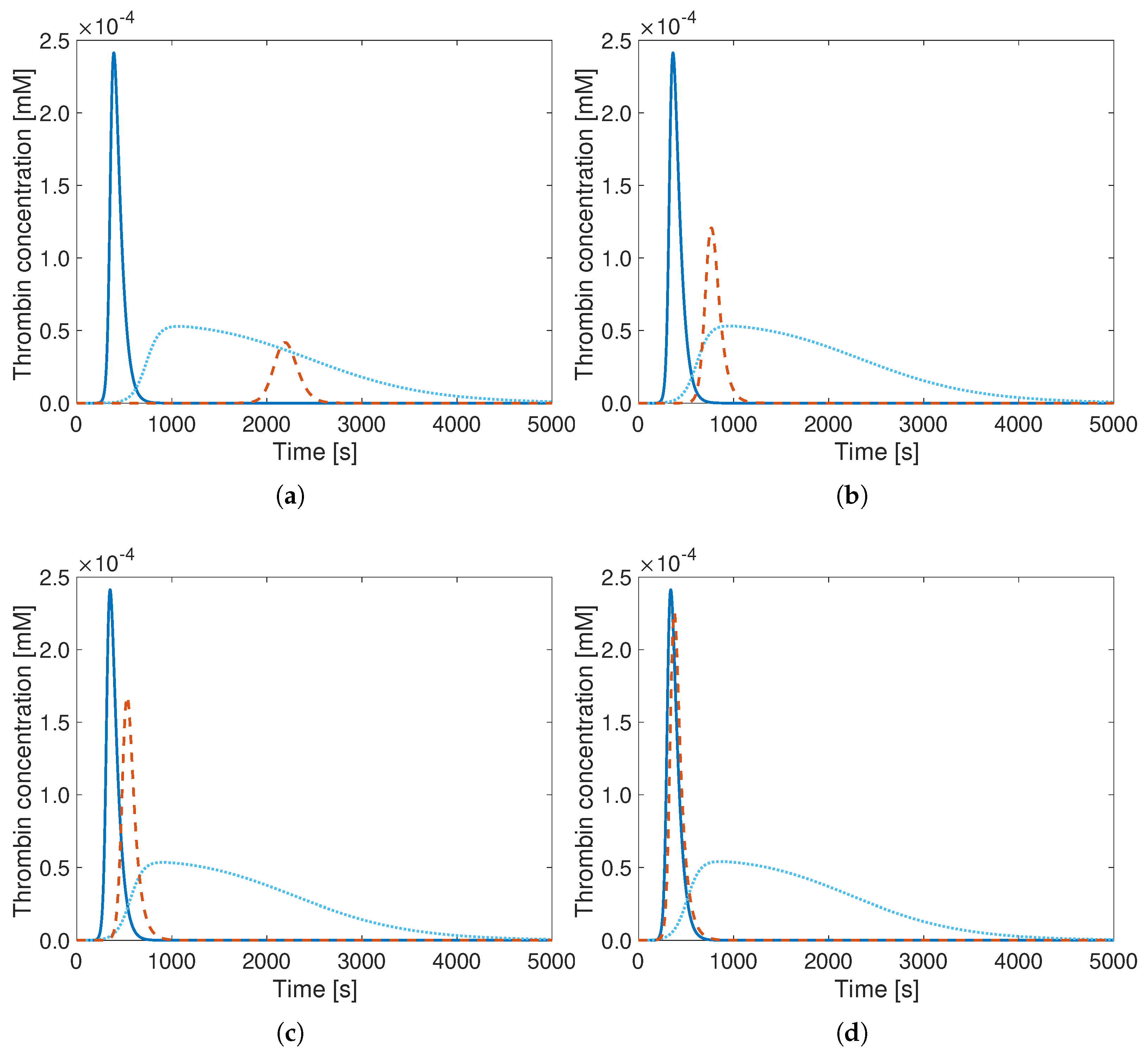
3. Results
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALBORZ | in-house hybrid code combining the lattice Boltzmann method with a finite-difference solver |
| CFD | computational fluid dynamics |
| INACT | inactive product |
| LBM | lattice Boltzmann method |
| PT | prothrombin |
| SSSD | sum of squared distances |
| TF | tissue factor |
| TG | thrombin generation |
| TH | thrombin |
References
- Mokdad, A.H.; Ballestros, K.; Echko, M.; Glenn, S.; Olsen, H.E.; Mullany, E.; Lee, A.; Khan, A.R.; Ahmadi, A.; Ferrari, A.J.; et al. The State of US Health, 1990–2016: Burden of Diseases, Injuries, and Risk Factors Among US States. JAMA 2018, 319, 1444–1472. [Google Scholar] [CrossRef]
- ISTH Steering Committee for World Thrombosis Day. Thrombosis: A major contributor to the global disease burden. J. Thromb. Haemost. 2014, 12, 1580–1590. [Google Scholar] [CrossRef] [PubMed]
- Barco, S.; Mahmoudpour, S.H.; Valerio, L.; Klok, F.A.; Münzel, T.; Middeldorp, S.; Ageno, W.; Cohen, A.T.; Hunt, B.J.; Konstantinides, S.V. Trends in mortality related to pulmonary embolism in the European Region, 2000–15: Analysis of vital registration data from the WHO Mortality Database. Lancet Respir. Med. 2020, 8, 277–287. [Google Scholar] [CrossRef] [PubMed]
- Beckmann, M.G.; Hooper, W.C.; Critchley, S.E.; Ortel, T.L. Venous Thromboembolism: A Public Health Concern. Am. J. Prev. Med. 2010, 38, 495–501. [Google Scholar] [CrossRef]
- Kulcsár, Z.; Houdart, E.; Bonafe, A.; Parker, G.; Millar, J.; Goddard, A.; Renowden, S.; Gál, G.; Turowski, B.; Mitchell, K.; et al. Intra-aneurysmal thrombosis as a possible cause of delayed aneurysm rupture after flow-diversion treatment. AJNR Am. J. Neuroradiol. 2010, 32, 20–25. [Google Scholar] [CrossRef] [PubMed]
- Hockin, M.F.; Jones, K.C.; Everse, S.J.; Mann, K.G. A model for the stoichiometric regulation of blood coagulation. J. Biol. Chem. 2002, 277, 18322–18333. [Google Scholar] [CrossRef]
- Chatterjee, M.S.; Denney, W.S.; Jing, H.; Diamond, S.L. Systems biology of coagulation initiation: Kinetics of thrombin generation in resting and activated human blood. PLoS Comput. Biol. 2010, 6, e1000950. [Google Scholar] [CrossRef]
- Ngoepe, M.N.; Ventikos, Y. Computational modelling of clot development in patient-specific cerebral aneurysm cases. J. Thromb. Haemost. 2016, 14, 262–272. [Google Scholar] [CrossRef]
- Wagenvoord, R.; Hemker, P.W.; Hemker, H.C. The limits of simulation of the clotting system. J. Thromb. Haemost. 2006, 4, 1331–1338. [Google Scholar] [CrossRef]
- Kuharsky, A.; Fogelson, A. Surface-mediated control of blood coagulation: The role of binding site densities and platelet deposition. Biophys. J. 2001, 80, 1050–1074. [Google Scholar] [CrossRef]
- Leiderman, K.; Fogelson, A. Grow with the flow: A spatial-temporal model of platelet deposition and blood coagulation under flow. Math. Med. Biol. 2010, 28, 47–84. [Google Scholar] [CrossRef] [PubMed]
- Flamm, M.H.; Colace, T.V.; Chatterjee, M.S.; Jing, H.; Zhou, S.; Jaeger, D.; Brass, L.F.; Sinno, T.; Diamond, S.L. Multiscale prediction of patient-specific platelet function under flow. Blood 2012, 120, 190–198. [Google Scholar] [CrossRef]
- Anand, M.; Rajagopal, K.; Rajagopal, K. A model incorporating some of the mechanical and biochemical factors underlying clot formation and dissolution in flowing blood. Comput. Math. Methods Med. 2003, 5, 183–218. [Google Scholar] [CrossRef]
- Biasetti, J.; Spazzini, P.; Swedenborg, J.; Gasser, T. An integrated fluid-chemical model towards modeling the formation of intra-luminal thrombus in abdominal aortic aneurysms. Front. Physiol. 2012, 3, 266. [Google Scholar] [CrossRef]
- Jones, K.; Mann, K. A model for the tissue factor pathway to thrombin. J. Biol. Chem. 1994, 269, 23367–23373. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Nayak, S.; Martin, S.W.; Heatherington, A.C.; Vicini, P.; Hua, F. A quantitative systems pharmacology model of blood coagulation network describes in vivo biomarker changes in non-bleeding subjects. J. Thromb. Haemost. 2016, 14, 2430–2445. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Yang, S.; Sun, X.; Ma, T.; Zheng, Y.; Liu, X. Nitric Oxide Distribution Correlates with Intraluminal Thrombus in Abdominal Aortic Aneurysm: A Computational Study. Bioengineering 2025, 12, 191. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Xi, Y.; Sun, A.; Deng, X.; Chen, Z.; Fan, Y. A New Mathematical Numerical Model to Evaluate the Risk of Thrombosis in Three Clinical Ventricular Assist Devices. Bioengineering 2022, 9, 235. [Google Scholar] [CrossRef]
- Komiya, K.; Imada, S.; Ujihara, Y.; Sugita, S.; Nakamura, M. Predictive Methods for Thrombus Formation in the Treatment of Aortic Dissection and Cerebral Aneurysms: A Comprehensive Review. Bioengineering 2024, 11, 871. [Google Scholar] [CrossRef]
- Turányi, T.; Tomlin, A.S. Analysis of Kinetic Reaction Mechanisms; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Kovács, M.; Papp, M.; Turányi, T.; Nagy, T. A novel active parameter selection strategy for the efficient optimization of combustion mechanisms. Proc. Combust. Inst. 2023, 39, 5259–5267. [Google Scholar] [CrossRef]
- Kovács, M.; Papp, M.; Szanthoffer, A.; Zsély, I.; Nagy, T.; Turányi, T. Optimization of a methanol/NOx combustion mechanism based on a large amount of experimental data. Fuel 2024, 375, 132544. [Google Scholar] [CrossRef]
- Elliott, L.; Ingham, D.; Kyne, A.; Mera, N.; Pourkashanian, M.; Wilson, C. Genetic algorithms for optimisation of chemical kinetics reaction mechanisms. Prog. Energy Combust. Sci. 2004, 30, 297–328. [Google Scholar] [CrossRef]
- Harris, S.; Elliott, L.; Ingham, D.; Pourkashanian, M.; Wilson, C. The optimisation of reaction rate parameters for chemical kinetic modelling of combustion using genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 190, 1065–1090. [Google Scholar] [CrossRef]
- Elliott, L.; Ingham, D.; Kyne, A.; Mera, N.; Pourkashanian, M.; Wilson, C. A real coded genetic algorithm for the optimization of reaction rate parameters or chemical kinetic modelling in a perfectly stirred reactor. In Proceedings of the 4th Annual Conference on Genetic and Evolutionary Computation, New York, NY, USA, 9–13 July 2002; pp. 138–144. Available online: https://dl.acm.org/doi/10.5555/2955491.2955709 (accessed on 8 October 2025).
- Methling, T.; Braun-Unkhoff, M.; Riedel, U. A novel linear transformation model for the analysis and optimisation of chemical kinetics. Combust. Theory Model. 2017, 21, 503–528. [Google Scholar] [CrossRef]
- Methling, T.; Braun-Unkhoff, M.; Riedel, U. An optimised chemical kinetic model for the combustion of fuel mixtures of syngas and natural gas. Fuel 2020, 262, 116611. [Google Scholar] [CrossRef]
- Tyurin, K.; Khanin, M. Optimality principle and determination of kinetic constants for biochemical reactions. Math. Med. Biol. 2005, 22, 1–14. [Google Scholar] [CrossRef]
- Wang, Y.; Luan, J.; Luo, K.; Fan, J.; Zhu, T. Model reduction of coagulation cascade based on genetic algorithm. Int. J. Numer. Methods Biomed. Eng. 2022, 38, e3652. [Google Scholar] [CrossRef] [PubMed]
- Chelle, P.; Morin, C.; Montmartin, A.; Piot, M.; Cournil, M.; Tardy-Poncet, B. Evaluation and calibration of in silico models of thrombin generation using experimental data from healty and haemophilic subjects. Bull. Math. Biol. 2018, 80, 1989–2025. [Google Scholar] [CrossRef]
- Perini, F.; Brakora, J.; Reitz, R.; Cantore, G. Development of reduced and optimized reaction mechanisms based on genetic algorithms and element flux analysis. Combust. Flame 2012, 159, 103–119. [Google Scholar] [CrossRef]
- Franken, T.; Netzer, C.; Mauss, F.; Pasternak, M.; Seidel, L.; Borg, A.; Lehtiniemi, H.; Matrisciano, A.; Kulzer, A.C. Multi-objective optimization of water injection in spark-ignition engines using the stochastic reactor model with tabulated chemistry. Int. J. Engine Res. 2019, 20, 1089–1100. [Google Scholar] [CrossRef]
- Hansen, K.; Shadden, S. Automated reduction of blood coagulation models. Int. J. Numer. Meth. Biomed. Eng. 2019, 35, e3220. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.A.; Huang, F.; Thévenin, D. Lattice Boltzmann model for simulation of flow in intracranial aneurysms considering non-Newtonian effects. Phys. Fluids 2022, 34, 073105. [Google Scholar] [CrossRef]
- Mann, K.; Everse, S.J.; Hockin, M.F.; Jones, K.C. Blood Clotting Predictor. U.S. Patent 20,060,015,261, 19 January 2006. [Google Scholar]
- Butenas, S.; van’t Veer, C.; Mann, G.K. “Normal” thrombin generation. Blood 1999, 94, 2169–2178. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.A.; Abdelsamie, A.; Darabiha, N.; Thévenin, D. Low-Mach hybrid lattice Boltzmann Finite Differences solver for combustion in complex flows. Phys. Fluids 2020, 32, 077105. [Google Scholar] [CrossRef]
- Eshghinejadfard, A.; Daróczy, L.; Janiga, G.; Thévenin, D. Calculation of the permeability in porous media using the lattice Boltzmann method. Int. J. Heat Fluid Flow 2016, 62, 93–103. [Google Scholar] [CrossRef]
- Janiga, G.; Daróczy, L.; Berg, P.; Thévenin, D.; Skalej, M.; Beuing, O. An automatic CFD-based flow diverter optimization principle for patient-specific intracranial aneurysms. J. Biomech. 2015, 48, 3846–3852. [Google Scholar] [CrossRef]
- Berg, P.; Iosif, C.; Ponsonnard, S.; Yardin, C.; Janiga, G.; Mounayer, C. Endothelialization of over- and undersized flow-diverter stents at covered vessel side branches: An in vivo and in silico study. J. Biomech. 2016, 49, 4–12. [Google Scholar] [CrossRef]
- Thévenin, D.; Janiga, G. Optimization and Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-objective optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Mann, K.; Brummel-Ziedins, K.; Undas, A.; Butenas, S. Does the genotype predict the phenotype? Evaluations of the hemostatic proteome. J. Thromb. Haemost. 2004, 2, 1727–1734. [Google Scholar] [CrossRef]
- van’t Veer, C.; Mann, K.G. Regulation of Tissue Factor Initiated Thrombin Generation by the Stoichiometric Inhibitors Tissue Factor Pathway Inhibitor, Antithrombin-III, and Heparin Cofactor-II. J. Biol. Chem. 1997, 272, 4367–4377. [Google Scholar] [CrossRef] [PubMed]
| Step | Reaction Pathway | Forward Reaction Rate [mM−1s−1] | Backward Reaction Rate [s−1] |
|---|---|---|---|
| 1 | TF + VII TF–VII | 3.20 | |
| 2 | TF + VIIa TF–VIIa | ||
| 3 | TF–VIIa + VII TF–VIIa + VIIa | – | |
| 4 | Xa + VII Xa + VIIa | – | |
| 5 | TH + VII TH + VIIa | 23 | – |
| 6 | TF–VIIa + X TF–VIIa–X | 1.05 | |
| 7 | TF–VIIa–X TF–VIIa–Xa | 6 [mM] | – |
| 8 | TF–VIIa + Xa TF–VIIa–Xa | 19 | |
| 9 | TF–VIIa + IX TF–VIIa–IX | 2.4 | |
| 10 | TF–VIIa–IX TF–VIIa + IXa | 1.8 | – |
| 11 | Xa + PT Xa + TH | 7.5 | – |
| 12 | TH + VIII TH + VIIIa | – | |
| 13 | VIIIa + IXa IXa–VIIIa | ||
| 14 | IXa–VIIIa + X IXa–VIIIa–X | ||
| 15 | IXa–VIIIa–X IXa–VIIIa + Xa | 8.20 | – |
| 16 | VIIIa VIIIa1L + VIIIa2 | [s−1] | 22 [mM−1] |
| 17 | IXa–VIIIa–X VIIIa1L + VIIIa2 + X + IXa | [s−1] | – |
| 18 | IXa–VIIIa VIIIa1L + VIIIa + IXa | [mM] | – |
| 19 | TH + V TH + Va | – | |
| 20 | Xa + Va Xa–Va | 0.2 | |
| 21 | Xa–Va + PT Xa–Va–PT | 103 | |
| 22 | Xa–Va–PT Xa–Va + mTH | 63.5 [mM] | – |
| 23 | mTH + Xa–Va TH + Xa–Va | – | |
| 24 | Xa + TFPI Xa–TFPI | ||
| 25 | TF–VIIa–Xa + TFPI TF–VIIa–Xa–TFPI | ||
| 26 | TF–VIIa + Xa–TFPI TF–VIIa–Xa–TFPI | – | |
| 27 | Xa + AT INACT | 1.5 | – |
| 28 | mTH + AT INACT | 7.1 | – |
| 29 | IXa + AT INACT | 0.49 | – |
| 30 | TH + AT INACT | 7.1 | – |
| 31 | TF–VIIa + AT INACT | 0.23 | – |
| Species | Initial Concentration [mM] | Diffusion Coefficients [m2s−1] |
|---|---|---|
| TF | ||
| TH | 0 | |
| PT | ||
| FVII | ||
| FVIIa | ||
| TF-FVII | 0 | |
| TF-FVIIa | 0 | |
| TF-FVIIa-FXa | 0 | |
| TF-FVIIa-FXa-TFPI | 0 | |
| TF-FVIIa-FX | 0 | |
| FX | ||
| FXa | 0 | |
| TFPI | ||
| FXa-TFPI | 0 | |
| FIX | ||
| FIXa | 0 | |
| FVIII | ||
| FVIIIa | 0 | |
| FVIIIa1L | 0 | |
| FVIIIa2 | 0 | |
| TF-FVIIa-FIX | 0 | |
| FIXa-FVIIIa | 0 | |
| FIXa-FVIIIa-FX | 0 | |
| FV | ||
| FVa | 0 | |
| FXa-FVa | 0 | |
| mTH | 0 | |
| AT | ||
| INACT | 0 | |
| FXa-FVa-PT | 0 |
| Reaction Pathway | Forward Reaction Rate [] | kcat [s−1] | KM [mM] |
|---|---|---|---|
| X + TF → Xa-Va + TF | |||
| PT + Xa-Va → TH + Xa-Va | |||
| V + TH → TH + Xa-Va | |||
| TH + AT → INACT |
| Reaction Pathway | Lower Limit | Upper Limit |
|---|---|---|
| kcat,1 | ||
| kM,1 | ||
| kcat,2 | ||
| kM,2 | ||
| kcat,3 | ||
| kM,3 | ||
| kf,4 |
| Reaction Rate Constant | Default Value | Improved Value |
|---|---|---|
| kcat,1 | ||
| kM,1 | ||
| kcat,2 | ||
| kM,2 | ||
| kcat,3 | ||
| kM,3 | ||
| kf,4 | ||
| SSSD (error) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Link, C.; Janiga, G.; Thévenin, D. Optimization of the Parameters of a Minimal Coagulation Model. Bioengineering 2025, 12, 1111. https://doi.org/10.3390/bioengineering12101111
Link C, Janiga G, Thévenin D. Optimization of the Parameters of a Minimal Coagulation Model. Bioengineering. 2025; 12(10):1111. https://doi.org/10.3390/bioengineering12101111
Chicago/Turabian StyleLink, Carolin, Gábor Janiga, and Dominique Thévenin. 2025. "Optimization of the Parameters of a Minimal Coagulation Model" Bioengineering 12, no. 10: 1111. https://doi.org/10.3390/bioengineering12101111
APA StyleLink, C., Janiga, G., & Thévenin, D. (2025). Optimization of the Parameters of a Minimal Coagulation Model. Bioengineering, 12(10), 1111. https://doi.org/10.3390/bioengineering12101111







