Adequate Segmentation in Marker-Based Motion Capture Studies for Hyperflexion and Hyperextension Lumbar Exercises
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethical Clearance
2.2. Participants
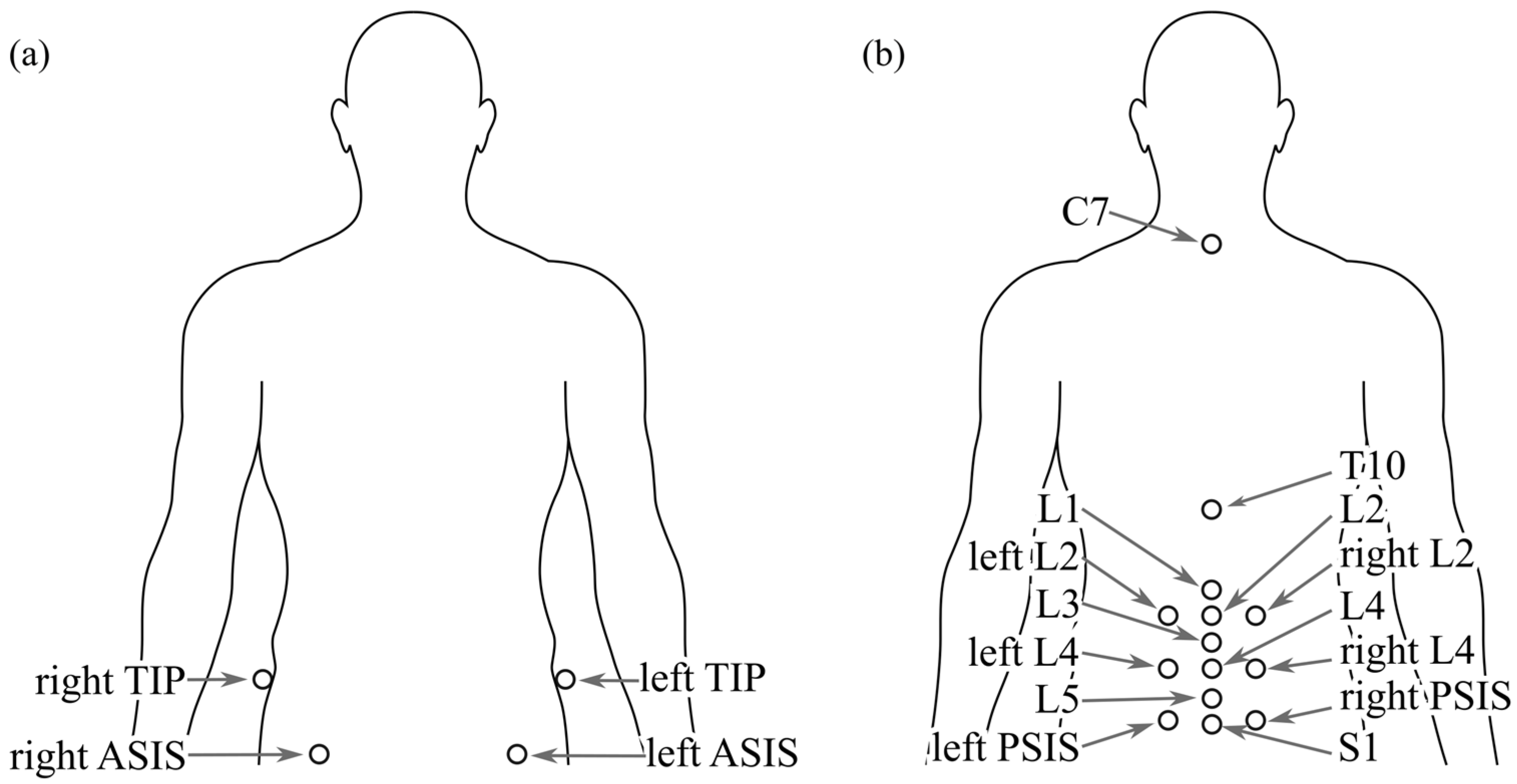
2.3. Data Capture
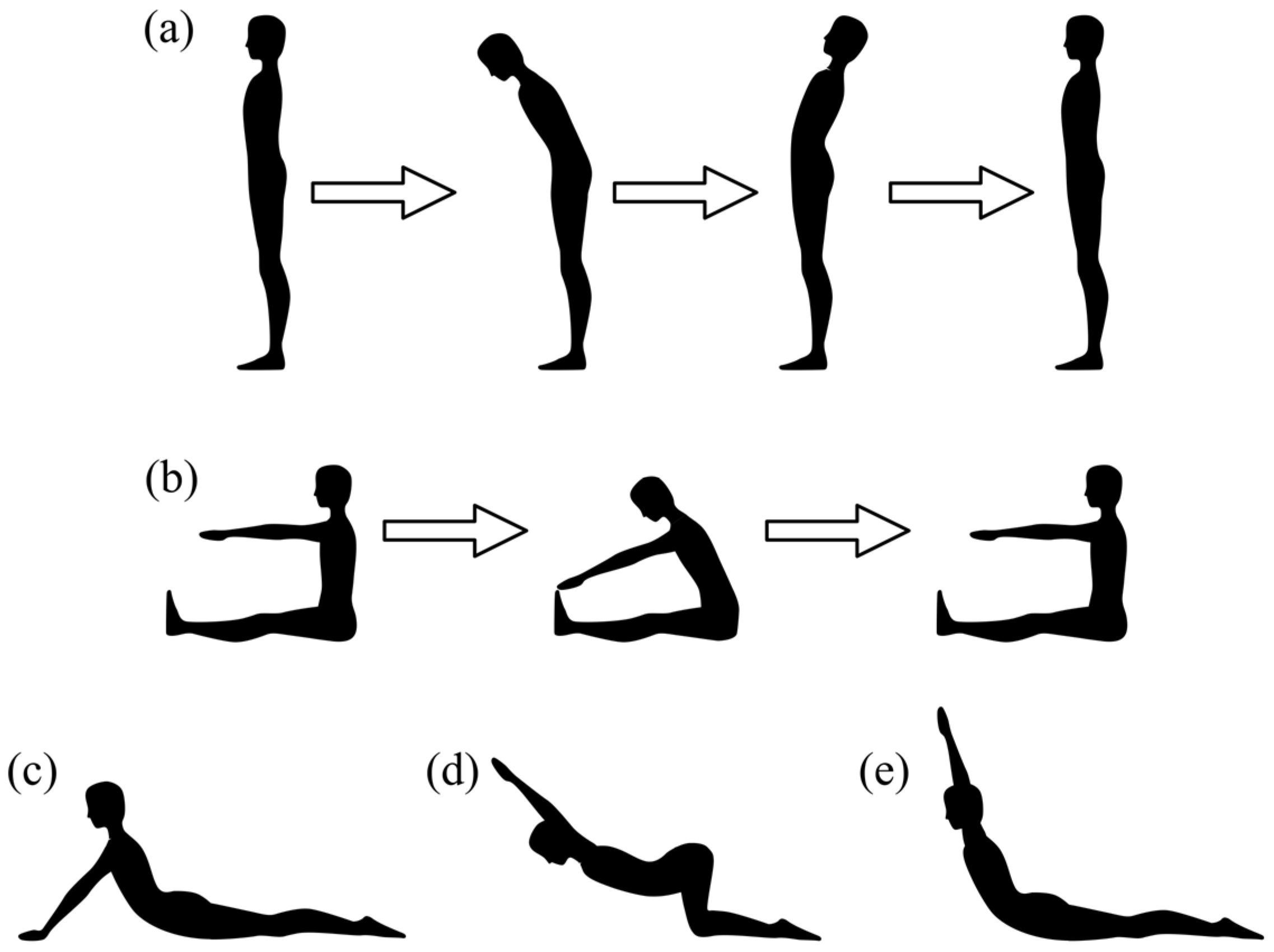
2.4. Exercises
2.5. Data Processing
2.6. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASIS | Anterior superior iliac spine |
| C7 | Seventh cervical vertebra |
| COB | Cobra posture |
| CUP | Cobra posture with arms up |
| F | Sitting flexion |
| FE | Flexion and extension |
| FSU | Functional spinal unit |
| L1 | First lumbar vertebra |
| L2 | Second lumbar vertebra |
| L3 | Third lumbar vertebra |
| L4 | Fourth lumbar vertebra |
| L5 | Fifth lumbar vertebra |
| PSIS | Posterior superior iliac spine |
| ROM | Range of motion |
| S1 | First sacral vertebra |
| SHO | Shoulder flexion stretching |
| STA | Static position |
| T1 | First thoracic vertebra |
| T10 | Tenth thoracic vertebra |
References
- Ball, J.R.; Harris, C.B.; Lee, J.; Vives, M.J. Lumbar Spine Injuries in Sports: Review of the Literature and Current Treatment Recommendations. Sports Med.-Open 2019, 5, 26. [Google Scholar] [CrossRef]
- Deng, C.; Yu, Q. A systematic review of cheerleading injuries: Epidemiological characteristics, biomechanical mechanisms, and prevention strategies. Front. Public Health 2025, 13, 1614164. [Google Scholar] [CrossRef]
- Thomas, R.E.; Thomas, B.C. A systematic review of injuries in gymnastics. Physician Sportsmed. 2019, 47, 96–121. [Google Scholar] [CrossRef]
- Gram, M.C.D.; Clarsen, B.; Bø, K. Injuries and illnesses among competitive Norwegian rhythmic gymnasts during preseason: A prospective cohort study of prevalence, incidence and risk factors. Br. J. Sports Med. 2021, 55, 231–236. [Google Scholar] [CrossRef]
- Swain, C.T.; Bradshaw, E.J.; Ekegren, C.L.; Orishimo, K.F.; Kremenic, I.J.; Liederbach, M.; Hagins, M. Multi-segment spine range of motion in dancers with and without recent low back pain. Gait Posture 2019, 70, 53–58. [Google Scholar] [CrossRef] [PubMed]
- Uršej, E.; Zaletel, P. Injury Occurrence in Modern and Hip-Hop Dancers: A Systematic Literature Review. Slov. J. Public Health 2020, 59, 195. [Google Scholar] [CrossRef]
- Xu, A.L.; Suresh, K.V.; Lee, R.J. Progress in Cheerleading Safety: Update on the Epidemiology of Cheerleading Injuries Presenting to US Emergency Departments, 2010–2019. Orthop. J. Sports Med. 2021, 9, 23259671211038895. [Google Scholar] [CrossRef] [PubMed]
- Sobrino, F.J.; Guillén, P. Overuse Injuries in Professional Ballet: Influence of Age and Years of Professional Practice. Orthop. J. Sports Med. 2017, 5, 2325967117712704. [Google Scholar] [CrossRef]
- Hooker, Q.L.; Lanier, V.M.; van Dillen, L.R. Consistent differences in lumbar spine alignment between low back pain subgroups and genders during clinical and functional activity sitting tests. Musculoskelet. Sci. Pract. 2021, 52, 102336. [Google Scholar] [CrossRef] [PubMed]
- Roch, P.J.; Wagner, M.; Weiland, J.; Gezzi, R.; Spiering, S.; Lehmann, W.; Saul, D.; Weiser, L.; Viezens, L.; Wachowski, M.M. Total disc arthroplasties change the kinematics of functional spinal units during lateral bending. Clin. Biomech. 2020, 73, 130–139. [Google Scholar] [CrossRef]
- Errabity, A.; Calmels, P.; Han, W.S.; Bonnaire, R.; Pannetier, R.; Convert, R.; Molimard, J. The effect of low back pain on spine kinematics: A systematic review and meta-analysis. Clin. Biomech. 2023, 108, 106070. [Google Scholar] [CrossRef]
- Eyssartier, C.; Billard, P.; Robert, M.; Thoreux, P.; Sauret, C. Which typical floor movements of men’s artistic gymnastics result in the most extreme lumbar lordosis and ground reaction forces? Sports Biomech. 2022, 24, 638–653. [Google Scholar] [CrossRef] [PubMed]
- McKinnon, C.D.; Callaghan, J.P. The relationship between external thoracopelvic angle and lumbar segmental axial twist angle using an ultrasound imaging technique. Hum. Mov. Sci. 2021, 78, 102824. [Google Scholar] [CrossRef] [PubMed]
- Romero-Flores, C.F.; Bustamante-Bello, R.; Bencomo, M.M.; Martinez-Ríos, E.A.; Montesinos, L. Optical Marker-Based Motion Capture of the Human Spine: A Scoping Review of Study Design and Outcomes. Ann. Biomed. Eng. 2024, 52, 2373–2387. [Google Scholar] [CrossRef] [PubMed]
- McKinnon, C.D.; Callaghan, J.P. Validation of an Ultrasound Protocol to Measure Intervertebral Axial Twist during Functional Twisting Movements in Isolated Functional Spinal Units. Ultrasound Med. Biol. 2019, 45, 642–649. [Google Scholar] [CrossRef]
- Zhang, C.; Mannen, E.M.; Sis, H.L.; Cadel, E.S.; Wong, B.M.; Wang, W.; Cheng, B.; Friis, E.A.; Anderson, D.E. Moment-rotation behavior of intervertebral joints in flexion-extension, lateral bending, and axial rotation at all levels of the human spine: A structured review and meta-regression analysis. J. Biomech. 2020, 100, 109579. [Google Scholar] [CrossRef]
- Chastain, K.; Gepner, B.; Moreau, D.; Koerber, B.; Forman, J.; Hallman, J.; Kerrigan, J. Effect of axial compression on stiffness and deformation of human lumbar spine in flexionextension. Traffic Inj. Prev. 2023, 24 (Suppl. S1), S55–S61. [Google Scholar] [CrossRef]
- Valentin, S.; Licka, T.F. Spinal Motion and Muscle Activity during Active Trunk Movements—Comparing Sheep and Humans Adopting Upright and Quadrupedal Postures. PLoS ONE 2016, 11, e0146362. [Google Scholar] [CrossRef]
- Mahdavi, A.; Rasti, S. Dynamic Flexion-Extension Magnetic Resonance Imaging of the Cervical Spine: An Evolutionary Tool for Diagnosis and Management of Cervical Spondylotic Myelopathy. World Neurosurg. 2024, 184, 138–147. [Google Scholar] [CrossRef]
- Barnamehei, H.; Zhou, Y.; Zhang, X.; Vasavada, A.N. Inverse kinematics in cervical spine models: Effects of scaling and model degrees of freedom for extension and flexion movements. J. Biomech. 2024, 175, 112302. [Google Scholar] [CrossRef]
- Beaudette, S.M.; Zwambag, D.P.; Graham, R.B.; Brown, S.H.M. Discriminating spatiotemporal movement strategies during spine flexion-extension in healthy individuals. Spine J. 2019, 19, 1264–1275. [Google Scholar] [CrossRef]
- Sonvico, L.; Spencer, S.M.; Fawcett, L.; Bucke, J.; Heneghan, N.R.; Rushton, A. Investigation of optimal lumbar spine Posture during a simulated landing task in elite gymnasts. Int. J. Sports Phys. Ther. 2019, 14, 65–73. [Google Scholar] [CrossRef]
- Azari, F.; Arjmand, N.; Shirazi-Adl, A.; Rahimi-Moghaddam, T. A combined passive and active musculoskeletal model study to estimate L4-L5 load sharing. J. Biomech. 2018, 70, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Fayad, J.; Eltes, P.E.; Lazary, A.; Cristofolini, L.; Stagni, R. Stereophotogrammetric approaches to multi-segmental kinematics of the thoracolumbar spine: A systematic review. BMC Musculoskelet. Disord. 2022, 23, 1080. [Google Scholar] [CrossRef] [PubMed]
- Kudo, S.; Fujimoto, M.; Sato, T.; Nagano, A. Determination of the optimal number of linked rigid-bodies of the trunk during walking and running based on Akaike’s information criterion. Gait Posture 2020, 77, 264–268. [Google Scholar] [CrossRef]
- Zemp, R.; List, R.; Gülay, T.; Elsig, J.P.; Naxera, J.; Taylor, W.R.; Lorenzetti, S. Soft tissue artefacts of the human back: Comparison of the sagittal curvature of the spine measured using skin markers and an open upright MRI. PLoS ONE 2014, 9, e95426. [Google Scholar] [CrossRef]
- Yamamoto, I.; Panjabi, M.M.; Oxland, T. Three-dimensional movements of the whole lumbar spine and lumbosacral joint. Spine 1989, 14, 1256–1260. [Google Scholar] [CrossRef] [PubMed]
- Tomezzoli, A.; Agouram, A.; Chalamet, B.; Pialat, J.B.; Duprey, S.; Cunin, V.; Fréchède, B. Predicting cervico-thoraco-lumbar vertebra positions from cutaneous markers: Combining local frame and postural predictors improves robustness to posture. J. Biomech. 2024, 164, 111961. [Google Scholar] [CrossRef] [PubMed]
- Leardini, A.; Biagi, F.; Merlo, A.; Belvedere, C.; Benedetti, M.G. Multi-segment trunk kinematics during locomotion and elementary exercises. Clin. Biomech. 2011, 26, 562–571. [Google Scholar] [CrossRef]
- Hagins, M.; Swain, C.T.V.; Orishimo, K.F.; Kremenic, I.J.; Liederbach, M. Motion of the multi-segmented spine in elite dancers during passé and arabesque. Gait Posture 2021, 88, 198–202. [Google Scholar] [CrossRef]
- Ignasiak, D.; Rüeger, A.; Ferguson, S.J. Multi-segmental thoracic spine kinematics measured dynamically in the young and elderly during flexion. Hum. Mov. Sci. 2017, 54, 230–239. [Google Scholar] [CrossRef] [PubMed]
- Mörl, F.; Blickhan, R. Three-dimensional relation of skin markers to lumbar vertebrae of healthy subjects in different postures measured by open MRI. Eur. Spine J. 2006, 15, 742–751. [Google Scholar] [CrossRef] [PubMed]
- Xi, X.; Ling, Z.; Wang, C.; Gu, C.; Zhan, X.; Yu, H.; Lu, S.; Tsai, T.-Y.; Yu, Y.; Cheng, L. Lumbar segment-dependent soft tissue artifacts of skin markers during in vivo weight-bearing forward–Backward bending. Front. Bioeng. Biotechnol. 2022, 10, 960063. [Google Scholar] [CrossRef] [PubMed]
- Zander, T.; Pan, F.; Schmidt, H. Which is the best-suited landmark to assess the thoracic orientation? J. Biomech. 2020, 102, 109545. [Google Scholar] [CrossRef]


| Gender (n) | Age (years) | Height (cm) | Weight (kg) | BMI |
|---|---|---|---|---|
| males (6) | 19.67 ± 1.11 | 178.47 ± 8.08 | 75.02 ± 13.81 | 23.45 ± 3.28 |
| females (11) | 20.18 ± 1.8 | 160.27 ± 6.58 | 53.92 ± 18.84 | 20.93 ± 7.32 |
| Model Comparison | |||||||
|---|---|---|---|---|---|---|---|
| 1 vs. 2 | 1 vs. 3 | 1 vs. 4 | 2 vs. 3 | 2 vs. 4 | 3 vs. 4 | Relative Lumbar Lordosis (deg) | |
| STA | |||||||
| 0.76 ± 0.65 | 0.74 ± 0.31 | 0.76 ± 0.30 | 0.69 ± 0.42 | 0.66 ± 0.48 | 1.00 ± 0.01 | ||
| FE in flexion | |||||||
| 0% | 1.00 ± 0.00 | 0.78 ± 0.25 | 0.75 ± 0.33 | 0.78 ± 0.25 | 0.75 ± 0.33 | 0.99 ± 0.09 | −13.74 ± 11.75 |
| 25% | 0.94 ± 0.34 | 0.78 ± 0.26 | 0.77 ± 0.28 | 0.76 ± 0.31 | 0.75 ± 0.34 | 1.00 ± 0.01 | −3.34 ± 8.61 |
| 50% | 1.00 ± 0.00 | 0.82 ± 0.22 | 0.81 ± 0.25 | 0.82 ± 0.22 | 0.81 ± 0.25 | 1.00 ± 0.01 | 3.29 ± 8.91 |
| 75% | 0.94 ± 0.34 | 0.93 ± 0.11 | 0.92 ± 0.12 | 0.87 ± 0.33 | 0.87 ± 0.32 | 1.00 ± 0.01 | 20.84 ± 19.05 |
| 100% | 0.91 ± 0.41 | 0.96 ± 0.12 | 0.96 ± 0.11 | 0.89 ± 0.38 | 0.89 ± 0.39 | 1.00 ± 0.00 | 31.98 ± 26.82 |
| FE in extension | |||||||
| 0% | 0.94 ± 0.34 | 0.97 ± 0.10 | 0.97 ± 0.10 | 0.91 ± 0.35 | 0.91 ± 0.35 | 1.00 ± 0.00 | 32.31 ± 27.18 |
| 25% | 0.91 ± 0.41 | 0.87 ± 0.19 | 0.88 ± 0.17 | 0.83 ± 0.32 | 0.83 ± 0.33 | 1.00 ± 0.00 | 15.40 ± 14.73 |
| 50% | 1.00 ± 0.00 | 0.87 ± 0.14 | 0.87 ± 0.15 | 0.87 ± 0.14 | 0.87 ± 0.15 | 1.00 ± 0.00 | 1.47 ± 11.37 |
| 75% | 1.00 ± 0.00 | 0.80 ± 0.22 | 0.79 ± 0.23 | 0.80 ± 0.22 | 0.79 ± 0.23 | 1.00 ± 0.01 | −7.32 ± 10.66 |
| 100% | 1.00 ± 0.00 | 0.78 ± 0.25 | 0.75 ± 0.33 | 0.78 ± 0.25 | 0.75 ± 0.33 | 0.99 ± 0.09 | −13.65 ± 11.80 |
| F in flexion | |||||||
| 0% | 0.88 ± 0.47 | 0.97 ± 0.12 | 0.97 ± 0.16 | 0.90 ± 0.39 | 0.91 ± 0.38 | 1.00 ± 0.01 | 34.94 ± 23.10 |
| 25% | 1.00 ± 0.00 | 0.99 ± 0.02 | 0.99 ± 0.01 | 0.99 ± 0.02 | 0.99 ± 0.01 | 1.00 ± 0.00 | 41.40 ± 18.48 |
| 50% | 0.94 ± 0.34 | 0.97 ± 0.10 | 0.97 ± 0.12 | 0.94 ± 0.25 | 0.94 ± 0.24 | 1.00 ± 0.00 | 50.30 ± 16.77 |
| 75% | 0.88 ± 0.47 | 0.96 ± 0.12 | 0.95 ± 0.15 | 0.89 ± 0.38 | 0.89 ± 0.36 | 1.00 ± 0.00 | 56.42 ± 15.69 |
| 100% | 0.76 ± 0.65 | 0.96 ± 0.09 | 0.95 ± 0.11 | 0.78 ± 0.57 | 0.79 ± 0.55 | 1.00 ± 0.00 | 57.30 ± 16.51 |
| F in extension | |||||||
| 0% | 0.79 ± 0.61 | 0.96 ± 0.08 | 0.96 ± 0.10 | 0.81 ± 0.53 | 0.81 ± 0.51 | 1.00 ± 0.00 | 57.16 ± 16.63 |
| 25% | 0.82 ± 0.57 | 0.96 ± 0.10 | 0.95 ± 0.12 | 0.84 ± 0.48 | 0.84 ± 0.46 | 1.00 ± 0.00 | 55.88 ± 16.04 |
| 50% | 0.97 ± 0.24 | 0.93 ± 0.19 | 0.94 ± 0.17 | 0.92 ± 0.22 | 0.94 ± 0.18 | 1.00 ± 0.02 | 47.50 ± 17.06 |
| 75% | 0.88 ± 0.47 | 0.97 ± 0.11 | 0.97 ± 0.14 | 0.89 ± 0.41 | 0.90 ± 0.40 | 1.00 ± 0.01 | 39.29 ± 15.67 |
| 100% | 0.88 ± 0.47 | 0.97 ± 0.12 | 0.97 ± 0.16 | 0.90 ± 0.39 | 0.91 ± 0.38 | 1.00 ± 0.01 | 34.95 ± 23.10 |
| COB | |||||||
| 1.00 ± 0.00 | 0.90 ± 0.15 | 0.90 ± 0.16 | 0.90 ± 0.15 | 0.90 ± 0.16 | 1.00 ± 0.00 | −17.91 ± 17.87 | |
| SHO | |||||||
| 0.91 ± 0.41 | 0.83 ± 0.25 | 0.83 ± 0.23 | 0.79 ± 0.34 | 0.79 ± 0.34 | 1.00 ± 0.01 | −14.98 ± 20.68 | |
| CUP | |||||||
| 0.94 ± 0.34 | 0.95 ± 0.06 | 0.94 ± 0.06 | 0.89 ± 0.33 | 0.90 ± 0.31 | 1.00 ± 0.01 | −18.30 ± 28.91 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero-Flores, C.F.; Bustamante-Bello, R.; Moya Bencomo, M.; Zenteno Aguirrezabal, I. Adequate Segmentation in Marker-Based Motion Capture Studies for Hyperflexion and Hyperextension Lumbar Exercises. Bioengineering 2025, 12, 1087. https://doi.org/10.3390/bioengineering12101087
Romero-Flores CF, Bustamante-Bello R, Moya Bencomo M, Zenteno Aguirrezabal I. Adequate Segmentation in Marker-Based Motion Capture Studies for Hyperflexion and Hyperextension Lumbar Exercises. Bioengineering. 2025; 12(10):1087. https://doi.org/10.3390/bioengineering12101087
Chicago/Turabian StyleRomero-Flores, Claudia F., Rogelio Bustamante-Bello, Marcos Moya Bencomo, and Iñaki Zenteno Aguirrezabal. 2025. "Adequate Segmentation in Marker-Based Motion Capture Studies for Hyperflexion and Hyperextension Lumbar Exercises" Bioengineering 12, no. 10: 1087. https://doi.org/10.3390/bioengineering12101087
APA StyleRomero-Flores, C. F., Bustamante-Bello, R., Moya Bencomo, M., & Zenteno Aguirrezabal, I. (2025). Adequate Segmentation in Marker-Based Motion Capture Studies for Hyperflexion and Hyperextension Lumbar Exercises. Bioengineering, 12(10), 1087. https://doi.org/10.3390/bioengineering12101087






