Implicit Is Not Enough: Explicitly Enforcing Anatomical Priors inside Landmark Localization Models
Abstract
1. Introduction
Contribution
- We use Differentiable Spatial to Numerical Transform (DSNT) [30] coordinate regression. DSNT has no disconnect between loss computation and desired metrics and retains the spatial generalization property of heatmap regression.
- The computational costs are reduced by combining the optimization strategies of [25,26] and designing an efficient pipeline of upscaling and downscaling operations within GAFFA. This is necessary to make our method computationally feasible, as we use higher resolution inputs and a larger number of landmarks than [25,26].
- We refine the marginal energy equation used in GAFFA, e.g., returning back from logarithmic space is not necessary for finding the location of the highest pixel intensity.
- The data augmentation scheme is extended with occlusion perturbations [24], which increases the overall ALL performance and robustness against occlusions.
2. Methods
2.1. Dataset
2.2. Initial Landmark Localization with Heatmap Regression
2.3. Explicit Landmark Refinement with Markov Random Fields
2.4. End-to-End Trainable Global Anatomical Feasibility Filter and Analysis
2.4.1. Prior Anatomical Knowledge and GAFFA
2.4.2. Numerical Realization
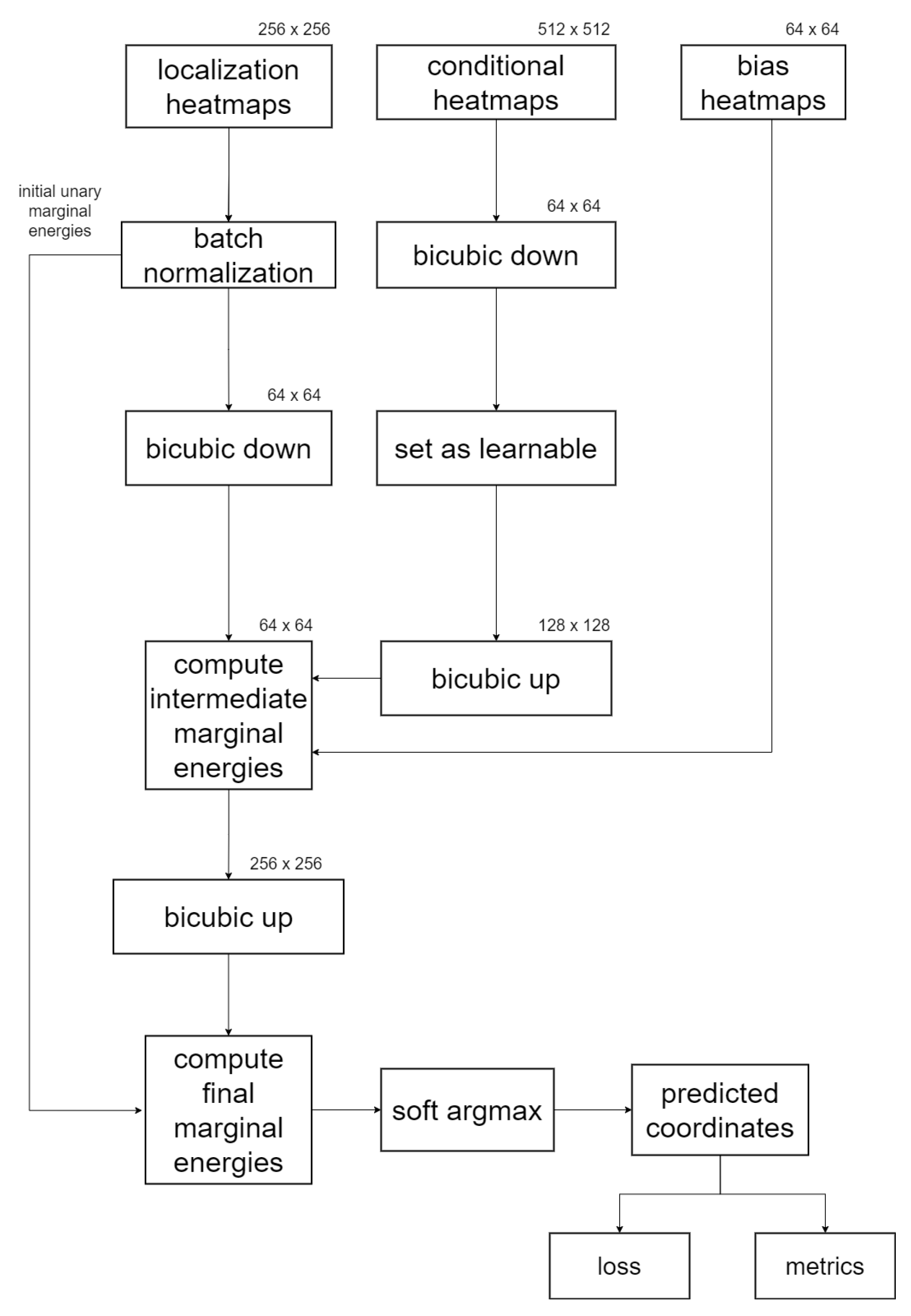
2.4.3. GAFFA Landmark Refinement Flowchart
2.4.4. Comparison with SCN and Graphical Model
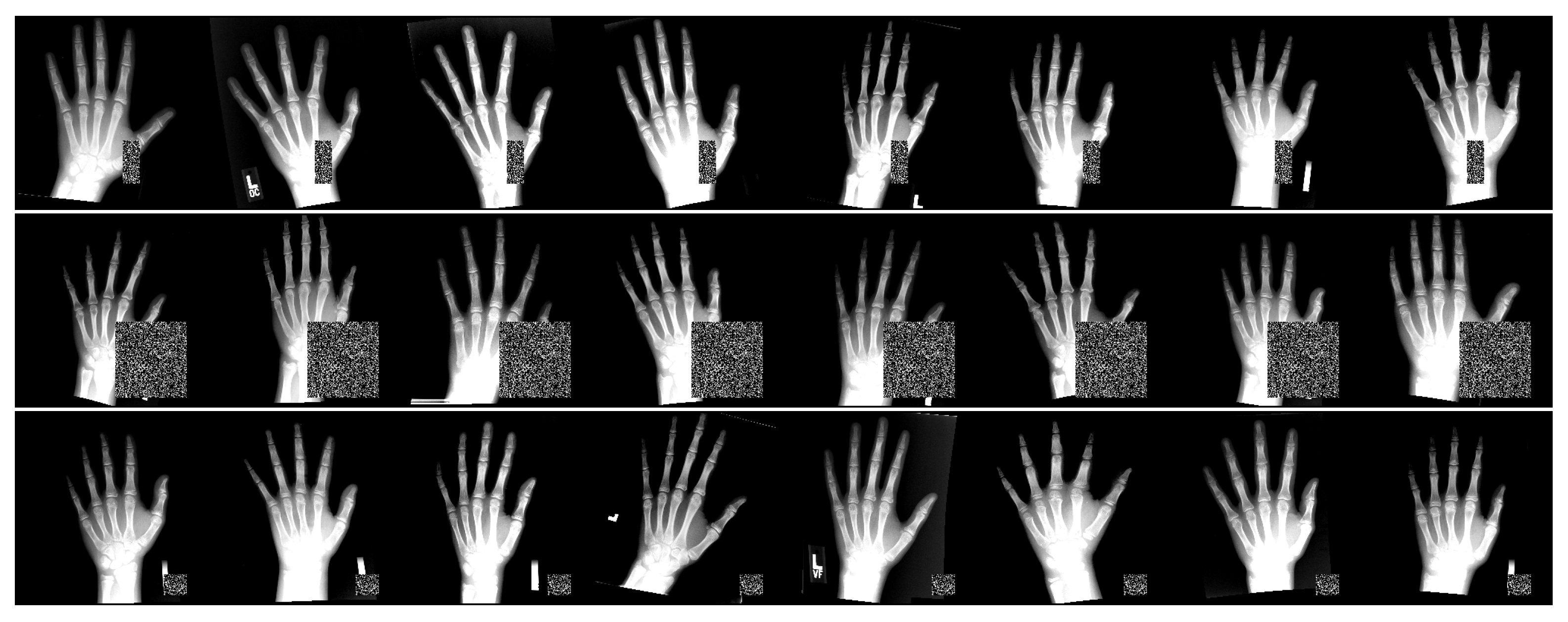
2.5. Rich-Representation Learning with Occlusions
3. Experimental Setup
3.1. Evaluation Metrics
3.2. Preprocessing and Data Augmentation
3.3. Model Training
3.4. Occlusion Test Setting Details
4. Results
4.1. Rich-Representation Learning with Occlusions
4.2. Landmark Refinement Methods and Standard Test Setting
4.3. Landmark Refinement Methods and Occlusion Test Setting
4.4. Comparison to State-of-the-Art
4.5. Qualitative Results of GAFFA and Outlier Analysis
5. Discussion
5.1. Rich-Representation Learning with Occlusions
5.2. Landmark Refinement Methods
5.2.1. Graphical Model
5.2.2. SpatialConfiguration-Net
5.2.3. Global Anatomical Feasibility Filter and Analysis
6. Conclusions
Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALL | Anatomical Landmark Localization |
| CPU | Central Processing Unit |
| GPU | Graphics Processing Unit |
| CNN | Convolutional Neural Network |
| SCN | SpatialConfiguration-Net |
| GM | Graphical Model |
| GAFFA | Global Anatomical Feasibility Filter and Analysis |
| MRF | Markov Random Field |
| GMM | Gaussian Mixture Model |
| LBP | Loopy Belief Propagation |
| FFT | Fast Fourier Transform |
| MSE | Mean Squared Error |
| DSNT | Differentiable Spatial to Numerical Transform |
| MD | Median |
| SD | Standard Deviation |
| WO | Without Artificial Occlusions |
References
- Lu, G.; Shu, H.; Bao, H.; Kong, Y.; Zhang, C.; Yan, B.; Zhang, Y.; Coatrieux, J. CMF-Net: Craniomaxillofacial Landmark Localization on CBCT Images using Geometric Constraint and Transformer. Phys. Med. Biol. 2023, 68, 095020. [Google Scholar] [CrossRef]
- Wang, C.W.; Huang, C.T.; Lee, J.H.; Li, C.H.; Chang, S.W.; Siao, M.J.; Lai, T.M.; Ibragimov, B.; Vrtovec, T.; Ronneberger, O.; et al. A benchmark for comparison of dental radiography analysis algorithms. Med. Image Anal. 2016, 31, 63–76. [Google Scholar] [CrossRef] [PubMed]
- Oh, K.; Oh, I.; Le, V.N.T.; Lee, D. Deep Anatomical Context Feature Learning for Cephalometric Landmark Detection. IEEE J. Biomed. Health Inform. 2020, 25, 806–817. [Google Scholar] [CrossRef]
- Rakosi, T. An Atlas and Manual of Cephalometric Radiography; Lea & Febiger: Philadelphia, PA, USA, 1982. [Google Scholar]
- Oktay, O.; Bai, W.; Guerrero, R.; Rajchl, M.; de Marvao, A.; O’Regan, D.P.; Cook, S.A.; Heinrich, M.P.; Glocker, B.; Rueckert, D. Stratified Decision Forests for Accurate Anatomical Landmark Localization in Cardiac Images. IEEE Trans. Med. Imaging 2017, 36, 332–342. [Google Scholar] [CrossRef]
- Urschler, M.; Zach, C.; Ditt, H.; Bischof, H. Automatic Point Landmark Matching for Regularizing Nonlinear Intensity Registration: Application to Thoracic CT Images. In Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), Copenhagen, Denmark, 1–6 October 2006; Volume 9, pp. 710–717. [Google Scholar] [CrossRef]
- Tiulpin, A.; Melekhov, I.; Saarakkala, S. KNEEL: Knee Anatomical Landmark Localization using Hourglass Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhu, J.; Zhu, J.; Zhou, A.; Shao, H. Bone Anatomical Landmark Localization with Cascaded Spatial Configuration Network. Meas. Sci. Technol. 2022, 33, 065401. [Google Scholar] [CrossRef]
- Glocker, B.; Feulner, J.; Criminisi, A.; Haynor, D.R.; Konukoglu, E. Automatic localization and identification of vertebrae in arbitrary field-of-view CT scans. In Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), Nice, France, 1–5 October 2012; pp. 590–598. [Google Scholar] [CrossRef]
- Donner, R.; Menze, B.H.; Bischof, H.; Langs, G. Global Localization of 3D Anatomical Structures by pre-filtered Hough Forests and Discrete Optimization. Med. Image Anal. 2013, 17, 1304–1314. [Google Scholar] [CrossRef]
- Potesil, V.; Kadir, T.; Platsch, G.; Brady, M. Personalized graphical models for anatomical landmark localization in whole-body medical images. Int. J. Comput. Vis. 2015, 111, 29–49. [Google Scholar] [CrossRef]
- Urschler, M.; Ebner, T.; Štern, D. Integrating Geometric Configuration and Appearance Information into a Unified Framework for Anatomical Landmark Localization. Med. Image Anal. 2018, 43, 23–36. [Google Scholar] [CrossRef]
- Ghesu, F.C.; Georgescu, B.; Zheng, Y.; Grbic, S.; Maier, A.; Hornegger, J.; Comaniciu, D. Multi-scale deep reinforcement learning for real-time 3D-landmark detection in CT scans. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 176–189. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Payer, C.; Štern, D.; Bischof, H.; Urschler, M. Integrating Spatial Configuration into Heatmap Regression based CNNs for Landmark Localization. Med. Image Anal. 2019, 54, 207–219. [Google Scholar] [CrossRef] [PubMed]
- Ao, Y.; Wu, H. Feature Aggregation and Refinement Network for 2D Anatomical Landmark Detection. J. Digit. Imaging 2023, 36, 547–561. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Zhao, R.; Leung, F.H.F.; Banerjee, S.; Lam, K.; Zheng, Y.; Ling, S.H. Landmark Localization from Medical Images with Generative Distribution Prior. IEEE Trans. Med. Imaging 2024, 43, 2679–2692. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Weng, C.; Huang, Y.; Fu, C.; Yeh, Y.; Yeh, C.; Tsai, T. Automatic Recognition of Whole-Spine Sagittal Alignment and Curvature Analysis through a Deep Learning Technique. Eur. Spine J. 2022, 31, 2092–2103. [Google Scholar] [CrossRef] [PubMed]
- Ham, G.; Oh, K. Learning Spatial Configuration Feature for Landmark Localization in Hand X-rays. Electronics 2023, 12, 4038. [Google Scholar] [CrossRef]
- Zhu, H.; Yao, Q.; Zhou, S.K. DATR: Domain-Adaptive Transformer for Multi-Domain Landmark Detection. arXiv 2022, arXiv:2203.06433. [Google Scholar] [CrossRef]
- Viriyasaranon, T.; Ma, S.; Choi, J. Anatomical Landmark Detection Using a Multiresolution Learning Approach with a Hybrid Transformer-CNN Model. In Proceedings of the Medical Image Computing and Computer Assisted Intervention (MICCAI), Vancouver, BC, Canada, 8–12 October 2023; pp. 433–443. [Google Scholar] [CrossRef]
- Guo, M.; Xu, T.; Liu, J.; Liu, Z.; Jiang, P.; Mu, T.; Zhang, S.; Martin, R.R.; Cheng, M.; Hu, S. Attention Mechanisms in Computer Vision: A Survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Kang, J.; Oh, K.; Oh, I. Accurate Landmark Localization for Medical Images using Perturbations. Appl. Sci. 2021, 11, 10277. [Google Scholar] [CrossRef]
- Gdoura, A.; Degünther, M.; Lorenz, B.; Effland, A. Combining CNNs and Markov-like Models for Facial Landmark Detection with Spatial Consistency Estimates. J. Imaging 2023, 9, 104. [Google Scholar] [CrossRef]
- Tompson, J.; Jain, A.; LeCun, Y.; Bregler, C. Joint Training of a Convolutional Network and a Graphical Model for Human Pose Estimation. Adv. Neural Inf. Process. Syst. 2014, 27, 1–9. [Google Scholar]
- Kindermann, R.; Snall, J.L. Markov Random Fields and Their Applications; American Mathematical Society: Providence, RI, USA, 1980. [Google Scholar]
- McLachlan, G.J.; Rathnayake, S. On the Number of Components in a Gaussian Mixture Model. In Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery; Wiley: Hoboken, NJ, USA, 2014; Volume 4, pp. 341–355. [Google Scholar] [CrossRef]
- Wainwright, M.J.; Jordan, M.I. Graphical Models, Exponential Families, and Variational Inference. Found. Trends Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef]
- Nibali, A.; He, Z.; Morgan, S.; Prendergast, L. Numerical Coordinate Regression with Convolutional Neural Networks. arXiv 2018, arXiv:1801.07372. [Google Scholar] [CrossRef]
- Szeliski, R.; Zabih, R.; Scharstein, D.; Veksler, O.; Kolmogorov, V.; Agarwala, A.; Tappen, M.; Rother, C. A Comparative Study of Energy Minimization Methods for Markov Random Fields with Smoothness-Based Priors. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1068–1080. [Google Scholar] [CrossRef] [PubMed]
- Ebner, T.; Štern, D.; Donner, R.; Bischof, H.; Urschler, M. Towards Automatic Bone Age Estimation from MRI: Localization of 3D Anatomical Landmarks. In Proceedings of the Medical Image Computing and Computer Assisted Intervention (MICCAI), Boston, MA, USA, 14–18 September 2014; pp. 421–428. [Google Scholar] [CrossRef]
- Štern, D.; Payer, C.; Urschler, M. Automated Age Estimation from MRI Volumes of the Hand. Med. Image Anal. 2019, 58, 101538. [Google Scholar] [CrossRef] [PubMed]
- Štern, D.; Payer, C.; Giuliani, N.; Urschler, M. Automatic Age Estimation and Majority Age Classification From Multi-Factorial MRI Data. IEEE J. Biomed. Health Inform. 2019, 23, 1392–1403. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6 July–11 July 2015; Volume 37, pp. 448–456. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; Volume 30, p. 3. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kolmogorov, V. Convergent Tree-Reweighted Message Passing for Energy Minimization. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1568–1583. [Google Scholar] [CrossRef]
- Kschischang, F.; Frey, B.; Loeliger, H.A. Factor Graphs and the Sum-Product Algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Criminisi, A.; Shotton, J. Decision Forests for Computer Vision and Medical Image Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hadzic, A.; Urschler, M.; Press, J.A.; Riedl, R.; Rugani, P.; Štern, D.; Kirnbauer, B. Evaluating a Periapical Lesion Detection CNN on a Clinically Representative CBCT Dataset-A Validation Study. J. Clin. Med. 2023, 13, 197. [Google Scholar] [CrossRef]





| Method | (in mm) | #Or (%Or) | ||||
|---|---|---|---|---|---|---|
| MD | SD | r > 2 mm | r > 4 mm | r > 10 mm | ||
| U-Net Gaussian Blobs | 0.47 | 0.69 | ±0.71 | 1787 (5.40%) | 236 (0.71%) | 2 (0.006%) |
| + Occlusion Train | 0.49 | 0.69 | ±0.66 | 1534 (4.63%) | 161 (0.49%) | 2 (0.006%) |
| U-Net Laplacian Blobs | 0.47 | 0.69 | ±0.70 | 1678 (5.07%) | 219 (0.66%) | 2 (0.006%) |
| + Occlusion Train | 0.50 | 0.69 | ±0.66 | 1540 (4.65%) | 148 (0.45%) | 2 (0.006%) |
| SCN Gaussian Blobs | 0.48 | 0.70 | ±0.74 | 1795 (5.42%) | 260 (0.79%) | 5 (0.015%) |
| + Occlusion Train | 0.49 | 0.69 | ±0.66 | 1576 (4.76%) | 152 (0.46%) | 2 (0.006%) |
| Method | (in mm) | #Or (%Or) | ||||
|---|---|---|---|---|---|---|
| MD | SD | r > 2 mm | r > 4 mm | r > 10 mm | ||
| U-Net | 0.49 | 0.69 | ±0.66 | 1534 (4.63%) | 161 (0.49%) | 2 (0.006%) |
| U-Net+GM | 0.67 | 0.83 | ±0.66 | 1790 (5.41%) | 158 (0.48%) | 2 (0.006%) |
| SCN | 0.49 | 0.69 | ±0.66 | 1576 (4.76%) | 152 (0.46%) | 2 (0.006%) |
| U-Net+GAFFA | 0.49 | 0.69 | ±0.66 | 1552 (4.69%) | 158 (0.48%) | 2 (0.006%) |
| U-Net+GAFFA | 0.50 | 0.70 | ±0.65 | 1572 (4.75%) | 142 (0.43%) | 1 (0.003%) |
| U-Net+GAFFA Lapl. Blobs | 0.49 | 0.69 | ±0.66 | 1525 (4.61%) | 174 (0.53%) | 2 (0.006%) |
| U-Net+GAFFA Lapl. Blobs | 0.51 | 0.71 | ±0.65 | 1548 (4.67%) | 143 (0.43%) | 1 (0.003%) |
| Method | (in mm) | #Or (%Or) | ||||
|---|---|---|---|---|---|---|
| MD | SD | r > 2 mm | r > 4 mm | r > 10 mm | ||
| U-Net WO | 0.52 | 3.80 | ±18.96 | 3935 (11.88%) | 2275 (6.87%) | 1442 (4.35%) |
| SCN WO | 0.54 | 3.18 | ±11.08 | 4274 (12.90%) | 2679 (8.09%) | 2180 (6.58%) |
| U-Net | 0.53 | 0.84 | ±2.03 | 2495 (7.53%) | 562 (1.70%) | 22 (0.07%) |
| U-Net+GM | 0.70 | 0.95 | ±1.06 | 2767 (8.36%) | 560 (1.69%) | 18 (0.05%) |
| SCN | 0.53 | 0.94 | ±2.56 | 2621 (7.91%) | 736 (2.22%) | 131 (0.40%) |
| U-Net+GAFFA | 0.53 | 0.83 | ±1.54 | 2482 (7.50%) | 581 (1.75%) | 18 (0.05%) |
| U-Net+GAFFA | 0.55 | 0.83 | ±1.14 | 2499 (7.55%) | 546 (1.65%) | 20 (0.06%) |
| U-Net+GAFFA Lapl. Blobs | 0.53 | 0.81 | ±1.09 | 2465 (7.44%) | 577 (1.74%) | 15 (0.05%) |
| U-Net+GAFFA Lapl. Blobs | 0.55 | 0.83 | ±1.00 | 2493 (7.53%) | 512 (1.55%) | 13 (0.04%) |
| Method | (mm) | |||||
|---|---|---|---|---|---|---|
| MD | SD | r > 2 mm | r > 4 mm | r > 10 mm | ||
| 1024 × 1216 input size | ||||||
| Viriyasaranon et al. [22] * | ? | 0.56 | ±0.58 | ? (3.17%) | ? (0.37%) | ? (0.0%) |
| 800 × 640 input size | ||||||
| Oh et al. [3] (from [20]) | ? | 0.63 | ±0.71 | 1301 (3.93%) | 109 (0.33%) | 3 (0.01%) |
| Kang et al. [24] | ? | 0.64 | ±0.64 | 1311 (3.96%) | 112 (0.34%) | 6 (0.02%) |
| Ham et al. [20] | ? | 0.61 | ±0.61 | 1231 (3.72%) | 102 (0.31%) | 3 (0.01%) |
| 512 × 512 input size | ||||||
| Payer et al. [15] | 0.43 | 0.66 | ±0.74 | 1659 (5.01%) | 241 (0.73%) | 3 (0.01%) |
| Huang et al. [17] | ? | 0.72 | ±0.74 | 1861 (5.62%) | 168 (0.51%) | 3 (0.01%) |
| 256 × 256 input size | ||||||
| U-Net+GAFFA (Ours) | 0.50 | 0.70 | ±0.65 | 1572 (4.75%) | 142 (0.43%) | 1 (0.003%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joham, S.J.; Hadzic, A.; Urschler, M. Implicit Is Not Enough: Explicitly Enforcing Anatomical Priors inside Landmark Localization Models. Bioengineering 2024, 11, 932. https://doi.org/10.3390/bioengineering11090932
Joham SJ, Hadzic A, Urschler M. Implicit Is Not Enough: Explicitly Enforcing Anatomical Priors inside Landmark Localization Models. Bioengineering. 2024; 11(9):932. https://doi.org/10.3390/bioengineering11090932
Chicago/Turabian StyleJoham, Simon Johannes, Arnela Hadzic, and Martin Urschler. 2024. "Implicit Is Not Enough: Explicitly Enforcing Anatomical Priors inside Landmark Localization Models" Bioengineering 11, no. 9: 932. https://doi.org/10.3390/bioengineering11090932
APA StyleJoham, S. J., Hadzic, A., & Urschler, M. (2024). Implicit Is Not Enough: Explicitly Enforcing Anatomical Priors inside Landmark Localization Models. Bioengineering, 11(9), 932. https://doi.org/10.3390/bioengineering11090932







