Efficient Multi-View Graph Convolutional Network with Self-Attention for Multi-Class Motor Imagery Decoding
Abstract
1. Introduction
- (1)
- We constructed different representation of brain views based on physical distance and functional connection, which can sufficiently express the topological relationship of brain regions in MI signals for subsequent spatial feature extraction.
- (2)
- We designed a residual graph convolutional network called ResChebyNet by combing the advantage of the residual learning and Chebyshev functions. In order to avoid the gradient vanishing problem caused by the increase of the layers of the graph convolutional network.
- (3)
- We developed an adaptive-weighted fusion (Awf) module for collaborative integration of features extracted from different brain views, which can enhance the reliability and accuracy of feature fusion.
- (4)
- We introduced the multi-head self-attention method in the classification framework, which can extend the receptive field of MI signals to a global scale and effectively enhance the expression ability of important features to improve decoding accuracy.
2. Methods
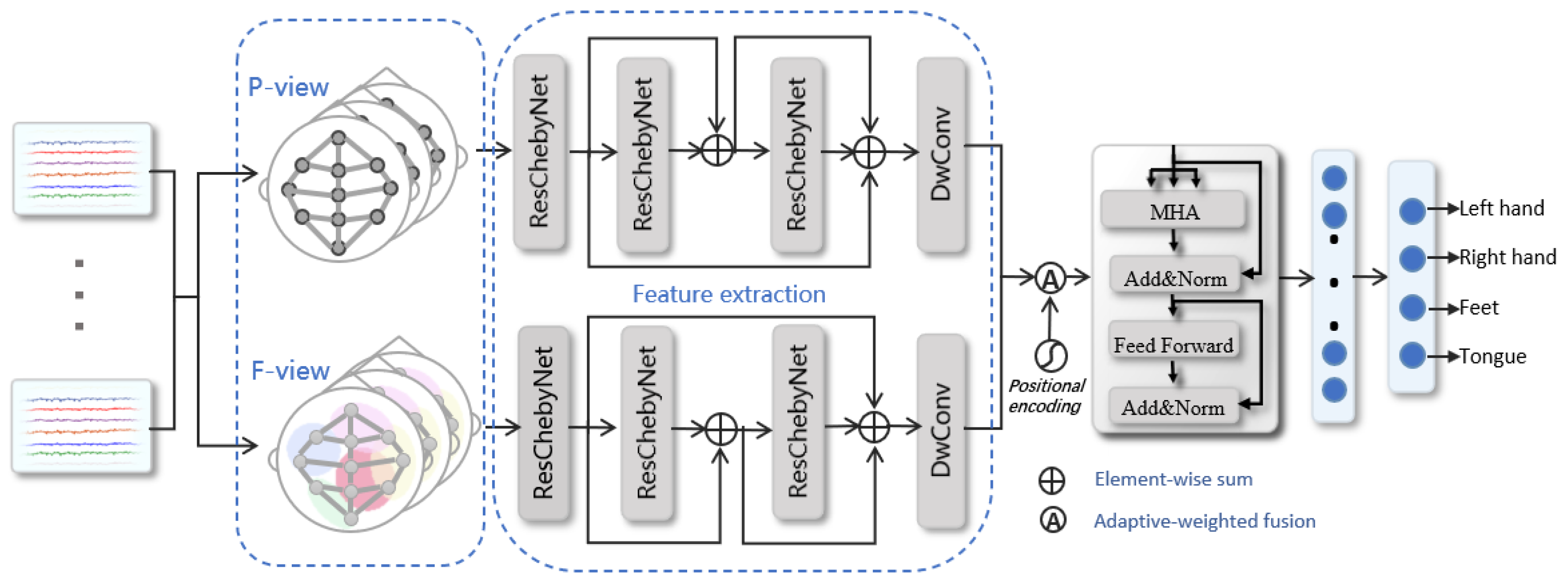
2.1. Overall Architecture
2.2. Multi-View on Brain Graph
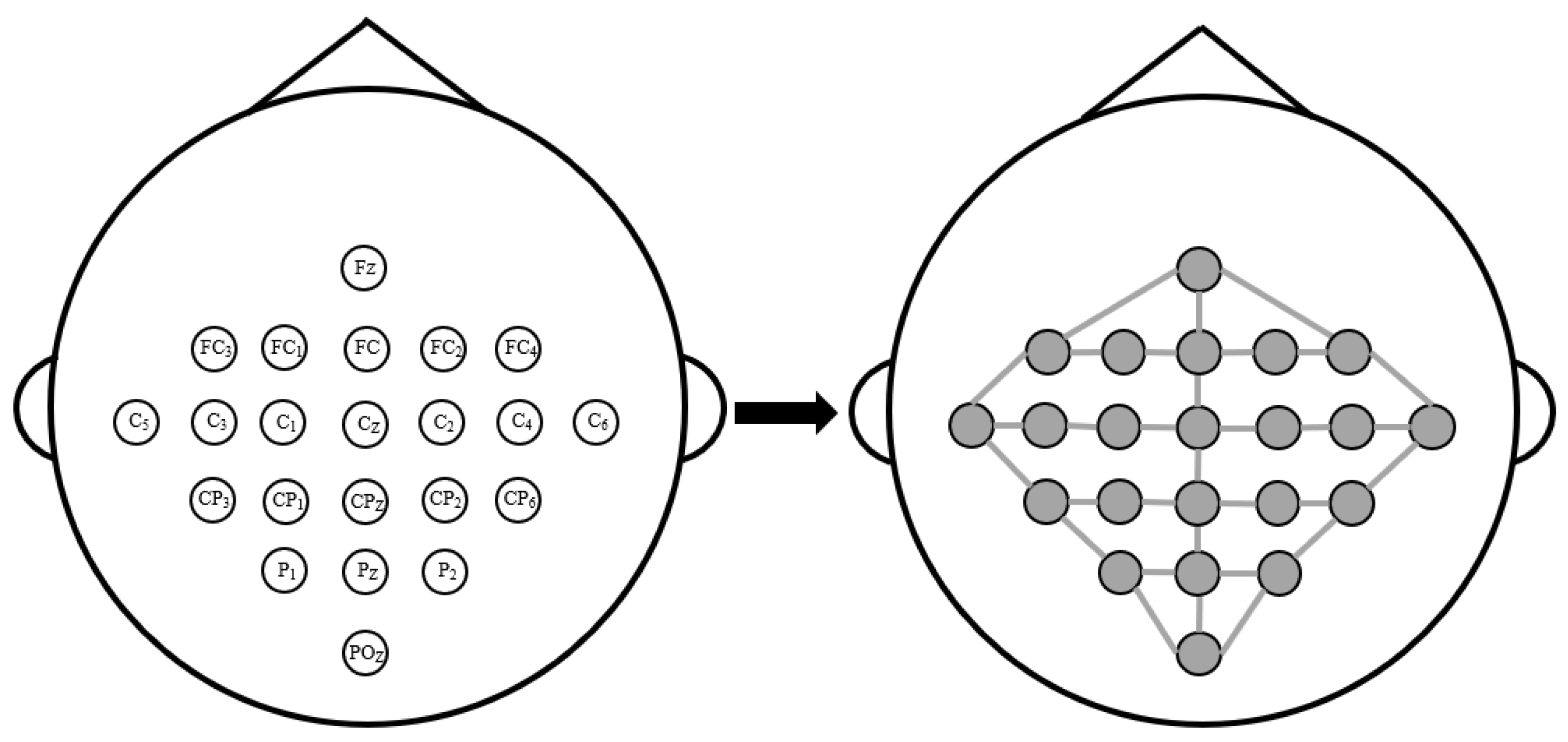
2.2.1. Physical-Distance-Based Brain View
2.2.2. Functional-Connectivity-Based Brain View
2.3. Spatial–Temporal Feature Extraction
2.3.1. Spatial Feature Extraction
2.3.2. Temporal Feature Extraction
2.4. Adaptive-Weighted Fusion
2.5. Self-Attention Feature Selection
2.6. Classification
3. Experiments and Results
3.1. Dataset
3.1.1. BCI Competition IV 2a Dataset
3.1.2. OpenBMI Dataset
3.2. Experimental Setup
3.3. Compared Methods
- DeepConvNet [12]: DeepConvNet is a general-purpose architecture which combines temporal convolution and spatial convolution operations. It consists of five convolutional layers. We trained this model in the same way as the original paper.
- Sinc-ShallowNet [37]: This method extracts features of EEG signals by stacking temporal sinc-convolutional layers and spatial convolutional layers. We reproduced the author’s design and obtained comparable performance.
- G-CRAM [18]: G-CRAM constructs three graph structures through the positioning information of EEG nodes and use a convolutional recurrent model for feature extraction. We adjusted the input format based on the original paper.
- BiLSTM-GCN [38]: BiLSTM-GCN uses the BiLSTM with the attention model to extract features and uses the GCN model based on Pearson’s matrix for feature learning. We performed corresponding reproduction operations according to the design of the original paper.
- EEG-Conformer [39]: The method consists of three parts: a convolution block, a self-attention block, and a fully connected classifier. We performed corresponding reproduction operations according to the published code in the paper.
3.4. Results
3.4.1. Comparison Experiments
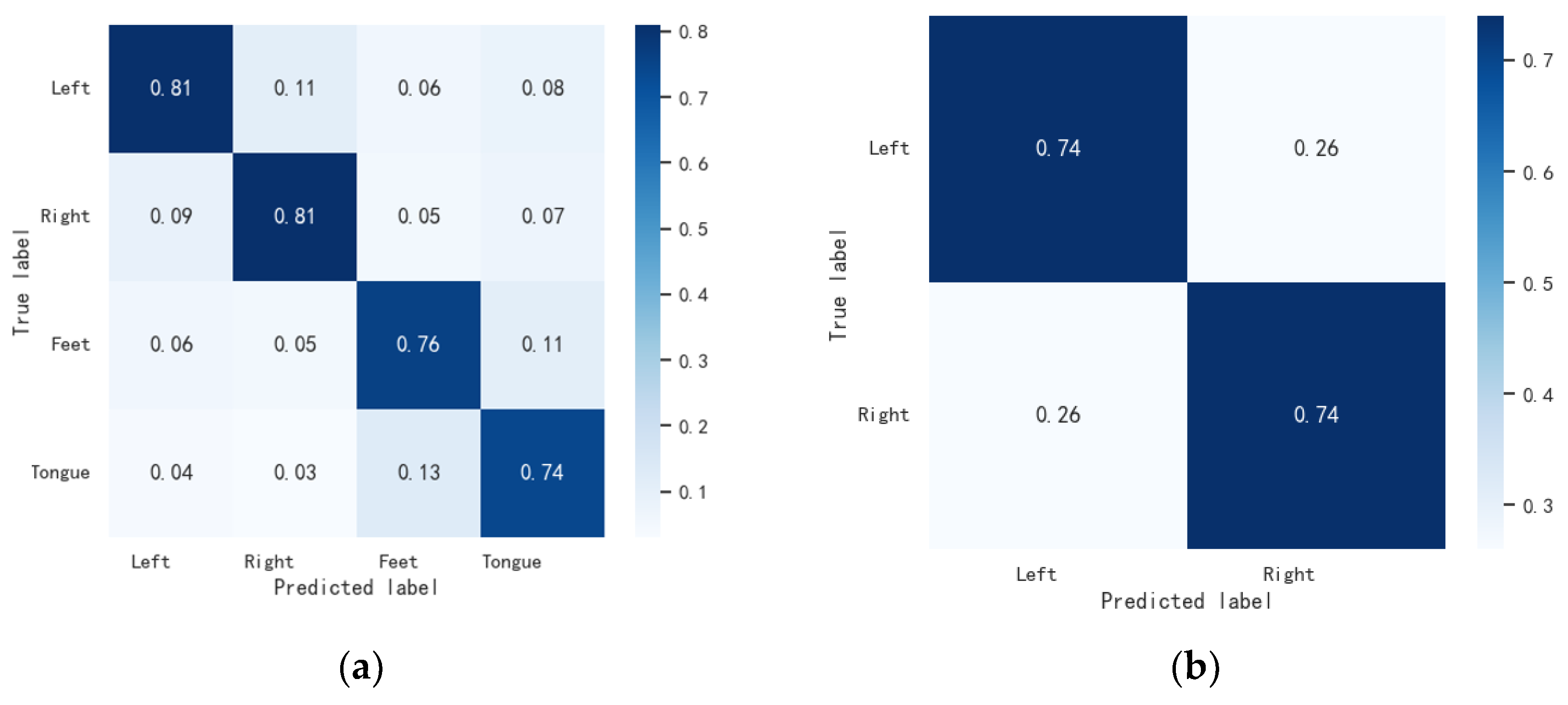
3.4.2. Confusion Matrix
3.4.3. Ablation Study
3.4.4. Visualization
4. Discussion
4.1. Visualization of the Brain Topographical Map
4.2. Selection of Parameters
4.3. Ablation Study of the Adaptive-Weighted Fusion
4.4. The Influence of Different Attention Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aggarwal, S.; Chugh, N. Review of machine learning techniques for EEG based brain computer interface. Arch. Comput. Methods Eng. 2022, 29, 3001–3020. [Google Scholar] [CrossRef]
- Orban, M.; Elsamanty, M.; Guo, K.; Zhang, S.; Yang, H. A review of brain activity and EEG-based brain–computer interfaces for rehabilitation application. Bioengineering 2022, 9, 768. [Google Scholar] [CrossRef]
- Grazia, A.; Wimmer, M.; Müller-Putz, G.R.; Wriessnegger, S.C. Neural suppression elicited during motor imagery following the observation of biological motion from point-light walker stimuli. Front. Hum. Neurosci. 2022, 15, 788036. [Google Scholar] [CrossRef] [PubMed]
- Chaddad, A.; Wu, Y.; Kateb, R.; Bouridane, A. Electroencephalography signal processing: A comprehensive review and analysis of methods and techniques. Sensors 2023, 23, 6434. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, M.P.; Hosseini, A.; Ahi, K. A review on machine learning for EEG signal processing in bioengineering. IEEE Rev. Biomed. Eng. 2020, 14, 204–218. [Google Scholar] [CrossRef]
- Rithwik, P.; Benzy, V.K.; Vinod, A.P. High accuracy decoding of motor imagery directions from EEG-based brain computer interface using filter bank spatially regularised common spatial pattern method. Biomed. Signal Process. Control 2022, 72, 103241. [Google Scholar] [CrossRef]
- Quadrianto, N.; Cuntai, G.; Dat, T.H.; Xue, P. Sub-band Common Spatial Pattern (SBCSP) for Brain-Computer Interface. In Proceedings of the 2007 3rd International IEEE/EMBS Conference on Neural Engineering, Kohala Coast, HI, USA, 2–5 May 2007; pp. 2–7. [Google Scholar]
- Kumar, S.; Sharma, A.; Mamun, K.; Tsunoda, T. A Deep Learning Approach for Motor Imagery EEG Signal Classification. In Proceedings of the 2016 3rd Asia-Pacific World Congress on Computer Science and Engineering (APWC on CSE), Nadi, Fiji, 10–12 December 2016; pp. 34–39. [Google Scholar]
- Yannick, R.; Hubert, B.; Isabela, A.; Alexandre, G.; Falk, T.H.; Jocelyn, F. Deep learning-based electroencephalography analysis: A systematic review. J. Neural Eng. 2019, 16, 051001. [Google Scholar]
- Dai, G.; Zhou, J.; Huang, J.; Wang, N. HS-CNN: A CNN with hybrid convolution scale for EEG motor imagery classification. J. Neural Eng. 2020, 17, 016025. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Ding, M.; Zhang, R.; Xiu, C. Motor imagery EEG classification algorithm based on CNN-LSTM feature fusion network. Biomed. Signal Process. Control 2022, 72, 103342. [Google Scholar] [CrossRef]
- Schirrmeister, R.; Gemein, L.; Eggensperger, K.; Hutter, F.; Ball, T. Deep learning with convolutional neural networks for decoding and visualization of EEG pathology. In Proceedings of the 2017 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 2 December 2017; pp. 1–7. [Google Scholar]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain–computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef]
- Izzuddin, T.A.; Safri, N.M.; Othman, M.A. Compact convolutional neural network (CNN) based on SincNet for end-to-end motor imagery decoding and analysis. Biocybern. Biomed. Eng. 2021, 41, 1629–1645. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Zhang, D.; Chen, K.; Jian, D.; Yao, L. Motor imagery classification via temporal attention cues of graph embedded EEG signals. IEEE J. Biomed. Health Inform. 2020, 24, 2570–2579. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, H.; Wu, Z.; Zhang, Y.; Li, T. Adaptive spatiotemporal graph convolutional networks for motor imagery classification. IEEE Signal Process. Lett. 2021, 28, 219–223. [Google Scholar] [CrossRef]
- Hou, Y.; Jia, S.; Lun, X.; Hao, Z.; Shi, Y.; Li, Y.; Lv, J. GCNs-net: A graph convolutional neural network approach for decoding time-resolved eeg motor imagery signals. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 7312–7322. [Google Scholar] [CrossRef]
- Galassi, A.; Lippi, M.; Torroni, P. Attention in natural language processing. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4291–4308. [Google Scholar] [CrossRef]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.-H.; Martin, R.R.; Cheng, M.-M.; Hu, S.-M. Attention mechanisms in computer vision: A survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Li, D.; Xu, J.; Wang, J.; Fang, X.; Ji, Y. A multi-scale fusion convolutional neural network based on attention mechanism for the visualization analysis of EEG signals decoding. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 2615–2626. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, X.; Wu, Z.; Sun, B.; Li, T. Motor imagery recognition with automatic EEG channel selection and deep learning. J. Neural Eng. 2021, 18, 016004. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Jin, J.; Xu, R.; Li, S.; Zuo, C.; Sun, H.; Cichocki, A. Distinguishable spatial-spectral feature learning neural network framework for motor imagery-based brain–computer interface. J. Neural Eng. 2021, 18, 0460e4. [Google Scholar] [CrossRef]
- Yu, Z.; Chen, W.; Zhang, T. Motor imagery EEG classification algorithm based on improved lightweight feature fusion network. Biomed. Signal Process. Control 2022, 75, 103618. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Zhao, L.; Li, B.; Hu, W.; Yu, J.; Zhang, Y.D. 3DCANN: A spatio-temporal convolution attention neural network for EEG emotion recognition. IEEE J. Biomed. Health Inform. 2021, 26, 5321–5331. [Google Scholar] [CrossRef] [PubMed]
- Eldele, E.; Chen, Z.; Liu, C.; Wu, M.; Kwoh, C.K.; Li, X.; Guan, C. An attention-based deep learning approach for sleep stage classification with single-channel EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 809–818. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. JMLR Org. 2015, 37, 448–456. [Google Scholar]
- Ye, Z.; Li, Z.; Li, G.; Zhao, H. Dual-channel deep graph convolutional neural networks. Front. Artif. Intell. 2024, 7, 1290491. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Tangermann, M.; Müller, K.-R.; Aertsen, A.; Birbaumer, N.; Braun, C.; Brunner, C.; Leeb, R.; Mehring, C.; Miller, K.J.; Müller-Putz, G.R.; et al. Review of the BCI Competition IV. Front. Neurosci. 2012, 6, 55. [Google Scholar] [CrossRef]
- Lee, M.-H.; Kwon, O.-Y.; Kim, Y.-J.; Kim, H.-K.; Lee, Y.-E.; Williamson, J.; Fazli, S.; Lee, S.-W. EEG dataset and OpenBMI toolbox for three BCI paradigms: An investigation into BCI illiteracy. GigaScience 2019, 8, giz002. [Google Scholar] [CrossRef]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Borra, D.; Fantozzi, S.; Magosso, E. Interpretable and lightweight convolutional neural network for EEG decoding: Application to movement execution and imagination. Neural Netw. 2020, 129, 55–74. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Jia, S.; Lun, X.; Zhang, S.; Chen, T.; Wang, F.; Lv, J. Deep feature mining via the attention-based bidirectional long short term memory graph convolutional neural network for human motor imagery recognition. Front. Bioeng. Biotechnol. 2022, 9, 706229. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Q.; Liu, B.; Gao, X. EEG conformer: Convolutional transformer for EEG decoding and visualization. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 710–719. [Google Scholar] [CrossRef]
- Laurens, V.D.M.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar]
- Zhang, Q.L.; Yang, Y.B. Sa-net: Shuffle attention for deep convolutional neural networks. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 2235–2239. [Google Scholar]






| Dataset | Method | Year | Average Acc (%) | Kappa | Std |
|---|---|---|---|---|---|
| BCIC IV 2a | DeepConvNet | 2017 | 66.87 | 0.59 | 15.03 |
| EEGNet | 2018 | 68.18 | 0.57 | 14.25 | |
| Sinc-ShallowNet | 2020 | 73.34 | 0.65 | 12.80 | |
| G-CRAM | 2020 | 72.53 | 0.64 | 12.35 | |
| BiLSTM-GCN | 2022 | 73.65 | 0.67 | 12.06 | |
| EEG-Conformer | 2023 | 75.37 | 0.69 | 12.74 | |
| MGCANet | — | 78.26 | 0.70 | 10.50 | |
| OpenBMI | DeepConvNet | 2017 | 60.08 | 0.31 | 14.95 |
| EEGNet | 2018 | 68.17 | 0.39 | 13.06 | |
| Sinc-ShallowNet | 2020 | 68.64 | 0.36 | 13.90 | |
| G-CRAM | 2020 | 68.05 | 0.36 | 14.21 | |
| BiLSTM-GCN | 2022 | 67.92 | 0.39 | 15.14 | |
| EEG-Conformer | 2023 | 66.45 | 0.35 | 14.32 | |
| MGCANet | — | 73.68 | 0.45 | 12.82 |
| Dataset | w/o P-View (%) | w/o F-View (%) | w/o Res (%) | w/o Awf (%) | w/o MHA (%) | MGCANet |
|---|---|---|---|---|---|---|
| BCIC IV 2a | 74.83 | 74.67 | 75.21 | 77.39 | 75.60 | 78.26 |
| OpenBMI | 69.95 | 70.39 | 69.72 | 72.65 | 71.14 | 73.68 |
| Parameter | Value | BCIC IV 2a (%) | OpenBMI (%) |
|---|---|---|---|
| K | 1 | 74.34 | 71.17 |
| 2 | 76.58 | 71.45 | |
| 3 | 78.26 | 73.68 | |
| 4 | 74.03 | 70.92 | |
| Number of layers | 1 | 75.18 | 70.60 |
| 2 | 76.72 | 71.61 | |
| 3 | 78.26 | 73.68 | |
| 4 | 72.51 | 69.24 | |
| Numbers of Heads | 1 | 77.65 | 72.75 |
| 4 | 77.73 | 73.16 | |
| 6 | 78.04 | 73.51 | |
| 8 | 78.26 | 73.68 | |
| 10 | 77.48 | 72.24 | |
| Max norm | 0.1 | 73.63 | 71.90 |
| 0.2 | 75.84 | 72.44 | |
| 0.5 | 78.26 | 73.68 | |
| 1.0 | 73.19 | 71.07 |
| Method | Fusion | BCIC IV 2a (%) | OpenBMI (%) |
|---|---|---|---|
| MGCANet | add | 76.48 | 72.24 |
| concat | 77.25 | 72.85 | |
| proposed | 78.26 | 73.68 |
| Dataset | Method | Average Acc (%) | Std (%) |
|---|---|---|---|
| BCIC IV 2a | SE | 73.95 | 15.76 |
| ECA | 76.67 | 11.08 | |
| SA | 77.20 | 12.28 | |
| MHA | 78.26 | 10.50 | |
| OpenBMI | SE | 70.24 | 16.03 |
| ECA | 72.52 | 13.24 | |
| SA | 71.43 | 12.95 | |
| MHA | 73.68 | 12.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, X.; Wang, D.; Xu, M.; Chen, J.; Wu, S. Efficient Multi-View Graph Convolutional Network with Self-Attention for Multi-Class Motor Imagery Decoding. Bioengineering 2024, 11, 926. https://doi.org/10.3390/bioengineering11090926
Tan X, Wang D, Xu M, Chen J, Wu S. Efficient Multi-View Graph Convolutional Network with Self-Attention for Multi-Class Motor Imagery Decoding. Bioengineering. 2024; 11(9):926. https://doi.org/10.3390/bioengineering11090926
Chicago/Turabian StyleTan, Xiyue, Dan Wang, Meng Xu, Jiaming Chen, and Shuhan Wu. 2024. "Efficient Multi-View Graph Convolutional Network with Self-Attention for Multi-Class Motor Imagery Decoding" Bioengineering 11, no. 9: 926. https://doi.org/10.3390/bioengineering11090926
APA StyleTan, X., Wang, D., Xu, M., Chen, J., & Wu, S. (2024). Efficient Multi-View Graph Convolutional Network with Self-Attention for Multi-Class Motor Imagery Decoding. Bioengineering, 11(9), 926. https://doi.org/10.3390/bioengineering11090926






