Adaptive Detection in Real-Time Gait Analysis through the Dynamic Gait Event Identifier
Abstract
1. Introduction
- High-precision multi-event real-time gait detection: We present a novel gait detection method suitable for complex settings, characterized by high precision and the ability to handle multiple events in real time. This method not only elevates the accuracy in identifying crucial gait events but also showcases its applicability and adaptability across dynamic and varying scenarios, being responsive to diverse gait events.
- Innovative weighted sleep time approach: We introduce an innovative weighted sleep time approach, which, by dynamically modulating the algorithm’s sensitivity and dormancy period, significantly enhances the accuracy and adaptability in detecting gait events.
- Adaptive threshold decision-making: We have developed an adaptive threshold decision-making rule aimed at real-time adjustment of detection thresholds for gait events. This rule is particularly effective in adapting to changes in the amplitude of gait curves across various scenarios, thus substantially improving the overall performance and adaptability in gait event detection.
2. Method
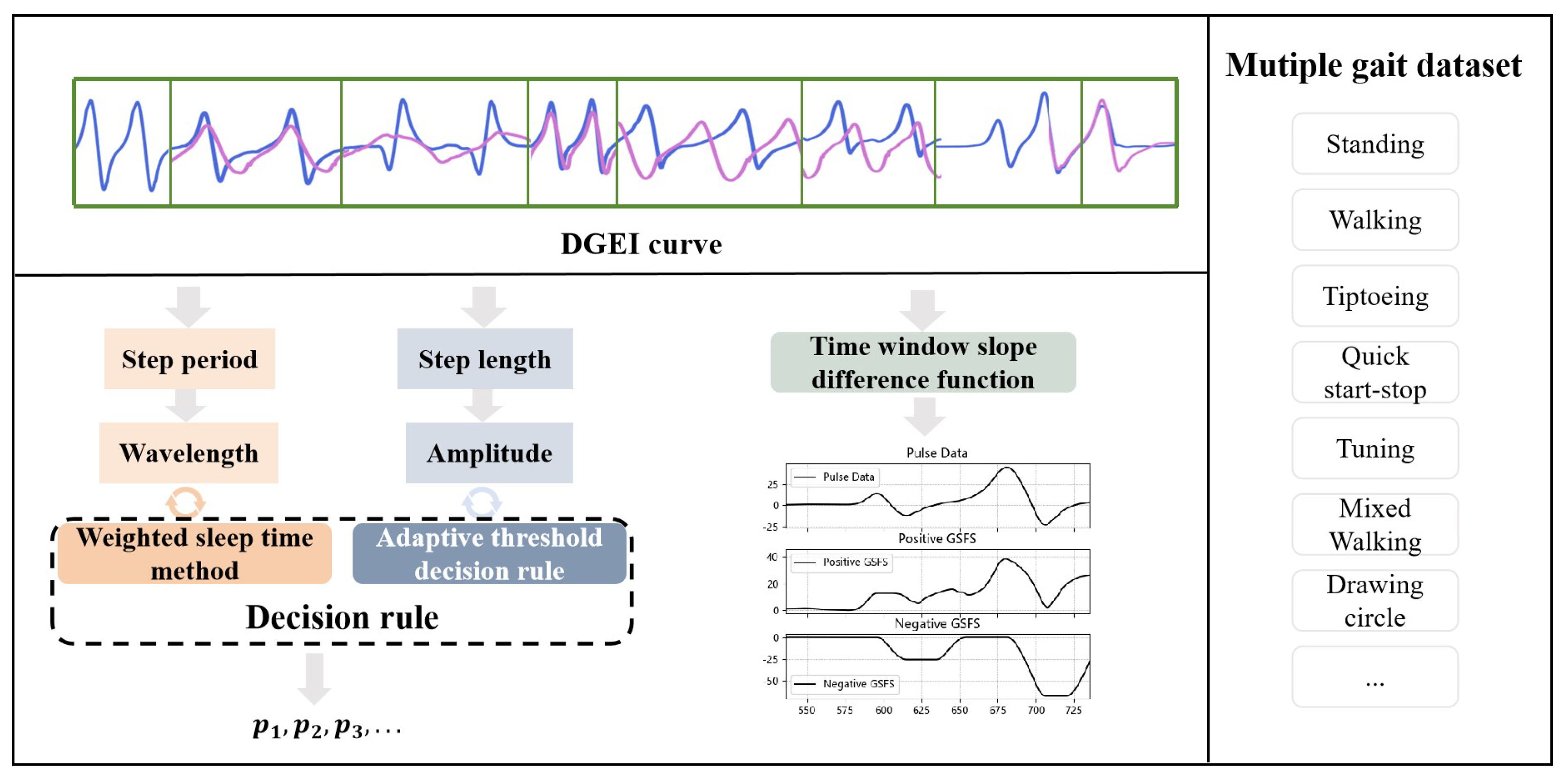
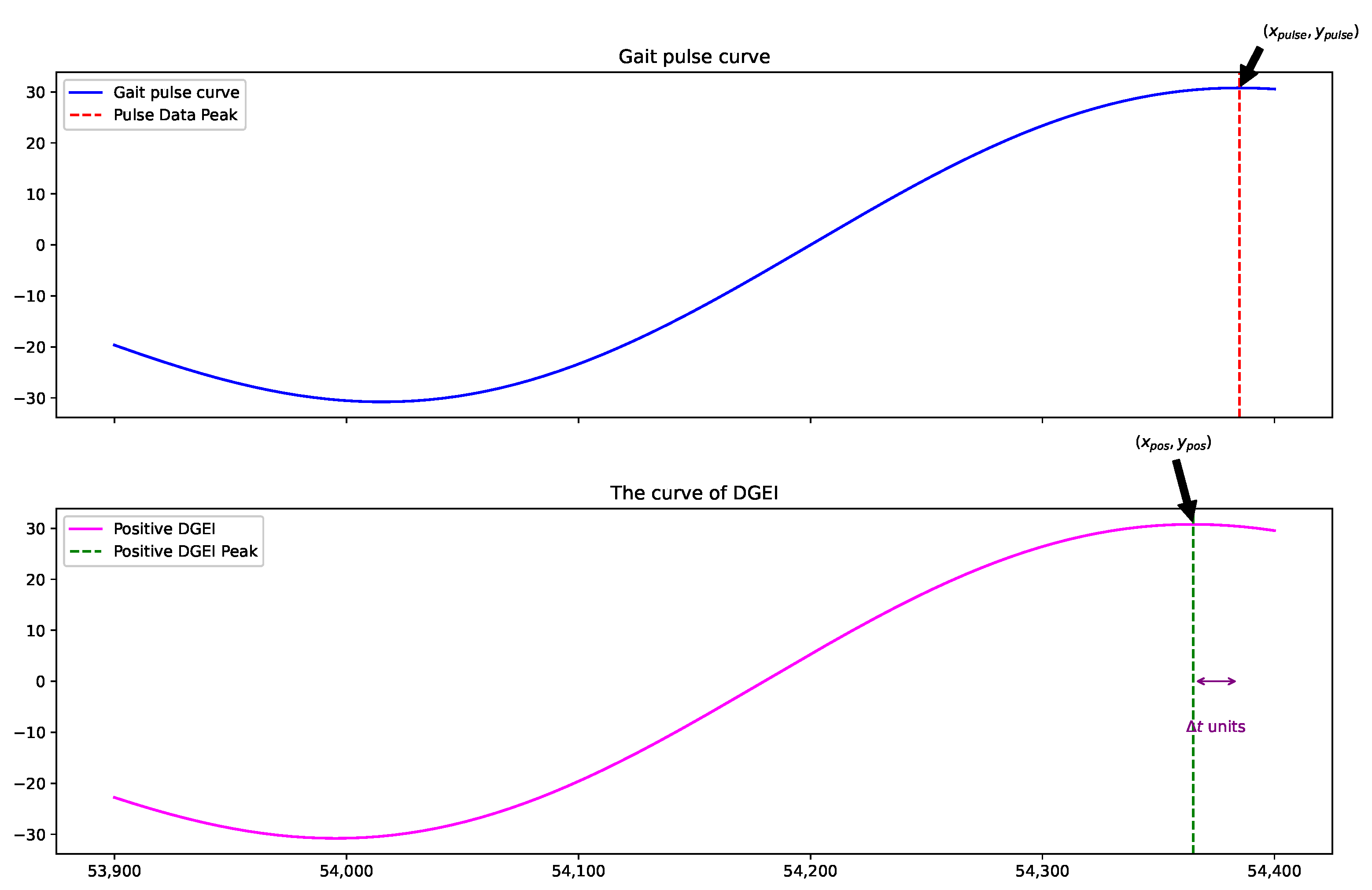
2.1. Dynamic Gait Event Identifier
- represents the change in Euler angles between consecutive gait data points, signifying the instantaneous gait dynamics.
- denotes the time interval between these data points, reflecting the temporal aspect of gait changes.
- and are weighting coefficients designed to balance the immediate gait changes against their rate over time, thereby accommodating the diverse dynamics of gait patterns. These coefficients are defined as follows:
- is the standard deviation of the immediate changes in Euler angles (), a statistical measure capturing the variability within the gait data.
- represents the mean rate of change in the Euler angles, encapsulating the average velocity of gait alterations across the dataset.
- sets the threshold, distinguishing between positive and negative gait events in the context of the algorithm’s classification process.
2.2. Weighted Sleep Time Method
2.3. Adaptive Threshold Decision Rules
3. Experiment
3.1. Data Gathering
3.2. Evaluation Indicator
3.3. Optimization Methodology
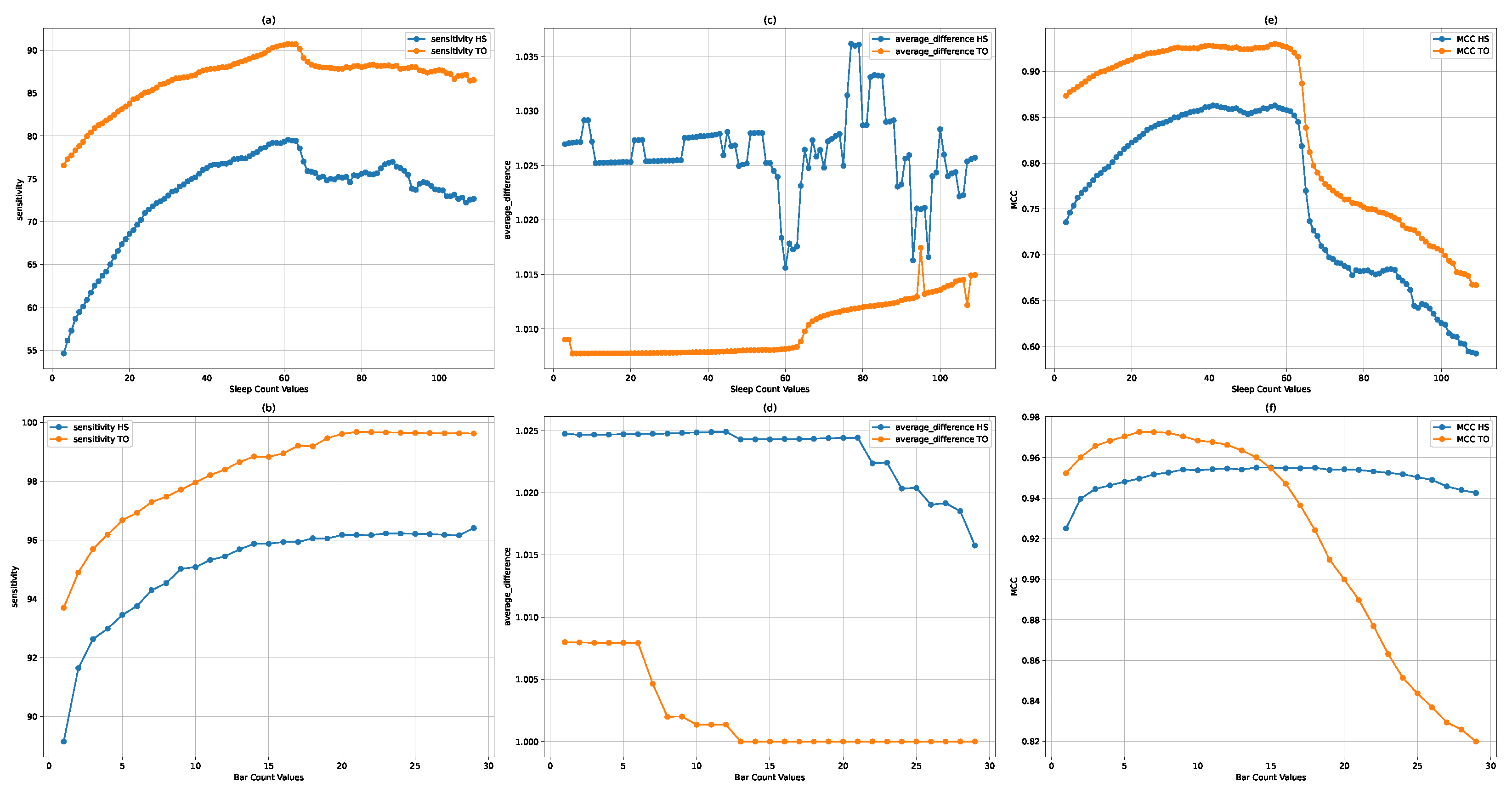
3.3.1. Optimization of Sleeptime
- Sensitivity analysis: The sensitivity metric, which indicates the true positive rate of detecting gait events, showed peak values for both toe-off (TO) and heel strike (HS) events in the range of 60 to 63 s. This suggests an optimal balance between event detection capability and the algorithm’s responsiveness within this sleeptime interval.
- Average difference optimization: The average difference, reflecting the precision in localizing detected events, reached its optimum at a sleeptime of 60 s. This optimal point signifies the highest alignment between detected events and their actual occurrences, thereby minimizing localization error.
- MCC performance: The Matthews correlation coefficient, a comprehensive measure of classification accuracy, exhibited optimal performance within the 55 to 60 s range. Given the MCC’s value in assessing the balance between various aspects of binary classification performance, this finding underscores the efficacy of the DGEI methodology within the specified sleeptime range.
3.3.2. Optimization of Bar
- MCC considerations: The MCC metric, which offers a balanced evaluation of the algorithm’s classification capabilities, identified the 5 to 10 range as optimal. This interval demonstrates a robust performance across detecting true positives and negatives while minimizing errors.
- Sensitivity insights: For the sensitivity metric, values above 8 consistently achieved a performance exceeding 95%. This high sensitivity indicates the algorithm’s effective detection of gait events at higher bar settings.
- Average difference analysis: The average difference across varying bar values showed minimal variation, suggesting that this metric was less sensitive to changes in the bar parameter. This stability implies that the bar setting’s impact on event localization precision is comparatively uniform.
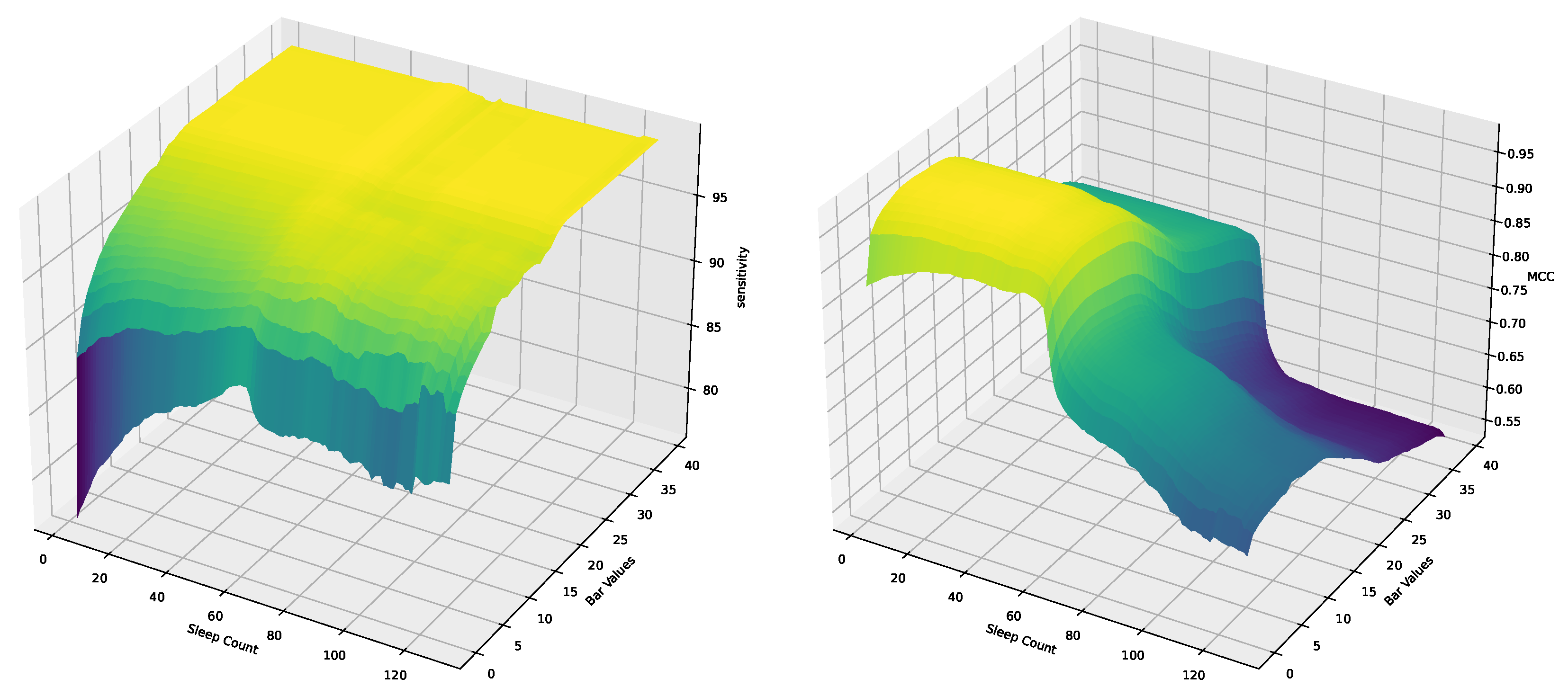
3.3.3. Coupling Analysis of Hyperparameters
- 1.
- Surface analysis: The plots showed smooth surfaces without abrupt changes or discontinuities, suggesting that the interaction between sleeptime and bar does not lead to sudden performance degradations within the explored ranges.
- 2.
- Optimal region identification: A region of the surface consistently demonstrated superior performance across all metrics, located around sleeptime = 60 and bar = 9. This observation confirms the previously determined optimal settings but also emphasizes their robustness in conjunction with one another.
- 3.
- Coupling effect: While varying one hyperparameter affected the performance metrics, the changes were gradual and predictable, indicating a low coupling effect.
3.4. Peak Detection
- 1.
- For the normal gait mode, including scenarios like “Sequential Ambulation + Standard Locomotion”, “Accelerated Initiation − Cessation (Universal)”, and “Standard Locomotion”, the DGEI method exhibited high accuracy. The detection rate, sensitivity, and positive predictive value (PPV) approached or reached 100%. This indicates the DGEI method’s effectiveness in identifying standard gait events.
- 2.
- In highly dynamic gait events, the scenario “Accelerated Initiation − Cessation + Rotational Movement” also nearly achieved perfect scores, demonstrating DGEI’s capability to maintain high accuracy and detection rates even in contexts with rapid changes in gait patterns.
- 3.
- Moreover, in the concatenated data, all “walking start” (WS) and “walking pause” (WP) events were identified and detected, indicating DGEI’s clear discernment of gait cessation and initiation. Tremors during stationary phases were effectively screened and ignored by WS and WP events, explaining the high accuracy in detection.
- 4.
- For the “Static Posture” activity, a detection rate of zero was as expected, since no gait activity occurs in this scenario, thus no heel strike (HS) or toe-off (TO) events are produced. This result confirms DGEI’s specificity, as it correctly does not misidentify stationary states as gait events.
- 5.
- In abnormal gait modes, such as “Dragging” and “Extension Beyond Normal Limits”, the DGEI method showed some reduction in sensitivity. Particularly in the “Dragging” activity, despite a still high detection rate, sensitivity dropped to 68.75%. This decrease could be attributed to the irregularities in the gait pattern affecting the performance of the DGEI method, leading to reduced detection efficacy.
- 6.
- In pathological gait simulations such as “Flexural Rigidity” and “Neurological Disorder Gait”, the DGEI method still demonstrated relatively high detection rates and sensitivity, indicating its applicability for certain pathological gait events.
- 7.
- The DGEI method exhibited very low mean absolute difference (MAD) values in most gait activities, particularly in scenarios like “Sequential Ambulation + Standard Locomotion”, “Accelerated Initiation − Cessation (Universal)”, and “Standard Locomotion”, where the MAD was almost zero. This implies that there was no deviation between the time points generated by the algorithm and those manually annotated, indicating very high accuracy.
- 8.
- For the “Dragging” activity, the MAD value significantly increased to 3.32 samples. This is an important indicator that the algorithm might struggle to accurately identify gait events in irregular gait patterns, leading to larger time discrepancies.
3.5. Error Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Liu, Y.; Wang, X. Efficient Gait Trajectory Prediction Method Based on Soft Constraint Weighted Template Matching: Work-in-Progress. In Proceedings of the 2023 International Conference on Hardware/Software Codesign and System Synthesis (CODES+ISSS), Hamburg, Germany, 17–22 September 2023; pp. 46–47. [Google Scholar]
- Zhu, Q.; Liu, Y.; Liu, M.; Zhang, S.; Chen, G.; Meng, H. Intelligent planning and research on urban traffic congestion. Future Internet 2021, 13, 284. [Google Scholar] [CrossRef]
- Seo, K. Real-Time Estimation of Walking Speed and Stride Length Using an IMU Embedded in a Robotic Hip Exoskeleton. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 12665–12671. [Google Scholar]
- Qin, S.; Yan, J.; Chen, X.; Li, W.; Li, P.; Liu, Z. Assessing the Stability of Human Gait Based on a Human Electrostatic Field Detection System. IEEE Sens. J. 2024, 24, 11036–11047. [Google Scholar] [CrossRef]
- Bejarano, N.C.; Ambrosini, E.; Pedrocchi, A.; Ferrigno, G.; Monticone, M.; Ferrante, S. A novel adaptive, real-time algorithm to detect gait events from wearable sensors. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 23, 413–422. [Google Scholar] [CrossRef]
- Tan, X.; Zhang, B.; Liu, G.; Zhao, X.; Zhao, Y. Cadence-insensitive soft exoskeleton design with adaptive gait state detection and iterative force control. IEEE Trans. Autom. Sci. Eng. 2021, 19, 2108–2121. [Google Scholar] [CrossRef]
- Celik, Y.; Stuart, S.; Woo, W.L.; Godfrey, A. Gait analysis in neurological populations: Progression in the use of wearables. Med. Eng. Phys. 2021, 87, 9–29. [Google Scholar] [CrossRef]
- Fastier-Wooller, J.W.; Lyons, N.; Vu, T.H.; Pizzolato, C.; Rybachuk, M.; Itoh, T.; Dao, D.V.; Maharaj, J.; Dau, V.T. Flexible Iron-On Sensor Embedded in Smart Sock for Gait Event Detection. ACS Appl. Mater. Interfaces 2023, 16, 1638–1649. [Google Scholar] [CrossRef] [PubMed]
- Yifan, L.; Xing, L.; Zhongyan, W.; Xu, Y.; Xingjun, W. Improving performance of human action intent recognition: Analysis of gait recognition machine learning algorithms and optimal combination with inertial measurement units. Comput. Biol. Med. 2023, 163, 107192. [Google Scholar] [CrossRef]
- Pang, D.; Guan, Z.; Luo, T.; Su, W.; Dou, R. Real-time detection of road manhole covers with a deep learning model. Sci. Rep. 2023, 13, 16479. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Kuruvithadam, K.; Schaer, A.; Stoneham, R.; Chatzipirpiridis, G.; Easthope, C.A.; Barry, G.; Martin, J.; Pané, S.; Nelson, B.J.; et al. An intelligent in-shoe system for gait monitoring and analysis with optimized sampling and real-time visualization capabilities. Sensors 2021, 21, 2869. [Google Scholar] [CrossRef]
- Coelho, C.N.; Kuusela, A.; Li, S.; Zhuang, H.; Ngadiuba, J.; Aarrestad, T.K.; Loncar, V.; Pierini, M.; Pol, A.A.; Summers, S. Automatic heterogeneous quantization of deep neural networks for low-latency inference on the edge for particle detectors. Nat. Mach. Intell. 2021, 3, 675–686. [Google Scholar] [CrossRef]
- Xu, D.; Quan, W.; Zhou, H.; Sun, D.; Baker, J.S.; Gu, Y. Explaining the differences of gait patterns between high and low-mileage runners with machine learning. Sci. Rep. 2022, 12, 2981. [Google Scholar] [CrossRef] [PubMed]
- Sonko, S.; Etukudoh, E.A.; Ibekwe, K.I.; Ilojianya, V.I.; Daudu, C.D. A comprehensive review of embedded systems in autonomous vehicles: Trends, challenges, and future directions. World J. Adv. Res. Rev. 2024, 21, 2009–2020. [Google Scholar] [CrossRef]
- Gerhardsson, K.M.; Laike, T. User acceptance of a personalised home lighting system based on wearable technology. Appl. Ergon. 2021, 96, 103480. [Google Scholar] [CrossRef] [PubMed]
- Driessen, J.J.; Laffranchi, M.; De Michieli, L. A reduced-order closed-loop hybrid dynamic model for design and development of lower limb prostheses. Wearable Technol. 2023, 4, e10. [Google Scholar] [CrossRef]
- Skinner, J.W.; Lee, H.K.; Hass, C.J. Evaluation of gait termination strategy in individuals with essential tremor and parkinson’s disease. Gait Posture 2022, 92, 338–342. [Google Scholar] [CrossRef] [PubMed]
- de la Iglesia, D.H.; Mendes, A.S.; González, G.V.; Jiménez-Bravo, D.M.; de Paz Santana, J.F. Connected elbow exoskeleton system for rehabilitation training based on virtual reality and context-aware. Sensors 2020, 20, 858. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhu, Q.; Cao, F.; Chen, J.; Lu, G. High-resolution remote sensing image segmentation framework based on attention mechanism and adaptive weighting. ISPRS Int. J. Geo-Inf. 2021, 10, 241. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, G.; Chen, J.; Zhu, Q. Exploration of internal and external factors of swimmers’ performance based on biofluid mechanics and computer simulation. Int. J. Environ. Res. Public Health 2021, 18, 6471. [Google Scholar] [CrossRef] [PubMed]
- Koo, D.K.; Kwon, J.W. Biomechanical Analysis of Unplanned Gait Termination According to a Stop-Signal Task Performance: A Preliminary Study. Brain Sci. 2023, 13, 304. [Google Scholar] [CrossRef]
- Webber, J.T.; Raichlen, D.A. The role of plantigrady and heel-strike in the mechanics and energetics of human walking with implications for the evolution of the human foot. J. Exp. Biol. 2016, 219, 3729–3737. [Google Scholar] [CrossRef]
- Henderson, G.; Beerse, M.; Liang, H.; Ferreira, D.; Wu, J. Improvement in overground walking after treadmill-based gait training in a child with agenesis of the corpus callosum. Phys. Ther. 2020, 100, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Muhamad, M.; Razak, A.; Halim, A.; Idros, M.M.; Osman, F.; Al Junid, S.; Chee, S.P. Design and Implementation of Wearable IMU Sensor System for Heel-Strike and Toe-Off Gait Parameter Measurement. In Proceedings of the 2023 IEEE International Conference on Applied Electronics and Engineering (ICAEE), Shah Alam, Malaysia, 23–23 September 2023; pp. 1–5. [Google Scholar]
- Li, W.; Lu, W.; Sha, X.; Xing, H.; Lou, J.; Sun, H.; Zhao, Y. Wearable gait recognition systems based on MEMS pressure and inertial sensors: A review. IEEE Sens. J. 2021, 22, 1092–1104. [Google Scholar] [CrossRef]
- Uchitomi, H.; Ming, X.; Zhao, C.; Ogata, T.; Miyake, Y. Classification of mild Parkinson’s disease: Data augmentation of time-series gait data obtained via inertial measurement units. Sci. Rep. 2023, 13, 12638. [Google Scholar] [CrossRef] [PubMed]
- Maas, S.A.; Göcking, T.; Stojan, R.; Voelcker-Rehage, C.; Kutz, D.F. Synchronization of Neurophysiological and Biomechanical Data in a Real-Time Virtual Gait Analysis System (GRAIL): A Proof-of-Principle Study. Sensors 2024, 24, 3779. [Google Scholar] [CrossRef] [PubMed]
- Skvortsov, D.; Chindilov, D.; Painev, N.; Rozov, A. Heel-Strike and Toe-Off Detection Algorithm Based on Deep Neural Networks Using Shank-Worn Inertial Sensors for Clinical Purpose. J. Sens. 2023, 2023, 7538611. [Google Scholar] [CrossRef]
- Molina-Rueda, F.; Fernández-González, P.; Cuesta-Gómez, A.; Koutsou, A.; Carratalá-Tejada, M.; Miangolarra-Page, J.C. Test–Retest Reliability of a Conventional Gait Model for Registering Joint Angles during Initial Contact and Toe-Off in Healthy Subjects. Int. J. Environ. Res. Public Health 2021, 18, 1343. [Google Scholar] [CrossRef]
- Slade, P.; Kochenderfer, M.J.; Delp, S.L.; Collins, S.H. Personalizing exoskeleton assistance while walking in the real world. Nature 2022, 610, 277–282. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Zhu, H. Hyper-parameter optimization: A review of algorithms and applications. arXiv 2020, arXiv:2003.05689. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011, 24, 2546–2554. [Google Scholar]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Alibrahim, H.; Ludwig, S.A. Hyperparameter optimization: Comparing genetic algorithm against grid search and bayesian optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 1551–1559. [Google Scholar]
- Reuter, A.S.; Schindler, M. Motion capture systems and their use in educational research: Insights from a systematic literature review. Educ. Sci. 2023, 13, 167. [Google Scholar] [CrossRef]
- Manupibul, U.; Tanthuwapathom, R.; Jarumethitanont, W.; Kaimuk, P.; Limroongreungrat, W.; Charoensuk, W. Integration of force and IMU sensors for developing low-cost portable gait measurement system in lower extremities. Sci. Rep. 2023, 13, 10653. [Google Scholar] [CrossRef] [PubMed]


| Gait Variation | Sample Size | Detection Rate | Average Deviation | Sensitivity |
|---|---|---|---|---|
| Sequential Ambulation + Standard Locomotion | 554 | 100.00% | 0.00 | 99.46% |
| Standard Locomotion + Rotational Movement | 440 | 99.32% | 0.15 | 95.21% |
| Accelerated Initiation − Cessation + Rotational Movement | 109 | 92.66% | 0.00 | 82.79% |
| Accelerated Initiation − Cessation (Universal) | 51 | 100.00% | 0.00 | 89.47% |
| Standard Locomotion | 31 | 100.00% | 0.00 | 96.88% |
| Static Posture | 53 | 0.00% | 0.00 | 0.00% |
| Flexural Rigidity | 0 | 94.55% | 11.81 | 96.30% |
| Floor Cleaning Activity | 55 | 78.79% | 0.96 | 85.25% |
| Circular Drawing Motion | 66 | 100.00% | 1.41 | 95.92% |
| Digitigrade Locomotion | 47 | 100.00% | 0.00 | 98.00% |
| Neurological Disorder Gait | 58 | 100.00% | 0.00 | 95.08% |
| Extension Beyond Normal Limits | 49 | 90.57% | 1.38 | 87.27% |
| Overall | 1513 | 97.82% | 0.58 | 94.33% |
| Gait Variation | Sample Size | Detection Rate | Average Deviation | Sensitivity |
|---|---|---|---|---|
| Sequential Ambulation + Standard Locomotion | 556 | 100.00% | 0.00 | 99.82% |
| Standard Locomotion + Rotational Movement | 457 | 99.12% | 0.22 | 98.26% |
| Accelerated Initiation − Cessation + Rotational Movement | 121 | 100.00% | 0.00 | 99.18% |
| Accelerated Initiation − Cessation (Universal) | 57 | 100.00% | 0.00 | 100.00% |
| Standard Locomotion | 33 | 100.00% | 0.00 | 100.00% |
| Static Posture | 0 | 0.00% | 0.00 | 0.00% |
| Flexural Rigidity | 53 | 94.34% | 0.00 | 98.04% |
| Floor Cleaning Activity | 62 | 88.71% | 3.32 | 68.75% |
| Circular Drawing Motion | 48 | 100.00% | 0.00 | 100.00% |
| Digitigrade Locomotion | 49 | 100.00% | 0.00 | 98.00% |
| Neurological Disorder Gait | 61 | 98.36% | 0.00 | 100.00% |
| Extension Beyond Normal Limits | 53 | 100.00% | 0.00 | 85.48% |
| Overall | 1550 | 99.03% | 0.18 | 96.91% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, X.; Zhu, Q.; Chen, Y.; Yang, Y.; Xie, H.; Wang, Y.; Wang, X. Adaptive Detection in Real-Time Gait Analysis through the Dynamic Gait Event Identifier. Bioengineering 2024, 11, 806. https://doi.org/10.3390/bioengineering11080806
Liu Y, Liu X, Zhu Q, Chen Y, Yang Y, Xie H, Wang Y, Wang X. Adaptive Detection in Real-Time Gait Analysis through the Dynamic Gait Event Identifier. Bioengineering. 2024; 11(8):806. https://doi.org/10.3390/bioengineering11080806
Chicago/Turabian StyleLiu, Yifan, Xing Liu, Qianhui Zhu, Yuan Chen, Yifei Yang, Haoyu Xie, Yichen Wang, and Xingjun Wang. 2024. "Adaptive Detection in Real-Time Gait Analysis through the Dynamic Gait Event Identifier" Bioengineering 11, no. 8: 806. https://doi.org/10.3390/bioengineering11080806
APA StyleLiu, Y., Liu, X., Zhu, Q., Chen, Y., Yang, Y., Xie, H., Wang, Y., & Wang, X. (2024). Adaptive Detection in Real-Time Gait Analysis through the Dynamic Gait Event Identifier. Bioengineering, 11(8), 806. https://doi.org/10.3390/bioengineering11080806








