Near-Infrared Forearm Vascular Width Calculation Using Radius Estimation of Tangent Circle
Abstract
1. Introduction
2. Related Works
2.1. Image Enhancement
2.2. Calculation of Vascular Width
3. Proposed Computational Method
4. Proposed Vascular Width Calculation Method
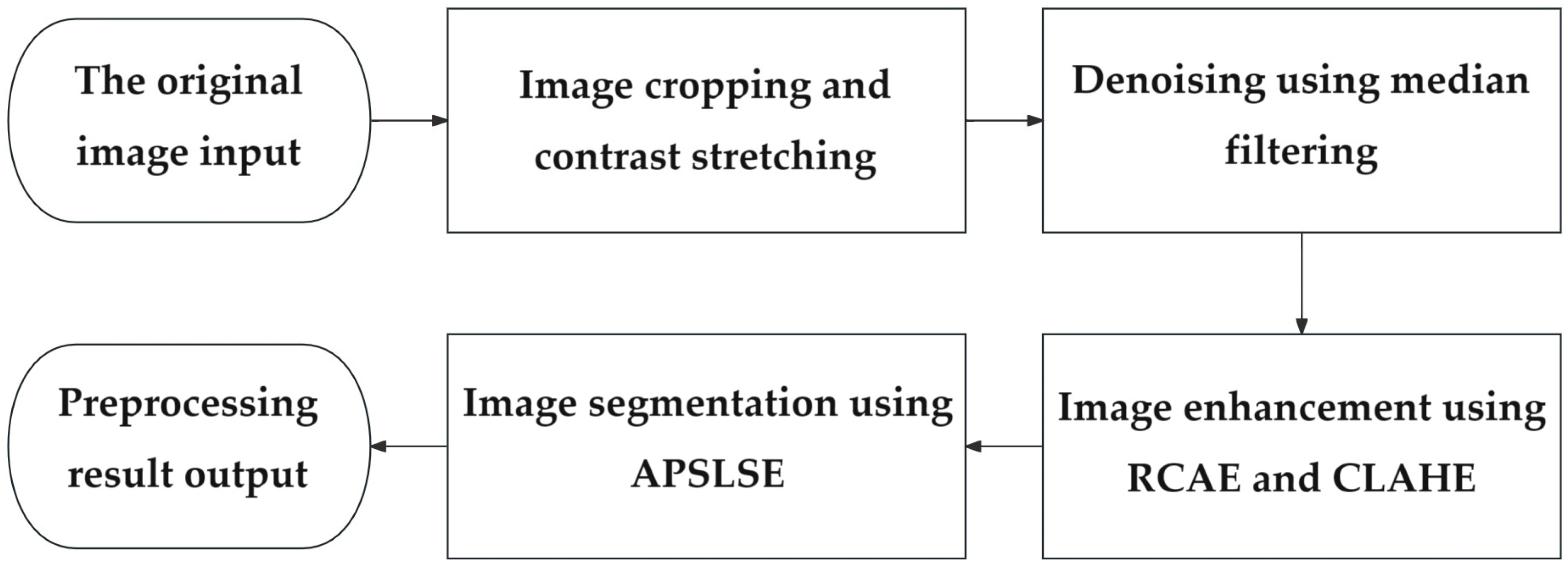
4.1. Image Preprocessing
4.2. Extraction of the Vascular Skeleton
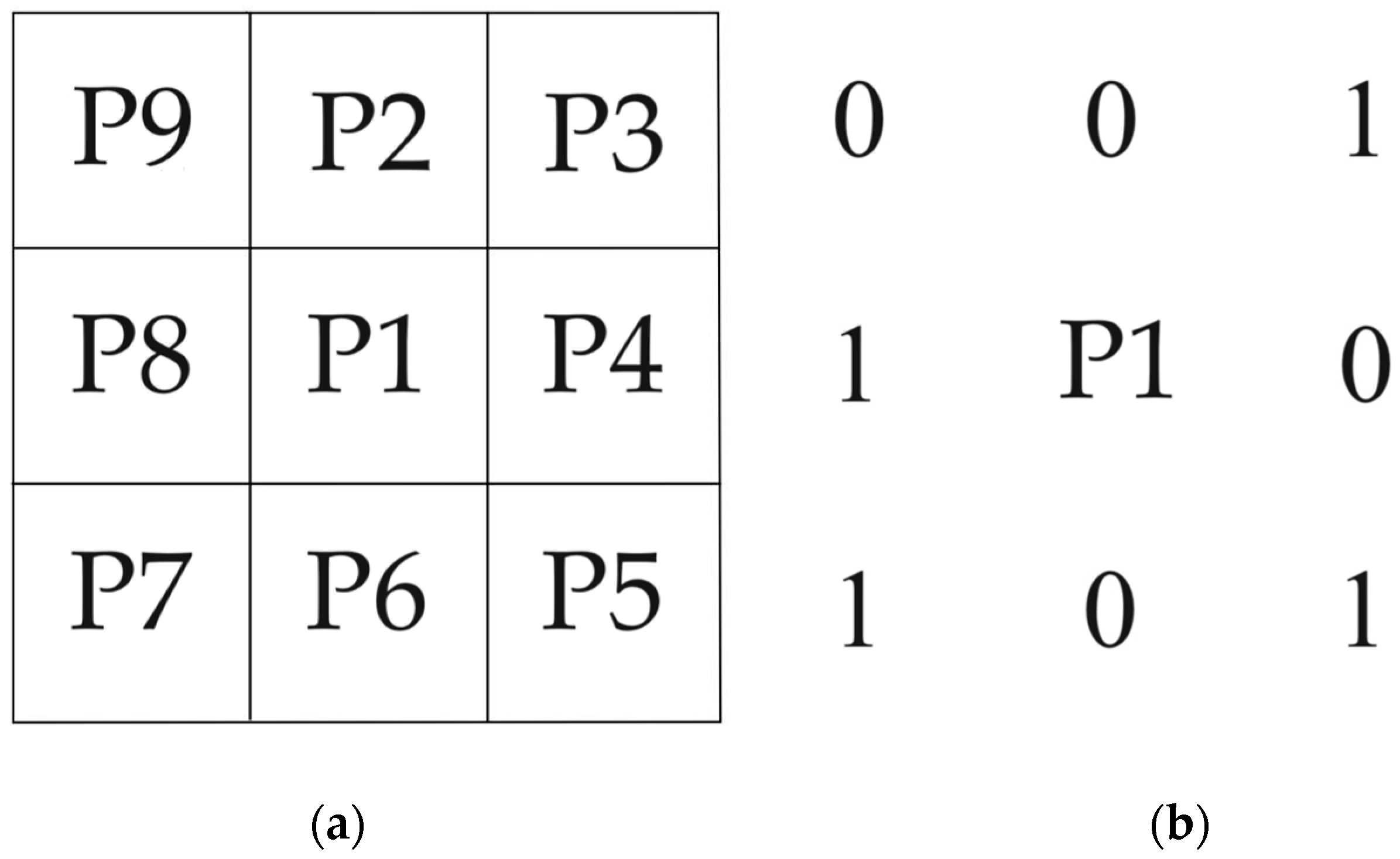
- The first round of iteration: for each pixel P1, the algorithm checks the surrounding eight pixels. The pixel P1 that simultaneously meets the following four conditions will be marked as pending deletion.
- (1)
- The number of white pixels in adjacent pixels around P1 ranges from two to six.
- (2)
- The number of changes in adjacent pixels P2, P3, P4, P5, P6, P7, P8, and P9 around P1 shall not exceed one.
- (3)
- The number of white pixels in adjacent pixels P2, P4, and P6 around P1 should not be less than one.
- (4)
- The number of white pixels in adjacent pixels P4, P6, and P8 around P1 should not be less than one.
- For each foreground pixel P1, the algorithm checks the surrounding eight pixels again. The pixel P1 that simultaneously meets the following four conditions are marked for deletion.
- (1)
- The number of white pixels in adjacent pixels around P1 ranges from two to six.
- (2)
- The number of changes in adjacent pixels P2, P3, P4, P5, P6, P7, P8, and P9 around P1 shall not exceed one.
- (3)
- The number of white pixels in adjacent pixels P2, P4, and P8 around P1 should not be less than one.
- (4)
- The number of white pixels in adjacent pixels P2, P6, and P8 around P1 should not be less than one.
- After the first and second iterations, the algorithm removes all foreground pixels marked as pending deletion from the image.
- The algorithm checks whether the image has changed after the deletion operation. If the image has not changed, it indicates that the refinement has been completed and the algorithm can be terminated; otherwise, the algorithm returns to the first iteration and proceeds to the next iteration.
4.3. Vascular Edge Detection
- Denoising: to reduce the impact of noise, Gaussian filtering is first applied to the image. The Gaussian filtering can blur images, making noise more evenly distributed in the image. The formula for a Gaussian filter is shown in Formula (4), where G(x, y) is the output of the Gaussian filter, x and y are the spatial coordinates of the filter, and η is the standard deviation of the Gaussian kernel.
- Gradient estimation: Canny uses Sobel and other operators to calculate gradient amplitude and direction on the smoothed image. The gradient direction can help determine the direction of edges. The calculation formulas for gradient amplitude GM and gradient direction GD are shown in Formulas (5) and (6), respectively, where Gx is the gradient of the image in the x direction and Gy is the gradient in the y direction.
- Non-maximum suppression: a type of suppression is applied to the gradient map, filtering out non-edge pixels and making blurry boundaries clearer. This process preserves the local maximum values in the gradient direction of each pixel and filters out other values.
- Dual threshold detection: both a high threshold and a low threshold are considered in Canny. If the gradient amplitude of a pixel is greater than the high threshold, it is marked as a strong edge. On the other hand, if the gradient amplitude is between the low and high thresholds, it is marked as a weak edge. Otherwise, it will be marked as a non-edge.
- Edge tracking: based on the connectivity of strong edges, the weak edges connected to them are marked as edges, while other weak edges are deleted.
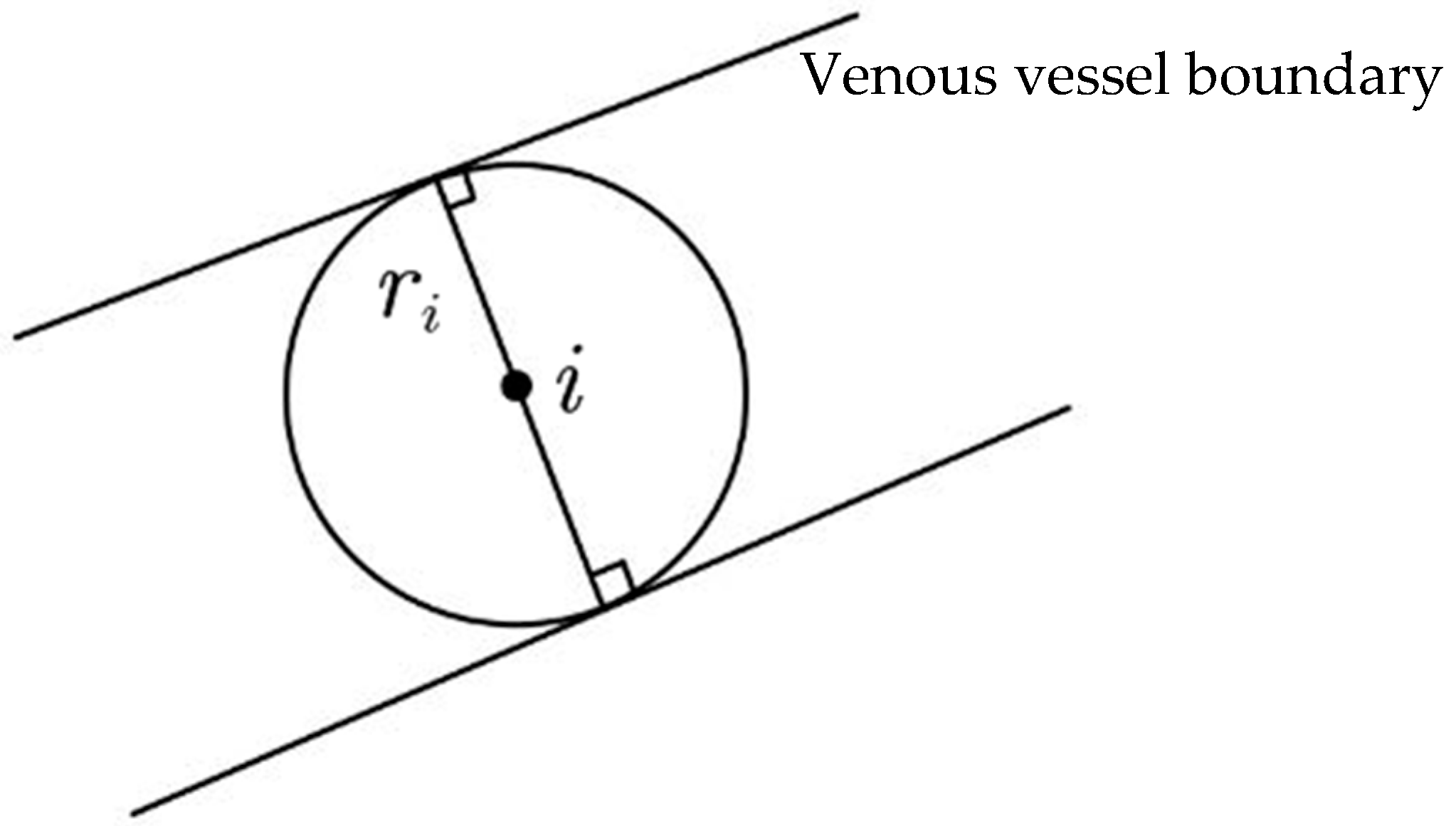
4.4. The RETC Algorithm
5. Experiments and Discussion
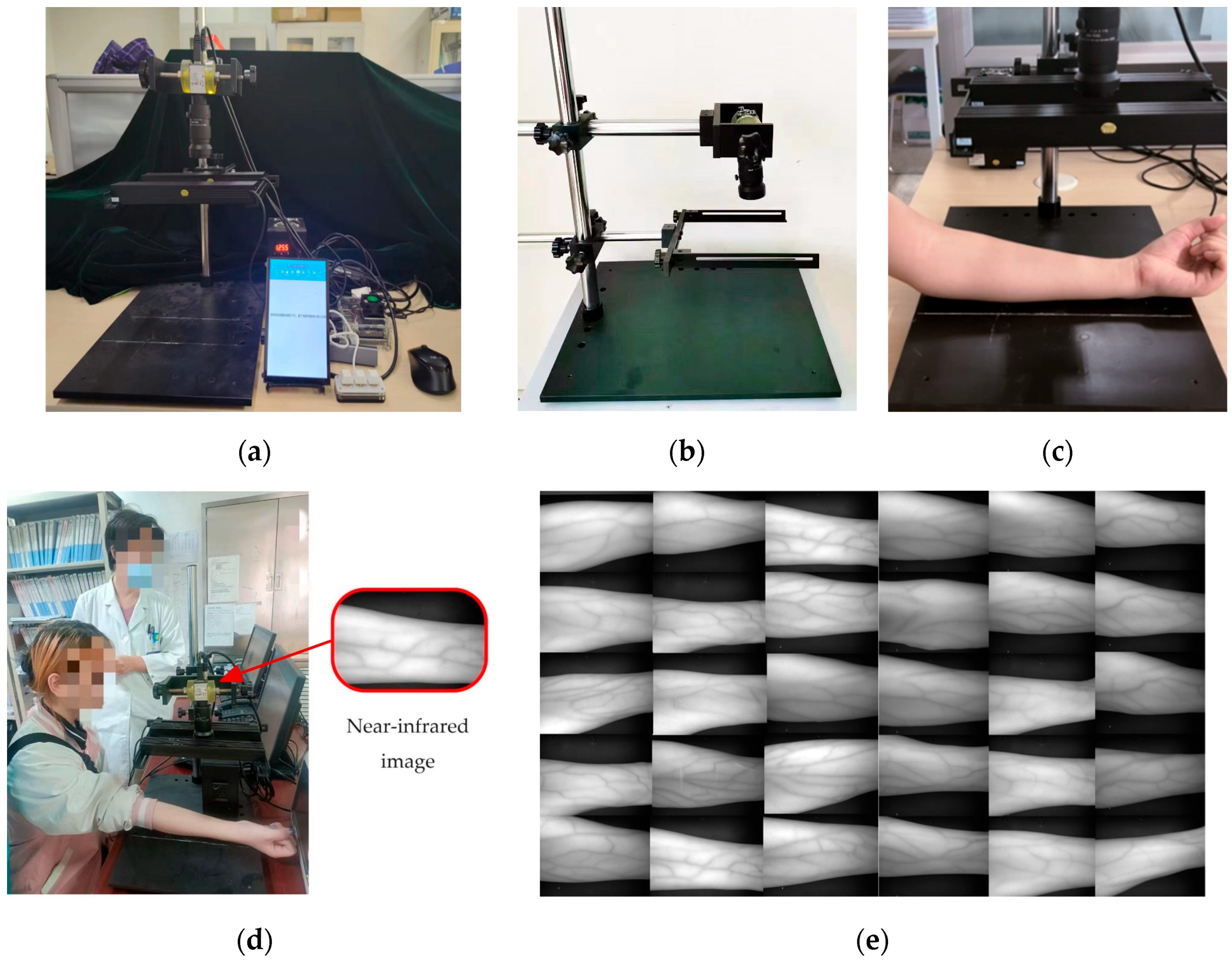
5.1. Experiment System and Data
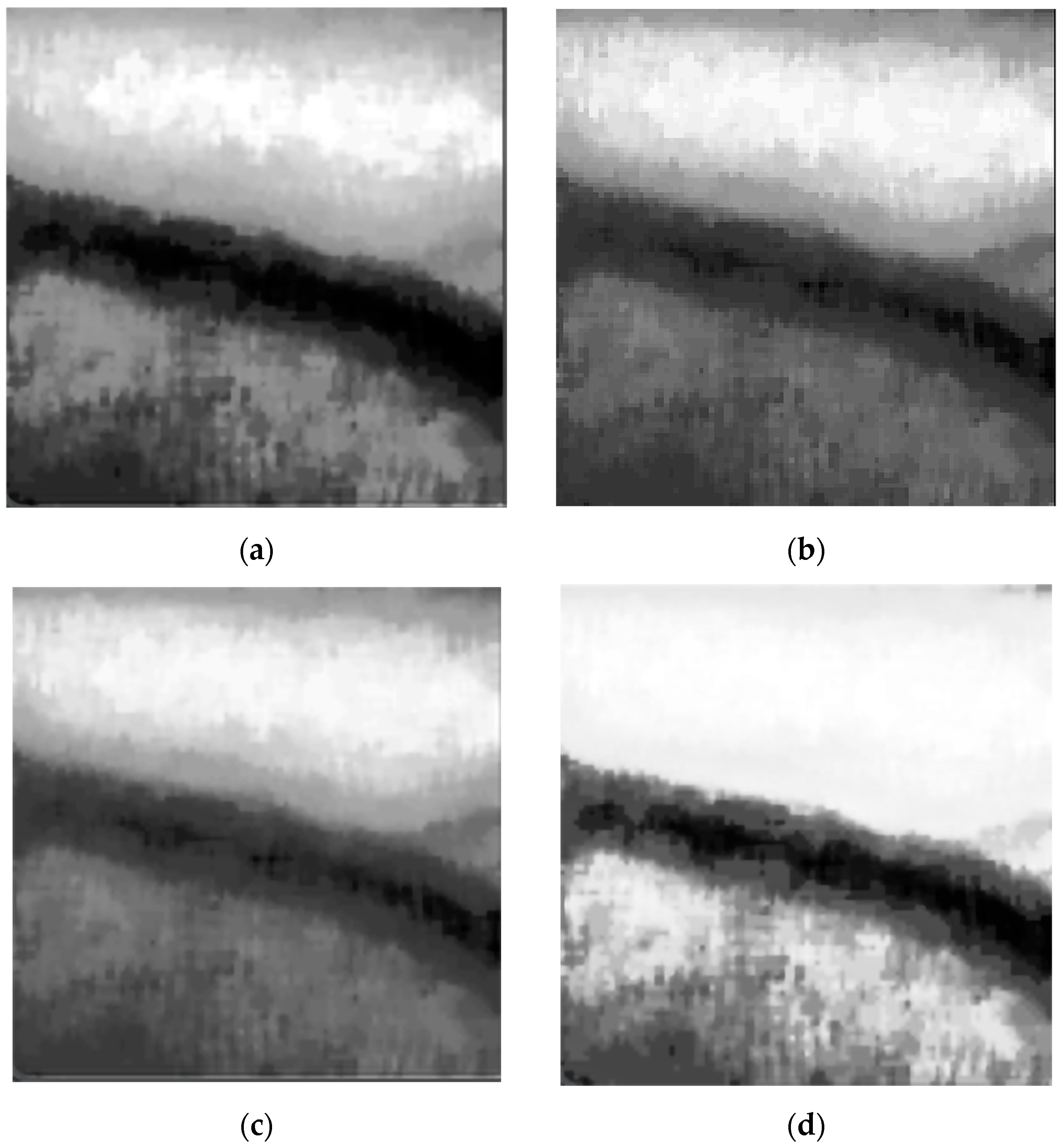
5.2. Evaluation of Image Enhancement Algorithm
5.3. Evaluation of Vascular Skeleton Extraction Algorithm
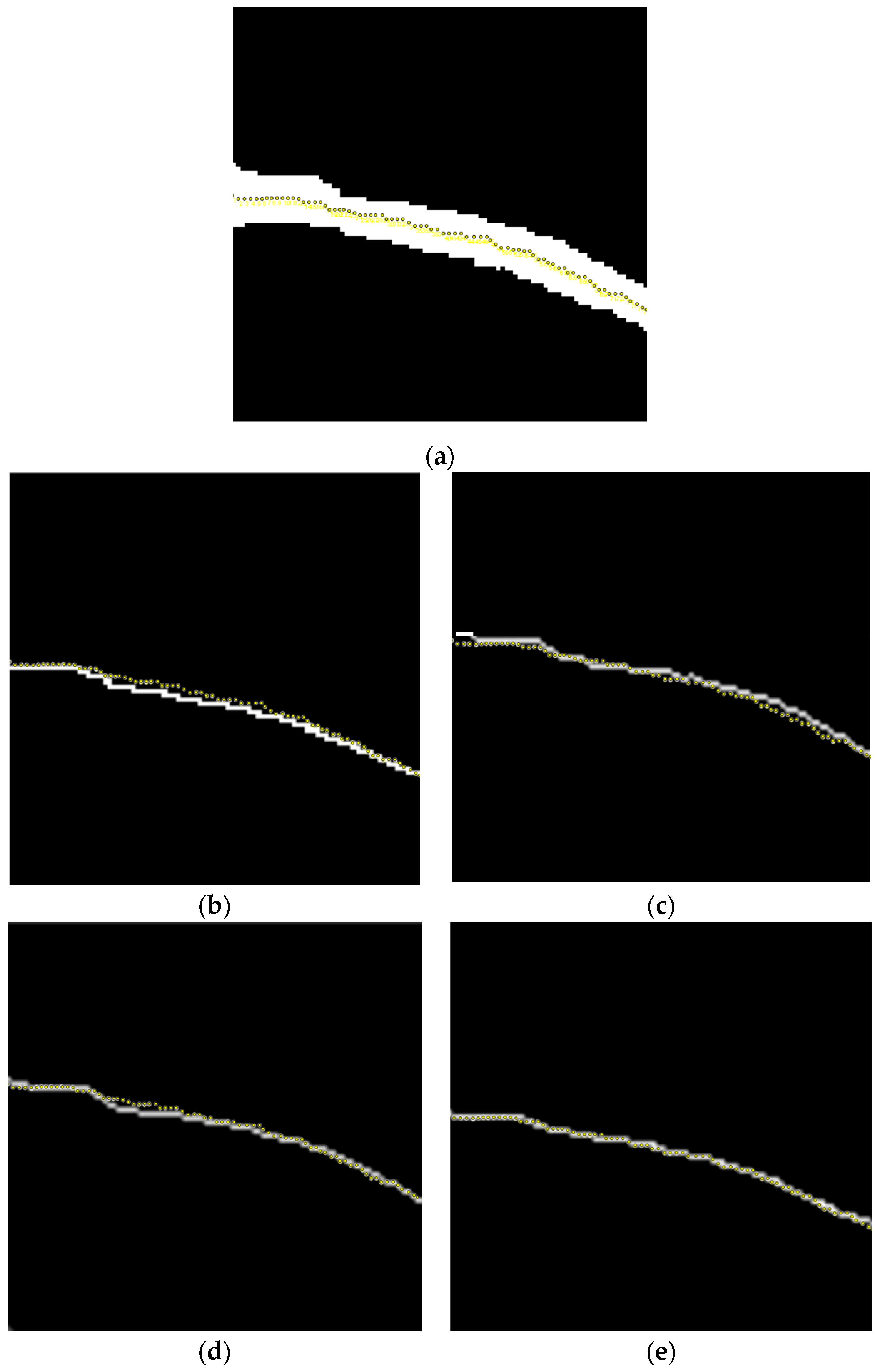
5.4. Evaluation of Vascular Edge Detection Algorithm
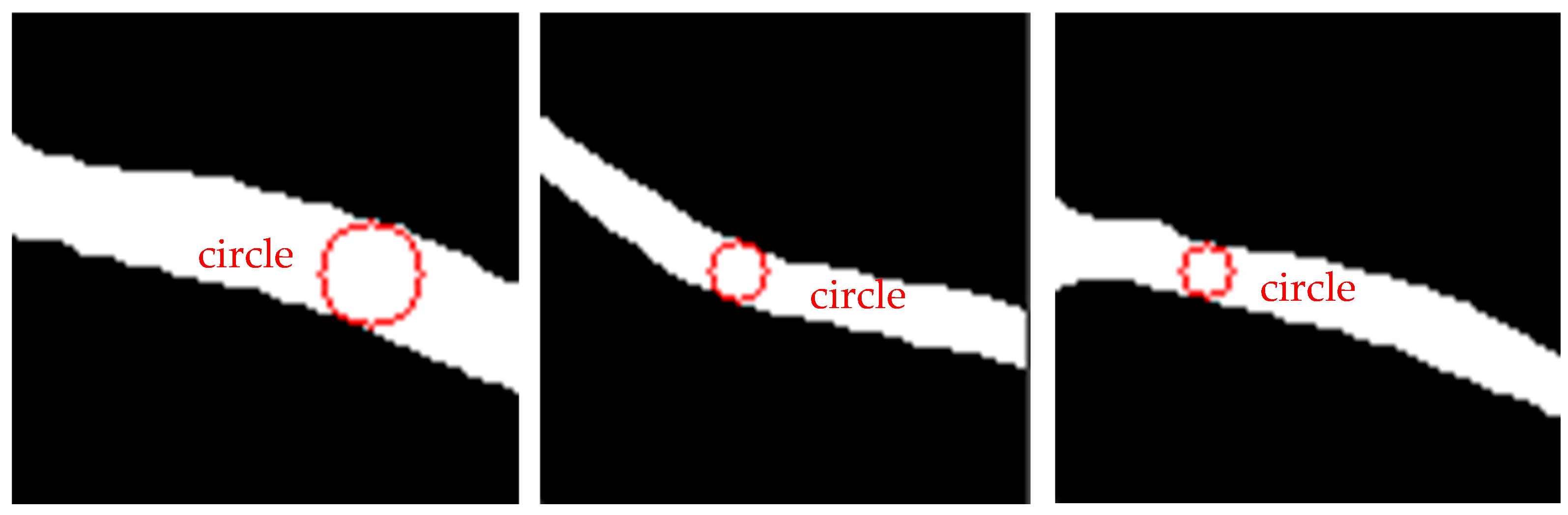
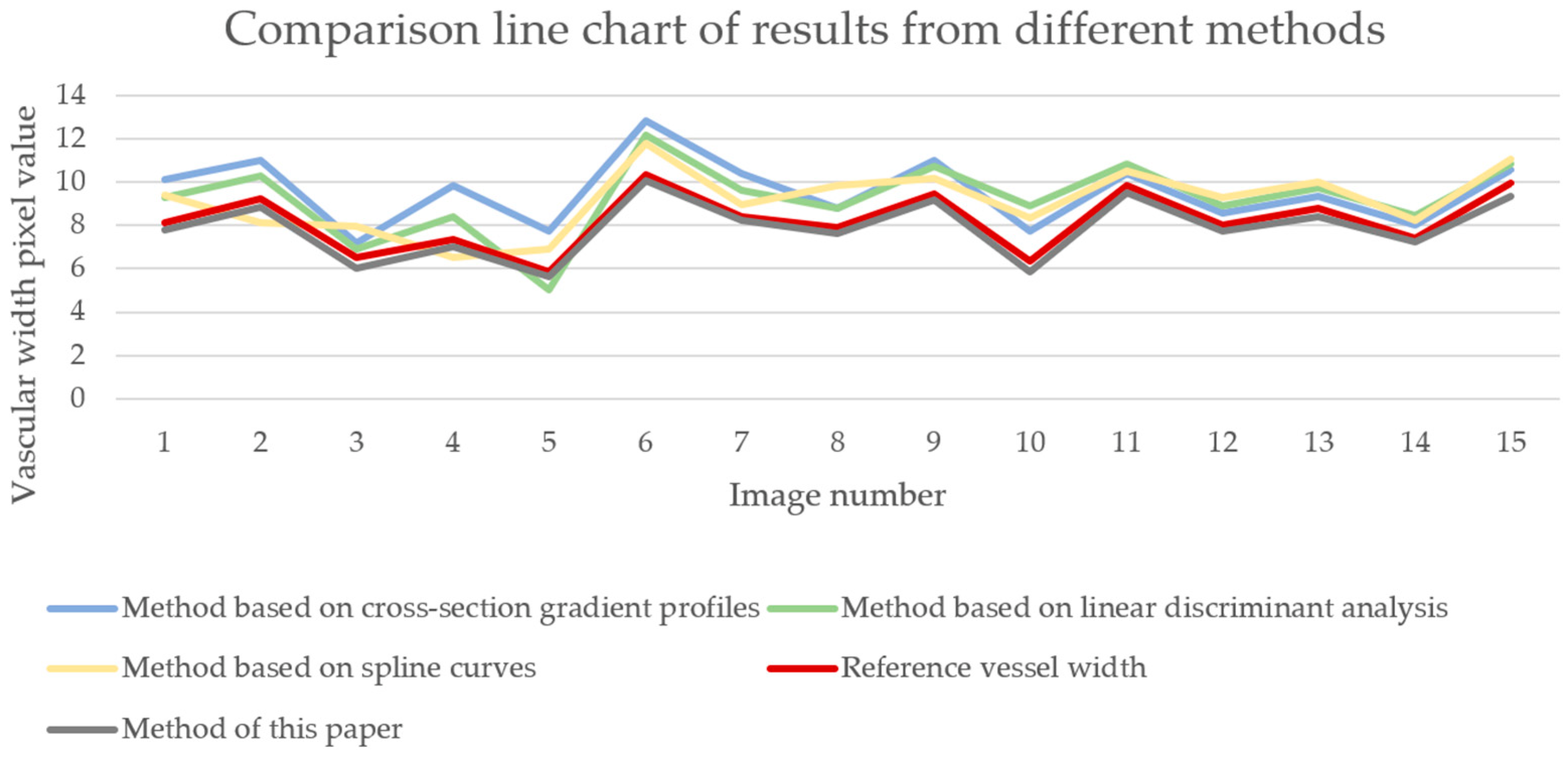
5.5. Evaluation of RETC Algorithm
5.6. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Pseudocode for the Zhang–Suen Refinement Algorithm
Appendix B. Numerical Calculation Methods for the Roberts, Sobel, and Prewitt Operators
Appendix C. Pseudocode for RETC Algorithm
References
- Matsushita, K.; Ballew, S.H.; Wang, A.Y.; Kalyesubula, R.; Schaeffner, E.; Agarwal, R. Epidemiology and risk of cardiovascular disease in populations with chronic kidney disease. Nat. Rev. Nephrol. 2022, 18, 696–707. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, P.-J.; Wang, R.-L.; Hu, F.-K.; Tsai, F.-R.; Chiu, C.-C.; Chiang, W.-F.; Wu, K.-L.; Li, Y.-K.; Chan, J.-S.; Chu, C.-M.; et al. Biomedical evaluation of early chronic kidney disease in the air force: Building a predictive model from the Taiwan military health service. Bioengineering 2024, 11, 231. [Google Scholar] [CrossRef] [PubMed]
- Foreman, K.J.; Marquez, N.; Dolgert, A.; Fukutaki, K.; Fullman, N.; McGaughey, M.; Pletcher, M.A.; Smith, A.E.; Tang, K.; Yuan, C.W.; et al. Forecasting life expectancy, years of life lost, and all-cause and cause-specific mortality for 250 causes of death: Reference and alternative scenarios for 2016-40 for 195 countries and territories. Lancet 2018, 392, 2052–2090. [Google Scholar] [CrossRef] [PubMed]
- Romagnani, P.; Remuzzi, G.; Glassock, R.; Levin, A.; Jager, K.J.; Tonelli, M.; Massy, Z.; Wanner, C.; Anders, H.J. Chronic kidney disease. Nat. Rev. Dis. Primers 2017, 23, 17088. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, A.; Branco, C.; Sant’Ana, M.; Costa, C.; Silva, B.; Fonseca, J.; Outerelo, C.; Gameiro, J. Hypoalbuminaemia and one-year mortality in haemodialysis patients with heart failure: A cohort analysis. J. Clin. Med. 2021, 10, 4518. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, V.; Khademian, M.H.; Masoumi, S.J.; Morvaridi, M.R.; Ezzatzadegan, J.S. Factors influencing survival time of hemodialysis patients; time to event analysis using parametric models: A cohort study. BMC Nephrol. 2019, 20, 215. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Tang, X.; Shen, A.; Sun, B.; Yu, S. Research progress on nocturnal hemodialysis. Acad. J. Second Mil. Med. Univ. 2017, 38, 982–986. [Google Scholar]
- Zhang, W.; Zhang, M.; Wang, M.; Chen, J. Recent advances on vascular calcification of arteriovenous fistula in hemodialysis. Chin. J. Nephrol. 2018, 34, 391–395. [Google Scholar]
- Kim, J.M.; Ko, H.; Kim, M.S. Predicting factors for early failure of vascular access in hemodialysis patients. Ann. Surg. Treat. Res. 2024, 106, 255–262. [Google Scholar] [CrossRef]
- Li, C.; Hu, H. The role of stent grafts in hemodialysis vascular access. J. Mod. Med. Health 2022, 38, 440–445. [Google Scholar]
- Yun, G.K.; Hyun, S.L.; Hyun, S.K.; Jeongsu, K.; Hyun, Y.P. Temporary arteriovenous fistula compression for clinical decision-making in patients on hemodialysis with significant aortic stenosis. J. Cardiovasc. Imaging 2023, 31, 118–120. [Google Scholar]
- Buffet-García, J.; Vicente-Campos, D.; López-Redondo, M.; Sánchez-Jorge, S.; Álvarez-González, J.; Plaza-Manzano, G.; Seijas-Fernández, T.; Valera-Calero, J.A. Association between gray-scale ultrasound imaging and serological creatine kinase for quantifying exercise-induced muscle damage: An observational study. Bioengineering 2024, 11, 40. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-W.; Hong, S.-U.; Lee, J.-H.; Park, S.-Y. Estimation of validity of a-mode ultrasound for measurements of muscle thickness and muscle quality. Bioengineering 2024, 11, 149. [Google Scholar] [CrossRef] [PubMed]
- Sui, M.; Mao, Y.; Sun, J. Live face detection based on near-infrared image features. Autom. Instrum. 2021, 9, 25–29. [Google Scholar]
- Koichi, A.; Yuta, H.; Chawan, K.; Keiko, O.O.; Norimichi, T. Monitoring respiratory state from near-infrared face video images. Artif. Life Robot. 2024, 29, 197–203. [Google Scholar]
- Cong, M.; Wu, T.; Liu, D.; Yang, D.; Du, Y. Prostate MR/TRUS image segmentation and registration methods based on supervised learning. Chin. J. Eng. 2020, 42, 1362–1371. [Google Scholar]
- Ma, B.; Jiang, S.; Yin, D.; Shen, H.; Ban, X.; Huang, H.; Wang, H.; Xue, W.; Feng, H. Image segmentation metric and its application in the analysis of microscopic image. Chin. J. Eng. 2021, 43, 137–149. [Google Scholar]
- Lam, L.; Lee, S.; Suen, C.Y. Thinning methodologies-a comprehensive survey. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 869–885. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, R.; Chen, D.; Dong, Y.; Fu, Z.; Luan, Q. Improved Canny edge detection method based on self-adaptive threshold. J. Optoelectron. Laser 2024, 35, 164–170. [Google Scholar]
- Dhal, K.G.; Das, A.; Ray, S. Histogram equalization variants as optimization problems: A review. Arch. Comput. Methods Eng. 2021, 28, 1471–1496. [Google Scholar] [CrossRef]
- Panetta, K.; Zhou, Y.; Agaian, S.; Jia, H. Nonlinear Unsharp Masking for Mammogram Enhancement. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 918–928. [Google Scholar] [CrossRef] [PubMed]
- Ling, J.; Chen, J.; Li, H. FDT: Improving the transferability of adversarial examples with frequency domain transformation. Comput. Secur. 2024, 144, 103942. [Google Scholar] [CrossRef]
- Midtskogen, S.; Valin, J. The Av1 Constrained Directional Enhancement Filter (CDEF). In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 1193–1197. [Google Scholar]
- Wen, X.; Zhao, J.; Liang, X. Image enhancement of finger-vein patterns based on wavelet denoising and histogram template equalization. J. Jilin Univ. (Sci. Ed.) 2008, 46, 291–292. [Google Scholar]
- Yang, C.; Shang, H.; Jia, C.; Huang, L. Adaptive unsharp masking method based on region segmentation. Opt. Precis. Eng. 2003, 11, 188–192. [Google Scholar]
- Yang, S.; Yang, J.; Song, Y. Finger vein image enhancement algorithm based on wavelet transform. Mod. Electron. Technol. 2013, 36, 73–75. [Google Scholar]
- Wang, Y.; Deng, G.; Xia, Y.; Zhang, L.; Liu, Y.; Zhang, W. Vascular image enhancement using steerable filters. J. Syst. Simul. 2018, 30, 2095–2101. [Google Scholar]
- Yakno, M.; Saleh, J.M.; Rosdi, B.A. Low contrast hand vein image enhancement. In Proceedings of the IEEE International Conference on Signal and Image Processing Applications, Kuala Lumpur, Malaysia, 16–18 November 2011; pp. 390–392. [Google Scholar]
- Shin, K.; Park, Y.; Nguyen, D.; Park, K. Finger-vein image enhancement using a fuzzy-based fusion method with Gabor and Retinex filtering. Sensors 2014, 14, 3095–3129. [Google Scholar] [CrossRef]
- Truc, P.; Khan, M.; Lee, Y.; Lee, S.; Kim, T. Vessel enhancement filter using directional filter bank. Comput. Vis. Image Underst. 2009, 113, 101–112. [Google Scholar] [CrossRef]
- Delibasis, K.K.; Kechriniotis, I.A.; Tsonos, C.; Assimakis, N. Automatic model-based tracing algorithm for vessel segmentation and diameter estimation. Comput. Methods Programs Biomed. 2010, 100, 108–122. [Google Scholar] [CrossRef]
- Sun, G.; Liu, X.; Wang, S. Width measurement for pathological vessels in retinal images using centerline correction and k-means clustering. Measurement 2019, 139, 185–195. [Google Scholar] [CrossRef]
- Xu, X.; Reinhardt, J.M.; Hu, Q.; Bakall, B.; Tlucek, P.S.; Bertelsen, G.; Abramoff, M.D. Retinal vessel width measurement at branchings using an improved electric field theory-based graph approach. PLoS ONE 2012, 7, e49668. [Google Scholar]
- Xu, X.; Niemeijer, M.; Song, Q.; Garvin, M.K.; Reinhardt, J.M.; Abramoff, M.D. Retinal vessel width measurements based on a graph-theoretic method. In Proceedings of the IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Chicago, IL, USA, 30 March–2 April 2011; pp. 641–644. [Google Scholar]
- Pakter, H.; Ferlin, E.; Fuchs, S.; Maestri, M.; Moraes, R.; Nunes, G.; Moreira, L.; Gus, M.; Fuchs, F. Measuring arteriolar-to-venous ratio in retinal photography of patients with hypertension: Development and application of a new semi-automated method. Am. J. Hypertens. 2005, 18, 417–421. [Google Scholar] [CrossRef] [PubMed]
- Yao, C. Research and Application of Retinal Image Segmentation Methods. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2009. [Google Scholar]
- Lupaşcu, C.A.; Tegolo, D.; Trucco, E. Accurate estimation of retinal vessel width using bagged decision trees and an extended multiresolution hermite model. Med. Image Anal. 2013, 17, 1164–1180. [Google Scholar] [CrossRef] [PubMed]
- Ren, H. Near-Infrared Vein Image Feature Enhancement and Visualization Algorithm. Master’s Thesis, China University of Mining and Technology, Beijing, China, 2014. [Google Scholar]
- Wang, L.; Meng, Q.; Guo, Y.; Jiao, Q. Measurement of coronary artery diameter on DSA image based on Hessian matrix. Chin. J. Med. Phys. 2019, 36, 1182–1186. [Google Scholar]
- Wang, C.; Li, Y.; Liu, B.; Xiang, H.; Xu, K.; Zheng, G.; Chen, M.; Zhang, D. Research on vessel diameter measurement based on clustering algorithm. Opt. Technol. 2021, 47, 37–44. [Google Scholar]
- Chen, J.; Zhao, L.; Li, D.; Wan, T. Automated detection and quantification of coronary artery stenoses based on vessel tree segmentation in X-ray angiography. Chin. J. Biomed. Eng. 2019, 38, 266–272. [Google Scholar]
- Zhang, Y.; Chen, X. Research on infrared image denoising method based on residual convolutional autoencoder (RCAE). Inf. Technol. Inf. 2019, 12, 242–244. [Google Scholar]
- Francis, M.; Jose, A.; Devadhas, G.G.; Avinashe, K.K. A novel technique for forearm blood vein detection and enhancement. Biomed. Res. 2017, 28, 2913–2919. [Google Scholar]
- Zhang, T.Y.; Suen, C.Y. A fast parallel algorithm for thinning digital patterns. Commun. ACM 1984, 27, 236–239. [Google Scholar] [CrossRef]
- Thapa, S.; Lomholt, M.; Krog, J.; Cherstvy, A.; Metzler, R. Bayesian analysis of single-particle tracking data using the nested-sampling algorithm: Maximum-likelihood model selection applied to stochastic-diffusivity data. Phys. Chem. Chem. Phys. 2018, 20, 29018–29037. [Google Scholar] [CrossRef] [PubMed]
- Bhawna, D.; Neetu, M.; Megha, M. Hybrid Particle Swarm Optimized and Fuzzy C Means Clustering based segmentation technique for investigation of COVID-19 infected chest CT. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2023, 11, 197–204. [Google Scholar]
- Fu, L.; Ju, J.; Yang, Q. RSS type-set fault diagnosis method for TE process. J. Shenyang Univ. Technol. 2021, 40, 6–11. [Google Scholar]
- Kushwaha, S.; Amuthachenthiru, K.; Geetha, K.; Narasimharao, J.; Kumar, D.M.; Gadde, S.S. Development of advanced noise filtering techniques for medical image enhancement. In Proceedings of the 2024 5th International Conference on Intelligent Communication Technologies and Virtual Mobile Networks (ICICV), Tirunelveli, India, 11–12 March 2024; pp. 906–912. [Google Scholar]
- Alwazzan, M.J.; Ismael, M.A.; Ahmed, A.N. A hybrid algorithm to enhance colour retinal fundus images using a Wiener filter and CLAHE. J. Digit. Imaging 2021, 34, 750–759. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, H.; Tian, Z.; Geng, W. Near-infrared vascular image segmentation using improved level set method. Infrared Phys. Technol. 2023, 131, 104678. [Google Scholar] [CrossRef]
- Li, D. Optimization Design of image edge detection based on Sobel operator. Dig. Technol. Appl. 2017, 11, 137–138. [Google Scholar]
- Yao, Z.; Chu, X.; Fan, J.; Wang, F. Research on effective wave height inversion of X-band radar based on Prewitt operator. Syst. Eng. Electron. 2022, 44, 1182–1187. [Google Scholar]
- Jiao, J. Laser reproduction method of digital media based on Roberts edge detection. J. Laser 2022, 43, 197–200. [Google Scholar]
- Wang, W.; Jiang, M.; Zhao, W. Improved edge detection algorithm based on Canny operator. Chin. J. Sci. Technol. Pap. 2017, 12, 910–915. [Google Scholar]
- Zhou, L.; Shen, J.; Liao, W.; Wang, Y. Retinal vessel segmentation based on centerline extraction. J. Biomed. Eng. Res. 2012, 29, 1–6. [Google Scholar]
- Chen, L. Analysis of digital X-ray image enhancement method based on histogram equalization. Shanghai Chem. Ind. 2023, 48, 26–29. [Google Scholar]
- Cheng, T.; Lu, X.; Yi, Q.; Tao, Z.; Zhang, Z. An infrared image enhancement method combining single-scale Retinex with guided filtering. Infrared Technol. 2021, 43, 1081–1088. [Google Scholar]
- Xia, Y.; Xiao, B.; Zhu, Y. Research on information filling card recognition method based on fuzzy Hit-Miss transform. J. Comput. Appl. Res. 2009, 26, 1822–1824. [Google Scholar]
- Yang, W.; Guo, K.; Wei, Y. An effective eight-neighborhood lookup-based fingerprint image thinning algorithm. J. Sichuan Univ. Sci. Eng. (Nat. Sci. Ed.) 2008, 2, 61–63. [Google Scholar]
- You, S.; Zhang, H.; Zhou, Y.; Zhang, X. Repair of breakpoints on centerline of welding seam structured light based on Hilditch algorithm. J. Heat Treat. Technol. 2020, 49, 134–138+145. [Google Scholar]
- Guo, Y.; Ma, X. Measurement method of change rate of retinal vascular width difference in fundus images. Chin. J. Sci. Instrum. 2016, 37, 912–919. [Google Scholar]
- Li, Q.; You, J.; Zhang, D. Vessel segmentation and width estimation in retinal images using multiscale production of matched filter responses. Expert Syst. Appl. 2012, 39, 7600–7610. [Google Scholar] [CrossRef]
- Khan, T.M.; Khan, M.A.; Rehman, N.U.; Naveed, K.; Afridi, I.U.; Naqvi, S.S.; Raazak, I. Width-wise vessel bifurcation for improved retinal vessel segmentation. Biomed. Signal Process. Control 2022, 71, 103169. [Google Scholar] [CrossRef]
- Alvarado-Carrillo, D.E.; Dalmau-Cedeño, O.S. Width Attention based Convolutional Neural Network for Retinal Vessel Segmentation. Expert Syst. Appl. 2022, 209, 118313. [Google Scholar] [CrossRef]
- Wu, H.; Wang, S. Abnormal data recognition algorithm for GNSS deformation monitoring. Sci-Tech Innov. Prod. 2019, 1, 30–34. [Google Scholar] [CrossRef]
- Janczyk, M.; Pfister, R. Understanding Inferential Statistics–From A for Significance Test to Z for Confidence Interval, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2023; pp. 97–155. [Google Scholar]
- Jia, D.; Hao, L.; Zhou, S.; Li, S. A new approach to centerlines and widths measurement of blood vessels in x-ray angiogram. Chin. J. Biomed. Eng. 2007, 2, 214–219+225. [Google Scholar]
- Kumar, D.K.; Aliahmad, B.; Hao, H. Retinal vessel diameter measurement using unsupervised linear discriminant analysis. Int. Sch. Res. Not. 2012, 2012, 151369. [Google Scholar] [CrossRef]
- Roysam, B.; Stewart, C.; Fritzsche, K. Determining retinal vessel widths and detection of width changes. In Automated Image Detection of Retinal Pathology; CRC Press: Boca Raton, FL, USA, 2009; pp. 269–304. [Google Scholar]




| Methods | ||
|---|---|---|
| Circular structure [61] | 0.49 | 0.16 |
| Graph theory [34] | 1.12 | 0.30 |
| Cubic spline fitting [35] | 1.31 | 0.28 |
| Decision Tree [37] | 2.14 | 0.42 |
| Multi-scale matched filtering [62] | 1.05 | 0.57 |
| BM3D and multi-scale line detection [63] | 0.83 | 0.24 |
| WA-Net [64] | 0.41 | 0.22 |
| Method of this paper | 0.36 | 0.10 |
| Features | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Gender | male | male | male | male | male | female | female | female | female | female |
| Age | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| Height (cm) | 182 | 163 | 175 | 165 | 180 | 156 | 160 | 160 | 162 | 172 |
| Weight (kg) | 62 | 62 | 56 | 60 | 75 | 44 | 52 | 65 | 60 | 56 |
| Vascular width | 10.57 | 8.46 | 8.09 | 9.2 | 9.12 | 7.82 | 8.72 | 9.02 | 9.29 | 8.73 |
| Reference vascular width | 11.2 | 8.7 | 8.5 | 9.6 | 9.4 | 8.1 | 9.2 | 9.5 | 9.9 | 9.1 |
| accuracy | 0.94 | 0.97 | 0.95 | 0.96 | 0.97 | 0.97 | 0.95 | 0.95 | 0.94 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Q.; Liu, H.; Tian, Z.; Wang, S.; Li, Q.; Yi, D. Near-Infrared Forearm Vascular Width Calculation Using Radius Estimation of Tangent Circle. Bioengineering 2024, 11, 801. https://doi.org/10.3390/bioengineering11080801
Ji Q, Liu H, Tian Z, Wang S, Li Q, Yi D. Near-Infrared Forearm Vascular Width Calculation Using Radius Estimation of Tangent Circle. Bioengineering. 2024; 11(8):801. https://doi.org/10.3390/bioengineering11080801
Chicago/Turabian StyleJi, Qianru, Haoting Liu, Zhen Tian, Song Wang, Qing Li, and Dewei Yi. 2024. "Near-Infrared Forearm Vascular Width Calculation Using Radius Estimation of Tangent Circle" Bioengineering 11, no. 8: 801. https://doi.org/10.3390/bioengineering11080801
APA StyleJi, Q., Liu, H., Tian, Z., Wang, S., Li, Q., & Yi, D. (2024). Near-Infrared Forearm Vascular Width Calculation Using Radius Estimation of Tangent Circle. Bioengineering, 11(8), 801. https://doi.org/10.3390/bioengineering11080801








