Machine Learning Meets Meta-Heuristics: Bald Eagle Search Optimization and Red Deer Optimization for Feature Selection in Type II Diabetes Diagnosis
Abstract
1. Introduction
Review of Related Works
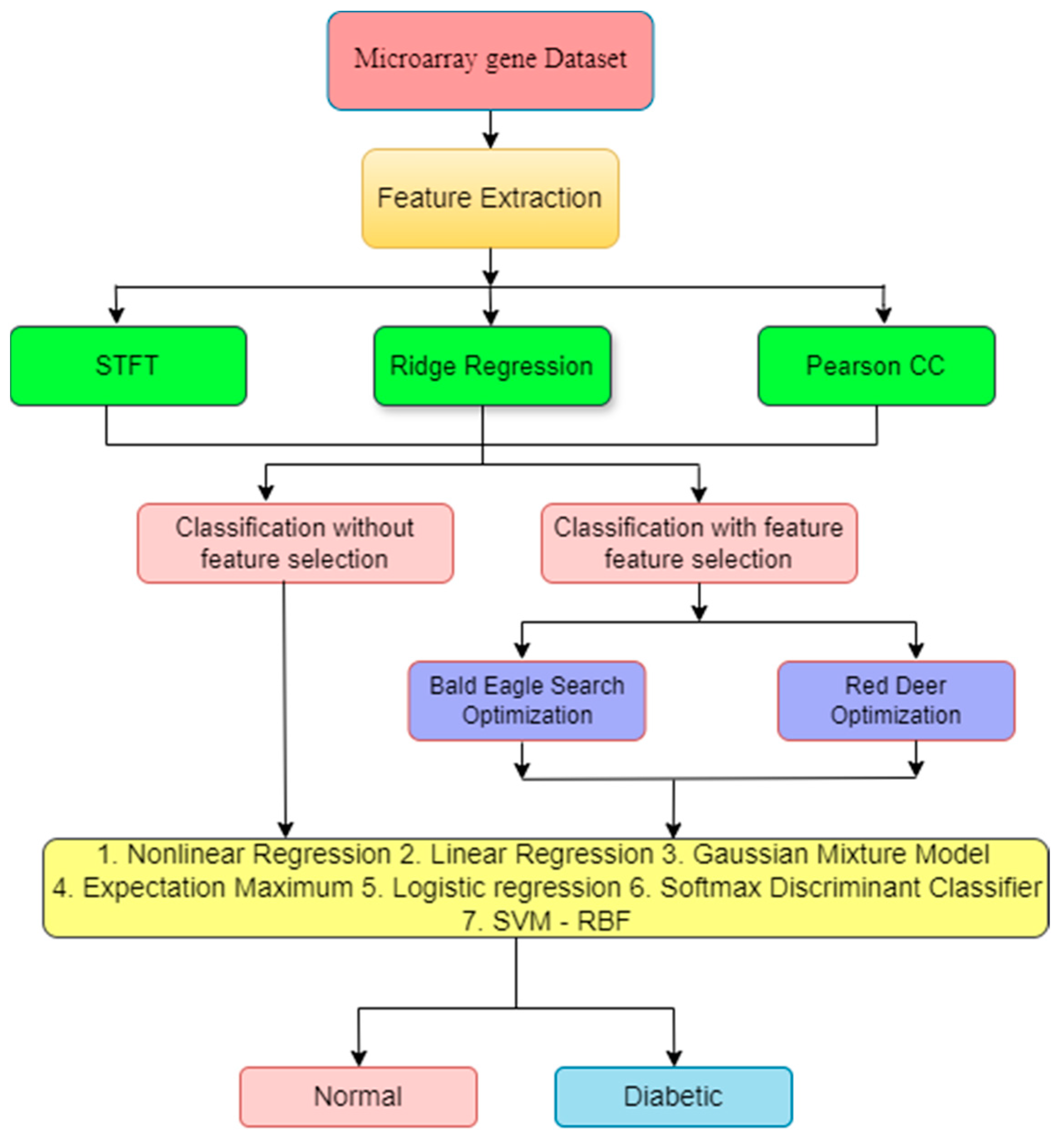
2. Materials and Methods
2.1. Dataset Details
2.2. Need for Feature Extraction (FE)
2.2.1. Short-Time Fourier Transform (STFT)
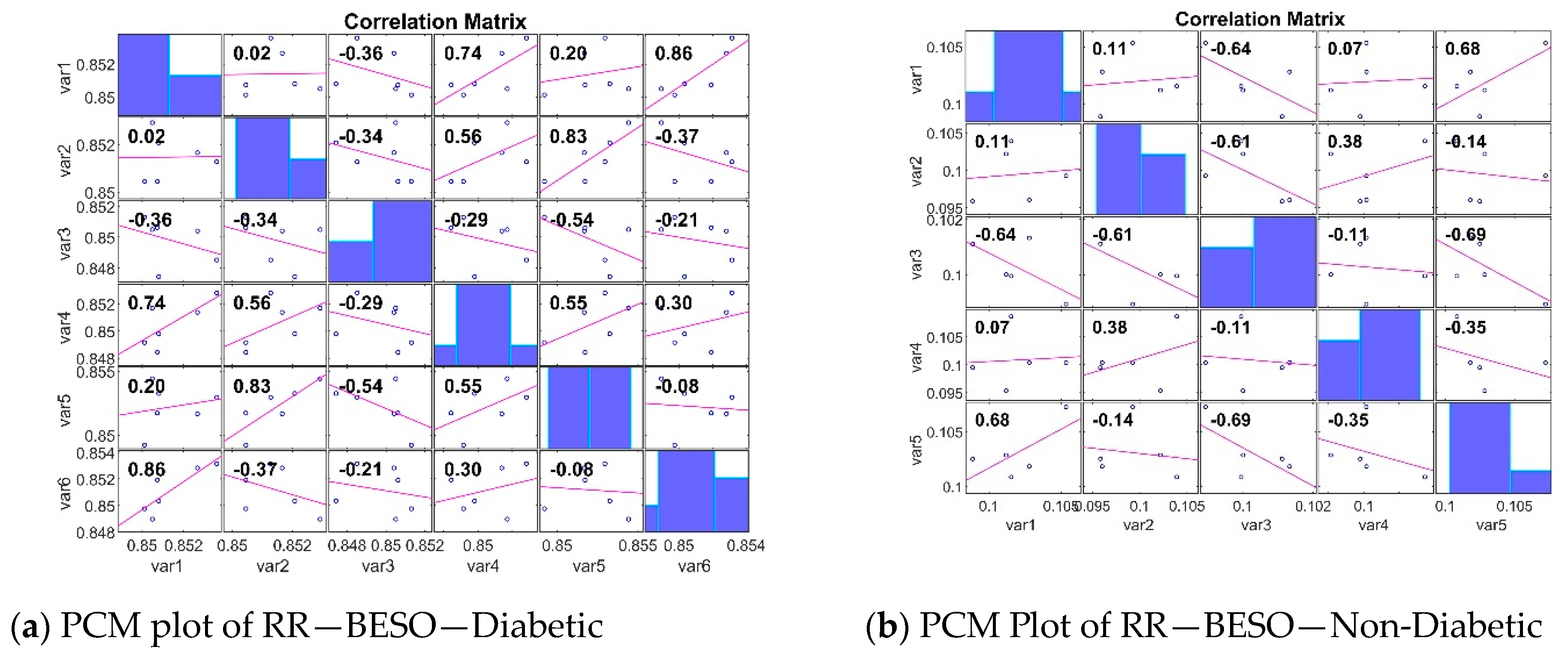
2.2.2. Ridge Regression (RR)
- represents the locally estimated coefficient vector for a specific data subset.
- denotes the design matrix for the i-th data subset.
- represents the outcome vector for the i-th data subset.
- is the regularization parameter for the local Ridge Regression on the i-th subset.
- I is the identity matrix with the same dimension as .
- represents the final combined coefficient vector obtained from all data subsets.
- represents the weight assigned to the local estimator from the i-th data subset.
- represents the locally estimated coefficient vector for the i-th data subset (as defined earlier).
2.2.3. Pearson’s Correlation Coefficient (PCC)
3. Feature Selection Method
3.1. Bald Eagle Search Optimization (BESO)
- Step 1: Simulating Exploration: Selecting the Search Area
- Step 2: Intensifying the Search
- Step 3: Convergence
3.2. Red Deer Optimization (RDO)
4. The RDO Algorithm
- (a)
- Initialization: Each RD is described by a set of variables, analogous to its genes. The number of variables (XNvar) corresponds to the number of genes. The values of these variables represent the potential contribution of each gene to diabetes detection, for instance, the set XNvar to 50, which means to account for investigations.
- (b)
- Roaring: In the “roar stage”, each RD representing a potential gene selection for diabetes detection can explore its surrounding solution space based on the microarray gene data. Imagine each RD has neighboring solutions in this multidimensional space. Here, a RD can adjust its position, which means gene selection within this local area. The algorithm evaluates the fitness of both the original and the adjusted positions using a fitness function reflecting how well the gene selection differentiates between diabetic and non-diabetic cases.
- (c)
- Roar:
- (d)
- Creation phase of harems:
- (e)
- The mating phase in RDO occurs in three key scenarios: 1. Commander Mating Within Harems—Each commander has the opportunity to mate with a specific proportion (α) of the hinds within its harem. This mating metaphorically represents the creation of new gene selections based on combinations of the commander’s strong selection and those of the hinds. 2. Commander Expansion Beyond Harems—Commanders can potentially mate with hinds from other harems. A random harem is chosen, and its commander has the chance to “mate” with a certain percentage (β) (which lies between 0 and 1) of the hinds in other harems. 3. Stag Mating—Stags also have a chance to contribute. They can mate with the closest hind, regardless of harem boundaries. This allows even less successful gene selections to potentially contribute to the next generation, introducing some level of diversity. By incorporating these three mating scenarios, RDO explores a combination of promising gene selections, ventures beyond established solutions, and maintains some level of diversity through stag mating.
- (f)
- Mating phase—New solutions are created. This process combines the strengths of existing gene selections from commanders, hinds, and even stags, promoting a balance between inheritance and exploration. This approach helps refine the population towards more effective gene selections for diabetes detection using your microarray gene data.
- (g)
- Building the next generation—RDO employs a two-pronged approach to select individuals for the next generation. A portion of the strongest RD is automatically selected for the next generation. These individuals represent the most promising gene selections identified so far. Additional members for the next generation are chosen from the remaining hinds and the newly generated offspring. This selection process often utilizes techniques like fitness tournaments or roulette wheels, which favor individuals with better fitness values.
- (h)
- RDO’s stopping criterion to determine the number of Iterations—a set number of iterations can be predetermined as the stopping point. The algorithm might stop if it identifies a solution that surpasses a certain threshold of quality for differentiating diabetic and non-diabetic segregation. A time limit might also be set as the stopping criterion. The parameters of each value involved in this algorithm are described in Table 4.
Analyzing the Impact of Feature Extraction Methods Using Statistical Measures
5. Classifiers
5.1. Non-Linear Regression
5.2. Linear Regression
5.3. Gaussian Mixture Models
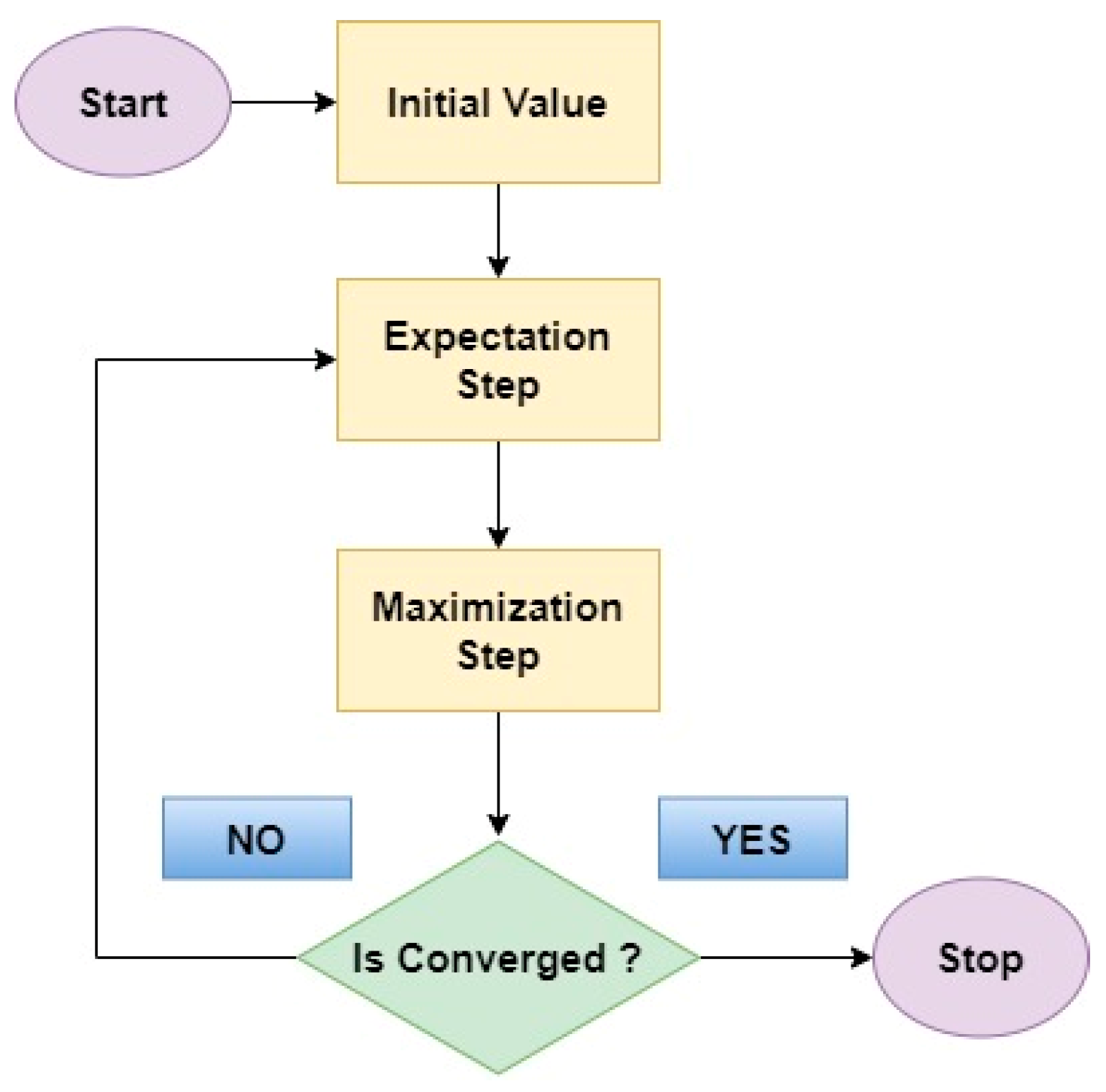
5.4. Expectation Maximum
- Expectation Step: In this initial step, the EM algorithm estimates the missing information, or hidden factors based on the currently available data and the current model parameters.
- Maximization Step: With the estimated missing values in place, the EM algorithm then refines the model parameters by considering the newly completed data.
5.5. Logistic Regression
5.6. Softmax Discriminant Classifier
5.7. Support Vector Machine (Radial Basis Function)
5.8. Selection of Classifiers Parameters through Training and Testing
6. Classifiers Training and Testing
- TP (True Positive): Catches diabetic patients.
- TN (True Negative): Identifies healthy people.
- FP (False Positive): Mistakes a healthy person for diabetic.
- FN (False Negative): Misses a diabetic person.
Selection of Targets
7. Outcomes and Findings
7.1. Computational Complexity
7.2. Limitations
7.3. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saeedi, P.; Petersohn, I.; Salpea, P.; Malanda, B.; Karuranga, S.; Unwin, N.; Colagiuri, S.; Guariguata, L.; Motala, A.A.; Ogurtsova, K.; et al. Global and regional diabetes prevalence estimates for 2019 and projections for 2030 and 2045: Results from the International Diabetes Federation Diabetes Atlas. Diabetes Res. Clin. Pract. 2019, 157, 107843. [Google Scholar] [CrossRef] [PubMed]
- Mohan, V.; Sudha, V.; Shobana, S.; Gayathri, R.; Krishnaswamy, K. Are unhealthy diets contributing to the rapid rise of type 2 diabetes in India? J. Nutr. 2023, 153, 940–948. [Google Scholar] [CrossRef]
- Oberoi, S.; Kansra, P. Economic menace of diabetes in India: A systematic review. Int. J. Diabetes Dev. Ctries. 2020, 40, 464–475. [Google Scholar] [CrossRef] [PubMed]
- American Diabetes Association Professional Practice Committee. 2. Classification and diagnosis of diabetes: Standards of Medical Care in Diabetes—2022. Diabetes Care 2022, 45 (Suppl. 1), S17–S38. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ding, J.; Zhi, D.U.; Gu, K.; Wang, H. Identification of type 2 diabetes based on a ten-gene biomarker prediction model constructed using a support vector machine algorithm. BioMed Res. Int. 2022, 2022, 1230761. [Google Scholar] [CrossRef] [PubMed]
- Mahendran, N.; Durai Raj Vincent, P.M.; Srinivasan, K.; Chang, C.-Y. Machine learning based computational gene selection models: A survey, performance evaluation, open issues, and future research directions. Front. Genet. 2020, 11, 603808. [Google Scholar] [CrossRef] [PubMed]
- Shivahare, B.D.; Singh, J.; Ravi, V.; Chandan, R.R.; Alahmadi, T.J.; Singh, P.; Diwakar, M. Delving into Machine Learning’s Influence on Disease Diagnosis and Prediction. Open Public Health J. 2024, 17, e18749445297804. [Google Scholar] [CrossRef]
- Chellappan, D.; Rajaguru, H. Detection of Diabetes through Microarray Genes with Enhancement of Classifiers Performance. Diagnostics 2023, 13, 2654. [Google Scholar] [CrossRef]
- Gowthami, S.; Reddy, R.V.S.; Ahmed, M.R. Exploring the effectiveness of machine learning algorithms for early detection of Type-2 Diabetes Mellitus. Meas. Sens. 2024, 31, 100983.c. [Google Scholar]
- Tasin, I.; Nabil, T.U.; Islam, S.; Khan, R. Diabetes prediction using machine learning and explainable AI techniques. Healthc. Technol. Lett. 2023, 10, 1–10. [Google Scholar] [CrossRef]
- Frasca, M.; La Torre, D.; Pravettoni, G.; Cutica, I. Explainable and interpretable artificial intelligence in medicine: A systematic bibliometric review. Discov. Artif. Intell. 2024, 4, 15. [Google Scholar] [CrossRef]
- Chaddad, A.; Peng, J.; Xu, J.; Bouridane, A. Survey of explainable AI techniques in healthcare. Sensors 2023, 23, 634. [Google Scholar] [CrossRef] [PubMed]
- Hussain, F.; Hussain, R.; Hossain, E. Explainable artificial intelligence (XAI): An engineering perspective. arXiv 2021, arXiv:2101.03613. [Google Scholar]
- Markus, A.F.; Kors, J.A.; Rijnbeek, P.R. The role of explainability in creating trustworthy artificial intelligence for health care: A comprehensive survey of the terminology, design choices, and evaluation strategies. J. Biomed. Inform. 2021, 113, 103655. [Google Scholar] [CrossRef] [PubMed]
- Hira, Z.M.; Gillies, D.F. A review of feature selection and feature extraction methods applied on microarray data. Adv. Bioinform. 2015, 2015, 198363. [Google Scholar] [CrossRef] [PubMed]
- Daliri, M.R. Feature selection using binary particle swarm optimization and support vector machines for medical diagnosis. Biomed. Tech./Biomed. Eng. 2012, 57, 395–402. [Google Scholar] [CrossRef] [PubMed]
- Alhussan, A.A.; Abdelhamid, A.A.; Towfek, S.K.; Ibrahim, A.; Eid, M.M.; Khafaga, D.S.; Saraya, M.S. Classification of diabetes using feature selection and hybrid Al-Biruni earth radius and dipper throated optimization. Diagnostics 2023, 13, 2038. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.A.; Govindasamy, R. Performance and evaluation of classification data mining techniques in diabetes. Int. J. Comput. Sci. Inf. Technol. 2015, 6, 1312–1319. [Google Scholar]
- Lawi, A.; Syarif, S. Performance evaluation of naive Bayes and support vector machine in type 2 diabetes Mellitus gene expression microarray data. J. Phys. Conf. Ser. 2019, 1341, 042018. [Google Scholar]
- Jakka, A.; Jakka, V.R. Performance evaluation of machine learning models for diabetes prediction. Int. J. Innov. Technol. Explor. Eng. Regul. Issue 2019, 8, 1976–1980. [Google Scholar]
- Yang, T.; Zhang, L.; Yi, L.; Feng, H.; Li, S.; Chen, H.; Zhu, J.; Zhao, J.; Zeng, Y.; Liu, H. Ensemble learning models based on noninvasive features for type 2 diabetes screening: Model development and validation. JMIR Med. Inform. 2020, 8, e15431. [Google Scholar] [CrossRef] [PubMed]
- Marateb, H.R.; Mansourian, M.; Faghihimani, E.; Amini, M.; Farina, D. A hybrid intelligent system for diagnosing microalbuminuria in type 2 diabetes patients without having to measure urinary albumin. Comput. Biol. Med. 2014, 45, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.-M.; Huang, K.-Y.; Lee, T.-Y.; Weng, J. An interpretable rule-based diagnostic classification of diabetic nephropathy among type 2 diabetes patients. BMC Bioinform. 2015, 16 (Suppl. 1), S5. [Google Scholar] [CrossRef]
- Chikh, M.A.; Saidi, M.; Settouti, N. Diagnosis of diabetes diseases using an Artificial Immune Recognition System2 (AIRS2) with fuzzy K-nearest neighbor. J. Med. Syst. 2012, 36, 2721–2729. [Google Scholar] [CrossRef] [PubMed]
- Luo, G. Automatically explaining machine learning prediction results: A demonstration on type 2 diabetes risk prediction. Health Inf. Sci. Syst. 2016, 4, 2. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Lim, D.H.; Kim, Y. Classification and prediction on the effects of nutritional intake on overweight/obesity, dyslipidemia, hypertension and type 2 diabetes mellitus using deep learning model: 4–7th Korea national health and nutrition examination survey. Int. J. Environ. Res. Public Health 2021, 18, 5597. [Google Scholar] [CrossRef] [PubMed]
- Kalagotla, S.K.; Gangashetty, S.V.; Giridhar, K. A novel stacking technique for prediction of diabetes. Comput. Biol. Med. 2021, 135, 104554. [Google Scholar] [CrossRef] [PubMed]
- Sarwar, M.A.; Kamal, N.; Hamid, W.; Shah, M.A. Prediction of diabetes using machine learning algorithms in healthcare. In Proceedings of the 2018 24th International Conference on Automation and Computing (ICAC), Newcastle Upon Tyne, UK, 6–7 September 2018. [Google Scholar] [CrossRef]
- Li, J.; Chen, Q.; Hu, X.; Yuan, P.; Cui, L.; Tu, L.; Cui, J.; Huang, J.; Jiang, T.; Ma, X.; et al. Establishment of noninvasive diabetes risk prediction model based on tongue features and machine learning techniques. Int. J. Med. Inform. 2021, 149, 104429. [Google Scholar] [CrossRef] [PubMed]
- Prajapati, S.; Das, H.; Gourisaria, M.K. Feature selection using differential evolution for microarray data classification. Discov. Internet Things 2023, 3, 12. [Google Scholar] [CrossRef]
- Alsattar, H.A.; Zaidan, A.A.; Zaidan, B.B. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Hilal, A.M.; Alrowais, F.; Al-Wesabi, F.N.; Marzouk, R. Red Deer Optimization with Artificial Intelligence Enabled Image Captioning System for Visually Impaired People. Comput. Syst. Sci. Eng. 2023, 46, 1929–1945. [Google Scholar] [CrossRef]
- Horng, J.-T.; Wu, L.-C.; Liu, B.-J.; Kuo, J.-L.; Kuo, W.-H.; Zhang, J.J. An expert system to classify microarray gene expression data using gene selection by decision tree. Expert Syst. Appl. 2009, 36, 9072–9081. [Google Scholar] [CrossRef]
- Shaik, B.S.; Naganjaneyulu, G.V.S.S.K.R.; Chandrasheker, T.; Narasimhadhan, A. A method for QRS delineation based on STFT using adaptive threshold. Procedia Comput. Sci. 2015, 54, 646–653. [Google Scholar] [CrossRef]
- Bar, N.; Nikparvar, B.; Jayavelu, N.D.; Roessler, F.K. Constrained Fourier estimation of short-term time-series gene expression data reduces noise and improves clustering and gene regulatory network predictions. BMC Bioinform. 2022, 23, 330. [Google Scholar] [CrossRef] [PubMed]
- Imani, M.; Ghassemian, H. Ridge regression-based feature extraction for hyperspectral data. Int. J. Remote Sens. 2015, 36, 1728–1742. [Google Scholar] [CrossRef]
- Paul, S.; Drineas, P. Feature selection for ridge regression with provable guarantees. Neural Comput. 2016, 28, 716–742. [Google Scholar] [CrossRef]
- Prabhakar, S.K.; Rajaguru, H.; Ryu, S.; Jeong, I.C.; Won, D.O. A holistic strategy for classification of sleep stages with EEG. Sensors 2022, 22, 3557. [Google Scholar] [CrossRef] [PubMed]
- Mehta, P.; Bukov, M.; Wang, C.-H.; Day, A.G.; Richardson, C.; Fisher, C.K.; Schwab, D.J. A high-bias, low-variance introduction to machine learning for physicists. Phys. Rep. 2019, 810, 1–124. [Google Scholar] [CrossRef]
- Li, G.; Zhang, A.; Zhang, Q.; Wu, D.; Zhan, C. Pearson correlation coefficient-based performance enhancement of broad learning system for stock price prediction. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2413–2417. [Google Scholar] [CrossRef]
- Mu, Y.; Liu, X.; Wang, L. A Pearson’s correlation coefficient based decision tree and its parallel implementation. Inf. Sci. 2018, 435, 40–58. [Google Scholar] [CrossRef]
- Grace Elizabeth Rani, T.G.; Jayalalitha, G. Complex patterns in financial time series through Higuchi’s fractal dimension. Fractals 2016, 24, 1650048. [Google Scholar] [CrossRef]
- Rehan, I.; Rehan, K.; Sultana, S.; Rehman, M.U. Fingernail Diagnostics: Advancing type II diabetes detection using machine learning algorithms and laser spectroscopy. Microchem. J. 2024, 201, 110762. [Google Scholar] [CrossRef]
- Wang, J.; Ouyang, H.; Zhang, C.; Li, S.; Xiang, J. A novel intelligent global harmony search algorithm based on improved search stability strategy. Sci. Rep. 2023, 13, 7705. [Google Scholar] [CrossRef]
- Fard, A.F.; Hajiaghaei-Keshteli, M. Red Deer Algorithm (RDA); a new optimization algorithm inspired by Red Deers’ mating. Int. Conf. Ind. Eng. 2016, 12, 331–342. [Google Scholar]
- Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M.; Tavakkoli-Moghaddam, R. Red deer algorithm (RDA): A new nature-inspired meta-heuristic. Soft Comput. 2020, 24, 14637–14665. [Google Scholar] [CrossRef]
- Bektaş, Y.; Karaca, H. Red deer algorithm based selective harmonic elimination for renewable energy application with unequal DC sources. Energy Rep. 2022, 8, 588–596. [Google Scholar] [CrossRef]
- Kumar, A.P.; Valsala, P. Feature Selection for high Dimensional DNA Microarray data using hybrid approaches. Bioinformation 2013, 9, 824. [Google Scholar] [CrossRef]
- Zhang, G.; Allaire, D.; Cagan, J. Reducing the Search Space for Global Minimum: A Focused Regions Identification Method for Least Squares Parameter Estimation in Nonlinear Models. J. Comput. Inf. Sci. Eng. 2023, 23, 021006. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998; Volume 326. [Google Scholar]
- Prabhakar, S.K.; Rajaguru, H.; Lee, S.-W. A comprehensive analysis of alcoholic EEG signals with detrend fluctuation analysis and post classifiers. In Proceedings of the 2019 7th International Winter Conference on Brain-Computer Interface (BCI), Gangwon, Republic of Korea, 18–20 February 2019. [Google Scholar]
- Llaha, O.; Rista, A. Prediction and Detection of Diabetes using Machine Learning. In Proceedings of the 20th International Conference on Real-Time Applications in Computer Science and Information Technology (RTA-CSIT), Tirana, Albania, 21–22 May 2021; pp. 94–102. [Google Scholar]
- Hamid, I.Y. Prediction of Type 2 Diabetes through Risk Factors using Binary Logistic Regression. J. Al-Qadisiyah Comput. Sci. Math. 2020, 12, 1. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, X.; Xu, L.; Ding, F. Expectation–maximization algorithm for bilinear systems by using the Rauch–Tung–Striebel smoother. Automatica 2022, 142, 110365. [Google Scholar] [CrossRef]
- Moon, T.K. The expectation-maximization algorithm. IEEE Signal Process. Mag. 1996, 13, 47–60. [Google Scholar] [CrossRef]
- Adiwijaya; Wisesty, U.N.; Lisnawati, E.; Aditsania, A.; Kusumo, D.S. Dimensionality reduction using principal component analysis for cancer detection based on microarray data classification. J. Comput. Sci. 2018, 14, 1521–1530. [Google Scholar] [CrossRef]
- Peng, C.-Y.J.; Lee, K.L.; Ingersoll, G.M. An introduction to logistic regression analysis and reporting. J. Educ. Res. 2002, 96, 3–14. [Google Scholar] [CrossRef]
- Zang, F.; Zhang, J.S. Softmax Discriminant Classifier. In Proceedings of the 3rd International Conference on Multimedia Information Networking and Security, Shanghai, China, 4–6 November 2011; pp. 16–20. [Google Scholar]
- Yao, X.; Panaye, A.; Doucet, J.; Chen, H.; Zhang, R.; Fan, B.; Liu, M.; Hu, Z. Comparative classification study of toxicity mechanisms using support vector machines and radial basis function neural networks. Anal. Chim. Acta 2005, 535, 259–273. [Google Scholar] [CrossRef]
- Ortiz-Martínez, M.; González-González, M.; Martagón, A.J.; Hlavinka, V.; Willson, R.C.; Rito-Palomares, M. Recent developments in biomarkers for diagnosis and screening of type 2 diabetes mellitus. Curr. Diabetes Rep. 2022, 22, 95–115. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, A.E.; Warner, T.A.; Guillén, L.A. Accuracy assessment in convolutional neural network-based deep learning remote sensing studies—Part 1: Literature review. Remote Sens. 2021, 13, 2450. [Google Scholar] [CrossRef]
- Maniruzzaman, M.; Kumar, N.; Abedin, M.M.; Islam, M.S.; Suri, H.S.; El-Baz, A.S.; Suri, J.S. Comparative approaches for classifi-cation of diabetes mellitus data: Machine learning paradigm. Comput. Methods Programs Biomed. 2017, 152, 23–34. [Google Scholar] [CrossRef] [PubMed]
- Hertroijs, D.F.L.; Elissen, A.M.J.; Brouwers, M.C.G.J.; Schaper, N.C.; Köhler, S.; Popa, M.C.; Asteriadis, S.; Hendriks, S.H.; Bilo, H.J.; Ruwaard, D.; et al. A risk score including body mass index, glycated hemoglobin and triglycerides predicts future glycemic control in people with type 2 diabetes. Diabetes Obes. Metab. 2017, 20, 681–688. [Google Scholar] [CrossRef] [PubMed]
- Deo, R.; Panigrahi, S. Performance assessment of machine learning based models for diabetes prediction. In Proceedings of the 2019 IEEE Healthcare Innovations and Point of Care Technologies, (HI-POCT), Bethesda, MD, USA, 20–22 November 2019. [Google Scholar]
- Akula, R.; Nguyen, N.; Garibay, I. Supervised machine learning based ensemble model for accurate prediction of type 2 diabetes. In Proceedings of the 2019 Southeast Con, Huntsville, AL, USA, 11–14 April 2019. [Google Scholar]
- Xie, Z.; Nikolayeva, O.; Luo, J.; Li, D. Building risk prediction models for type 2 diabetes using machine learning techniques. Prev. Chronic Dis. 2019, 16, E130. [Google Scholar] [CrossRef]
- Bernardini, M.; Morettini, M.; Romeo, L.; Frontoni, E.; Burattini, L. Early temporal prediction of type 2 diabetes risk condition from a general practitioner electronic health record: A multiple instance boosting approach. Artif. Intell. Med. 2020, 105, 101847. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Niu, M.; Wang, C.; Wang, Z. Nonlaboratory based risk assessment model for type 2 diabetes mellitus screening in Chinese rural population: A joint bagging boosting model. IEEE J. Biomed. Health Inform. 2021, 25, 4005–4016. [Google Scholar] [CrossRef] [PubMed]

| S. No. | Author and Year | Database | Feature Extraction/Dimensionality Reduction Technique | Classifiers Used | Evaluation Metrics | Limitations |
|---|---|---|---|---|---|---|
| 1 | Kumar, D. A., and Govindasamy, R. (2015) [18] | UCI repository | - | Support Vector Regression Bayes Net Naive Bayes Decision Table | 79.81% accuracy | The study only used the Pima Indians Diabetes Dataset (PIDD) from the UCI Machine Learning Repository, which may limit the generalizability of the findings to other diabetes datasets or real-world scenarios. |
| 2 | Lawi, A. and Syarif, S. (2019, October) [19] | GSE18732 Mircoarray gene expression data | Entropy and Resampling (SMOTE) | Naïve Bayes, SVM: Linear, RBF, Polynomial | SVM uses RBF kernel achieved 97.22% accuracy | The limited dataset size of only 2000 customer reviews, which may not be sufficient to fully evaluate the performance of the Naive Bayes and SVM classifiers. |
| 3 | Jakka et al. (2019) [20] | PIMA Dataset | - | KNN—K-Nearest Neighbor DT—Decision Tree Naive Bayes SVM LR—Logistic Regression RF—Random Forest | Accuracy: 73, 70, 75, 66, 78, 74 | Potentially remove irrelevant or redundant features from the dataset. |
| 4 | Yang et al. (2020) [21] | NHANES (National Health and Nutrition Examination Survey) database | Binary Logistic Regression | Linear discriminant analysis, Support Vector Machine Random Forest | Accuracy: 75, 74, 74 | The inability to clearly separate type 1 and type 2 diabetes, the unbalanced dataset, and the relatively low positive predictive value of the models. |
| 5 | Marateb et al. (2014) [22] | Tested on a sample size of 200 patients with type 2 diabetes in a cross-sectional study | Multimethods (machine learning, fuzzy logic, expert system) | SVM DT NB | Accuracy = 92%, 89%, 85% | Without a larger-scale validation, the true capabilities and limitations of the proposed hybrid intelligent system for diagnosing microalbuminuria remain uncertain. |
| 6 | Huang et al. (2015) [23] | Clinical and genotyping data study involving 345 type 2 diabetic patients (185 with diabetic nephropathy and 160 without diabetic nephropathy) | Clinical + Genetic Analysis | DT RF NB SVM | For DT—accuracy = 65.2% sensitivity = 63.2% specificity = 67.2% | A larger and more diverse dataset would be needed to further validate and refine the proposed Decision Tree-based model to identify diabetic nephropathy. |
| 7 | Chikh et al. (2012) [24] | UCI machine learning repository | Artificial Immune Recognition System | KNN CRISP Fuzzy | Accuracy = 89.10% | The article does not provide a detailed comparison of the MAIRS2 method with other commonly used machine learning techniques for diabetes diagnosis. |
| 8 | Luo, G. (2016) [25] | Electronic medical record dataset from the Practice Fusion diabetes classification competition containing patient records from all 50 states in the United States | Champion machine learning model | SVM | AUC = 0.884 Accuracy = 77.6% | Lack of model interpretability. |
| 9 | Kim et al. (2021) [26] | Aged 40–69 years from the combined dataset of the 4th to 7th KNHANES (from 2007 to 2018) | - | Deep Neural Network, logistic regression, Decision Tree | Accuracy: 80%, 80%, 71% | The study lacks detailed discussion on the specific parameters and variables used in the Deep Neural Network (DNN) model. |
| 10 | Kalagotla et al. (2021) [27] | PIMA Dataset | Stacking multilayer perceptron, Support Vector Machine Logistic Regression | Accuracy: 78 Precision: 72 Sensitivity: 51 F1 score: 60 | The study did not explore the impact of different hyperparameters or feature engineering techniques on the performance of the proposed models, which could influence the overall results. | |
| 11 | Sarwar et al. (2018) [28] | Pima Indians Diabetes Dataset | - | K-Nearest Neighbors (KNN), Naive Bayes (NB), Support Vector Machine (SVM), Decision Tree (DT), Logistic Regression (LR) and Random Forest (RF) | Accuracy: 0.77, 0.74, 0.77, 0.71, 0.74, 0.71 | Lack of discussion on the potential biases present in the dataset used for predictive analytics. |
| 12 | Li et al. (2021) [29] | 1512 subjects were recruited from the hospital | Genetic Algorithm | Extreme gradient boosting (GBT) | AUC (ROC): 0.91 precision: 0.82 sensitivity: 0.80 F1 score: 0.77 | Limits the generalizability of the models, especially the deep learning models which typically require large datasets to perform optimally. |
| Dataset Details | Status of the Data | Total No of Genes (per Patients) | After Feature Extraction—For All Three Methods (per Patients) | After Feature Selection—For All Two Methods (per Patients) |
|---|---|---|---|---|
| Nordic Islet Transplantation Program | Imbalanced Diabetic—20 Non-Diabetic—57 | 28,960 | 2870 × 1 | 287 × 1 |
| Statistical Parameters | STFT | Ridge Regression | Pearson CC | |||
|---|---|---|---|---|---|---|
| Dia P | Non-Dia P | Dia P | Non-Dia P | Dia P | Non-Dia P | |
| Mean | 40.7681 | 40.7863 | 0.0033 | 0.0025 | 0.0047 | 0.0045 |
| Variance | 11,745.67 | 11,789.27 | 1.3511 | 1.3746 | 0.0004 | 0.0004 |
| Skewness | 19.2455 | 19.2461 | 0.0284 | −0.0032 | 0.0038 | −0.0317 |
| Kurtosis | 388.5211 | 388.5372 | 0.6909 | 0.9046 | −0.1658 | −0.0884 |
| Sample Entropy | 11.0014 | 11.0014 | 11.4868 | 11.4868 | 11.4868 | 11.4868 |
| Shannon Entropy | 0 | 0 | 3.9818 | 3.9684 | 2.8979 | 2.9848 |
| Higuchi’s Fractal Dimension | 1.1097 | 1.1104 | 2.007 | 2.0093 | 1.9834 | 1.9659 |
| CCA | 0.4031 | 0.0675 | 0.0908 | |||
| S. No. | Parameters | Values | S. No. | Parameters | Values |
|---|---|---|---|---|---|
| 1. | Initial population (I) | 100 | 6. | Beta (β) | 0.4 |
| 2. | Maximum time of simulation | 10 (s) | 7. | Gamma (γ) | 0.7 |
| 3. | Number of males (M) | 15 | 8. | Roar | 0.25 |
| 4. | Number of hinds (H) | I M | 9. | Fight | 0.4 |
| 5. | Alpha (α) | 0.85 | 10. | Mating | 0.77 |
| Feature Selection | DR Techniques | STFT | Ridge Regression | Pearson CC | |||
|---|---|---|---|---|---|---|---|
| Class | Dia P | Non-Dia P | Dia P | Non-Dia P | Dia P | Non-Dia P | |
| BESO | p value < 0.05 | 0.4673 | 0.3545 | 0.2962 | 0.2599 | 0.3373 | 0.3178 |
| RDO | p value < 0.05 | 0.4996 | 0.4999 | 0.4999 | 0.4883 | 0.4999 | 0.4999 |
| Clinical Situation | Predicted Values | ||
|---|---|---|---|
| Dia | Non-Dia | ||
| Real Values | Class of Dia | TP | FN |
| Class of Non-Dia | FP | TN | |
| Classifiers | STFT | Ridge Regression | Pearson CC | |||
|---|---|---|---|---|---|---|
| Train MSE | Test MSE | Train MSE | Test MSE | Train MSE | Test MSE | |
| NLR | 1.59 × 10−5 | 4.84 × 10−6 | 7.29 × 10−6 | 3.25 × 10−5 | 4.36 × 10−5 | 4.1 × 10−4 |
| LR | 1.18 × 10−5 | 3.61 × 10−6 | 1.16 × 10−5 | 1.94 × 10−5 | 9.61 × 10−6 | 3.84 × 10−4 |
| GMM | 1.05 × 10−5 | 2.89 × 10−6 | 1.02 × 10−5 | 1.48 × 10−5 | 2.02 × 10−5 | 8.41 × 10−4 |
| EM | 6.74 × 10−6 | 2.89 × 10−6 | 5.29 × 10−6 | 1.37 × 10−5 | 9.61 × 10−6 | 3.72 × 10−5 |
| LoR | 2.46 × 10−5 | 9 × 10−6 | 2.7 × 10−5 | 3.02 × 10−5 | 4 × 10−6 | 2.92 × 10−5 |
| SDC | 1.28 × 10−5 | 4 × 10−6 | 1.68 × 10−5 | 1.22 × 10−5 | 2.56 × 10−6 | 1.85 × 10−5 |
| SVM (RBF) | 1.88 × 10−6 | 1 × 10−6 | 2.56 × 10−6 | 4.41 × 10−6 | 3.6 × 10−7 | 4.41 × 10−6 |
| Classifiers | STFT | Ridge Regression | Pearson CC | |||
|---|---|---|---|---|---|---|
| Train MSE | Test MSE | Train MSE | Test MSE | Train MSE | Test MSE | |
| NLR | 1.43 × 10−5 | 5.29 × 10−5 | 1.44 × 10−5 | 2.21 × 10−5 | 9.41 × 10−5 | 7.06 × 10−5 |
| LR | 3.76 × 10−5 | 2.3 × 10−5 | 7.74 × 10−5 | 1.85 × 10−5 | 2.5 × 10−5 | 2.02 × 10−5 |
| GMM | 4.51 × 10−5 | 1.3 × 10−5 | 6.56 × 10−5 | 3.97 × 10−4 | 6.08 × 10−5 | 3.02 × 10−5 |
| EM | 3.4 × 10−5 | 1.37 × 10−5 | 5.18 × 10−5 | 3.14 × 10−4 | 1.6 × 10−7 | 1.3 × 10−5 |
| LoR | 9.97 × 10−6 | 4 × 10−6 | 9 × 10−6 | 1.76 × 10−5 | 4.9 × 10−7 | 1.68 × 10−5 |
| SDC | 2.21 × 10−5 | 1.6 × 10−5 | 2.81 × 10−6 | 2.81 × 10−4 | 8.1 × 10−7 | 8.65 × 10−5 |
| SVM (RBF) | 2.18 × 10−6 | 1.44 × 10−6 | 5.29 × 10−6 | 4.9 × 10−5 | 4.9 × 10−7 | 8.1 × 10−7 |
| Classifiers | STFT | Ridge Regression | Pearson CC | |||
|---|---|---|---|---|---|---|
| Train MSE | Test MSE | Train MSE | Test MSE | Train MSE | Test MSE | |
| NLR | 2.62 × 10−5 | 2.56 × 10−6 | 6.08 × 10−5 | 9 × 10−6 | 5.04 × 10−5 | 6.56 × 10−5 |
| LR | 4.85 × 10−5 | 1.96 × 10−6 | 6.24 × 10−5 | 6.4 × 10−5 | 2.25 × 10−6 | 1.09 × 10−5 |
| GMM | 9.01 × 10−6 | 4.41 × 10−6 | 2.12 × 10−5 | 2.25 × 10−6 | 6.25 × 10−6 | 1.22 × 10−5 |
| EM | 3.51 × 10−5 | 7.29 × 10−6 | 5.48 × 10−5 | 2.81 × 10−5 | 1.69 × 10−6 | 7.84 × 10−6 |
| LoR | 1.39 × 10−5 | 2.25 × 10−6 | 3.02 × 10−5 | 4.84 × 10−6 | 3.6 × 10−7 | 4 × 10−6 |
| SDC | 1.35 × 10−5 | 2.89 × 10−6 | 2.6 × 10−5 | 1.96 × 10−6 | 1.44 × 10−7 | 1.68 × 10−5 |
| SVM (RBF) | 4.25 × 10−7 | 3.6 × 10−7 | 8.1 × 10−7 | 9 × 10−8 | 4 × 10−8 | 2.5 × 10−7 |
| Classifiers | Description |
|---|---|
| NLR | The uniform weight is set to 0.4, while the bias is adjusted iteratively to minimize the sum of least square errors, with the criterion being the Mean Squared Error (MSE). |
| Linear Regression | The weight is uniformly set at 0.451, while the bias is adjusted to 0.003 iteratively to meet the Mean Squared Error (MSE) criterion. |
| GMM | The input sample’s mean covariance and tuning parameter are refined through EM steps, with MSE as the criterion. |
| EM | The likelihood probability is 0.13, the cluster probability is 0.45, and the convergence rate is 0.631, with the condition being MSE. |
| Logistic Regression | The criterion is MSE, with the condition being that the threshold Hθ(x) should be less than 0.48. |
| SDC | The parameter Γ is set to 0.5, alongside mean target values of 0.1 and 0.85 for each class. |
| SVM (RBF) | The settings include C as 1, the coefficient of the kernel function (gamma) as 100, class weights at 0.86, and the convergence criterion as MSE. |
| Metrics | Formula |
|---|---|
| Accuracy | |
| F1 Score | |
| Matthews Correlation Coefficient (MCC) | |
| Jaccard Metric | |
| Error Rate | ER = 1 − Accu |
| Kappa |
| Feature Extraction | Classifiers | Parameters | |||||
|---|---|---|---|---|---|---|---|
| Accu (%) | F1S (%) | MCC | Jaccard Metric (%) | Error Rate (%) | Kappa | ||
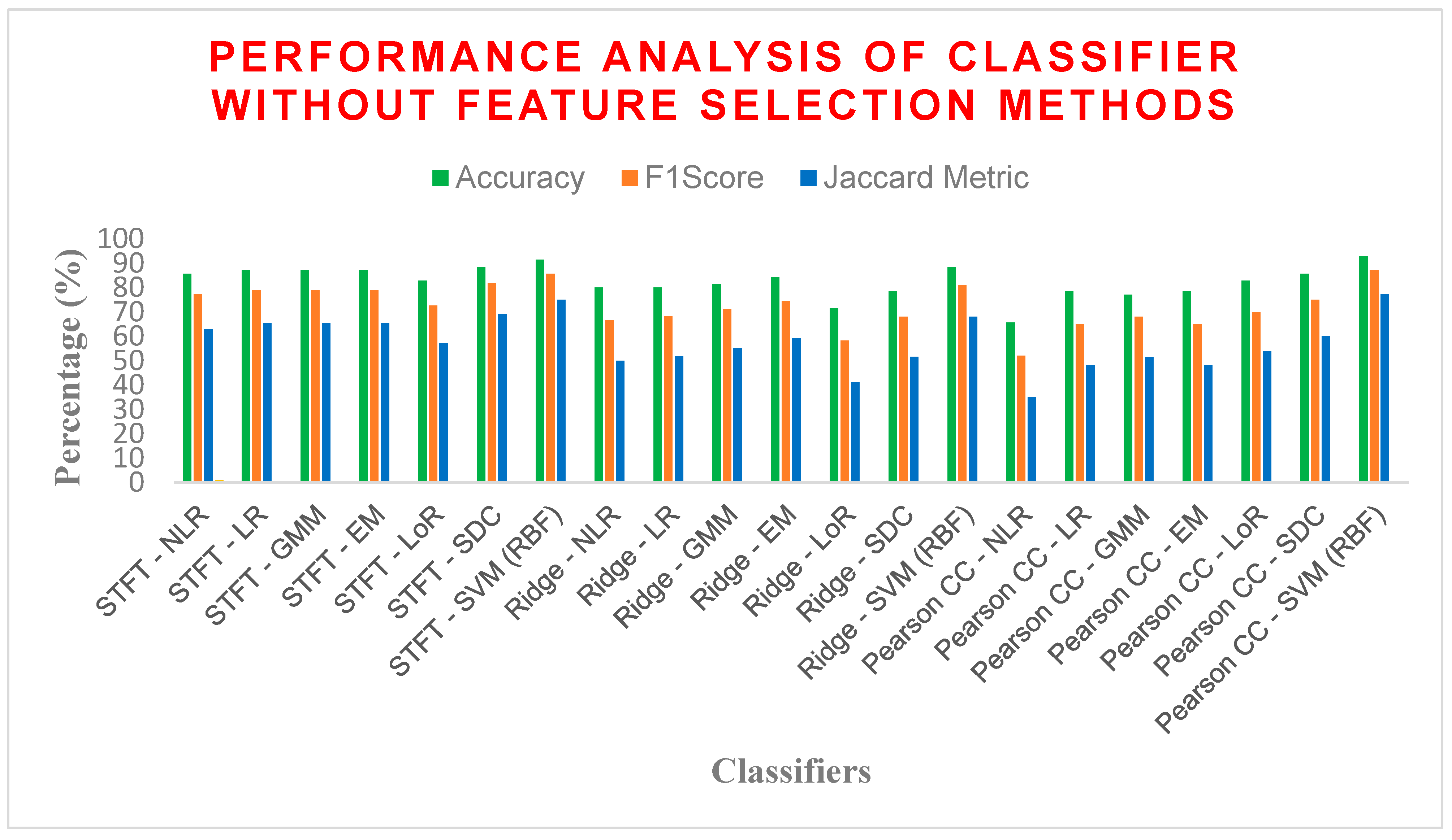
| STFT | NLR | 85.7142 | 77.2727 | 0.6757 | 62.9629 | 14.2857 | 0.6698 |
| LR | 87.1428 | 79.0697 | 0.7021 | 65.3846 | 12.8571 | 0.6985 | |
| GMM | 87.1428 | 79.0697 | 0.7021 | 65.3846 | 12.8571 | 0.6985 | |
| EM | 87.1428 | 79.0697 | 0.7021 | 65.3846 | 12.8571 | 0.6985 | |
| LoR | 82.8571 | 72.7272 | 0.6091 | 57.1428 | 17.1428 | 0.6037 | |
| SDC | 88.5714 | 81.8181 | 0.7423 | 69.2307 | 11.4285 | 0.7358 | |
| SVM (RBF) | 91.4285 | 85.7142 | 0.7979 | 75 | 8.57142 | 0.7961 | |
| Ridge Regression | NLR | 80 | 66.6667 | 0.5255 | 50 | 20 | 0.5242 |
| LR | 80 | 68.1818 | 0.5425 | 51.7241 | 20 | 0.5377 | |
| GMM | 81.4285 | 71.1111 | 0.5845 | 55.1724 | 18.5714 | 0.5767 | |
| EM | 84.2857 | 74.4186 | 0.6348 | 59.2592 | 15.7142 | 0.6315 | |
| LoR | 71.4286 | 58.3333 | 0.3873 | 41.1764 | 28.5714 | 0.375 | |
| SDC | 78.5714 | 68.0851 | 0.5383 | 51.6129 | 21.4285 | 0.5248 | |
| SVM (RBF) | 88.5714 | 80.9524 | 0.7298 | 68 | 11.4285 | 0.7281 | |
| Pearson CC | NLR | 65.7143 | 52 | 0.2829 | 35.1351 | 34.2857 | 0.2695 |
| LR | 78.5714 | 65.1162 | 0.5001 | 48.2758 | 21.4285 | 0.4976 | |
| GMM | 77.1429 | 68 | 0.5385 | 51.5151 | 22.8571 | 0.5130 | |
| EM | 78.5714 | 65.1162 | 0.5001 | 48.2758 | 21.4285 | 0.4976 | |
| LoR | 82.8571 | 70 | 0.58 | 53.8461 | 17.1428 | 0.58 | |
| SDC | 85.7142 | 75 | 0.65 | 60 | 14.2857 | 0.65 | |
| SVM (RBF) | 92.8571 | 87.1795 | 0.8228 | 77.2727 | 7.14285 | 0.8223 | |
| Feature Extraction | Classifiers | Parameters | |||||
|---|---|---|---|---|---|---|---|
| Accu (%) | F1S (%) | MCC | Jaccard Metric (%) | Error Rate (%) | Kappa | ||
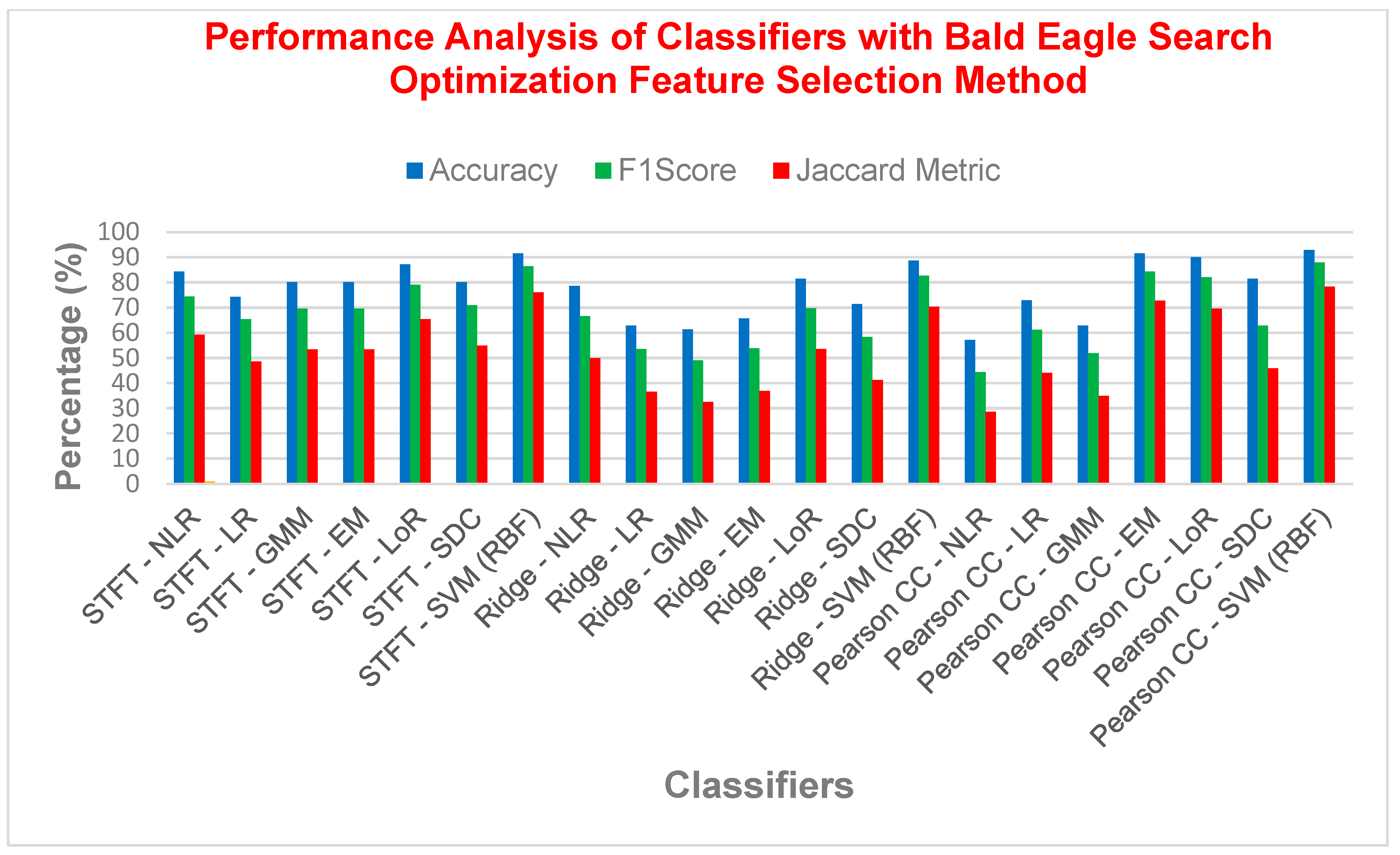
| STFT | NLR | 84.2857 | 74.4186 | 0.6347 | 59.2592 | 15.7142 | 0.6315 |
| LR | 74.2857 | 65.3846 | 0.4987 | 48.5714 | 25.7142 | 0.4661 | |
| GMM | 80 | 69.5652 | 0.5609 | 53.3333 | 20 | 0.5504 | |
| EM | 80 | 69.5652 | 0.5609 | 53.3333 | 20 | 0.5504 | |
| LoR | 87.1428 | 79.0697 | 0.7021 | 65.3846 | 12.8571 | 0.6985 | |
| SDC | 80 | 70.8333 | 0.5809 | 54.8387 | 20 | 0.5625 | |
| SVM (RBF) | 91.4285 | 86.3636 | 0.8089 | 76 | 8.57142 | 0.8018 | |
| Ridge Regression | NLR | 78.5714 | 66.6667 | 0.5185 | 50 | 21.4285 | 0.5116 |
| LR | 62.8571 | 53.5714 | 0.2982 | 36.5853 | 37.1428 | 0.2661 | |
| GMM | 61.4285 | 49.0566 | 0.2262 | 32.5 | 38.5714 | 0.2092 | |
| EM | 65.7142 | 53.8461 | 0.3083 | 36.8421 | 34.2857 | 0.2881 | |
| LoR | 81.4285 | 69.7674 | 0.5674 | 53.5714 | 18.5714 | 0.5645 | |
| SDC | 71.4285 | 58.3333 | 0.3872 | 41.1764 | 28.5714 | 0.375 | |
| SVM (RBF) | 88.5714 | 82.6087 | 0.7573 | 70.3703 | 11.4285 | 0.7431 | |
| Pearson CC | NLR | 57.1428 | 44.4444 | 0.1446 | 28.5714 | 42.8571 | 0.1322 |
| LR | 72.8571 | 61.2244 | 0.4310 | 44.1176 | 27.1428 | 0.4140 | |
| GMM | 62.8571 | 51.8518 | 0.2711 | 35 | 37.1428 | 0.2479 | |
| EM | 91.4285 | 84.2105 | 0.7855 | 72.7272 | 8.57142 | 0.7835 | |
| LoR | 90 | 82.0512 | 0.7517 | 69.5652 | 10 | 0.7512 | |
| SDC | 81.4285 | 62.8571 | 0.5174 | 45.8333 | 18.5714 | 0.5081 | |
| SVM (RBF) | 92.8571 | 87.8048 | 0.8280 | 78.2608 | 7.14285 | 0.8275 | |
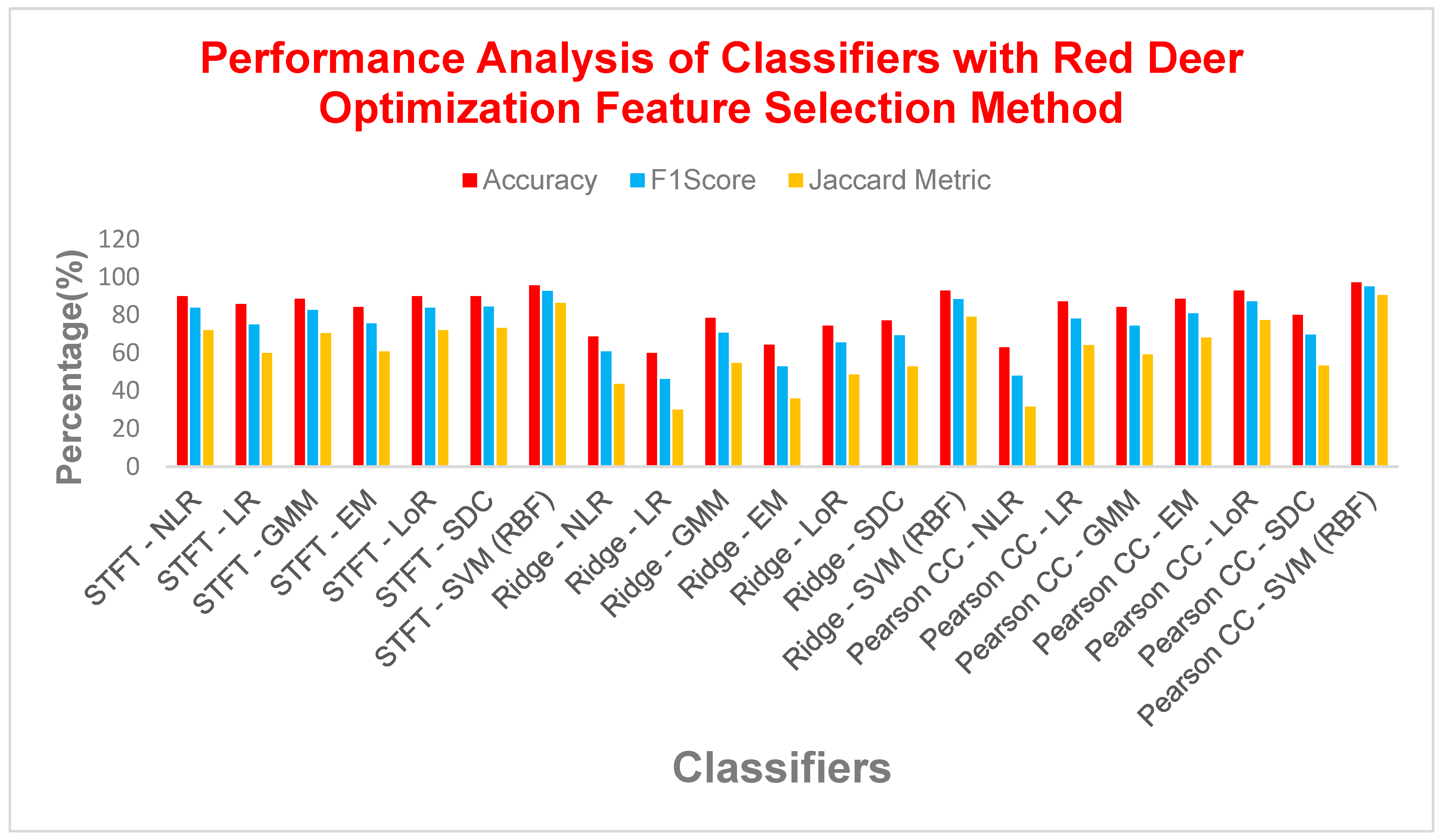
| Feature Extraction | Classifiers | Parameters | |||||
|---|---|---|---|---|---|---|---|
| Accu (%) | F1S (%) | MCC | Jaccard Metric (%) | Error Rate (%) | Kappa | ||
| STFT | NLR | 90 | 83.7209 | 0.7694 | 72 | 10 | 0.76555 |
| LR | 85.7142 | 75 | 0.65 | 60 | 14.2857 | 0.65 | |
| GMM | 88.5714 | 82.6087 | 0.7573 | 70.3703 | 11.4285 | 0.7431 | |
| EM | 84.2857 | 75.5555 | 0.6505 | 60.7142 | 15.7142 | 0.6418 | |
| LoR | 90 | 83.7209 | 0.7694 | 72 | 10 | 0.7655 | |
| SDC | 90 | 84.4444 | 0.7825 | 73.0769 | 10 | 0.7721 | |
| SVM (RBF) | 95.7142 | 92.6829 | 0.8971 | 86.3636 | 4.2857 | 0.8965 | |
| Ridge Regression | NLR | 68.5714 | 60.7142 | 0.4248 | 43.5897 | 31.4285 | 0.3790 |
| LR | 60 | 46.1538 | 0.1813 | 30 | 40 | 0.1694 | |
| GMM | 78.5714 | 70.5882 | 0.5820 | 54.5454 | 21.4285 | 0.5493 | |
| EM | 64.2857 | 52.8301 | 0.2895 | 35.8974 | 35.7142 | 0.2677 | |
| LoR | 74.2857 | 65.3846 | 0.4987 | 48.5714 | 25.7142 | 0.4661 | |
| SDC | 77.1428 | 69.2307 | 0.5622 | 52.9411 | 22.8571 | 0.5254 | |
| SVM (RBF) | 92.8571 | 88.3720 | 0.8367 | 79.1667 | 7.14285 | 0.8325 | |
| Pearson CC | NLR | 62.8571 | 48 | 0.2190 | 31.5789 | 37.1428 | 0.2086 |
| LR | 87.1428 | 78.0487 | 0.6901 | 64 | 12.8571 | 0.6896 | |
| GMM | 84.2857 | 74.4186 | 0.6347 | 59.2592 | 15.7142 | 0.6315 | |
| EM | 88.5714 | 80.9523 | 0.7298 | 68 | 11.4285 | 0.7281 | |
| LoR | 92.8571 | 87.1794 | 0.8228 | 77.2727 | 7.14285 | 0.8223 | |
| SDC | 80 | 69.5652 | 0.5609 | 53.3333 | 20 | 0.5504 | |
| SVM (RBF) | 97.1428 | 95 | 0.93 | 90.4761 | 2.85714 | 0.93 | |
| Classifiers | DR Method | ||
|---|---|---|---|
| STFT | Ridge Regression | Pearson CC | |
| NLR | O(n2 logn) | O(2n2 log2n) | O(2n2 log2n) |
| LR | O(n2 logn) | O(2n2log2n) | O(2n2 log2n) |
| GMM | O(n2 log2n) | O(2n3 log2n) | O(2n3 log2n) |
| EM | O(n3 logn) | O(2n3 log2n) | O(2n3 log2n) |
| LoR | O(2n2 logn) | O(2n2 log2n) | O(2n2 log2n) |
| SDC | O(n3 logn) | O(2n2 log2n) | O(2n2 log2n) |
| SVM (RBF) | O(2n4 log2n) | O(2n2 log4n) | O(2n2 log4n) |
| Classifiers | DR Method | ||
|---|---|---|---|
| STFT | Ridge Regression | Pearson CC | |
| NLR | O(n4 logn) | O(2n4 log2n) | O(2n4 log2n) |
| LR | O(n4 logn) | O(2n4 log2n) | O(2n4 log2n) |
| GMM | O(n4 log2n) | O(2n5 log2n) | O(2n5 log2n) |
| EM | O(n5 logn) | O(2n5 log2n) | O(2n5 log2n) |
| LoR | O(2n4 logn) | O(2n4 log2n) | O(2n4 log2n) |
| SDC | O(n5 logn) | O(2n4 log2n) | O(2n4 log2n) |
| SVM (RBF) | O(2n6 log2n) | O(2n4 log4n) | O(2n4 log4n) |
| Classifiers | DR Method | ||
|---|---|---|---|
| STFT | Ridge Regression | Pearson CC | |
| NLR | O(n5 logn) | O(2n5 log2n) | O(2n5 log2n) |
| LR | O(n5 logn) | O(2n5 log2n) | O(2n5 log2n) |
| GMM | O(n5 log2n) | O(2n6 log2n) | O(2n6 log2n) |
| EM | O(n6 logn) | O(2n6 log2n) | O(2n6 log2n) |
| LoR | O(2n5 logn) | O(2n5 log2n) | O(2n5 log2n) |
| SDC | O(n6 logn) | O(2n5 log2n) | O(2n5 log2n) |
| SVM (RBF) | O(2n7 log2n) | O(2n5 log4n) | O(2n5 log4n) |
| S. No. | Author (with Year) | Description of the Population | Data Sampling | Machine Learning Parameter | Accuracy (%) |
|---|---|---|---|---|---|
| 1. | This article | Nordic Islet Transplantation program | Tenfold cross-validation | STFT, RR, PCC, NLR, LR, LoR, GMM, EM, SDC, SVM (RBF) | 97.14 |
| 2. | Maniruzzaman et al. (2017) [62] | PIDD (Pima Indian diabetic dataset) | Cross-validation K2, K4, K5, K10, and JK | LDA, QDA, NB, GPC, SVM, ANN, AB, LoR, DT, RF | ACC: 92 |
| 3. | Hertroijs et al. (2018) [63] | Total: 105,814 Age (mean): greater than 18 | Training set of 90% and test set of 10% fivefold cross-validation | Latent Growth Mixture Modeling (LGMM) | ACC: 92.3 |
| 4. | Deo et al. (2019) [64] | Total: 140 diabetes: 14 imbalanced age: 12–90 | Training set of 70% and 30% test set with fivefold cross-validation, holdout validation | BT, SVM (L) | ACC: 91 |
| 5. | Akula et al. (2019) [65] | PIDD Practice Fusion Dataset total: 10,000 age: 18–80 | Training set: 800; test set: 10,000 | KNN, SVM, DT, RF, GB, NN, NB | ACC: 86 |
| 6. | Xie et al. (2019) [66] | Total: 138,146 diabetes: 20,467 age: 30–80 | Training set is approximately 67%, test set is approximately 33% | SVM, DT, LoR, RF, NN, NB | ACC: 81, 74, 81, 79, 82, 78 |
| 7. | Bernardini et al. (2020) [67] | Total: 252 diabetes: 252 age: 54–72 | Tenfold cross-validation | Multiple instance learning boosting | ACC: 83 |
| 8. | Zhang et al. (2021) [68] | Total: 37,730, diabetes: 9.4% age: 50–70 imbalanced | Training set is approximately 80% test set is approximately 20% Tenfold cross-validation | Bagging boosting, GBT, RF, GBM | ACC: 82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chellappan, D.; Rajaguru, H. Machine Learning Meets Meta-Heuristics: Bald Eagle Search Optimization and Red Deer Optimization for Feature Selection in Type II Diabetes Diagnosis. Bioengineering 2024, 11, 766. https://doi.org/10.3390/bioengineering11080766
Chellappan D, Rajaguru H. Machine Learning Meets Meta-Heuristics: Bald Eagle Search Optimization and Red Deer Optimization for Feature Selection in Type II Diabetes Diagnosis. Bioengineering. 2024; 11(8):766. https://doi.org/10.3390/bioengineering11080766
Chicago/Turabian StyleChellappan, Dinesh, and Harikumar Rajaguru. 2024. "Machine Learning Meets Meta-Heuristics: Bald Eagle Search Optimization and Red Deer Optimization for Feature Selection in Type II Diabetes Diagnosis" Bioengineering 11, no. 8: 766. https://doi.org/10.3390/bioengineering11080766
APA StyleChellappan, D., & Rajaguru, H. (2024). Machine Learning Meets Meta-Heuristics: Bald Eagle Search Optimization and Red Deer Optimization for Feature Selection in Type II Diabetes Diagnosis. Bioengineering, 11(8), 766. https://doi.org/10.3390/bioengineering11080766








