Cortical and Trabecular Bone Modeling and Implications for Bone Functional Adaptation in the Mammalian Tibia
Abstract
1. Introduction
2. Influencing Factors in Bone Modeling in Response to Mechanical Loading
3. Cortical Bone Modeling
3.1. Murine Studies
3.2. Large Mammals’ Studies
3.3. Human Studies
3.4. Summary
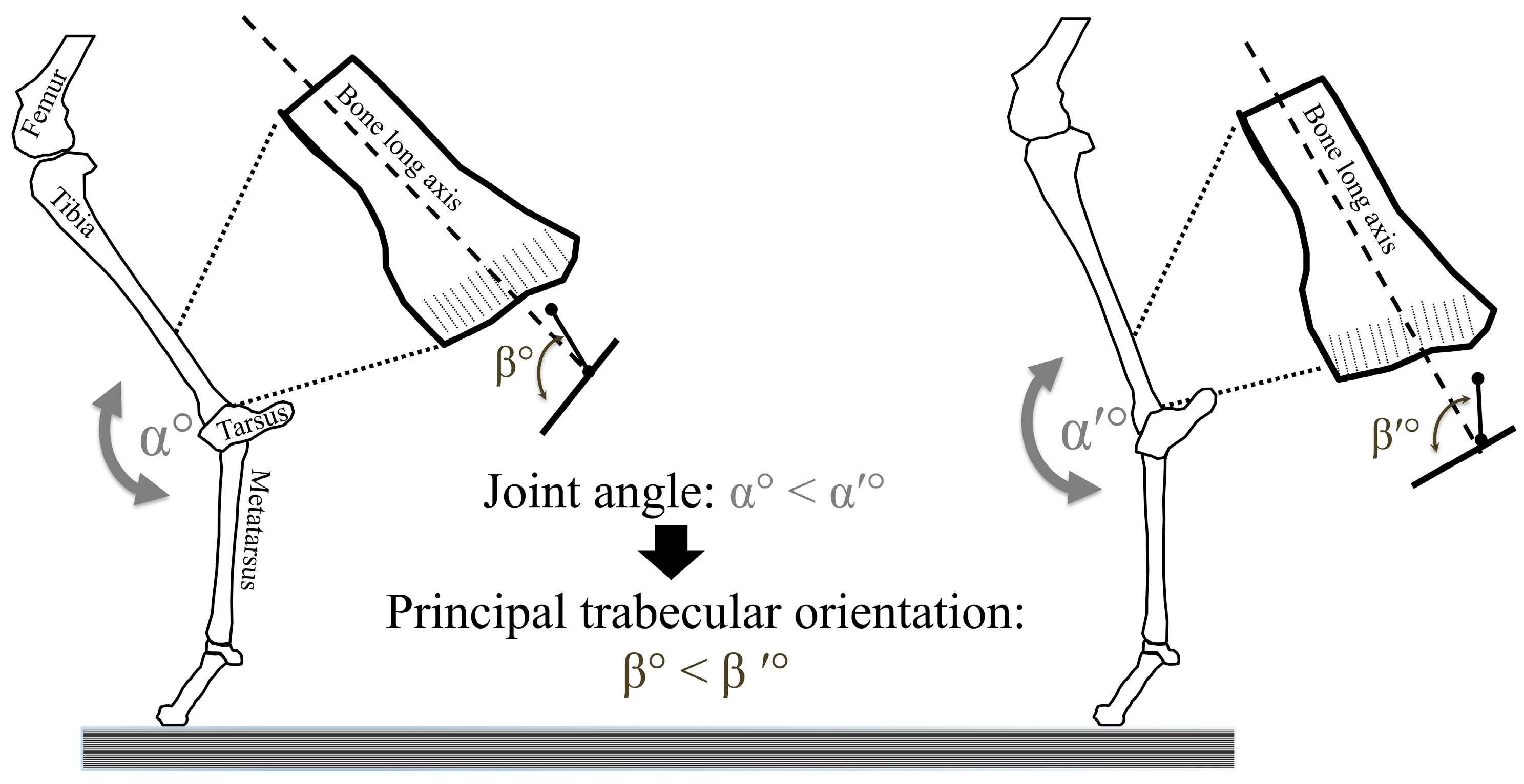
4. Trabecular Bone Modeling
4.1. Murine Studies
4.2. Large Mammals’ Studies
4.3. Human Studies
4.4. Summary
5. Integrated Cortical and Trabecular Bone Modeling Analysis
6. Clinical Importance
7. Limitations
8. Future Studies
9. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barak, M.M. Bone Modeling or Bone Remodeling: That Is the Question. Am. J. Phys. Anthropol. 2020, 172, 153–155. [Google Scholar] [CrossRef] [PubMed]
- Robling, A.G.; Castillo, A.B.; Turner, C.H. Biomechanical and Molecular Regulation of Bone Remodeling. Annu. Rev. Biomed. Eng. 2006, 8, 455–498. [Google Scholar] [CrossRef] [PubMed]
- Gabel, L.; Liphardt, A.-M.; Hulme, P.A.; Heer, M.; Zwart, S.R.; Sibonga, J.D.; Smith, S.M.; Boyd, S.K. Incomplete Recovery of Bone Strength and Trabecular Microarchitecture at the Distal Tibia 1 Year after Return from Long Duration Spaceflight. Sci. Rep. 2022, 12, 9446. [Google Scholar] [CrossRef] [PubMed]
- Bikle, D.D.; Halloran, B.P. The response of bone to unloading. J. Bone Miner. Metab. 1999, 17, 233–244. [Google Scholar] [CrossRef]
- Bolamperti, S.; Villa, I.; Rubinacci, A. Bone remodeling: An operational process ensuring survival and bone mechanical competence. Bone Res. 2022, 10, 48. [Google Scholar] [CrossRef] [PubMed]
- Hughes, J.M.; Castellani, C.M.; Popp, K.L.; Guerriere, K.I.; Matheny RW, J.; Nindl, B.C.; Bouxsein, M.L. The central role of osteocytes in the four adaptive pathways of bone’s mechanostat. Exerc. Sport Sci. Rev. 2020, 48, 140–148. [Google Scholar] [CrossRef] [PubMed]
- Hughes, J.M.; Popp, K.L.; Yanovich, R.; Bouxsein, M.L.; Matheny, R.W. The role of adaptive bone formation in the etiology of stress fracture. Exp. Biol. Med. 2017, 242, 897–906. [Google Scholar] [CrossRef] [PubMed]
- Kivell, T.L. A review of trabecular bone functional adaptation: What have we learned from trabecular analyses in extant hominoids and what can we apply to fossils? J. Anat. 2016, 228, 569–594. [Google Scholar] [CrossRef]
- Klein-Nulend, J.; Bakker, A.D.; Bacabac, R.G.; Vatsa, A.; Weinbaum, S. Mechanosensation and transduction in osteocytes. Bone 2013, 54, 182–190. [Google Scholar] [CrossRef]
- Loundagin, L.L.; Cooper DM, L. Towards novel measurements of remodeling activity in cortical bone: Implications for osteoporosis and related pharmaceutical treatments. Eur. Cells Mater. 2022, 43, 202–227. [Google Scholar] [CrossRef]
- Meakin, L.B.; Price, J.S.; Lanyon, L.E. The Contribution of Experimental In Vivo Models to Understanding the Mechanisms of Adaptation to Mechanical Loading in Bone. Front. Endocrinol. 2014, 5, 154. [Google Scholar] [CrossRef] [PubMed]
- Robling, A.G.; Turner, C.H. Mechanical signaling for bone modeling and remodeling. Crit. Rev. Eukaryot. Gene Expr. 2009, 19, 319–338. [Google Scholar] [CrossRef] [PubMed]
- Seeman, E. Bone modeling and remodeling. Crit. Rev. Eukaryot. Gene Expr. 2009, 19, 219–233. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, S.; Gross, T.S.; Bain, S.D. Bone mechanotransduction may require augmentation in order to strengthen the senescent skeleton. Ageing Res. Rev. 2012, 11, 353–360. [Google Scholar] [CrossRef] [PubMed]
- Tan VP, S.; Macdonald, H.M.; Kim, S.; Nettlefold, L.; Gabel, L.; Ashe, M.C.; McKay, H.A. Influence of physical activity on bone strength in children and adolescents: A systematic review and narrative synthesis. J. Bone Miner. Res. 2014, 29, 2161–2181. [Google Scholar] [CrossRef] [PubMed]
- Willie, B.M.; Zimmermann, E.A.; Vitienes, I.; Main, R.P.; Komarova, S.V. Bone adaptation: Safety factors and load predictability in shaping skeletal form. Bone 2020, 131, 115114. [Google Scholar] [CrossRef] [PubMed]
- Monaco, G.; van Dam, S.; Casal Novo Ribeiro, J.L.; Larbi, A.; de Magalhães, J.P. A Comparison of Human and Mouse Gene Co-Expression Networks Reveals Conservation and Divergence at the Tissue, Pathway and Disease Levels. BMC Evol. Biol. 2015, 15, 259. [Google Scholar] [CrossRef] [PubMed]
- Parfitt, A.M. Misconceptions (2): Turnover Is Always Higher in Cancellous than in Cortical Bone. Bone 2002, 30, 807–809. [Google Scholar] [CrossRef]
- Yang, H.; Xu, X.; Bullock, W.; Main, R.P. Adaptive Changes in Micromechanical Environments of Cancellous and Cortical Bone in Response to In Vivo Loading and Disuse. J. Biomech. 2019, 89, 85–94. [Google Scholar] [CrossRef]
- Yang, H.; Bullock, W.A.; Myhal, A.; DeShield, P.; Duffy, D.; Main, R.P. Cancellous Bone May Have a Greater Adaptive Strain Threshold than Cortical Bone. JBMR Plus 2021, 5, e10489. [Google Scholar] [CrossRef]
- Saers, J.P.P.; DeMars, L.J.; Stephens, N.B.; Jashashvili, T.; Carlson, K.J.; Gordon, A.D.; Shaw, C.N.; Ryan, T.M.; Stock, J.T. Combinations of Trabecular and Cortical Bone Properties Distinguish Various Loading Modalities between Athletes and Controls. Am. J. Phys. Anthropol. 2021, 174, 434–450. [Google Scholar] [CrossRef] [PubMed]
- Murray, A.A.; Erlandson, M.C. Tibial Cortical and Trabecular Variables Together Can Pinpoint the Timing of Impact Loading Relative to Menarche in Premenopausal Females. Am. J. Hum. Biol. 2022, 34, e23711. [Google Scholar] [CrossRef] [PubMed]
- Grimston, S.K.; Watkins, M.P.; Brodt, M.D.; Silva, M.J.; Civitelli, R. Enhanced Periosteal and Endocortical Responses to Axial Tibial Compression Loading in Conditional Connexin43 Deficient Mice. PLoS ONE 2012, 7, e44222. [Google Scholar] [CrossRef] [PubMed]
- Kelly, N.H.; Schimenti, J.C.; Ross, F.P.; van der Meulen, M.C.H. Transcriptional Profiling of Cortical versus Cancellous Bone from Mechanically-Loaded Murine Tibiae Reveals Differential Gene Expression. Bone 2016, 86, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.M.; Yeh, J.K.; Aloia, J.F.; Tierney, J.M.; Sprintz, S. Effect of Treadmill Exercise on Tibial Cortical Bone in Aged Female Rats: A Histomorphometry and Dual Energy X-ray Absorptiometry Study. Bone 1994, 15, 313–319. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.E.; Main, R.P.; Xu, Q.; Schmicker, T.L.; Schaffler, M.B.; Wright, T.M.; van der Meulen, M.C.H. Tibial Compression Is Anabolic in the Adult Mouse Skeleton despite Reduced Responsiveness with Aging. Bone 2011, 49, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Silva, M.J.; Brodt, M.D.; Lynch, M.A.; Stephens, A.L.; Wood, D.J.; Civitelli, R. Tibial Loading Increases Osteogenic Gene Expression and Cortical Bone Volume in Mature and Middle-Aged Mice. PLoS ONE 2012, 7, e34980. [Google Scholar] [CrossRef] [PubMed]
- Holguin, N.; Brodt, M.D.; Sanchez, M.E.; Silva, M.J. Aging Diminishes Lamellar and Woven Bone Formation Induced by Tibial Compression in Adult C57BL/6. Bone 2014, 65, 83–91. [Google Scholar] [CrossRef] [PubMed]
- Main, R.P.; Lynch, M.E.; van der Meulen, M.C.H. Load-Induced Changes in Bone Stiffness and Cancellous and Cortical Bone Mass Following Tibial Compression Diminish with Age in Female Mice. J. Exp. Biol. 2014, 217, 1775–1783. [Google Scholar] [CrossRef]
- Carriero, A.; Javaheri, B.; Kazeruni, N.B.; Pitsillides, A.A.; Shefelbine, S.J. Age and Sex Differences in Load-Induced Tibial Cortical Bone Surface Strain Maps. JBMR Plus 2021, 5, e10467. [Google Scholar] [CrossRef]
- Cullen, D.M.; Smith, R.T.; Akhter, M.P. Bone-Loading Response Varies with Strain Magnitude and Cycle Number. J. Appl. Physiol. 2001, 91, 1971–1976. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, Y.F.; Turner, C.H. Effects of Loading Frequency on Mechanically Induced Bone Formation. J. Bone Miner. Res. 2001, 16, 918–924. [Google Scholar] [CrossRef] [PubMed]
- De Souza, R.L.; Matsuura, M.; Eckstein, F.; Rawlinson, S.C.F.; Lanyon, L.E.; Pitsillides, A.A. Non-Invasive Axial Loading of Mouse Tibiae Increases Cortical Bone Formation and Modifies Trabecular Organization: A New Model to Study Cortical and Cancellous Compartments in a Single Loaded Element. Bone 2005, 37, 810–818. [Google Scholar] [CrossRef] [PubMed]
- Sugiyama, T.; Meakin, L.B.; Browne, W.J.; Galea, G.L.; Price, J.S.; Lanyon, L.E. Bones’ Adaptive Response to Mechanical Loading Is Essentially Linear between the Low Strains Associated with Disuse and the High Strains Associated with the Lamellar/Woven Bone Transition. J. Bone Miner. Res. 2012, 27, 1784–1793. [Google Scholar] [CrossRef]
- Weatherholt, A.M.; Fuchs, R.K.; Warden, S.J. Cortical and Trabecular Bone Adaptation to Incremental Load Magnitudes Using the Mouse Tibial Axial Compression Loading Model. Bone 2013, 52, 372–379. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Willie, B.M.; Beach, J.M.; Wright, T.M.; van der Meulen, M.C.H.; Bostrom, M.P.G. Trabecular Bone Adaptation to Loading in a Rabbit Model Is Not Magnitude-Dependent. J. Orthop. Res. 2013, 31, 930–934. [Google Scholar] [CrossRef] [PubMed]
- Berman, A.G.; Clauser, C.A.; Wunderlin, C.; Hammond, M.A.; Wallace, J.M. Structural and Mechanical Improvements to Bone Are Strain Dependent with Axial Compression of the Tibia in Female C57BL/6 Mice. PLoS ONE 2015, 10, e0130504. [Google Scholar] [CrossRef] [PubMed]
- Skedros, J.G.; Mason, M.W.; Bloebaum, R.D. Modeling and Remodeling in a Developing Artiodactyl Calcaneus: A Model for Evaluating Frost’s Mechanostat Hypothesis and Its Corollaries. Anat. Rec. 2001, 263, 167–185. [Google Scholar] [CrossRef]
- Turner, C.H.; Akhter, M.P.; Raab, D.M.; Kimmel, D.B.; Recker, R.R. A Noninvasive, In Vivo Model for Studying Strain Adaptive Bone Modeling. Bone 1991, 12, 73–79. [Google Scholar] [CrossRef]
- van der Meulen, M.C.H.; Morgan, T.G.; Yang, X.; Baldini, T.H.; Myers, E.R.; Wright, T.M.; Bostrom, M.P.G. Cancellous Bone Adaptation to In Vivo Loading in a Rabbit Model. Bone 2006, 38, 871–877. [Google Scholar] [CrossRef]
- Yang, H.; Embry, R.E.; Main, R.P. Effects of Loading Duration and Short Rest Insertion on Cancellous and Cortical Bone Adaptation in the Mouse Tibia. PLoS ONE 2017, 12, e0169519. [Google Scholar] [CrossRef] [PubMed]
- Bouchard, A.L.; Dsouza, C.; Julien, C.; Rummler, M.; Gaumond, M.-H.; Cermakian, N.; Willie, B.M. Bone Adaptation to Mechanical Loading in Mice Is Affected by Circadian Rhythms. Bone 2022, 154, 116218. [Google Scholar] [CrossRef] [PubMed]
- Mosley, J.R.; Lanyon, L.E. Strain Rate as a Controlling Influence on Adaptive Modeling in Response to Dynamic Loading of the Ulna in Growing Male Rats. Bone 1998, 23, 313–318. [Google Scholar] [CrossRef] [PubMed]
- Turner, C.H.; Forwood, M.R.; Otter, M.W. Mechanotransduction in Bone: Do Bone Cells Act as Sensors of Fluid Flow? FASEB J. 1994, 8, 875–878. [Google Scholar] [CrossRef] [PubMed]
- Burr, D.B.; Robling, A.G.; Turner, C.H. Effects of Biomechanical Stress on Bones in Animals. Bone 2002, 30, 781–786. [Google Scholar] [CrossRef] [PubMed]
- Robling, A.G.; Burr, D.B.; Turner, C.H. Partitioning a Daily Mechanical Stimulus into Discrete Loading Bouts Improves the Osteogenic Response to Loading. J. Bone Miner. Res. 2000, 15, 1596–1602. [Google Scholar] [CrossRef] [PubMed]
- Robling, A.G.; Burr, D.B.; Turner, C.H. Recovery Periods Restore Mechanosensitivity to Dynamically Loaded Bone. J. Exp. Biol. 2001, 204, 3389–3399. [Google Scholar] [CrossRef] [PubMed]
- LaMothe, J.M.; Zernicke, R.F. Rest Insertion Combined with High-Frequency Loading Enhances Osteogenesis. J. Appl. Physiol. 2004, 96, 1788–1793. [Google Scholar] [CrossRef]
- Srinivasan, S.; Ausk, B.J.; Poliachik, S.L.; Warner, S.E.; Richardson, T.S.; Gross, T.S. Rest-Inserted Loading Rapidly Amplifies the Response of Bone to Small Increases in Strain and Load Cycles. J. Appl. Physiol. 2007, 102, 1945–1952. [Google Scholar] [CrossRef]
- Sugiyama, T.; Price, J.S.; Lanyon, L.E. Functional Adaptation to Mechanical Loading in Both Cortical and Cancellous Bone Is Controlled Locally and Is Confined to the Loaded Bones. Bone 2010, 46, 314–321. [Google Scholar] [CrossRef]
- Gross, T.S.; Srinivasan, S.; Liu, C.C.; Clemens, T.L.; Bain, S.D. Noninvasive Loading of the Murine Tibia: An In Vivo Model for the Study of Mechanotransduction. J. Bone Miner. Res. 2002, 17, 493–501. [Google Scholar] [CrossRef]
- Fritton, J.C.; Myers, E.R.; Wright, T.M.; van der Meulen, M.C.H. Loading Induces Site-Specific Increases in Mineral Content Assessed by Microcomputed Tomography of the Mouse Tibia. Bone 2005, 36, 1030–1038. [Google Scholar] [CrossRef]
- Iwamoto, J.; Yeh, J.K.; Aloia, J.F. Differential Effect of Treadmill Exercise on Three Cancellous Bone Sites in the Young Growing Rat. Bone 1999, 24, 163–169. [Google Scholar] [CrossRef]
- Barak, M.M.; Lieberman, D.E.; Hublin, J.-J. A Wolff in Sheep’s Clothing: Trabecular Bone Adaptation in Response to Changes in Joint Loading Orientation. Bone 2011, 49, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
- Macdonald, H.M.; Cooper, D.M.L.; McKay, H.A. Anterior–Posterior Bending Strength at the Tibial Shaft Increases with Physical Activity in Boys: Evidence for Non-Uniform Geometric Adaptation. Osteoporos. Int. 2009, 20, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, D.E.; Devlin, M.J.; Pearson, O.M. Articular Area Responses to Mechanical Loading: Effects of Exercise, Age, and Skeletal Location. Am. J. Phys. Anthropol. 2001, 116, 266–277. [Google Scholar] [CrossRef]
- Lieberman, D.E.; Pearson, O.M.; Polk, J.D.; Demes, B.; Crompton, A.W. Optimization of Bone Growth and Remodeling in Response to Loading in Tapered Mammalian Limbs. J. Exp. Biol. 2003, 206, 3125–3138. [Google Scholar] [CrossRef]
- Brodt, M.D.; Silva, M.J. Aged Mice Have Enhanced Endocortical Response and Normal Periosteal Response Compared with Young-Adult Mice Following 1 Week of Axial Tibial Compression. J. Bone Miner. Res. 2010, 25, 2006–2015. [Google Scholar] [CrossRef]
- Akhter, M.P.; Cullen, D.M.; Pedersen, E.A.; Kimmel, D.B.; Recker, R.R. Bone Response to In Vivo Mechanical Loading in Two Breeds of Mice. Calcif. Tissue Int. 1998, 63, 442–449. [Google Scholar] [CrossRef] [PubMed]
- Judex, S.; Donahue, L.-R.; Rubin, C. Genetic Predisposition to Low Bone Mass Is Paralleled by an Enhanced Sensitivity to Signals Anabolic to the Skeleton. FASEB J. 2002, 16, 1280–1282. [Google Scholar] [CrossRef]
- Kodama, Y.; Dimai, H.P.; Wergedal, J.; Sheng, M.; Malpe, R.; Kutilek, S.; Beamer, W.; Donahue, L.R.; Rosen, C.; Baylink, D.J.; et al. Cortical Tibial Bone Volume in Two Strains of Mice: Effects of Sciatic Neurectomy and Genetic Regulation of Bone Response to Mechanical Loading. Bone 1999, 25, 183–190. [Google Scholar] [CrossRef] [PubMed]
- Kodama, Y.; Umemura, Y.; Nagasawa, S.; Beamer, W.G.; Donahue, L.R.; Rosen, C.R.; Baylink, D.J.; Farley, J.R. Exercise and Mechanical Loading Increase Periosteal Bone Formation and Whole Bone Strength in C57BL/6J Mice but Not in C3H/Hej Mice. Calcif. Tissue Int. 2000, 66, 298–306. [Google Scholar] [CrossRef] [PubMed]
- Wallace, I.J.; Demes, B.; Judex, S. Ontogenetic and Genetic Influences on Bone’s Responsiveness to Mechanical Signals. In Building Bones: Bone Formation and Development in Anthropology; Percival, C.J., Richtsmeier, J.T., Eds.; Cambridge Studies in Biological and Evolutionary Anthropology; Cambridge University Press: Cambridge, UK, 2017; pp. 233–253. ISBN 978-1-107-12278-9. [Google Scholar]
- Li, D.; Gromov, K.; Søballe, K.; Puzas, J.E.; O’Keefe, R.J.; Awad, H.; Drissi, H.; Schwarz, E.M. Quantitative Mouse Model of Implant-Associated Osteomyelitis and the Kinetics of Microbial Growth, Osteolysis, and Humoral Immunity. J. Orthop. Res. 2008, 26, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Holguin, N.; Brodt, M.D.; Sanchez, M.E.; Kotiya, A.A.; Silva, M.J. Adaptation of Tibial Structure and Strength to Axial Compression Depends on Loading History in Both C57BL/6 and BALB/c Mice. Calcif. Tissue Int. 2013, 93, 211–221. [Google Scholar] [CrossRef]
- Delaere, O.; Dhem, A.; Bourgois, R. Cancellous Bone and Mechanical Strength of the Femoral Neck. Arch. Orthop. Trauma. Surg. 1989, 108, 72–75. [Google Scholar] [CrossRef] [PubMed]
- Barak, M.M.; Weiner, S.; Shahar, R. Importance of the Integrity of Trabecular Bone to the Relationship between Load and Deformation of Rat Femora: An Optical Metrology Study. J. Mater. Chem. 2008, 18, 3855–3864. [Google Scholar] [CrossRef]
- Barak, M.M.; Weiner, S.; Shahar, R. The Contribution of Trabecular Bone to the Stiffness and Strength of Rat Lumbar Vertebrae. Spine 2010, 35, E1153–E1159. [Google Scholar] [CrossRef] [PubMed]
- Werner, C.; Iversen, B.F.; Therkildsen, M.H. Contribution of the Trabecular Component to Mechanical Strength and Bone Mineral Content of the Femoral Neck. An Experimental Study on Cadaver Bones. Scand. J. Clin. Lab. Investig. 1988, 48, 457–460. [Google Scholar] [CrossRef]
- Wallace, I.J.; Demes, B.; Mongle, C.; Pearson, O.M.; Polk, J.D.; Lieberman, D.E. Exercise-Induced Bone Formation Is Poorly Linked to Local Strain Magnitude in the Sheep Tibia. PLoS ONE 2014, 9, e99108. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Niinimäki, S.; Härkönen, L.; Puolakka, H.-L.; van den Berg, M.; Salmi, A.-K. Cross-Sectional Properties of Reindeer Long Bones and Metapodials Allow Identification of Activity Patterns. Archaeol. Anthropol. Sci. 2021, 13, 146. [Google Scholar] [CrossRef]
- Hughes, J.M.; Taylor, K.M.; Guerriere, K.I.; Smith, N.I.; Staab, J.S.; Walker, L.A.; Staab, J.E.; Bartlett, P.M.; Spiering, B.A.; Nguyen, V.T.; et al. Changes in Distal Tibial Microarchitecture during Eight Weeks of U.S. Army Basic Combat Training Differ by Sex and Race. JBMR Plus 2023, 7, e10719. [Google Scholar] [CrossRef] [PubMed]
- Demes, B.; Qin, Y.X.; Stern, J.T., Jr.; Larson, S.G.; Rubin, C.T. Patterns of Strain in the Macaque Tibia during Functional Activity. Am. J. Phys. Anthropol. 2001, 116, 257–265. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, D.E.; Polk, J.D.; Demes, B. Predicting Long Bone Loading from Cross-Sectional Geometry. Am. J. Phys. Anthropol. 2004, 123, 156–171. [Google Scholar] [CrossRef]
- Javaheri, B.; Razi, H.; Gohin, S.; Wylie, S.; Chang, Y.-M.; Salmon, P.; Lee, P.D.; Pitsillides, A.A. Lasting Organ-Level Bone Mechanoadaptation Is Unrelated to Local Strain. Sci. Adv. 2020, 6, eaax8301. [Google Scholar] [CrossRef] [PubMed]
- van Tol, A.F.; Schemenz, V.; Wagermaier, W.; Roschger, A.; Razi, H.; Vitienes, I.; Fratzl, P.; Willie, B.M.; Weinkamer, R. The Mechanoresponse of Bone Is Closely Related to the Osteocyte Lacunocanalicular Network Architecture. Proc. Natl. Acad. Sci. USA 2020, 117, 32251–32259. [Google Scholar] [CrossRef] [PubMed]
- Miller, C.J.; Trichilo, S.; Pickering, E.; Martelli, S.; Delisser, P.; Meakin, L.B.; Pivonka, P. Cortical Thickness Adaptive Response to Mechanical Loading Depends on Periosteal Position and Varies Linearly with Loading Magnitude. Front. Bioeng. Biotechnol. 2021, 9, 671606. [Google Scholar] [CrossRef] [PubMed]
- Shaw, C.N.; Stock, J.T. Extreme Mobility in the Late Pleistocene? Comparing Limb Biomechanics among Fossil Homo, Varsity Athletes and Holocene Foragers. J. Hum. Evol. 2013, 64, 242–249. [Google Scholar] [CrossRef] [PubMed]
- Fritton, J.C.; Myers, E.R.; Wright, T.M.; van der Meulen, M.C.H. Bone Mass Is Preserved and Cancellous Architecture Altered Due to Cyclic Loading of the Mouse Tibia after Orchidectomy. J. Bone Miner. Res. 2008, 23, 663–671. [Google Scholar] [CrossRef] [PubMed]
- Swift, J.M.; Gasier, H.G.; Swift, S.N.; Wiggs, M.P.; Hogan, H.A.; Fluckey, J.D.; Bloomfield, S.A. Increased Training Loads Do Not Magnify Cancellous Bone Gains with Rodent Jump Resistance Exercise. J. Appl. Physiol. 2010, 109, 1600–1607. [Google Scholar] [CrossRef]
- Barak, M.M.; Lieberman, D.E.; Hublin, J.-J. Of Mice, Rats and Men: Trabecular Bone Architecture in Mammals Scales to Body Mass with Negative Allometry. J. Struct. Biol. 2013, 183, 123–131. [Google Scholar] [CrossRef]
- Assif, L.; Chirchir, H. Trabecular Bone Morphology in Big Cats Reflects the Complex Diversity of Limb Use but Not Home Range Size or Daily Travel Distance. Anat. Rec. 2024, 307, 208–222. [Google Scholar] [CrossRef] [PubMed]
- Cazenave, M.; Nakatsukasa, M.; Mazurier, A.; Skinner, M.M. Identification of Functionally-Related Adaptations in the Trabecular Network of the Proximal Femur and Tibia of a Bipedally-Trained Japanese Macaque. Anthropol. Sci. 2024, 132, 13–26. [Google Scholar] [CrossRef]
- Volpato, V.; Viola, T.B.; Nakatsukasa, M.; Bondioli, L.; Macchiarelli, R. Textural Characteristics of the Iliac-Femoral Trabecular Pattern in a Bipedally Trained Japanese Macaque. Primates 2008, 49, 16–25. [Google Scholar] [CrossRef] [PubMed]
- Tanck, E.; Homminga, J.; van Lenthe, G.H.; Huiskes, R. Increase in Bone Volume Fraction Precedes Architectural Adaptation in Growing Bone. Bone 2001, 28, 650–654. [Google Scholar] [CrossRef] [PubMed]
- Raichlen, D.A.; Gordon, A.D.; Foster, A.D.; Webber, J.T.; Sukhdeo, S.M.; Scott, R.S.; Gosman, J.H.; Ryan, T.M. An Ontogenetic Framework Linking Locomotion and Trabecular Bone Architecture with Applications for Reconstructing Hominin Life History. J. Hum. Evol. 2015, 81, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Barak, M.M.; Lieberman, D.E.; Raichlen, D.; Pontzer, H.; Warrener, A.G.; Hublin, J.-J. Trabecular Evidence for a Human-like Gait in Australopithecus Africanus. PLoS ONE 2013, 8, e77687. [Google Scholar] [CrossRef]
- Barak, M.M.; Sherratt, E.; Lieberman, D.E. Using Principal Trabecular Orientation to Differentiate Joint Loading Orientation in the 3rd Metacarpal Heads of Humans and Chimpanzees. J. Hum. Evol. 2017, 113, 173–182. [Google Scholar] [CrossRef] [PubMed]
- Willie, B.M.; Birkhold, A.I.; Razi, H.; Thiele, T.; Aido, M.; Kruck, B.; Schill, A.; Checa, S.; Main, R.P.; Duda, G.N. Diminished Response to In Vivo Mechanical Loading in Trabecular and Not Cortical Bone in Adulthood of Female C57Bl/6 Mice Coincides with a Reduction in Deformation to Load. Bone 2013, 55, 335–346. [Google Scholar] [CrossRef] [PubMed]
- Sakai, J. How Synaptic Pruning Shapes Neural Wiring during Development and, Possibly, in Disease. Proc. Natl. Acad. Sci. USA 2020, 117, 16096–16099. [Google Scholar] [CrossRef]
- Dean, M.N.; Shahar, R. The structure-mechanics relationship and the response to load of the acellular bone of neoteleost fish: A review. J. Appl. Ichthyol. 2012, 28, 320–329. [Google Scholar] [CrossRef]
- Shahar, R.; Dean, M.N. The enigmas of bone without osteocytes. BoneKEy Rep. 2013, 2, 343. [Google Scholar] [CrossRef] [PubMed]
- Kranenbarg, S.; van Cleynenbreugel, T.; Schipper, H.; van Leeuwen, J. Adaptive bone formation in acellular vertebrae of sea bass (Dicentrarchus labrax L.). J. Exp. Biol. 2005, 208 Pt 18, 3493–3502. [Google Scholar] [CrossRef] [PubMed]
- Barak, M.M.; Black, M.A. A Novel Use of 3D Printing Model Demonstrates the Effects of Deteriorated Trabecular Bone Structure on Bone Stiffness and Strength. J. Mech. Behav. Biomed. Mater. 2018, 78, 455–464. [Google Scholar] [CrossRef] [PubMed]
- Wood, Z.; Lynn, L.; Nguyen, J.T.; Black, M.A.; Patel, M.; Barak, M.M. Are We Crying Wolff? 3D Printed Replicas of Trabecular Bone Structure Demonstrate Higher Stiffness and Strength during off-Axis Loading. Bone 2019, 127, 635–645. [Google Scholar] [CrossRef] [PubMed]
- Christen, P.; van Rietbergen, B.; Lambers, F.M.; Müller, R.; Ito, K. Bone Morphology Allows Estimation of Loading History in a Murine Model of Bone Adaptation. Biomech. Model. Mechanobiol. 2012, 11, 483–492. [Google Scholar] [CrossRef]
- Pais, A.; Moreira, C.; Belinha, J. The Biomechanical Analysis of Tibial Implants Using Meshless Methods: Stress and Bone Tissue Remodeling Analysis. Designs 2024, 8, 28. [Google Scholar] [CrossRef]
- Farage-O’Reilly, S.M.; Cheong, V.S.; Pickering, E.; Pivonka, P.; Bellantuono, I.; Kadirkamanathan, V.; Dall’Ara, E. The Loading Direction Dramatically Affects the Mechanical Properties of the Mouse Tibia. Front. Bioeng. Biotechnol. 2024, 12, 1335955. [Google Scholar] [CrossRef]
- Meslier, Q.A.; Shefelbine, S.J. Using Finite Element Modeling in Bone Mechanoadaptation. Curr. Osteoporos. Rep. 2023, 21, 105–116. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barak, M.M. Cortical and Trabecular Bone Modeling and Implications for Bone Functional Adaptation in the Mammalian Tibia. Bioengineering 2024, 11, 514. https://doi.org/10.3390/bioengineering11050514
Barak MM. Cortical and Trabecular Bone Modeling and Implications for Bone Functional Adaptation in the Mammalian Tibia. Bioengineering. 2024; 11(5):514. https://doi.org/10.3390/bioengineering11050514
Chicago/Turabian StyleBarak, Meir M. 2024. "Cortical and Trabecular Bone Modeling and Implications for Bone Functional Adaptation in the Mammalian Tibia" Bioengineering 11, no. 5: 514. https://doi.org/10.3390/bioengineering11050514
APA StyleBarak, M. M. (2024). Cortical and Trabecular Bone Modeling and Implications for Bone Functional Adaptation in the Mammalian Tibia. Bioengineering, 11(5), 514. https://doi.org/10.3390/bioengineering11050514






