Design Optimization and Tradeoff Analysis of an Actuated Continuum Probe for Pulmonary Nodule Localization and Resection
Abstract
1. Introduction
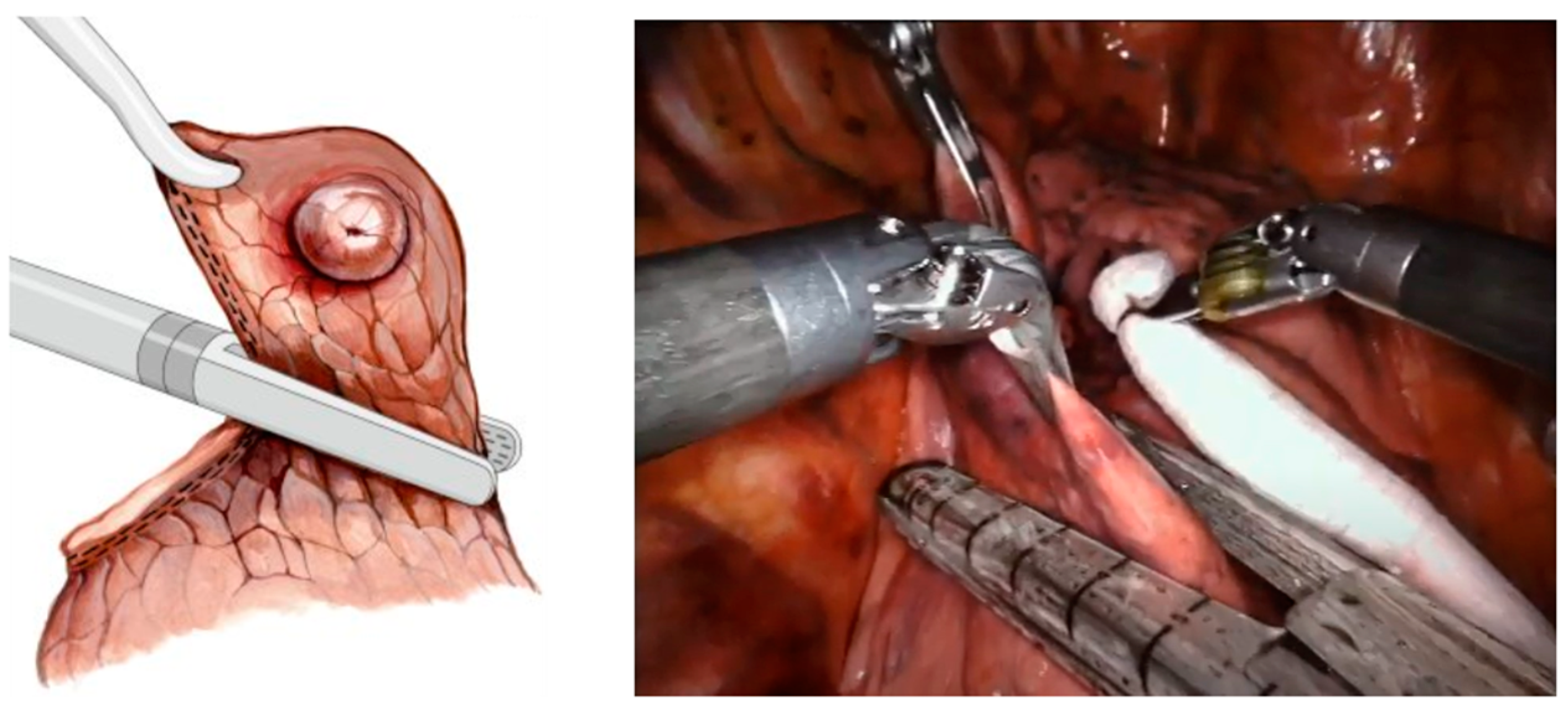
1.1. Wedge Resection of PNs
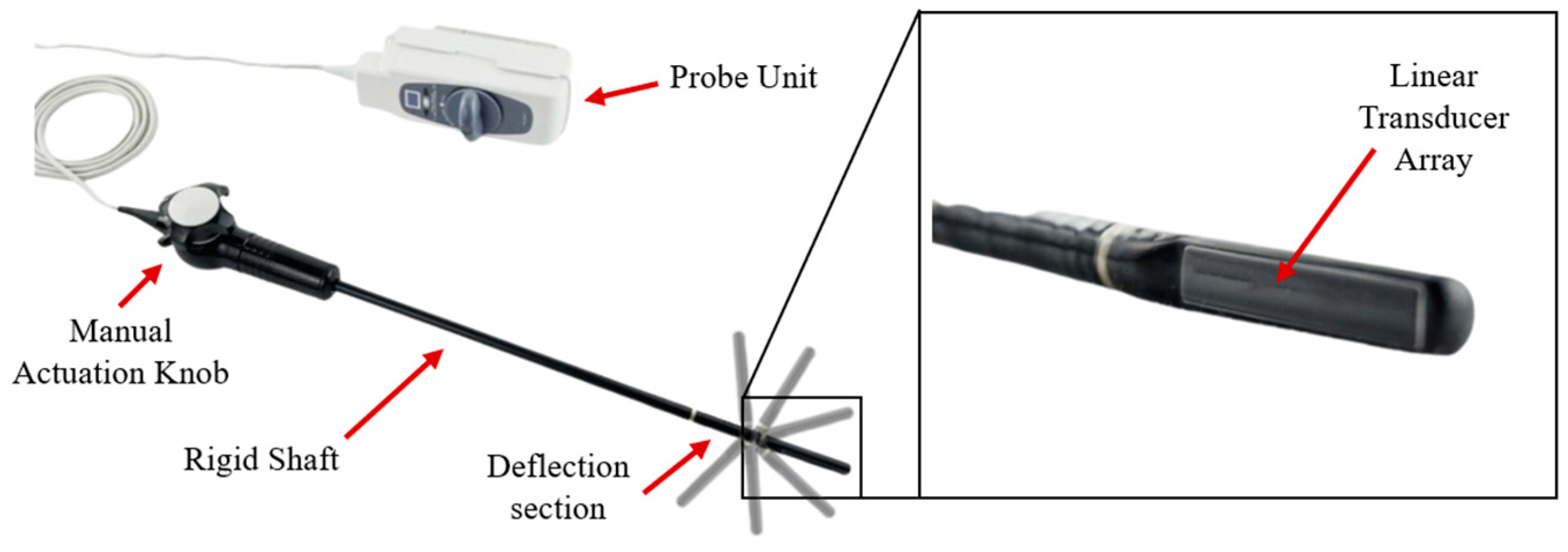
1.2. Probe Actuation
1.3. Research Objective
2. Materials and Methods
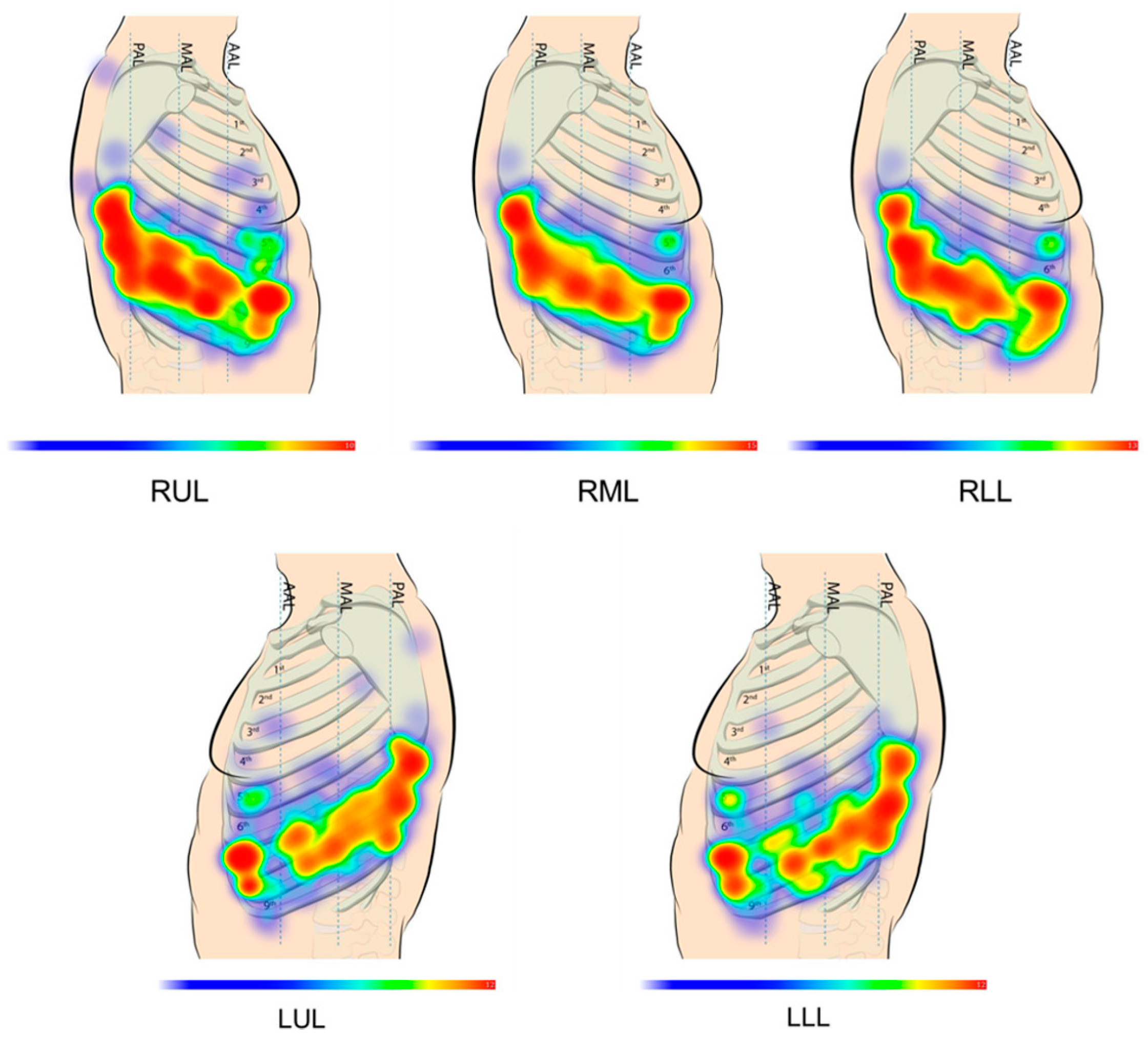
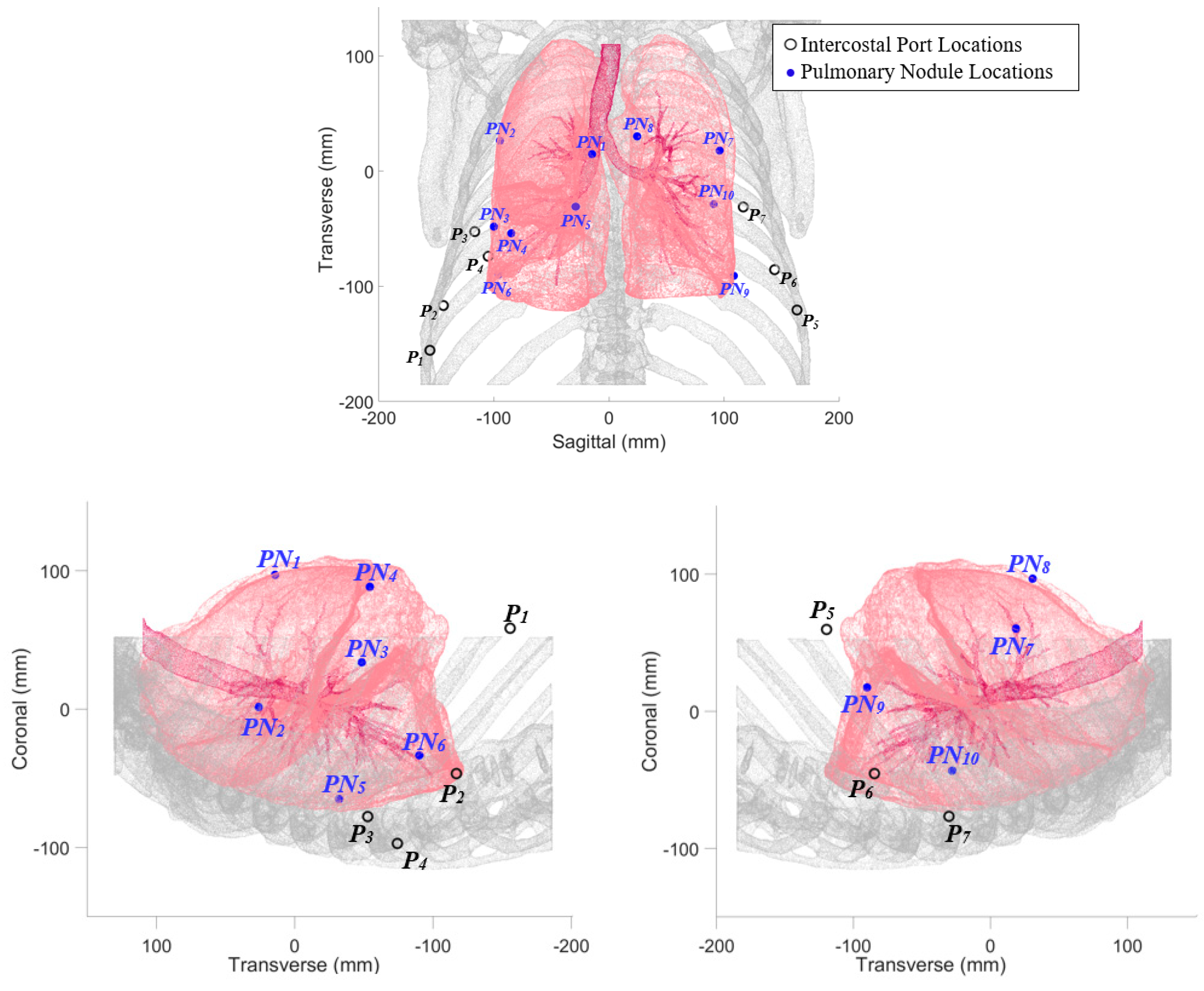
2.1. Probe Configuration Analysis
2.2. Design Variables and Constraints
2.3. MOGA-Based Design Optimization
3. Results
3.1. Optimal Probe Configuration
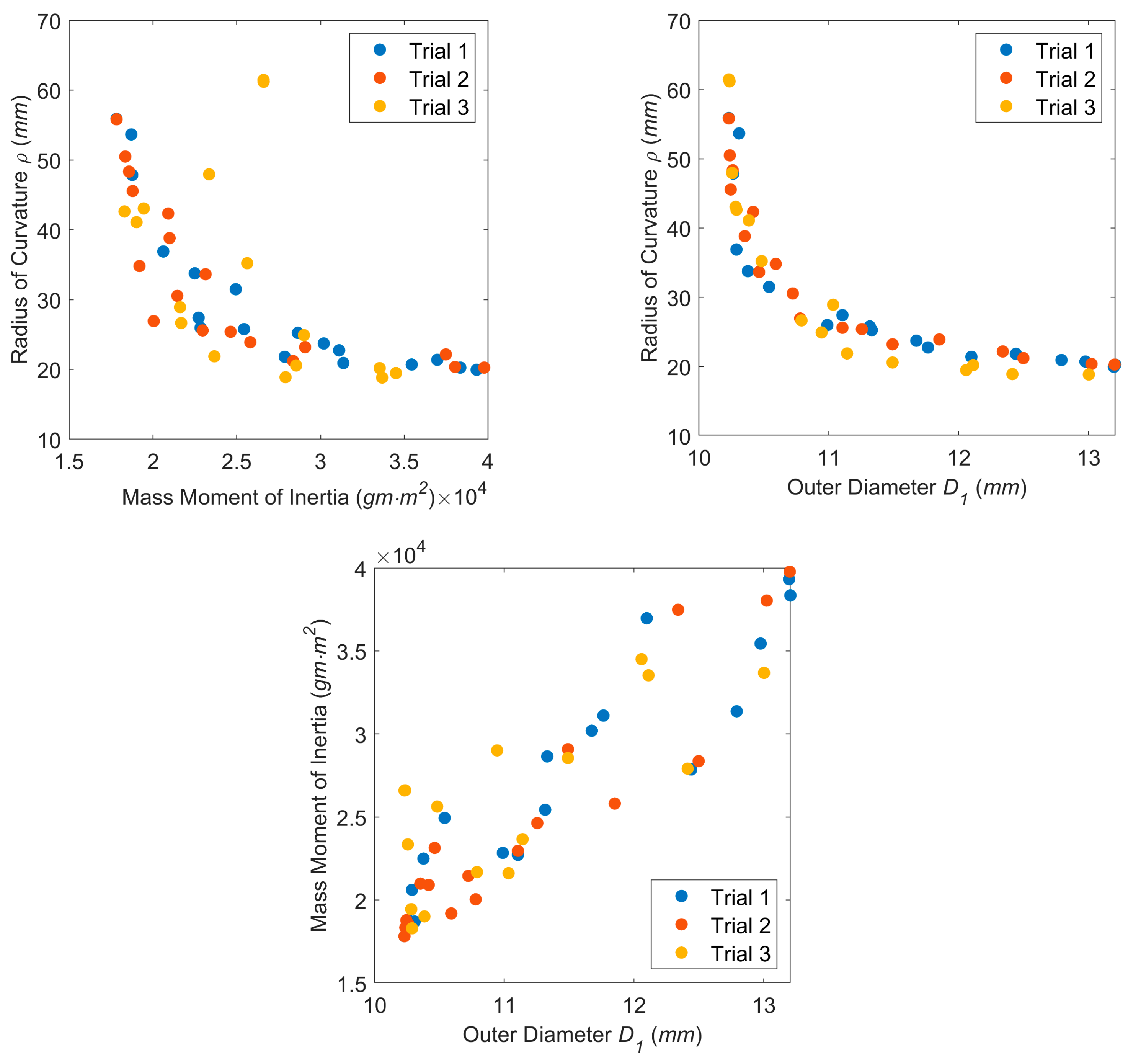
3.2. Design Optimization
3.3. Experimental Confirmation
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Lung Cancer. Available online: https://www.who.int/news-room/fact-sheets/detail/lung-cancer (accessed on 4 February 2024).
- Mayo Clinic. Lung Cancer. 2022. Available online: https://www.mayoclinic.org/diseases-conditions/lung-cancer/symptoms-causes/syc-20374620 (accessed on 4 May 2023).
- How to Detect Lung Cancer: Lung Cancer Tests. Available online: https://www.cancer.org/cancer/types/lung-cancer/detection-diagnosis-staging/how-diagnosed.html (accessed on 4 May 2023).
- Loverdos, K.; Fotiadis, A.; Kontogianni, C.; Iliopoulou, M.; Gaga, M. Lung nodules: A comprehensive review on current approach and management. Ann. Thorac. Med. 2019, 14, 226–238. [Google Scholar] [CrossRef] [PubMed]
- What Is a Lung Nodule?—American Thoracic Society. 2020. Available online: https://www.thoracic.org/patients/patient-resources/resources/lung-nodules-online.pdf (accessed on 4 May 2023).
- Ye, T.; Deng, L.; Wang, S.; Xiang, J.; Zhang, Y.; Hu, H.; Sun, Y.; Li, Y.; Shen, L.; Xie, L.; et al. Lung Adenocarcinomas Manifesting as Radiological Part-Solid Nodules Define a Special Clinical Subtype. J. Thorac. Oncol. 2019, 14, 617–627. [Google Scholar] [CrossRef] [PubMed]
- Cruickshank, A.; Stieler, G.; Ameer, F. Evaluation of the solitary pulmonary nodule. Intern. Med. J. 2019, 49, 306–315. [Google Scholar] [CrossRef] [PubMed]
- MacMahon, H.; Naidich, D.P.; Goo, J.M.; Lee, K.S.; Leung, A.N.C.; Mayo, J.R.; Mehta, A.C.; Ohno, Y.; Powell, C.A.; Prokop, M.; et al. Guidelines for Management of Incidental Pulmonary Nodules Detected on CT Images: From the Fleischner Society 2017. Radiology 2017, 284, 228–243. [Google Scholar] [CrossRef] [PubMed]
- Cornella, K.N.; Repper, D.C.; Palafox, B.A.; Razavi, M.K.; Loh, C.T.; Markle, K.M.; Openshaw, L.E. A Surgeon’s Guide for Various Lung Nodule Localization Techniques and the Newest Technologies. Innov. Technol. Tech. Cardiothorac. Vasc. Surg. 2021, 16, 26–33. [Google Scholar] [CrossRef] [PubMed]
- European Society of Thoracic Surgeons. Types of Pulmonary Resections. Available online: https://www.ests.org/about_ests/patient_information/diseases/pulmonary_nodules_and_lung_cancer/lung_cancer/treatment/pulmonary_resections.aspx#googtrans/en/en (accessed on 21 May 2023).
- Alberton, L.; Costas, K. Robotic Assisted Wedge Resection for Pulmonary Nodule Using Intraoperative ICG Tattoo; CTSNet, Inc.: Chicago, IL, USA, 2017; Available online: https://ctsnet.figshare.com/articles/media/Robotic_Assisted_Wedge_Resection_for_Pulmonary_Nodule_Using_Intraoperative_ICG_Tattoo/5147683/1 (accessed on 22 May 2023).
- Marra, A.; Yankulov, A. The role of new staplers in reducing the incidence of air leak. J. Thorac. Dis. 2023, 15, 893–900. [Google Scholar] [CrossRef] [PubMed]
- Oh, D.S.; Tisol, W.B.; Cesnik, L.; Crosby, A.; Cerfolio, R.J. Port Strategies for Robot-Assisted Lobectomy by High-Volume Thoracic Surgeons: A Nationwide Survey. Innov. Technol. Tech. Cardiothorac. Vasc. Surg. 2019, 14, 545–552. [Google Scholar] [CrossRef] [PubMed]
- Roshankhah, R.; Blackwell, J.; Ali, M.H.; Masuodi, B.; Egan, T.; Muller, M. Detecting pulmonary nodules by using ultrasound multiple scattering. J. Acoust. Soc. Am. 2021, 150, 4095–4102. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Gao, J.; Chen, C.; Zhi, X.; Liu, H.; Hong, N. Comparison between the application of microcoil and hookwire for localizing pulmonary nodules. Eur. Radiol. 2019, 29, 4036–4043. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, Z.; Huang, W.; Zhuang, J.; Lin, D.; Zhong, W.; Lan, B. Electromagnetic navigation bronchoscopic localization versus percutaneous CT-guided localization for thoracoscopic resection of small pulmonary nodules. Thorac. Cancer 2021, 12, 468–474. [Google Scholar] [CrossRef]
- Jiang, T.; Lin, M.; Zhao, M.; Zhan, C.; Li, M.; Feng, M.; Wang, Q. Preoperative Computed Tomography-Guided Localization for Pulmonary Nodules with Glue and Dye. Thorac. Cardiovasc. Surg. 2020, 68, 525–532. [Google Scholar] [CrossRef] [PubMed]
- Anayama, T.; Hirohashi, K.; Miyazaki, R.; Okada, H.; Kawamoto, N.; Yamamoto, M.; Sato, T.; Orihashi, K. Near-infrared dye marking for thoracoscopic resection of small-sized pulmonary nodules: Comparison of percutaneous and bronchoscopic injection techniques. J. Cardiothorac. Surg. 2018, 13, 5. [Google Scholar] [CrossRef] [PubMed]
- Powell, T.I.; Jangra, D.; Clifton, J.C.; Lara-Guerra, H.; Church, N.; English, J.; Evans, K.; Yee, J.; Coxson, H.; Mayo, J.R.; et al. Peripheral lung nodules: Fluoroscopically guided video-assisted thoracoscopic resection after computed tomography-guided localization using platinum microcoils. Ann. Surg. 2004, 240, 481–488, discussion 8–9. [Google Scholar] [CrossRef] [PubMed]
- Seitlinger, J.; Olland, A.; Guinard, S.; Massard, G.; Falcoz, P.-E. Conversion from video-assisted thoracic surgery (VATS) to thoracotomy during major lung resection: How does it affect perioperative outcomes? Interact. Cardiovasc. Thorac. Surg. 2021, 32, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Baig, M.Z.; Razi, S.S.; Agyabeng-Dadzie, K.; Stroever, S.; Muslim, Z.; Weber, J.; Herrera, L.J.; Bhora, F.Y. Robotic-assisted thoracoscopic surgery demonstrates a lower rate of conversion to thoracotomy than video-assisted thoracoscopic surgery for complex lobectomies. Eur. J. Cardio Thorac. Surg. 2022, 62, ezac281. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Xu, W.; Ren, H. Chapter 1—Slender Snake-Like Endoscopic Robots in Surgery; Academic Press: Cambridge, MA, USA, 2020; pp. 1–17. [Google Scholar]
- Jiajia, L.; Fuxin, D.; Yibin, L.; Yanqiang, L.; Tao, Z.; Gang, Z. A novel inverse kinematics algorithm using the Kepler oval for continuum robots. Appl. Math. Model. 2021, 93, 206–225. [Google Scholar] [CrossRef]
- Hong, W.; Xie, L.; Liu, J.; Sun, Y.; Li, K.; Wang, H. Development of a Novel Continuum Robotic System for Maxillary Sinus Surgery. IEEE/ASME Trans. Mechatron. 2018, 23, 1226–1237. [Google Scholar] [CrossRef]
- Lu, J.; Du, F.; Yang, F.; Zhang, T.; Lei, Y.; Wang, J. Kinematic modeling of a class of n-tendon continuum manipulators. Adv. Robot. 2020, 34, 1254–1271. [Google Scholar] [CrossRef]
- Crews, J.H.; Buckner, G.D. Design optimization of a shape memory alloy–actuated robotic catheter. J. Intell. Mater. Syst. Struct. 2012, 23, 545–562. [Google Scholar] [CrossRef]
- Salerno, M.; Zhang, K.; Menciassi, A.; Dai, J.S. A Novel 4-DOF Origami Grasper with an SMA-Actuation System for Minimally Invasive Surgery. IEEE Trans. Robot. 2016, 32, 484–498. [Google Scholar] [CrossRef]
- Alfalahi, H.; Renda, F.; Stefanini, C. Concentric Tube Robots for Minimally Invasive Surgery: Current Applications and Future Opportunities. IEEE Trans. Med. Robot. Bionics 2020, 2, 410–424. [Google Scholar] [CrossRef]
- Bruns, T.L.; Remirez, A.A.; Emerson, M.A.; Lathrop, R.A.; Mahoney, A.W.; Gilbert, H.B.; Liu, C.L.; Russell, P.T.; Labadie, R.F.; Weaver, K.D.; et al. A modular, multi-arm concentric tube robot system with application to transnasal surgery for orbital tumors. Int. J. Robot. Res. 2021, 40, 521–533. [Google Scholar] [CrossRef]
- ORTNER Medical Solutions. O. M. e.U. Aloka Ust-5536. Available online: https://www.ort-med.com/en/aloka-ust-5536/ (accessed on 20 July 2023).
- Schirmer, B.D. Intra-operative and laparoscopic ultrasound. In Surgical Treatment: Evidence-Based and Problem-Oriented; Holzheimer, R.G., Mannick, J.A., Eds.; Zuckschwerdt: Munich, Germany, 2001. Available online: https://www.ncbi.nlm.nih.gov/books/NBK6975/ (accessed on 4 May 2023).
- Hitachi, Ltd. Intraoperative Electronic Linear Probe UST-5536-7.5 (Compatible with Waterproof Cover) Instruction Manual; Hitachi, Ltd.: Tokyo, Japan, 2020. [Google Scholar]
- Holoxica. Lung CT Scan. Sketchfab. 4 July 2017. Available online: https://sketchfab.com/3d-models/lung-ct-scan-f7232f2e10524eacbfb8fd149d0550e0 (accessed on 10 July 2023).
- Gayzik, F.S.; Yu, M.M.; Danelson, K.A.; Slice, D.E.; Stitzel, J.D. Quantification of age-related shape change of the human rib cage through geometric morphometrics. J. Biomech. 2008, 41, 1545–1554. [Google Scholar] [CrossRef] [PubMed]
- McCullough, M. Design Optimization and Tradeoff Analysis of an Actuated Probe for Pulmonary Nodule Localization and Resection. Master’s Thesis, North Carolina State University, Raleigh, NC, USA, 2023. Available online: https://www.lib.ncsu.edu/resolver/1840.20/41346 (accessed on 4 May 2023).
- Genetic Algorithm Options. Genetic Algorithm Options—MATLAB & Simulink. Available online: https://www.mathworks.com/help/gads/genetic-algorithm-options.html (accessed on 2 January 2023).

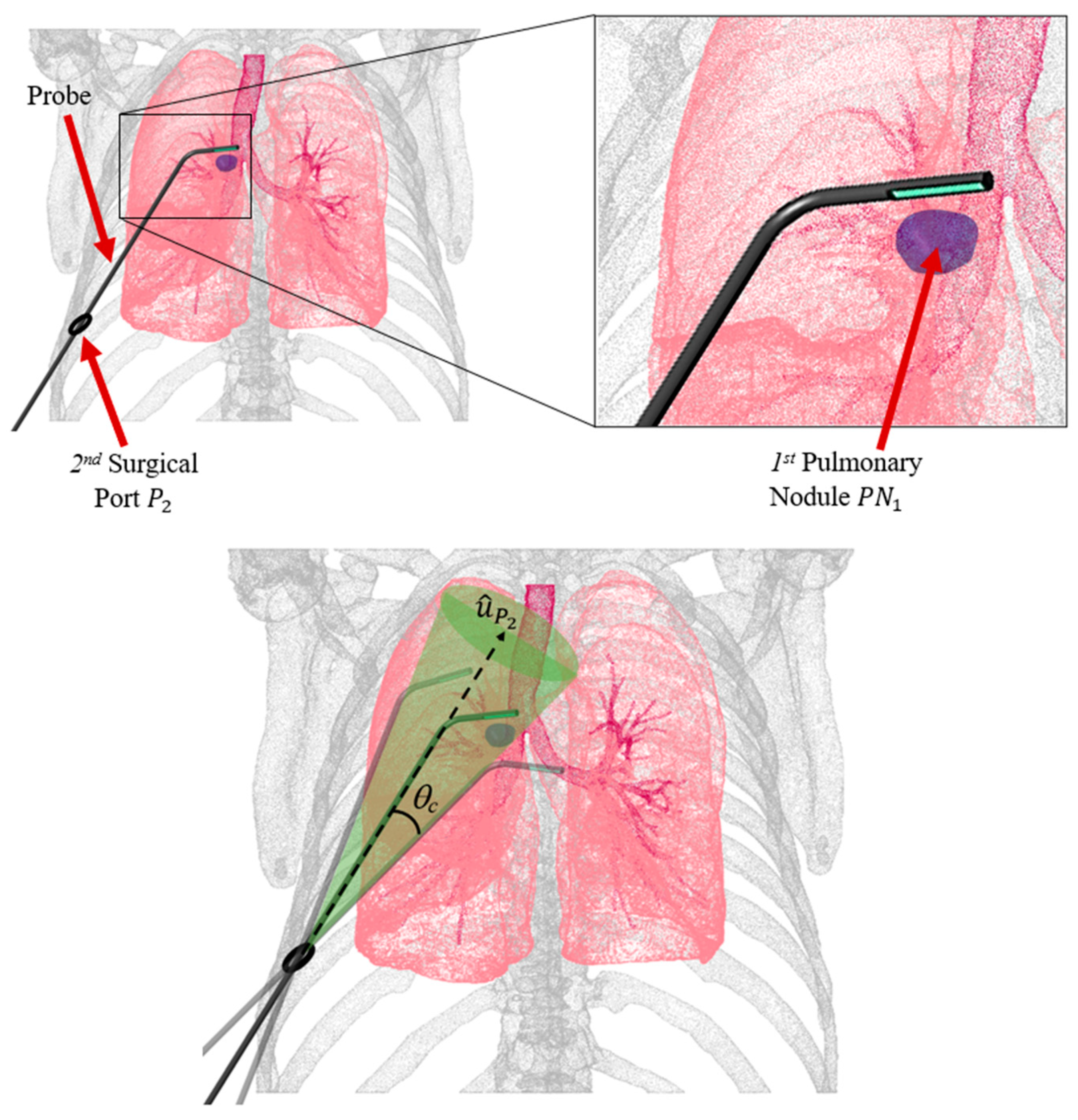
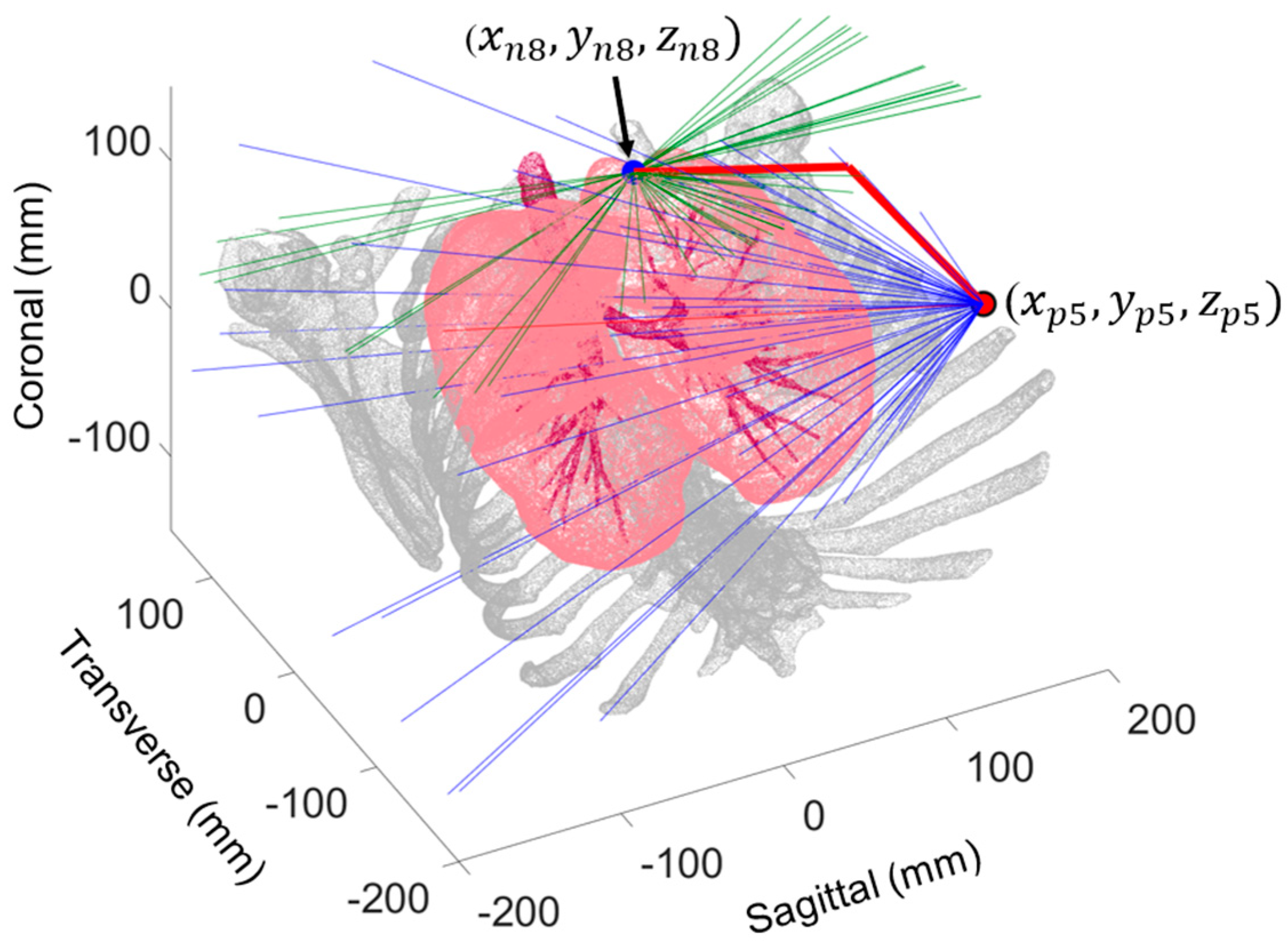

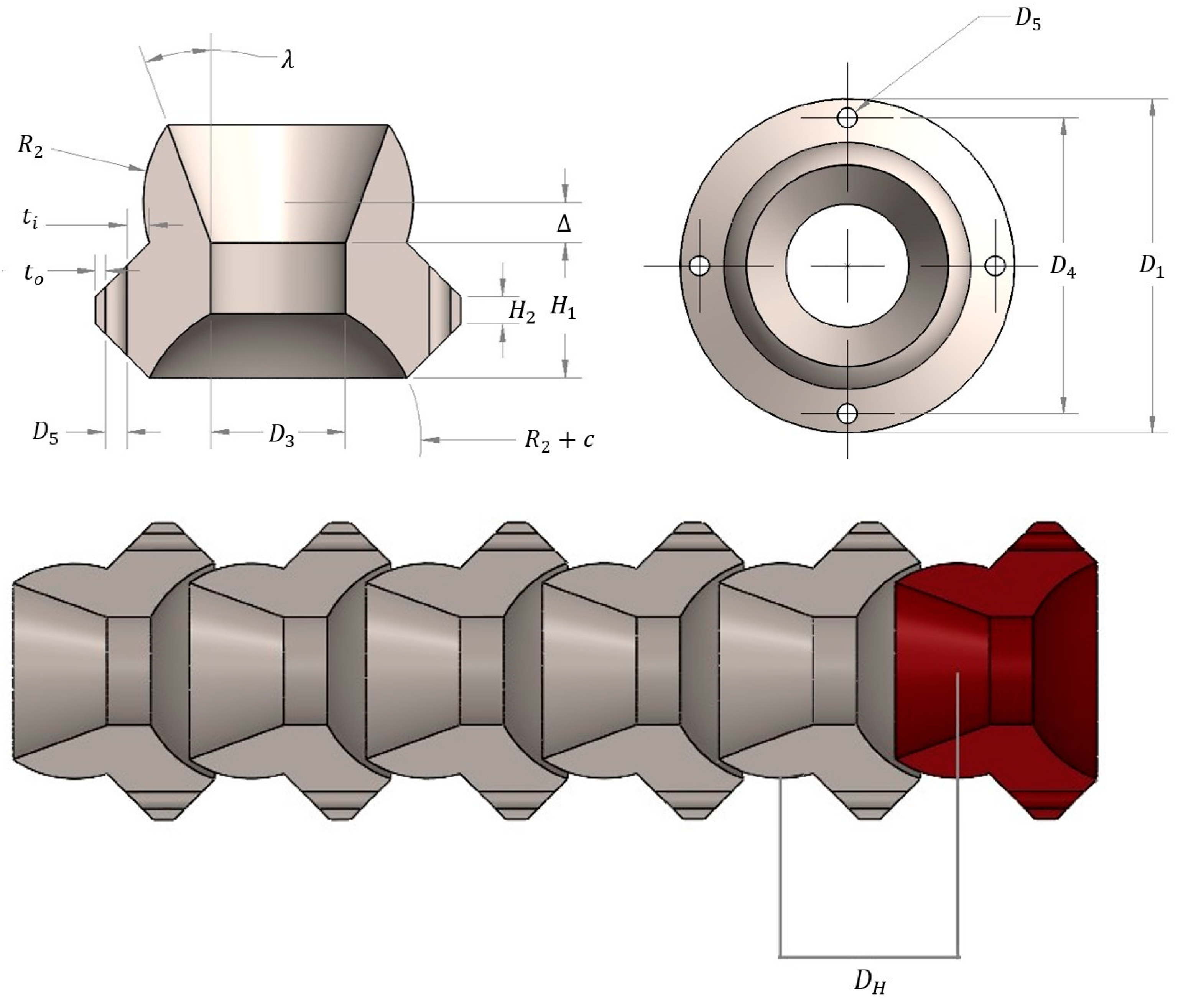

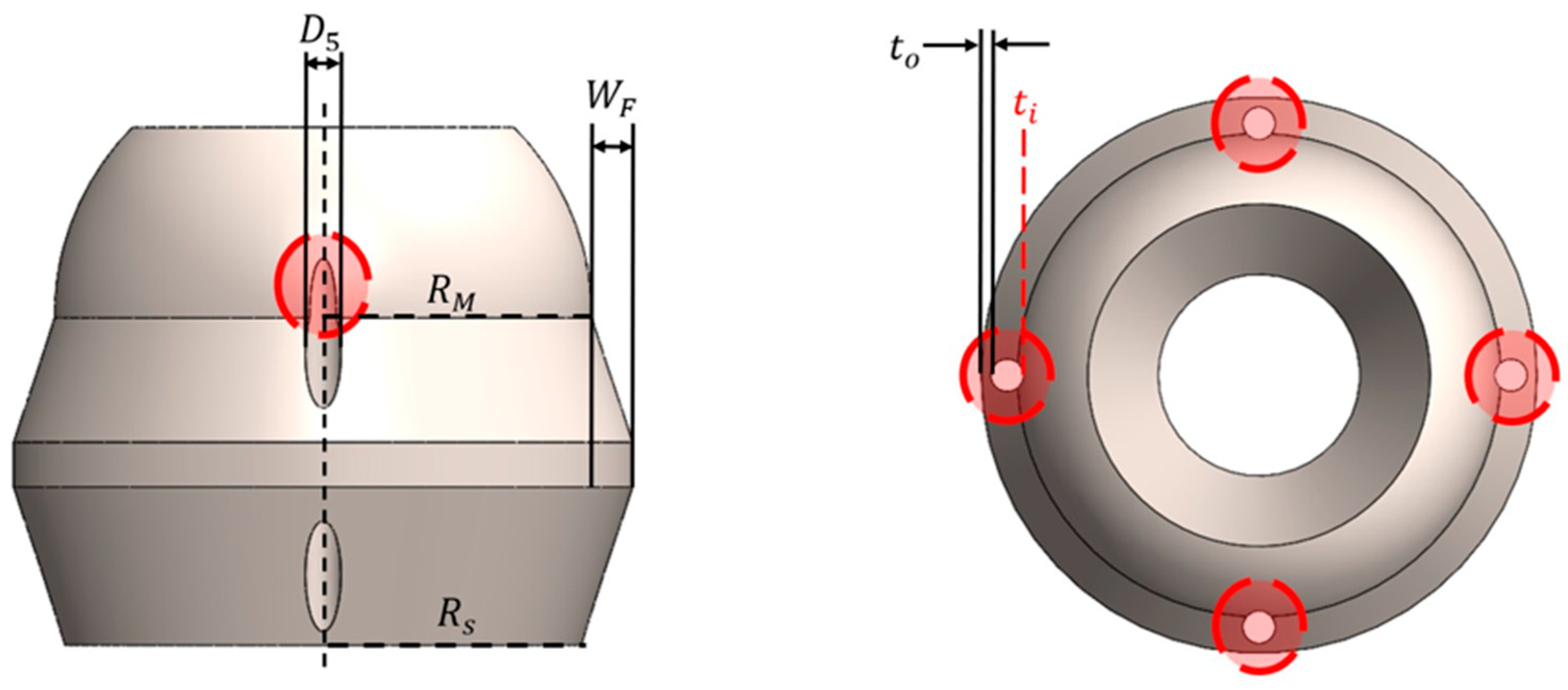






| Parameter | Description | Lower Bound | Upper Bound | Units |
|---|---|---|---|---|
| Spherical radius | 3.00 | 6.00 | mm | |
| Flange height | 2.00 | 12.00 | mm | |
| Flange chamfer height | 1.00 | 11.00 | mm | |
| Socket depth | 1.00 | 6.00 | mm | |
| Central lumen diameter * | 5.00 | 5.00 | mm | |
| Radial lumen diameter * | 0.80 | 0.80 | mm | |
| Socket radial clearance * | 0.03 | 0.03 | mm | |
| Flange to spherical center dist. | 0.01 | 3.00 | mm | |
| Flange chamfer angle | 15.0 | 40.0 | deg | |
| Central lumen chamfer angle | 15.0 | 75.0 | deg | |
| Flange inner wall thickness * | 0.10 | 0.10 | mm | |
| Flange outer wall thickness * | 0.25 | 0.25 | mm |
| PN Number | Lobe | Port Number | (mm) | (mm) | (mm) | (deg) | (mm) |
|---|---|---|---|---|---|---|---|
| 1 | RUL | 1 | 163.21 | 99.48 | 262.69 | 64.86 | 41.98 |
| 2 | RUL | 2 | 45.04 | 120.59 | 165.63 | 37.49 | 57.10 |
| 3 | RML | 2 | 56.93 | 58.97 | 115.9 | 18.97 | 29.08 |
| 4 | RML | 1 | 128.62 | 17.93 | 146.55 | 98.07 | 5.88 |
| 5 | RLL | 4 | 67.75 | 29.47 | 97.22 | 46.25 | 13.55 |
| 6 | RLL | 4 | 38.09 | 30.76 | 68.85 | 53.72 | 13.72 |
| 7 | LUL | 5 | 37.24 | 120.03 | 157.27 | 27.97 | 58.23 |
| 8 | LUL | 5 | 109.07 | 144.15 | 253.22 | 69.97 | 59.05 |
| 9 | LLL | 6 | 51.17 | 25.05 | 76.19 | 38.78 | 11.81 |
| 10 | LLL | 7 | 39.44 | 13.18 | 52.62 | 86.78 | 4.79 |
| Trial | Optimum | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Minimal | 5.14 | 1.28 | 6.18 | 54.07 | 2.29 | 20.12 | 4.75 | 19.94 | 39,321.51 | 13.20 |
| 1 | Minimal | 3.66 | 0.01 | 5.93 | 58.31 | 1.72 | 15.00 | 3.97 | 55.87 | 17,819.53 | 10.23 |
| 1 | Minimal | 3.66 | 0.01 | 5.93 | 58.31 | 1.72 | 15.00 | 3.97 | 55.87 | 17,819.53 | 10.23 |
| 2 | Minimal | 5.14 | 1.20 | 6.27 | 55.27 | 2.22 | 20.12 | 4.75 | 20.26 | 39,774.94 | 13.20 |
| 2 | Minimal | 3.66 | 0.01 | 5.93 | 58.31 | 1.72 | 15.02 | 3.96 | 55.82 | 17,822.57 | 10.23 |
| 2 | Minimal | 3.66 | 0.01 | 5.93 | 58.31 | 1.72 | 15.00 | 3.97 | 55.87 | 17,819.53 | 10.23 |
| 3 | Minimal | 4.89 | 1.15 | 5.18 | 41.11 | 2.49 | 18.08 | 4.64 | 18.83 | 33,678.06 | 13.00 |
| 3 | Minimal | 3.68 | 0.02 | 6.58 | 62.24 | 1.59 | 15.02 | 3.84 | 42.61 | 18,296.35 | 10.29 |
| 3 | Minimal | 3.67 | 0.01 | 7.33 | 56.60 | 3.39 | 15.00 | 3.89 | 61.46 | 26,597.28 | 10.23 |
| Design Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Performance Index | |||||||
| Univariate p-value: | <0.001 | <0.001 | <0.001 | 0.793 | 0.972 | <0.001 | <0.001 |
| Univariate p-value: | <0.001 | 0.591 | <0.001 | 0.000 | <0.001 | 0.753 | 0.500 |
| Univariate p-value: | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | 0.587 | 0.025 |
| Univariate : | 0.023 | 0.128 | 0.171 | 0.000 | 0.000 | 0.445 | 0.100 |
| Univariate : | 0.045 | 0.001 | 0.223 | 0.632 | 0.054 | 0.000 | 0.001 |
| Univariate : | 0.060 | 0.021 | 0.194 | 0.468 | 0.020 | 0.001 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McCullough, M.D.; Muller, M.; Egan, T.M.; Buckner, G.D. Design Optimization and Tradeoff Analysis of an Actuated Continuum Probe for Pulmonary Nodule Localization and Resection. Bioengineering 2024, 11, 417. https://doi.org/10.3390/bioengineering11050417
McCullough MD, Muller M, Egan TM, Buckner GD. Design Optimization and Tradeoff Analysis of an Actuated Continuum Probe for Pulmonary Nodule Localization and Resection. Bioengineering. 2024; 11(5):417. https://doi.org/10.3390/bioengineering11050417
Chicago/Turabian StyleMcCullough, Madison D., Marie Muller, Thomas M. Egan, and Gregory D. Buckner. 2024. "Design Optimization and Tradeoff Analysis of an Actuated Continuum Probe for Pulmonary Nodule Localization and Resection" Bioengineering 11, no. 5: 417. https://doi.org/10.3390/bioengineering11050417
APA StyleMcCullough, M. D., Muller, M., Egan, T. M., & Buckner, G. D. (2024). Design Optimization and Tradeoff Analysis of an Actuated Continuum Probe for Pulmonary Nodule Localization and Resection. Bioengineering, 11(5), 417. https://doi.org/10.3390/bioengineering11050417







