Analysis of Intracranial Aneurysm Haemodynamics Altered by Wall Movement
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of the Proposed FSI Case
2.1.1. A Simple but Versatile Geometry


2.1.2. Choice of Physical Parameters
2.1.3. Boundary Conditions
2.1.4. Quantities of Interest
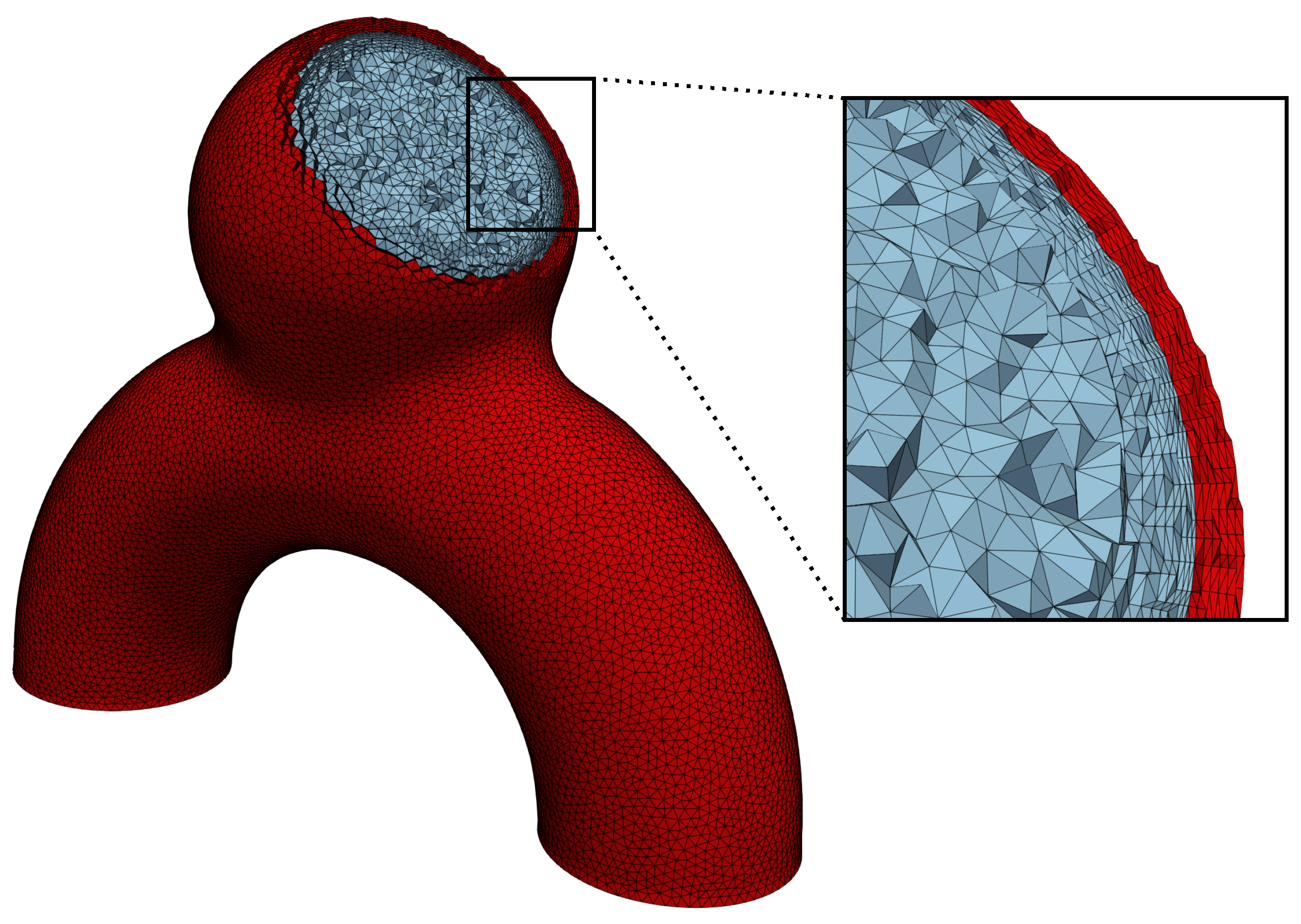
2.1.5. Meshing
2.2. Modelling the Physics
2.2.1. Fluid Mechanics
2.2.2. Solid Mechanics
2.2.3. Coupling
3. Results
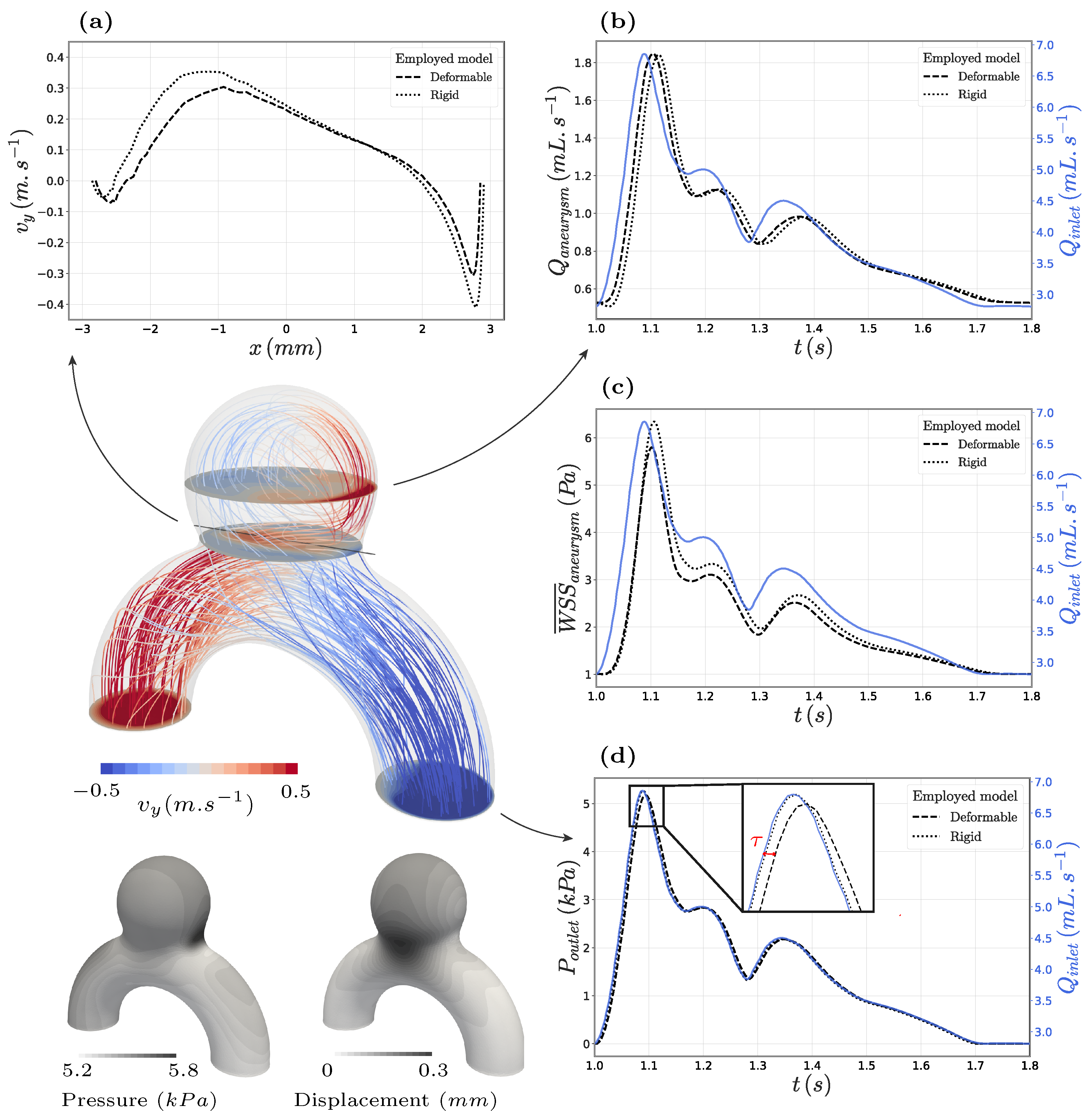
3.1. FSI in the Proposed Idealized Aneurysm
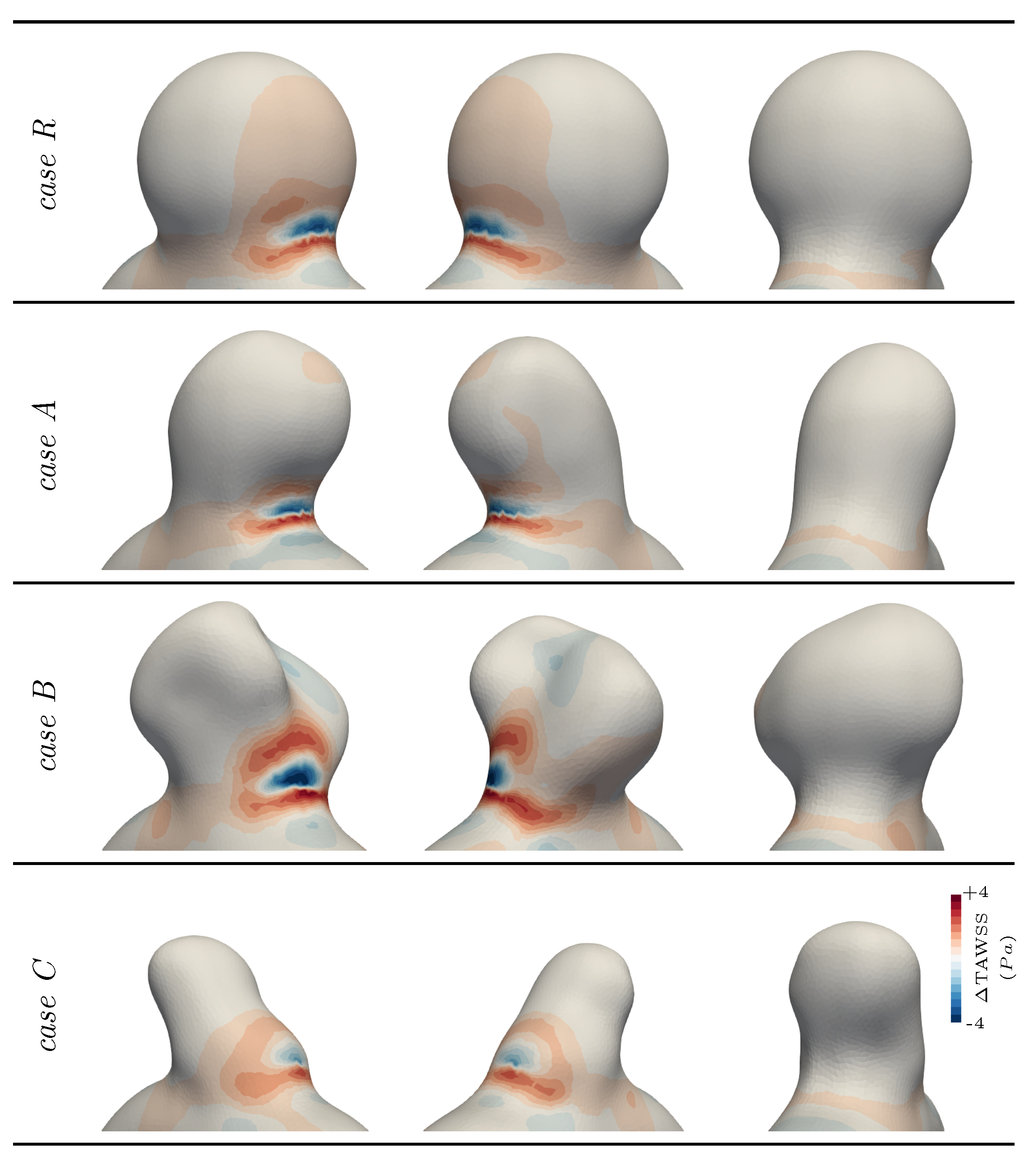
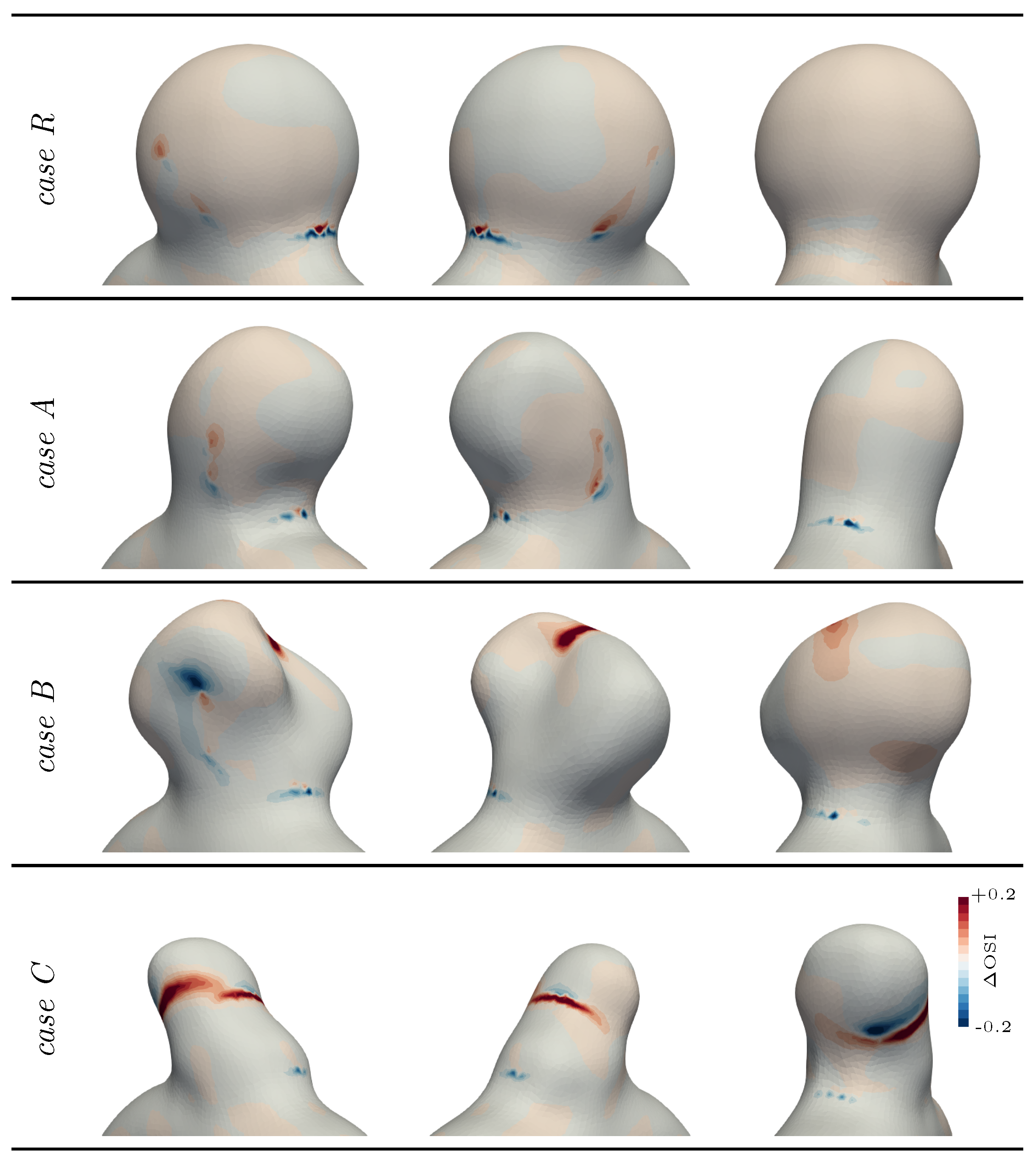
3.2. Exploring Different Bulge Shapes
4. Discussion
4.1. Impact of the Wall Modelling
4.2. Limitations and Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
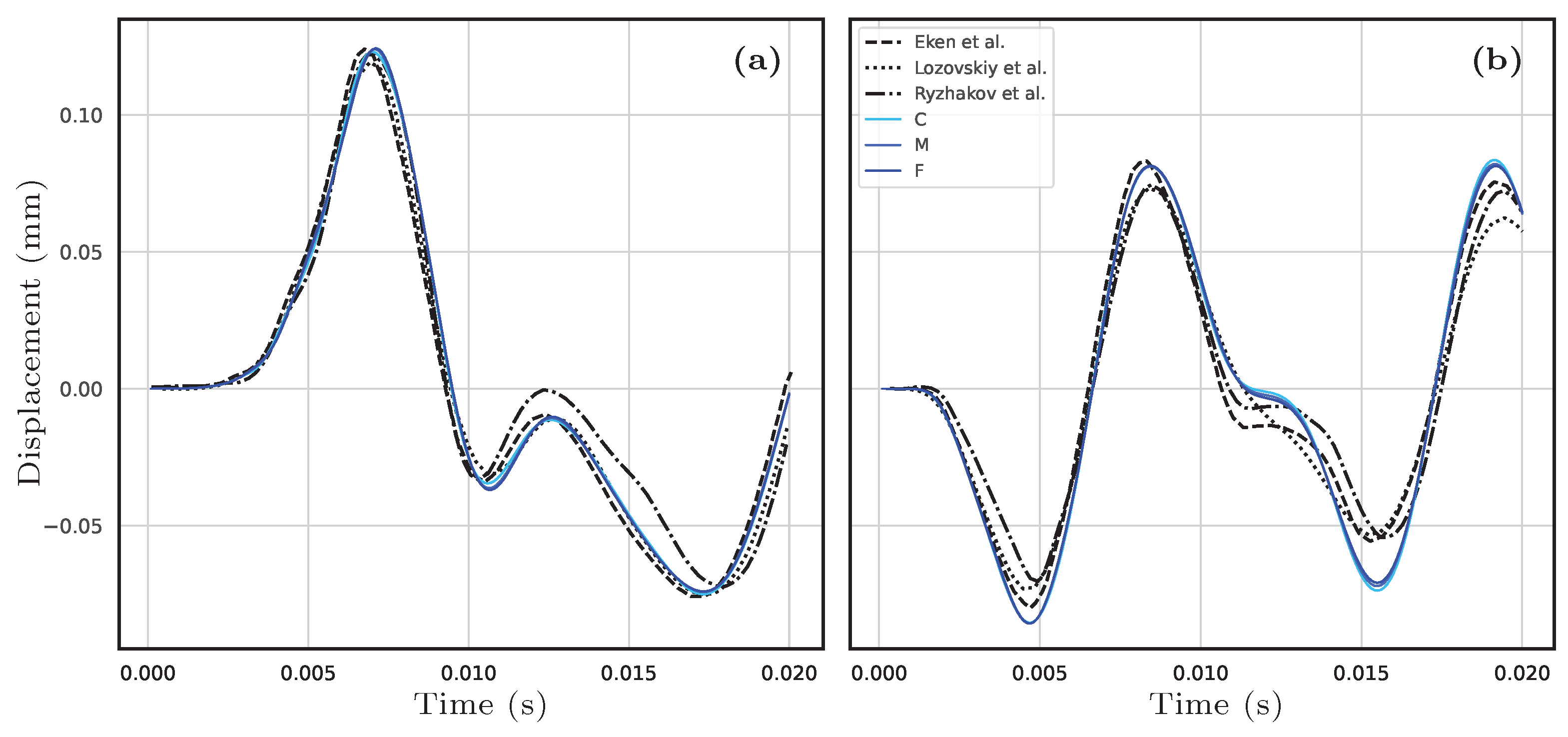
Appendix A. Framework Validation with the Pressure Wave Benchmark
| Mesh ID. | No. Layers in the Solid | (mm) | No. Elements in the Fluid Mesh | No. Elements in the Solid Mesh |
|---|---|---|---|---|
| C | 4 | 0.70 | 176k | 64k |
| M | 6 | 0.48 | 365k | 186k |
| F | 8 | 0.35 | 634k | 409k |


Appendix B. Convergence Study for the Proposed Case R
| Mesh ID. | (mm) | (mm) | No. Fluid Elements | No. Solid Layers | Solid Elements A.R. | No. Solid Elements |
|---|---|---|---|---|---|---|
| M1 | 0.39 | 0.046 | 0.12 M | 3 | 4.65 | 0.06M |
| M2 | 0.30 | 0.035 | 0.25 M | 4 | 4.76 | 0.13M |
| M3 | 0.22 | 0.026 | 0.50 M | 5 | 4.49 | 0.27M |
| M4 | 0.17 | 0.020 | 1.03 M | 6 | 4.08 | 0.56M |
| M5 | 0.13 | 0.015 | 2.05 M | 7 | 4.13 | 1.28M |

References
- Ingall, T.; Asplund, K.; Mähönen, M.; Bonita, R. A Multinational Comparison of Subarachnoid Hemorrhage Epidemiology in the WHO MONICA Stroke Study. Stroke 2000, 31, 1054–1061. [Google Scholar] [CrossRef]
- Vlak, M.H.; Algra, A.; Brandenburg, R.; Rinkel, G.J. Prevalence of unruptured intracranial aneurysms, with emphasis on sex, age, comorbidity, country, and time period: A systematic review and meta-analysis. Lancet Neurol. 2011, 10, 626–636. [Google Scholar] [CrossRef] [PubMed]
- Kotowski, M.; Naggara, O.; Darsaut, T.; Nolet, S.; Gevry, G.; Kouznetsov, E.; Raymond, J. Safety and occlusion rates of surgical treatment of unruptured intracranial aneurysms: A systematic review and meta-analysis of the literature from 1990 to 2011. J. Neurol. Neurosurg. Psychiatry 2012, 84, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Naggara, O.N.; Lecler, A.; Oppenheim, C.; Meder, J.F.; Raymond, J. Endovascular Treatment of Intracranial Unruptured Aneurysms: A Systematic Review of the Literature on Safety with Emphasis on Subgroup Analyses. Radiology 2012, 263, 828–835. [Google Scholar] [CrossRef] [PubMed]
- Niemann, U.; Berg, P.; Niemann, A.; Beuing, O.; Preim, B.; Spiliopoulou, M.; Saalfeld, S. Rupture Status Classification of Intracranial Aneurysms Using Morphological Parameters. In Proceedings of the IEEE 31st International Symposium on Computer-Based Medical Systems, Karlstad, Sweden, 18–21 June 2018; pp. 48–53. [Google Scholar] [CrossRef]
- Cebral, J.; Vázquez, M.; Sforza, D.; Houzeaux, G.; Tateshima, S.; Scrivano, E.; Bleise, C.; Lylyk, P.; Putman, C. Analysis of hemodynamics and wall mechanics at sites of cerebral aneurysm rupture. J. Neurointerventional Surg. 2014, 7, 530–536. [Google Scholar] [CrossRef]
- Meng, H.; Tutino, V.; Xiang, J.; Siddiqui, A. High WSS or Low WSS? Complex Interactions of Hemodynamics with Intracranial Aneurysm Initiation, Growth, and Rupture: Toward a Unifying Hypothesis. Am. J. Neuroradiol. 2014, 35, 1254–1262. [Google Scholar] [CrossRef]
- Janiga, G.; Berg, P.; Sugiyama, S.; Kono, K.; Steinman, D. The Computational Fluid Dynamics Rupture Challenge 2013—Phase I: Prediction of Rupture Status in Intracranial Aneurysms. Am. J. Neuroradiol. 2015, 36, 530–536. [Google Scholar] [CrossRef]
- Souche, A.; Valen-Sendstad, K. High-fidelity fluid structure interaction simulations of turbulent-like aneurysm flows reveals high-frequency narrowband wall vibrations: A stimulus of mechanobiological relevance? J. Biomech. 2022, 145, 111369. [Google Scholar] [CrossRef] [PubMed]
- Bruneau, D.; Steinman, D.; Valen-Sendstad, K. Understanding intracranial aneurysm sounds via high-fidelity fluid-structure-interaction modelling. Commun. Med. 2023, 3, 163. [Google Scholar] [CrossRef]
- Alam, M.; Seshaiyer, P. Impact of Contact Constraints on the Dynamics of Idealized Intracranial Saccular Aneurysms. Bioengineering 2019, 6, 77. [Google Scholar] [CrossRef]
- Alam, M.; Padmanabhan, S. Quantification of the Rupture Potential of Patient-Specific Intracranial Aneurysms under Contact Constraints. Bioengineering 2021, 8, 149. [Google Scholar] [CrossRef]
- Torii, R.; Oshima, M.; Kobayashi, T.; Takagi, K.; Tezduyar, T. Fluid-structure interaction modeling of blood flow and cerebral aneurysm: Significance of artery and aneurysm shapes. Comput. Methods Appl. Mech. Eng. 2009, 198, 3613–3621. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.C.; Zhang, Y.; Wang, W.; Liang, X.; Kvamsdal, T.; Brekken, R.; Isaksen, J. A fully-coupled fluid-structure interaction simulation of cerebral aneurysms. Comput. Mech. 2010, 46, 3–16. [Google Scholar] [CrossRef]
- Torii, R.; Oshima, M.; Kobayashi, T.; Takagi, K.; Tezduyar, T. Fluid-structure interaction modeling of a patient-specific cerebral aneurysm: Influence of structural modeling. Comput. Mech. 2008, 43, 151–159. [Google Scholar] [CrossRef]
- Torii, R.; Oshima, M.; Kobayashi, T.; Takagi, K.; Tezduyar, T.E. Influence of wall thickness on fluid–structure interaction computations of cerebral aneurysms. Int. J. Numer. Methods Biomed. Eng. 2010, 26, 336–347. [Google Scholar] [CrossRef]
- Voß, S.; Saalfeld, S.; Hoffmann, T.; Beuing, O.; Weigand, S.; Jachau, K.; Preim, B.; Thévenin, D.; Janiga, G.; Berg, P. Fluid-Structure Simulations of a Ruptured Intracranial Aneurysm: Constant versus Patient-Specific Wall Thickness. Comput. Math. Methods Med. 2016, 2016, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Valencia, A.; Burdiles, P.A.; Ignat, M.; Mura, J.; Bravo, E.; Rivera, R.; Sordo, J. Fluid Structural Analysis of Human Cerebral Aneurysm Using Their Own Wall Mechanical Properties. Comput. Math. Methods Med. 2013, 2013, 293128. [Google Scholar] [CrossRef] [PubMed]
- Barahona, J.; Valencia, A.; Torres, M. Study of the Hemodynamics Effects of an Isolated Systolic Hypertension (ISH) Condition on Cerebral Aneurysms Models, Using FSI Simulations. Appl. Sci. 2021, 11, 2595. [Google Scholar] [CrossRef]
- Vanrossomme, A.; Eker, O.; Thiran, J.P.; Courbebaisse, G.; Zouaoui Boudjeltia, K. Intracranial Aneurysms: Wall Motion Analysis for Prediction of Rupture. Am. J. Neuroradiol. 2015, 36, 1796–1802. [Google Scholar] [CrossRef]
- Hayakawa, M.; Tanaka, T.; Sadato, A.; Adachi, K.; Ito, K.; Hattori, N.; Omi, T.; Oheda, M.; Katada, K.; Murayama, K.; et al. Detection of Pulsation in Unruptured Cerebral Aneurysms by ECG-Gated 3D-CT Angiography (4D-CTA) with 320-Row Area Detector CT (ADCT) and Follow-up Evaluation Results: Assessment Based on Heart Rate at the Time of Scanning. Clin. Neuroradiol. 2013, 24, 145–150. [Google Scholar] [CrossRef]
- Zhou, J.; Guo, Q.; Chen, Y.; Lin, B.; Ding, S.; Zhao, H.; Pan, Y.; Wan, J.; Zhao, B. Irregular Pulsation of Intracranial Aneurysm Detected by Four-Dimensional CT Angiography and Associated With Small Aneurysm Rupture: A Single-Center Prospective Analysis. Front. Neurol. 2022, 13, 809286. [Google Scholar] [CrossRef]
- Stam, L.; Aquarius, R.; De Jong, G.; Slump, C.; Meijer, F.; Boogaarts, J. A review on imaging techniques and quantitative measurements for dynamic imaging of cerebral aneurysm pulsations. Sci. Rep. 2021, 11, 2175. [Google Scholar] [CrossRef]
- Finol, E.; Raut, S.; Jana, A.; de oliveira, V.; Muluk, S. The Importance of Patient-Specific Regionally Varying Wall Thickness in Abdominal Aortic Aneurysm Biomechanics. J. Biomech. Eng. 2013, 135, 081010. [Google Scholar] [CrossRef]
- Isaksen, J.; Bazilevs, Y.; Kvamsdal, T.; Zhang, Y.; Kaspersen, J.; Waterloo, K.; Romner, B.; Ingebrigtsen, T. Determination of Wall Tension in Cerebral Artery Aneurysms by Numerical Simulation. Stroke 2008, 39, 3172–3178. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, J.; Ohara, H. Clinicopathological study of cerebral aneurysms: Origin, rupture, repair, and growth. J. Neurosurg. 1978, 48, 505–514. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Wu, H.; Wang, J.; Mendieta, J.; Yu, H.; Xiang, Y.; Anbananthan, H.; Zhang, J.; Zhao, H.; Zhu, Z.; et al. Constrained Estimation of Intracranial Aneurysm Surface Deformation using 4D-CTA. Comput. Methods Programs Biomed. 2023, 244, 107975. [Google Scholar] [CrossRef]
- Kleinloog, R.; Zwanenburg, J.; Schermers, B.; Krikken, E.; Ruigrok, Y.; Luijten, P.; Visser, F.; Regli, L.; Rinkel, G.; Verweij, B. Quantification of Intracranial Aneurysm Volume Pulsation with 7T MRI. Am. J. Neuroradiol. 2018, 39, 713–719. [Google Scholar] [CrossRef]
- Illies, T.; Säring, D.; Kinoshita, M.; Fujinaka, T.; Bester, M.; Fiehler, J.; Tomiyama, N.; Watanabe, Y. Feasibility of Quantification of Intracranial Aneurysm Pulsation with 4D CTA with Manual and Computer-Aided Post-Processing. PLoS ONE 2016, 11, e0166810. [Google Scholar] [CrossRef]
- Robertson, A.M.; Duan, X.; Aziz, K.M.; Hill, M.R.; Watkins, S.C.; Cebral, J.R. Diversity in the Strength and Structure of Unruptured Cerebral Aneurysms. Ann. Biomed. Eng. 2015, 43, 1502–1515. [Google Scholar] [CrossRef]
- Wang, H.; Balzani, D.; Vedula, V.; Uhlmann, K.; Varnik, F. On the Potential Self-Amplification of Aneurysms Due to Tissue Degradation and Blood Flow Revealed From FSI Simulations. Front. Physiol. 2021, 12, 785780. [Google Scholar] [CrossRef]
- Baharoglu, M.; Schirmer, C.; Hoit, D.; Gao, B.; Malek, A. Aneurysm Inflow-Angle as a Discriminant for Rupture in Sidewall Cerebral Aneurysms Morphometric and Computational Fluid Dynamic Analysis. Stroke 2010, 41, 1423–1430. [Google Scholar] [CrossRef]
- Hassan, T.; Timofeev, E.; Saito, T.; Shimizu, H.; Ezura, M.; Matsumoto, Y.; Takayama, K.; Tominaga, T.; Takahashi, A. A proposed parent vessel geometry-based categorization of saccular intracranial aneurysms: Computational flow dynamics analysis of the risk factors for lesion rupture. J. Neurosurg. 2005, 103, 662–680. [Google Scholar] [CrossRef]
- Ramalho, S.; Moura, A.B.; Gambaruto, A.M.; Sequeira, A. Influence of Blood Rheology and Outflow Boundary Conditions in Numerical Simulations of Cerebral Aneurysms. In Mathematical Methods and Models in Biomedicine; Ledzewicz, U., Schättler, H., Friedman, A., Kashdan, E., Eds.; Springer: New York, NY, USA, 2013; pp. 149–175. [Google Scholar] [CrossRef]
- Baz, R.; Scheau, C.; Cosmin, N.; Bordei, P. Morphometry of the Entire Internal Carotid Artery on CT Angiography. Medicina 2021, 57, 832. [Google Scholar] [CrossRef]
- Baharoglu, M.; Lauric, A.; Gao, B.; Malek, A. Identification of a dichotomy in morphological predictors of rupture status between sidewall- and bifurcation-type intracranial aneurysms: Clinical article. J. Neurosurg. 2012, 116, 871–881. [Google Scholar] [CrossRef]
- Yang, X.; Xia, D.; Kin, T.; Igarashi, T. IntrA: 3D Intracranial Aneurysm Dataset for Deep Learning. In Proceedings of the The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Ford, M.D.; Alperin, N.; Lee, S.H.; Holdsworth, D.W.; Steinman, D.A. Characterization of volumetric flow rate waveforms in the normal internal carotid and vertebral arteries. Physiol. Meas. 2005, 26, 477. [Google Scholar] [CrossRef]
- Seymour, R.S.; Hu, Q.; Snelling, E.P. Blood flow rate and wall shear stress in seven major cephalic arteries of humans. J. Anat. 2020, 236, 522–530. [Google Scholar] [CrossRef]
- Frösen, J.; Piippo, A.; Paetau, A.; Kangasniemi, M.; Niemelä, M.; Hernesniemi, J.; Jääskeläinen, J. Remodeling of Saccular Cerebral Artery Aneurysm Wall Is Associated With Rupture Histological Analysis of 24 Unruptured and 42 Ruptured Cases. Stroke 2004, 35, 2287–2293. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.; Wang, Z.; Hoi, Y.; Gao, L.; Metaxa, E.; Swartz, D.; Kolega, J. Complex Hemodynamics at the Apex of an Arterial Bifurcation Induces Vascular Remodeling Resembling Cerebral Aneurysm Initiation. Stroke 2007, 38, 1924–1931. [Google Scholar] [CrossRef]
- Malek, A. Hemodynamic Shear Stress and Its Role in Atherosclerosis. JAMA 1999, 282, 2035. [Google Scholar] [CrossRef] [PubMed]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D Finite Element Mesh Generator with built-in Pre- and Post-Processing Facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Turek, S.; Hron, J. Proposal for Numerical Benchmarking of Fluid-Structure Interaction between an Elastic Object and Laminar Incompressible Flow. In Fluid-Structure Interaction; Bungartz, H.J., Schäfer, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 371–385. [Google Scholar]
- Formaggia, L.; Gerbeau, J.F.; Nobile, F.; Quarteroni, A. On the Coupling of 3D and 1D Navier-Stokes Equations for Flow Problems in Compliant Vessels. Comput. Methods Appl. Mech. Eng. 2000, 191, 561–582. [Google Scholar] [CrossRef]
- Hirt, C.; Amsden, A.; Cook, J. An arbitrary Lagrangian-Eulerian computing method for all flow speeds. J. Comput. Phys. 1974, 14, 227–253. [Google Scholar] [CrossRef]
- Hachem, E.; Rivaux, B.; Kloczko, T.; Digonnet, H.; Coupez, T. Stabilized finite element method for incompressible flows with high Reynolds number. J. Comput. Phys. 2010, 229, 8643–8665. [Google Scholar] [CrossRef]
- Babuška, I. Error-bounds for finite element method. Numer. Math. 1971, 16, 322–333. [Google Scholar] [CrossRef]
- Habchi, C.; Russeil, S.; Bougeard, D.; Harion, J.L.; Lemenand, T.; Ghanem, A.; Valle, D.D.; Peerhossaini, H. Partitioned solver for strongly coupled fluid–structure interaction. Comput. Fluids 2013, 71, 306–319. [Google Scholar] [CrossRef]
- Shamanskiy, A.; Simeon, B. Mesh moving techniques in fluid-structure interaction: Robustness, accumulated distortion and computational efficiency. Comput. Mech. 2021, 67, 583–600. [Google Scholar] [CrossRef]
- Chiandussi, G.; Bugeda, G.; Oñate, E. A simple method for automatic update of finite element meshes. Commun. Numer. Methods Eng. 2000, 16, 1–19. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. J. Elast. Phys. Sci. Solids 2000, 61, 1–48. [Google Scholar]
- Simo, J.; Taylor, R.; Pister, K. Variational and projection methods for the volume constraint in finite deformation elasto-plasticity. Comput. Methods Appl. Mech. Eng. 1985, 51, 177–208. [Google Scholar] [CrossRef]
- Nemer, R.; Larcher, A.; Coupez, T.; Hachem, E. Stabilized finite element method for incompressible solid dynamics using an updated Lagrangian formulation. Comput. Methods Appl. Mech. Eng. 2021, 384, 113923. [Google Scholar] [CrossRef]
- Felippa, C.; Park, K. Staggered transient analysis procedures for coupled mechanical systems: Formulation. Comput. Methods Appl. Mech. Eng. 1980, 24, 61–111. [Google Scholar] [CrossRef]
- Causin, P.; Gerbeau, J.; Nobile, F. Added-mass effect in the design of partitioned algorithms for fluid–structure problems. Comput. Methods Appl. Mech. Eng. 2005, 194, 4506–4527. [Google Scholar] [CrossRef]
- Förster, C.; Wall, W.; Ramm, E. Artificial added mass instabilities in sequential staggered coupling of nonlinear structures and incompressible viscous flows. Comput. Methods Appl. Mech. Eng. 2007, 196, 1278–1293. [Google Scholar] [CrossRef]
- Breuer, M.; De Nayer, G.; Münsch, M.; Gallinger, T.; Wüchner, R. Fluid–structure interaction using a partitioned semi-implicit predictor–corrector coupling scheme for the application of large-eddy simulation. J. Fluids Struct. 2012, 29, 107–130. [Google Scholar] [CrossRef]
- Eken, A.; Sahin, M. A parallel monolithic algorithm for the numerical simulation of large-scale fluid structure interaction problems. Int. J. Numer. Methods Fluids 2015, 80, 687–714. [Google Scholar] [CrossRef]
- Küttler, U.; Wall, W. Fixed-point fluid-structure interaction solvers with dynamic relaxation. Comput. Mech. 2008, 43, 61–72. [Google Scholar] [CrossRef]
- Hashimoto, T.; Meng, H.; Young, W. Intracranial aneurysms: Links among inflammation, hemodynamics and vascular remodeling. Neurol. Res. 2006, 28, 372–380. [Google Scholar] [CrossRef]
- Brambila-Solórzano, A.; Méndez-Lavielle, F.; Naude, J.L.; Martínez-Sánchez, G.J.; García-Rebolledo, A.; Hernández, B.; Escobar-del Pozo, C. Influence of Blood Rheology and Turbulence Models in the Numerical Simulation of Aneurysms. Bioengineering 2023, 10, 1170. [Google Scholar] [CrossRef]
- Grande Gutierrez, N.; Mathew, M.; McCrindle, B.; Tran, J.; Kahn, A.; Burns, J.; Marsden, A. Hemodynamic variables in aneurysms are associated with thrombotic risk in children with Kawasaki disease. Int. J. Cardiol. 2019, 281, 15–21. [Google Scholar] [CrossRef]
- Beppu, M.; Tsuji, M.; Ishida, F.; Shirakawa, M.; Suzuki, H.; Yoshimura, S. Computational Fluid Dynamics Using a Porous Media Setting Predicts Outcome after Flow-Diverter Treatment. AJNR. Am. J. Neuroradiol. 2020, 41, 2107–2113. [Google Scholar] [CrossRef]
- Paritala, P.; Anbananthan, H.; Hautaniemi, J.; Smith, M.; George, A.; Allenby, M.; Benitez, J.; Wang, J.; Maclachlan, L.; Liang, E.; et al. Reproducibility of the computational fluid dynamic analysis of a cerebral aneurysm monitored over a decade. Sci. Rep. 2023, 13, 219. [Google Scholar] [CrossRef]
- Robertson, A.M.; Sequeira, A.; Owens, R.G. Rheological models for blood. In Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System; Formaggia, L., Quarteroni, A., Veneziani, A., Eds.; Springer: Milan, Italy, 2009; pp. 211–241. [Google Scholar] [CrossRef]
- Beris, A.; Horner, J.; Jariwala, S.; Armstrong, M.; Wagner, N. Recent advances in blood rheology: A review. Soft Matter 2021, 17, 28. [Google Scholar] [CrossRef]
- Giannokostas, K.; Moschopoulos, P.; Varchanis, S.; Dimakopoulos, Y.; Tsamopoulos, J. Advanced Constitutive Modeling of the Thixotropic Elasto-Visco-Plastic Behavior of Blood: Description of the Model and Rheological Predictions. Materials 2020, 13, 4184. [Google Scholar] [CrossRef]
- Bols, J.; Degroote, J.; Trachet, B.; Verhegghe, B.; Segers, P.; Vierendeels, J. A computational method to assess the in vivo stresses and unloaded configuration of patient-specific blood vessels. J. Comput. Appl. Math. 2013, 246, 10–17. [Google Scholar] [CrossRef]
- Cebral, J.; Duan, X.; Chung, B.; Putnam, C.; Aziz, K.; Robertson, A. Wall Mechanical Properties and Hemodynamics of Unruptured Intracranial Aneurysms. Am. J. Neuroradiol. 2015, 36, 1695–1703. [Google Scholar] [CrossRef]
- Laurence, D.; Homburg, H.; Yan, F.; Tang, Q.; Fung, K.M.; Bohnstedt, B.; Holzapfel, G.; Lee, C.H. A Pilot Study on Biaxial Mechanical, Collagen Microstructural, and Morphological Characterizations of a Resected Human Intracranial Aneurysm Tissue. Sci. Rep. 2021, 11, 3525. [Google Scholar] [CrossRef] [PubMed]
- Acosta, J.M.; Cayron, A.F.; Dupuy, N.; Pelli, G.; Foglia, B.; Haemmerli, J.; Allémann, E.; Bijlenga, P.; Kwak, B.R.; Morel, S. Effect of Aneurysm and Patient Characteristics on Intracranial Aneurysm Wall Thickness. Front. Cardiovasc. Med. 2021, 8, 775307. [Google Scholar] [CrossRef] [PubMed]
- Parshin, D.; Lipovka, A.; Yunoshev, A.; Ovsyannikov, K.; Dubovoy, A.; Chupakhin, A. On the optimal choice of a hyperelastic model of ruptured and unruptured cerebral aneurysm. Sci. Rep. 2019, 9, 15865. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Perdikaris, P.; Karniadakis, G.E. Fractional modeling of viscoelasticity in 3D cerebral arteries and aneurysms. J. Comput. Phys. 2016, 323, 219–242. [Google Scholar] [CrossRef] [PubMed]
- Malan, A.; Oxtoby, O. An accelerated, fully-coupled, parallel 3D hybrid finite-volume fluid–structure interaction scheme. Comput. Methods Appl. Mech. Eng. 2013, 253, 426–438. [Google Scholar] [CrossRef]
- Ryzhakov, P.B.; Marti, J.; Dialami, N. A Unified Arbitrary Lagrangian–Eulerian Model for Fluid–Structure Interaction Problems Involving Flows in Flexible Channels. J. Sci. Comput. 2022, 90, 85. [Google Scholar] [CrossRef]
- Lozovskiy, A.; Olshanskii, M.A.; Vassilevski, Y.V. Analysis and assessment of a monolithic FSI finite element method. Comput. Fluids 2019, 179, 277–288. [Google Scholar] [CrossRef]
- Turek, S.; Hron, J.; Mádlík, M.; Razzaq, M.; Wobker, H.; Acker, J.F. Numerical Simulation and Benchmarking of a Monolithic Multigrid Solver for Fluid-Structure Interaction Problems with Application to Hemodynamics. In Fluid Structure Interaction II; Bungartz, H.J., Mehl, M., Schäfer, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 193–220. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goetz, A.; Jeken-Rico, P.; Chau, Y.; Sédat, J.; Larcher, A.; Hachem, E. Analysis of Intracranial Aneurysm Haemodynamics Altered by Wall Movement. Bioengineering 2024, 11, 269. https://doi.org/10.3390/bioengineering11030269
Goetz A, Jeken-Rico P, Chau Y, Sédat J, Larcher A, Hachem E. Analysis of Intracranial Aneurysm Haemodynamics Altered by Wall Movement. Bioengineering. 2024; 11(3):269. https://doi.org/10.3390/bioengineering11030269
Chicago/Turabian StyleGoetz, Aurèle, Pablo Jeken-Rico, Yves Chau, Jacques Sédat, Aurélien Larcher, and Elie Hachem. 2024. "Analysis of Intracranial Aneurysm Haemodynamics Altered by Wall Movement" Bioengineering 11, no. 3: 269. https://doi.org/10.3390/bioengineering11030269
APA StyleGoetz, A., Jeken-Rico, P., Chau, Y., Sédat, J., Larcher, A., & Hachem, E. (2024). Analysis of Intracranial Aneurysm Haemodynamics Altered by Wall Movement. Bioengineering, 11(3), 269. https://doi.org/10.3390/bioengineering11030269