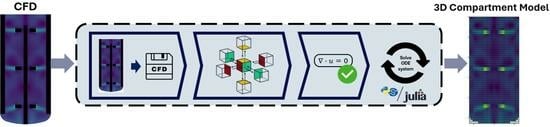
An Automatic Method for Generation of CFD-Based 3D Compartment Models: Towards Real-Time Mixing Simulations
Abstract
1. Introduction
2. Materials and Methods
2.1. Generating the Compartment Models
2.1.1. Interpolation
2.1.2. Enforcing Continuity
| Algorithm 1 Solving the continuity equation in all grid cells |
|
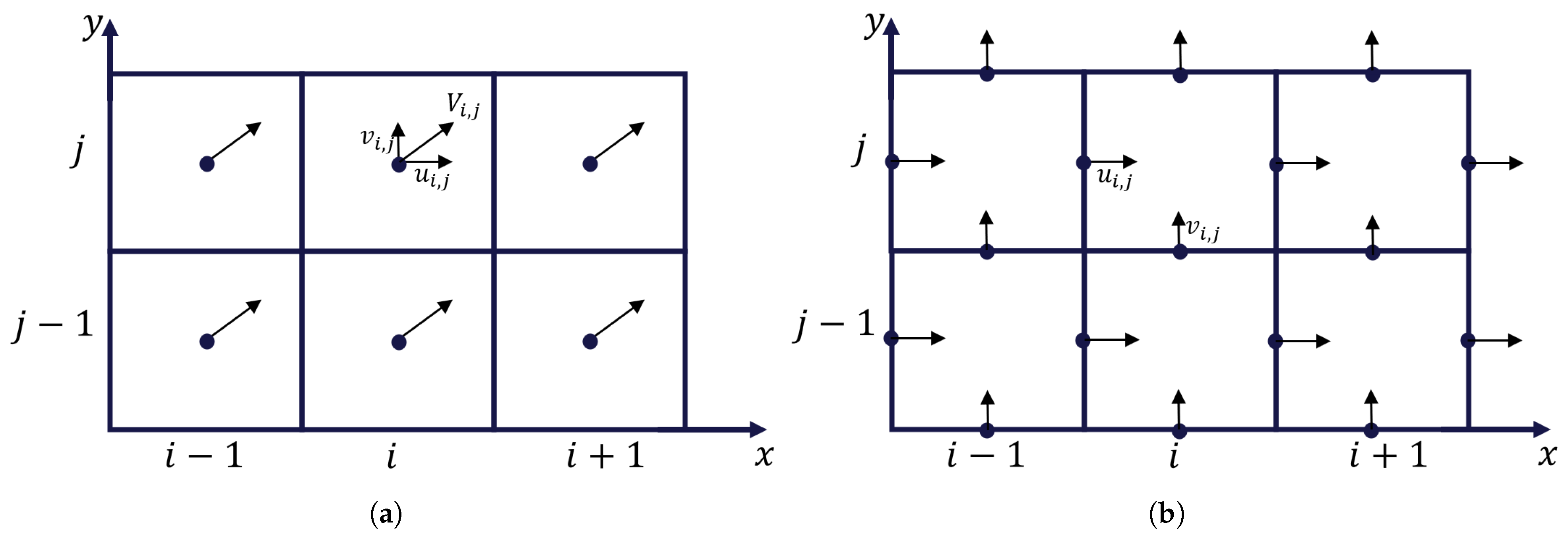
2.1.3. Converting Velocity Field to Volumes and Flows
- Grid resolution ();
- Relaxation factor for the Gauss–Seidel method (default: 1.7);
- Tolerance level for the RMS of the divergence (default: ).
2.2. Solving the System of Mass Balances
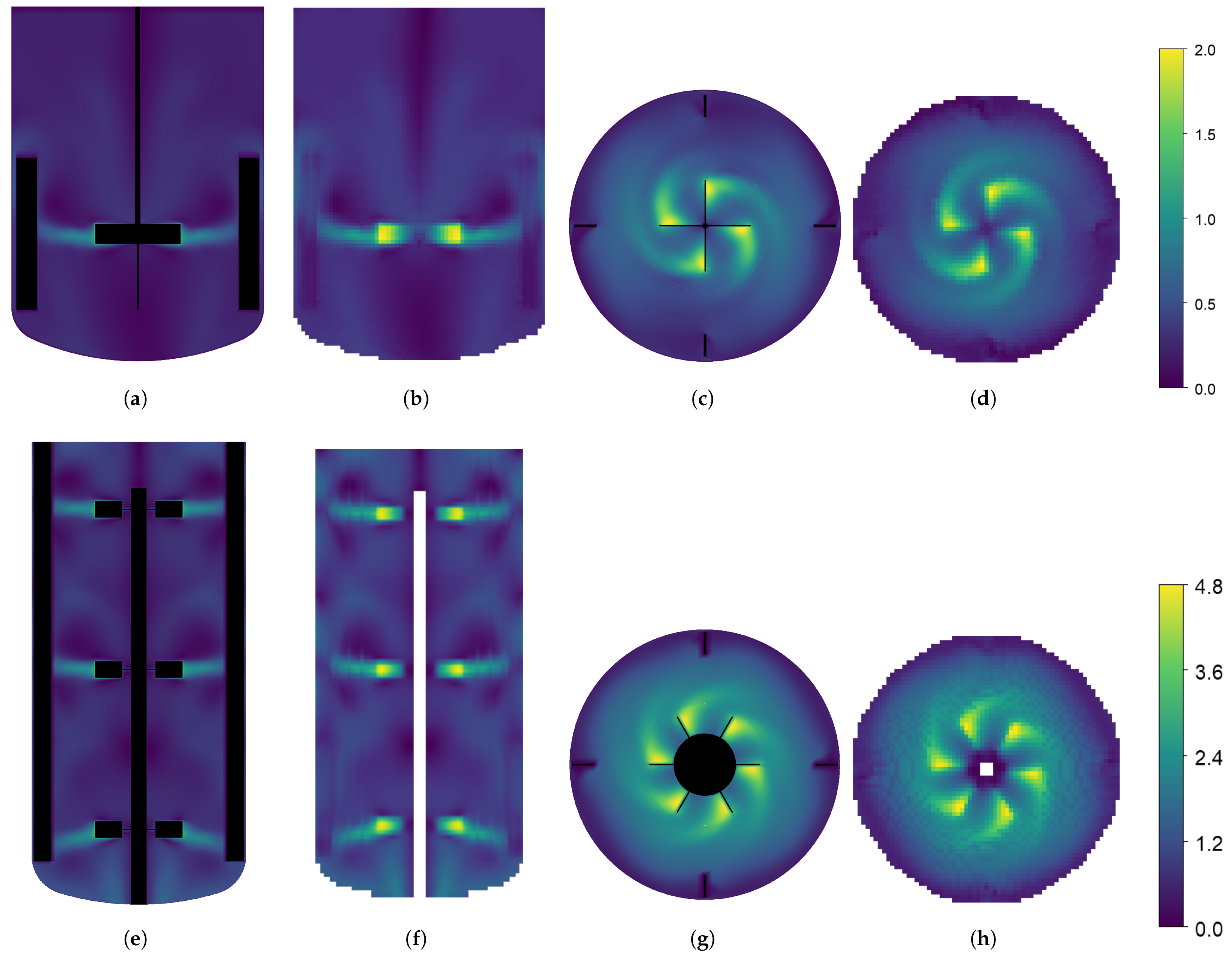
2.3. Case Study: Stirred Tanks
2.4. Coupling with a Biokinetic Model
3. Results
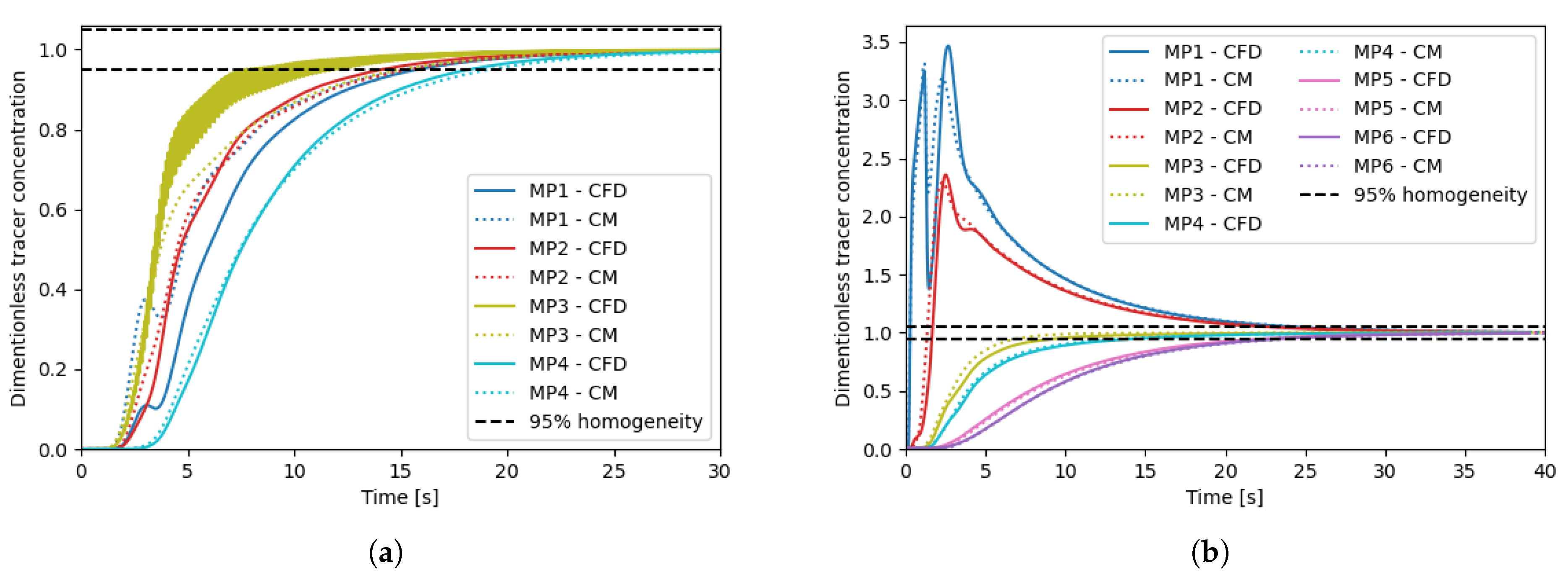
3.1. Case Study Mixing Time
3.2. Simulation of a Biological Process
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CM | Compartment Model |
| NaN | Not a Number |
| RMS | Root Mean Square |
| ODE | Ordinary Differential Equation |
| RPM | Rotations Per Minute |
| 0D | Zero Dimensional |
| 2D | Two Dimensional |
| 3D | Three Dimensional |
References
- Nadal-Rey, G.; McClure, D.D.; Kavanagh, J.M.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Understanding gradients in industrial bioreactors. Biotechnol. Adv. 2021, 46, 107660. [Google Scholar] [CrossRef] [PubMed]
- Dai, X.; Zhu, M.; Warren, M.; Balakrishnan, R.; Patsalo, V.; Okano, H.; Williamson, J.R.; Fredrick, K.; Wang, Y.P.; Hwa, T. Reduction of translating ribosomes enables Escherichia coli to maintain elongation rates during slow growth. Nat. Microbiol. 2016, 2, 16231. [Google Scholar] [CrossRef] [PubMed]
- Balakrishnan, R.; Mori, M.; Segota, I.; Zhang, Z.; Aebersold, R.; Ludwig, C.; Hwa, T. Principles of gene regulation quantitatively connect DNA to RNA and proteins in bacteria. Science 2022, 378, eabk2066. [Google Scholar] [CrossRef] [PubMed]
- Spann, R.; Glibstrup, J.; Pellicer-Alborch, K.; Junne, S.; Neubauer, P.; Roca, C.; Kold, D.; Lantz, A.E.; Sin, G.; Gernaey, K.V.; et al. CFD predicted pH gradients in lactic acid bacteria cultivations. Biotechnol. Bioeng. 2019, 116, 769–780. [Google Scholar] [CrossRef] [PubMed]
- Haringa, C.; Tang, W.; Wang, G.; Deshmukh, A.T.; van Winden, W.A.; Chu, J.; van Gulik, W.M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Computational fluid dynamics simulation of an industrial P. chrysogenum fermentation with a coupled 9-pool metabolic model: Towards rational scale-down and design optimization. Chem. Eng. Sci. 2018, 175, 12–24. [Google Scholar] [CrossRef]
- Nauha, E.K.; Kálal, Z.; Ali, J.M.; Alopaeus, V. Compartmental modeling of large stirred tank bioreactors with high gas volume fractions. Chem. Eng. J. 2018, 334, 2319–2334. [Google Scholar] [CrossRef]
- Bashiri, H.; Heniche, M.; Bertrand, F.; Chaouki, J. Compartmental modelling of turbulent fluid flow for the scale-up of stirred tanks. Can. J. Chem. Eng. 2014, 92, 1070–1081. [Google Scholar] [CrossRef]
- Bashiri, H.; Bertrand, F.; Chaouki, J. Development of a multiscale model for the design and scale-up of gas/liquid stirred tank reactors. Chem. Eng. J. 2016, 297, 277–294. [Google Scholar] [CrossRef]
- Moullec, Y.L.; Gentric, C.; Potier, O.; Leclerc, J.P. Comparison of systemic, compartmental and CFD modelling approaches: Application to the simulation of a biological reactor of wastewater treatment. Chem. Eng. Sci. 2010, 65, 343–350. [Google Scholar] [CrossRef]
- Wells, G.J.; Ray, W.H. Methodology for modeling detailed imperfect mixing effects in complex reactors. AIChE J. 2005, 51, 1508–1520. [Google Scholar] [CrossRef]
- Bisgaard, J.; Zahn, J.A.; Tajsoleiman, T.; Rasmussen, T.; Huusom, J.K.; Gernaey, K.V. General rights Data-based dynamic compartment model: Modeling of E. coli fed-batch fermentation in a 600 m3 bubble column. J. Ind. Microbiol. Biotechnol. 2023, 49, kuac021. [Google Scholar] [CrossRef]
- Bezzo, F.; Macchietto, S. A general methodology for hybrid multizonal/CFD models: Part II. Automatic zoning. Comput. Chem. Eng. 2004, 28, 513–525. [Google Scholar] [CrossRef]
- Spann, R.; Gernaey, K.V.; Sin, G. A compartment model for risk-based monitoring of lactic acid bacteria cultivations. Biochem. Eng. J. 2019, 151, 107293. [Google Scholar] [CrossRef]
- Liu, G.; Wilhite, B.A. A generalized zoning framework for development of CFD-based reduced-order compartment models. AIChE J. 2023, 69, e18063. [Google Scholar] [CrossRef]
- Rigopoulos, S.; Jones, A. A hybrid CFD-reaction engineering framework for multiphase reactor modelling: Basic concept and application to bubble column reactors. Chem. Eng. Sci. 2003, 58, 3077–3089. [Google Scholar] [CrossRef]
- Krychowska, A.; Kordas, M.; Konopacki, M.; Grygorcewicz, B.; Musik, D.; Wójcik, K.; Jędrzejczak-Silicka, M.; Rakoczy, R. Mathematical Modeling of Hydrodynamics in Bioreactor by Means of CFD-Based Compartment Model. Processes 2020, 8, 1301. [Google Scholar] [CrossRef]
- Delafosse, A.; Collignon, M.L.; Calvo, S.; Delvigne, F.; Crine, M.; Thonart, P.; Toye, D. CFD-based compartment model for description of mixing in bioreactors. Chem. Eng. Sci. 2014, 106, 76–85. [Google Scholar] [CrossRef]
- Tajsoleiman, T.; Spann, R.; Bach, C.; Gernaey, K.V.; Huusom, J.K.; Krühne, U. A CFD based automatic method for compartment model development. Comput. Chem. Eng. 2019, 123, 236–245. [Google Scholar] [CrossRef]
- Tarcsay, B.L.; Németh, S.; Chován, T.; Bárkányi, Á. Development of CFD based Compartment Models for Analysing High Risk Processes. Chem. Eng. Trans. 2022, 91, 487–492. [Google Scholar] [CrossRef]
- Massmann, T.; Kocks, C.; Parakenings, L.; Weber, B.; Jupke, A. Two-Dimensional CFD based compartment modeling for dynamic simulation of semi-batch crystallization processes in stirred tank reactors. Comput. Chem. Eng. 2020, 140, 106933. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Seidel, L. Ueber die Berechnung der wahrscheinlichsten Werthe solcher Unbekannten, zwischen welchen Bedingungs-Gleichungen bestehen. Astron. Nachrichten 1874, 84, 193–210. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Turbulent Schmidt numbers for CFD analysis with various types of flowfield. Atmos. Environ. 2007, 41, 8091–8099. [Google Scholar] [CrossRef]
- Gualtieri, C.; Angeloudis, A.; Bombardelli, F.; Jha, S.; Stoesser, T. On the values for the turbulent schmidt number in environmental flows. Fluids 2017, 2, 17. [Google Scholar] [CrossRef]
- Paul, E.L.; Atiemo-Obeng, V.A.; Kresta, S.M. Handbook of Industrial Mixing; Wiley-Blackwell: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Monod, J. The growth of bacterial cultures. Annu. Rev. Microbiol. 1949, 3, 371–394. [Google Scholar] [CrossRef]
- Kovárová-Kovar, K.; Egli, T. Growth Kinetics of Suspended Microbial Cells: From Single-Substrate-Controlled Growth to Mixed-Substrate Kinetics. Microbiol. Mol. Biol. Rev. 1998, 62, 646–666. [Google Scholar] [CrossRef] [PubMed]
- Titchener-Hooker, N. Bioprocess Engineering Principles (by Pauline M. Doran). Trends Biotechnol. 1995, 13. [Google Scholar]
- Stanbury, P.F.; Whitaker, A.; Hall, S.J. Principles of Fermentation Technology, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Nadal-Rey, G.; McClure, D.D.; Kavanagh, J.M.; Cassells, B.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Development of dynamic compartment models for industrial aerobic fed-batch fermentation processes. Chem. Eng. J. 2021, 420, 130402. [Google Scholar] [CrossRef]
- Perotto, S.; Rozza, G. Special Issue on Reduced Order Models in CFD. Int. J. Comput. Fluid Dyn. 2020, 34, 91–92. [Google Scholar] [CrossRef]


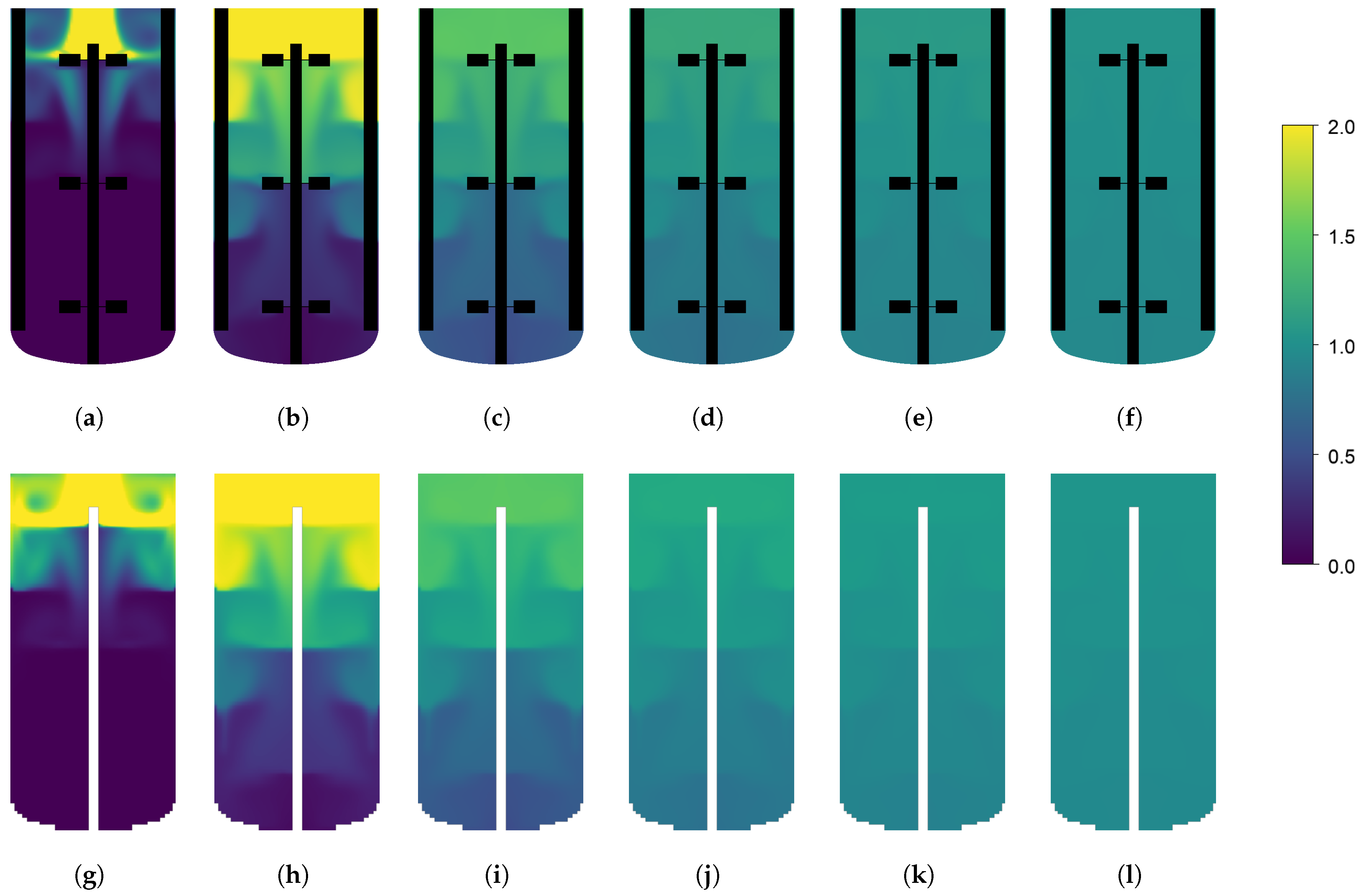
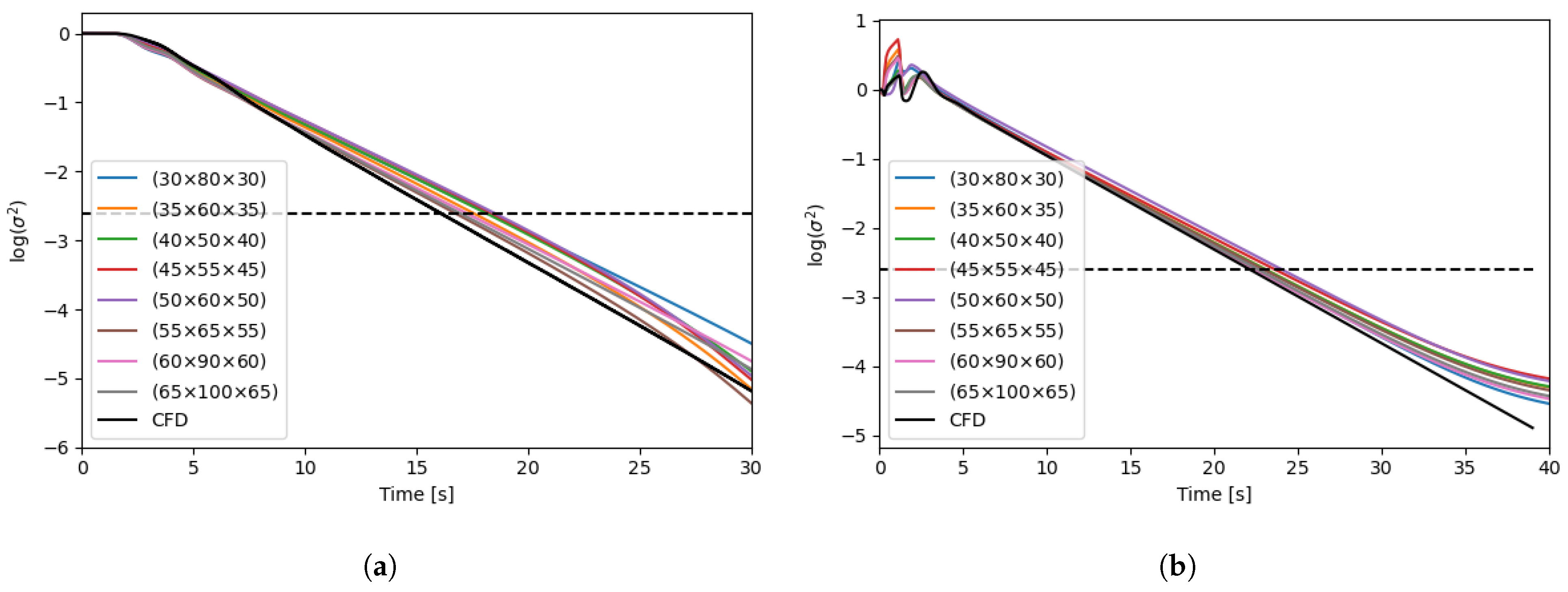
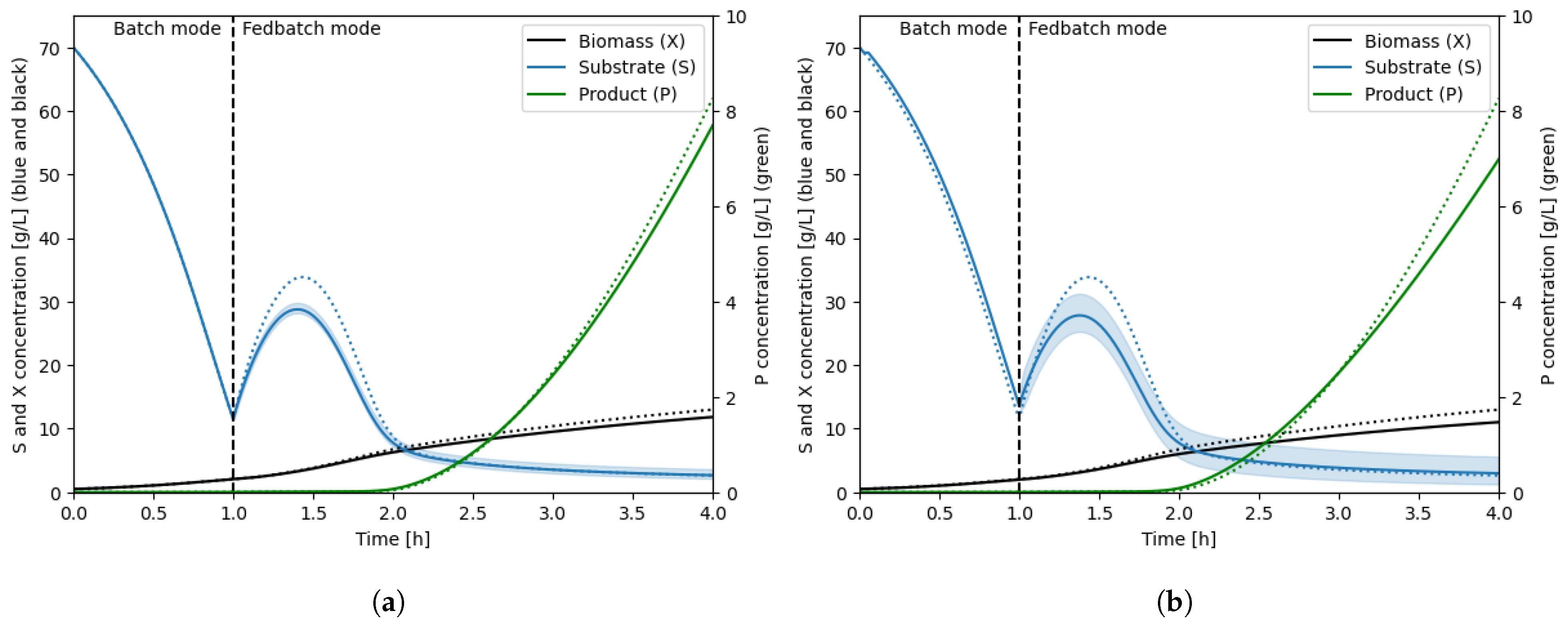
| Parameter | Reactor #1 | Reactor #2 |
|---|---|---|
| Total Volume | 16.355 L | 189.947 L |
| Inside height | 35 cm | 105.5 cm |
| Bottom type | rounded | rounded |
| Inside diameter | 25 cm | 48.8 cm |
| Impeller diameter | 8.5 cm | 20 cm |
| Number of impellers | 1 | 3 |
| Impeller type | Paddle | Rushton |
| Number of blades on impeller | 4 | 6 |
| Distance from top to impeller centre | 22.5 cm | 15.375, 51.875, 88.375 cm |
| Number of baffles | 4 | 4 |
| Baffle width | 2 cm | 4 cm |
| Baffle height | 15 cm | 95.5 cm |
| Agitator shaft diameter | 5 mm | 3.5 cm |
| Parameter | Value | Unit |
|---|---|---|
| 2 | ||
| 10 | ||
| 5 × | ||
| 0.03 | ||
| 2.8 × | ||
| 100 | ||
| 1 | ||
| Initial condition | Value | Unit |
| 0.5 | ||
| 70 | ||
| 0 |
| Reactor | ANSYS-CFX 2021R1 CFD Mesh | CM Python () | CM Julia () | CM Julia () |
|---|---|---|---|---|
| 16 L | 1455 | 22.59 | 10.05 | 0.641 |
| 190 L | 682 | 4.927 | 10.22 | 0.722 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Nepvou De Carfort, J.; Pinto, T.; Krühne, U. An Automatic Method for Generation of CFD-Based 3D Compartment Models: Towards Real-Time Mixing Simulations. Bioengineering 2024, 11, 169. https://doi.org/10.3390/bioengineering11020169
Le Nepvou De Carfort J, Pinto T, Krühne U. An Automatic Method for Generation of CFD-Based 3D Compartment Models: Towards Real-Time Mixing Simulations. Bioengineering. 2024; 11(2):169. https://doi.org/10.3390/bioengineering11020169
Chicago/Turabian StyleLe Nepvou De Carfort, Johan, Tiago Pinto, and Ulrich Krühne. 2024. "An Automatic Method for Generation of CFD-Based 3D Compartment Models: Towards Real-Time Mixing Simulations" Bioengineering 11, no. 2: 169. https://doi.org/10.3390/bioengineering11020169
APA StyleLe Nepvou De Carfort, J., Pinto, T., & Krühne, U. (2024). An Automatic Method for Generation of CFD-Based 3D Compartment Models: Towards Real-Time Mixing Simulations. Bioengineering, 11(2), 169. https://doi.org/10.3390/bioengineering11020169