Compensation Method for Missing and Misidentified Skeletons in Nursing Care Action Assessment by Improving Spatial Temporal Graph Convolutional Networks
Abstract
1. Introduction
2. Methods
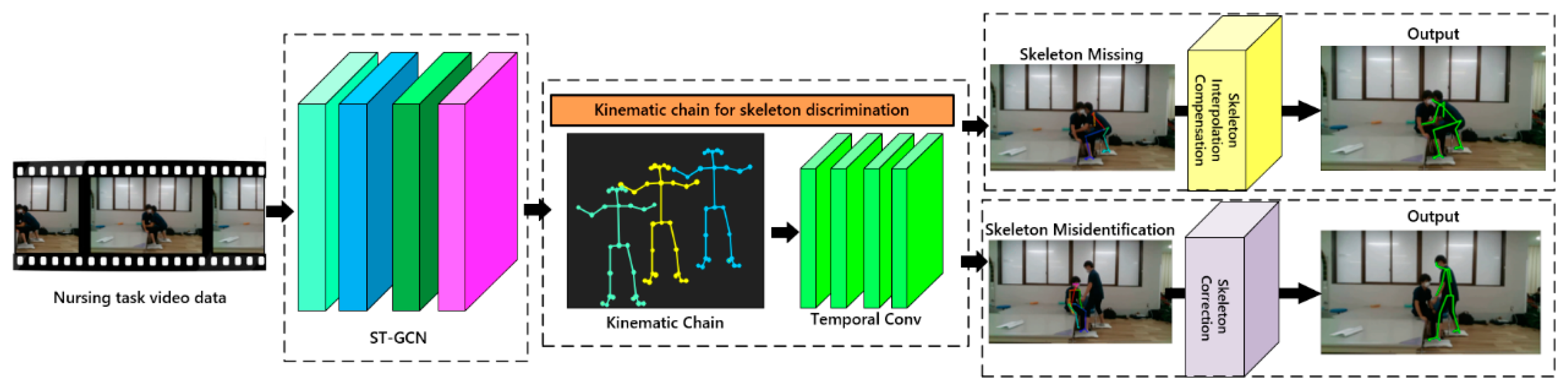
2.1. Overview
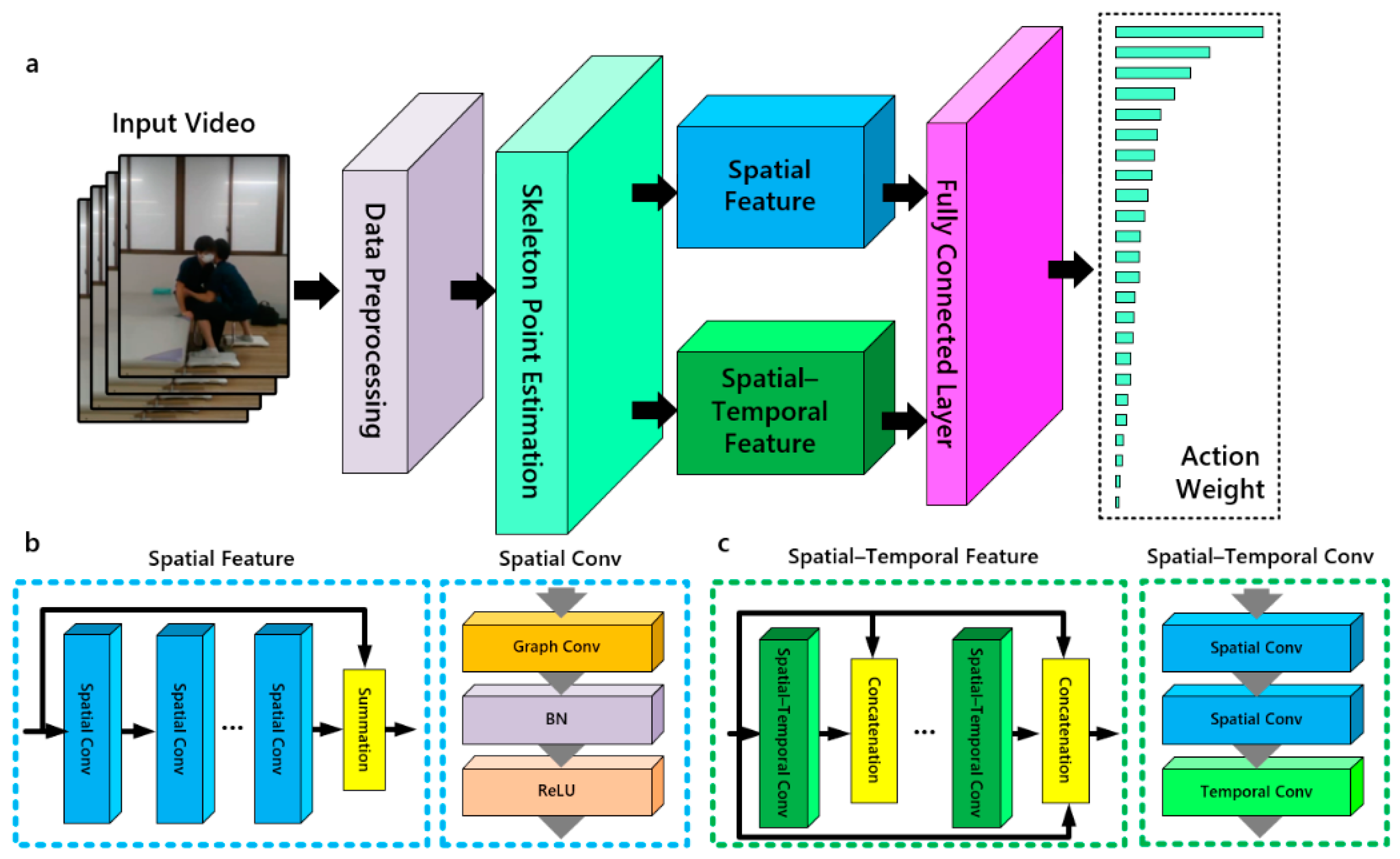
2.2. ST-GCN
2.3. Kinematic Chain for Skeleton Discrimination
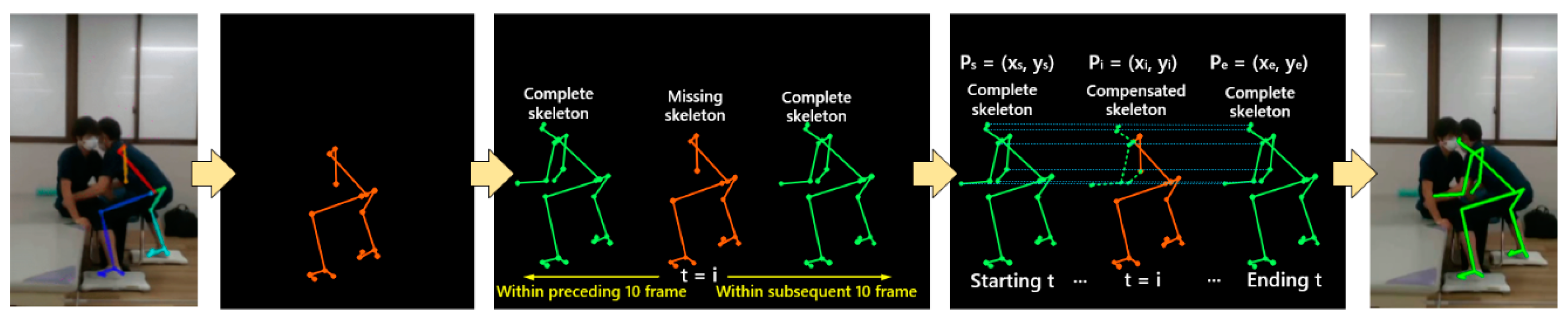
2.4. Skeleton Interpolation Compensation
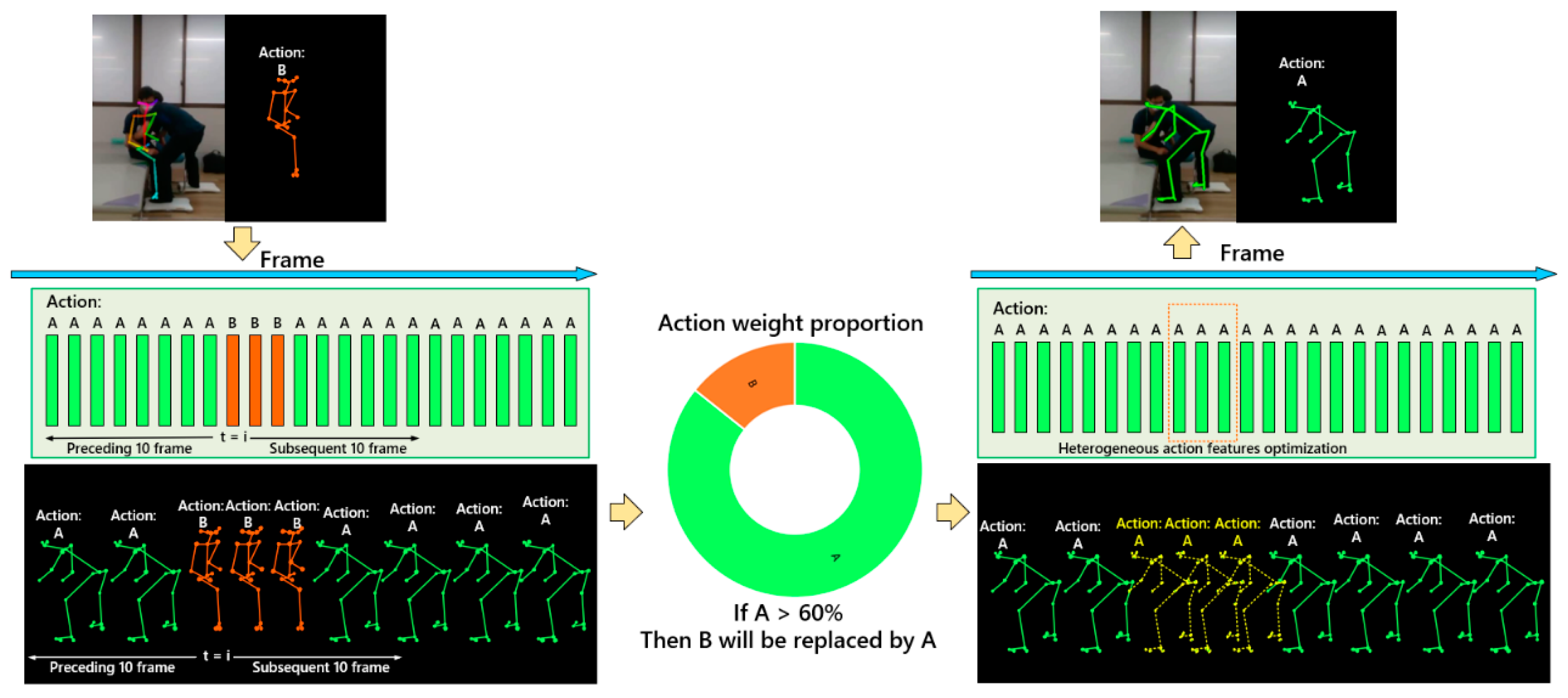
2.5. Skeleton Correction
2.6. Study Design
2.7. Joint Angle and Scoring Tool
2.8. Accuracy Verification
3. Results
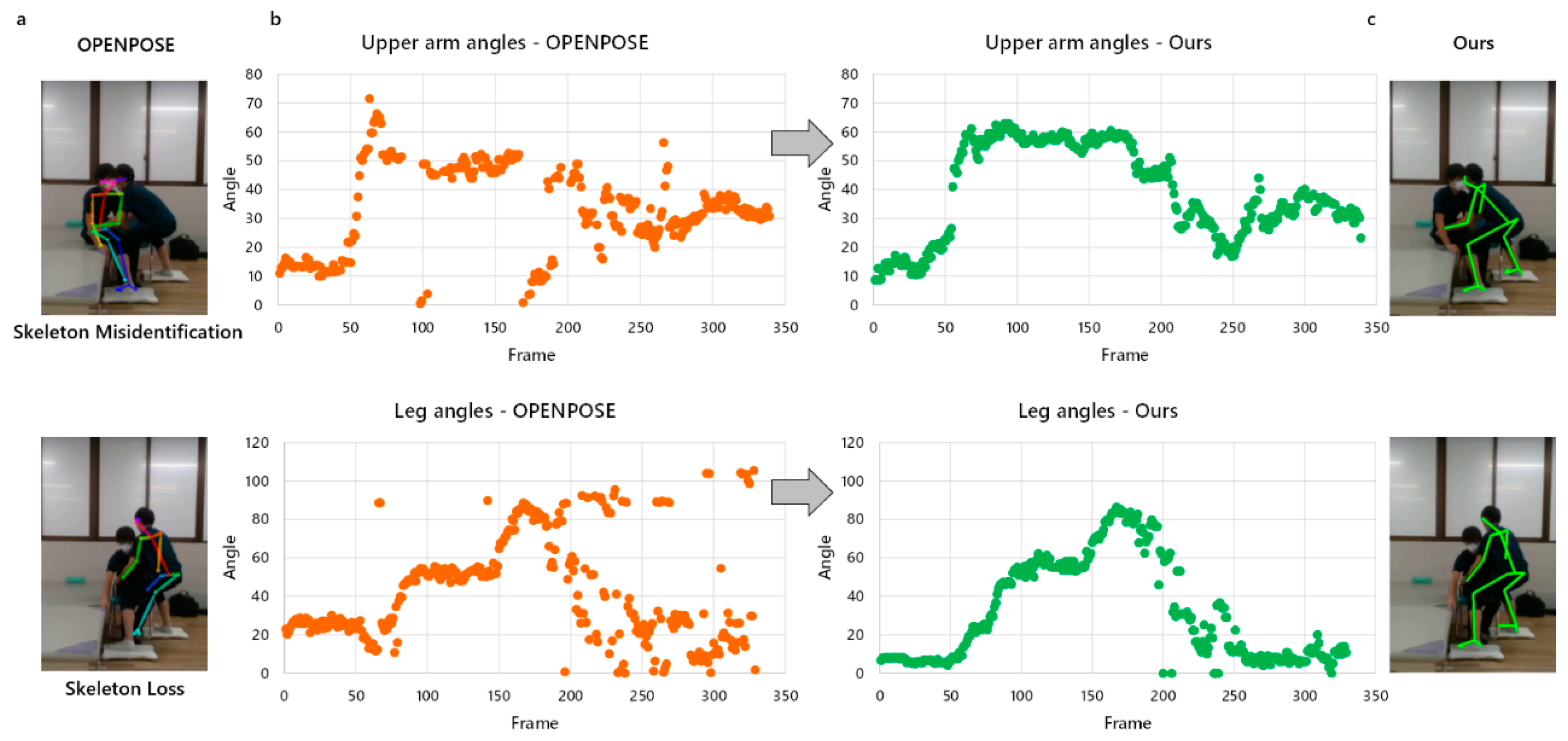
3.1. Missing and Misidentified Skeletons
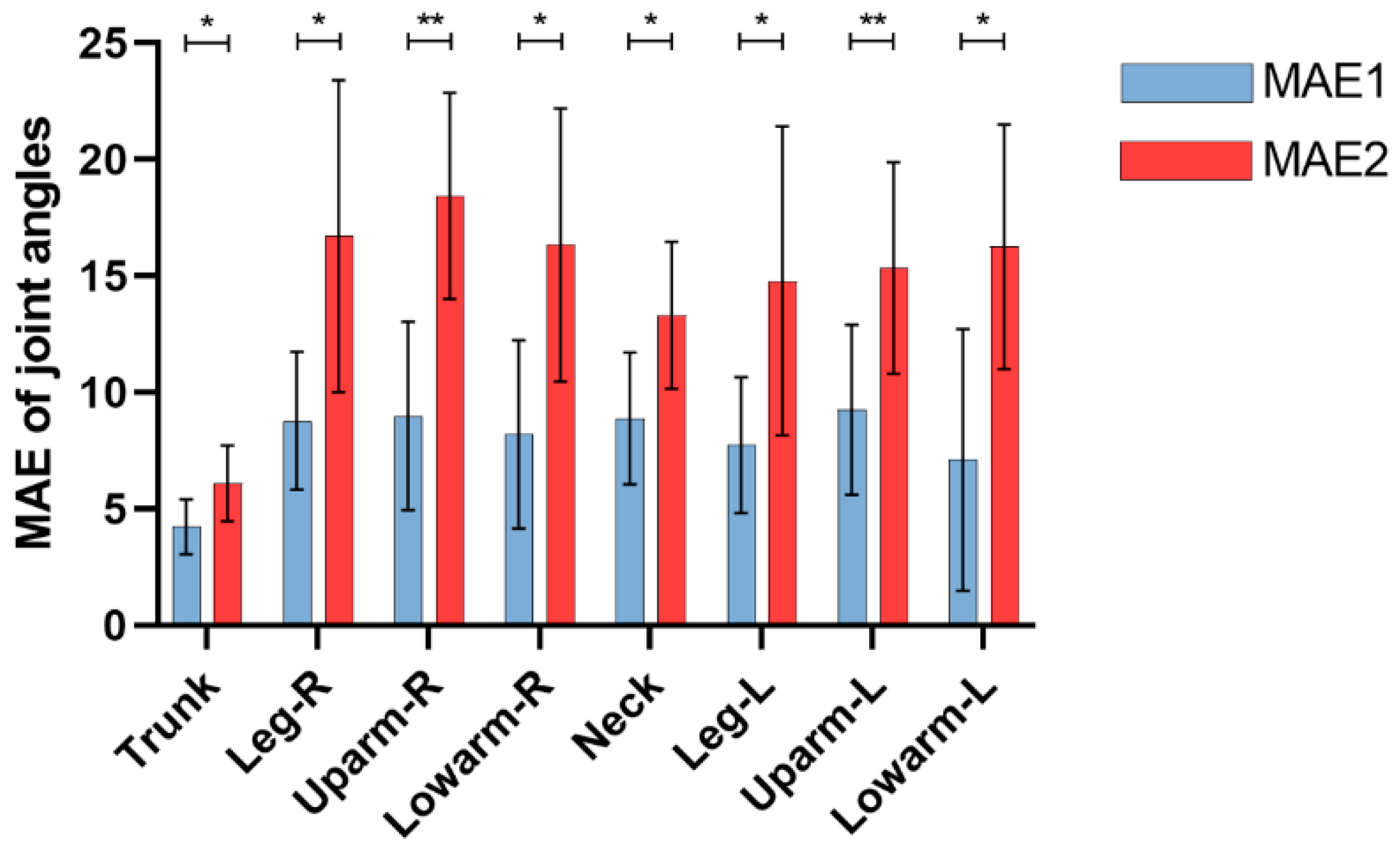
3.2. Joint Angles Error
3.3. REBA Score Error
4. Discussion
4.1. Main Findings and Contributions
4.2. Limitations
4.3. Directions for Further Research
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jacquier-Bret, J.; Gorce, P. Prevalence of Body Area Work-Related Musculoskeletal Disorders among Healthcare Professionals: A Systematic Review. Int. J. Environ. Res. Public Health 2023, 20, 841. [Google Scholar] [CrossRef]
- Heuel, L.; Lübstorf, S.; Otto, A.-K.; Wollesen, B. Chronic stress, behavioral tendencies, and determinants of health behaviors in nurses: A mixed-methods approach. BMC Public Health 2022, 22, 624. [Google Scholar] [CrossRef]
- Naidoo, R.N.; Haq, S.A. Occupational use syndromes. Best Pract. Res. Clin. Rheumatol. 2008, 22, 677–691. [Google Scholar] [CrossRef]
- Asuquo, E.G.; Tighe, S.M.; Bradshaw, C. Interventions to reduce work-related musculoskeletal disorders among healthcare staff in nursing homes; An integrative literature review. Int. J. Nurs. Stud. Adv. 2021, 3, 100033. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, H.; Quan, W.; Gusztav, F.; Wang, M.; Baker, J.S.; Gu, Y. Accurately and effectively predict the ACL force: Utilizing biomechanical landing pattern before and after-fatigue. Comput. Meth. Programs Biomed. 2023, 241, 107761. [Google Scholar] [CrossRef] [PubMed]
- McAtamney, L.; Corlett, E.N. RULA: A survey method for the investigation of work-related upper limb disorders. Appl. Ergon. 1993, 24, 91–99. [Google Scholar] [CrossRef] [PubMed]
- Hignett, S.; McAtamney, L. Rapid entire body assessment (REBA). Appl. Ergon. 2000, 31, 201–205. [Google Scholar] [CrossRef] [PubMed]
- Graben, P.R.; Schall, M.C., Jr.; Gallagher, S.; Sesek, R.; Acosta-Sojo, Y. Reliability Analysis of Observation-Based Exposure Assessment Tools for the Upper Extremities: A Systematic Review. Int. J. Environ. Res. Public Health 2022, 19, 10595. [Google Scholar] [CrossRef] [PubMed]
- Kee, D. Comparison of OWAS, RULA and REBA for assessing potential work-related musculoskeletal disorders. Int. J. Ind. Ergon. 2021, 83, 103140. [Google Scholar] [CrossRef]
- Kim, W.; Sung, J.; Saakes, D.; Huang, C.; Xiong, S. Ergonomic postural assessment using a new open-source human pose estimation technology (OpenPose). Int. J. Ind. Ergon. 2021, 84, 103164. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, H.; Quan, W.; Jiang, X.; Liang, M.; Li, S.; Ugbolue, U.C.; Baker, J.S.; Gusztav, F.; Ma, X.; et al. A new method proposed for realizing human gait pattern recognition: Inspirations for the application of sports and clinical gait analysis. Gait Posture 2024, 107, 293–305. [Google Scholar] [CrossRef]
- Lind, C.M.; Abtahi, F.; Forsman, M. Wearable Motion Capture Devices for the Prevention of Work-Related Musculoskeletal Disorders in Ergonomics—An Overview of Current Applications, Challenges, and Future Opportunities. Sensors 2023, 23, 4259. [Google Scholar] [CrossRef]
- Kalasin, S.; Surareungchai, W. Challenges of Emerging Wearable Sensors for Remote Monitoring toward Telemedicine Healthcare. Anal. Chem. 2023, 95, 1773–1784. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Nishida, N.; Morita, M.; Mitsuda, M.; Jiang, Z. Visualization of Caregiving Posture and Risk Evaluation of Discomfort and Injury. Appl. Sci. 2023, 13, 12699. [Google Scholar] [CrossRef]
- Yu, Y.; Umer, W.; Yang, X.; Antwi-Afari, M.F. Posture-related data collection methods for construction workers: A review. Autom. Constr. 2021, 124, 103538. [Google Scholar] [CrossRef]
- Xu, D.; Quan, W.; Zhou, H.; Sun, D.; Baker, J.S.; Gu, Y. Explaining the differences of gait patterns between high and low-mileage runners with machine learning. Sci. Rep. 2022, 12, 2981. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.A.; Mentiplay, B.F.; Hough, E.; Pua, Y.H. Three-dimensional cameras and skeleton pose tracking for physical function assessment: A review of uses, validity, current developments and Kinect alternatives. Gait Posture 2019, 68, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Kendall, A.; Grimes, M.; Cipolla, R. Posenet: A convolutional network for real-time 6-dof camera relocalization. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2938–2946. [Google Scholar]
- Güler, R.A.; Neverova, N.; Kokkinos, I. Densepose: Dense human pose estimation in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7297–7306. [Google Scholar]
- Huang, J.; Zhu, Z.; Huang, G. Multi-stage HRNet: Multiple stage high-resolution network for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime multi-person 2d pose estimation using part affinity fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7291–7299. [Google Scholar]
- Huang, C.C.; Nguyen, M.H. Robust 3D skeleton tracking based on openpose and a probabilistic tracking framework. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 4107–4112. [Google Scholar]
- Tsai, M.F.; Huang, S.H. Enhancing accuracy of human action Recognition System using Skeleton Point correction method. Multimed. Tools Appl. 2022, 81, 7439–7459. [Google Scholar] [CrossRef]
- Guo, X.; Dai, Y. Occluded joints recovery in 3d human pose estimation based on distance matrix. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 1325–1330. [Google Scholar]
- Kanazawa, A.; Zhang, J.Y.; Felsen, P.; Malik, J. Learning 3d human dynamics from video. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5614–5623. [Google Scholar]
- Yan, S.; Xiong, Y.; Lin, D. Spatial temporal graph convolutional networks for skeleton-based action recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; p. 32. [Google Scholar]
- Chen, Y.; Zhang, Z.; Yuan, C.; Li, B.; Deng, Y.; Hu, W. Channel-wise topology refinement graph convolution for skeleton-based action recognition. In Proceedings of the IEEE/CVF international conference on computer vision, Montreal, BC, Canada, 11–17 October 2021; pp. 13359–13368. [Google Scholar]
- Li, G.; Zhang, M.; Li, J.; Lv, F.; Tong, G. Efficient densely connected convolutional neural networks. Pattern Recognit. 2021, 109, 107610. [Google Scholar] [CrossRef]
- Wandt, B.; Ackermann, H.; Rosenhahn, B. A kinematic chain space for monocular motion capture. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Natarajan, B.; Elakkiya, R. Dynamic GAN for high-quality sign language video generation from skeletal poses using generative adversarial networks. Soft Comput. 2022, 26, 13153–13175. [Google Scholar] [CrossRef]
- Howarth, S.J.; Callaghan, J.P. Quantitative assessment of the accuracy for three interpolation techniques in kinematic analysis of human movement. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 847–855. [Google Scholar] [CrossRef] [PubMed]
- Gauss, J.F.; Brandin, C.; Heberle, A.; Löwe, W. Smoothing skeleton avatar visualizations using signal processing technology. SN Comput. Sci. 2021, 2, 429. [Google Scholar] [CrossRef]
- Miyajima, S.; Tanaka, T.; Imamura, Y.; Kusaka, T. Lumbar joint torque estimation based on simplified motion measurement using multiple inertial sensors. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 6716–6719. [Google Scholar]
- Liang, F.Y.; Gao, F.; Liao, W.H. Synergy-based knee angle estimation using kinematics of thigh. Gait Posture 2021, 89, 25–30. [Google Scholar] [CrossRef]
- Figueiredo, L.C.; Gratão, A.C.M.; Barbosa, G.C.; Monteiro, D.Q.; Pelegrini, L.N.d.C.; Sato, T.d.O. Musculoskeletal symptoms in formal and informal caregivers of elderly people. Rev. Bras. Enferm. 2021, 75, e20210249. [Google Scholar] [CrossRef]
- Yu, Y.; Li, H.; Yang, X.; Kong, L.; Luo, X.; Wong, A.Y.L. An automatic and non-invasive physical fatigue assessment method for construction workers. Autom. Constr. 2019, 103, 1–12. [Google Scholar] [CrossRef]
- Li, L.; Martin, T.; Xu, X. A novel vision-based real-time method for evaluating postural risk factors associated with musculoskeletal disorders. Appl. Ergon. 2020, 87, 103138. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhang, R.; Lee, C.-H.; Lee, Y.-C. An evaluation of posture recognition based on intelligent rapid entire body assessment system for determining musculoskeletal disorders. Sensors 2020, 20, 4414. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, H.; Quan, W.; Gusztav, F.; Baker, J.S.; Gu, Y. Adaptive neuro-fuzzy inference system model driven by the non-negative matrix factorization-extracted muscle synergy patterns to estimate lower limb joint movements. Comput. Meth. Programs Biomed. 2023, 242, 107848. [Google Scholar] [CrossRef]
- Yuan, H.; Zhou, Y. Ergonomic assessment based on monocular RGB camera in elderly care by a new multi-person 3D pose estimation technique (ROMP). Int. J. Ind. Ergon. 2023, 95, 103440. [Google Scholar] [CrossRef]
- Liu, P.L.; Chang, C.C. Simple method integrating OpenPose and RGB-D camera for identifying 3D body landmark locations in various postures. Int. J. Ind. Ergon. 2022, 91, 103354. [Google Scholar] [CrossRef]
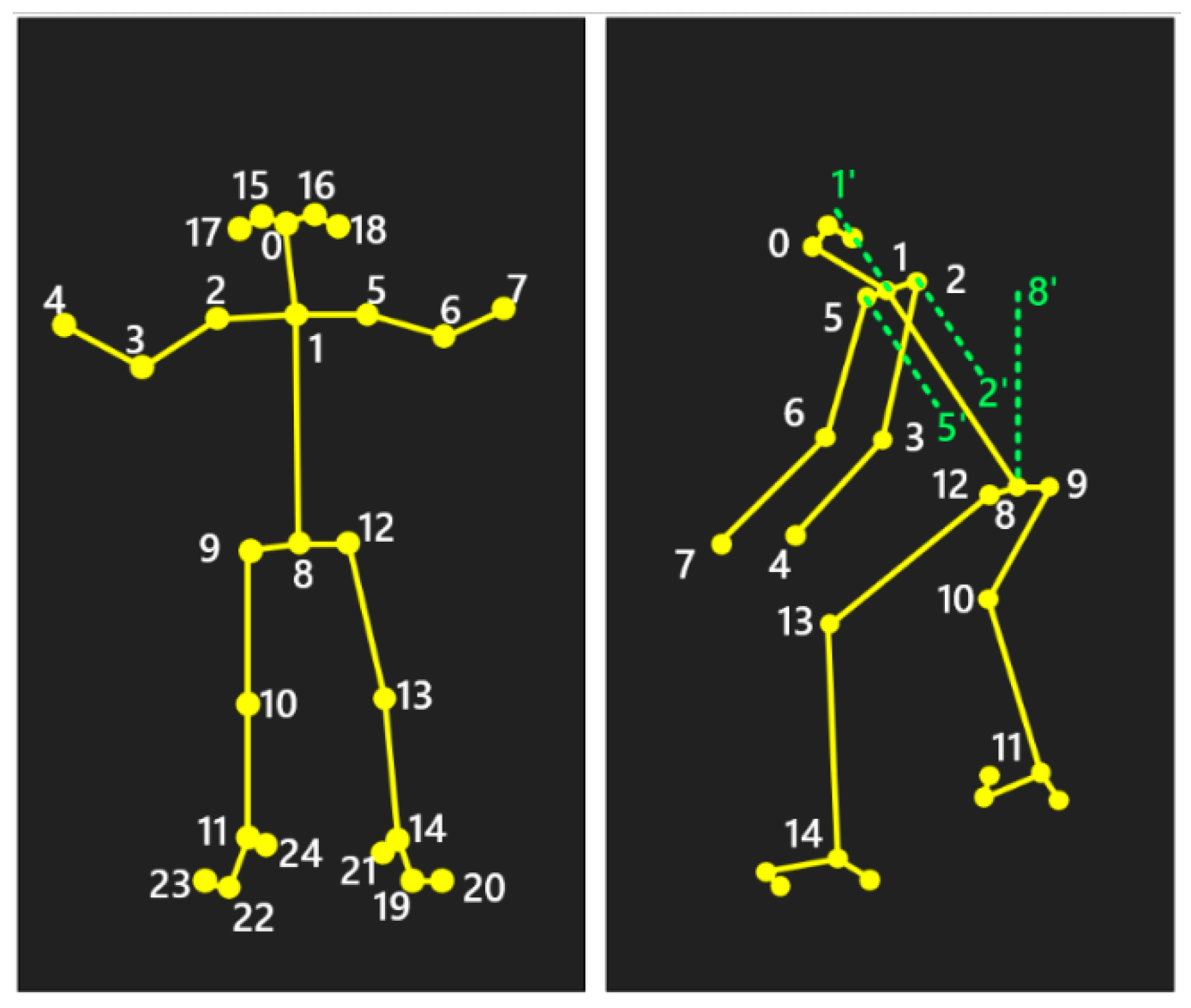
| Joint Angle | Involved Skeletal Points |
|---|---|
| Trunk flexion angle | ∠1, 8, 8′ |
| Neck flexion angle | ∠0, 1, 1′ |
| Left leg flexion angle | ∠12, 13, 14 |
| Right leg flexion angle | ∠9, 10, 11 |
| Left upper arm flexion angle | ∠5′, 5, 6 |
| Right upper arm flexion angle | ∠2′, 2, 3 |
| Left lower arm flexion angle | ∠5, 6, 7 |
| Right lower arm flexion angle | ∠2, 3, 4 |
| Action Level | REBA Score | Risk Level | Correction Suggestion |
|---|---|---|---|
| 0 | 1 | Negligible | None necessary |
| 1 | 2–3 | Low | Maybe necessary |
| 2 | 4–7 | Medium | Necessary |
| 3 | 8–10 | High | Necessary soon |
| 4 | 11–15 | Very high | Necessary now |
| Nursing Task Video | Frame 1 | Frame 2 | Frame i | Frame n | |
|---|---|---|---|---|---|
| OpenPose | Joint angle | Ao1 | Ao2 | Aoi | Aon |
| REBA | Ro1 | Ro2 | Roi | Ron | |
| Inertial sensors | Joint angle | As1 | As2 | Asi | Asn |
| REBA | Rs1 | Rs2 | Rsi | Rsn | |
| Ours | Joint angle | A1 | A2 | Ai | An |
| REBA | R1 | R2 | Ri | Rn | |
| Accuracy | Joint angle error | [Ao1, As1, A1] | [Ao2, As2, A2] | [Aoi, Asi, Ai] | [Aon, Asn, An] |
| REBA score error | [Ro1, Rs1, R1] | [Ro2, Rs2, R2] | [Roi, Rsi, Ri] | [Ron, Rsn, Rn] |
| Joints | Skeleton Missing Rate | Skeleton Misidentification Rate | ||
|---|---|---|---|---|
| OpenPose | Ours | OpenPose | Ours | |
| Trunk | 0.18% | 0.07% | 20.60% | 2.18% |
| Leg-R | 16.79% | 5.96% | ||
| Upper arm-R | 22.42% | 10.36% | ||
| Lower arm-R | 64.68% | 51.67% | ||
| Neck | 22.06% | 7.01% | ||
| Leg-L | 8.47% | 1.78% | ||
| Upper arm-L | 11.19% | 0.29% | ||
| Lower arm-L | 12.75% | 0.58% | ||
| Joints | Eangle1 (N = 8) | p-Value p1 | Eangle2 (N = 8) | p-Value p2 | Eangle3 (N = 8) | p-Value p3 |
|---|---|---|---|---|---|---|
| Trunk | −0.166 ± 18.526 | p = 0.628 | −0.019 ± 2.345 | p = 0.659 | −0.017 ± 18.800 | p = 0.961 |
| Leg-R | 3.880 ± 18.591 | p < 0.001 | −0.060 ± 2.324 | p = 0.160 | 0.882 ± 6.090 | p < 0.001 |
| Upper arm-R | 3.145 ± 10.742 | p < 0.001 | −0.186 ± 4.475 | p = 0.025 | 0.755 ± 10.136 | p < 0.001 |
| Lower arm-R | 3.969 ± 30.840 | p < 0.001 | −0.226 ± 4.427 | p = 0.006 | −0.108 ± 18.481 | p = 0.752 |
| Neck | −1.956 ± 14.891 | p < 0.001 | −0.072 ± 2.281 | p = 0.087 | 1.963 ± 14.436 | p < 0.001 |
| Leg-L | −1.069 ± 7.174 | p < 0.001 | −0.125 ± 4.512 | p = 0.134 | −4.098 ± 30.771 | p < 0.001 |
| Upper arm-L | −1.014 ± 10.605 | p < 0.001 | −0.059 ± 2.292 | p = 0.165 | 0.773 ± 9.903 | P < 0.001 |
| Lower arm-L | 2.473 ± 27.971 | p < 0.001 | 0.006 ± 4.586 | p = 0.942 | −3.001 ± 27.793 | p < 0.001 |
| Joints | EREBA1 (N = 8) | p-Value | EREBA2 (N = 8) | p-Value |
|---|---|---|---|---|
| Trunk | −0.001 ± 0.207 | p = 0.788 | 0 ± 0.159 | p = 1 |
| Leg-R | 0.255 ± 0.568 | p < 0.001 | 0.015 ± 0.465 | p = 0.066 |
| Upper arm-R | −0.176 ± 0.644 | p < 0.001 | −0.005 ± 0.302 | p = 0.296 |
| Lower arm-R | −0.154 ± 0.635 | p < 0.001 | 0.235 ± 0.448 | p < 0.001 |
| Neck | 0.003 ± 0.132 | p = 0.124 | −0.003 ± 0.395 | p = 0.638 |
| Leg-L | −0.027 ± 0.282 | p < 0.001 | 0.012 ± 0.506 | p = 0.186 |
| Upper arm-L | 0.013 ± 0.282 | p = 0.013 | 0.001 ± 0.186 | p = 0.619 |
| Lower arm-L | 0.098 ± 0.309 | p < 0.001 | 0.234 ± 0.508 | p = 0.325 |
| REBA | 0.116 ± 1.128 | p < 0.001 | −0.003 ± 0.208 | p = 0.373 |
| Joints | Acc | ||||
|---|---|---|---|---|---|
| OpenPose | Tsai et al. [23] | Guo et al. [24] | Kanazawa et al. [25] | Ours | |
| Trunk | 91.92% | 90.34% | 92.36% | 95.32% | 95.65% |
| Leg-R | 81.43% | 86.61% | 86.42% | 88.33% | 87.47% |
| Upper arm-R | 71.61% | 72.41% | 72.98% | 75.79% | 76.95% |
| Lower arm-R | 47.76% | 59.87% | 60.14% | 62.87% | 64.31% |
| Neck | 76.96% | 82.86% | 87.95% | 86.97% | 87.96% |
| Leg-L | 82.94% | 83.14% | 89.76% | 91.61% | 90.81% |
| Upper arm-L | 80.25% | 85.27% | 92.31% | 91.89% | 92.13% |
| Lower arm-L | 84.26% | 87.35% | 91.14% | 95.57% | 91.68% |
| REBA | 58.33% | 63.29% | 76.63% | 80.46% | 87.34% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Nishida, N.; Morita, M.; Sakai, T.; Jiang, Z. Compensation Method for Missing and Misidentified Skeletons in Nursing Care Action Assessment by Improving Spatial Temporal Graph Convolutional Networks. Bioengineering 2024, 11, 127. https://doi.org/10.3390/bioengineering11020127
Han X, Nishida N, Morita M, Sakai T, Jiang Z. Compensation Method for Missing and Misidentified Skeletons in Nursing Care Action Assessment by Improving Spatial Temporal Graph Convolutional Networks. Bioengineering. 2024; 11(2):127. https://doi.org/10.3390/bioengineering11020127
Chicago/Turabian StyleHan, Xin, Norihiro Nishida, Minoru Morita, Takashi Sakai, and Zhongwei Jiang. 2024. "Compensation Method for Missing and Misidentified Skeletons in Nursing Care Action Assessment by Improving Spatial Temporal Graph Convolutional Networks" Bioengineering 11, no. 2: 127. https://doi.org/10.3390/bioengineering11020127
APA StyleHan, X., Nishida, N., Morita, M., Sakai, T., & Jiang, Z. (2024). Compensation Method for Missing and Misidentified Skeletons in Nursing Care Action Assessment by Improving Spatial Temporal Graph Convolutional Networks. Bioengineering, 11(2), 127. https://doi.org/10.3390/bioengineering11020127







