A Gait Analysis in Professional Dancers: A Cross-Sectional Study
Abstract
1. Introduction
1.1. Related Work
Study Design and Objectives
- To determine discrepancies in temporal–spatial parameters, such as stride length, step width, and gait velocity, between professional dancers and non-dancers.
- To analyze joint kinematics, including joint angles and range of motion across the gait cycle, to identify precise distinctions in joint motion between the two groups.
- To evaluate ground reaction forces and their components, which will provide insight into the distribution of forces and load patterns experienced by professional dancers in contrast to non-dancers.
2. Methodology
Data Analysis
3. Results
3.1. The Result Comparing the Right and Left Angular Velocity of the Dancers and Non-Dancers
3.1.1. Regression Equations in the Context of This Study (Velocity)
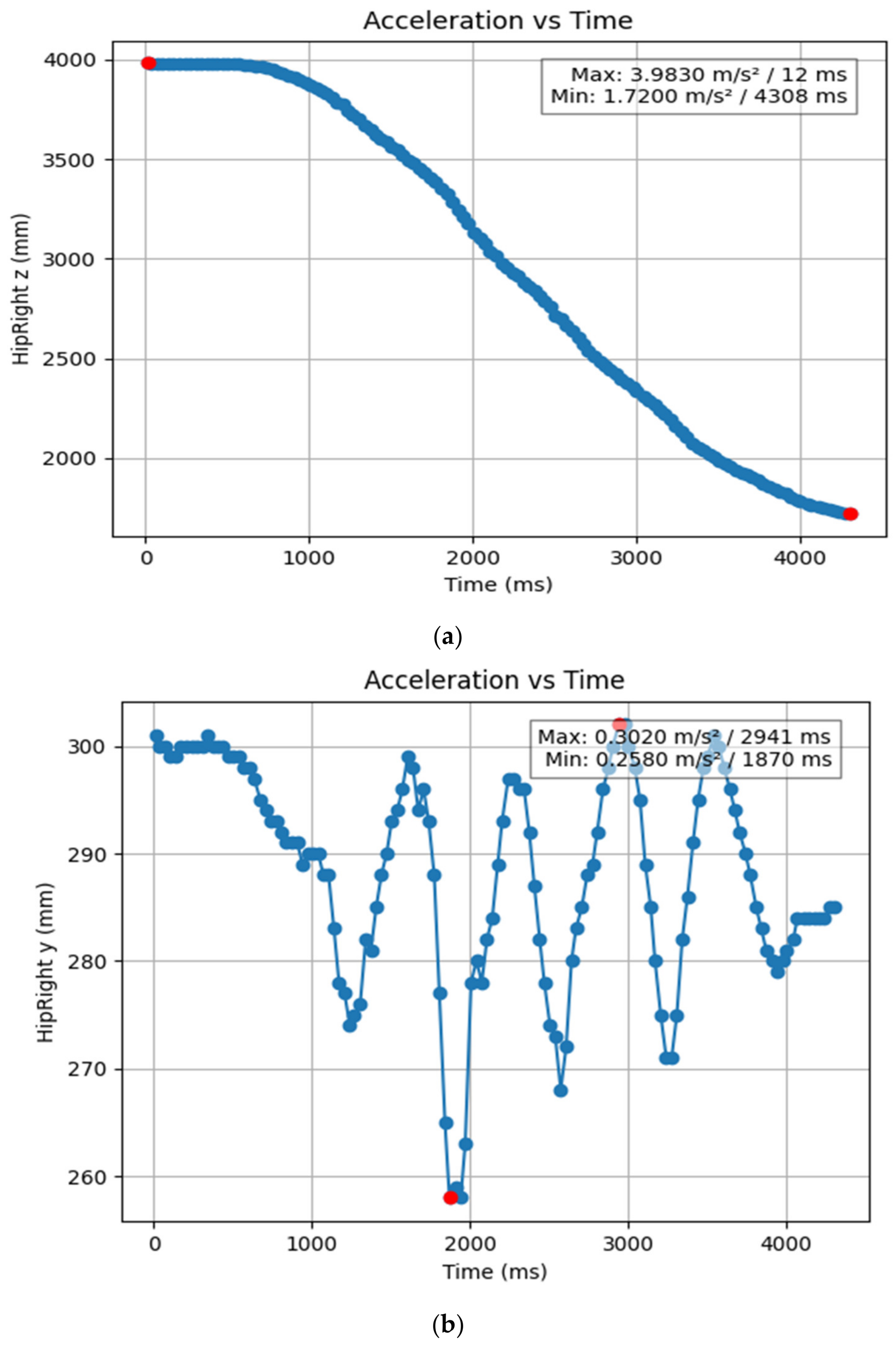
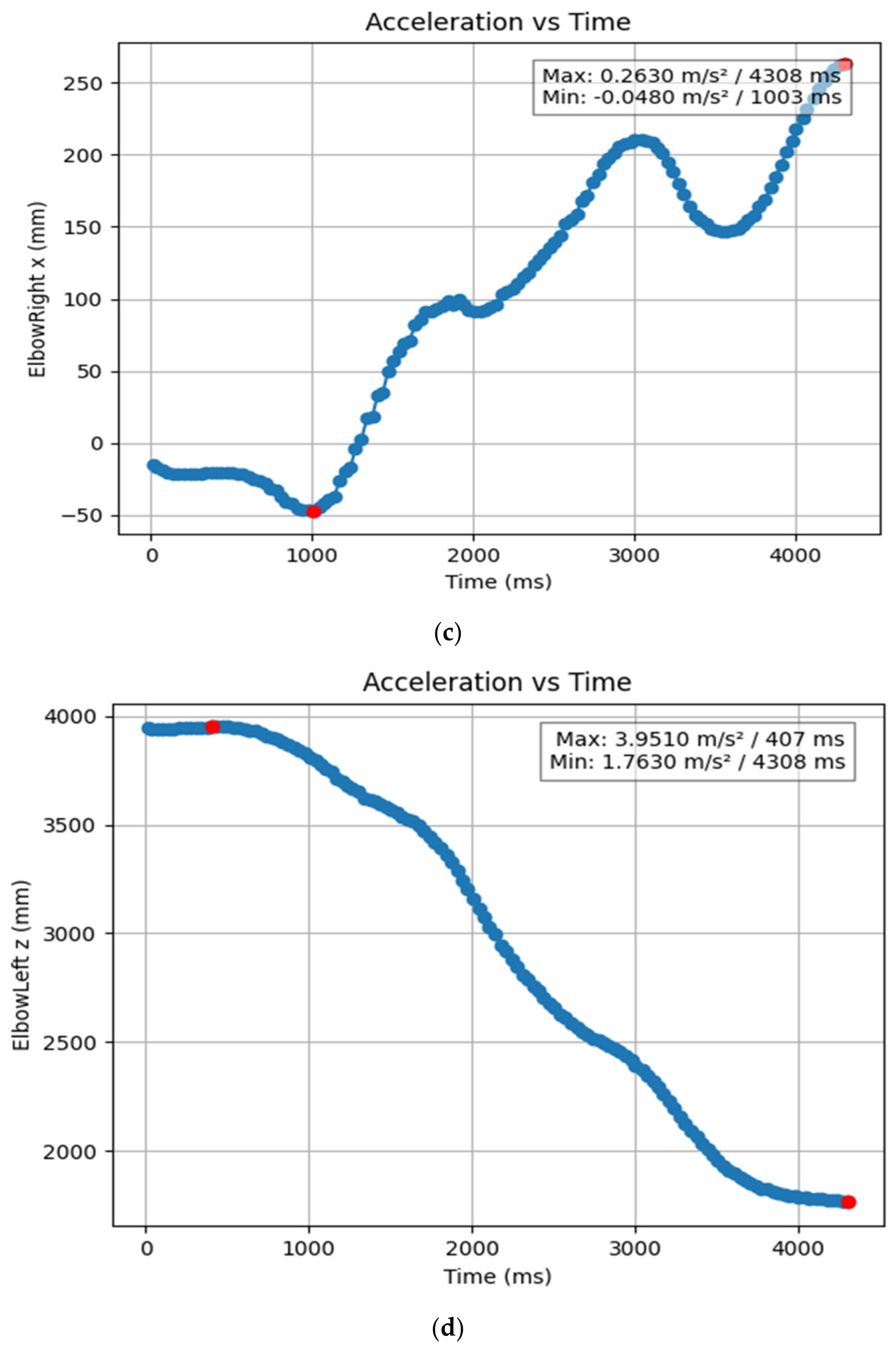
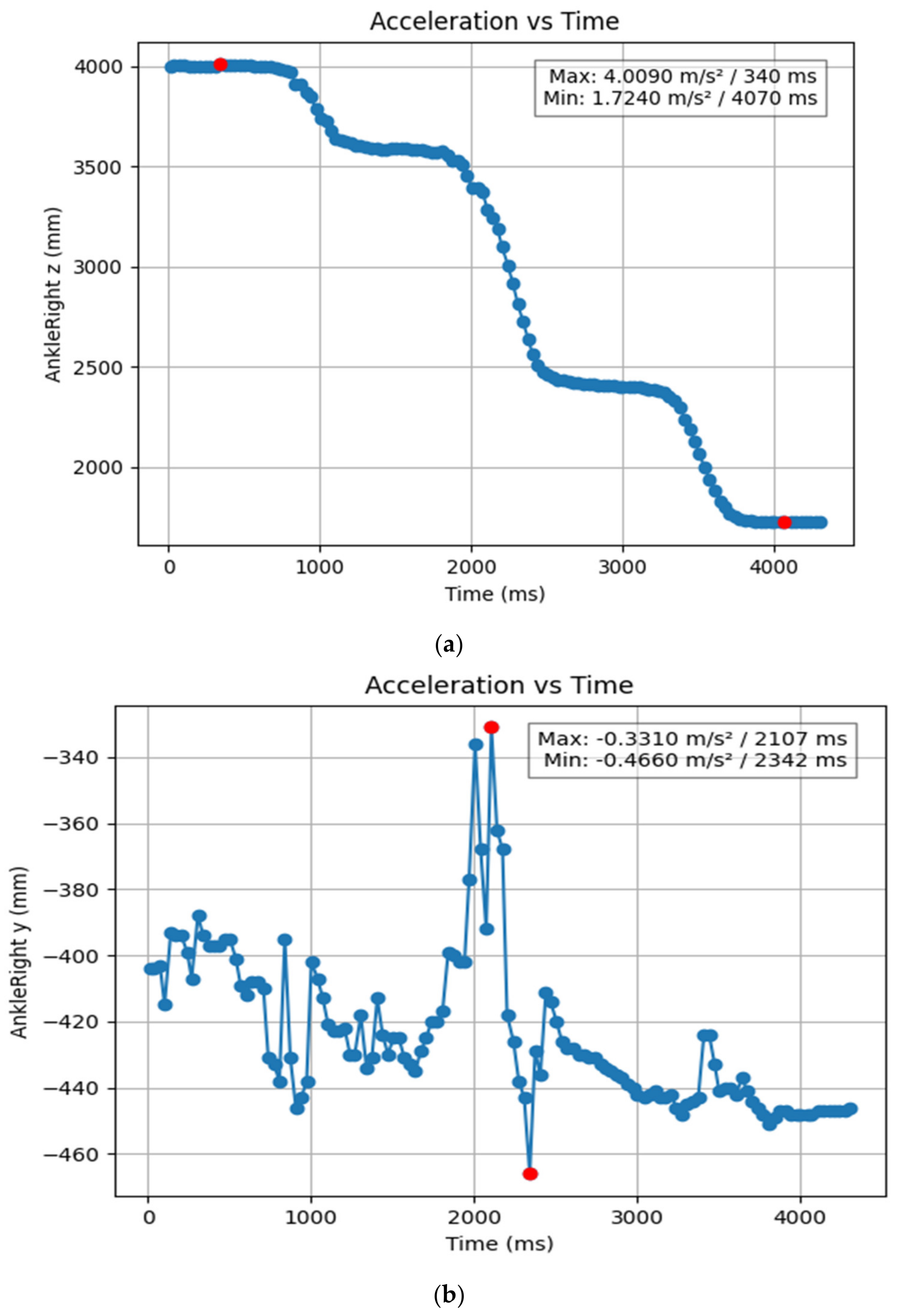
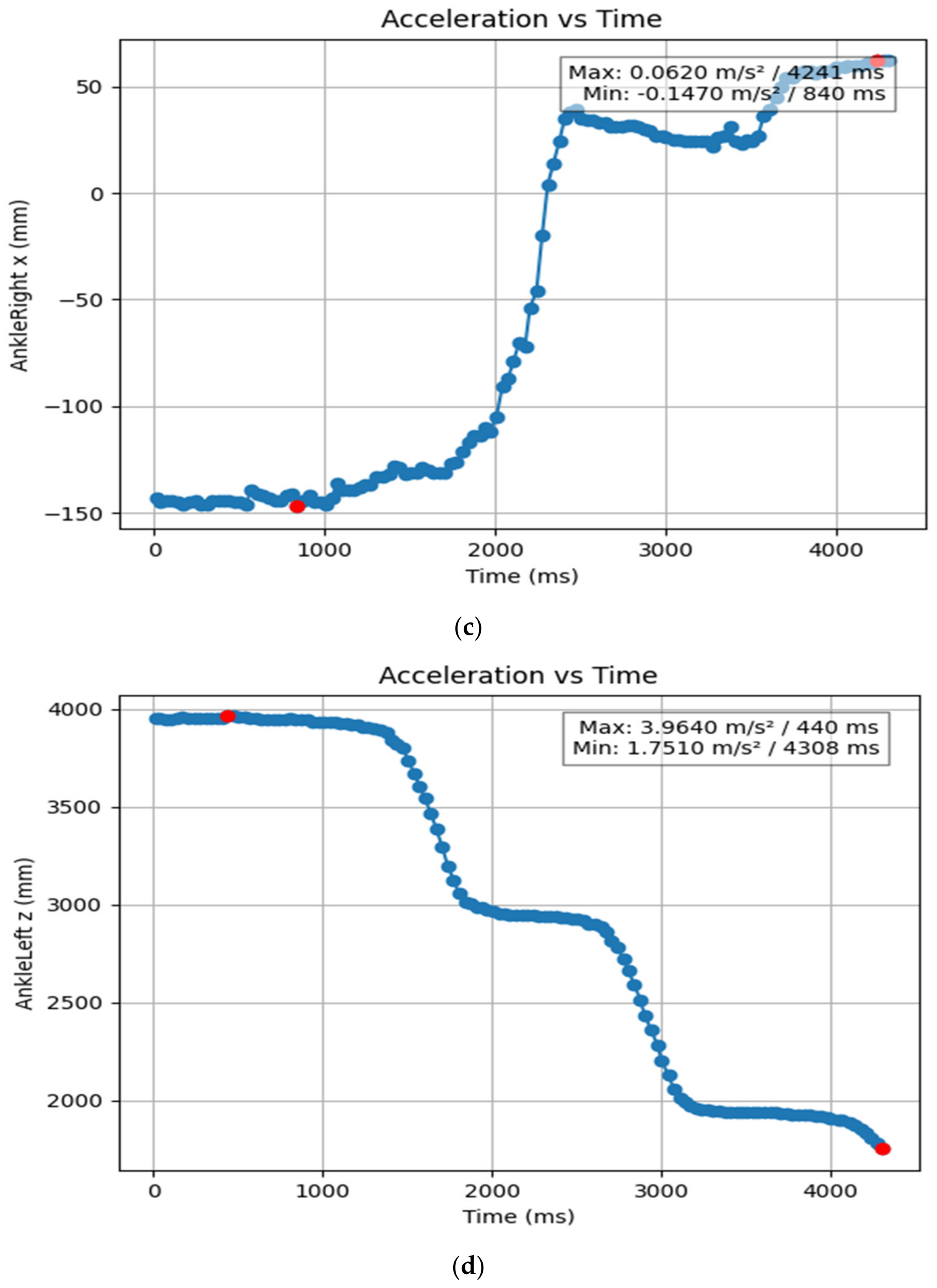
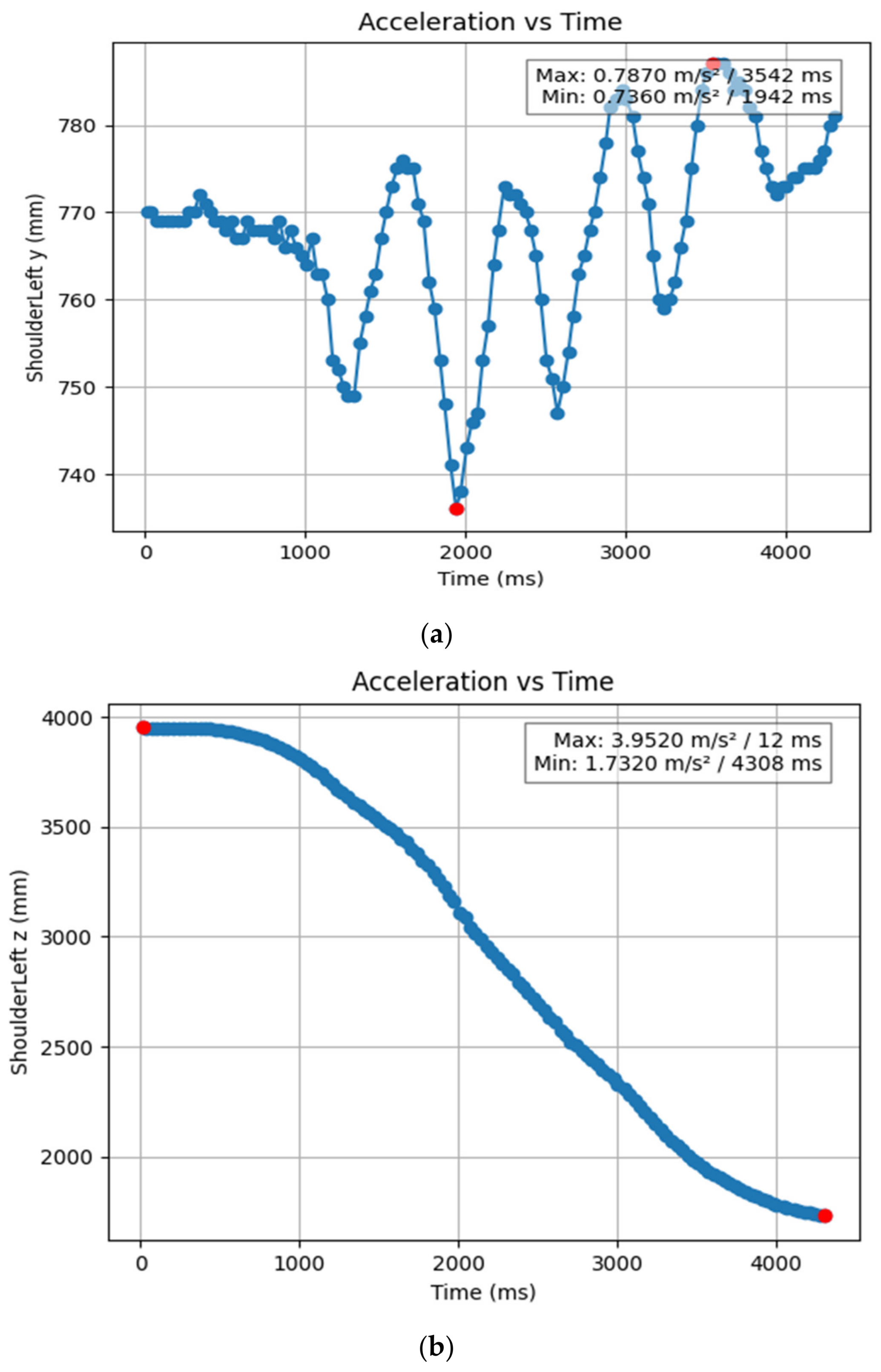
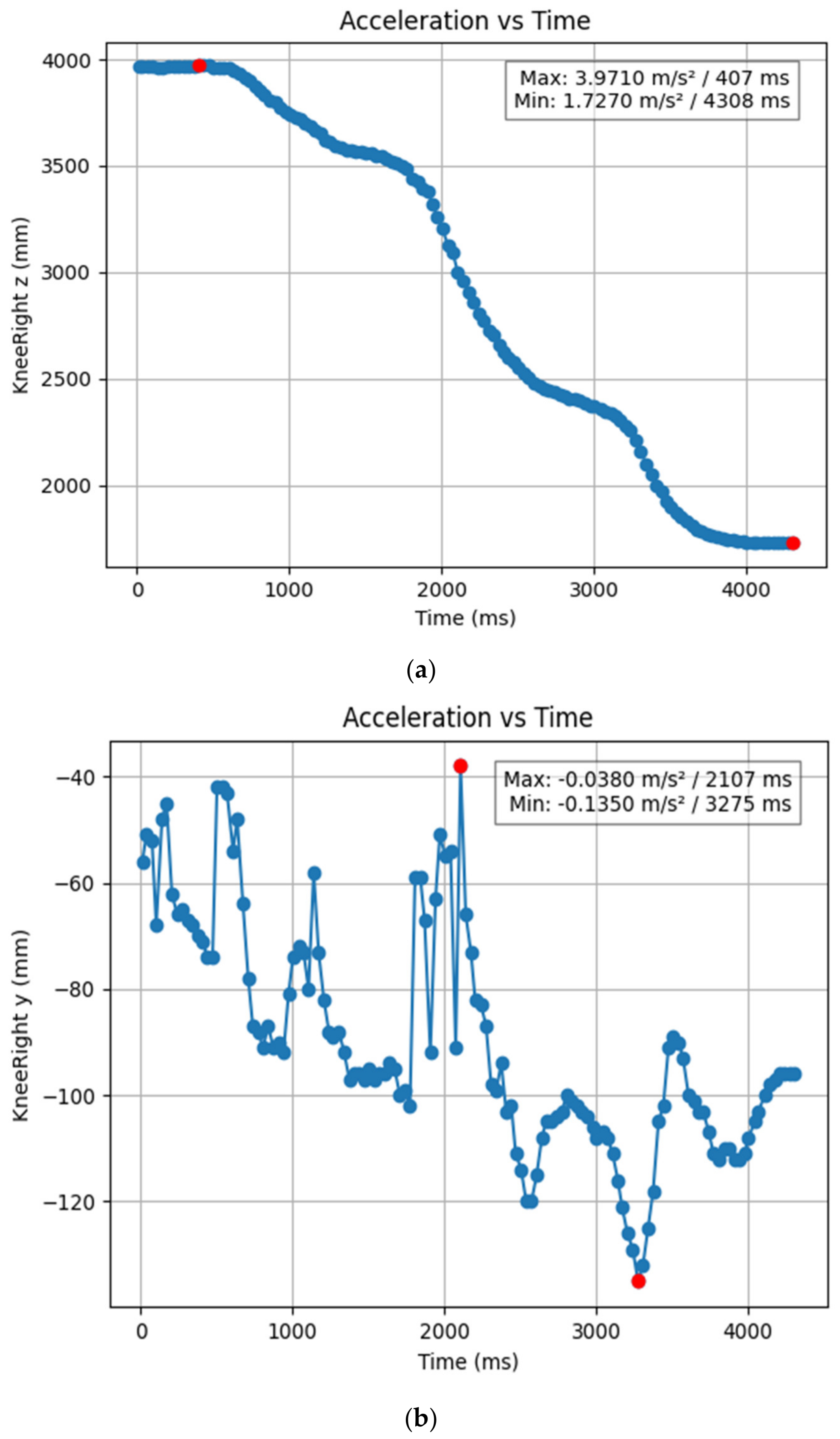
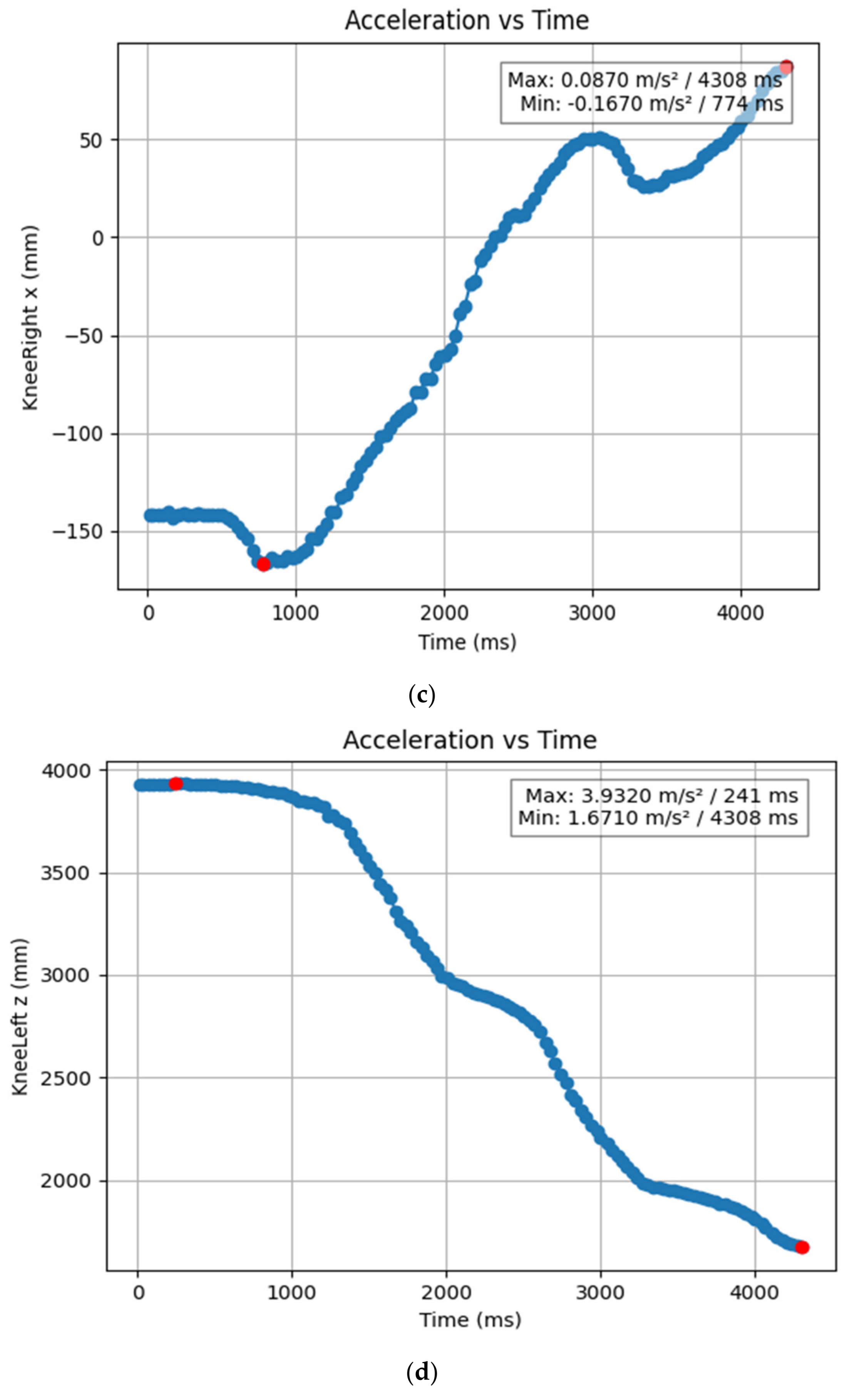
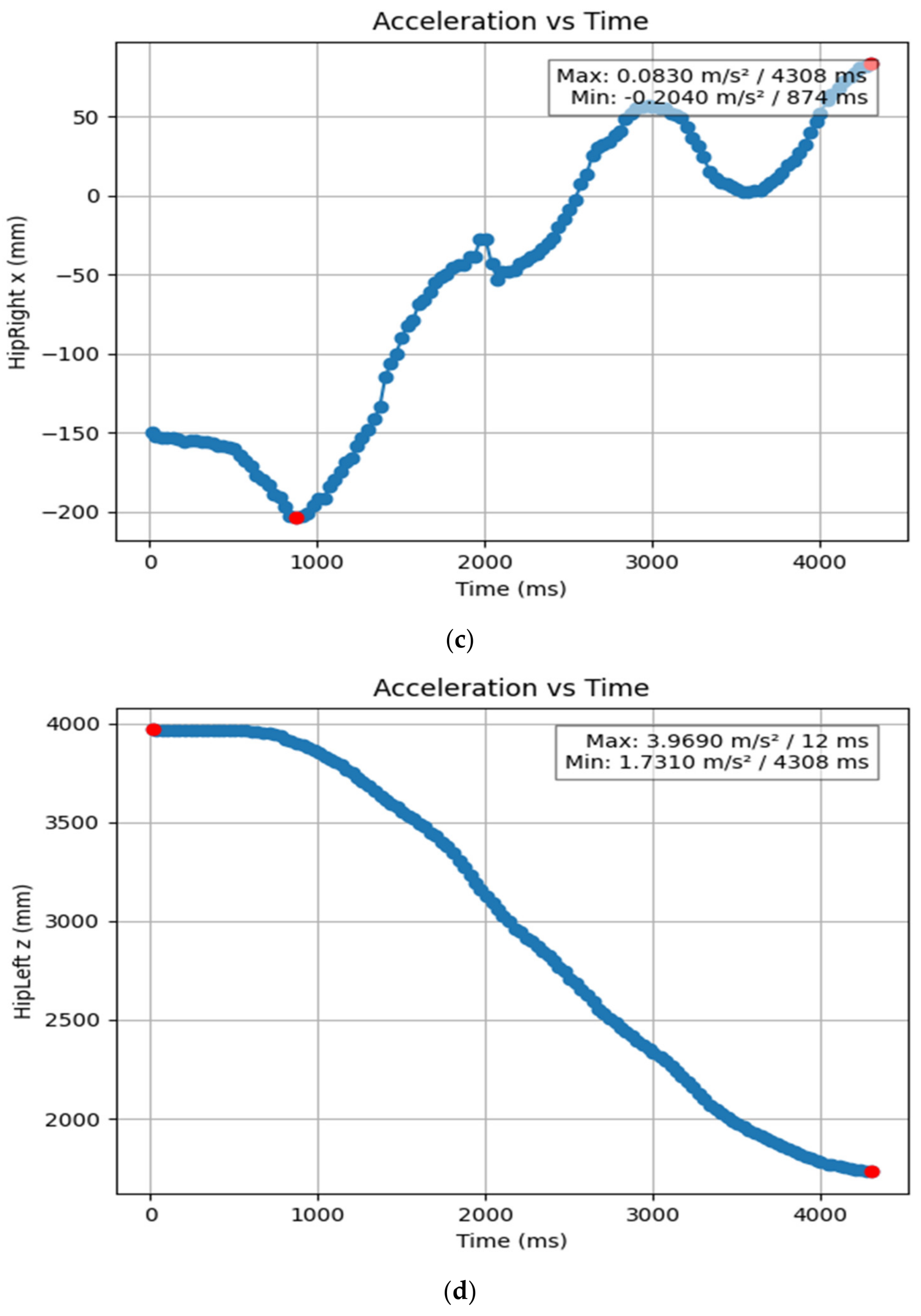
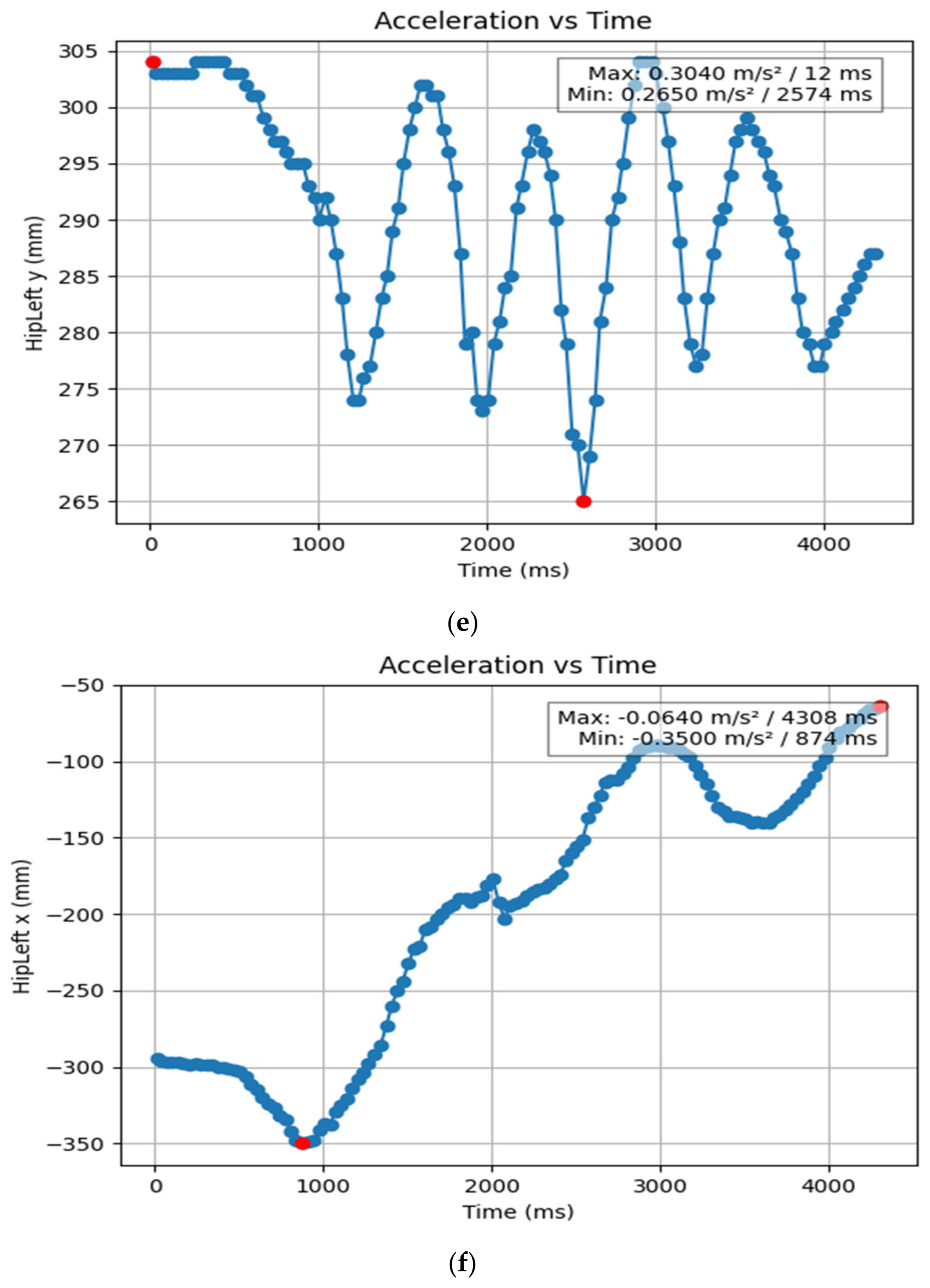
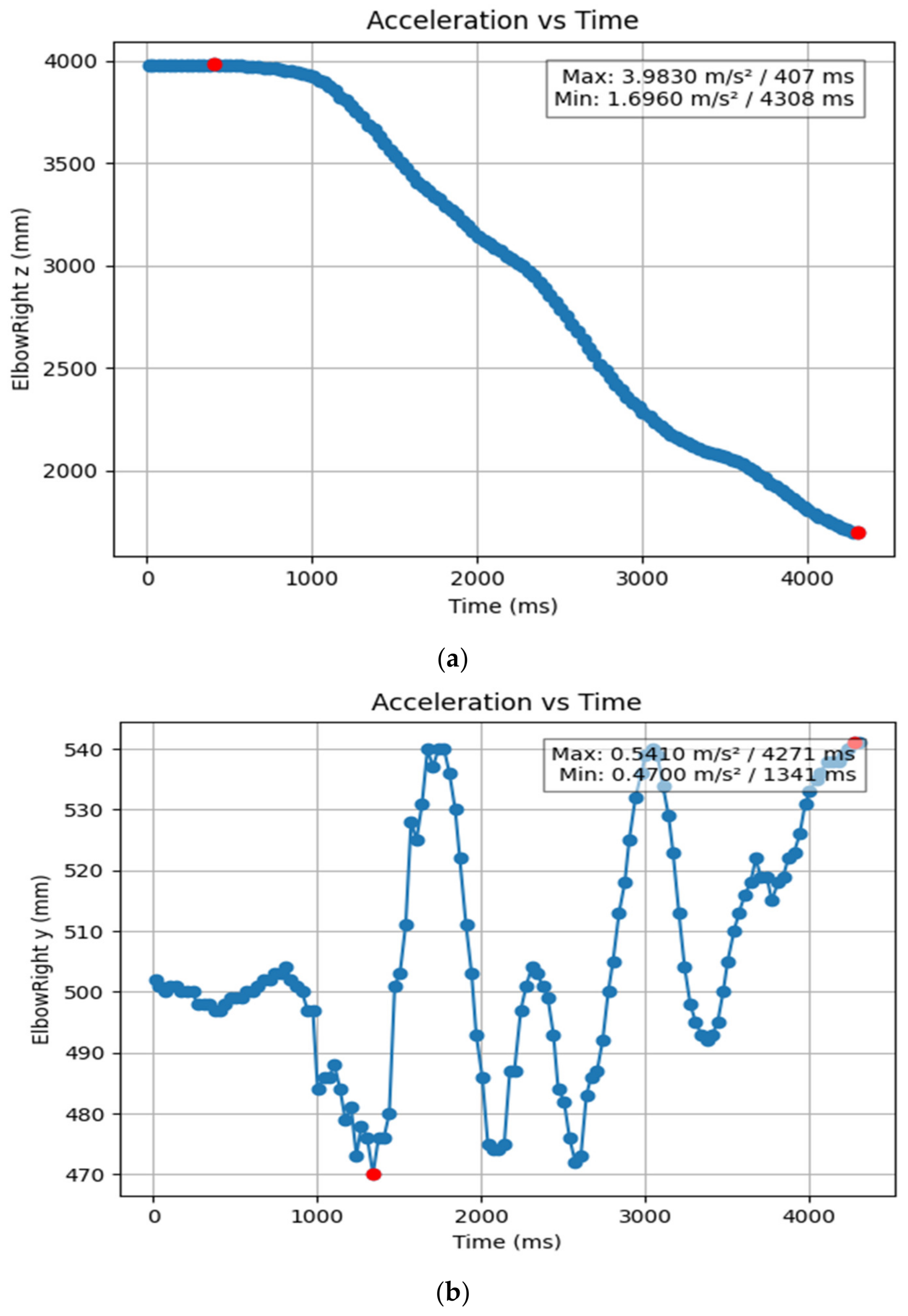
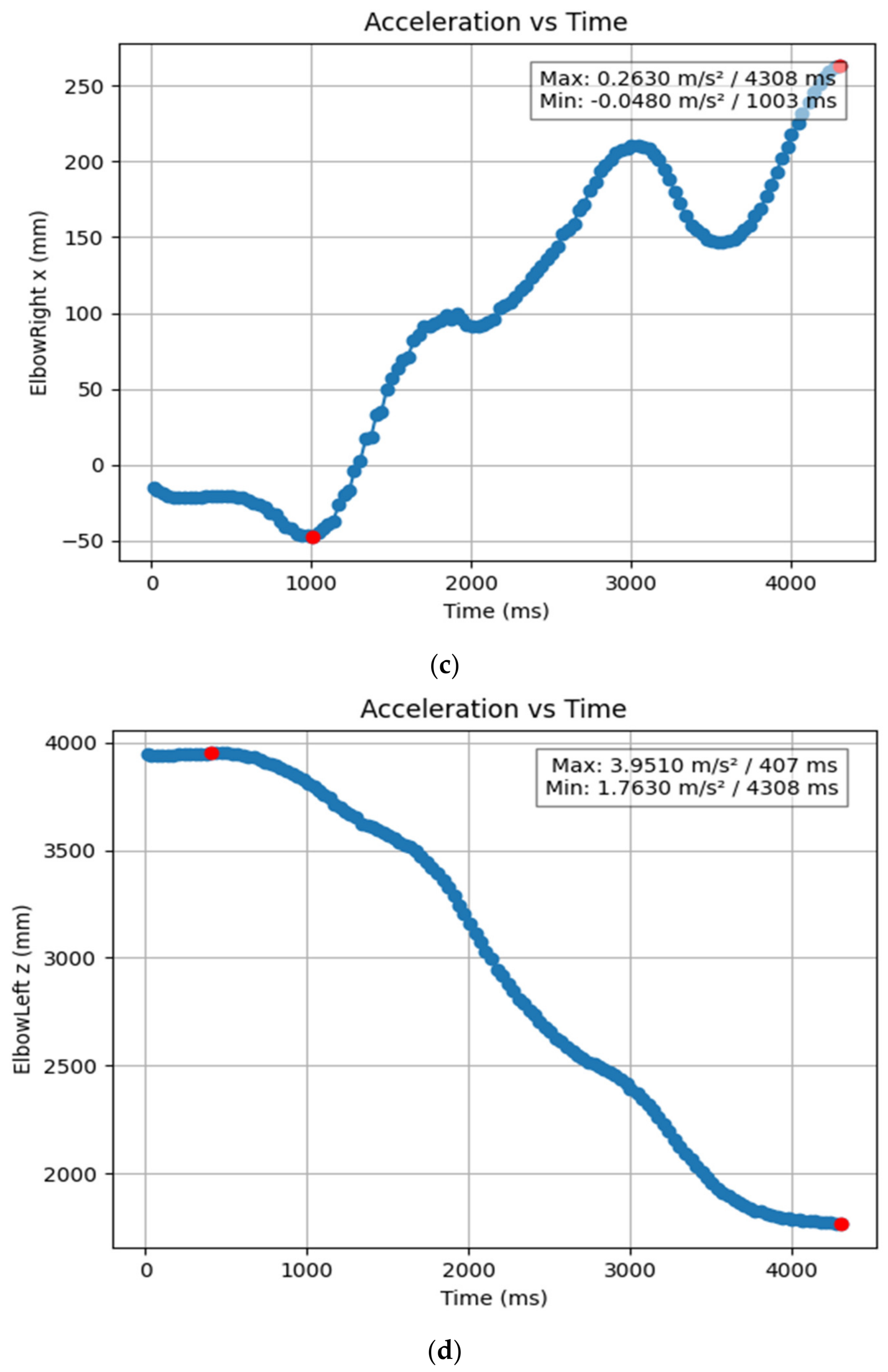
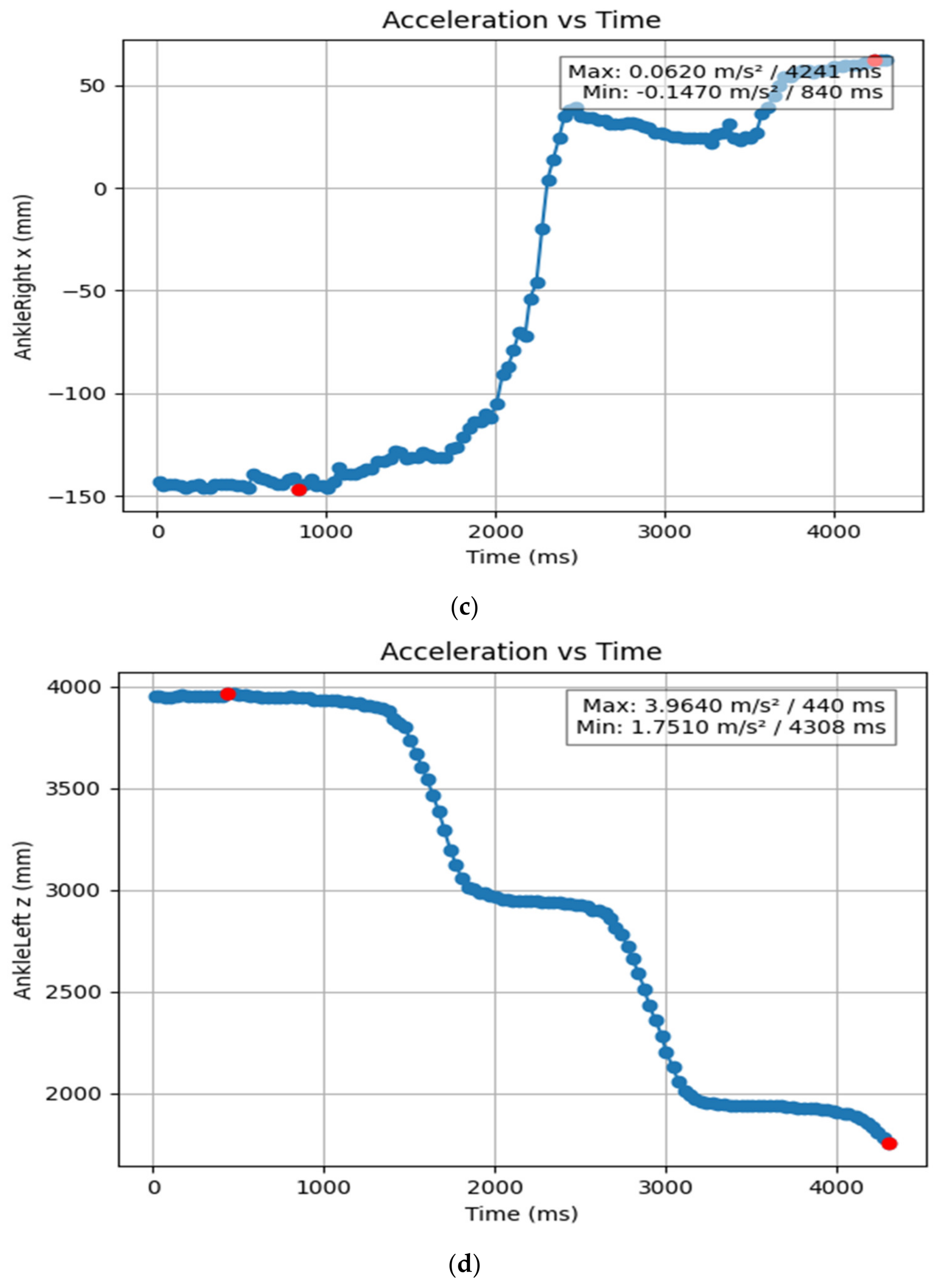
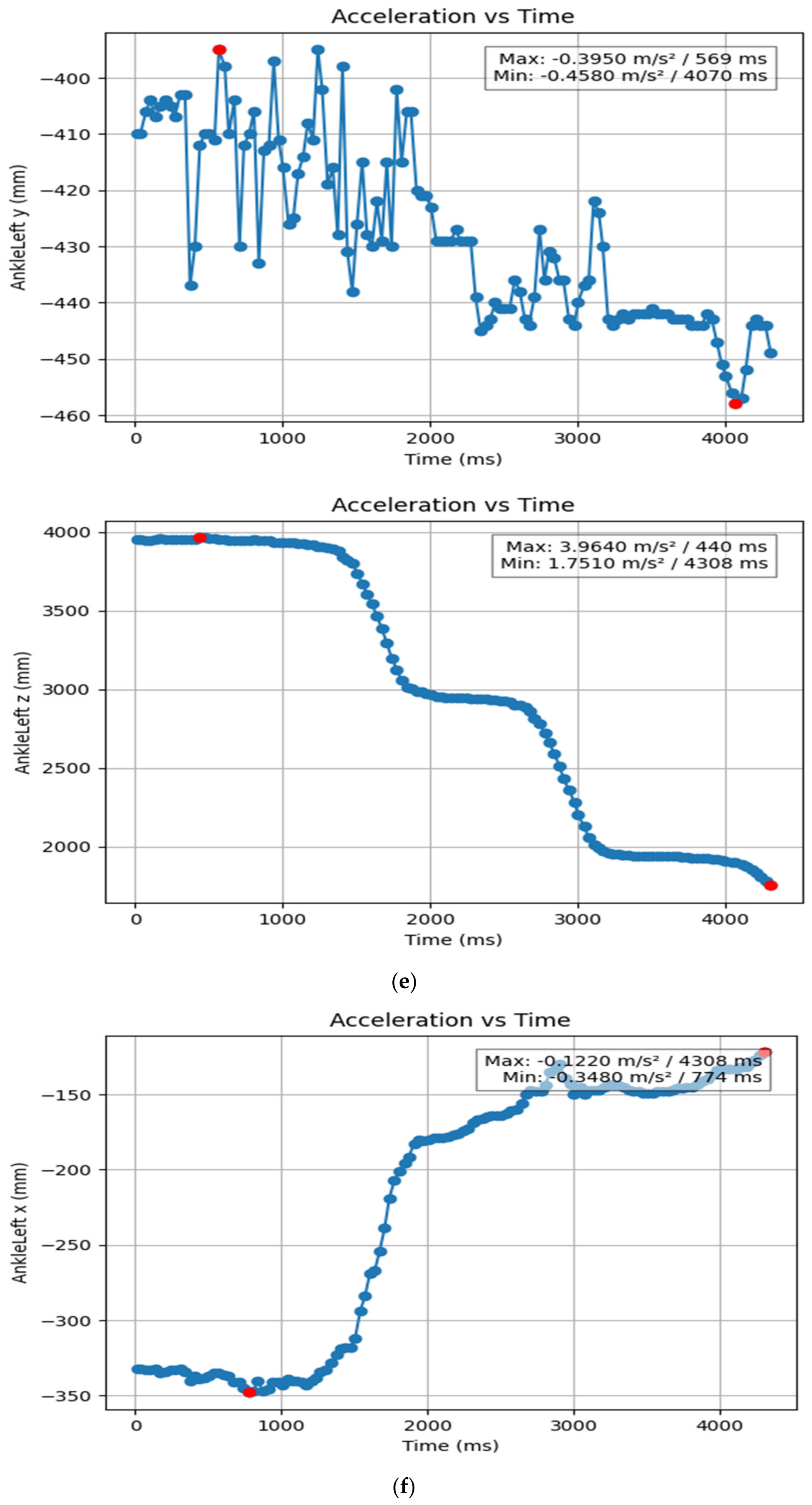
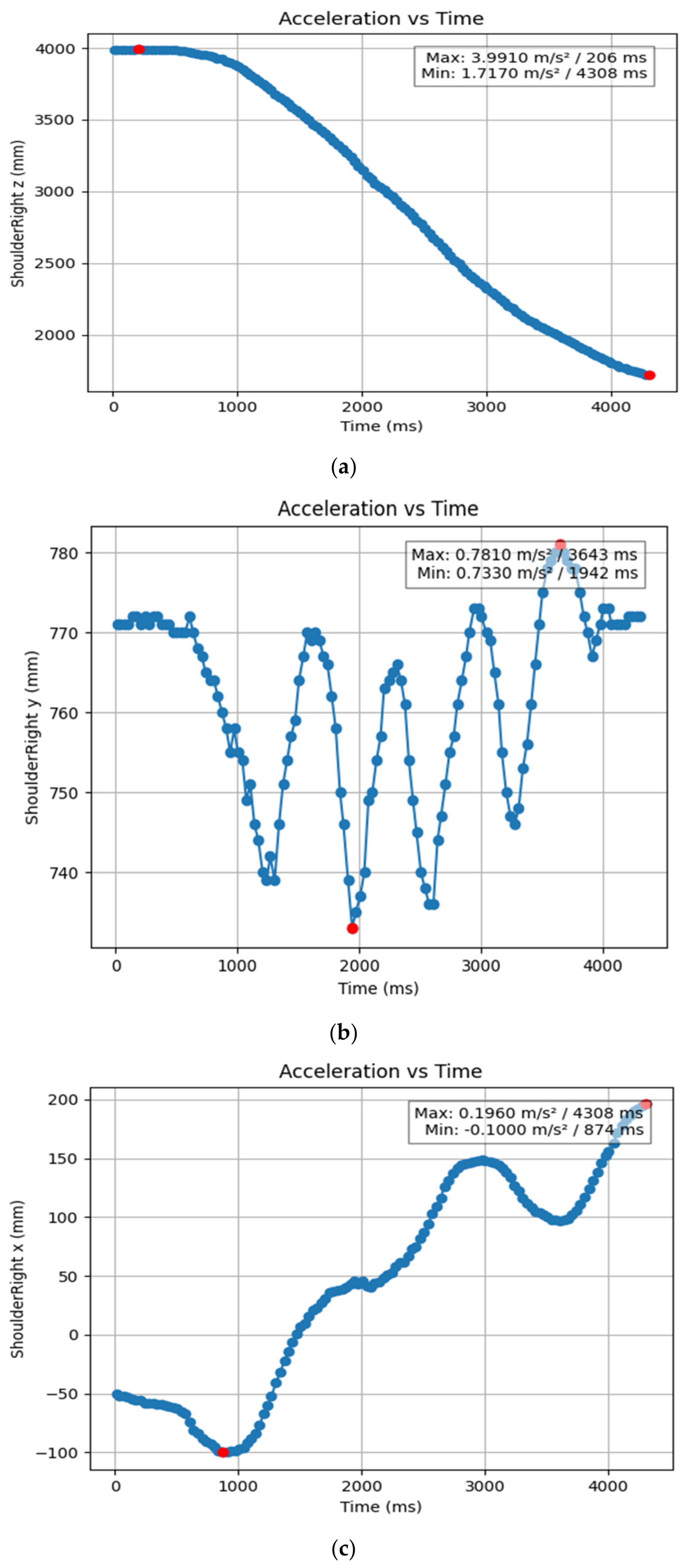
3.1.2. Acceleration Showing Maximum and Minimum Points to Various Angle Positions
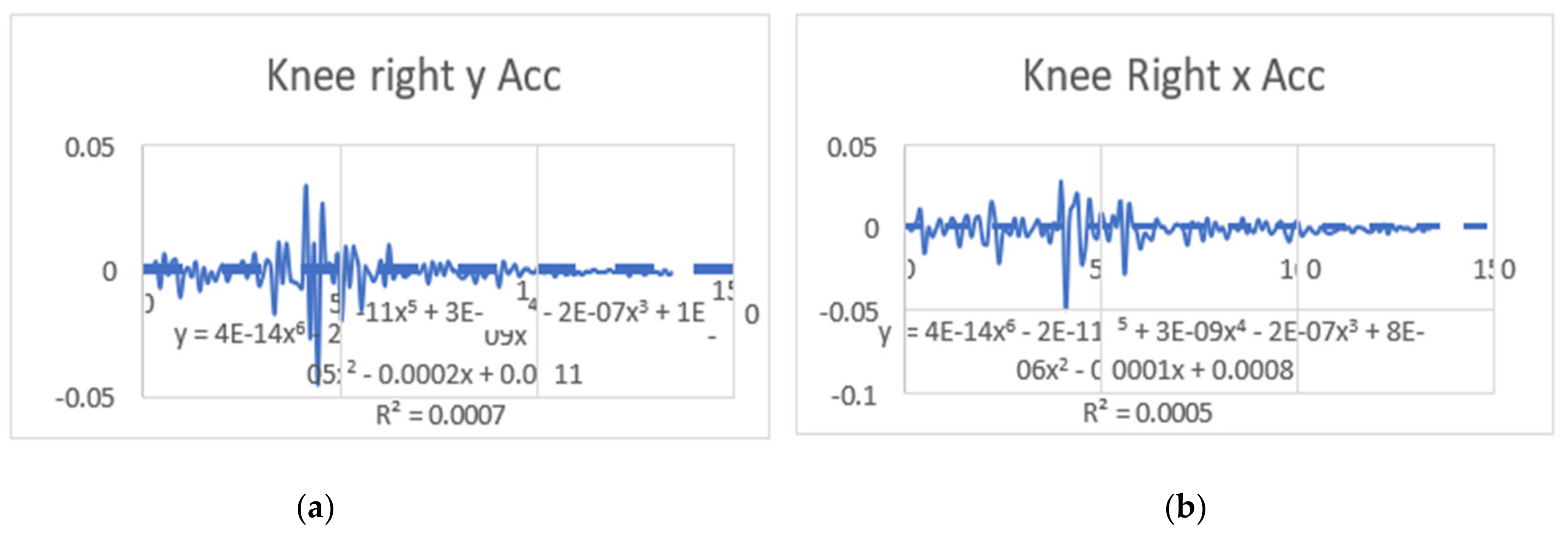
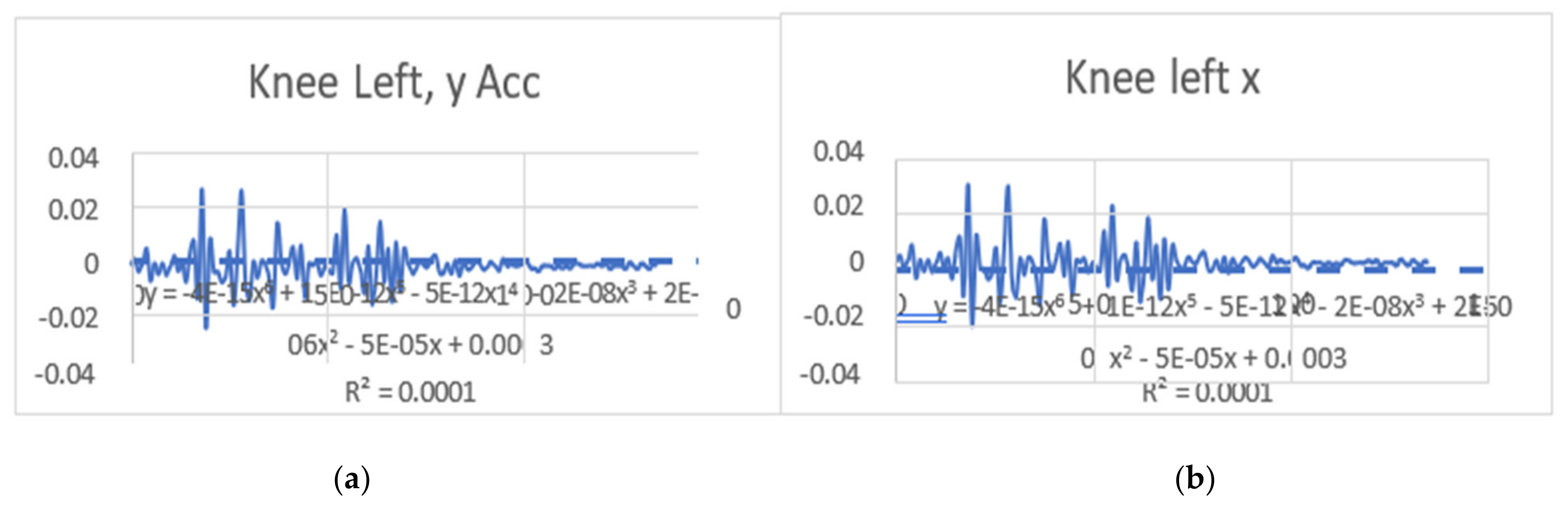
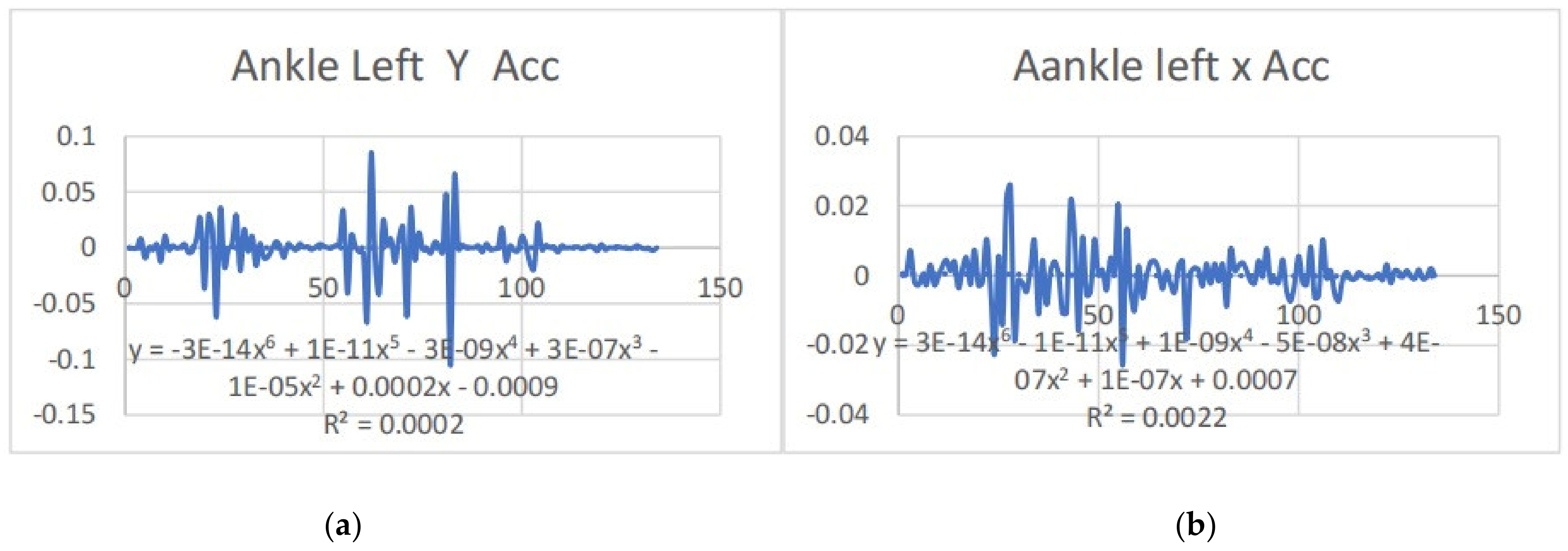
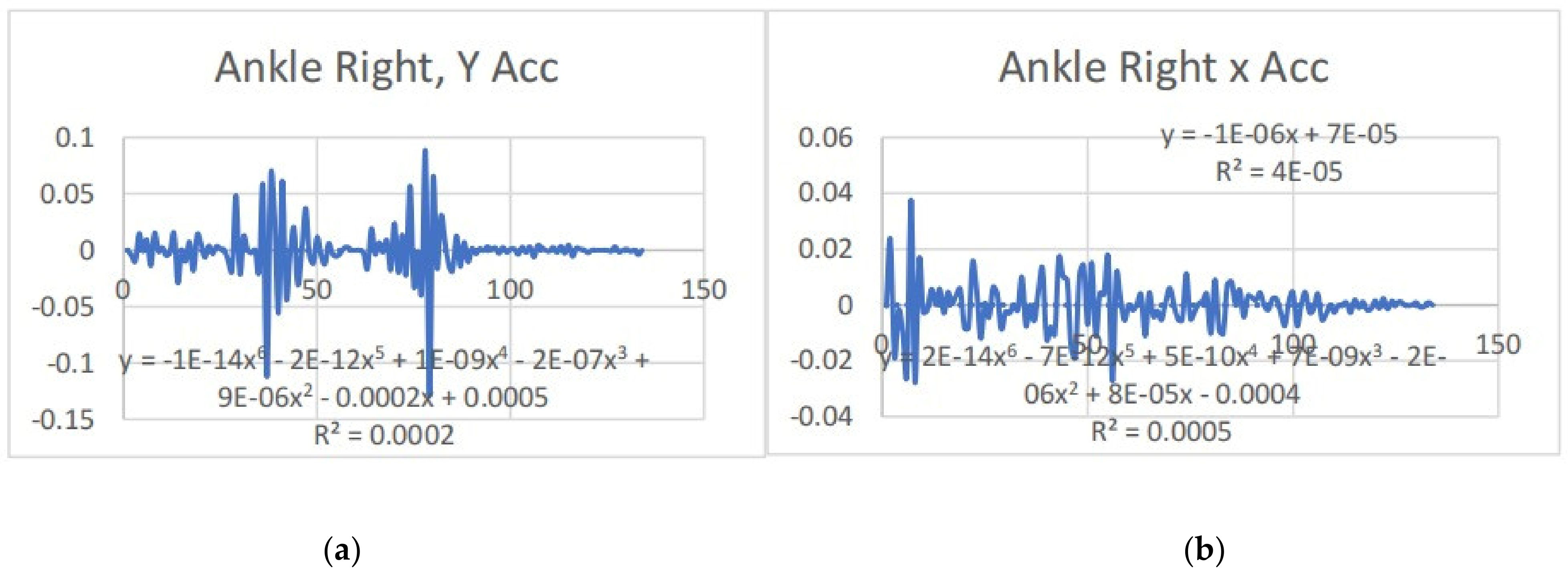
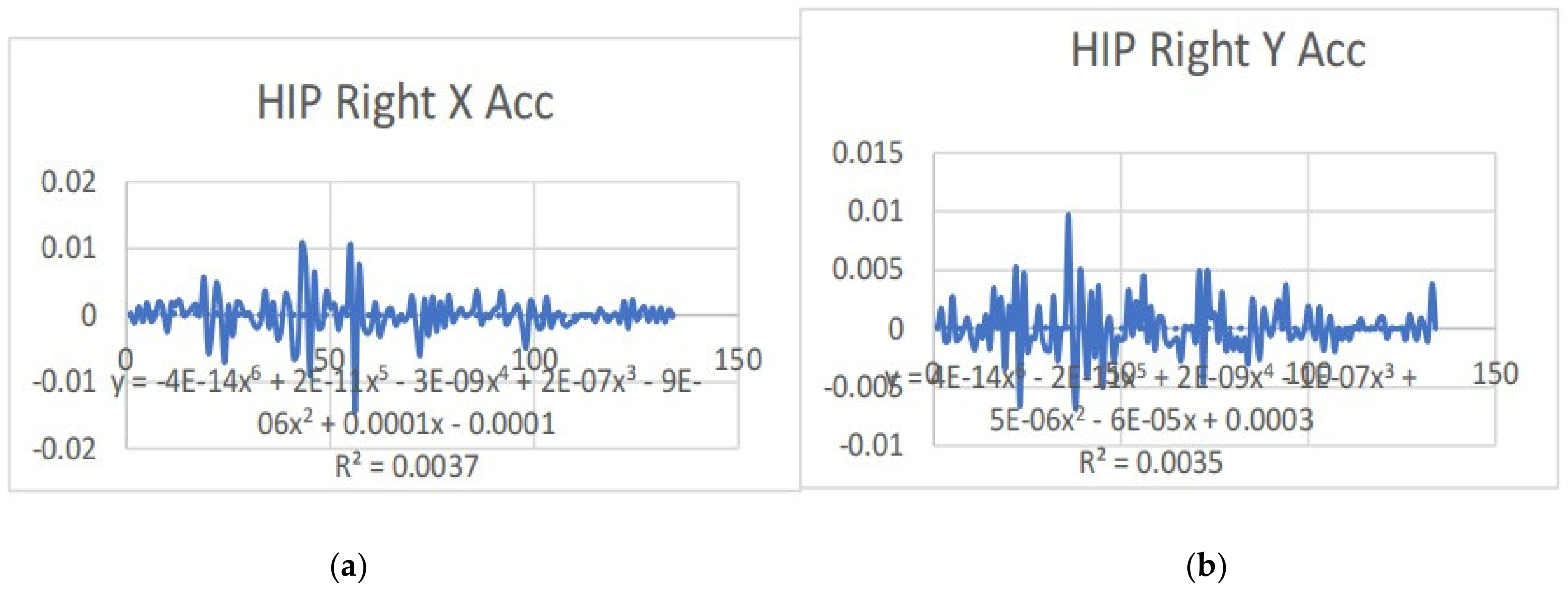
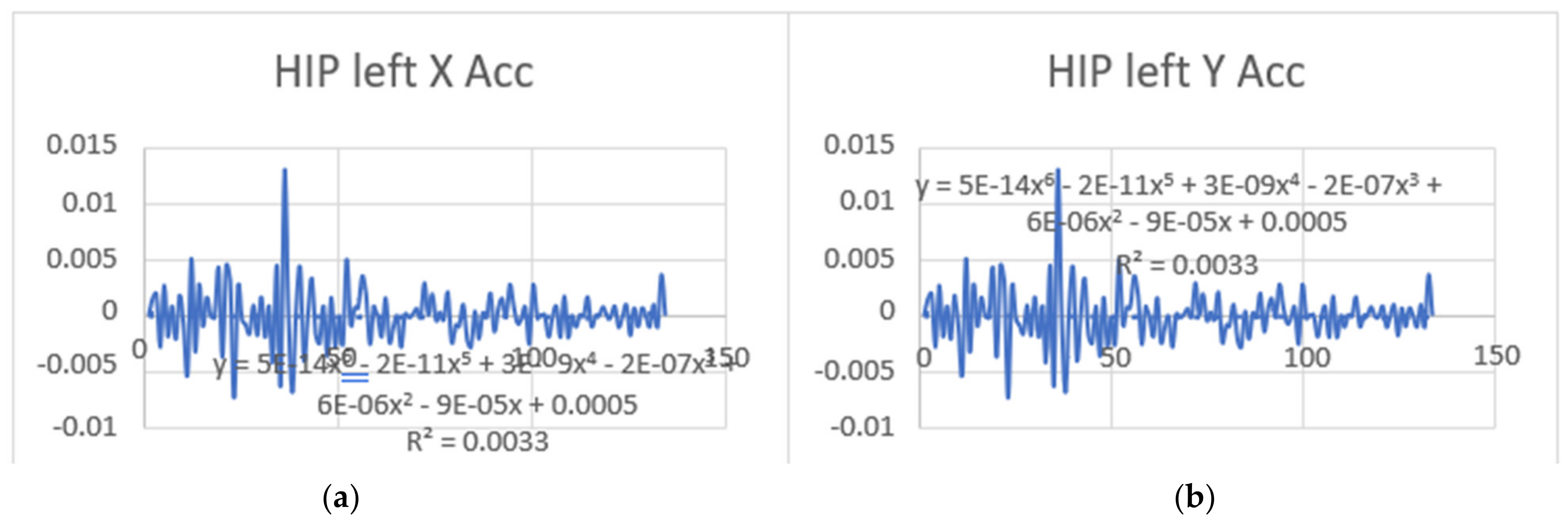
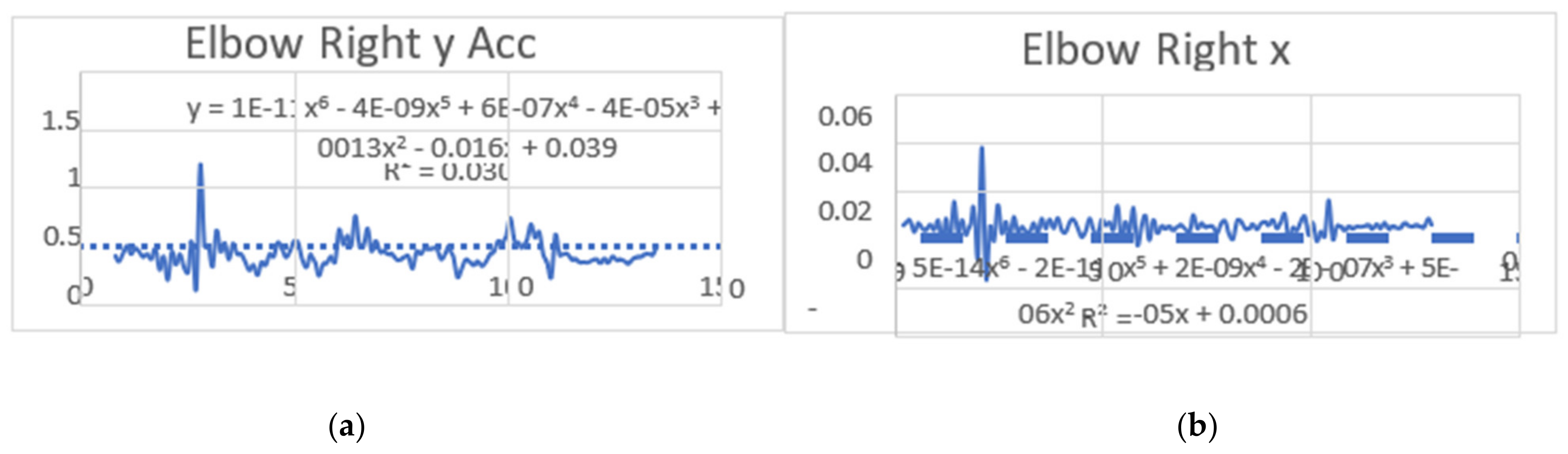
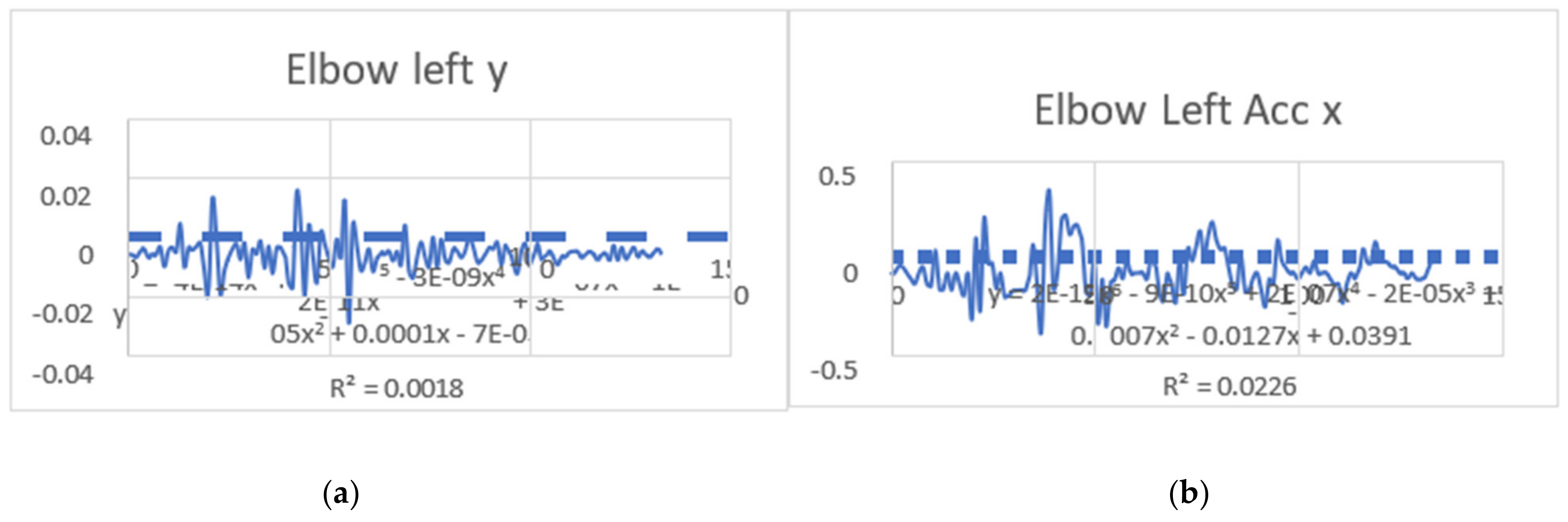
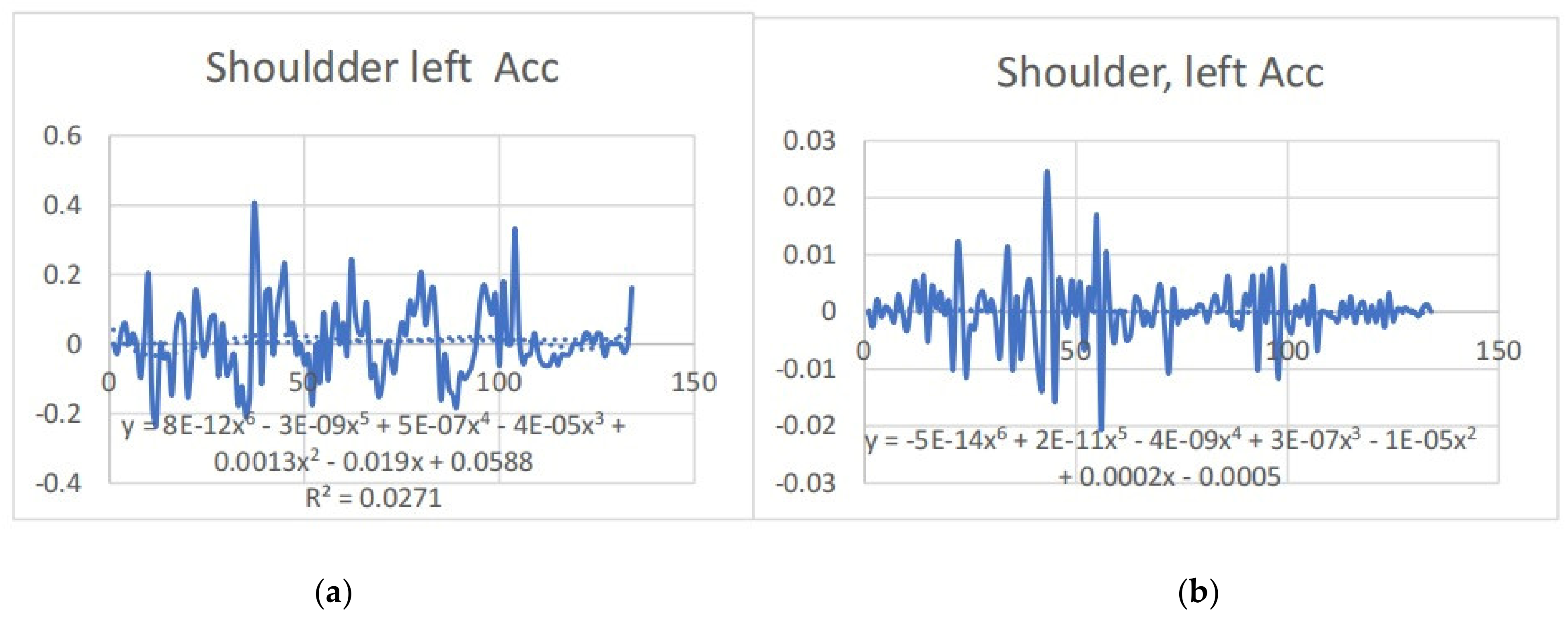
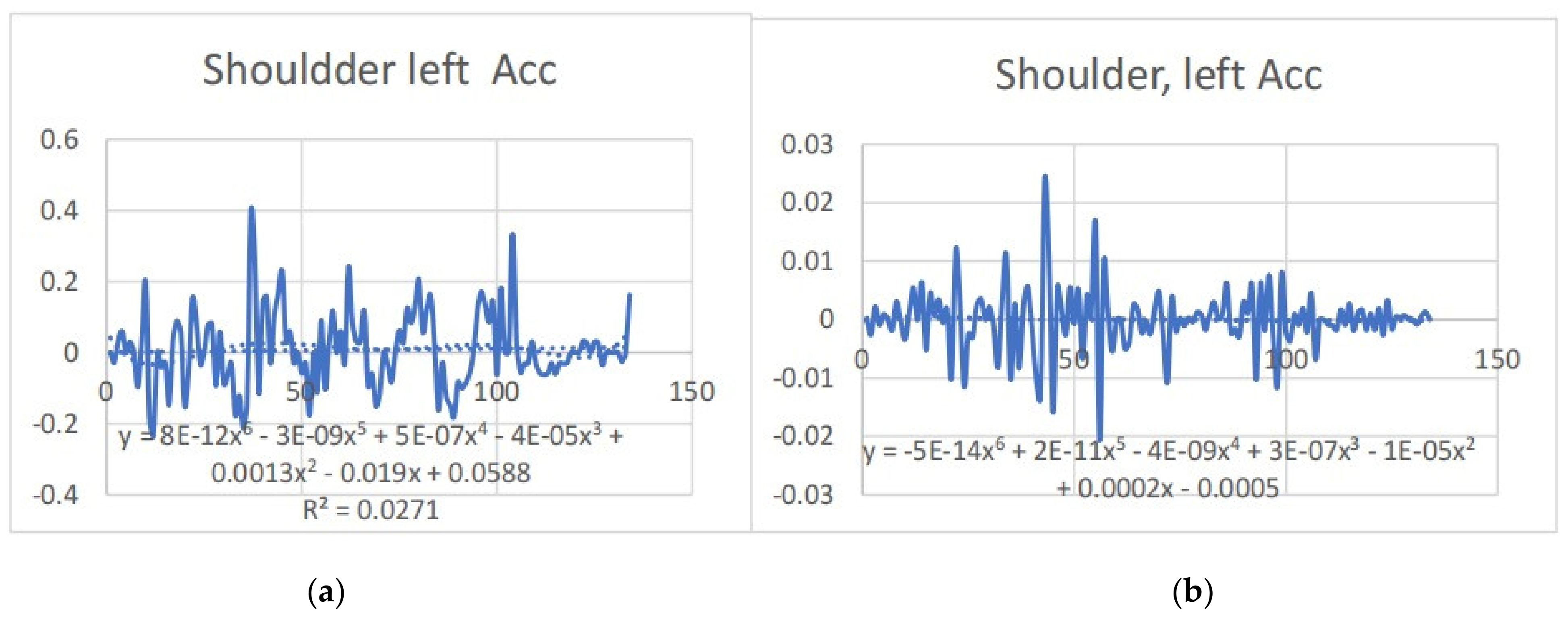
3.2. Acceleration Graphs with Regression Equation Lines
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Winter, D.A. The Biomechanics and Motor Control of Human Gait: Normal, Elderly, and Pathological; University of Waterloo Press: Waterloo, ON, Canada, 1991. [Google Scholar]
- Kadaba, M.P.; Ramakrishnan, H.K.; Wootten, M.E. Measurement of lower extremity kinematics during level walking. J. Orthop. Res. 1990, 8, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Gage, J.R. Gait analysis. An essential tool in the treatment of cerebral palsy. Clin. Orthop. Relat. Res. 1993, 264, 24–30. [Google Scholar] [CrossRef]
- Cappozzo, A.; Catani, F.; Della Croce, U.; Leardini, A. Position and orientation in space of bones during movement: Anatomical frame definition and determination. Clin. Biomech. 1995, 10, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Whittle, M.W. Gait Analysis: An Introduction; Butterworth-Heinemann: Oxford, UK, 1996. [Google Scholar]
- Baker, R. Gait analysis methods in rehabilitation. J. Neuroeng. Rehabil. 2007, 4, 1. [Google Scholar] [CrossRef]
- Zatsiorsky, V.M.; Seluyanov, V.N. The mass and inertia characteristics of the main segments of the human body. Biomechanics 1983, VIII-B, 1152–1159. [Google Scholar]
- Baker, R.; Rodda, J. Normal gait and gait analysis. In Management of Spinal Cord Injuries; Springer: Berlin/Heidelberg, Germany, 2002; pp. 153–172. [Google Scholar]
- Karamanidis, K.; Arampatzis, A. Biomechanical strategies of muscle-tendon interaction in walking and running: Implications for modeling and experimental studies. J. Biomech. 2015, 48, 2186–2192. [Google Scholar]
- Winter, D.A. Energy generation and absorption at the ankle and knee during fast, natural, and slow cadences. Clin. Orthop. Relat. Res. 1983, 175, 147–154. [Google Scholar] [CrossRef]
- Chiu, M.C.; Wang, M.-J. The effect of gait speed and gender on perceived exertion, muscle activity, joint motion of lower extremity, ground reaction force and heart rate during normal walking. Gait Posture 2007, 25, 385–392. [Google Scholar] [CrossRef]
- Perry, J.; Burnfield, J.M. Gait Analysis: Normal and Pathological Function; SLACK Incorporated: West Deptford, NJ, USA, 2010. [Google Scholar]
- Smith, P.J.; Gerrie, B.J.; Varner, K.E. Kinematic and kinetic comparison of ballet turns (pirouettes) on flat and relevé. J. Danc. Med. Sci. 2015, 19, 15–22. [Google Scholar] [CrossRef]
- Zeni, J.A., Jr.; Higginson, J. Differences in gait parameters between healthy subjects and persons with moderate and severe knee osteoarthritis: A result of altered walking speed? Clin. Biomech. 2009, 24, 372–378. [Google Scholar] [CrossRef]
- Ferber, R.; Osis, S.T. Etiology of iliotibial band friction syndrome in distance runners. Physiother. Theory Pract. 2015, 31, 566–581. [Google Scholar]
- Kirtley, C. Clinical Gait Analysis: Theory and Practice; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Novacheck, T.F. The biomechanics of running. Gait Posture 1998, 7, 77–95. [Google Scholar] [CrossRef] [PubMed]
- Della Croce, U.; Cappozzo, A.; Kerrigan, D.C.; Collins, J.J. Popliteal angle behavior during gait: A clinical and ex-perimental investigation. Gait Posture 1999, 9, 1–9. [Google Scholar]
- Rose, J.; Gamble, J.G.; Medeiros, J. Walking in cerebral palsy. Gait Posture 1993, 1, 11–20. [Google Scholar] [CrossRef]
- Sutherland, D.H.; Davids, J.R. Common gait abnormalities of the knee in cerebral palsy. Clin. Orthop. Relat. Res. 1993, 288, 139–147. [Google Scholar]
- Davis, R.B.; Ounpuu, S.; Tyburski, D.; Gage, J.R. A gait analysis data collection and reduction technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Burwitz, L.; Moore, P.M.; Wilkinson, D.M. Physiological and performance-related assessment of performance-related factors in sport. J. Sports Sci. 1994, 12, 93–109. [Google Scholar] [CrossRef] [PubMed]
- Waters, R.L.; Mulroy, S.; Gronley, J.K. The energy expenditure of normal and pathologic gait. Gait Posture 2003, 17, 264–268. [Google Scholar] [CrossRef]
- Hansford, H.J.; Cashin, A.G.; Wewege, M.A.; Ferraro, M.C.; McAuley, J.H.; Jones, M.D. Evaluation of journal policies to increase promotion of transparency and openness in sport science research. J. Sci. Med. Sport 2022, 25, 192–194. [Google Scholar] [CrossRef]
- Arnold, E.M.; Ward, S.R.; Lieber, R.L.; Delp, S.L. A model of the lower limb for analysis of human movement. Ann. Biomed. Eng. 2009, 38, 269–279. [Google Scholar] [CrossRef]
- Perry, J. Gait analysis: Normal and pathological function. J. Pediatr. Orthop. 1992, 12, 815–817. [Google Scholar] [CrossRef]
- Williams, S.J.; Kendall, L.R. A profile of sports science research (1983–2003). J. Sci. Med. Sport 2007, 10, 193–200. [Google Scholar] [CrossRef] [PubMed]

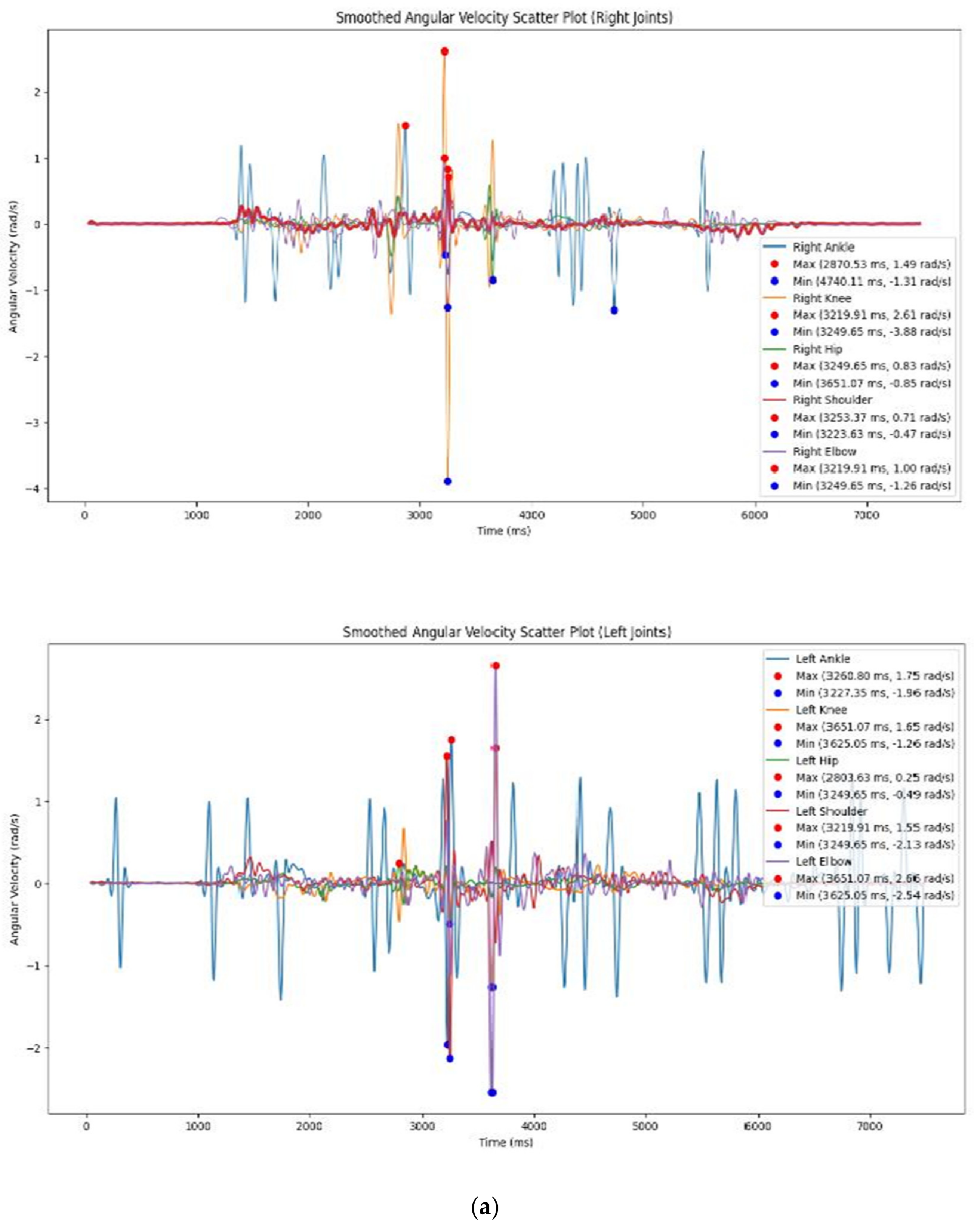
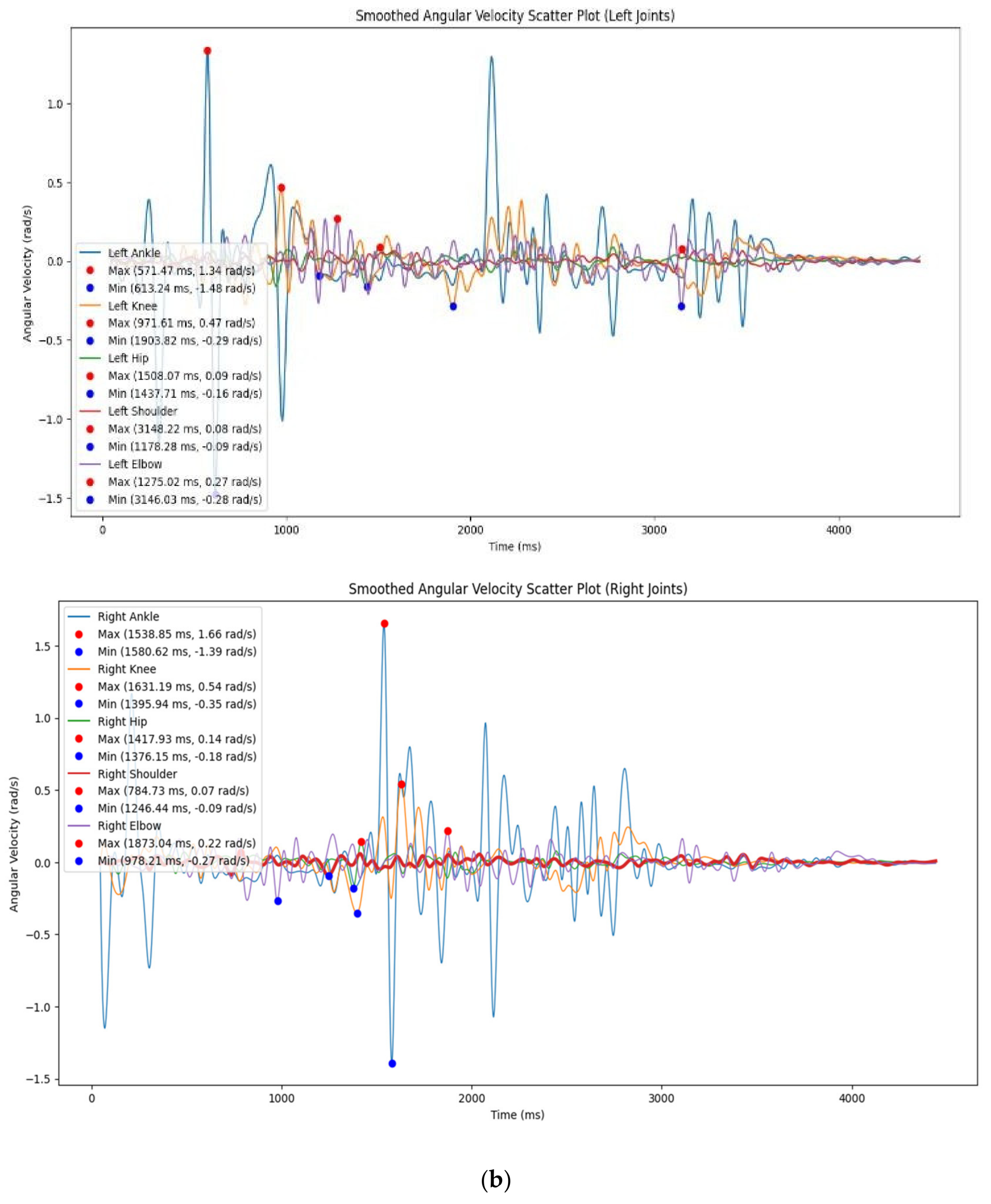
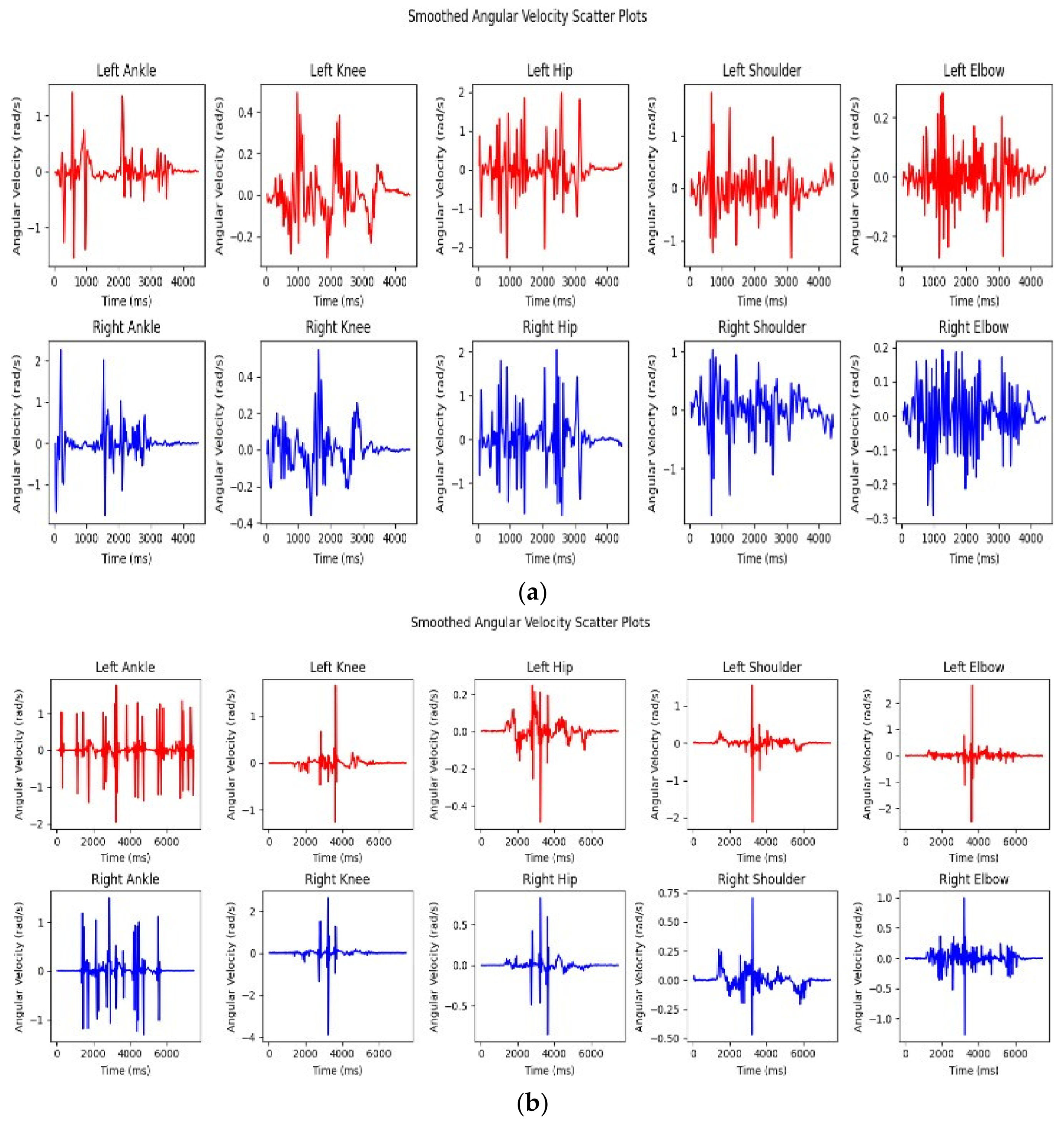













| Non-Dancer | Gait | Angular Velocity_Min | Angular_Velocity Max | Time_Min | Time_Max |
|---|---|---|---|---|---|
| Left Shoulder | −2.13 | 1.55 | 3249.65 | 3219.91 | |
| Right Shoulder | −0.47 | 0.71 | 3223.63 | 3253.37 | |
| Left Elbow | −2.54 | 2.66 | 3625.05 | 3651.07 | |
| Right Elbow | −1.26 | 1 | 3249.65 | 3219.91 | |
| Left Hip | −0.49 | 0.25 | 3249.65 | 2803.63 | |
| Right Hip | −0.85 | 0.83 | 3651.07 | 3249.65 | |
| Left Knee | −1.26 | 1.65 | 3625.05 | 3651.07 | |
| Right Knee | −3.88 | 2.61 | 3249.65 | 3219.91 | |
| Left Ankle | −1.96 | 1.75 | 3227.35 | 3260.8 | |
| Right Ankle | −1.31 | 1.49 | 4740.11 | 2870.53 |
| Dancer | Gait | Angular Velocity_min | Angular Velocity_max | Time_min | Tim_max |
|---|---|---|---|---|---|
| Left Shoulder | −0.09 | 0.08 | 1178.28 | 3148.22 | |
| Right Sholder | −0.09 | 0.07 | 1246.44 | 784.73 | |
| Left Elbow | −0.28 | 0.27 | 3146.03 | 1275.02 | |
| Right Elbow | −0.27 | 0.22 | 978.21 | 1873.04 | |
| Left Hip | −0.16 | 0.09 | 1437.71 | 1508.07 | |
| Right Hip | −0.18 | 0.14 | 1376.15 | 1417.93 | |
| Left Knee | −0.29 | 0.47 | 1903.82 | 971.61 | |
| Right Knee | −0.35 | 0.54 | 1395.94 | 1631.19 | |
| Left Ankle | −1.48 | 1.34 | 613.24 | 571.47 | |
| Right Ankle | −1.39 | 1.66 | 1580.62 | 1538.85 |
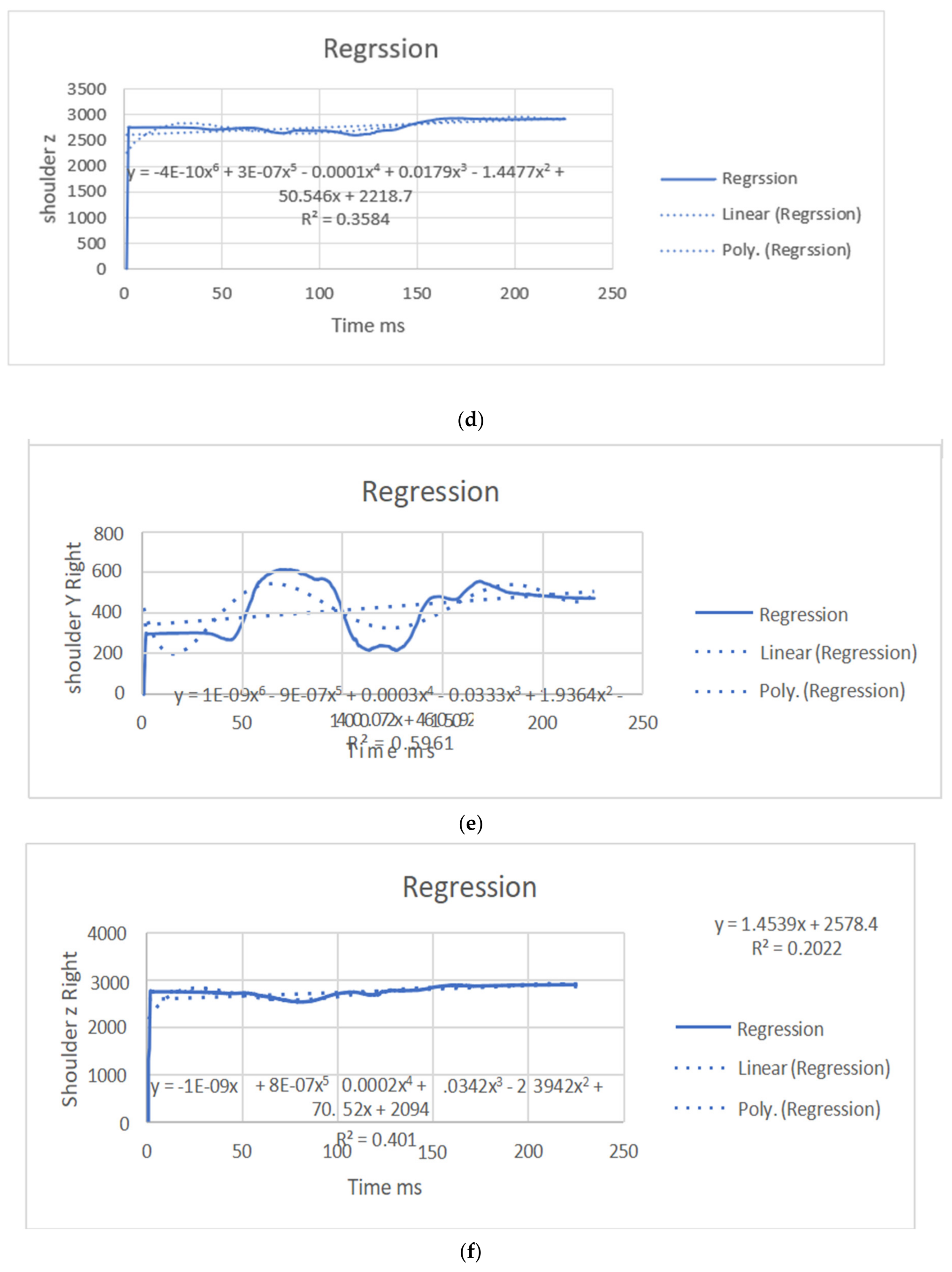
| Left | Poly-Regression Equation | Slope | Right | Poly-Regression Equation | Slope |
|---|---|---|---|---|---|
| Shoulder x | y = 1E-09 × 6 − 1E-06 × 5 + 0.0003x4 − 0.0352x3 + 2.1241x2 − 47.302x + 193.92 R2 = 0.6182 | y = 0.6507x − 3.006 R2 = 0.1171 | shoulder x | y = 1E-09x6 − 9E-07x5 + 0.0003x4 − 0.0333x3 + 1.9364x2 − 40.072x + 460.92 | y = 0.7381x + 337.02 R2 = 0.1457 |
| Shoulder y | y = 1E-10x6 − 9E-08x5 + 2E-05x4 − 0.0021x3 + 0.0979x2 − 0.099x + 250.78 R2 = 0.3963 | y = −0.0319x + 320.66 R2 = 0.0012 | shoulder y | y = 1E-09x6 − 9E-07x5 + 0.0003x4 − 0.0333x3 + 1.9364x2 − 40.072x + 460.92 R2 = 0.5961 | y = 0.7381x + 337.02 R2 = 0.1457 |
| Shoulder z | y = −4E-10x6 + 3E-07x5 − 0.0001x4 + 0.0179x3 − 1.4477x2 + 50.546x + 2218.7 R2 = 0.3584 | y = 1.3928x + 2620.9 R2 = 0.1822 | shoulder y | y = −1E-09x6 + 8E-07x5 − 0.0002x4 + 0.0342x3 − 2.3942x2 + 70.852x + 2094.2 | y = 1.4539x + 2578.4 R2 = 0.2022 |
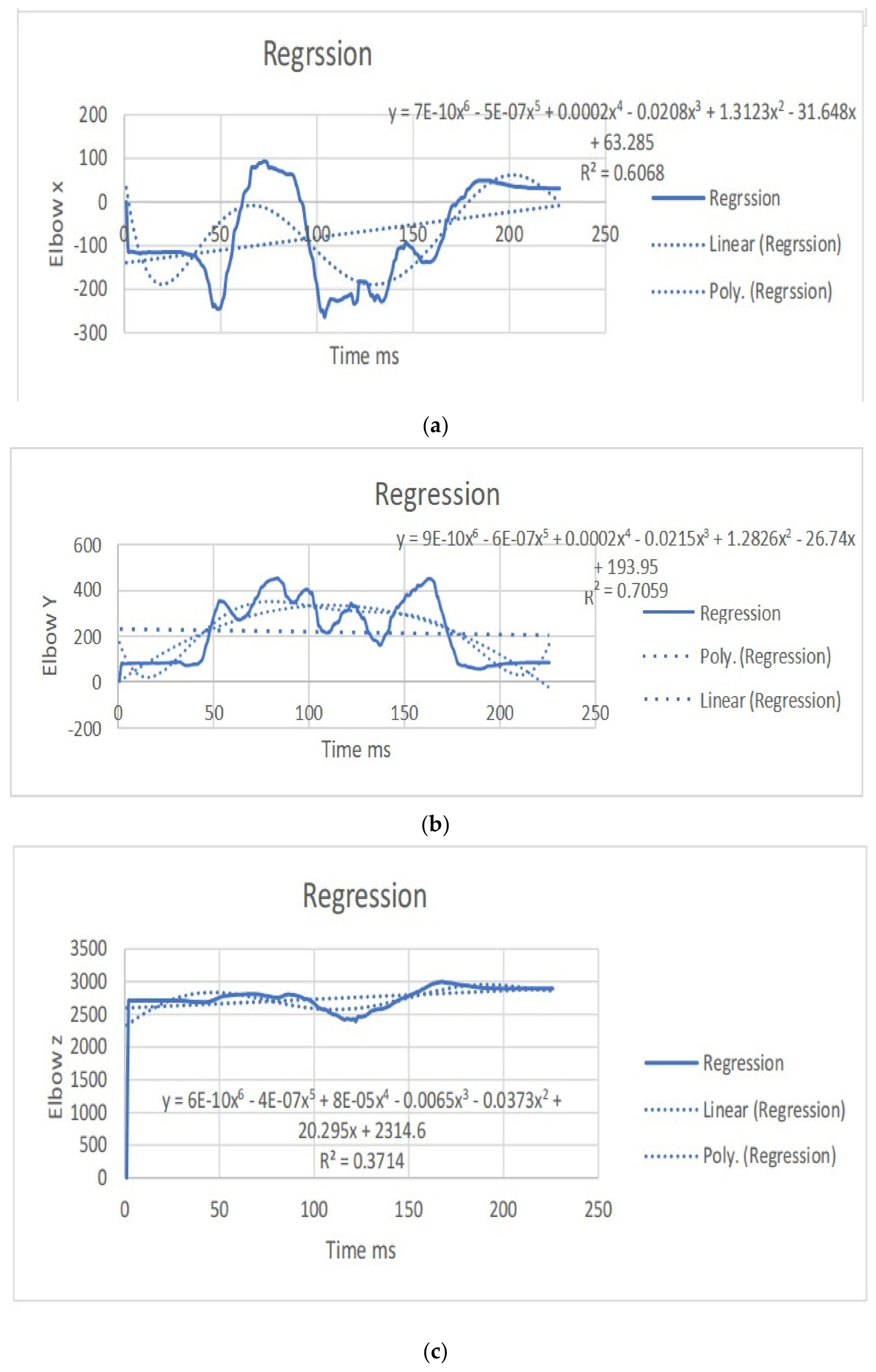
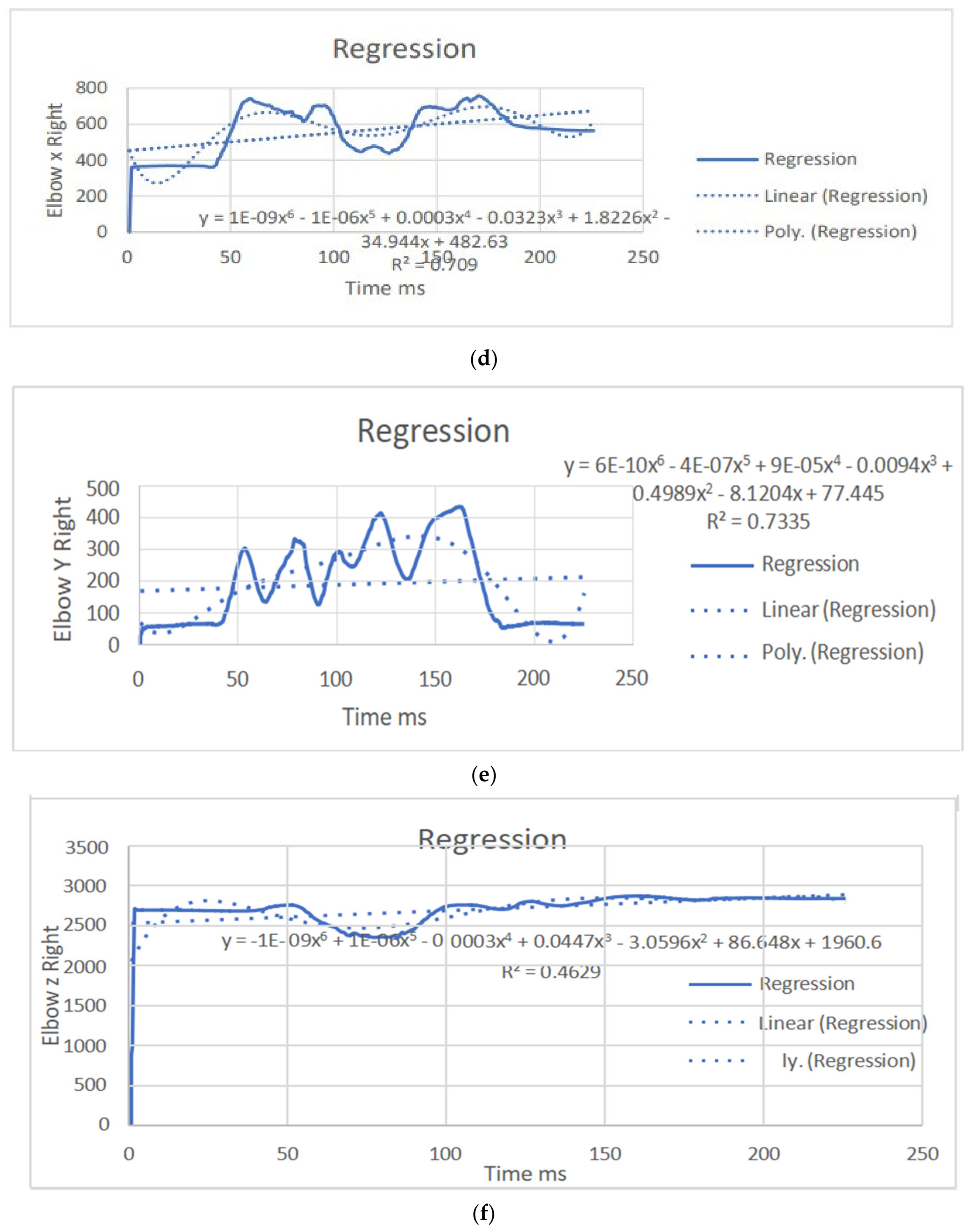
| Elbow x | y = 7E-10x6 − 5E-07x5 + 0.0002x4 − 0.0208x3 + 1.3123x2 − 31.648x + 63.285 R2 = 0.6068 | y = 0.5824x − 139.74 R2 = 0.1299 | elbow x | y = 1E-09x6 − 1E-06x5 + 0.0003x4 − 0.0323x3 + 1.8226x2 − 34.944x + 482.63 R2 = 0.709 | y = 0.9853x + 451.97 R2 = 0.2351 |
| Elbow y | y = 9E-10x6 − 6E-07x5 + 0.0002x4 − 0.0215x3 + 1.2826x2 − 26.74x + 193.95 R2 = 0.7059 | y = − 0.1198x + 229.51 R2 = 0.0033 | elbow y | y = 6E-10x6 − 4E-07x5 + 9E-05x4 − 0.0094x3 + 0.4989x2 − 8.1204x + 77.445 R2 = 0.7335 | y = 0.194x + 168.92 R2 = 0.0102 |
| Elbow z | y = 6E-10x6 − 4E-07x5 + 8E-05x4 − 0.0065x3 − 0.0373x2 + 20.295x + 2314.6 R2 = 0.3714 | y = 1.3233x + 2598.5 R2 = 0.137 | elbow z | y = −1E-09x6 + 1E-06x5 − 0.0003x4 + 0.0447x3 − 3.0596x2 + 86.648x + 1960.6 R2 = 0.4629 | y = 1.5943x + 2518.2 R2 = 0.2049 |
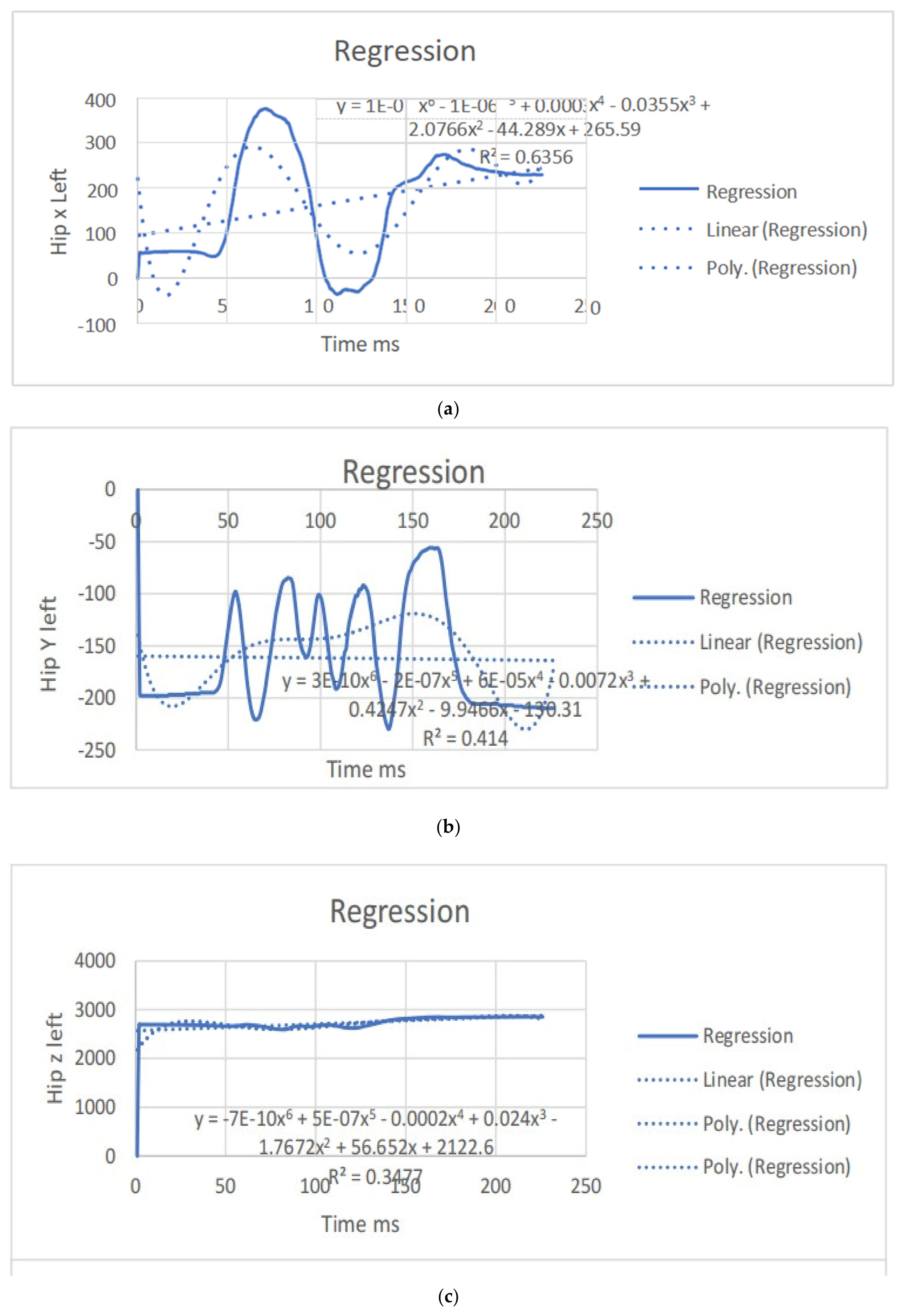
| Hip x | y = 1E-09x6 − 1E-06x5 + 0.0003x4 − 0.0355x3 + 2.0766x2 − 44.289x + 265.59 R2 = 0.6356 | y = 0.6655x + 93.149 R2 = 0.1287 | hip x | y = 1E-09x6 − 1E-06x5 + 0.0003x4 − 0.0332x3 + 1.9213x2 − 39.799x + 386.81 R2 = 0.6154 | y = 0.6643x + 252.81 R2 = 0.131 |
| Hip y | y = 3E-10x6 − 2E-07x5 + 6E-05x4 − 0.0072x3 + 0.4247x2 − 9.9466x − 130.31 R2 = 0.414 | y = − 0.0188x − 159.83 R2 = 0.0006 | hip y | y = 3E-10x6 − 2E-07x5 + 5E-05x4 − 0.0063x3 + 0.3608x2 − 8.2405x − 135.68 R2 = 0.3956 | y = −0.0023x − 160.38 R2 = 9E-06 |
| Hip z | y = −7E-10x6 + 5E-07x5 − 0.0002x4 + 0.024x3 − 1.7672x2 + 56.652x + 2122.6 R2 = 0.3477 | y = 1.3895x + 2566.4 R2 = 0.202 | hip x | y = −9E-10x6 + 7E-07x5 − 0.0002x4 + 0.0286x3 − 2.0299x2 + 62.143x + 2086.5 R2 = 0.3598 | y = 1.3919x + 2551.6 R2 = 0.2049 |
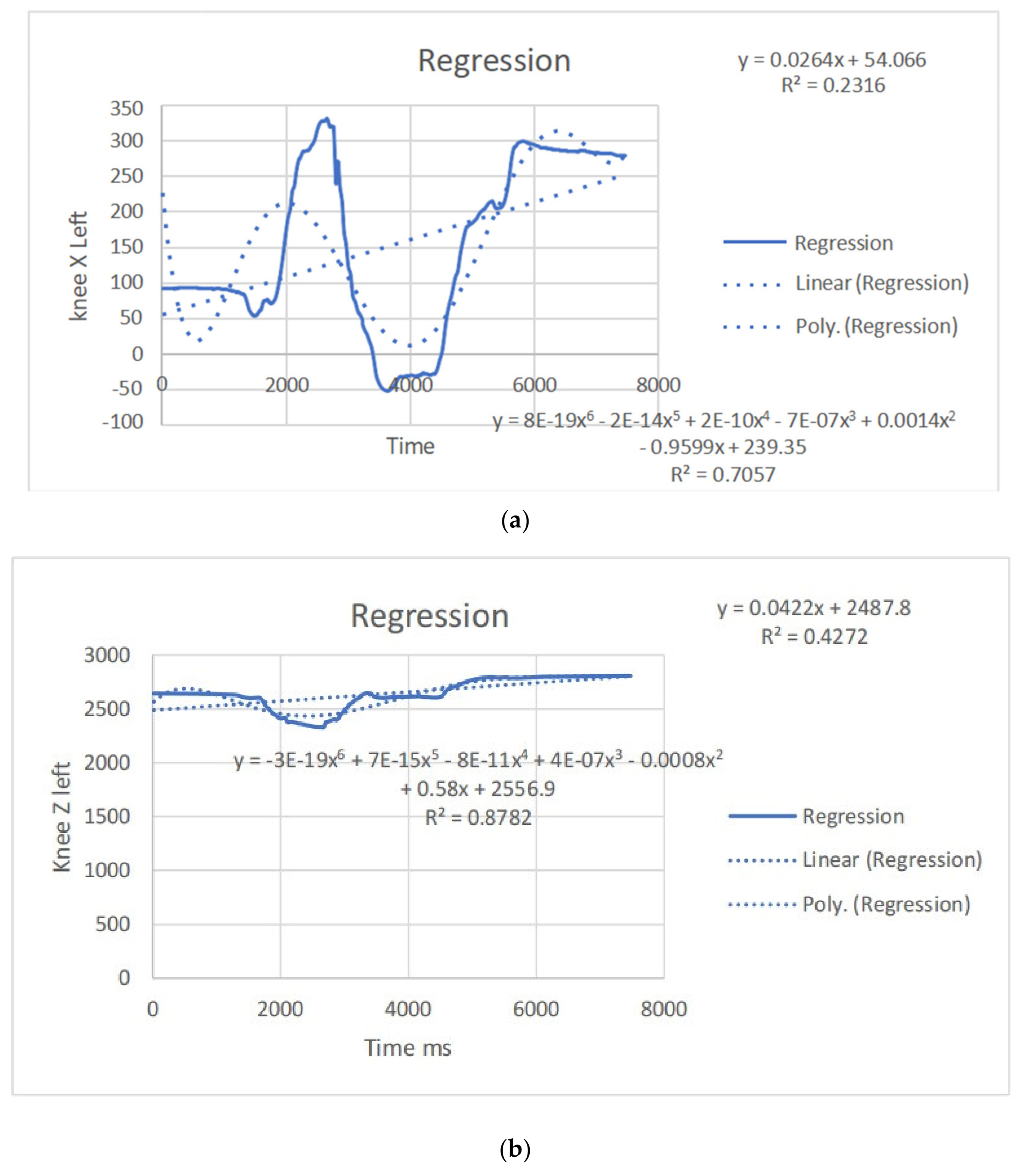
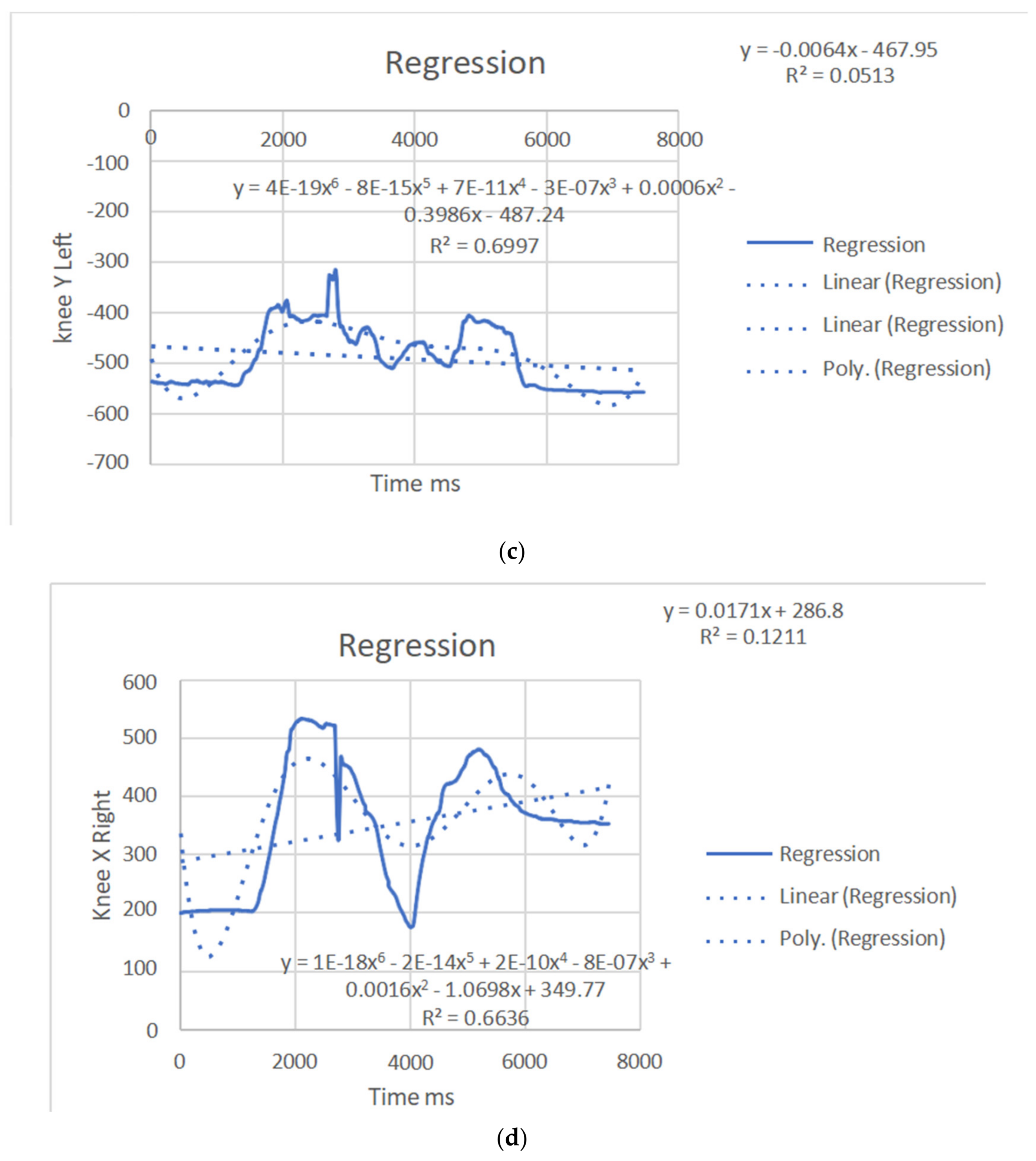
| Knee x | y = 8E-19x6 − 2E-14x5 + 2E-10x4 − 7E-07x3 + 0.0014x2 − 0.9599x + 239.35 R2 = 0.7057 | y = 0.0264x + 54.066 R2 = 0.2316 | knee x | y = 1E-18x6 − 2E-14x5 + 2E-10x4 − 8E-07x3 + 0.0016x2 − 1.0698x + 349.77 R2 = 0.6636 | y = 0.0171x + 286.8 R2 = 0.1211 |
| Knee y | y = 4E-19x6 − 8E-15x5 + 7E-11x4 − 3E-07x3 + 0.0006x2 − 0.3986x − 487.24 R2 = 0.6997 | y = − 0.0064x − 467.95 R2 = 0.0513 | knee y | y = −2E-20x6 + 6E-16x5 − 6E-12x4 + 2E-08x3 − 9E-06x2 + 0.0137x − 558.69 R2 = 0.774 | y = −0.0013x − 488.99 R2 = 0.0021 |
| Knee z | y = −3E-19x6 + 7E-15x5 − 8E-11x4 + 4E-07x3 − 0.0008x2 + 0.58x + 2556.9 R2 = 0.8782 | y = 0.0422x + 2487.8 R2 = 0.4272 | knee z | y = 5E-19x6 − 1E-14x5 + 9E-11x4 − 3E-07x3 + 0.0004x2 − 0.253x + 2678.1 R2 = 0.8788 | y = 0.0336x + 2517.1 R2 = 0.3122 |
| Ankle x | y = 8E-19x6 − 2E-14x5 + 2E-10x4 − 8E-07x3 + 0.0015x2 − 1.0479x + 249.71 R2 = 0.5062 | y = 0.0242x + 75.242 R2 = 0.151 | ankle x | y = 9E-19x6 − 2E-14x5 + 2E-10x4 − 7E-07x3 + 0.0013x2 − 0.8189x + 317.65 R2 = 0.5931 | y = 0.02x + 268.69 R2 = 0.1924 |
| Ankle y | y = 3E-19x6 − 8E-15x5 + 7E-11x4 − 3E-07x3 + 0.0006x2 − 0.4268x − 772.93 R2 = 0.6686 | y = − 0.0133x − 774.4 R2 = 0.2372 | ankle y | y = −2E-19x6 + 5E-15x5 − 4E-11x4 + 2E-07x3 − 0.0003x2 + 0.182x − 863.2 R2 = 0.6649 | y = −0.0077x − 802.72 R2 = 0.1081 |
| Ankle z | y = − 7E-19x6 + 2E-14x5 − 2E-10x4 + 8E-07x3 − 0.0016x2 + 1.1437x + 2440.4 R2 = 0.8088 | y = 0.0499x + 2428.1 R2 = 0.3469 | ankle z | y = 8E-19x6 − 2E-14x5 + 2E-10x4 − 6E-07x3 + 0.001x2 − 0.6664x + 2706.6 R2 = 0.7414 | y = 0.0307x + 2507.5 R2 = 0.2011 |
| Column Name | Time (m/s) Min | Time (m/s) Max | Acceleration of Min, mm/s2 | Acceleration of Max, mm/s2 |
|---|---|---|---|---|
| ShoulderLeft x (mm) | 3.674 | 2.407 | −0.118 | 0.294 |
| ShoulderLeft y (mm) | 4.517 | 4.039 | 0.237 | 0.43 |
| ShoulderLeft z (mm) | 3.875 | 5.639 | 2.614 | 2.947 |
| ElbowLeft x (mm) | 3.422 | 2.374 | −0.264 | 0.093 |
| ElbowLeft y (mm) | 6.238 | 2.738 | 0.054 | 0.45 |
| ElbowLeft z (mm) | 4.006 | 5.506 | 2.395 | 2.997 |
| ElbowRight x (mm) | 0.014 | 5.605 | 0.359 | 0.758 |
| ElbowRight y (mm) | 0.014 | 5.338 | 0.05 | 0.432 |
| ElbowRight z (mm) | 2.773 | 5.273 | 2.34 | 2.863 |
| ShoulderRight x (mm) | 4.174 | 2.24 | 0.215 | 0.612 |
| ShoulderRight y (mm) | 2.139 | 5.273 | 0.229 | 0.427 |
| ShoulderRight z (mm) | 2.607 | 7.275 | 2.526 | 2.89 |
| HipLeft x (mm) | 3.674 | 2.308 | −0.035 | 0.376 |
| HipLeft y (mm) | 4.517 | 5.238 | −0.23 | −0.056 |
| HipLeft z (mm) | 2.674 | 7.139 | 2.593 | 2.855 |
| KneeLeft x (mm) | 3.638 | 2.674 | −0.052 | 0.33 |
| KneeLeft y (mm) | 6.81 | 2.81 | −0.561 | −0.318 |
| KneeLeft z (mm) | 2.607 | 7.405 | 2.329 | 2.806 |
| AnkleLeft x (mm) | 3.121 | 2.674 | −0.103 | 0.452 |
| AnkleLeft y (mm) | 6.474 | 2.073 | −0.897 | −0.642 |
| AnkleLeft z (mm) | 2.207 | 7.308 | 2.194 | 2.786 |
| HipRight x (mm) | 3.674 | 2.308 | 0.132 | 0.528 |
| HipRight y (mm) | 4.517 | 5.206 | −0.228 | −0.045 |
| HipRight z (mm) | 2.674 | 7.34 | 2.561 | 2.839 |
| KneeRight x (mm) | 4.039 | 2.106 | 0.175 | 0.532 |
| KneeRight y (mm) | 6.774 | 3.488 | −0.562 | −0.37 |
| KneeRight z (mm) | 2.773 | 7.405 | 2.351 | 2.812 |
| AnkleRight x (mm) | 4.006 | 5.106 | 0.168 | 0.544 |
| AnkleRight y (mm) | 5.939 | 3.911 | −0.892 | −0.714 |
| ElbowRight x (mm) | 0.014 | 5.605 | 0.359 | 0.758 |
| Column Name | Time (m/s2) of Min | Time (m/s2) of Max | Acceleration of Min mm/s2 | Acceleration of Max, mm/s2 |
|---|---|---|---|---|
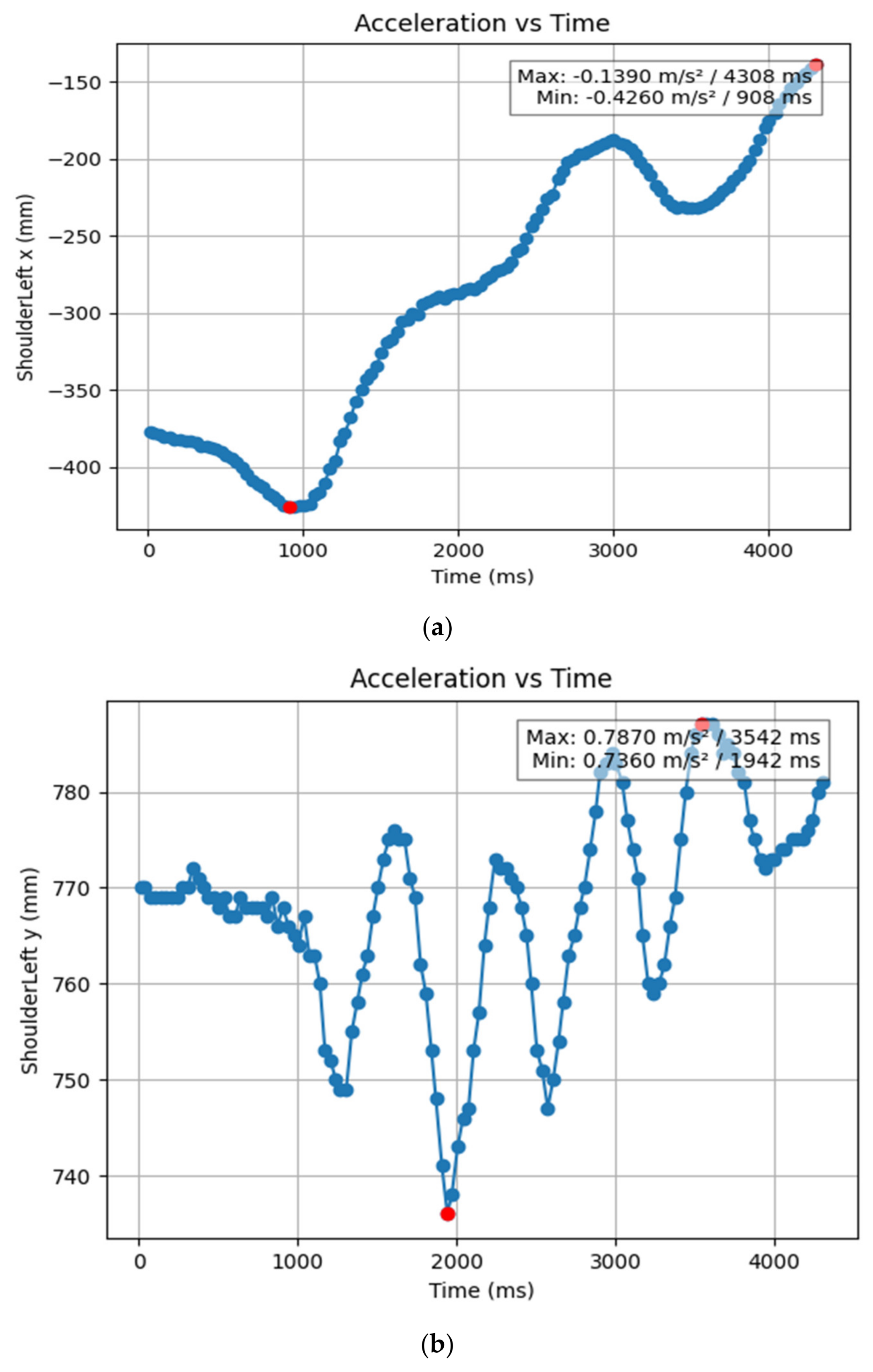
| ShoulderLeft x (mm) | 0.908 | 4.308 | −0.426 | −0.139 |
| ShoulderLeft y (mm) | 1.942 | 3.542 | 0.736 | 0.787 |
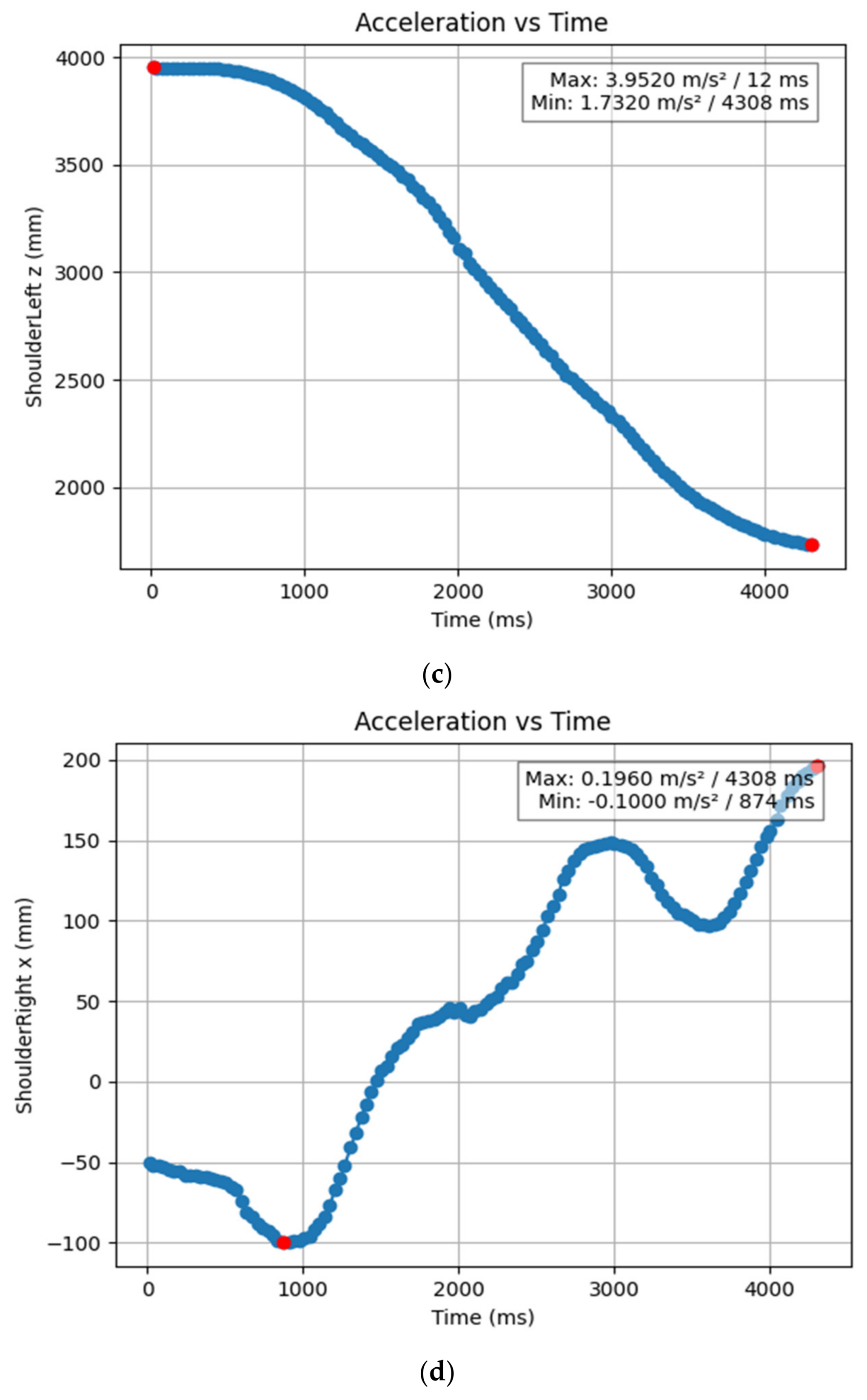
| ShoulderLeft z (mm) | 4.308 | 0.012 | 1.732 | 3.952 |
| ElbowLeft x (mm) | 0.908 | 4.308 | −0.5 | −0.207 |
| ElbowLeft y (mm) | 2.007 | 3.704 | 0.47 | 0.561 |
| ElbowLeft z (mm) | 4.308 | 0.407 | 1.763 | 3.951 |
| ShoulderRight x (mm) | 0.874 | 4.308 | −0.1 | 0.196 |
| ShoulderRight y (mm) | 1.942 | 3.643 | 0.733 | 0.781 |
| ShoulderRight z (mm) | 4.308 | 0.206 | 1.717 | 3.991 |
| ElbowRight x (mm) | 1.003 | 4.308 | −0.048 | 0.263 |
| ElbowRight y (mm) | 1.341 | 4.271 | 0.47 | 0.541 |
| ElbowRight z (mm) | 4.308 | 0.407 | 1.696 | 3.983 |
| HipLeft x (mm) | 0.874 | 4.308 | −0.35 | −0.064 |
| HipLeft y (mm) | 2.574 | 0.012 | 0.265 | 0.304 |
| HipLeft z (mm) | 4.308 | 0.012 | 1.731 | 3.969 |
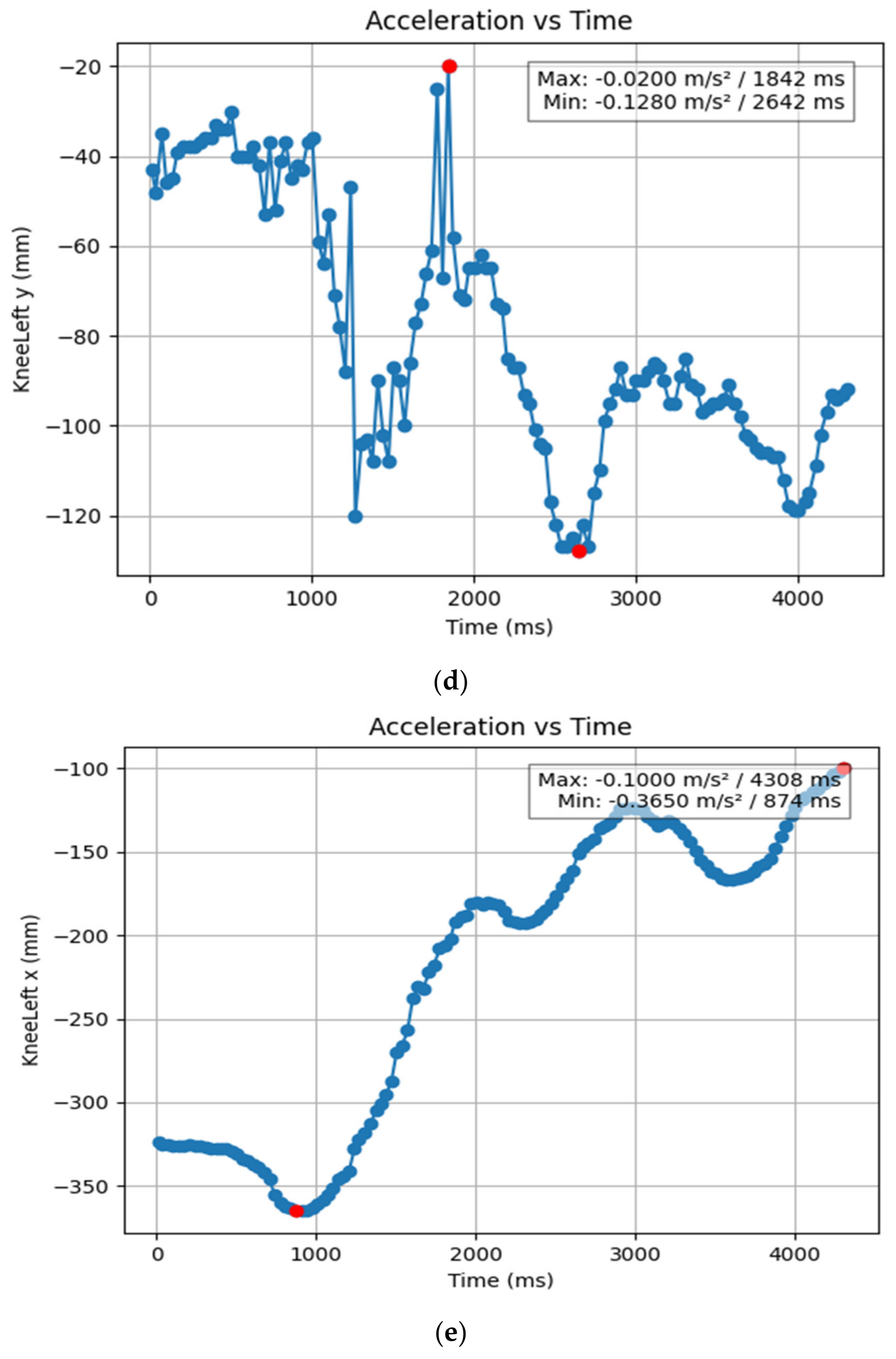
| KneeLeft x (mm) | 0.874 | 4.308 | −0.365 | −0.1 |
| KneeLeft y (mm) | 2.642 | 1.842 | −0.128 | −0.02 |
| KneeLeft z (mm) | 4.308 | 0.241 | 1.671 | 3.932 |
| AnkleLeft x (mm) | 0.774 | 4.308 | −0.348 | −0.122 |
| AnkleLeft y (mm) | 4.07 | 0.569 | −0.458 | −0.395 |
| AnkleLeft z (mm) | 4.308 | 0.44 | 1.751 | 3.964 |
| HipRight x (mm) | 0.874 | 4.308 | −0.204 | 0.083 |
| HipRight y (mm) | 1.87 | 2.941 | 0.258 | 0.302 |
| HipRight z (mm) | 4.308 | 0.012 | 1.72 | 3.983 |
| KneeRight x (mm) | 0.774 | 4.308 | −0.167 | 0.087 |
| KneeRight y (mm) | 3.275 | 2.107 | −0.135 | −0.038 |
| KneeRight z (mm) | 4.308 | 0.407 | 1.727 | 3.971 |
| AnkleRight x (mm) | 0.84 | 4.241 | −0.147 | 0.062 |
| AnkleRight y (mm) | 2.342 | 2.107 | −0.466 | −0.331 |
| AnkleRight z (mm) | 4.07 | 0.34 | 1.724 | 4.009 |
| Left | Poly-Regression Equation | Slope | Right | Poly-Regression Equation | Slope |
|---|---|---|---|---|---|
| Shoulder x | y = −5E-14x6 + 2E-11x5 − 4E-09x4 + 3E-07x3 − 1E-05x2 + 0.0002x − 0.0005 R2 = 0.0017 | y = −3E-06x + 0.0003 R2 = 0.0005 | shoulder x | y = 8E-12x6 − 3E-09x5 + 5E-07x4 − 4E-05x3 + 0.0013x2 − 0.019x + 0.0588 R2 = 0.0271 | y = 0.0001x + 0.0008 R2 = 0.0015 |
| Shoulder y | y = 9E-14x6 − 4E-11x5 + 5E-09x4 − 4E-07x3 + 1E-05x2 − 0.0002x + 0.0007 R2 = 0.0077 | y = −3E-06x + 0.0003 R2 = 0.0005 | shoulder y | y = 7E-12x6 − 2E-09x5 + 2E-07x4 − 2E-06x3 − 0.0006x2 + 0.0262x − 0.107 R2 = 0.1474 | y = −0.0009x + 0.1613 R2 = 0.0353 |
| Elbow x | y = 2E-12x6 − 9E-10x5 + 2E-07x4 − 2E-05x3 + 0.0007x2 − 0.0127x + 0.0391 R2 = 0.0226 | y = 0.0002x − 0.0055 R2 = 0.0048 | elbow x | y = 5E-14x6 − 2E-11x5 + 2E-09x4 − 2E-07x3 + 5E-06x2 − 7E-05x + 0.0006 R2 = 0.0019 | y = −1E-06x + 0.0002 R2 = 5E-05 |
| Elbow y | y = −4E-14x6 + 2E-11x5 − 3E-09x4 + 3E-07x3 − 1E-05x2 + 0.0001x − 7E-05 R2 = 0.0018 | y = −3E-06x + 0.0002 R2 = 0.0003 | elbow y | y = 1E-11x6 − 4E-09x5 + 6E-07x4 − 4E-05x3 + 0.0013x2 − 0.016x + 0.039 R2 = 0.0304 | y = −4E-05x + 0.0086 R2 = 1E-04 |
| Hip x | y = 5E-14x6 − 2E-11x5 + 3E-09x4 − 2E-07x3 + 6E-06x2 − 9E-05x + 0.0005 R2 = 0.0033 | y = −3E-07x + 8E-05 R2 = 3E-05 | hip x | y = −4E-14x6 + 2E-11x5 − 3E-09x4 + 2E-07x3 − 9E-06x2 + 0.0001x − 0.0001 R2 = 0.0037 | y = −3E-06x + 0.0002 R2 = 0.0012 |
| Hip y | y = 5E-14x6 − 2E-11x5 + 3E-09x4 − 2E-07x3 + 6E-06x2 − 9E-05x + 0.0005 R2 = 0.0033 | y = −3E-07x + 8E-05 R2 = 3E-05 | hip y | y = 4E-14x6 − 2E-11x5 + 2E-09x4 − 1E-07x3 + 5E-06x2 − 6E-05x + 0.0003 R2 = 0.0035 | y = 2E-07x + 4E-05 R2 = 2E-05 |
| Knee x | y = −4E-15x6 + 1E-12x5 − 5E-12x4 − 2E-08x3 + 2E-06x2 − 5E-05x + 0.0003 R2 = 0.0001 | y = 4E-07x − 4E-05 R2 = 7E-06 | knee x | y = 4E-14x6 − 2E-11x5 + 3E-09x4 − 2E-07x3 + 8E-06x2 − 0.0001x + 0.0008 R2 = 0.0005 | y = −3E-06x + 0.0002 R2 = 0.0002 |
| Knee y | y = −4E-15x6 + 1E-12x5 − 5E-12x4 − 2E-08x3 + 2E-06x2 − 5E-05x + 0.0003 R2 = 0.0001 | y = 4E-07x − 4E-05 R2 = 7E-06 | knee y | y = 4E-14x6 − 2E-11x5 + 3E-09x4 − 2E-07x3 + 1E-05x2 − 0.0002x + 0.0011 R2 = 0.0007 | y = 9E-07x − 0.0001 R2 = 2E-05 |
| Ankle x | y = 3E-14x6 − 1E-11x5 + 1E-09x4 − 5E-08x3 + 4E-07x2 + 1E-07x + 0.0007 R2 = 0.0022 | y = −6E-06x + 0.0005 R2 = 0.001 | ankle x | y = 2E-14x6 − 7E-12x5 + 5E-10x4 + 7E-09x3 − 2E-06x2 + 8E-05x − 0.0004 R2 = 0.0005 | y = −1E-06x + 7E-05 R2 = 4E-05 |
| Ankle y | y = −3E-14x6 + 1E-11x5 − 3E-09x4 + 3E-07x3 − 1E-05x2 + 0.0002x − 0.0009 R2 = 0.0002 | y = −1E-06x + 0.0001 R2 = 7E-06 | ankle y | y = −1E-14x6 − 2E-12x5 + 1E-09x4 − 2E-07x3 + 9E-06x2 − 0.0002x + 0.0005 R2 = 0.0002 | y = 1E-06x − 0.0003 R2 = 4E-06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Obi, M.F.; Gina, W.; Goswami, T. A Gait Analysis in Professional Dancers: A Cross-Sectional Study. Bioengineering 2024, 11, 1102. https://doi.org/10.3390/bioengineering11111102
Obi MF, Gina W, Goswami T. A Gait Analysis in Professional Dancers: A Cross-Sectional Study. Bioengineering. 2024; 11(11):1102. https://doi.org/10.3390/bioengineering11111102
Chicago/Turabian StyleObi, Manghe Fidelis, Walther Gina, and Tarun Goswami. 2024. "A Gait Analysis in Professional Dancers: A Cross-Sectional Study" Bioengineering 11, no. 11: 1102. https://doi.org/10.3390/bioengineering11111102
APA StyleObi, M. F., Gina, W., & Goswami, T. (2024). A Gait Analysis in Professional Dancers: A Cross-Sectional Study. Bioengineering, 11(11), 1102. https://doi.org/10.3390/bioengineering11111102







