Enhanced CAD Detection Using Novel Multi-Modal Learning: Integration of ECG, PCG, and Coupling Signals
Abstract
1. Introduction
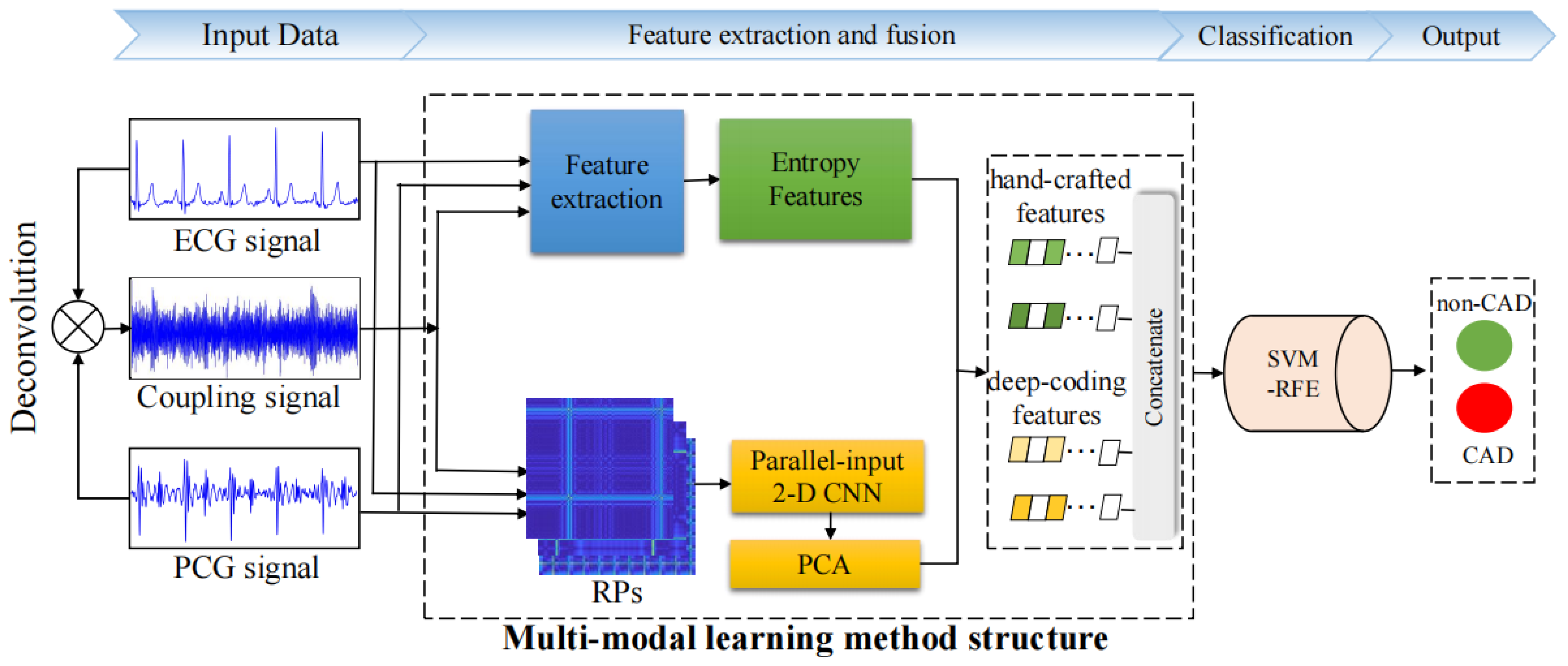
- This study proposes a multi-modal learning method to enhance the precision of CAD detection by integrating ECG, PCG, and their novel coupling signals. The method initially generates a novel coupling signal based on the deconvolution of ECG and PCG, and then it extracts nonlinear features, including various entropy features and recurrence deep-coding features from multi-modal signals to capture global and local information.
- The proposed model designs a novel parallel-input 2-D CNN model to encode the deep representations of multi-modal RPs, enabling detailed analysis of cardiac state changes.
2. Materials and Methods
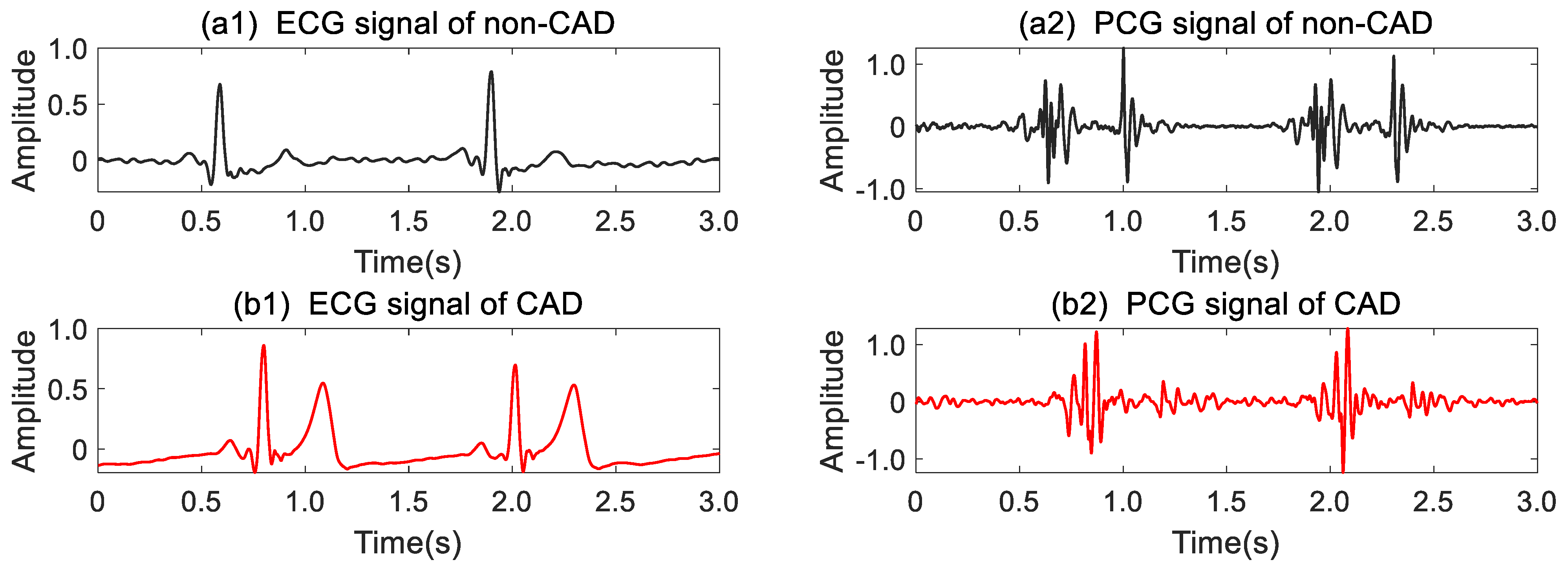
2.1. Data Preprocessing
2.2. ECG–PCG Coupling Signal Evaluation
2.3. Feature Extraction
2.3.1. Entropy Features
- ApEn [22] is a nonlinear analytical tool used to statistically quantify the regularity of the new signal patterns. Through phase space reconstruction and the new signal pattern generation, ApEn is calculated by comparing similar distances between all new patterns, which is defined as follows:where N represents the number of sample points in a signal, m denotes the embedding dimension, r is the threshold value, and C indicates the probability of similar distances between any two new patterns.
- 2.
- SampEn, an improvement algorithm of ApEn, overcomes the limitations of ApEn by excluding the probability of identical patterns [23]. It is also a prevalent tool used to measure the complexity of time series. It is calculated as follows:where N denotes the number of sample points in signals, m is the embedding dimension, r is the threshold parameter, and B represents the probability of similar patterns.
- 3.
- FuzzyEn [30] introduces a fuzzy membership function to improve the SampEn algorithm. In the process of FuzzyEn calculation, the fuzzy similar distance Sij replaces the actual distance of the new patterns, which is defined aswhere dij denotes the distance between the new patterns. As was proven, incorporating the fuzzy membership function notably enhances FuzzyEn stability and consistency [31]. During the calculation of ApEn, SampEn, and FuzzyEn in this study, m was set to 2 and r was 0.2 times the standard deviation of the input signal [32].
- 4.
- DistEn [25] measures the complexity of the distance matrix by using empirical probability distribution functions (ePDF). Evaluation of ePDF mainly relies on the histogram of a predefined bin size B. It is defined by Shannon’s formula:
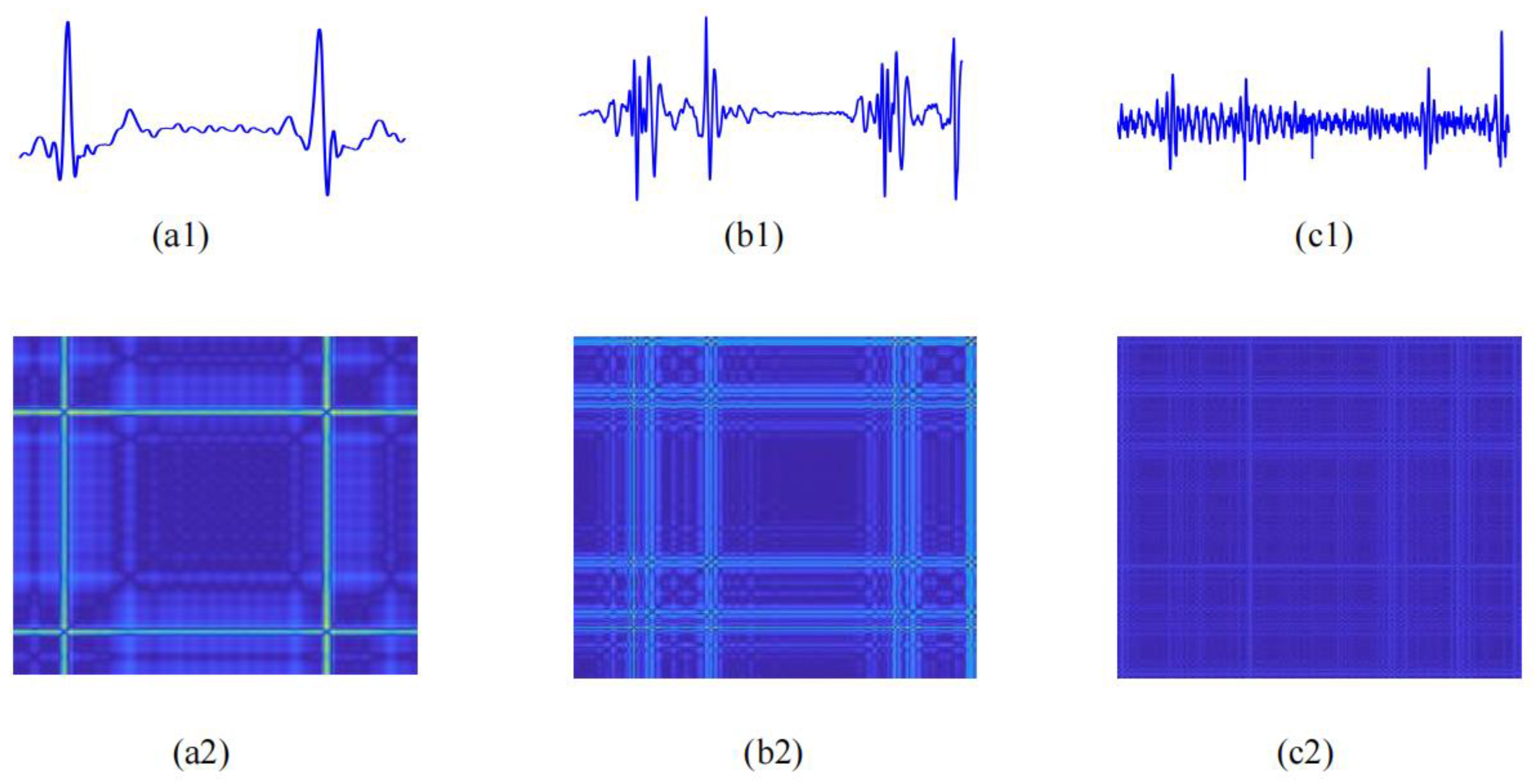
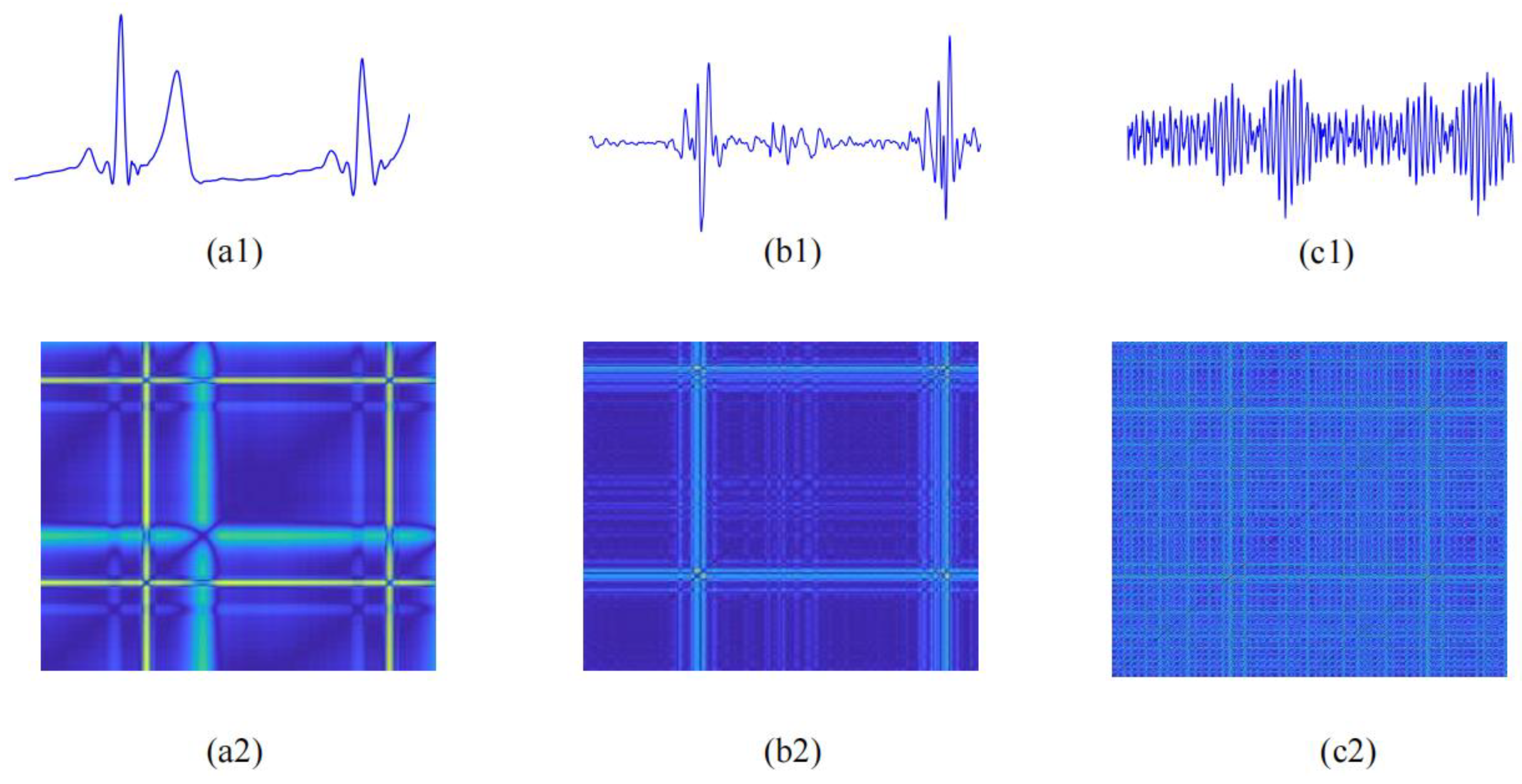
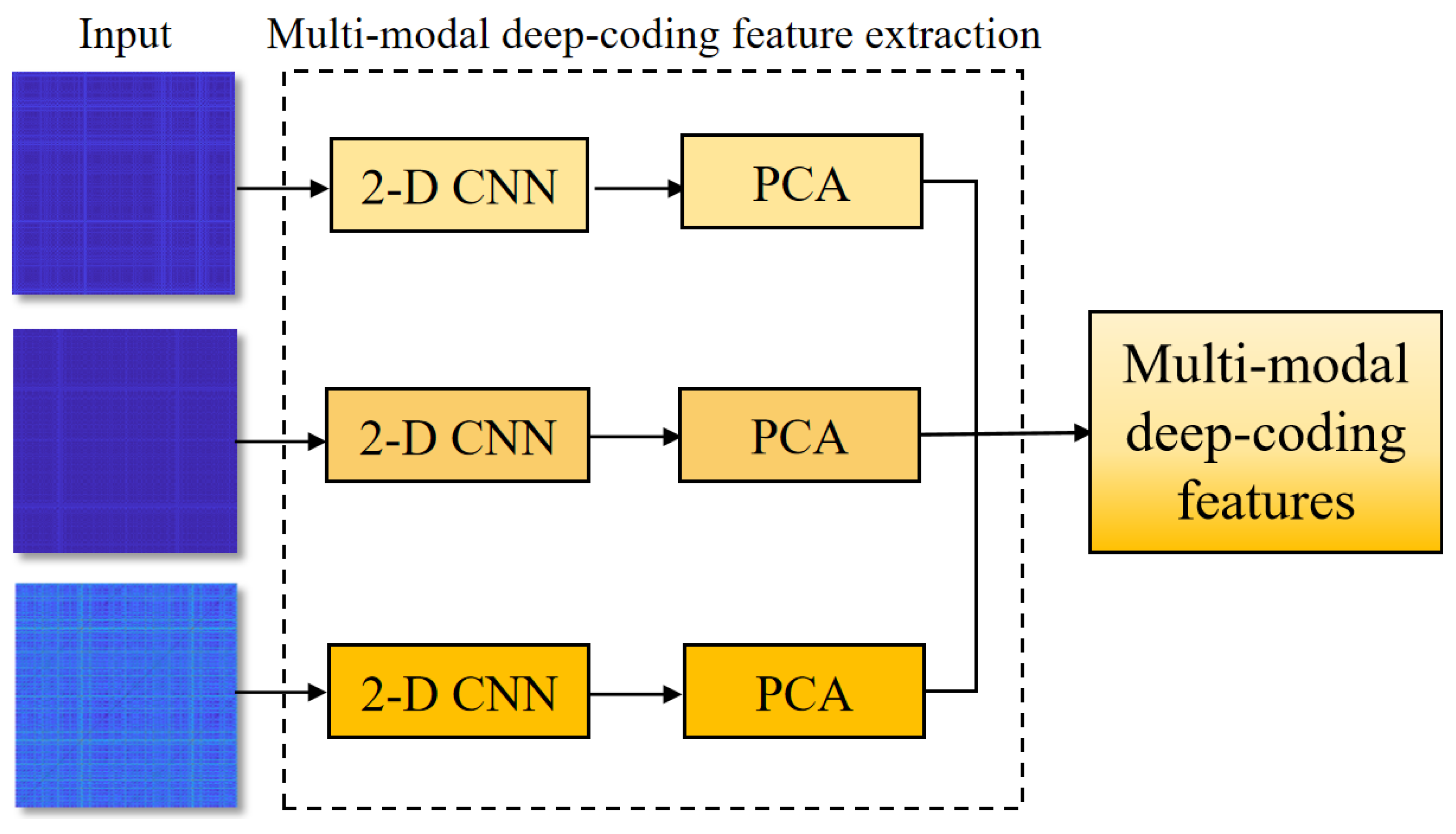
2.3.2. Recurrence Deep-Coding Features
Recurrence Plot Construction
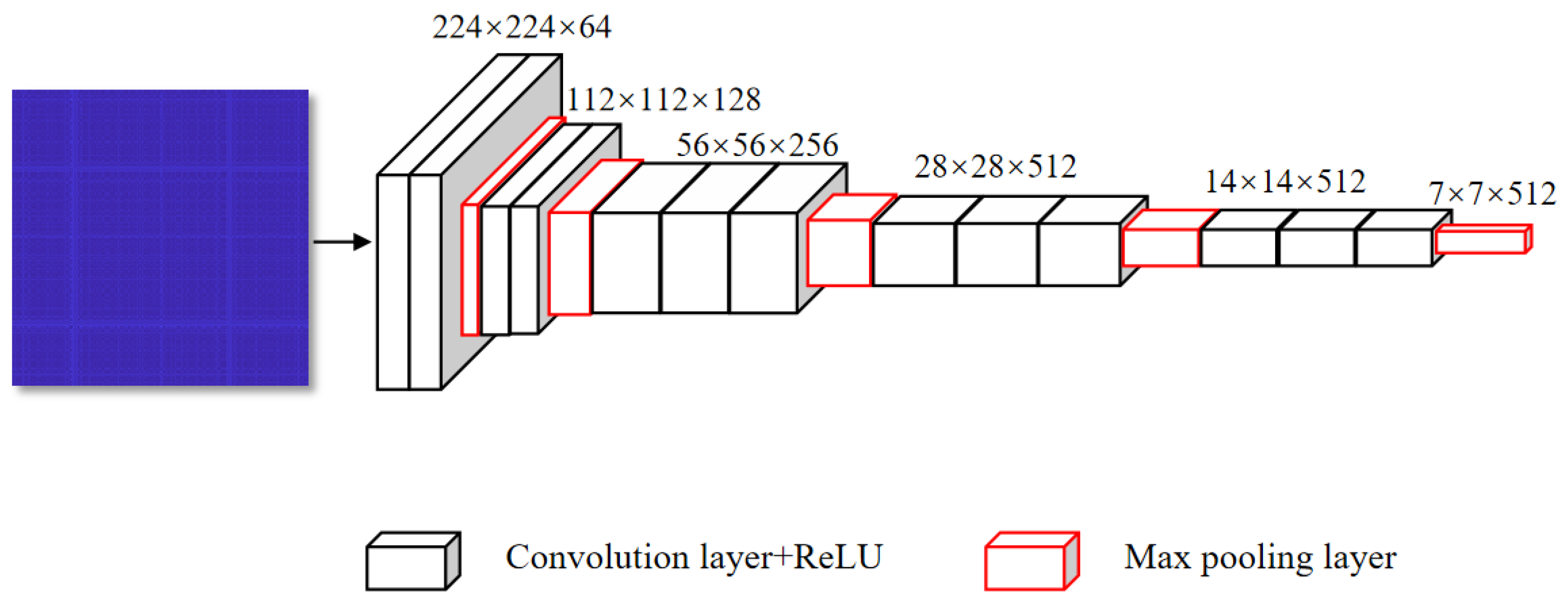
Parallel-Input CNN Framework
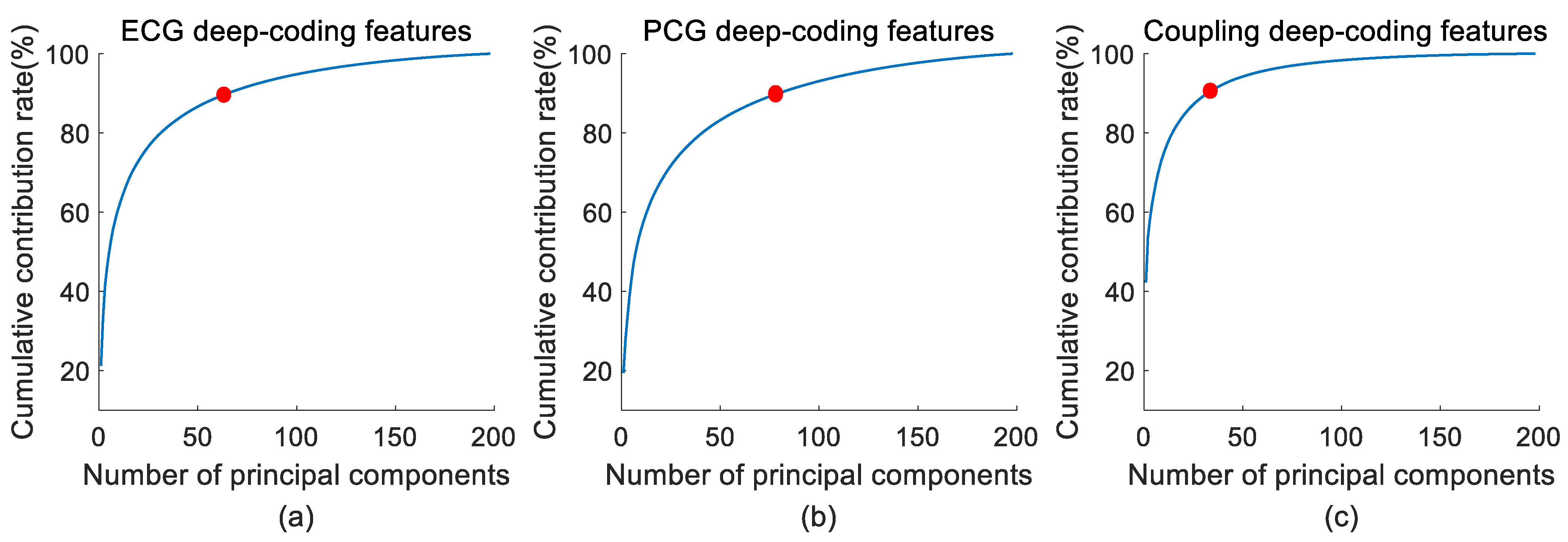
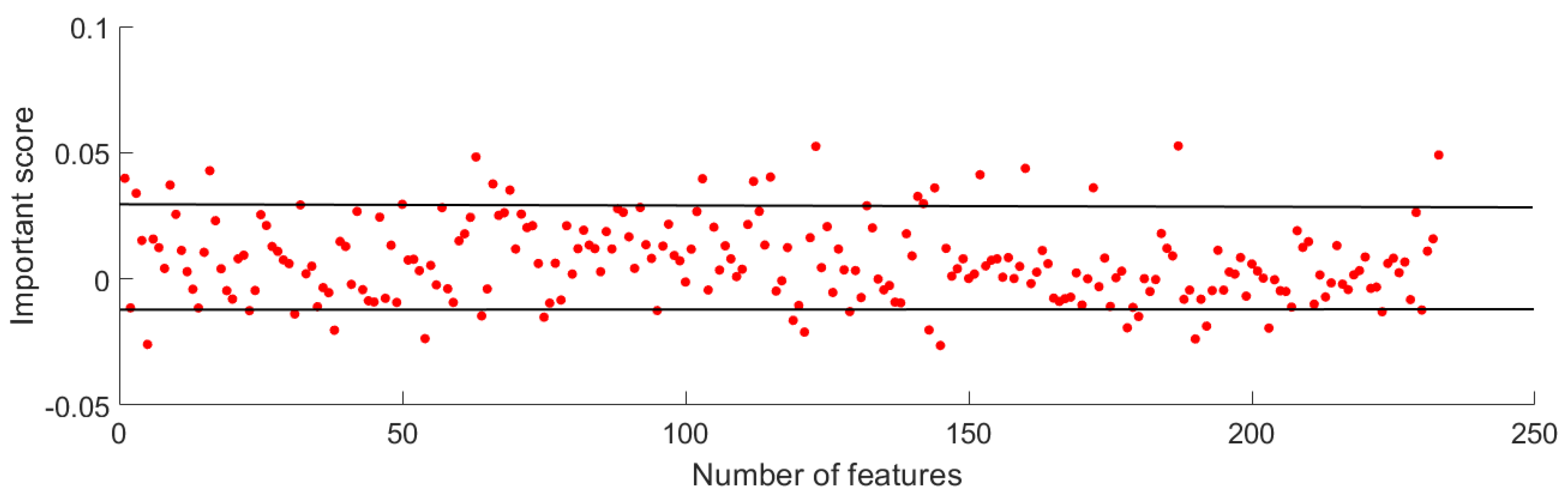
2.4. Feature Reduction
2.5. Statistical Analysis
2.6. Classification
2.7. Performance Evaluation
3. Results
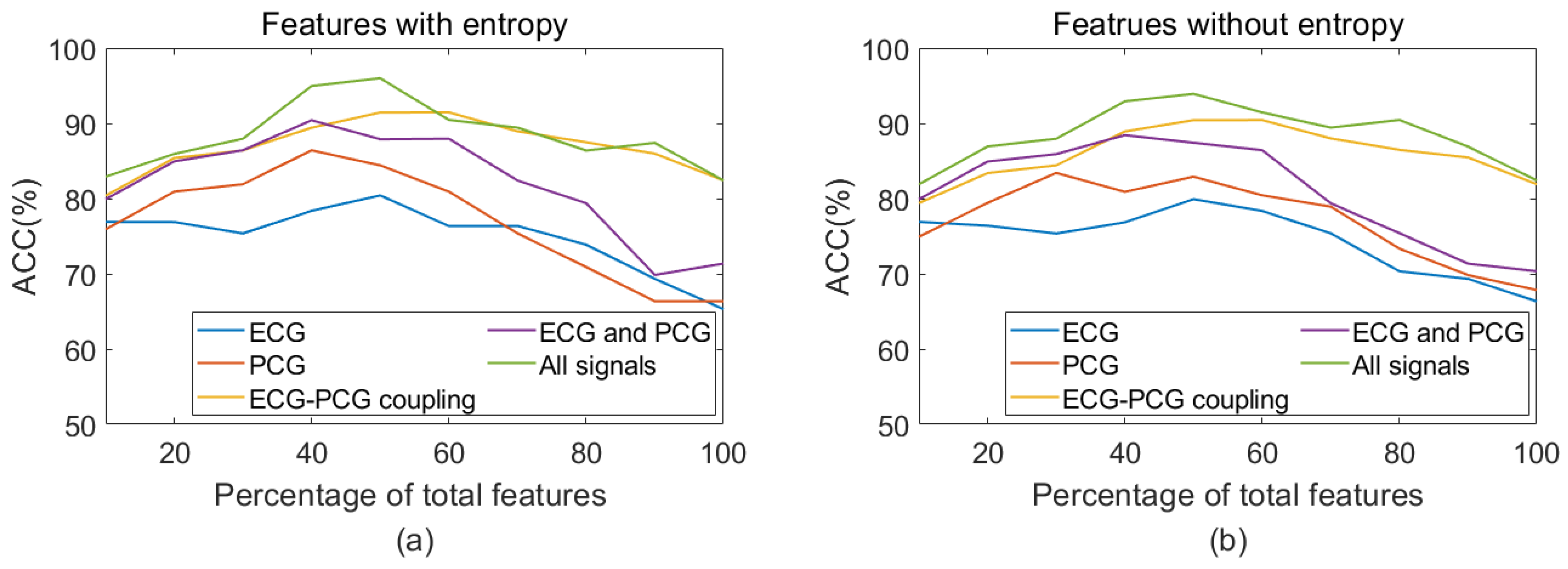
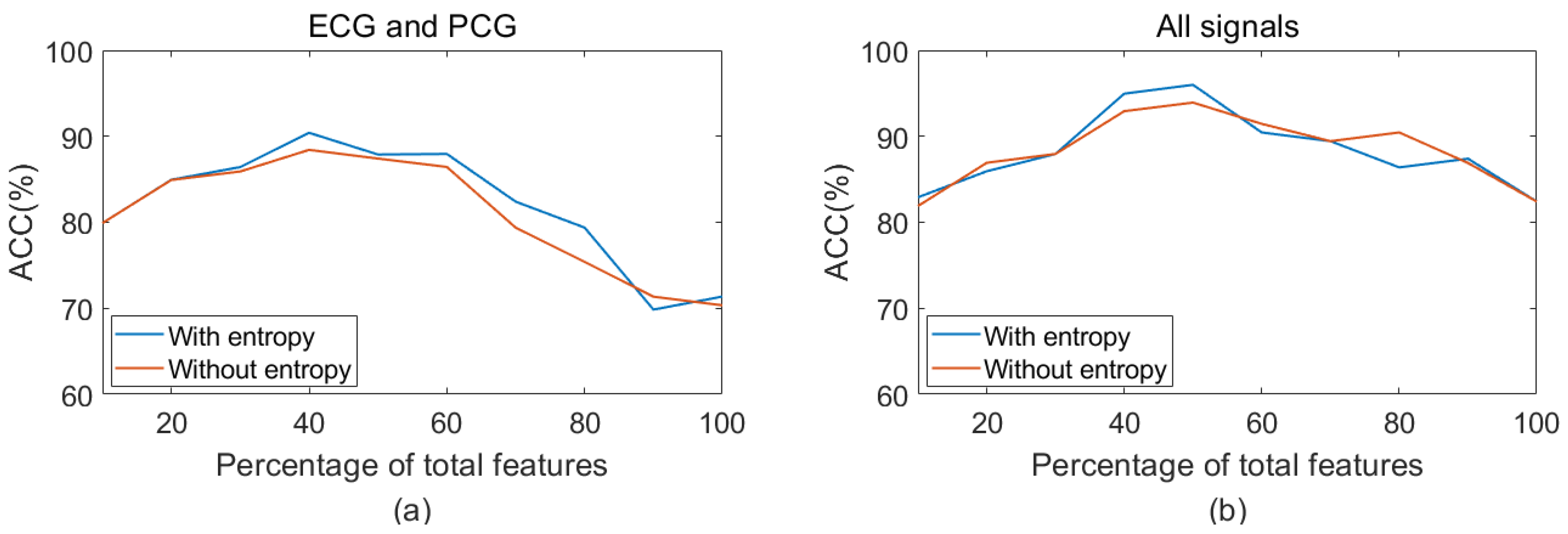
3.1. Feature Reduction Results
3.2. Statistical Analysis Results
3.3. Classification Results
3.4. Classification Results of a Different Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pathak, A.; Samanta, P.; Mandana, K.; Saha, G. Detection of coronary artery atherosclerotic disease using novel features from synchrosqueezing transform of phonocardiogram. Biomed. Signal Process. Control. 2020, 62, 102055. [Google Scholar] [CrossRef]
- Lih, O.S.; Jahmunah, V.; San, T.R.; Ciaccio, E.J.; Yamakawa, T.; Tanabe, M.; Kobayashi, M.; Faust, O.; Acharya, U.R. Comprehensive electrocardiographic diagnosis based on deep learning. Artif. Intell. Med. 2020, 103, 101789. [Google Scholar] [CrossRef]
- Cury, R.C.; Abbara, S.; Achenbach, S.; Agatston, A.; Berman, D.S.; Budoff, M.J.; Dill, K.E.; Jacobs, J.E.; Maroules, C.D.; Rubin, G.D.; et al. CAD-RADSTM coronary artery disease—Reporting and data system. An expert consensus document of the society of cardiovascular computed tomography (SCCT), the american college of radiology (ACR) and the north american society for cardiovascular imaging (NASCI). Endorsed by the American college of cardiology. J. Cardiovasc. Comput. Tomogr. 2016, 10, 269–281. [Google Scholar] [PubMed]
- Yoshida, H.; Yokoyama, K.; Maruvama, Y.; Yamanoto, H.; Yoshida, S.; Hosoya, T. Investigation of coronary artery calcification and stenosis by coronary angiography (CAG) in haemodialysis patients. Nephrol. Dial. Transplant. 2006, 21, 1451–1452. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, H.; Ren, G.; Yu, X.; Wang, D.; Wu, S. Discrimination of the diastolic murmurs in coronary heart disease and in valvular disease. IEEE Access 2020, 8, 160407–160413. [Google Scholar] [CrossRef]
- Giddens, D.P.; Mabon, R.F.; Cassanova, R.A. Measurements of disordered flows distal to subtotal vascular stenosis in the thoracic aortas of dogs. Circ. Res. 1976, 39, 112–119. [Google Scholar] [CrossRef] [PubMed]
- Akay, Y.M.; Akay, M.; Welkowitz, W.; Semmlow, J.L.; Kostis, J.B. Noninvasive acoustical detection of coronary artery disease: A comparative study of signal processing methods. IEEE Trans. Biomed. Eng. 1993, 40, 571–578. [Google Scholar] [CrossRef]
- Leasure, M.; Jain, U.; Butchy, A.; Otten, J.; Covalesky, V.; McCormick, D.; Mintz, G. Deep learning algorithm predicts angiographic coronary artery disease in stable patients using only a standard 12-lead electrocardiogram. Can. J. Cardiol. 2021, 37, 1715–1724. [Google Scholar] [CrossRef]
- Alizadehsani, R.; Zangooei, M.H.; Hosseini, M.J.; Habibi, J.; Khosravi, A.; Roshanzamir, M.; Khozeimeh, F.; Sarrafzadegan, N.; Nahavandi, S. Coronary artery disease detection using computational intelligence methods. Knowl.-Based Syst. 2016, 109, 187–197. [Google Scholar] [CrossRef]
- Li, J.; Ke, L.; Du, Q.; Chen, X.; Ding, X. Multi-modal cardiac function signals classification algorithm based on improved D-S evidence theory. Biomed. Signal Process. Control 2022, 71, 103078. [Google Scholar] [CrossRef]
- Zarrabi, M.; Parsaei, H.; Boostani, R.; Zare, A.; Dorfeshan, Z.; Zarrabi, K.; Kojuri, J. A system for accurately predicting the risk of myocardial infarction using PCG, ECG and clinical features. Biomed. Eng. 2017, 29, 1750023. [Google Scholar] [CrossRef]
- Tan, J.H.; Hagiwara, Y.; Pang, W.; Lim, I.; Oh, S.L.; Adam, M.; Tan, R.S.; Chen, M.; Acharya, U.R. Application of stacked convolutional and long short-term memory network for accurate identification of CAD ECG signals. Comput. Biol. Med. 2018, 94, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Hagiwara, Y.; Koh, J.E.W.; Oh, S.L.; Tan, J.H.; Adam, M.; Tan, R.S. Entropies for automated detection of coronary artery disease using ECG signals: A review. Biocybern. Biomed. Eng. 2018, 38, 373–384. [Google Scholar] [CrossRef]
- Tschannen, M.; Kramer, T.; Marti, G.; Heinzmann, M.; Wiatowski, T. Heart sound classification using deep structured features. In Proceedings of the 2016 Computing in Cardiology Conference, (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 565–568. [Google Scholar]
- Noman, F.; Ting, C.M.; Salleh, S.H.; Ombao, H. Short-segment heart sound classification using an ensemble of deep convolutional neural networks. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing, (ICASSP), Brighton, UK, 12–17 May 2019; pp. 1318–1322. [Google Scholar]
- Baydoun, M.; Safatly, L.; Ghaziri, H.; Hajj, A.E. Analysis of heart sound anomalies using ensemble learning. Biomed. Signal Process. Control 2020, 62, 102019. [Google Scholar] [CrossRef]
- Humayun, A.I.; Ghaffarzadegan, S.; Ansari, M.I.; Feng, Z.; Hasan, T. Towards domain invariant heart sound abnormality detection using learnable filterbanks. IEEE J. Biomed. Health Inf. 2019, 24, 2189–2198. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Cherif, L.H.; Debbal, S.M.; Bereksi-Reguig, F. Choice of the wavelet analyzing in the phonocardiogram signal analysis using the discrete and the packet wavelet transform. Expert. Syst. Appl. 2010, 37, 913–918. [Google Scholar] [CrossRef]
- Liu, T.T.; Li, P.; Liu, Y.Y.; Zhang, H.; Li, Y.Y.; Wang, X.P.; Jiao, Y.; Liu, C.; Karmakar, C.; Liang, X.; et al. Detection of Coronary Artery Disease Using Multi-Domain Feature Fusion of Multi-Channel Heart Sound Signals. Entropy 2021, 23, 642. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Dawes, G.S.; Moulden, M.; Sheil, O. Approximate entropy, a statistic of regularity, applied to fetal heart rate data before and during labor. Obst. Gynecol. 1992, 80, 763–768. [Google Scholar]
- Tang, H.; Jiang, Y.; Li, T.; Wang, X. Identification of pulmonary hypertension using entropy measure analysis of heart sound signal. Entropy 2018, 20, 389. [Google Scholar] [CrossRef]
- Zhang, D.; She, J.; Zhang, Z.; Yu, M. Effects of acute hypoxia on heart rate variability, sample entropy and cardiorespiratory phase synchronization. Biomed. Eng. Online 2014, 13, 73. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Li, P.; Liu, C.; Liu, C.; Li, K.; Li, K.; Zheng, D.; Zheng, D.; Liu, C.; Liu, C.; et al. Assessing the complexity of short-term heartbeat interval series by distribution entropy. Med. Biol. Eng. Comput. 2015, 53, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Mathunjwa, B.M.; Lin, Y.T.; Lin, C.H.; Abbod, M.F.; Shieh, J.S. ECG arrhythmia classification by using a recurrence plot and convolutional neural network. Biomed. Signal Process. Control 2021, 64, 102262. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.; Zhang, Z.; Xing, Y.; Liu, X.; Dong, R.; He, Y.; Xia, L.; Liu, F. Recurrence Plot-Based Approach for Cardiac Arrhythmia Classification Using Inception-ResNet-v2. Front Physiol. 2021, 17, 648950. [Google Scholar] [CrossRef]
- Li, P.; Li, K.; Liu, C.; Zheng, D.; Li, Z.M.; Liu, C. Detection of coupling in short physiological series by a joint distribution entropy method. IEEE. Trans. Biomed. Eng. 2016, 63, 2231–2242. [Google Scholar] [CrossRef]
- Dong, H.W.; Wang, X.P.; Liu, Y.Y.; Sun, C.F.; Jiao, Y.; Zhao, L.; Zhao, S.; Xing, M.; Zhang, H.; Liu, C. Non-destructive detection of CAD stenosis severity using ECG-PCG coupling analysis. Biomed. Signal Process. Control 2023, 86, 105328. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2008, 31, 61–68. [Google Scholar] [CrossRef]
- Castiglioni, P.; Rienzo, M.D. How the Threshold “r” Influences Approximate Entropy Analysis of Heart-Rate Variability. In Proceedings of the 2008 Computers in Cardiology, Bologna, Italy, 14–17 September 2008; pp. 561–564. [Google Scholar]
- Yang, H. Multiscale Recurrence Quantification Analysis of Spatial Cardiac Vectorcardiogram Signals. IEEE Trans. Biomed. Eng. 2011, 58, 339–347. [Google Scholar]
- Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M.; Gertych, A.; Tan, R.S. A deep convolutional neural network model to classify heartbeats. Comput. Biol. Med. 2017, 89, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Wei, S.; Tang, H.; Liu, C. Multivariable fuzzy measure entropy analysis for heart rate variability and heart sound amplitude variability. Entropy 2016, 18, 430. [Google Scholar] [CrossRef]
- Soroush, M.Z.; Maghooli, K.; Setarehdan, S.K.; Nasrabadi, A.M. Emotion recognition through EEG phase space dynamics and Dempster-Shafer theory. Med. Hypotheses 2019, 127, 34–45. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, X.; Liu, C.; Liu, Y.; Li, P.; Yao, L.; Li, H.; Wang, J.; Jiao, Y. Detection of coronary artery disease using multi-modal feature fusion and hybrid feature selection. Physiol. Meas. 2020, 41, 115007. [Google Scholar] [CrossRef]
- Kaveh, A.; Chung, W. Automated classification of coronary atherosclerosis using single lead ECG. In Proceedings of the 2013 IEEE Conference on Wireless Sensor (ICWISE), Kuching, Malaysia, 2–4 December 2013; pp. 108–113. [Google Scholar]
- Samanta, P.; Pathak, A.; Mandana, K.; Saha, G. Classification of coronary artery diseased and normal subjects using multi-channel phonocardiogram signal. Biocybern. Biomed. Eng. 2019, 39, 426–443. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.P.; Liu, C.C.; Zeng, Q.; Zheng, Y.; Chu, X.; Yao, L.; Wang, J.; Jiao, Y.; Karmakar, C. A fusion framework based on multi-domain features and deep learning features of phonocardiagram for coronary artery disease detection. Comput. Biol. Med. 2020, 120, 103733. [Google Scholar] [CrossRef]
- Pathak, A.; Samanta, P.; Mandana, K.; Saha, G. An improved method to detect coronary artery disease using phonocardiogram signals in noisy environment. Appl. Acoust. 2020, 164, 107242. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.P.; Liu, C.C.; Zeng, Q.; Li, P.; Jiao, Y. Integrating multi-domain deep features of electrocardiogram and phonocardiogram for coronary artery disease detection. Comput. Biol. Med. 2021, 138, 104914. [Google Scholar] [CrossRef]

| Characteristics | Non-CAD | CAD |
|---|---|---|
| Age | 61 ± 10 | 62 ± 10 |
| Male/female | 30/34 | 89/46 |
| Height | 164 ± 7 | 166 ± 8 |
| Weight | 69 ± 12 | 71 ± 11 |
| Heart rate | 72 ± 12 | 75 ± 16 |
| Systolic blood pressure | 134 ± 15 | 133 ± 16 |
| Diastolic blood pressure | 80 ± 11 | 82 ± 12 |
| Index | Layer | Index | Layer |
|---|---|---|---|
| 1 | conv3_64 | 10 | max-pooling_2 |
| 2 | conv3_64 | 11 | conv3_512 |
| 3 | max-pooling_2 | 12 | conv3_512 |
| 4 | conv3_128 | 13 | conv3_512 |
| 5 | conv3_128 | 14 | max-pooling_2 |
| 6 | max-pooling_2 | 15 | conv3_512 |
| 7 | conv3_256 | 16 | conv3_512 |
| 8 | conv3_256 | 17 | conv3_512 |
| 9 | conv3_256 | 18 | max-pooling_2 |
| Feature | Type | p-Value | Feature | Type | p-Value |
|---|---|---|---|---|---|
| RD-pcg23 | Deep-coding | 0.0384 | RD-coupl22 | Deep-coding | 0.0470 |
| RD-pcg32 | Deep-coding | 0.0491 | RD-coup23 | Deep-coding | 0.0418 |
| RD-pcg40 | Deep-coding | 0.0431 | RD-coup26 | Deep-coding | 0.0427 |
| RD-pcg46 | Deep-coding | 0.0134 | RD-coup27 | Deep-coding | 0.0444 |
| RD-pcg51 | Deep-coding | 0.0028 | RD-coupl29 | Deep-coding | 0.0335 |
| RD-pcg57 | Deep-coding | 0.0082 | RD-coupl30 | Deep-coding | 2.54 × 10−5 |
| RD-pcg58 | Deep-coding | 0.0271 | RD-coupl31 | Deep-coding | 0.0421 |
| RD-pcg69 | Deep-coding | 0.0117 | RD-coupl32 | Deep-coding | 0.0311 |
| RD-pcg76 | Deep-coding | 0.0318 | RD-coupl33 | Deep-coding | 0.0014 |
| RD-ecg9 | Deep-coding | 0.0268 | RD-coupl34 | Deep-coding | 0.0311 |
| RD-ecg17 | Deep-coding | 0.0037 | RD-coupl35 | Deep-coding | 0.0014 |
| RD-ecg21 | Deep-coding | 0.0022 | ApEn-pcg-1 | Entropy | 2.39 × 10−4 |
| RD-ecg29 | Deep-coding | 0.0176 | SampEn-pcg-1 | Entropy | 2.38 × 10−4 |
| RD-ecg36 | Deep-coding | 0.0174 | FuzzyEn-pcg-1 | Entropy | 2.41 × 10−4 |
| RD-ecg43 | Deep-coding | 4.66 × 10−7 | DistEn-pcg-1 | Entropy | 2.39 × 10−4 |
| RD-ecg63 | Deep-coding | 0.0142 | ApEn-s1-s2s | Entropy | 0.0295 |
| RD-ecg64 | Deep-coding | 0.0418 | SampEn-pcg | Entropy | 0.0194 |
| RD-coupl13 | Deep-coding | 0.0478 | FuzzyEn-pcg | Entropy | 0.0298 |
| RD-coupl15 | Deep-coding | 0.0307 | DistEn-pcg | Entropy | 0.0433 |
| RD-coupl16 | Deep-coding | 0.0199 | SampEn-ecg | Entropy | 0.032 |
| RD-coupl20 | Deep-coding | 0.023 | SampEn-coupl | Entropy | 0.032 |
| With Entropy | Without Entropy | |||||||
|---|---|---|---|---|---|---|---|---|
| ACC (%) | SEN (%) | SPE (%) | F1 (%) | ACC (%) | SEN (%) | SPE (%) | F1 (%) | |
| Single ECG | 80.41 ± 2.85 | 89.63 ± 3.63 | 61.15 ± 12.42 | 66.07 ± 8.10 | 79.90 ± 3.54 | 90.37 ± 2.96 | 57.95 ± 9.94 | 64.58 ± 7.67 |
| Single PCG | 86.41 ± 4.15 | 96.29 ± 4.68 | 65.64 ± 14.19 | 74.85 ± 9.27 | 84.41 ± 4.34 | 92.59 ± 3.31 | 67.18 ± 8.94 | 73.30 ± 7.93 |
| Single coupling | 91.44 ± 2.56 | 94.81 ± 5.54 | 84.48 ± 4.67 | 86.54 ± 3.40 | 90.42 ± 3.44 | 95.56 ± 2.77 | 79.49 ± 9.86 | 83.89 ± 6.59 |
| ECG and PCG | 90.42 ± 3.45 | 95.56 ± 2.77 | 79.36 ± 9.32 | 79.97 ± 5.99 | 89.42 ± 3.04 | 93.33 ± 4.32 | 81.03 ± 9.21 | 82.74 ± 5.97 |
| All signals | 95.96 ± 3.05 | 100.00 ± 0.00 | 87.31 ± 9.67 | 92.93 ± 5.60 | 93.97 ± 4.89 | 98.52 ± 1.81 | 84.36 ± 1.61 | 89.10 ± 9.74 |
| Model | ACC (%) | SEN (%) | SPE (%) | F1 (%) |
|---|---|---|---|---|
| ResNet50-based model | 90.96 ± 2.89 | 94.81 ± 1.81 | 82.82 ± 5.71 | 85.45 ± 4.80 |
| Our model | 95.96 ± 3.05 | 100.00 ± 0.00 | 87.31 ± 9.67 | 92.93 ± 5.60 |
| Author | Data | Method | Result (%) |
|---|---|---|---|
| Liu et al. [20] | Self-collected 21CAD/15non-CAD | Multi-channel PCG; time domain, frequency domain, and nonlinear domain features; SVM | ACC:90.9 SPE:93.0 SEN:87.9 |
| Kaveh et al. [38] | MIT-BIH 43CAD/46non-CAD | ECG; time domain and frequency domain features; SVM | ACC:88.0 SPE:92.6 SEN:84.2 |
| Samanta et al. [39] | Self-collected 29CAD/37non-CAD | PCG; time domain and frequency domain features; CNN | ACC:82.6 SPE:79.6 SEN:85.6 |
| Li et al. [40] | Self-collected 135CAD/60non-CAD | PCG; multi-domain features; deep features; MLP | ACC:90.4 SPE:83.4 SEN:93.7 |
| Pathak et al. [41] | Self-collected 40 Normal/40 CAD | PCG; imaginary part of cross power spectral density; SVM | ACC: 75.0 SPE: 73.5 SEN: 76.5 |
| This study | Self-collected 135CAD/64non-CAD | ECG and PCG; entropy; RP; deep learning and SVM | ACC:95.96 SPE:87.43 SEN: 100.00 |
| This study | Self-collected 64CAD/64non-CAD | ECG and PCG; entropy; RP; deep learning and SVM | ACC:94.32 SPE: 93.44 SEN: 96.12 |
| Author | Classifier | Input | Result (%) |
|---|---|---|---|
| Studies on ECG classification using the PhysioNet dataset | |||
| Kumar et al. [12] | SVM | Time-frequency features | ACC: 99.60 |
| Tan et al. [13] | 1-D CNN | ECG signal | ACC:99.85 |
| Acharya et al. [14] | 1-D CNN | Entropy features | ACC:99.27 |
| This study | SVM | Entropy, recurrence deep-coding features | ACC: 99.85 |
| Studies on PCG classification using the PhysioNet/CinC Challenge 2016 dataset | |||
| Tschannen et al. [15] | 1-D CNN | Time features, frequency features | ACC: 87.00 |
| Noman et al. [16] | 2-D CNN | MFCCs image | ACC: 88.80 |
| Baydoun et al. [17] | Boosting and bagging model | Time-frequency features, statistical features | ACC: 91.50 |
| This study | SVM | Entropy, recurrence deep-coding features | ACC: 94.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Liu, X.; Liu, C.; Wang, X.; Liu, Y.; Zhao, S.; Zhang, M. Enhanced CAD Detection Using Novel Multi-Modal Learning: Integration of ECG, PCG, and Coupling Signals. Bioengineering 2024, 11, 1093. https://doi.org/10.3390/bioengineering11111093
Sun C, Liu X, Liu C, Wang X, Liu Y, Zhao S, Zhang M. Enhanced CAD Detection Using Novel Multi-Modal Learning: Integration of ECG, PCG, and Coupling Signals. Bioengineering. 2024; 11(11):1093. https://doi.org/10.3390/bioengineering11111093
Chicago/Turabian StyleSun, Chengfa, Xiaolei Liu, Changchun Liu, Xinpei Wang, Yuanyuan Liu, Shilong Zhao, and Ming Zhang. 2024. "Enhanced CAD Detection Using Novel Multi-Modal Learning: Integration of ECG, PCG, and Coupling Signals" Bioengineering 11, no. 11: 1093. https://doi.org/10.3390/bioengineering11111093
APA StyleSun, C., Liu, X., Liu, C., Wang, X., Liu, Y., Zhao, S., & Zhang, M. (2024). Enhanced CAD Detection Using Novel Multi-Modal Learning: Integration of ECG, PCG, and Coupling Signals. Bioengineering, 11(11), 1093. https://doi.org/10.3390/bioengineering11111093







