Advancing Barrett’s Esophagus Segmentation: A Deep-Learning Ensemble Approach with Data Augmentation and Model Collaboration
Abstract
1. Introduction
2. Materials and Methods
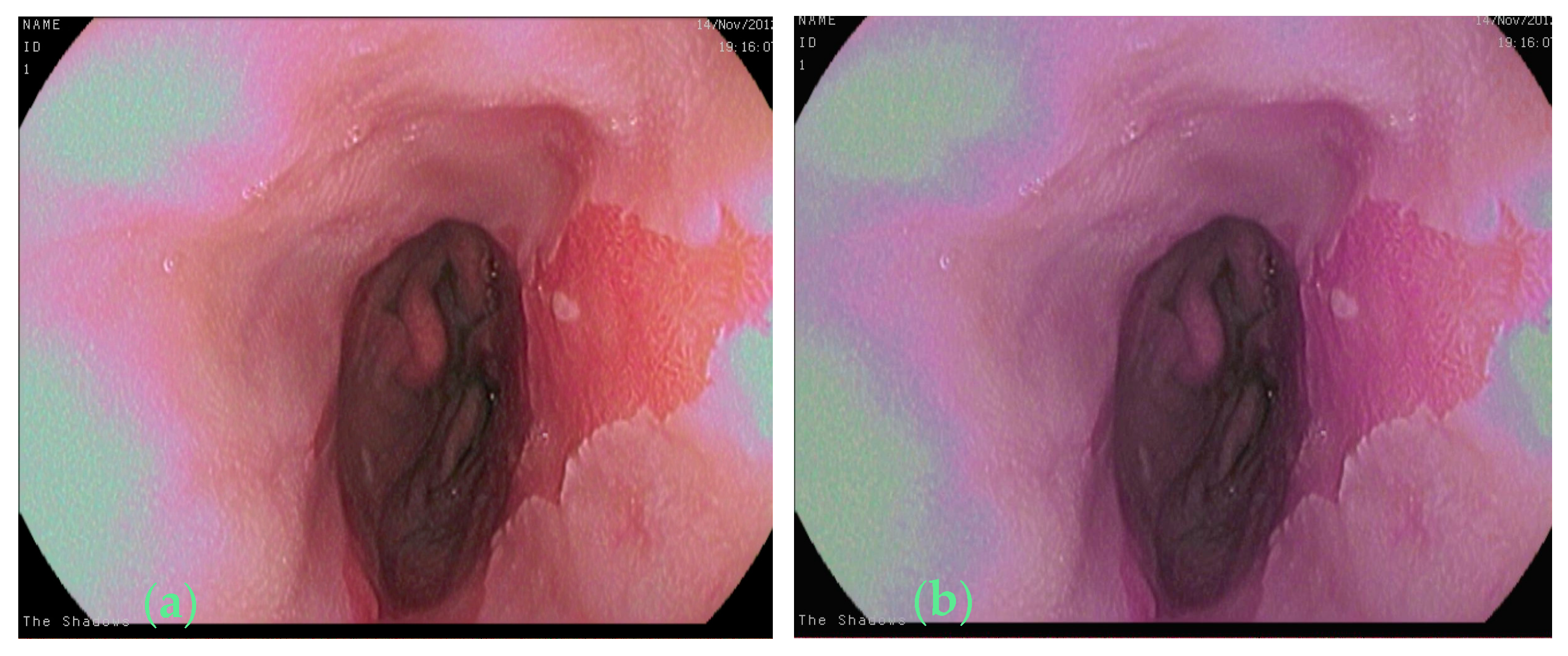
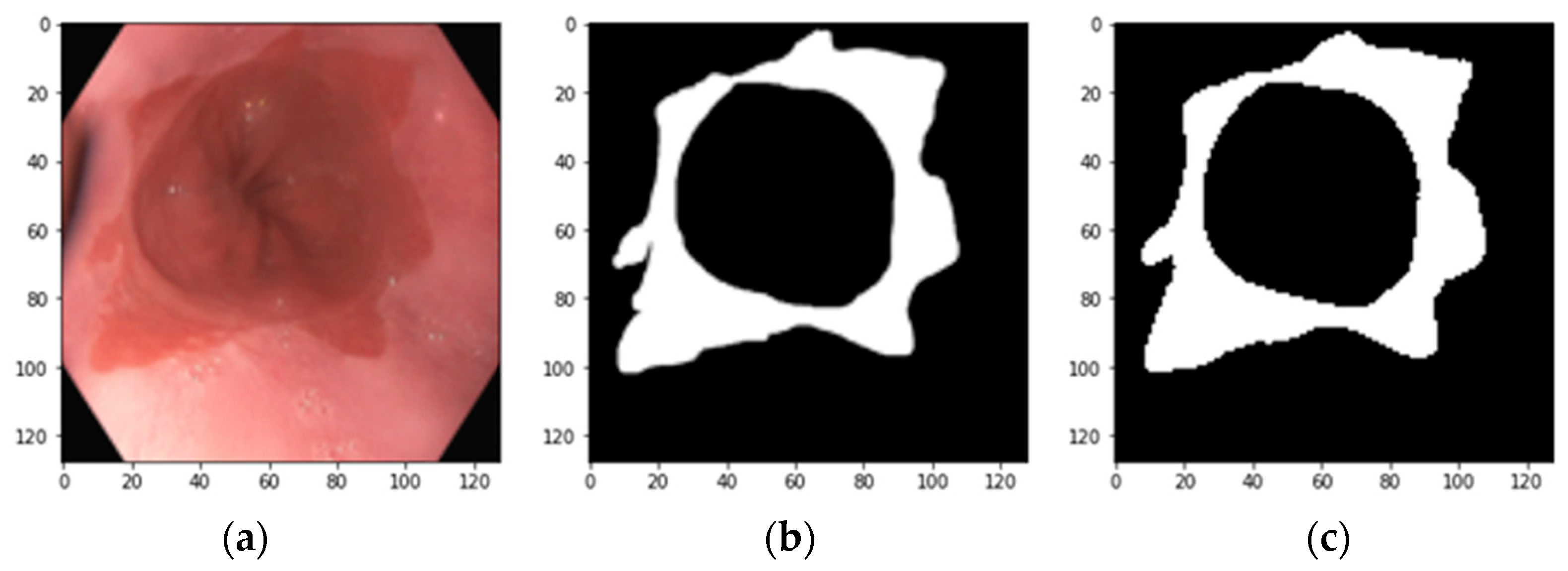
2.1. Raw Images and the Annotation Method
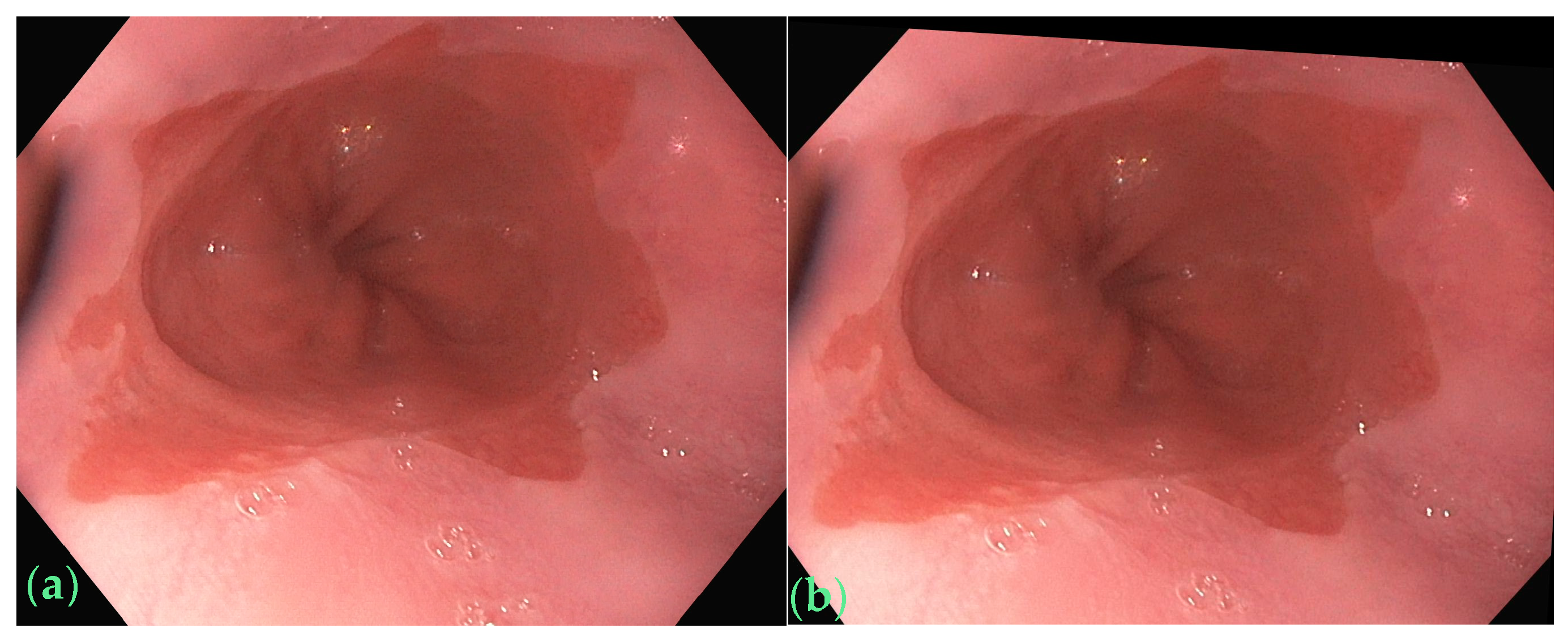
2.2. Data Augmentation
2.2.1. Step 1: Data Augmentation to Create Dataset-192
2.2.2. Step 2: Data Augmentation to Create Dataset-360
2.3. The Implementation Platform
- model = models.unet_2d((128, 128, 3), filter_num = [64, 128, 256, 512, 1024];
- n_labels = 1;
- stack_num_down = 2, stack_num_up = 2;
- activation = ‘ReLU’;
- output_activation = ‘Sigmoid’;
- batch_norm = True, pool = False, unpool = False;
- backbone = ‘DenseNet121’, weights = ‘imagenet’;
- freeze_backbone = True, freeze_batch_norm = True;
- name = ‘unet’)
- model.compile(loss = ‘binary_crossentropy’, optimizer = Adam(learning_rate = 1 × 10−5),
- metrics = [‘accuracy’, losses.dice_coef])
2.3.1. Model and Backbone Network
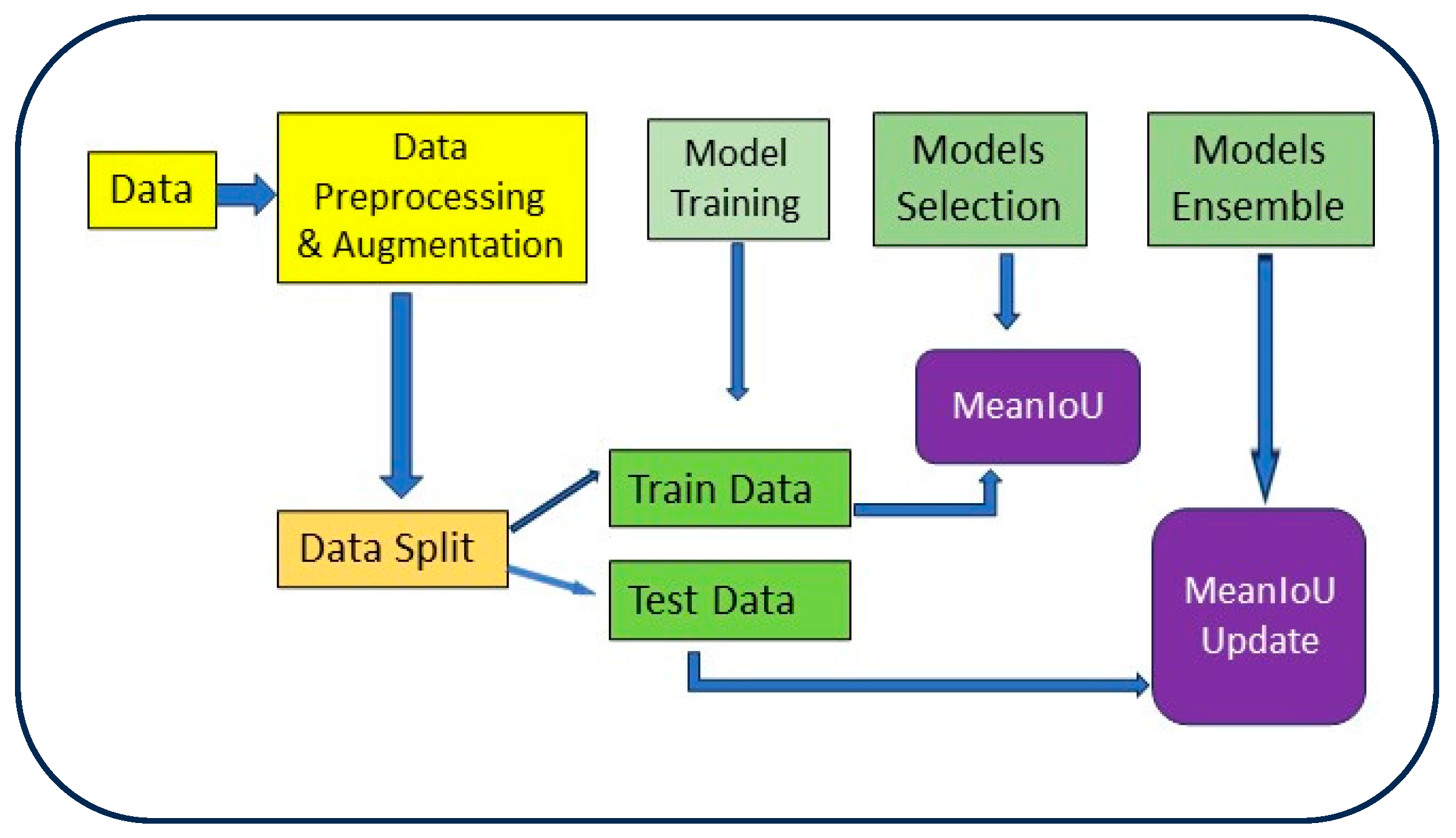
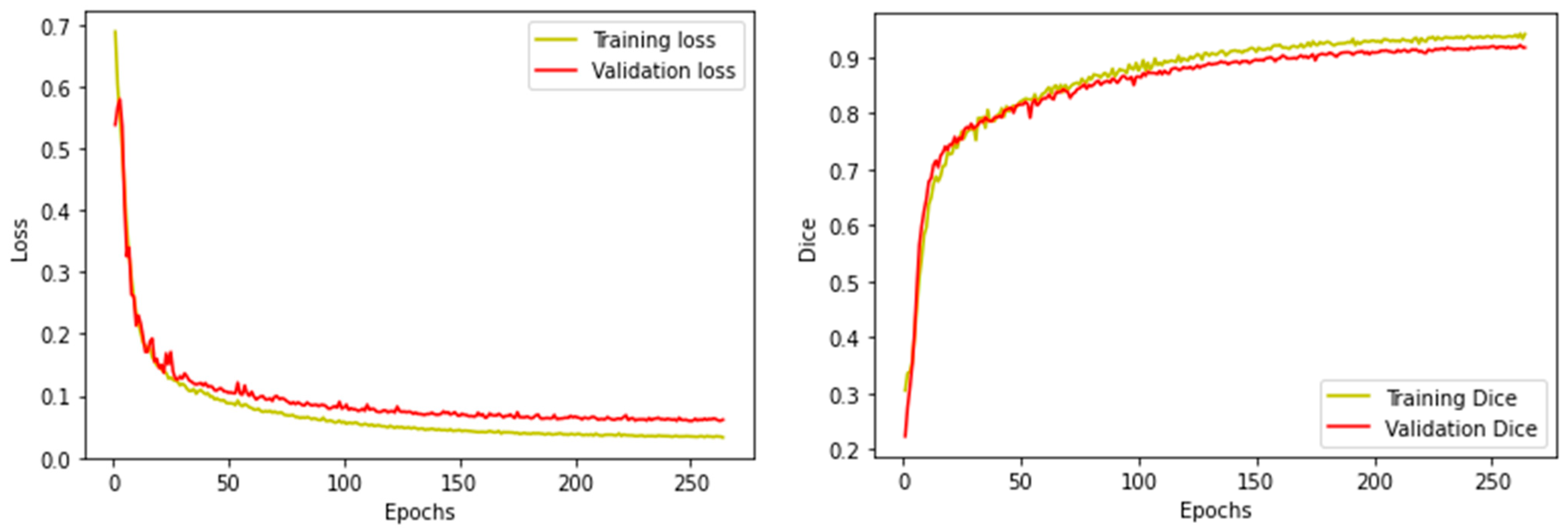
2.3.2. Model Training and Testing Process
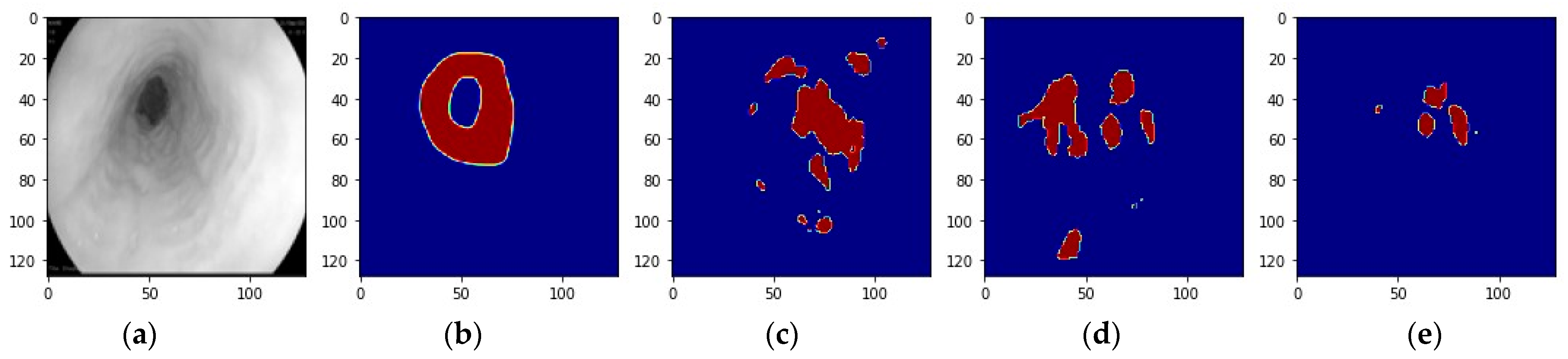
2.4. Model Ensemble
3. Results
3.1. Individual Model Performance
3.2. Ensemble Performance
3.3. Backbone-Based Ensemble Comparison
3.4. Comparison with Deeplabv3+
3.5. Grid Search Ensemble
3.6. Model Ensemble from Scratch
3.7. Saturation of Learning Rate and Ensemble Learning via Grid Search
- Model 1: Unet with a backbone VGG16;
- Model 2: Unet with a backbone DenseNet121;
- Model 3: Attention Unet with a backbone DenseNet121;
- Model 4: deeplabv3+ with a backbone VGG16;
- Model 5: deeplabv3+ with a backbone VGG19;
- Model 6: deeplabv3+with a backbone DenseNet169;
- Model 7: deeplabv3+ with a backbone DenseNet201.
4. Discussion
4.1. Model Selection and Performance
4.2. Impact of Data Augmentation
4.3. Models with vs. without a Backbone
4.4. Ensemble Strategies
4.5. Comparison with Deeplabv3
4.6. Training Saturation and Ensemble Learning
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Halvorsen, K.; Winther, M.H.; Næss, T.C.; Smedsrud, K.; Eide, K.E.; Johannessen, G.; Aabakken, P.; Gilja, L.A.; Cascio, D.; Wallace, M.J. The HyperKvasir dataset for multi-class image classification and segmentation in gastroenterology. Sci. Data 2019, 6, 1–9. [Google Scholar]
- Vulpoi, R.-A.; Luca, M.; Ciobanu, A.; Olteanu, A.; Barboi, O.-B.; Drug, V.L. Artificial Intelligence in Digestive Endoscopy—Where Are We and Where Are We Going? Diagnostics 2022, 12, 927. [Google Scholar] [CrossRef] [PubMed]
- de Groof, A.J.; Struyvenberg, M.R.; van der Putten, J.; van der Sommen, F.; Fockens, K.N.; Curvers, W.L.; Zinger, S.; Pouw, R.E.; Coron, E.; Baldaque-Silva, F.; et al. Deep-learning system detects neoplasia in patients with Barrett’s esophagus with higher accuracy than endoscopisnts in a multistep training and validation study with benchmarking. Gastroenterology 2020, 158, 915–929.e4. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, R.; Requa, J.; Dao, T.; Ninh, A.; Tran, E.; Mai, D.; Lugo, M.; Chehade, N.E.H.; Chang, K.J.; Karnes, W.E.; et al. Artificial intelligence using convolutional neural networks for real-time detection of early esophageal neoplasia in Barrett’s esophagus (with video). Gastrointest. Endosc. 2020, 91, 1264–1271. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Punn, N.S.; Agarwal, S. Modality specific U-Net variants for biomedical image segmentation: A survey. Artif. Intell. Rev. 2022, 55, 5845–5889. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Advances in Neural Information Processing Systems (NeurIPS); Cornell University: Ithaca, NY, USA, 2014; pp. 2357–2365. [Google Scholar]
- Pan, W.; Li, X.; Wang, W.; Zhou, L.; Wu, J.; Ren, T.; Liu, C.; Lv, M.; Su, S.; Tang, Y. Identification of Barrett’s esophagus in endoscopic images using deep learning. BMC Gastroenterol. 2021, 21, 479. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Santiago, Chile, 11–18 December 2015. [Google Scholar]
- Sha, Y. 2021: Keras-Unet-Collection. GitHub Repository. Available online: https://zenodo.org/records/5449801 (accessed on 4 September 2021).
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Lecture Notes in Computer Science; DLMIA 2018/ML-CDS 2018, LNCS 11045; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–11. [Google Scholar] [CrossRef]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Alom, M.Z.; Hasan, M.; Yakopcic, C.; Taha, T.M.; Asari, V.K. Recurrent Residual Convolutional Neural Network based on U-Net (R2U-Net) for Medical Image Segmentation. arXiv 2018, arXiv:1802.06955. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 630–645. [Google Scholar]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Ibtehaz, N.; Rahman, M.S. MultiResUNet: Rethinking the U-Net Architecture for Multimodal Biomedical Image Segmentation. arXiv 2019, arXiv:1902.04049. Available online: https://arxiv.org/abs/1902.04049 (accessed on 29 October 2021).



| Model Backbone | Unet | Unet2plus | Attension Unet | Deeplab v3+ | Ensemble |
|---|---|---|---|---|---|
| VGG16 | 0.81 | 0.51 | 0.80 | 0.77 | 0.81 |
| VGG19 | 0.80 | 0.46 | 0.78 | 0.76 | 0.81 |
| ResNet50 | 0.56 | 0.42 | 0.58 | 0.52 | |
| ResNet101 | 0.53 | 0.42 | 0.53 | 050 | |
| ResNet152 | 0.59 | 0.42 | 0.58 | 0.55 | |
| ResNet50V2 | 0.83 | 0.81 | 0.83 | 0.85 | |
| ResNet101V2 | 0.83 | 0.78 | 0.80 | 0.83 | |
| ResNet152V2 | 0.83 | 0.77 | 0.80 | 0.83 | |
| DenseNet121 | 0.85 | 0.83 | 0.84 | 0.86 | |
| DenseNet169 | 0.84 | 0.84 | 0.85 | 0.78 | 0.86 |
| DenseNet201 | 0.83 | 0.83 | 0.83 | 0.78 | 0.85 |
| Ensemble | 0.87 | 0.76 | 0.80 | 0.80 |
| Model Backbone | Unet | Unet 2plus | Attension Unet | Deeplab v3+ | Ensemble |
|---|---|---|---|---|---|
| VGG16 | 0.90 | 0.75 | 0.88 | 0.89 | 0.90 |
| VGG19 | 0.88 | 0.73 | 0.84 | 0.90 | 0.89 |
| ResNet50 | 0.65 | 0.47 | 0.68 | 0.79 | 0.77 |
| ResNet101 | 0.69 | 0.51 | 0.69 | 0.76 | 0.73 |
| ResNet152 | 0.71 | 0.44 | 0.62 | 0.71 | |
| ResNet50V2 | 0.86 | 0.84 | 0.87 | 0.88 | |
| ResNet101V2 | 0.87 | 0.82 | 0.86 | 0.88 | |
| ResNet152 V2 | 0.83 | 0.76 | 0.84 | 0.84 | |
| DenseNet121 | 0.88 | 0.87 | 0.88 | 0.89 | |
| DenseNet169 | 0.86 | 0.86 | 0.87 | 0.90 | 0.89 |
| DenseNet201 | 0.88 | 0.86 | 0.88 | 0.90 | 0.90 |
| Ensemble | 0.90 | 0.87 | 0.90 | 0.90 |
| Metrics | IoU | Dice | F1-Score |
|---|---|---|---|
| UNet | 0.82 | 0.76 | 0.82 |
| Deeplabv3+ | 0.77 | 0.68 | 0.78 |
| Metrics | IoU | Dice | F1-Score |
|---|---|---|---|
| UNet | 0.90 | 0.87 | 0.91 |
| Deeplabv3+ | 0.89 | 0.87 | 0.91 |
| Model | Backbones | Average Ensemble |
|---|---|---|
| Unet | VGG16 ResNet50V2 DenseNet121 | 0.86 |
| Unet 2plus | VGG16 ResNet50V2 DenseNet169 | 0.84 |
| Attension Unet | VGG16 ResNet50V2 DenseNet169 | 0.84 |
| Deeplabv3+ | VGG16, DenseNet169 DenseNet201 | 0.80 |
| Model | Backbones | Average Ensemble | Weighted Ensemble | Weighted Ratio |
|---|---|---|---|---|
| Unet | VGG16 ResNet101V2 DenseNet121 | 0.91 | 0.91 | [0.3, 0.2, 0.3] |
| Unet 2plus | VGG16 ResNet50V2 DenseNet121 | 0.87 | 0.88 | [0.1, 0.3, 0.4] |
| Attension Unet | VGG16 ResNet50V2 DenseNet121 | 0.90 | 0.90 | [0.4, 0.1, 0.3] |
| Deeplabv3+ | VGG16 ResNet50 DenseNet201 | 0.90 | 0.91 | [0.4,0.0, 0.4] |
| Model | Unet | Unet2plus | Attention Unet | R2Unet | Ensemble |
|---|---|---|---|---|---|
| MeanIoU | 0.80 | 0.80 | 0.82 | 0.78 | 0.83 |
| Model | Unet | Unet2plus | Attention Unet | R2Unet | Ensemble |
|---|---|---|---|---|---|
| MeanIoU | 0.88 | 0.82 | 0.84 | 0.87 | 0.89 |
| Models | meanIoU | Epochs |
|---|---|---|
| Model 1 | 0.90 | 264 |
| Model 2 | 0.89 | 175 |
| Model 3 | 0.89 | 153 |
| Model 4 | 0.90 | 264 |
| Model 5 | 0.90 | 249 |
| Model 6 | 0.91 | 306 |
| Model 7 | 0.90 | 202 |
| Model Combinations | Average Ensemble meanIoU |
|---|---|
| [model 1, model 3, model 6] | 0.918 |
| [model 3, model 5, model 6] | 0.917 |
| [model 1, model 5, model 6] | 0.917 |
| [model 1, model 6, model 7] | 0.917 |
| [model 1, model 4, model 6] | 0.916 |
| [model 1, model 3, model 5] | 0.916 |
| Model Combinations | Average Ensemble meanIoU |
|---|---|
| [model 1, model 6] | 0.917 |
| [model 1, model 7] | 0.914 |
| [model 3, model 6] | 0.914 |
| [model 5, model 6] | 0.913 |
| [model 4, model 6] | 0.913 |
| [model 1, model 5] | 0.913 |
| Model Combinations | Weighted Ensemble meanIoU | Weight Ratio |
|---|---|---|
| [model 1, model 3, model 6] | 0.936 | [0.4, 0.0, 0.2] |
| [model 1, model 6] | 0.936 | [0.4, 0.2] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-D.; Tsai, C.M. Advancing Barrett’s Esophagus Segmentation: A Deep-Learning Ensemble Approach with Data Augmentation and Model Collaboration. Bioengineering 2024, 11, 47. https://doi.org/10.3390/bioengineering11010047
Lee J-D, Tsai CM. Advancing Barrett’s Esophagus Segmentation: A Deep-Learning Ensemble Approach with Data Augmentation and Model Collaboration. Bioengineering. 2024; 11(1):47. https://doi.org/10.3390/bioengineering11010047
Chicago/Turabian StyleLee, Jiann-Der, and Chih Mao Tsai. 2024. "Advancing Barrett’s Esophagus Segmentation: A Deep-Learning Ensemble Approach with Data Augmentation and Model Collaboration" Bioengineering 11, no. 1: 47. https://doi.org/10.3390/bioengineering11010047
APA StyleLee, J.-D., & Tsai, C. M. (2024). Advancing Barrett’s Esophagus Segmentation: A Deep-Learning Ensemble Approach with Data Augmentation and Model Collaboration. Bioengineering, 11(1), 47. https://doi.org/10.3390/bioengineering11010047








