Online Ergonomic Evaluation in Realistic Manual Material Handling Task: Proof of Concept
Abstract
:1. Introduction
2. Materials and Methods
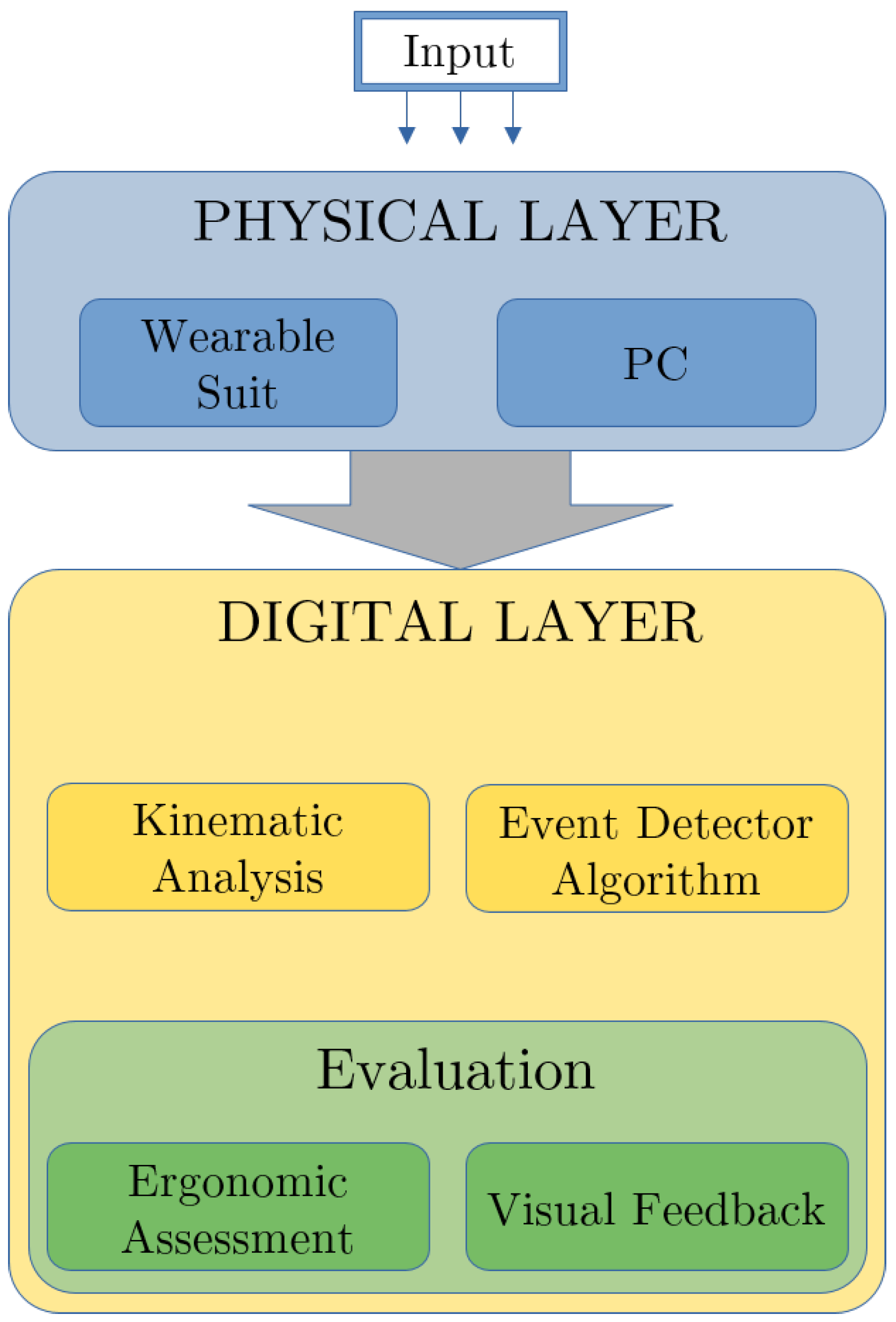
2.1. On-LI Architecture
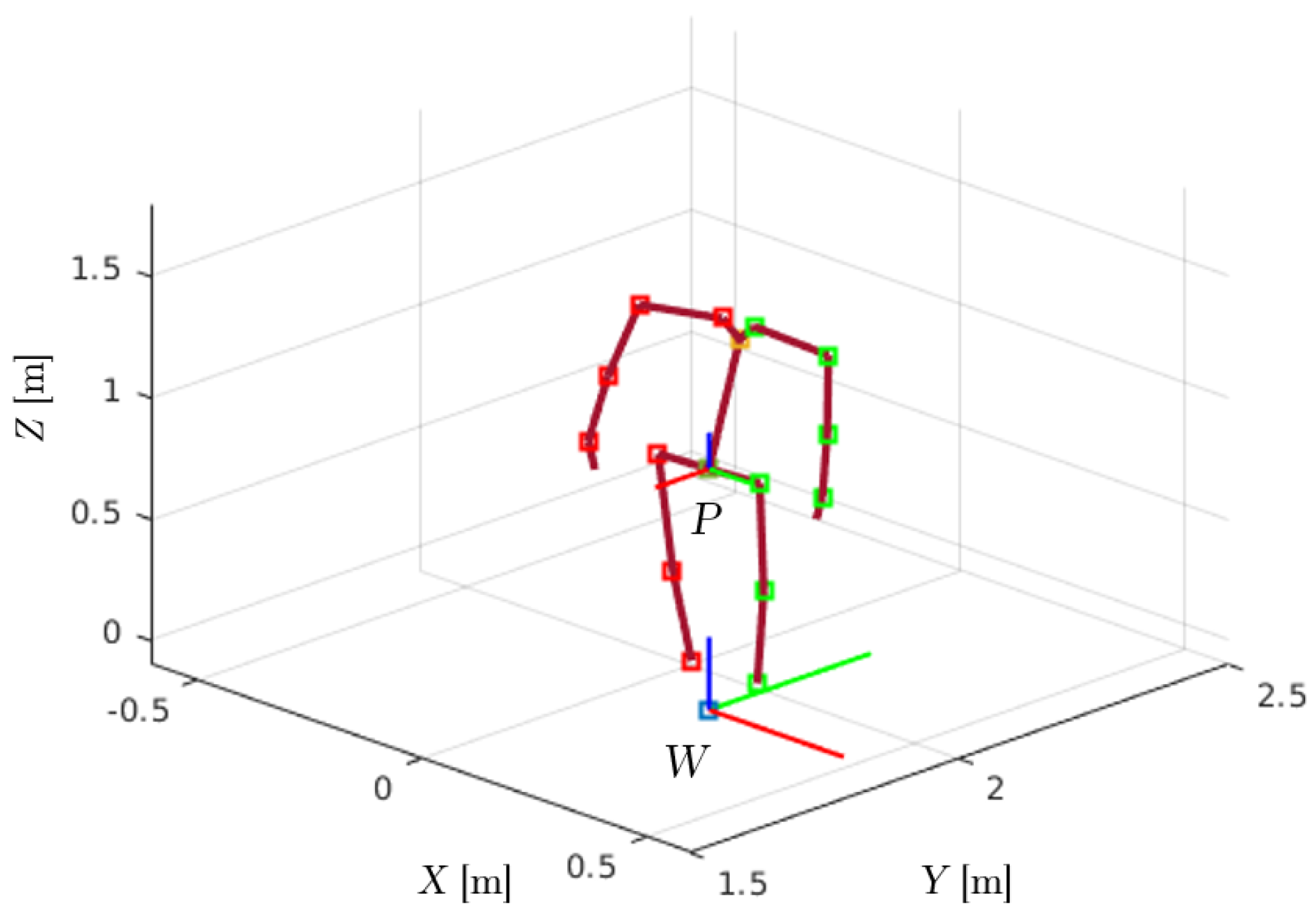
2.2. Kinematic Analysis
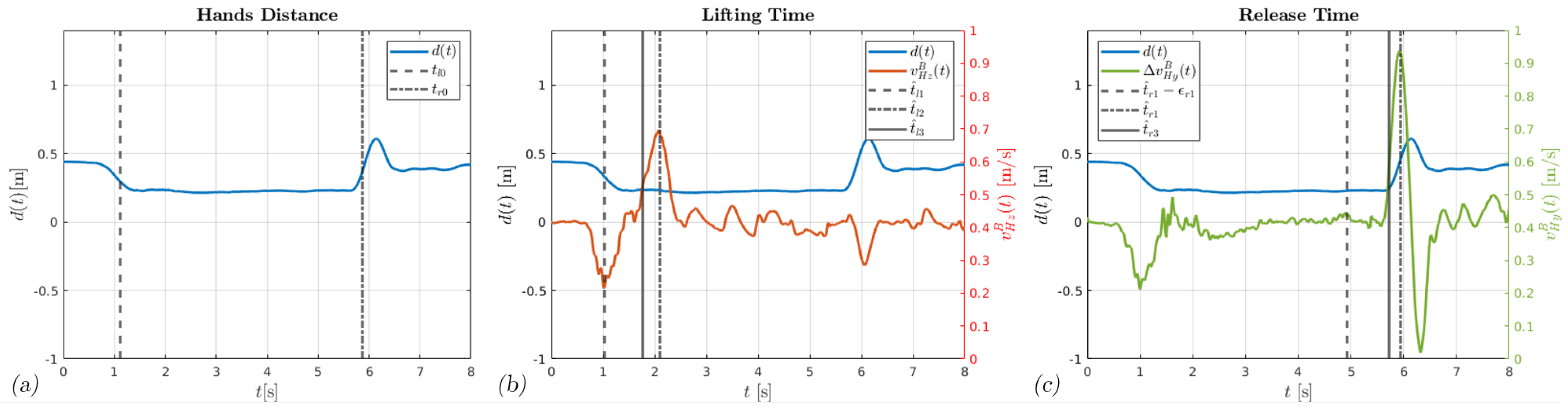
2.3. Event Detector Algorithm
2.4. Ergonomic Assessment: Digital Algorithm
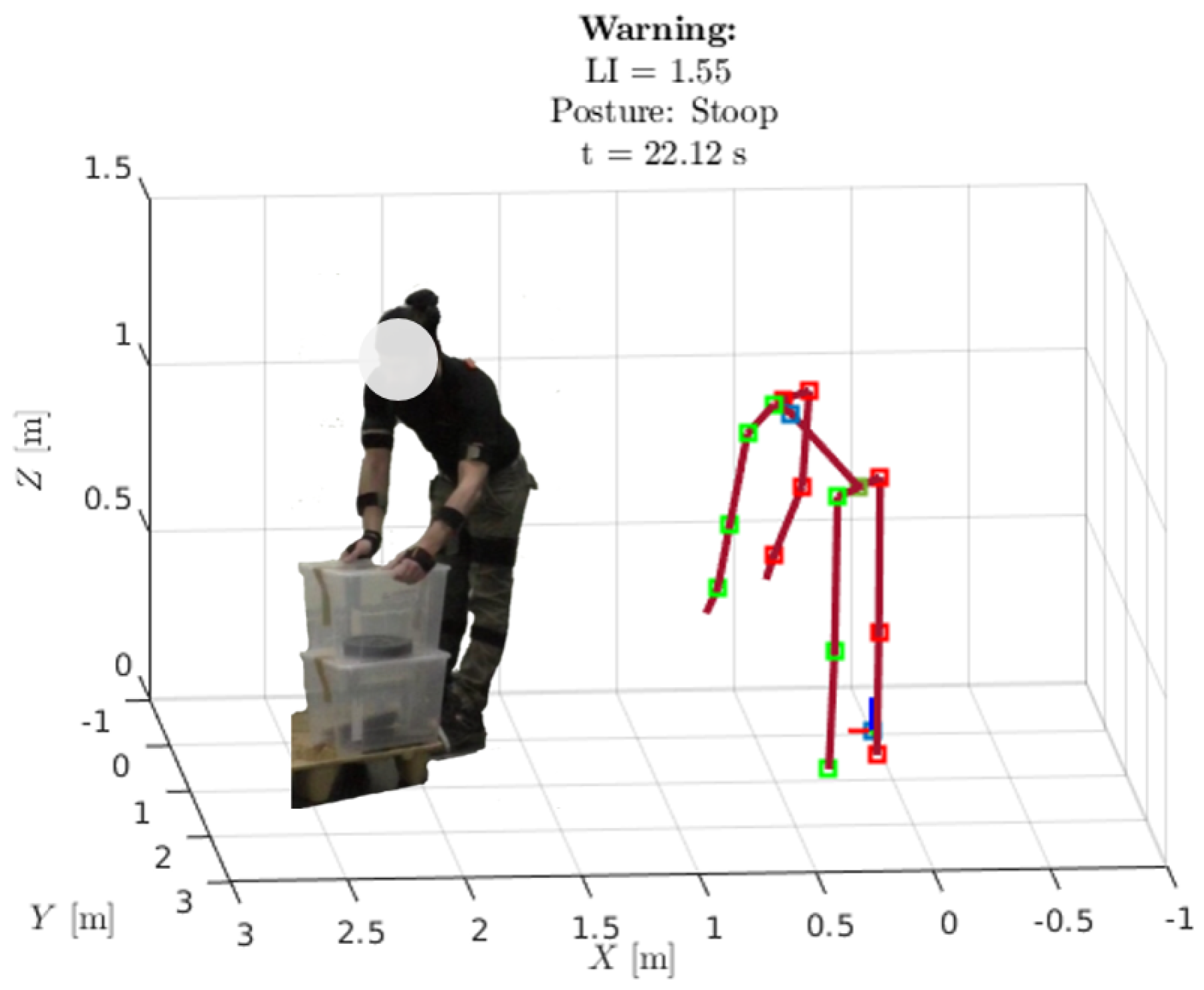
2.5. Visual Feedback
3. Experimental Assessment
3.1. Subjects and Data Collection
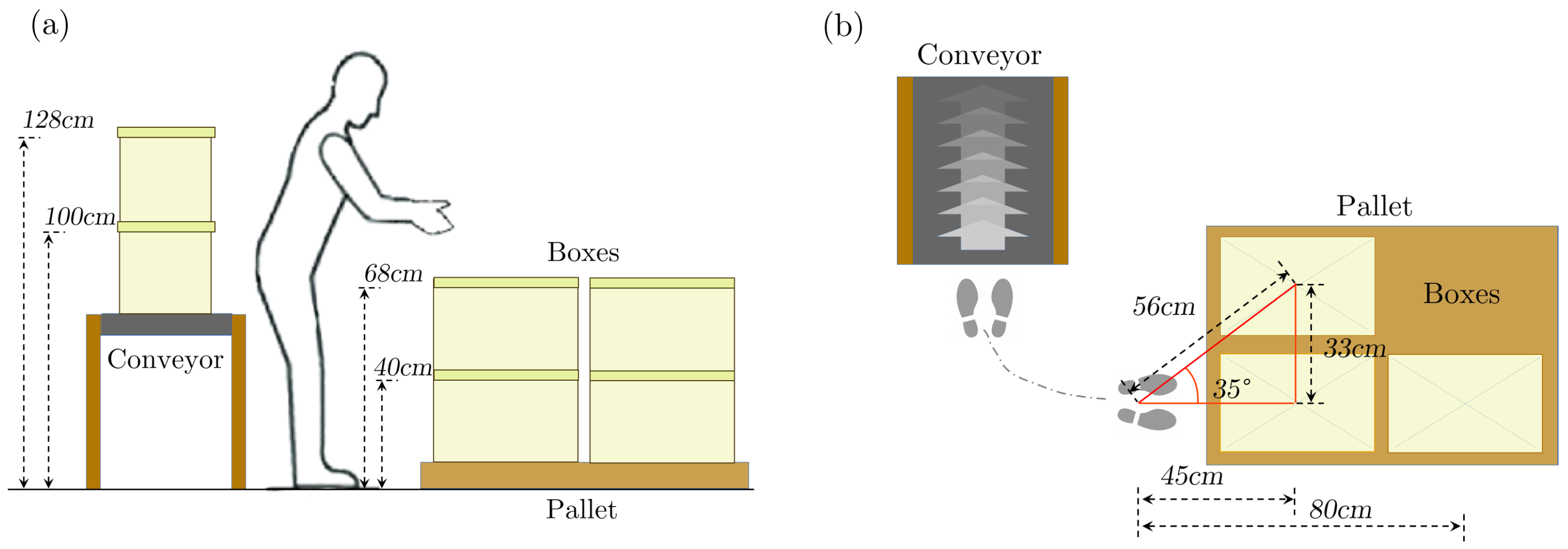
3.2. Experimental Protocol
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WMSD | Work-related musculoskeletal disorder |
| MMH | Manual material handling |
| NIOSH | National Institute for Occupational Safety and Health |
| TACOS | Time-based assessment computerized strategy |
| OCRA | Occupational repetitive action |
| RULA | Rapid upper limb assessment |
| EAWS | Ergonomic assessment worksheet |
| On-LI | Online Lifting Index |
| IMU | Inertial measurement unit |
| EDA | Event detector algorithm |
| DoFs | Degree(s) of freedom |
| RWL | Recommended weight limit |
| LI | Lifting Index |
| MT | Motion tracker |
References
- Schneider, E.; Irastorza, X.; Copsey, S. Work-Related Musculoskeletal Disorders in the EU—Facts and Figures; European Agency for Safety and Health at Work: Bilbao, Spain, 2010. [Google Scholar]
- Vos, T.; Abajobir, A.A.; Abate, K.H.; Abbafati, C.; Abbas, K.M.; Abd-Allah, F.; Abdulkader, R.S.; Abdulle, A.M.; Abebo, T.A.; Abera, S.F.; et al. Global, regional, and national incidence, prevalence, and years lived with disability for 328 diseases and injuries for 195 countries, 1990–2016: A systematic analysis for the Global Burden of Disease Study 2016. Lancet 2017, 390, 1211–1259. [Google Scholar] [CrossRef] [PubMed]
- de Kok, J.; Vroonhof, P.; Snijders, J.; Roullis, G.; Clarke, M.; Peereboom, K.; van Dorst, P.; Isusi, I. Work-Related Musculoskeletal Disorders: Prevalence, Costs and Demographics in the EU; Technical Report; European Agency for Safety and Health at Work: Bilbao, Spain, 2019. [Google Scholar]
- Bevan, S. Economic impact of musculoskeletal disorders (MSDs) on work in Europe. Best Pract. Res. Clin. Rheumatol. 2015, 29, 356–373. [Google Scholar] [CrossRef] [PubMed]
- Rudy, T.E.; Weiner, D.K.; Lieber, S.J.; Slaboda, J.; Boston, J.R. The impact of chronic low back pain on older adults: A comparative study of patients and controls. Pain 2007, 131, 293–301. [Google Scholar] [CrossRef] [PubMed]
- Coyte, P.C.; Asche, C.V.; Croxford, R.; Chan, B. The economic cost of musculoskeletal disorders in Canada. Arthritis Rheum. Off. J. Am. Coll. Rheumatol. 1998, 11, 315–325. [Google Scholar] [CrossRef] [PubMed]
- Lee, P. The economic impact of musculoskeletal disorders. Qual. Life Res. 1994, 3, S85–S91. [Google Scholar] [CrossRef] [PubMed]
- Buckle, P. Ergonomics and musculoskeletal disorders: Overview. Occup. Med. 2005, 55, 164–167. [Google Scholar] [CrossRef] [PubMed]
- Pieper, C.; Schröer, S.; Eilerts, A.L. Evidence of workplace interventions—A systematic review of systematic reviews. Int. J. Environ. Res. Public Health 2019, 16, 3553. [Google Scholar] [CrossRef]
- National Institute for Occupational Safety and Health. Division of Physical Sciences and Engineering. NIOSH, Manual of Analytical Methods; US Department of Health and Human Services, Public Health Service, Centers: Washington, DC, USA, 1994.
- Waters, T.; Occhipinti, E.; Colombini, D.; Alvarez-Casado, E.; Fox, R. Variable lifting index (vli) a new method for evaluating variable lifting tasks. Hum. Factors 2016, 58, 695–711. [Google Scholar] [CrossRef]
- Garg, A.; Kapellusch, J.M. The cumulative lifting index (CULI) for the revised NIOSH lifting equation: Quantifying risk for workers with job rotation. Hum. Factors 2016, 58, 683–694. [Google Scholar] [CrossRef]
- Colombini, D.; Occhipinti, E. Working Posture Assessment: The TACOS (Time-Based Assessment Computerized Strategy) Method; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Occhipinti, E. OCRA: A concise index for the assessment of exposure to repetitive movements of the upper limbs. Ergonomics 1998, 41, 1290–1311. [Google Scholar] [CrossRef]
- Garg, A.; Moore, J.S.; Kapellusch, J.M. The strain index to analyze jobs for risk of distal upper extremity disorders: Model validation. In Proceedings of the 2007 IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 2–4 December 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 497–499. [Google Scholar]
- Humadi, A.; Nazarahari, M.; Ahmad, R.; Rouhani, H. In-field instrumented ergonomic risk assessment: Inertial measurement units versus Kinect V2. Int. J. Ind. Ergon. 2021, 84, 103147. [Google Scholar] [CrossRef]
- Cole, D.; Rivilis, I.; Van Eerd, D.; Cullen, K.; Irvin, E.; Kramer, D. Effectiveness of Participatory Ergonomic Interventions: A Systematic Review; Institute for Work & Health: Toronto, ON, Canada, 2005. [Google Scholar]
- ISO 11228-1:2003; Ergonomics—Manual Handling—Part 1: Lifting and Carrying. ISO: Geneva, Switzerland, 2003.
- Rybnikár, F.; Kačerová, I.; Hořejší, P.; Šimon, M. Ergonomics Evaluation Using Motion Capture Technology—Literature Review. Appl. Sci. 2022, 13, 162. [Google Scholar] [CrossRef]
- Tirupachuri, Y.; Ramadoss, P.; Rapetti, L.; Latella, C.; Darvish, K.; Traversaro, S.; Pucci, D. Online non-collocated estimation of payload and articular stress for real-time human ergonomy assessment. IEEE Access 2021, 9, 123260–123279. [Google Scholar] [CrossRef]
- Colim, A.; Faria, C.; Braga, A.C.; Sousa, N.; Rocha, L.; Carneiro, P.; Costa, N.; Arezes, P. Towards an ergonomic assessment framework for industrial assembly workstations—A case study. Appl. Sci. 2020, 10, 3048. [Google Scholar] [CrossRef]
- Kim, W.; Lorenzini, M.; Balatti, P.; Nguyen, P.D.; Pattacini, U.; Tikhanoff, V.; Peternel, L.; Fantacci, C.; Natale, L.; Metta, G.; et al. Adaptable workstations for human-robot collaboration: A reconfigurable framework for improving worker ergonomics and productivity. IEEE Robot. Autom. Mag. 2019, 26, 14–26. [Google Scholar] [CrossRef]
- Marin, A.G.; Shourijeh, M.S.; Galibarov, P.E.; Damsgaard, M.; Fritzsch, L.; Stulp, F. Optimizing contextual ergonomics models in human-robot interaction. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–9. [Google Scholar]
- Peternel, L.; Kim, W.; Babič, J.; Ajoudani, A. Towards ergonomic control of human-robot co-manipulation and handover. In Proceedings of the 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017; pp. 55–60. [Google Scholar]
- Harari, Y.; Riemer, R.; Bechar, A. Differences in spinal moments, kinematics and pace during single-task and combined manual material handling jobs. Appl. Ergon. 2019, 81, 102871. [Google Scholar] [CrossRef]
- Lorenzini, M.; Kim, W.; Ajoudani, A. An online multi-index approach to human ergonomics assessment in the workplace. IEEE Trans. Hum. Mach. Syst. 2022, 52, 812–823. [Google Scholar] [CrossRef]
- Malaisé, A.; Maurice, P.; Colas, F.; Ivaldi, S. Online Human Activity Recognition for Ergonomics Assessment. In Proceedings of the JNRH 2018-Journées Nationales de la Robotique Humanoïde, Nancy, France, 14–15 June 2018. [Google Scholar]
- Malaisé, A.; Maurice, P.; Colas, F.; Ivaldi, S. Activity recognition for ergonomics assessment of industrial tasks with automatic feature selection. IEEE Robot. Autom. Lett. 2019, 4, 1132–1139. [Google Scholar] [CrossRef]
- Maurice, P.; Malaisé, A.; Amiot, C.; Paris, N.; Richard, G.J.; Rochel, O.; Ivaldi, S. Human movement and ergonomics: An industry-oriented dataset for collaborative robotics. Int. J. Robot. Res. 2019, 38, 1529–1537. [Google Scholar] [CrossRef]
- UNI ISO 11228-1:2022; Ergonomics—Manual Handling—Part 1: Lifting, Lowering and Carrying. Ente Nazionale Italiano di Unificazione (UNI): Milan, Italy, 2022.
- Di Natali, C.; Mattila, J.; Kolu, A.; De Vito, P.; Gauttier, S.; Morata, M.; Garcia, M.; Caldwell, D. Smart tools for railway inspection and maintenance work, performance and safety improvement. Transp. Res. Procedia 2023, 72, 3070–3077. [Google Scholar] [CrossRef]
- Poliero, T.; Lazzaroni, M.; Toxiri, S.; Di Natali, C.; Caldwell, D.G.; Ortiz, J. Applicability of an active back-support exoskeleton to carrying activities. Front. Robot. AI 2020, 7, 579963. [Google Scholar] [CrossRef] [PubMed]
- Poliero, T.; Sposito, M.; Toxiri, S.; Di Natali, C.; Iurato, M.; Sanguineti, V.; Caldwell, D.G.; Ortiz, J. Versatile and non-versatile occupational back-support exoskeletons: A comparison in laboratory and field studies. Wearable Technol. 2021, 2, e12. [Google Scholar] [CrossRef]
- Waters, T.R.; Lu, M.L.; Piacitelli, L.A.; Werren, D.; Deddens, J.A. Efficacy of the revised NIOSH lifting equation to predict risk of low back pain due to manual lifting: Expanded cross-sectional analysis. J. Occup. Environ. Med. 2011, 53, 1061–1067. [Google Scholar] [CrossRef] [PubMed]



| Lifting Index | Risk Magnitude | Recommendation |
|---|---|---|
| ≤1.00 | Very Low | No modification required |
| – | Low | Pay attention to frequency of execution, excessively heavy loads, and/or awkward postures that are held for too long |
| – | Moderate | Redesign tasks and workplaces according to priorities to reduce the Lifting Index |
| – | High | It is highly necessary to modify the task to reduce the Lifting Index |
| >3.00 | Very High | It is critically important to change the task immediately to reduce the Lifting Index |
| Box | Hands Height | Vertical Travel | Horizontal Distance | Twist | Grasp | Frequency | Single Limb | Load | LI |
|---|---|---|---|---|---|---|---|---|---|
| (cm) | (cm) | (cm) | (deg) | (G,S,P) | (Lifting/Minute) | (Yes/No) | (kg) | ||
| FH | 68 | 32 | 45 | 0 | S | 6 | No | 10 | 1.13 |
| FL | 40 | 88 | 45 | 0 | S | 6 | No | 10 | 1.33 |
| LH | 68 | 32 | 56 | 22 | S | 6 | No | 10 | 1.44 |
| LL | 40 | 88 | 56 | 22 | S | 6 | No | 10 | 1.77 |
| RH | 68 | 32 | 65 (63*) | 0 | S | 6 | No | 10 | 1.52 |
| RL | 40 | 88 | 65 (63*) | 0 | S | 6 | No | 10 | 1.79 |
| Box | Hands Height | Vertical Travel | Horizontal Distance | Twist | Grasp | Frequency | Single Limb | Load | LI |
|---|---|---|---|---|---|---|---|---|---|
| (cm) | (cm) | (cm) | (deg) | (G,S,P) | (Lifting/Minute) | (Yes/No) | (kg) | ||
| FH | 70 ± 6 | 34 ± 4 | 47 ± 8 | 2 ± 4 | S | 6 | No | 10 | 1.23 ± 0.16 |
| FL | 44 ± 5 | 79 ± 2 | 45 ± 7 | 3 ± 5 | S | 6 | No | 10 | 1.27 ± 0.16 |
| LH | 67 ± 4 | 38 ± 3 | 56 ± 7 | 26 ± 10 | S | 6 | No | 10 | 1.52 ± 0.17 |
| LL | 42 ± 4 | 79 ± 4 | 42 ± 7 | 24 ± 11 | S | 6 | No | 10 | 1.61 ± 0.26 |
| RH | 70 ± 8 | 39 ± 7 | 67 ± 5 (63*) | -2 ± 3 | S | 6 | No | 10 | 1.54 ± 0.09 |
| RL | 46 ± 8 | 75 ± 6 | 61 ± 6 (63*) | 2 ± 3 | S | 6 | No | 10 | 1.69 ± 0.11 |
| Box | Hands Height | Vertical Travel | Horizontal Distance | Twist | LI | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Abs. Err. | Rel. Err. | Abs. Err. | Rel. Err. | Abs. Err. | Rel. Err. | Abs. Err. | Rel. Err. | Abs. Err. | Rel. Err. | |
| (cm) | (%) | (cm) | (%) | (cm) | (%) | (deg) | (%) | (%) | ||
| FH | 2 | 2.5 | 2 | 1.1 | 2 | 3.2 | 2 | 1.4 | 0.1 | 3.3 |
| FL | 4 | 5.0 | 9 | 5.1 | 0 | 0 | 3 | 2.2 | 0.06 | 2.0 |
| LH | 1 | 1.2 | 6 | 3.4 | 0 | 0 | 4 | 2.9 | 0.08 | 2.6 |
| LL | 2 | 2.5 | 9 | 5.1 | 14 | 22.2 | 2 | 1.4 | 0.15 | 5 |
| RH | 2 | 2.5 | 7 | 4.0 | 2 | 6.3 | 2 | 1.4 | 0.02 | 0.6 |
| RL | 6 | 7.5 | 13 | 7.4 | 4 | 3.2 | 2 | 1.4 | 0.1 | 3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leggieri, S.; Fanti, V.; Caldwell, D.G.; Di Natali, C. Online Ergonomic Evaluation in Realistic Manual Material Handling Task: Proof of Concept. Bioengineering 2024, 11, 14. https://doi.org/10.3390/bioengineering11010014
Leggieri S, Fanti V, Caldwell DG, Di Natali C. Online Ergonomic Evaluation in Realistic Manual Material Handling Task: Proof of Concept. Bioengineering. 2024; 11(1):14. https://doi.org/10.3390/bioengineering11010014
Chicago/Turabian StyleLeggieri, Sergio, Vasco Fanti, Darwin G. Caldwell, and Christian Di Natali. 2024. "Online Ergonomic Evaluation in Realistic Manual Material Handling Task: Proof of Concept" Bioengineering 11, no. 1: 14. https://doi.org/10.3390/bioengineering11010014
APA StyleLeggieri, S., Fanti, V., Caldwell, D. G., & Di Natali, C. (2024). Online Ergonomic Evaluation in Realistic Manual Material Handling Task: Proof of Concept. Bioengineering, 11(1), 14. https://doi.org/10.3390/bioengineering11010014







