A Fast Calibration Method for Pneumotachograph with a 3L Syringe
Abstract
1. Introduction
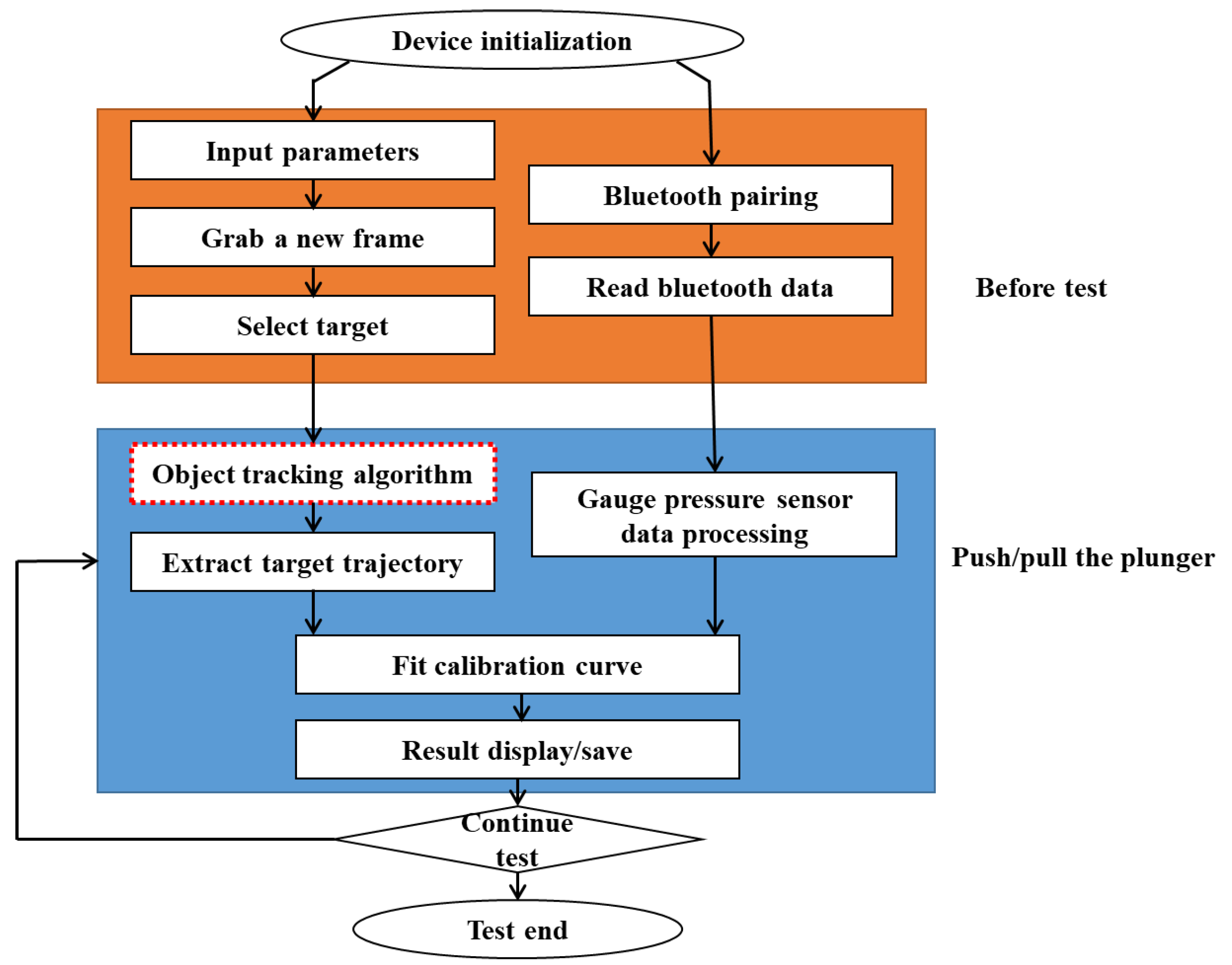
2. Methods
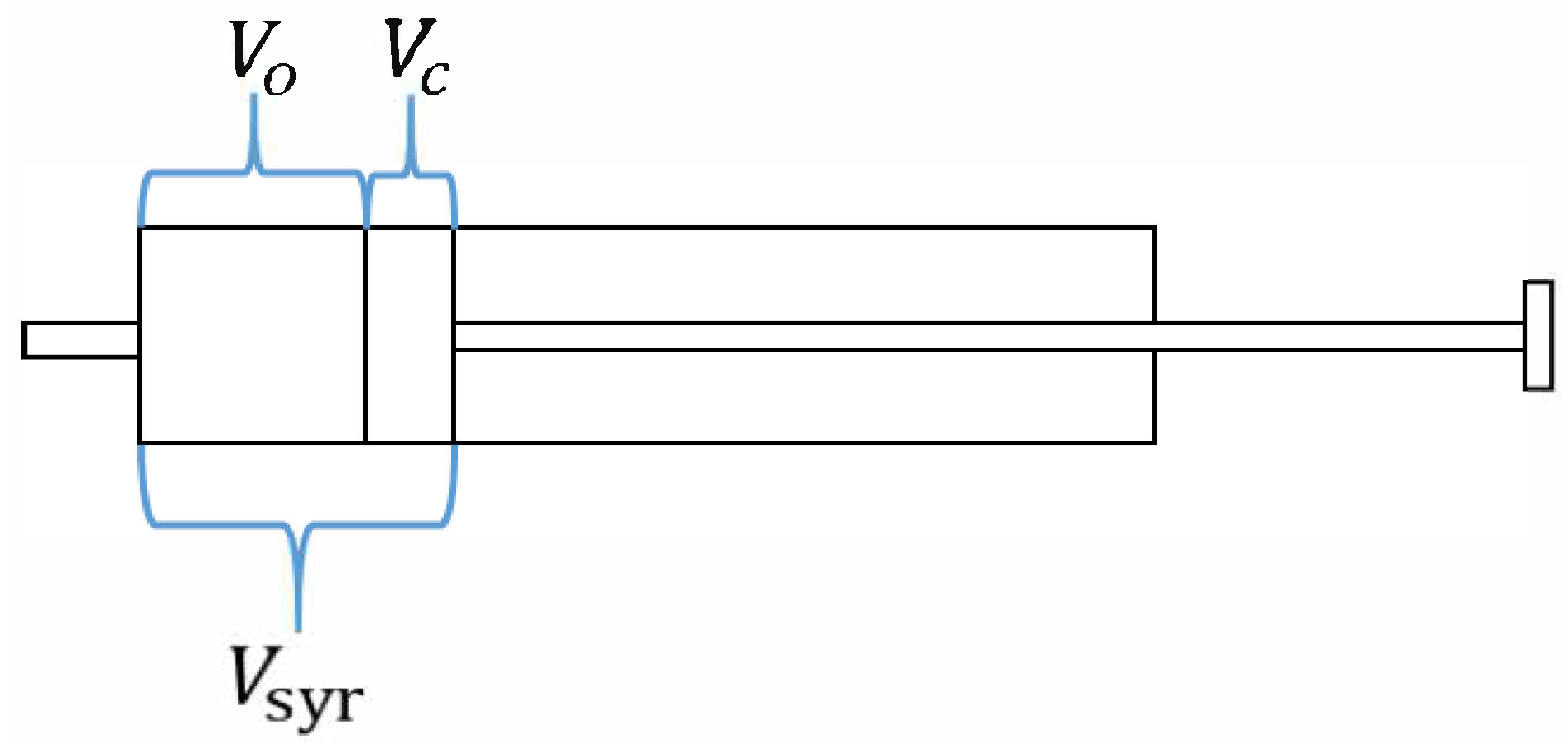
2.1. Tapping Position Optimization
2.1.1. Presumptions
- The air in the 3L syringe is set as the ideal gas, which satisfies the ideal gas state equation;
- The friction between the plunger and the cylinder wall is relatively small and can be ignored;
- The gas in the cylinder cavity has no heat exchange with the outside world. It is an adiabatic process. The gas temperature is the ambient temperature;
- Cylinder leakage can be ignored.
2.1.2. Governing Equations
2.1.3. Dynamic Mesh Method and Boundary Conditions
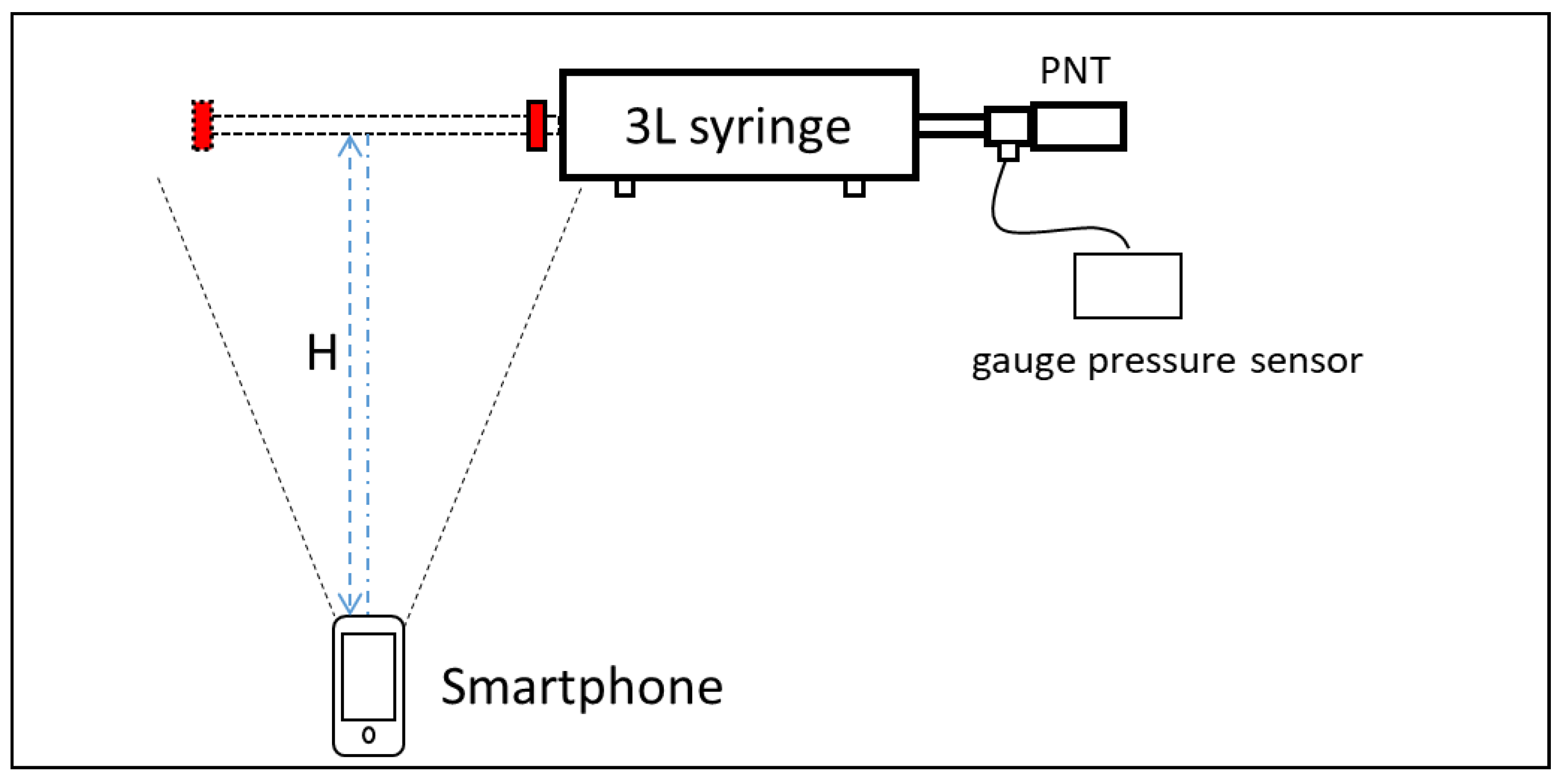
2.2. Experimental Method
2.2.1. Experiment 1: Validation of Tapping Position
2.2.2. Experiment 2: Validation of the Calibration System
2.2.3. Experiment 3: The Correction for Real Output Flow
2.2.4. Experiment 4: Validation of Calibration Accuracy
3. Results and Discussion
3.1. Tapping Position Optimization Results
3.2. Experiment 1: Validation of Tapping Position
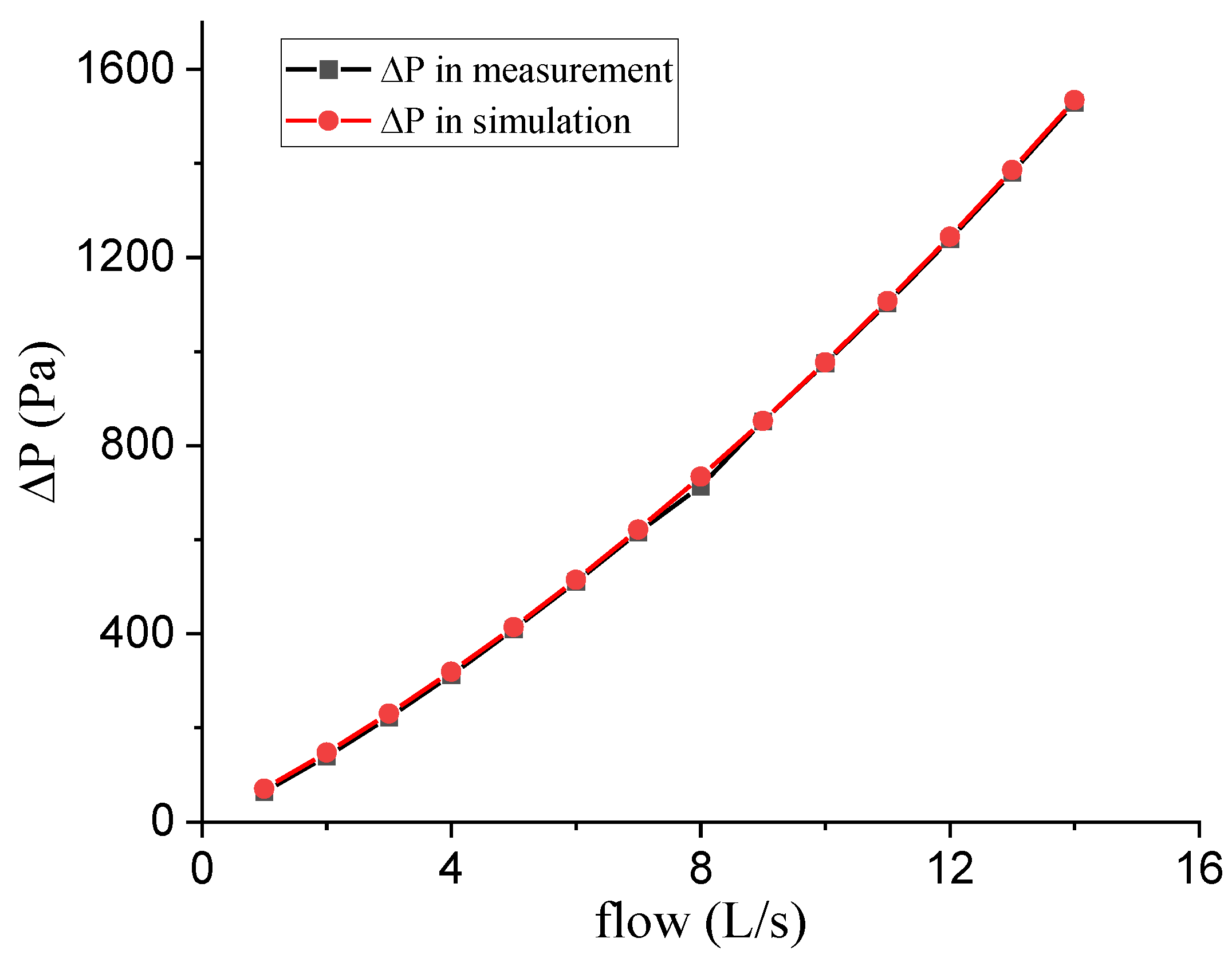
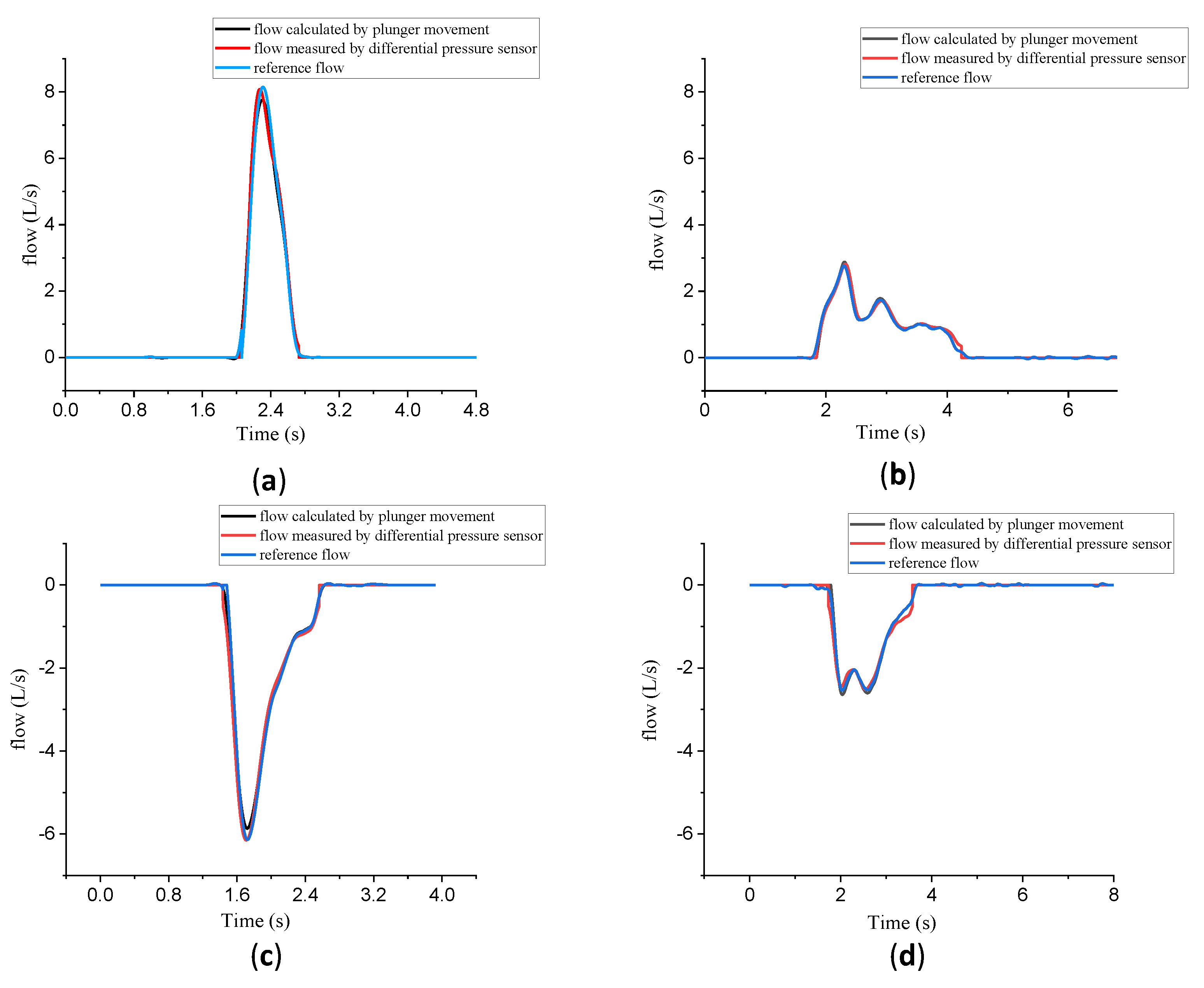
3.3. Experiment 2: Validation of the Calibration System
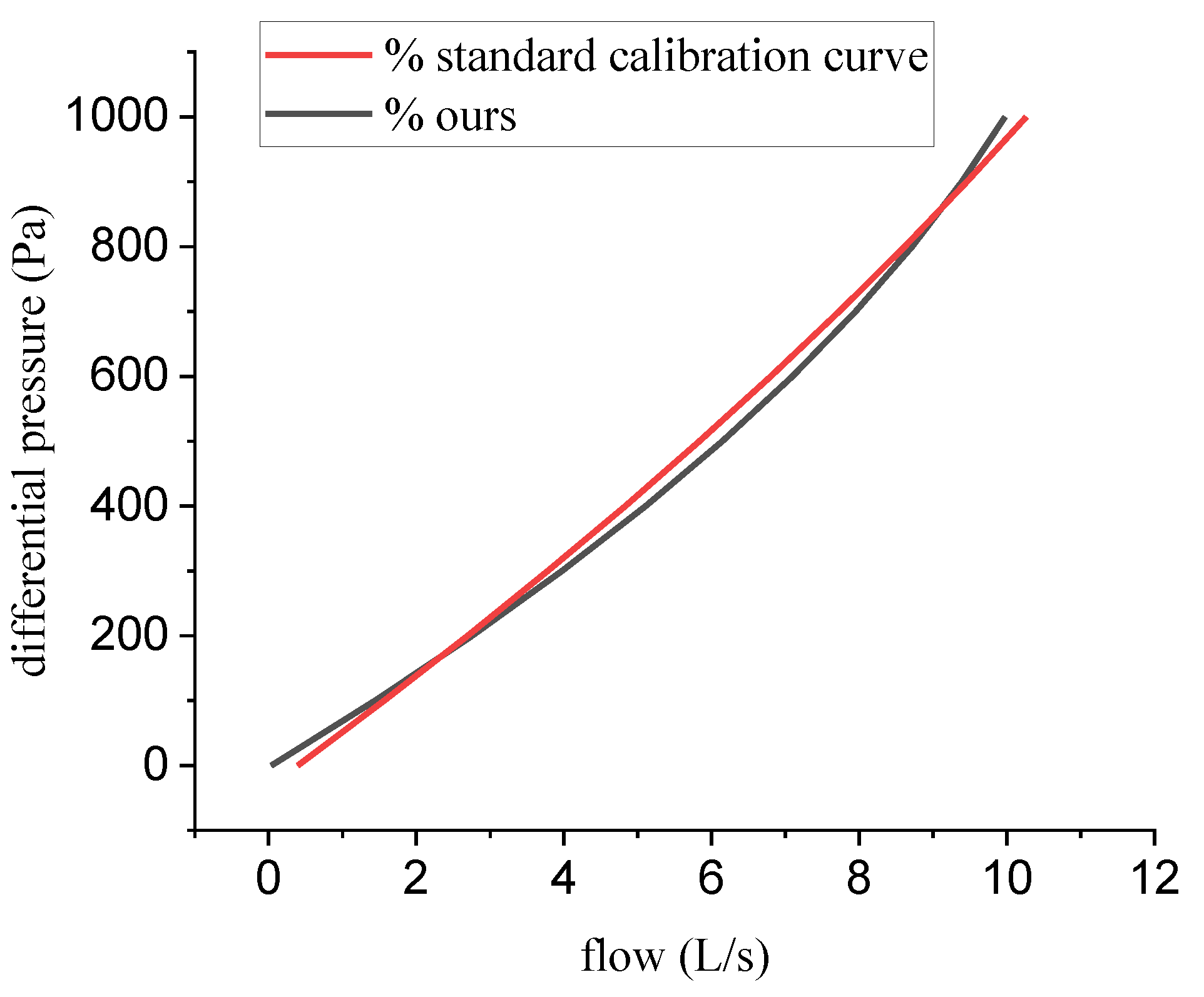
3.4. Experiment 3: The Correction for Real Output Flow
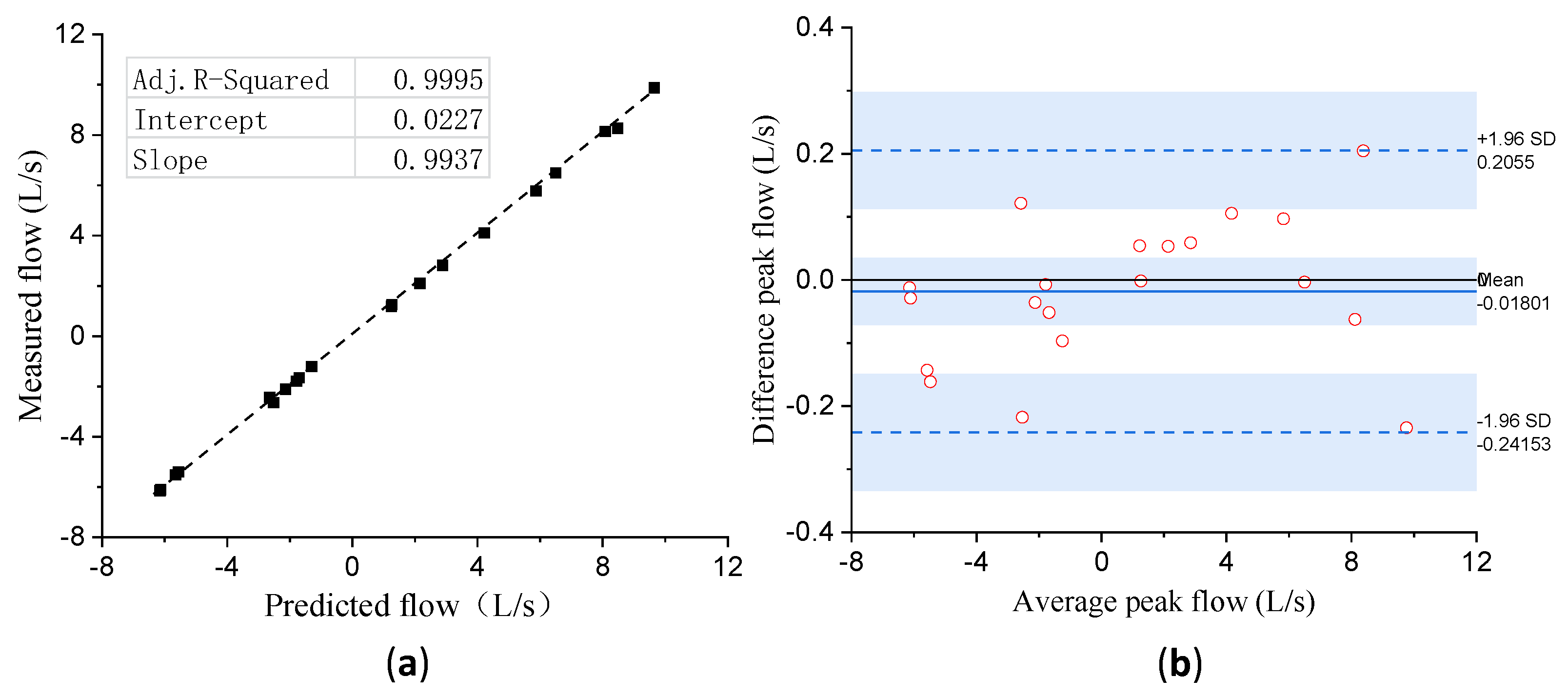
3.5. Experiment 4: Validation of Calibration Accuracy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Senior, R.M.; Anthonisen, N.R. Chronic obstructive pulmonary disease (COPD). Am. J. Respir. Crit. Care Med. 1998, 157, S139–S147. [Google Scholar] [CrossRef] [PubMed]
- Doña, E.; Reinoso-Arija, R.; Carrasco-Hernandez, L.; Doménech, A.; Dorado, A.; Lopez-Campos, J.L. Exploring Current Concepts and Challenges in the Identification and Management of Early-Stage COPD. J. Clin. Med. 2023, 12, 5293. [Google Scholar] [CrossRef] [PubMed]
- Leving, M.T.; Kocks, J.; Bosnic-Anticevich, S.; Dekhuijzen, R.; Usmani, O.S. Relationship between peak inspiratory flow and patient and disease characteristics in individuals with COPD—A systematic scoping review. Biomedicines 2022, 10, 458. [Google Scholar] [CrossRef] [PubMed]
- Al Rajeh, A.M.; Hurst, J.R. Monitoring of physiological parameters to predict exacerbations of chronic obstructive pulmonary disease (COPD): A systematic review. J. Clin. Med. 2016, 5, 108. [Google Scholar] [CrossRef] [PubMed]
- Gilbey, J.D.; Wilson, M. Measurement of gas flow and volume. Anaesth. Intensive Care Med. 2021, 22, 37–41. [Google Scholar] [CrossRef]
- Brooker, G. A Telespirometer for the Developing World. Electronics 2020, 9, 275. [Google Scholar] [CrossRef]
- Schena, E.; Lupi, G.; Cecchini, S.; Silvestri, S. Linearity dependence on oxygen fraction and gas temperature of a novel Fleisch pneumotachograph for neonatal ventilation at low flow rates. Measurement 2012, 45, 2064–2071. [Google Scholar] [CrossRef]
- Mandal, N. Respirometers including spirometer, pneumotachograph and peak flow meter. Anaesth. Intensive Care Med. 2006, 7, 1–5. [Google Scholar] [CrossRef]
- Schena, E.; Massaroni, C.; Saccomandi, P.; Cecchini, S. Flow measurement in mechanical ventilation: A review. Med. Eng. Phys. 2015, 37, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Miller, M.R.; Hankinson, J.; Brusasco, V.; Burgos, F.; Casaburi, R.; Coates, A.; Crapo, R.; Enright, P.; Grinten, C.P.M.V.D.; Gustafsson, P.A. Standardisation of spirometry. Eur. Respir. J. 2005, 26, 319–338. [Google Scholar] [CrossRef] [PubMed]
- Boros, P.W.; Maciejewski, A.; Nowicki, M.M.; Wesołowski, S. Comparability of portable and desktop spirometry: A randomized, parallel assignment, open-label clinical trial. Adv. Respir. Med. 2022, 90, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Yeh, M.P.; Gardner, R.M.; Adams, T.D.; Yanowitz, F.G. Computerized determination of pneumotachometer characteristics using a calibrated syringe. J. Appl. Physiol. 1982, 53, 280–285. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Turner, M.J.; Yem, J.S.; Baker, A.B. Calibration of pneumotachographs using a calibrated syringe. J. Appl. Physiol. 2003, 95, 571–576. [Google Scholar] [CrossRef] [PubMed]
- Biselli, P.J.C.; Nóbrega, R.S.; Soriano, F.G. Nonlinear flow sensor calibration with an accurate syringe. Sensors 2018, 18, 2163. [Google Scholar] [CrossRef]
- Quelhas, A.; Motta-Ribeiro, G.; Pino, A.; Giannella-Neto, A.; Jandre, F. Pneumotachograph Calibration: Influence of Regularization Methods on Parameter Estimation and the Use of Alternative Calibration Models. In Proceedings of the Brazilian Congress on Biomedical Engineering, Vitoria, Brazil, 26–30 October 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 961–968. [Google Scholar]
- Navajas, D.; Roca, J.; Farré, R.; Rotger, M. Gas compression artefacts when testing peak expiratory flow meters with mechanically-driven syringes. Eur. Respir. J. 1997, 10, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Hankinson, J.; Reynolds, J.; Das, M.; Viola, J. Method to produce American Thoracic Society flow-time waveforms using a mechanical pump. Eur. Respir. J. 1997, 10, 690–694. [Google Scholar] [CrossRef] [PubMed]
- Cross, T.J.; Kelley, E.F.; Hardy, T.A.; Isautier, J.M.; Johnson, B.D. The syringe potentiometer: A low-cost device for pneumotachograph calibration. J. Appl. Physiol. 2019, 127, 1150–1162. [Google Scholar] [CrossRef] [PubMed]
- Sadrehaghighi, I. Dynamic & Adaptive Meshing. CFD Open Series, Patch. 2021, Volume 2. Available online: https://www.academia.edu/44183574/Dynamic_and_Adaptive_Meshing (accessed on 24 July 2023).
- Ma, X.; Fan, Z.; Da, X. Dynamic Mesh Method for Two-Dimensional Synthetic Jet. Procedia Eng. 2012, 31, 422–427. [Google Scholar] [CrossRef]
- Semin, N.; Ibrahim, R.A.B.; Abdul, R.I. In-cylinder flow through piston-port engines modeling using dynamic mesh. J. Appl. Sci. Res. 2008, 4, 58–64. [Google Scholar]
- Xv, Y.F.; Su, T.X.; Cui, J.J. Transient Analysis of Flow Field in Cylinder of an Engine. Adv. Mater. Res. 2011, 311, 2169–2173. [Google Scholar] [CrossRef]
- ANSYS Fluent. ANSYS Fluent UDF Manual; ANSYS Inc.: Washington, PA, USA, 2015. [Google Scholar]
- ANSYS Fluent. 12.0 User’s Guide; ANSYS Inc.: Washington, PA, USA, 2009; Volume 6, p. 552. [Google Scholar]
- Leichter, I.; Lindenbaum, M.; Rivlin, E. Mean shift tracking with multiple reference color histograms. Comput. Vis. Image Underst. 2010, 114, 400–408. [Google Scholar] [CrossRef]
- Chu, J.H.; Zhai, X.P.; Su, G.N.; Chen, C.L. Real-time object tracking based on android platform. Adv. Mater. Res. 2012, 403, 1438–1441. [Google Scholar] [CrossRef]
- Singh, P.; Deepak, B.; Sethi, T.; Murthy, M.D.P. Real-time object detection and tracking using color feature and motion. In Proceedings of the 2015 International Conference on Communications and Signal Processing (ICCSP), Melmaruvathur, India, 2–4 April 2015; pp. 1236–1241. [Google Scholar]
- Porikli, F.; Yilmaz, A. Object detection and tracking. In Video Analytics for Business Intelligence; Springer: Berlin/Heidelberg, Germany, 2012; pp. 3–41. [Google Scholar]
- Panchal, P.; Prajapati, G.; Patel, S.; Shah, H.; Nasriwala, J. A review on object detection and tracking methods. Int. J. Res. Emerg. Sci. Technol. 2015, 2, 7–12. [Google Scholar]
- Lewis, G.N.; Randall, M.; Pitzer, K.S.; Brewer, L. Thermodynamics; Courier Dover Publications: Mineola, NY, USA, 2020. [Google Scholar]





| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average ± Standard Deviation | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Push | 3.0038 | 3.0040 | 3.0114 | 3.0107 | 3.0143 | 3.0115 | 3.0135 | 3.0114 | 3.0126 | 3.0131 | 3.0106 ± 0.003715 |
| Pull | 3.0001 | 2.9932 | 3.0000 | 3.0030 | 3.0031 | 2.9999 | 2.9961 | 3.0013 | 2.9998 | 2.9971 | 2.9994 ± 0.003093 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Qiu, X.; Zhang, H.; Xu, L.; Lu, S.; Du, L.; Chen, X.; Fang, Z. A Fast Calibration Method for Pneumotachograph with a 3L Syringe. Bioengineering 2023, 10, 1053. https://doi.org/10.3390/bioengineering10091053
Li Y, Qiu X, Zhang H, Xu L, Lu S, Du L, Chen X, Fang Z. A Fast Calibration Method for Pneumotachograph with a 3L Syringe. Bioengineering. 2023; 10(9):1053. https://doi.org/10.3390/bioengineering10091053
Chicago/Turabian StyleLi, Yueqi, Xin Qiu, Hao Zhang, Lirui Xu, Saihu Lu, Lidong Du, Xianxiang Chen, and Zhen Fang. 2023. "A Fast Calibration Method for Pneumotachograph with a 3L Syringe" Bioengineering 10, no. 9: 1053. https://doi.org/10.3390/bioengineering10091053
APA StyleLi, Y., Qiu, X., Zhang, H., Xu, L., Lu, S., Du, L., Chen, X., & Fang, Z. (2023). A Fast Calibration Method for Pneumotachograph with a 3L Syringe. Bioengineering, 10(9), 1053. https://doi.org/10.3390/bioengineering10091053







