GNN-surv: Discrete-Time Survival Prediction Using Graph Neural Networks
Abstract
:1. Introduction
- We design and construct a sophisticated cancer patient similarity network that integrates both genomic and clinical features, enabling a better understanding of patient characteristics and relationships.
- We propose GNN-surv, a novel GNN that incorporates discrete-time survival models. We demonstrate its broad applicability via experiments across two different survival models and three types of GNN layers.
- We empirically show the superior performance of GNN-surv in survival prediction for two urologic cancers, thereby showing its potential for broader application in oncological research.
2. Materials and Methods
2.1. Dataset
2.2. Patient Similarity Graph
| Feature | BLCA | KIRC | |
|---|---|---|---|
| Number of Patients | 400 | 313 | |
| Age | <65 years | 147 (36.8%) | 193 (61.7%) |
| ≥65 years | 253 (63.2%) | 120 (38.3%) | |
| Gender | Male | 295 (73.8%) | 201 (64.2%) |
| Female | 105 (26.2%) | 112 (35.8%) | |
| Stage T (Primary tumor) | Negative (Stages T0–2) | 148 (37.6%) | 196 (62.6%) |
| Positive (Stages T3–4) | 246 (62.4%) | 117 (37.4%) | |
| Stage N (Regional lymph nodes) | Negative (Stage N0) | 261 (67.4%) | 244 (87.8%) |
| Positive (Stage N1–3) | 126 (32.6%) | 34 (12.2%) | |
| Stage M (Distant metastasis) | Negative (Stage M0) | 340 (86.1%) | 258 (82.7%) |
| Positive (Stage M1) | 55 (13.9%) | 54 (17.3%) | |
| Overall survival (OS) | Survival days (Mean ± SD 1) | 810.5 ± 833.8 | 1310.3 ± 1062.7 |
| Uncensored patients | 173 (43.7%) | 102 (32.8%) | |
| Censored patients | 223 (56.3%) | 209 (67.2%) | |
2.3. Graph Neural Networks for Survival Prediction
2.3.1. Graph Convolutional Networks (GCN)
2.3.2. GraphSAGE
2.3.3. Graph Attention Networks (GAT)
2.3.4. Discrete-Time Survival Models
2.4. Performance Evaluation
3. Results
3.1. Experimental Setting
3.2. Hyperparameter Optimization in Graph Construction
3.3. Survival Prediction Performance
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leung, K.M.; Elashoff, R.M.; Afifi, A.A. Censoring issues in survival analysis. Annu. Rev. Public Health 1997, 18, 83–104. [Google Scholar] [CrossRef] [PubMed]
- Van Wieringen, W.N.; Kun, D.; Hampel, R.; Boulesteix, A.L. Survival prediction using gene expression data: A review and comparison. Comput. Stat. Data Anal. 2009, 53, 1590–1603. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–202. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B.; Blackstone, E.H.; Lauer, M.S. Random survival forests. Ann. Appl. Stat. 2008, 2, 841–860. [Google Scholar] [CrossRef]
- Efron, B. Logistic regression, survival analysis, and the Kaplan-Meier curve. J. Am. Stat. Assoc. 1988, 83, 414–425. [Google Scholar] [CrossRef]
- Allison, P.D. Discrete-time methods for the analysis of event histories. Sociol. Methodol. 1982, 13, 61–98. [Google Scholar] [CrossRef]
- Burke, H.B.; Goodman, P.H.; Rosen, D.B.; Henson, D.E.; Weinstein, J.N.; Harrell, F.E., Jr.; Marks, J.R.; Winchester, D.P.; Bostwick, D.G. Artificial neural networks improve the accuracy of cancer survival prediction. Cancer 1997, 79, 857–862. [Google Scholar] [CrossRef]
- Ahmed, F.E. Artificial neural networks for diagnosis and survival prediction in colon cancer. Mol. Cancer 2005, 4, 29. [Google Scholar] [CrossRef]
- Sun, D.; Wang, M.; Li, A. A multimodal deep neural network for human breast cancer prognosis prediction by integrating multi-dimensional data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 16, 841–850. [Google Scholar] [CrossRef]
- Lundin, M.; Lundin, J.; Burke, H.; Toikkanen, S.; Pylkkänen, L.; Joensuu, H. Artificial neural networks applied to survival prediction in breast cancer. Oncology 1999, 57, 281–286. [Google Scholar] [CrossRef]
- Lopez-Garcia, G.; Jerez, J.M.; Franco, L.; Veredas, F.J. Transfer learning with convolutional neural networks for cancer survival prediction using gene-expression data. PLoS ONE 2020, 15, e0230536. [Google Scholar] [CrossRef] [PubMed]
- Kvamme, H.; Borgan, Ø.; Scheel, I. Time-to-event prediction with neural networks and Cox regression. arXiv 2019, arXiv:1907.00825. [Google Scholar]
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol. 2018, 18, 24. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Zame, W.; Yoon, J.; Van Der Schaar, M. Deephit: A deep learning approach to survival analysis with competing risks. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Brown, C.C. On the use of indicator variables for studying the time-dependence of parameters in a response-time model. Biometrics 1975, 31, 863–872. [Google Scholar] [CrossRef] [PubMed]
- Gensheimer, M.F.; Narasimhan, B. A scalable discrete-time survival model for neural networks. PeerJ 2019, 7, e6257. [Google Scholar] [CrossRef]
- Khan, F.M.; Zubek, V.B. Support vector regression for censored data (SVRc): A novel tool for survival analysis. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 863–868. [Google Scholar]
- Gao, J.; Lyu, T.; Xiong, F.; Wang, J.; Ke, W.; Li, Z. MGNN: A multimodal graph neural network for predicting the survival of cancer patients. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 1697–1700. [Google Scholar]
- Gao, J.; Lyu, T.; Xiong, F.; Wang, J.; Ke, W.; Li, Z. Predicting the survival of cancer patients with multimodal graph neural network. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 19, 699–709. [Google Scholar] [CrossRef]
- Qiu, L.; Kang, D.; Wang, C.; Guo, W.; Fu, F.; Wu, Q.; Xi, G.; He, J.; Zheng, L.; Zhang, Q.; et al. Intratumor graph neural network recovers hidden prognostic value of multi-biomarker spatial heterogeneity. Nat. Commun. 2022, 13, 4250. [Google Scholar] [CrossRef]
- Liang, B.; Gong, H.; Lu, L.; Xu, J. Risk stratification and pathway analysis based on graph neural network and interpretable algorithm. BMC Bioinform. 2022, 23, 394. [Google Scholar] [CrossRef]
- Goldman, M.J.; Craft, B.; Hastie, M.; Repečka, K.; McDade, F.; Kamath, A.; Banerjee, A.; Luo, Y.; Rogers, D.; Brooks, A.N.; et al. Visualizing and interpreting cancer genomics data via the Xena platform. Nat. Biotechnol. 2020, 38, 675–678. [Google Scholar] [CrossRef]
- Zhu, X.; Zhou, X.; Zhang, Y.; Sun, X.; Liu, H.; Zhang, Y. Reporting and methodological quality of survival analysis in articles published in Chinese oncology journals. Medicine 2017, 96, e9204. [Google Scholar] [CrossRef]
- Kim, S.Y.; Choe, E.K.; Shivakumar, M.; Kim, D.; Sohn, K.A. Multi-layered network-based pathway activity inference using directed random walks: Application to predicting clinical outcomes in urologic cancer. Bioinformatics 2021, 37, 2405–2413. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Mezlini, A.M.; Demir, F.; Fiume, M.; Tu, Z.; Brudno, M.; Haibe-Kains, B.; Goldenberg, A. Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 2014, 11, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Kvamme, H.; Borgan, Ø. Continuous and discrete-time survival prediction with neural networks. Lifetime Data Anal. 2021, 27, 710–736. [Google Scholar] [CrossRef] [PubMed]
- Biganzoli, E.; Boracchi, P.; Mariani, L.; Marubini, E. Feed forward neural networks for the analysis of censored survival data: A partial logistic regression approach. Stat. Med. 1998, 17, 1169–1186. [Google Scholar] [CrossRef]
- Yu, C.N.; Greiner, R.; Lin, H.C.; Baracos, V. Learning patient-specific cancer survival distributions as a sequence of dependent regressors. In Proceedings of the 25th Conference on Neural Information Processing Systems, Granada, Spain, 12–14 December 2011; Volume 24. [Google Scholar]
- Antolini, L.; Boracchi, P.; Biganzoli, E. A time-dependent discrimination index for survival data. Stat. Med. 2005, 24, 3927–3944. [Google Scholar] [CrossRef]
- Graf, E.; Schmoor, C.; Sauerbrei, W.; Schumacher, M. Assessment and comparison of prognostic classification schemes for survival data. Stat. Med. 1999, 18, 2529–2545. [Google Scholar] [CrossRef]
- Gerds, T.A.; Schumacher, M. Consistent estimation of the expected Brier score in general survival models with right-censored event times. Biom. J. 2006, 48, 1029–1040. [Google Scholar] [CrossRef]
- Hinkle, D.E.; Wiersma, W.; Jurs, S.G. Applied Statistics for the Behavioral Sciences; Houghton Mifflin College Division: Boston, MA, USA, 2003; Volume 663. [Google Scholar]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. In Proceedings of the ICLR Workshop on Representation Learning on Graphs and Manifolds, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
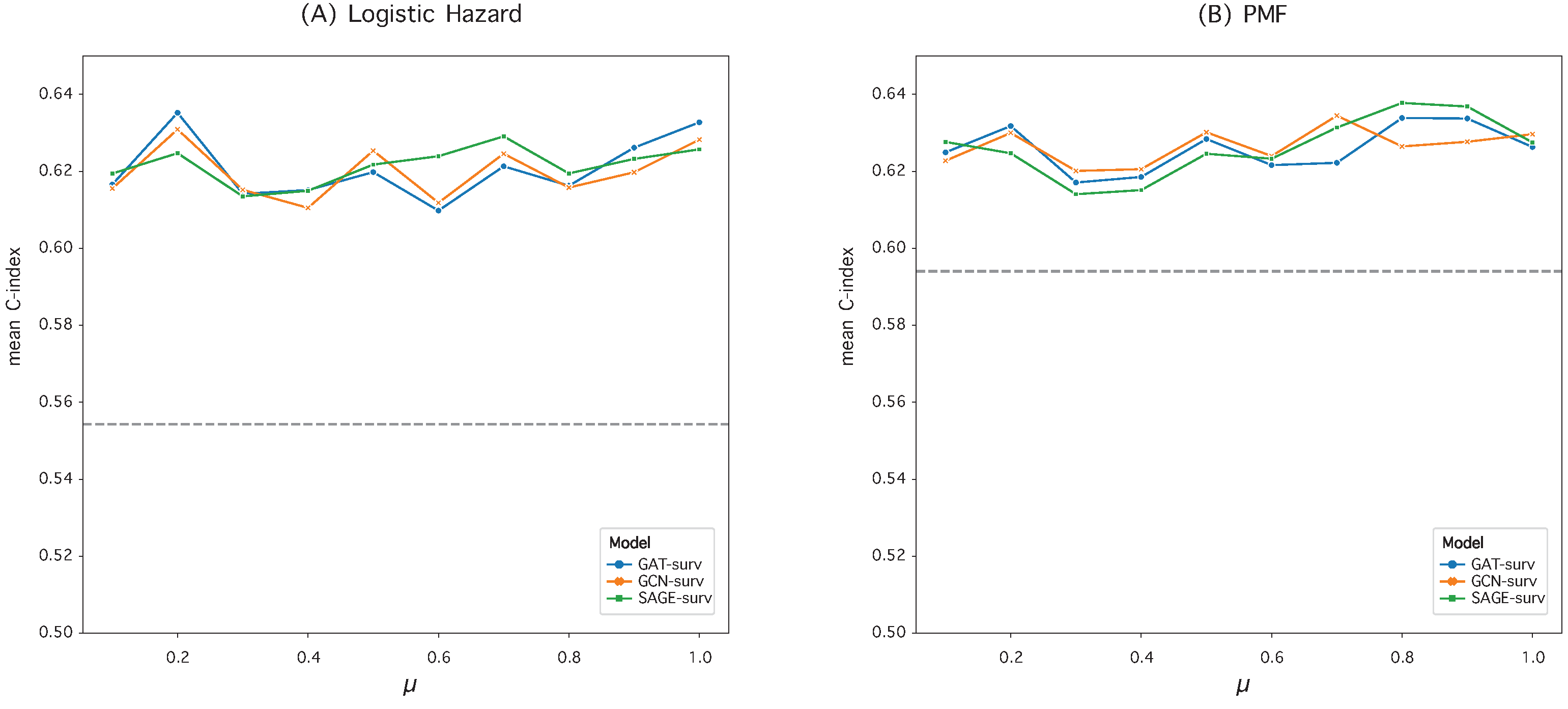
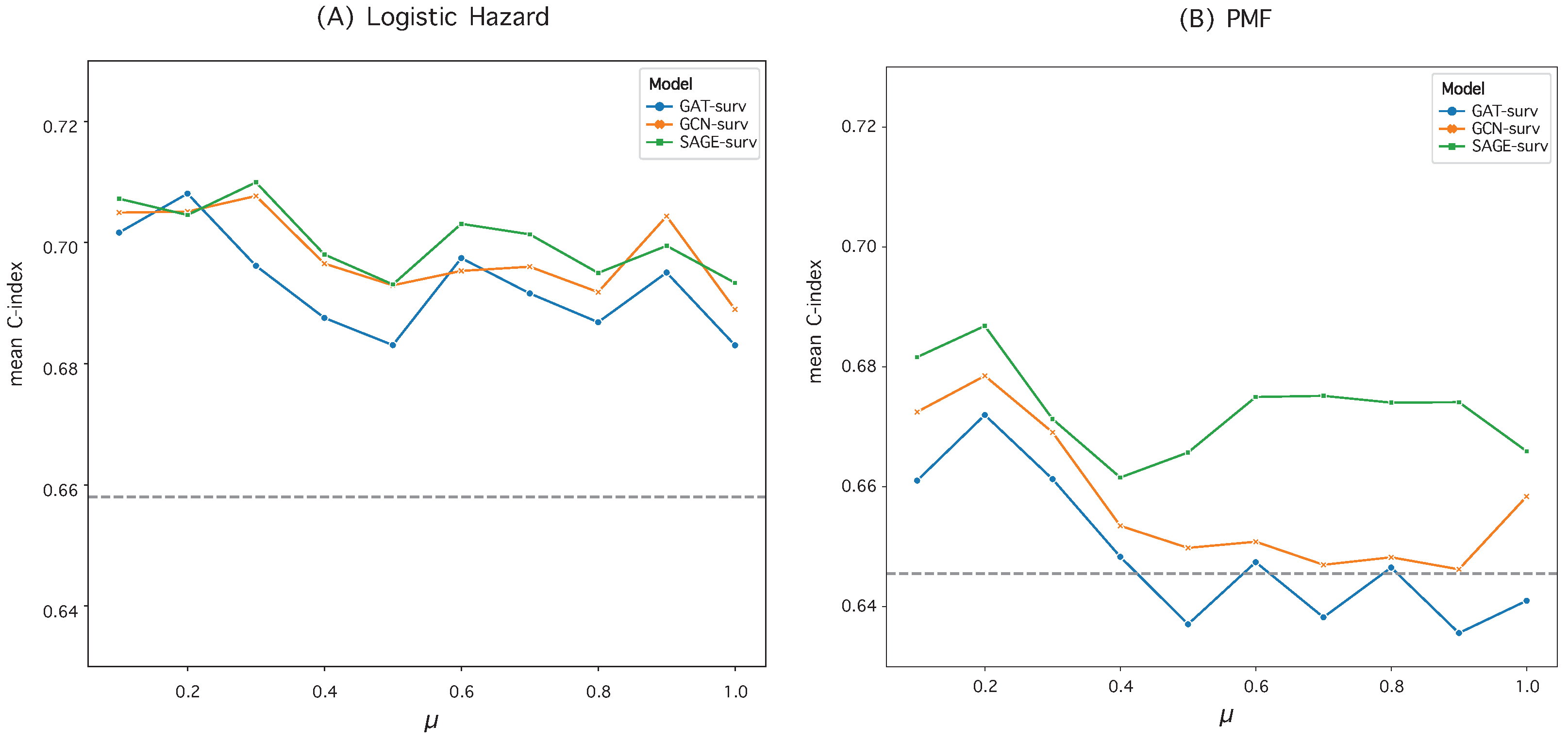

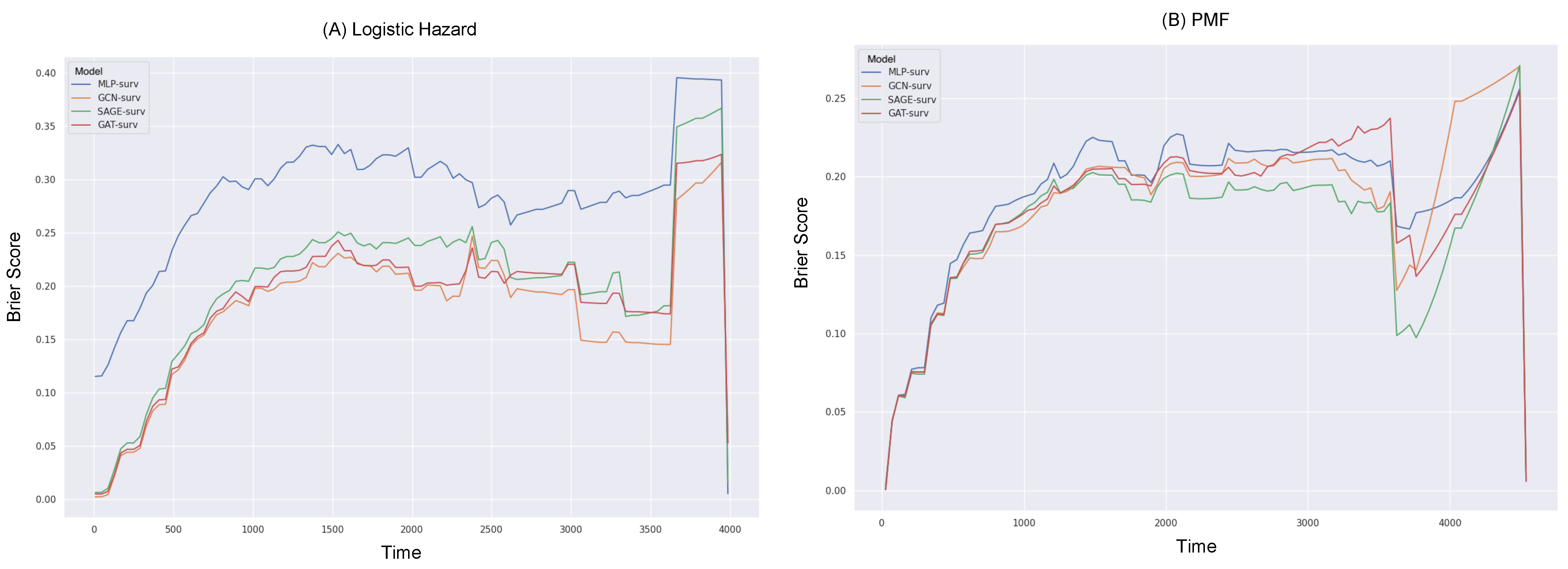
| Logistic Hazard () | PMF () | |||
|---|---|---|---|---|
| Model | IBS | IBS | ||
| MLP-surv | 0.5543 ± 0.0689 | 0.3183 ± 0.0497 | 0.5941 ± 0.0629 | 0.2324 ± 0.0222 |
| GCN-surv | 0.6309 ± 0.0481 | 0.2331 ± 0.0358 | 0.6265 ± 0.0493 | 0.2130 ± 0.0231 |
| SAGE-surv | 0.6247 ± 0.0505 | 0.2331 ± 0.0389 | 0.6378 ± 0.0415 | 0.2140 ± 0.0238 |
| GAT-surv | 0.6352 ± 0.0520 | 0.2341 ± 0.0365 | 0.6339 ± 0.0451 | 0.2154 ± 0.0229 |
| Logistic Hazard () | PMF () | |||
|---|---|---|---|---|
| Model | IBS | IBS | ||
| MLP-surv | 0.6581 ± 0.0559 | 0.2577 ± 0.0902 | 0.6455 ± 0.0516 | 0.2022 ± 0.0174 |
| GCN-surv | 0.7077 ± 0.0373 | 0.1965 ± 0.0240 | 0.6785 ± 0.0464 | 0.1964 ± 0.0195 |
| SAGE-surv | 0.7099 ± 0.0409 | 0.1955 ± 0.0269 | 0.6868 ± 0.047 | 0.1859 ± 0.0222 |
| GAT-surv | 0.6962 ± 0.0362 | 0.2018 ± 0.0260 | 0.672 ± 0.05 | 0.1958 ± 0.0233 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.Y. GNN-surv: Discrete-Time Survival Prediction Using Graph Neural Networks. Bioengineering 2023, 10, 1046. https://doi.org/10.3390/bioengineering10091046
Kim SY. GNN-surv: Discrete-Time Survival Prediction Using Graph Neural Networks. Bioengineering. 2023; 10(9):1046. https://doi.org/10.3390/bioengineering10091046
Chicago/Turabian StyleKim, So Yeon. 2023. "GNN-surv: Discrete-Time Survival Prediction Using Graph Neural Networks" Bioengineering 10, no. 9: 1046. https://doi.org/10.3390/bioengineering10091046
APA StyleKim, S. Y. (2023). GNN-surv: Discrete-Time Survival Prediction Using Graph Neural Networks. Bioengineering, 10(9), 1046. https://doi.org/10.3390/bioengineering10091046







