Continuous Motion Estimation of Knee Joint Based on a Parameter Self-Updating Mechanism Model
Abstract
:1. Introduction
- A self-adaptive optimized DBN, depending on the original sEMG signals of different subjects, was built to complete the reconstruction of sEMG sequences.
- An adaptive regression model fused with BPNN was established to achieve the optimal estimation of continuous joint angle.
- A parameter self-updating mechanism was applied to update the model parameters using a small amount of data from new subjects to satisfy personalized demand.
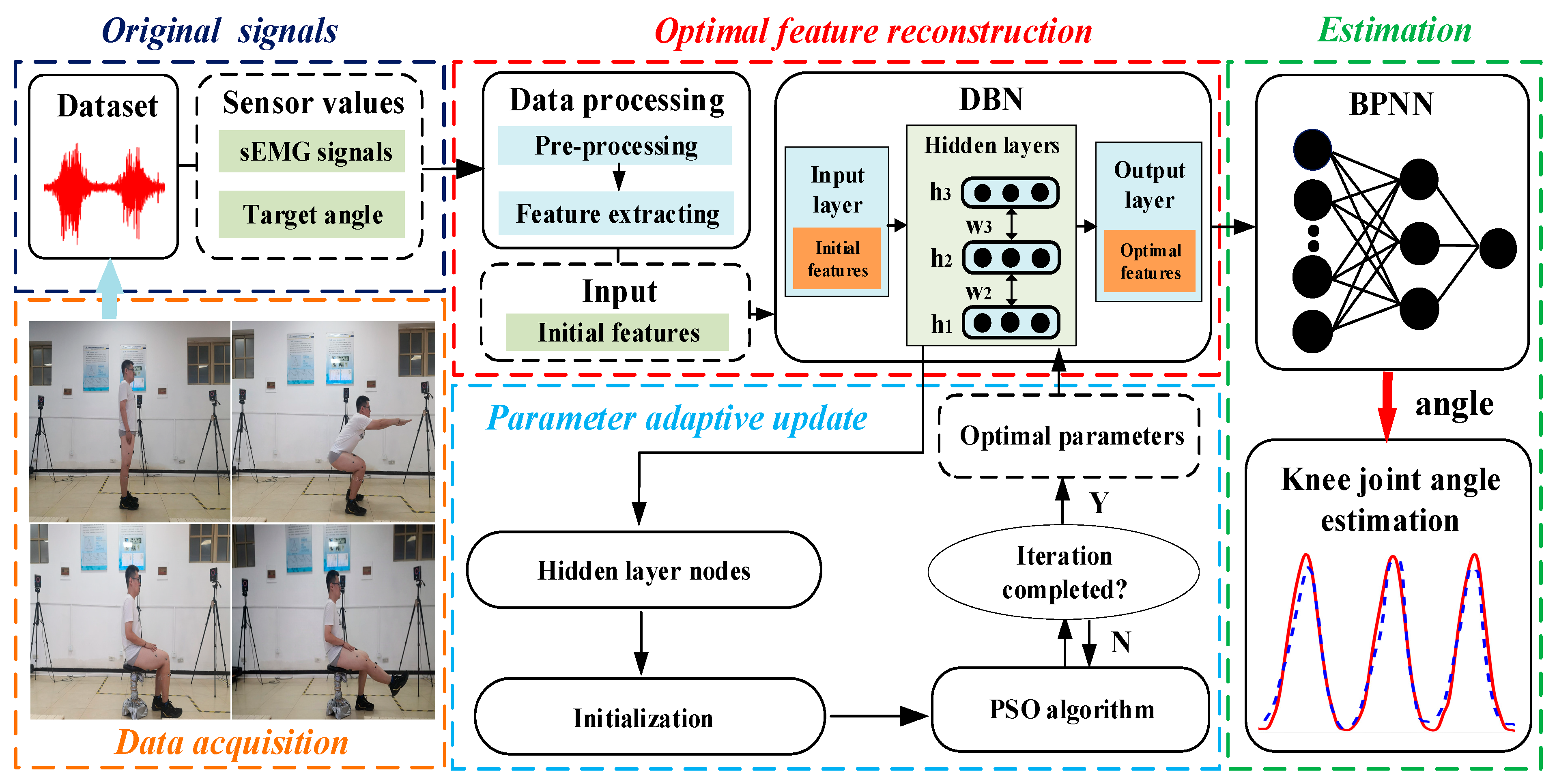
2. Materials and Methods
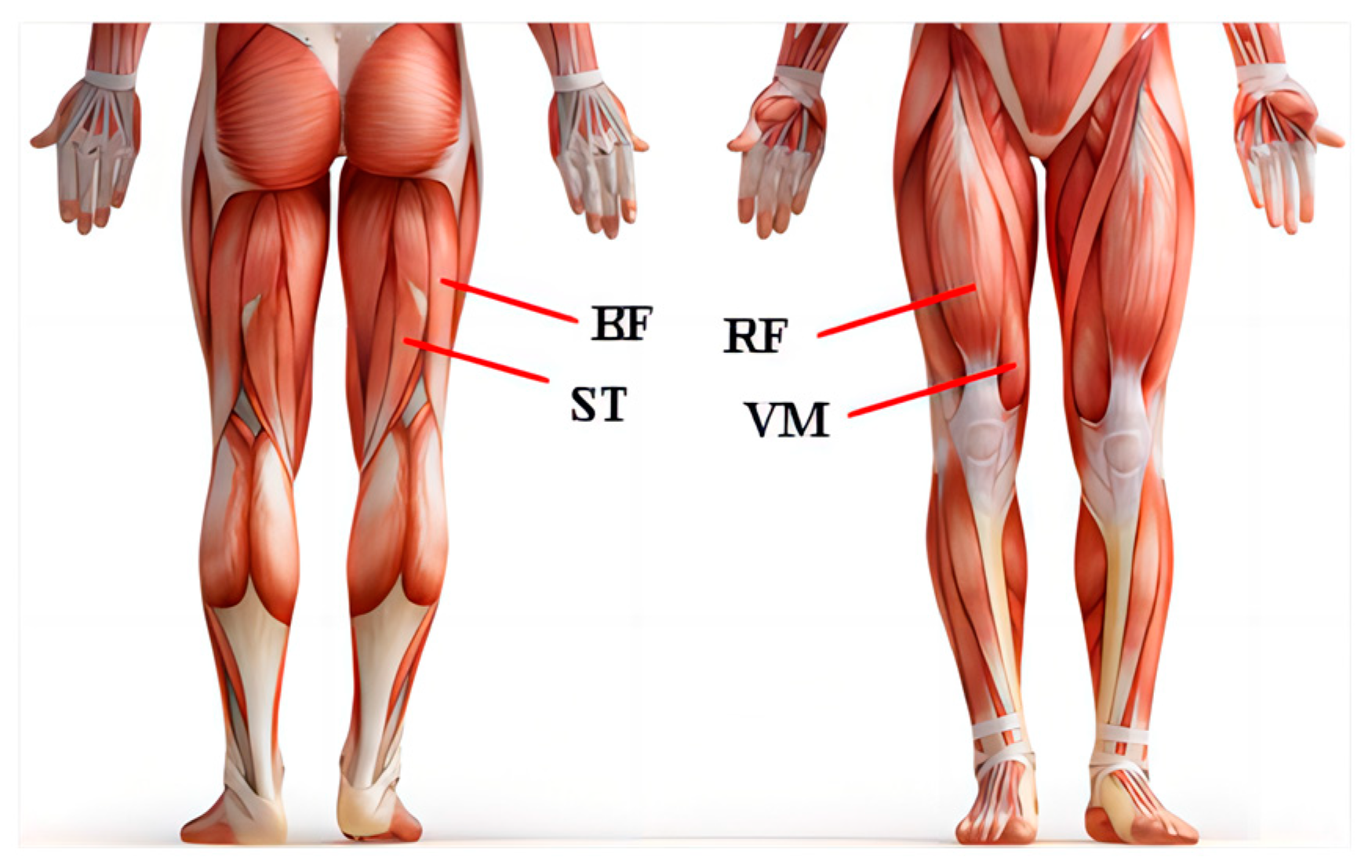
2.1. Data Acquisition and Pre-Processing
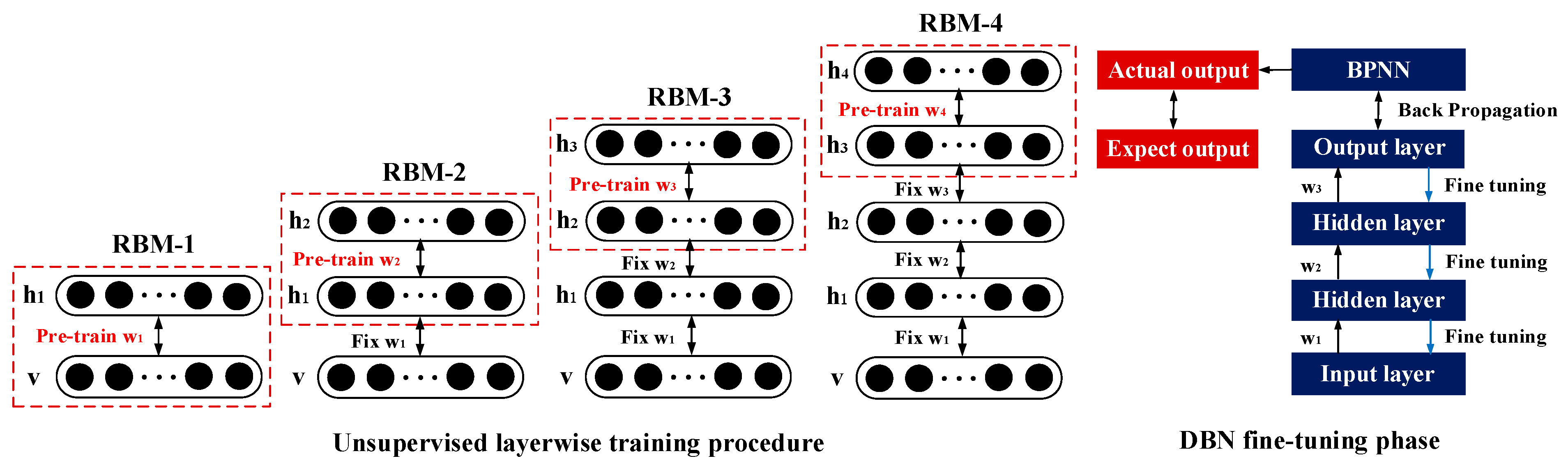
2.2. Feature Reconstruction by DBN
2.3. DBN Adaptive Optimization Fused with the PSO Algorithm
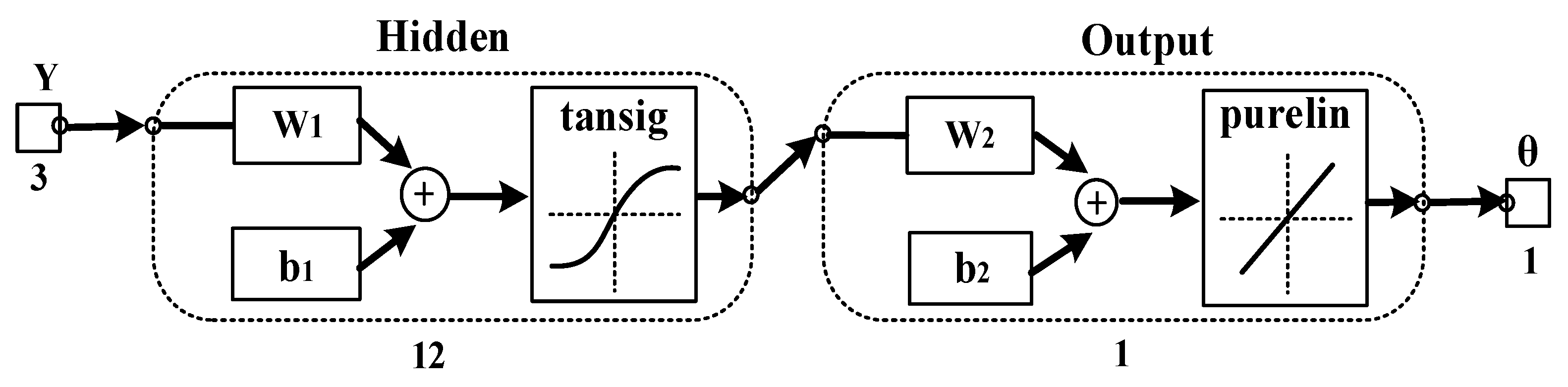
2.4. Construction of the Adaptive Regression Model
2.5. Result Evaluation Indicators
3. Experiments and Results
3.1. Subjects
3.2. Experimental Procedure
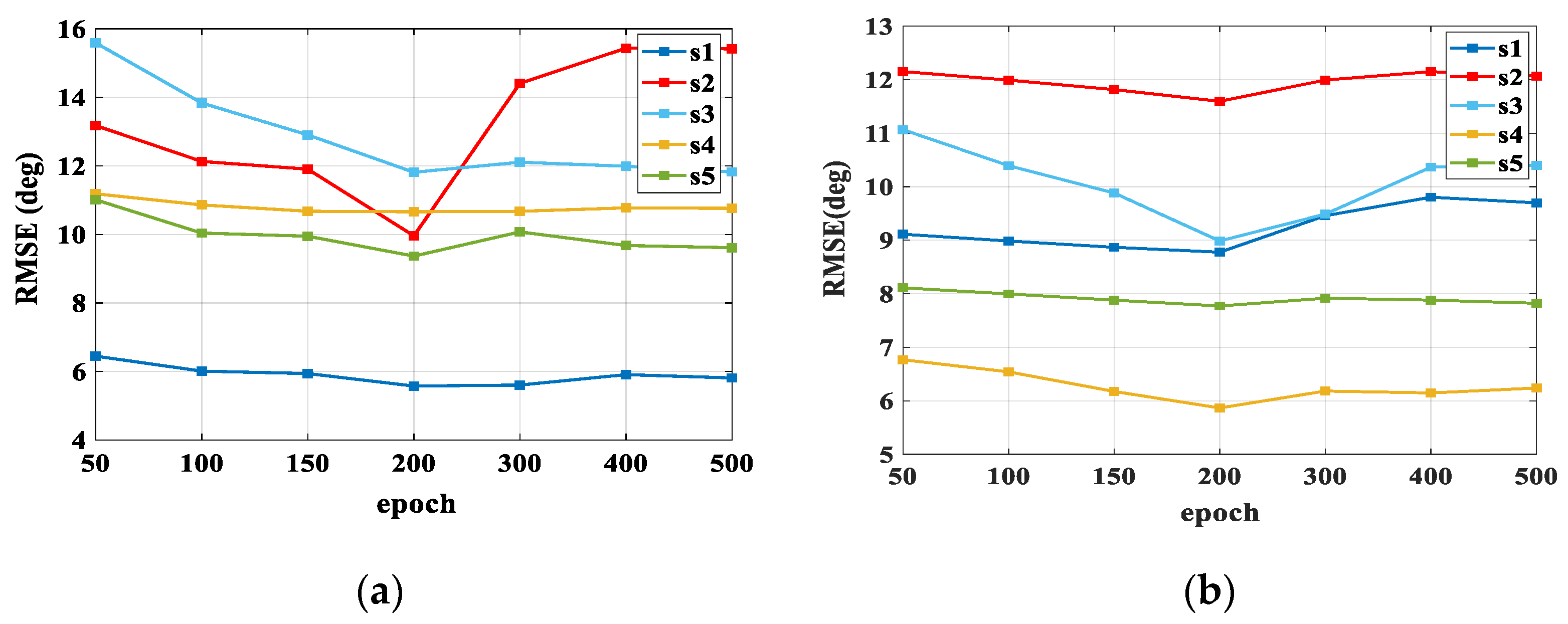
3.3. Model Training
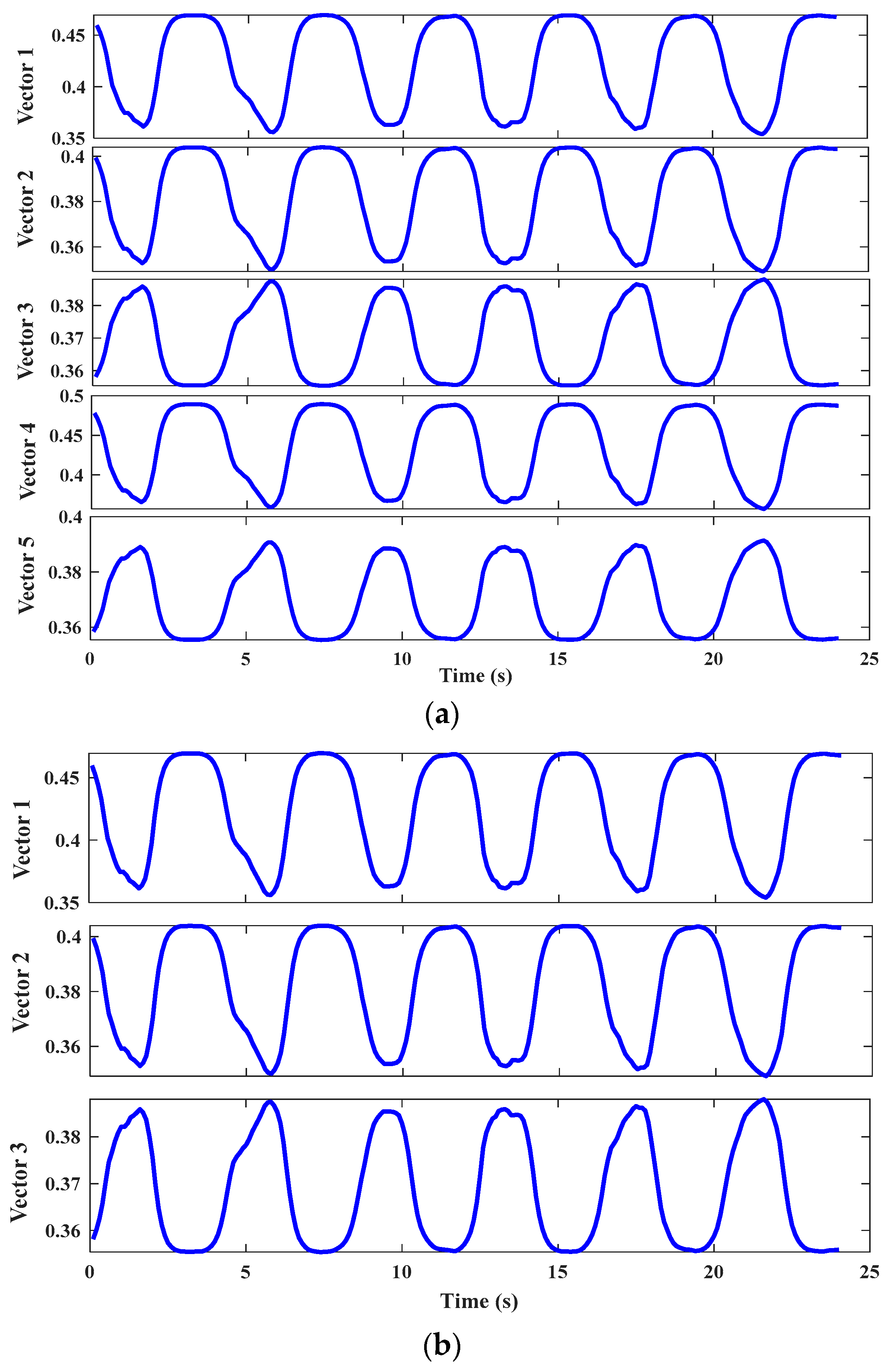
3.4. Comparison of Estimated Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, Q.C.; Xiong, A.B.; Zhao, X.G.; Han, J.D. A review on researches and applications of sEMG-based motion intent recognition methods. Acta Autom. Sin. 2016, 42, 13–25. [Google Scholar]
- Li, K.X.; Zhang, J.H.; Wang, L.F.; Zhang, M.L.; Li, J.Y.; Bao, S.C. A review of the key technologies for sEMG-based human-robot interaction systems. Biomed. Signal Process. Control 2020, 62, 102074. [Google Scholar] [CrossRef]
- Han, J.D.; Ding, Q.C.; Xiong, A.B.; Zhao, X.G. A state-space EMG model for the estimation of continuous joint movements. IEEE Trans. Ind. Electron. 2015, 62, 4267–4275. [Google Scholar] [CrossRef]
- Li, K.X.; Zhang, J.H.; Liu, X.; Zhang, M.L. Estimation of continuous elbow joint movement based on human physiological structure. Biomed. Eng. OnLine 2019, 18, 31. [Google Scholar] [CrossRef] [PubMed]
- Li, K.X.; Liu, X.; Zhang, J.H.; Zhang, M.L.; Hou, Z.M. Continuous Motion and Time-varying Stiffness Estimation of the Human Elbow Joint Based on sEMG. J. Mech. Med. Biol. 2019, 19, 307–312. [Google Scholar] [CrossRef]
- Xi, X.G.; Jiang, W.J.; Hua, X.; Wang, H.J.; Yang, C.; Zhao, Y.B.; Miran, S.M.; Luo, Z.Z. Simultaneous and Continuous Estimation of Joint Angles Based on Surface Electromyography State-Space Model. IEEE Sen. J. 2021, 21, 8089–8099. [Google Scholar] [CrossRef]
- Ding, Q.C.; Han, J.D.; Zhao, X.G. Continuous estimation of human multi-joint angles from sEMG using a state-space model. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1518–1528. [Google Scholar] [CrossRef]
- Tang, Z.C.; Yu, H.N.; Cang, S. Impact of load variation on joint angle estimation from surface EMG signals. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 1342–1350. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Li, P.F.; Hou, Z.G.; Lu, Z.; Chen, Y.X.; Li, Q.L.; Tan, M. sEMG-based continuous estimation of joint angles of human legs by using BP neural networks. Neurocomputing 2012, 78, 139–148. [Google Scholar] [CrossRef]
- LI, Z.Y.; Zhang, D.H.; Zhao, X.G.; Wang, F.Y.; Zhang, B.; Ye, D.; Han, J.D. A Temporally Smoothed MLP Regression Scheme for Continuous Knee/Ankle Angles Estimation by Using Multi-Channel sEMG. IEEE Access 2020, 8, 47433–47444. [Google Scholar] [CrossRef]
- Masayuki, Y.; Ryohei, K.; Masao, Y. An evaluation of hand-force prediction using artificial neural-network regression models of surface EMG signals for handwear devices. J. Sens. 2017, 2017, 3980906. [Google Scholar]
- Triwiyanto, T.; Wahyunggoro, O.; Nugroho, H.A.; Herianto, H. Muscle fatigue compensation of the electromyography signal for elbow joint angle estimation using adaptive feature. Comput. Electron. Eng. 2018, 71, 284–293. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, R.; Chen, W.; Xiong, C. Simultaneous and continuous estimation of shoulder and elbow kinematics from surface EMG signals. Front. Neurosci. 2017, 11, 280. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Miran, S.M.; Xi, X.; Xue, A. Surface Electromyography Based Estimation of Knee Joint Angle by Using Correlation Dimension of Wavelet Coefficient. IEEE Access 2019, 7, 60522–60531. [Google Scholar] [CrossRef]
- Xie, H.L.; Li, G.C.; Zhao, X.F.; Li, F. Prediction of limb joint angles based on multi-source signals by GS-GRNN for exoskeleton wearer. Sensors 2020, 20, 1104. [Google Scholar] [CrossRef]
- Xiao, F.Y.; Wang, Y.; He, L.G.; Wang, H.; Li, W.H. Motion Estimation from Surface Electromyogram Using Adaboost Regression and Average Feature Values. IEEE Access 2019, 7, 13121–13134. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, J.T.; Peng, C.; Yin, Y.H. Evolving Gaussian Process Autoregression Based Learning of Human Motion Intent Using Improved Energy Kernel Method of EMG. IEEE Trans. Biomed. Eng. 2019, 66, 2556–2565. [Google Scholar] [CrossRef]
- Gui, K.; Liu, H.H.; Zhang, D.G. A practical and adaptive method to achieve EMG-Based torque estimation for a robotic exoskeleton. IEEE/ASME Trans. Mech. 2019, 24, 483–494. [Google Scholar] [CrossRef]
- Anari, S.; Sarshar, N.T.; Mahjoori, N.; Dorosti, S.; Rezaie, A. Review of Deep Learning Approaches for Thyroid Cancer Diagnosis. Math. Probl. Eng. 2022, 2022, 5052435. [Google Scholar] [CrossRef]
- Kasgari, A.B.; Safavi, S.; Nouri, M.; Hou, J.; Sarshar, N.T.; Ranjbarzadeh, R. Point-of-Interest Preference Model Using an Attention Mechanism in a Convolutional Neural Network. Bioengineering 2023, 10, 495. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.C.; Zhang, X.D.; Cheng, Y.; Xi, N. Surface EMG based continuous estimation of human lower limb joint angles by using deep belief networks. Biomed. Signal Process. Control 2018, 40, 335–342. [Google Scholar] [CrossRef]
- Chai, Y.; Liu, K.; Li, C.; Shi, T. A Novel Method based on Long Short Term Memory Network and Discrete-Time Zeroing Neural Algorithm for Upper-Limb Continuous Estimation Using sEMG Signals. Biomed. Signal Process. Control 2020, 67, 102416. [Google Scholar] [CrossRef]
- Gautam, A.; Panwar, M.; Biswas, D.; Acharyya, A. MyoNet: A transferlearning-based LRCN for lower limb movement recognition and knee joint angle prediction for remote monitoring of rehabilitation progress from sEMG. IEEE J. Trans. Eng. Health Med. 2020, 8, 1–10. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Y.; Song, Q.; Wang, C. Continuous estimation of knee joint angle based on surface electromyography using a long short-term memory neural network and time-advanced feature. Sensors 2020, 20, 4966. [Google Scholar] [CrossRef]
- Ma, C.F.; Lin, C.; Samuel, O.W.; Xua, L.S.; Li, G.L. Continuous estimation of upper limb joint angle from sEMG signals based on SCA-LSTM deep learning approach. Biomed. Signal Process. Control 2020, 61, 102024. [Google Scholar] [CrossRef]
- Huang, Y.C.; He, Z.X.; Liu, Y.X. Real-time intended knee joint motion prediction by deep recurrent neural networks. IEEE Sens. J. 2019, 19, 11503–11509. [Google Scholar] [CrossRef]
- Yang, W.; Yang, D.; Liu, Y.; Liu, H. Decoding simultaneous multi-DOF wrist movements from raw EMG signals using a convolutional neural network. IEEE Trans. Hum.-Mach. Syst. 2019, 49, 411–420. [Google Scholar] [CrossRef]
- Lichtwark, G.A.; Bougoulias, K.; Wilson, A.M. Muscle fascicle and series elastic element length changes along the length of the human gastrocnemius during walking and running. J. Biomech. 2007, 40, 157–164. [Google Scholar] [CrossRef] [PubMed]
- Omuro, K.; Shiba, Y.; Obuchi, S.; Takahira, N. Effect of ankle weights on EMG activity of the semitendinosus and knee stability during walking by community-dwelling elderly. Rigakuryoho Kagaku 2011, 26, 55–59. [Google Scholar] [CrossRef]
- Barbero, M.; Rainoldi, A.; Merletti, R. Atlas of Muscle Innervation Zones: Understanding Surface EMG and Its Applications; Springer: Milan, Italy, 2012; ISBN 978-88-470-2462-5. [Google Scholar]
- Besomi, M.; Hodges, P.W.; Dieën, J.V.; Carson, R.G.; Clancy, E.A.; Disselhorst-Klug, A. Consensus for experimental design in electromyography (CEDE) project: Electrode selection matrix. J. Electromyogr. Kinesiol. 2019, 48, 128–144. [Google Scholar] [CrossRef]
- Luca, C.J.D. The use of surface electromyography in biomechanics. J. Appl. Biomech. 1997, 13, 135–163. [Google Scholar] [CrossRef]
- DeLuca, C.J. Myoelectrical manifestations of localized muscular fatigue in humans. Crit. Rev. Biomed. Eng. 1984, 11, 251–279. [Google Scholar]
- Micera, S.; Carpaneto, J.; Raspopovic, S. Control of Hand Prostheses Using Peripheral Information. IEEE Rev. Biomed. Eng. 2010, 3, 48–68. [Google Scholar] [CrossRef]
- Simão, M.; Mendes, N.; Gibaru, O.; Neto, P. A Review on Electromyography Decoding and Pattern Recognition for Human-Machine Interaction. IEEE Access 2019, 7, 39564–39582. [Google Scholar] [CrossRef]
- Oskoei, M.A.; Hu, H. Myoelectric control systems—A survey. Biomed. Signal Process. Control 2007, 2, 275–294. [Google Scholar] [CrossRef]
- Englehart, K.; Hudgins, B. A robust, real-time control scheme for multifunction myoelectric control. IEEE Trans. Biomed. Eng. 2003, 50, 848–854. [Google Scholar] [CrossRef] [PubMed]
- Farina, D.; Merletti, R. Comparison of algorithms for estimation of EMG variables during voluntary isometric contractions. J. Electromyogr. Kinesiol. 2000, 10, 337–349. [Google Scholar] [CrossRef]
- Pan, T.Y.; Tsai, W.L.; Chang, C.Y.; Yeh, C.W.; Hu, M.C. A Hierarchical Hand Gesture Recognition Framework for Sports Referee Training-Based EMG and Accelerometer Sensors. IEEE Trans. Cyber. 2020, 52, 3172–3183. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, X.; Cao, S.; Zhang, X.; Chen, X. Exploration of Chinese sign language recognition using wearable sensors based on deep belief net. IEEE J. Biomed. Health Inf. 2020, 24, 1310–1320. [Google Scholar] [CrossRef]
- Shahbaba, B. Analysis of Variance (ANOVA): An Introduction to Statistics through Biological Data; Springer: New York, NY, USA, 2012; pp. 221–234. [Google Scholar]
- Wang, F.; Wei, X.T.; Qin, H. Estimation of Lower Limb Continuous Movements Based on sEMG and LSTM. J. Northeast. Univ. 2020, 41, 7. [Google Scholar]






| Subject | Squat | Knee Flex/Ext | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number of Neurons in Each Layer | Time/s | Number of Neurons in Each Layer | Time/s | |||||||
| S1 | 37 | 26 | 16 | 5 | 31.7 | 8 | 48 | 11 | 44 | 40.4 |
| S2 | 34 | 32 | 29 | 35 | 43.4 | 34 | 41 | 14 | 17 | 29.3 |
| S3 | 2 | 41 | 48 | 32 | 36.6 | 38 | 2 | 42 | 49 | 42.0 |
| S4 | 5 | 40 | 25 | 34 | 39.0 | 18 | 14 | 40 | 19 | 34.1 |
| S5 | 2 | 49 | 46 | 42 | 41.1 | 17 | 28 | 37 | 32 | 41.4 |
| Subject | Model | Squat | Knee Flex/Ext | ||||
|---|---|---|---|---|---|---|---|
| RMSE | CC | R2 | RMSE | CC | R2 | ||
| 1 | PSO-DBN-BP | 5.57 ± 0.44 | 0.99 ± 0.01 | 0.97 ± 0.01 | 8.71 ± 0.16 | 0.93 ± 0.01 | 0.88 ± 0.01 |
| DBN-BP | 6.37 ± 1.04 | 0.98 ± 0.01 | 0.96 ± 0.01 | 9.09 ± 0.36 | 0.92 ± 0.01 | 0.85 ± 0.01 | |
| BPNN | 8.79 ± 2.71 | 0.94 ± 0.04 | 0.89 ± 0.07 | 9.84 ± 1.22 | 0.89 ± 0.03 | 0.79 ± 0.05 | |
| 2 | PSO-DBN-BP | 9.96 ± 0.51 | 0.95 ± 0.01 | 0.90 ± 0.01 | 8.34 ± 0.17 | 0.93 ± 0.01 | 0.88 ± 0.01 |
| DBN-BP | 11.72 ± 1.28 | 0.93 ± 0.01 | 0.86 ± 0.02 | 12.06 ± 0.41 | 0.90 ± 0.01 | 0.84 ± 0.02 | |
| BPNN | 12.90 ± 1.45 | 0.90 ± 0.01 | 0.81 ± 0.04 | 12.64 ± 0.47 | 0.88 ± 0.02 | 0.81 ± 0.02 | |
| 3 | PSO-DBN-BP | 11.82 ± 0.10 | 0.95 ± 0.01 | 0.90 ± 0.01 | 6.09 ± 0.34 | 0.96 ± 0.01 | 0.93 ± 0.01 |
| DBN-BP | 13.53 ± 2.61 | 0.93 ± 0.03 | 0.85 ± 0.06 | 7.21 ± 1.18 | 0.95 ± 0.02 | 0.89 ± 0.04 | |
| BPNN | 21.71 ± 1.40 | 0.81 ± 0.02 | 0.66 ± 0.03 | 8.77 ± 0.99 | 0.92 ± 0.02 | 0.85 ± 0.04 | |
| 4 | PSO-DBN-BP | 10.49 ± 0.15 | 0.95 ± 0.01 | 0.90 ± 0.01 | 5.87 ± 0.34 | 0.97 ± 0.01 | 0.95 ± 0.01 |
| DBN-BP | 10.86 ± 0.24 | 0.94 ± 0.01 | 0.89 ± 0.01 | 6.75 ± 1.30 | 0.95 ± 0.02 | 0.91 ± 0.04 | |
| BPNN | 12.32 ± 0.99 | 0.93 ± 0.01 | 0.87 ± 0.01 | 8.12 ± 0.86 | 0.93 ± 0.02 | 0.87 ± 0.03 | |
| 5 | PSO-DBN-BP | 9.29 ± 0.33 | 0.96 ± 0.01 | 0.93 ± 0.01 | 7.77 ± 0.23 | 0.93 ± 0.01 | 0.86 ± 0.01 |
| DBN-BP | 10.22 ± 0.62 | 0.95 ± 0.01 | 0.91 ± 0.02 | 8.07 ± 0.39 | 0.91 ± 0.01 | 0.84 ± 0.01 | |
| BPNN | 14.97 ± 1.24 | 0.88 ± 0.02 | 0.78 ± 0.04 | 8.64 ± 0.75 | 0.90 ± 0.02 | 0.82 ± 0.04 | |
| Overall | PSO-DBN-BP | 9.42 ± 0.31 | 0.96 ± 0.01 | 0.92 ± 0.01 | 7.36 ± 0.25 | 0.94 ± 0.01 | 0.90 ± 0.01 |
| DBN-BP | 10.54 ± 1.16 | 0.95 ± 0.01 | 0.89 ± 0.02 | 8.64 ± 0.61 | 0.93 ± 0.01 | 0.87 ± 0.02 | |
| BPNN | 14.14 ± 1.56 | 0.89 ± 0.02 | 0.80 ± 0.04 | 9.60 ± 0.86 | 0.90 ± 0.02 | 0.83 ± 0.04 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, K.; Zhang, J.; Cao, J. Continuous Motion Estimation of Knee Joint Based on a Parameter Self-Updating Mechanism Model. Bioengineering 2023, 10, 1028. https://doi.org/10.3390/bioengineering10091028
Li J, Li K, Zhang J, Cao J. Continuous Motion Estimation of Knee Joint Based on a Parameter Self-Updating Mechanism Model. Bioengineering. 2023; 10(9):1028. https://doi.org/10.3390/bioengineering10091028
Chicago/Turabian StyleLi, Jiayi, Kexiang Li, Jianhua Zhang, and Jian Cao. 2023. "Continuous Motion Estimation of Knee Joint Based on a Parameter Self-Updating Mechanism Model" Bioengineering 10, no. 9: 1028. https://doi.org/10.3390/bioengineering10091028
APA StyleLi, J., Li, K., Zhang, J., & Cao, J. (2023). Continuous Motion Estimation of Knee Joint Based on a Parameter Self-Updating Mechanism Model. Bioengineering, 10(9), 1028. https://doi.org/10.3390/bioengineering10091028





