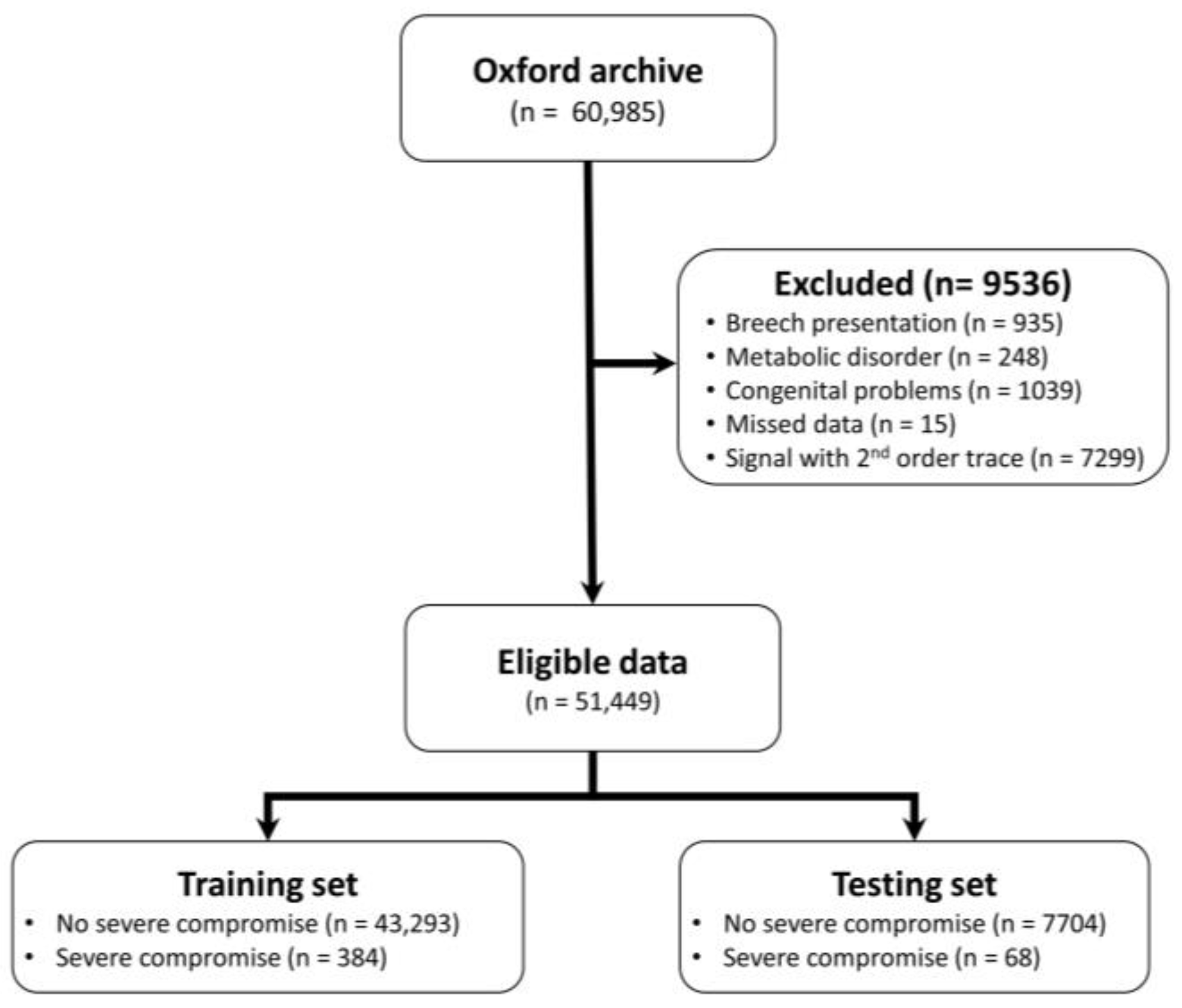
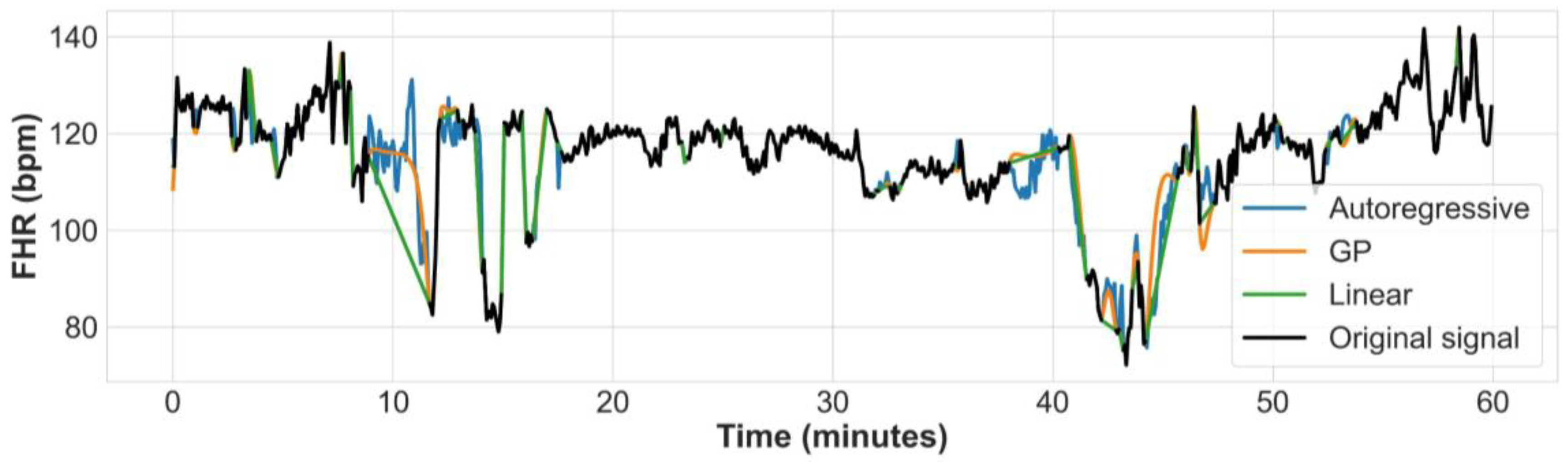
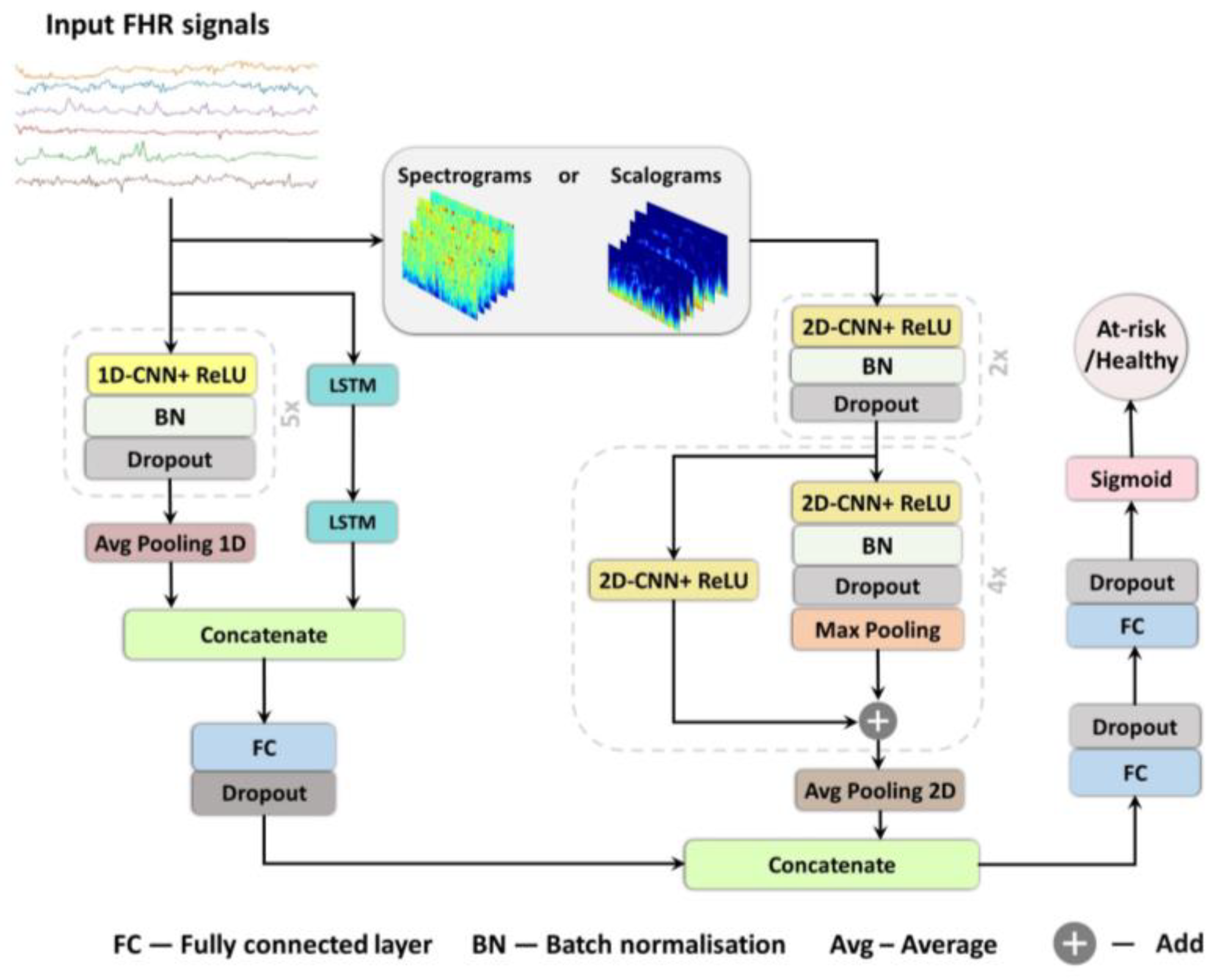
1. Introduction
Cardiotocography (CTG) is a continuous and simultaneous measurement of fetal heart rate (FHR) and maternal uterine contraction signals. CTG is commonly performed during or preceding labour to assess fetal wellbeing and reduce its mortality and morbidity [
1]. Interpretation of the CTG patterns requires assessing the FHR baseline, variability, accelerations, and decelerations by a trained clinician. However, due to the complexity of CTG signals, visual interpretation is often challenging and imprecise [
2], leading to miss diagnoses [
3,
4]. In the United Kingdom (UK), each year between 2015 to 2018, on average 125 intrapartum still births, 154 neonatal deaths, and 854 severe injuries were registered [
5]. These adverse outcomes frequently lead to litigation. In England, in 2020/2021, over £4.1 billion was spent on settling obstetric claims, 59% of which were clinical negligence payments [
6]. Enhancing the accuracy of CTG interpretation has the potential to enable clinicians to intervene earlier, thereby potentially preventing some of these adverse outcomes. This, in turn, can alleviate the substantial financial burden on the healthcare system. Globally in 2019, an estimated 2 million babies were stillborn [
7]. Most these adverse outcomes that occurred during intrapartum periods are potentially preventable with CTG monitoring and appropriate interventions.
CTG remains at the center of the decision-making process in intrapartum fetal monitoring despite its limitations, as there is no other technology or method that has been shown to be as effective in assessing fetal well-being during labour. CTG is typically performed at maternity admission units/triage wards or after admission to the labour ward and in some countries like Sweden it is routinely performed, while in others, such as the UK, CTG is not recommended for low-risk births (about 40% of all) [
8,
9]. Under some circumstances, the initial 20–30 min CTG recording is called ‘admission CTG’ [
10], and its role is controversial: some studies show that it may increase the incidence of unnecessary caesarean sections, especially in ‘low risk’ pregnancies [
10], while others report its benefit in the decision to perform caesarean delivery when administered routinely to all births [
8]. This lack of consensus can be attributed to the imprecision of current clinical guidelines and the poor sensitivity and specificity of the available tools to interpret CTG patterns. During the evaluation of 27,000 high-risk births, our team noted significant differences in the first-hour CTG features (extracted using objective computerized methods) and clinical risk factors between births with severe compromise and those without severe compromise [
11].
Several automated methods have been proposed to address the subjective visual interpretation of CTG recordings [
12,
13,
14,
15]. Research efforts have been devoted to developing techniques that can automatically detect characteristics of the CTG signal [
16,
17,
18,
19]. These studies focus on detecting or quantifying abnormal patterns by mimicking what clinical rules and guidelines suggest or what experts do during their visual assessment. Such methods are commercially available but have not shown clinical benefit in randomised clinical trials [
20,
21] and have not been widely adopted. Other studies have used advanced signal processing techniques to extract multiple features from the CTG signal alone or in conjunction with clinical risk factors and apply machine learning approaches, including hierarchical Dirichlet process mixture models [
22], logistic regression [
23], neural networks [
24], support vector machines [
14,
25], random forests [
15], Bayesian classifier [
26], and XGBoost [
15,
27], to find patterns from the extracted features. One of the key issues with the conventional machine learning models is that they require careful design of feature extractors that transform the input CTG signal into compact representations or feature vectors [
28].
More recent studies on computerised CTG analysis apply modern deep learning (DL) techniques [
12,
29,
30,
31]. Convolutional Neural Networks (CNN) are among the most notable DL approaches that learn automatically abstract hierarchical representations directly from the input data using multiple hidden layers [
28]. CNN models have been extensively applied in various medical data analysis tasks involving image and time series analysis [
32,
33]. Long Short-Term Memory (LSTM) networks are another class of DL models suitable for analysing sequential (time series) data [
34]. Most previous works incorporating deep learning methods for the CTG analysis have used primarily 1D-CNN based networks. For example, Comert et al. [
12], and Baghel et al. [
31] analysed the last 90 min CTG data of the CTU-UHB open-access dataset [
35], using 1D CNNs. Zhao et al. [
12] reported better performance on the same dataset when implementing 2D CNNs by firstly transforming the CTG signal into 2D images using recurrence plots. More recently, Liu et al. [
36] proposed attention based CNN-LSTM network with features of discrete wavelet transformation to analyse the CTU-UHB dataset. However, these studies have been evaluated mostly on small datasets (40–160 abnormal birth outcomes), which are prone to large within-class variability and between-class similarity, resulting in a model with poor generalisation performance. Furthermore, although the proposed deep learning models are valid, due to absence of a distinct holdout (testing) sets in the CTU-UHB dataset and the less rigorous evaluation approach adopted (using the whole dataset for the cross validation instead of only on the training set), the results should be interpreted with caution. On a much larger dataset, Petrozziello et al. [
37] and Mohannad et al. [
38] evaluated the performance of CNNs to classify CTGs. Petrozziello et al. [
37] achieved promising performance using multimodal 1D CNNs to predict cord acidemia from the last hour CTG signal. Mohannad et al. [
38] applied a multi-input CNN network to analyse CTG plots of the initial 30 min of the last 50 min before delivery and gestational age to predict foetuses with a low Apgar score. Overall, previous studies on analysis of CTG using deep learning approaches focused on the last hour recordings mostly using small datasets.
In this study, we present three deep learning models for prediction of birth outcome using FHR traces recorded around the onset of labour in both: the time domain, implementing a combination of 1D CNNs and LSTMs; and in the frequency domain, employing a 2D CNNs [
33,
39]. The models are trained to classify new-borns with and without severe compromise at birth. To our knowledge, this study represents a pioneering effort in the application of deep learning techniques for analyzing CTG traces during early labour. Given the absence of published results from computer-based methods, we conducted a comparison of our findings with the existing standards of clinical care. We hypothesise that DL methods trained with a large clinical dataset of CTGs from around the onset of labour could hold the potential to ultimately assist clinicians in identifying foetuses who are already compromised or are vulnerable at labour onset and may thus be at high risk for further injury during labour.
4. Discussion
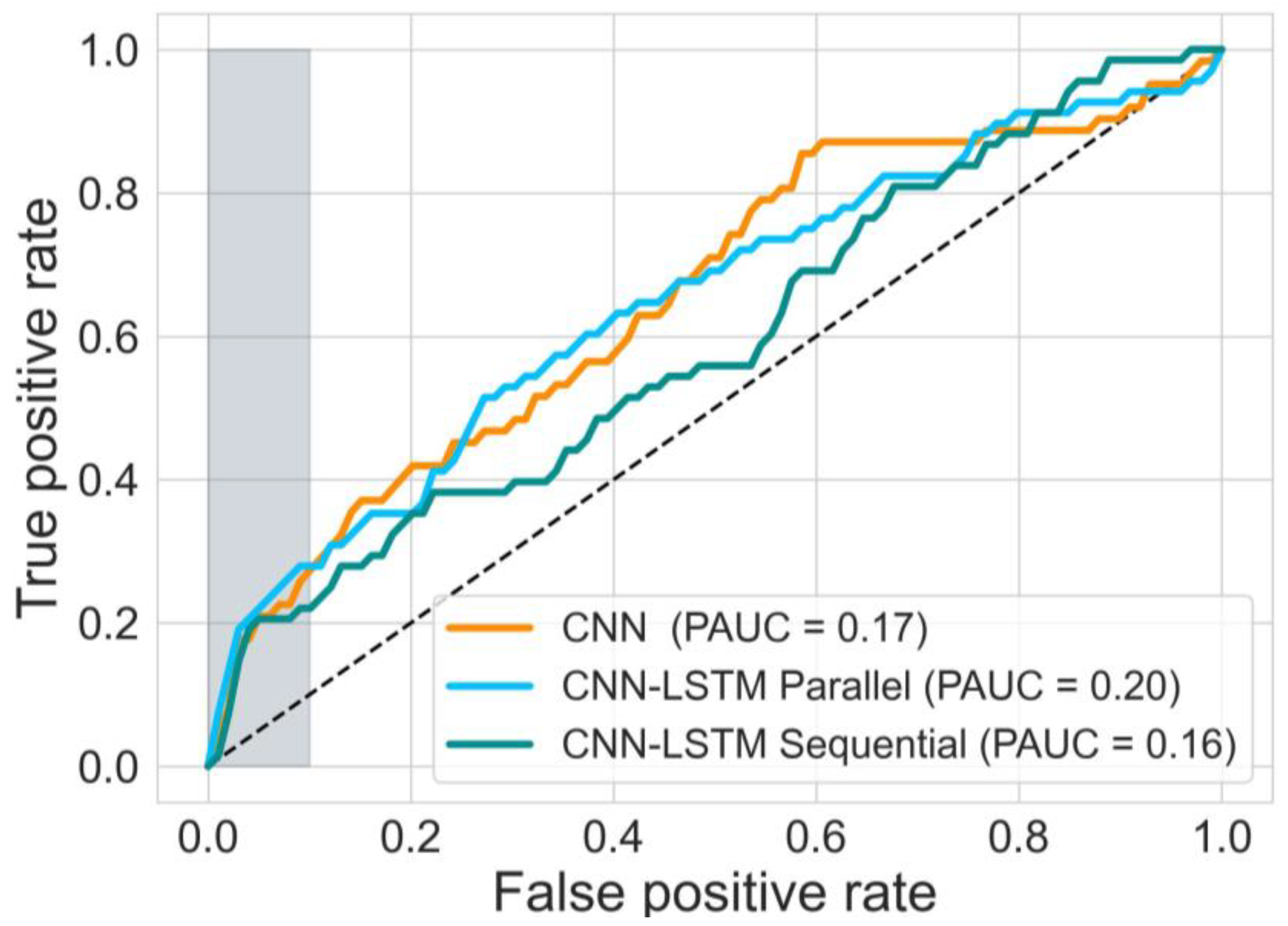
This study investigates the potential of implementing different deep learning architectures for predicting births with and without severe compromise outcomes, using the first 20 min of the FHR signals of more than 51,000 births, recorded as per clinical practice in a UK hospital during 1993–2012. From the designed and proposed DL architectures, the 1D-CNN-LSTM parallel topology model achieved superior classification performance compared to the other two developed models: 2D-CNN; and the multimodal architectures (combined 1D-CNN-LSTM and 2D-CNN). The suboptimal performance of the 2D-CNNs could be attributed to the lack of informative features in the time-frequency representations of the FHR signal. The post-hoc analysis also indicates that the performance of the 1D-CNN-LSTM model is not biased to signal loss, and its predictions are related to a degree to low STV values, which aligns with the clinical expectation of what is important in the initial FHR [
11].
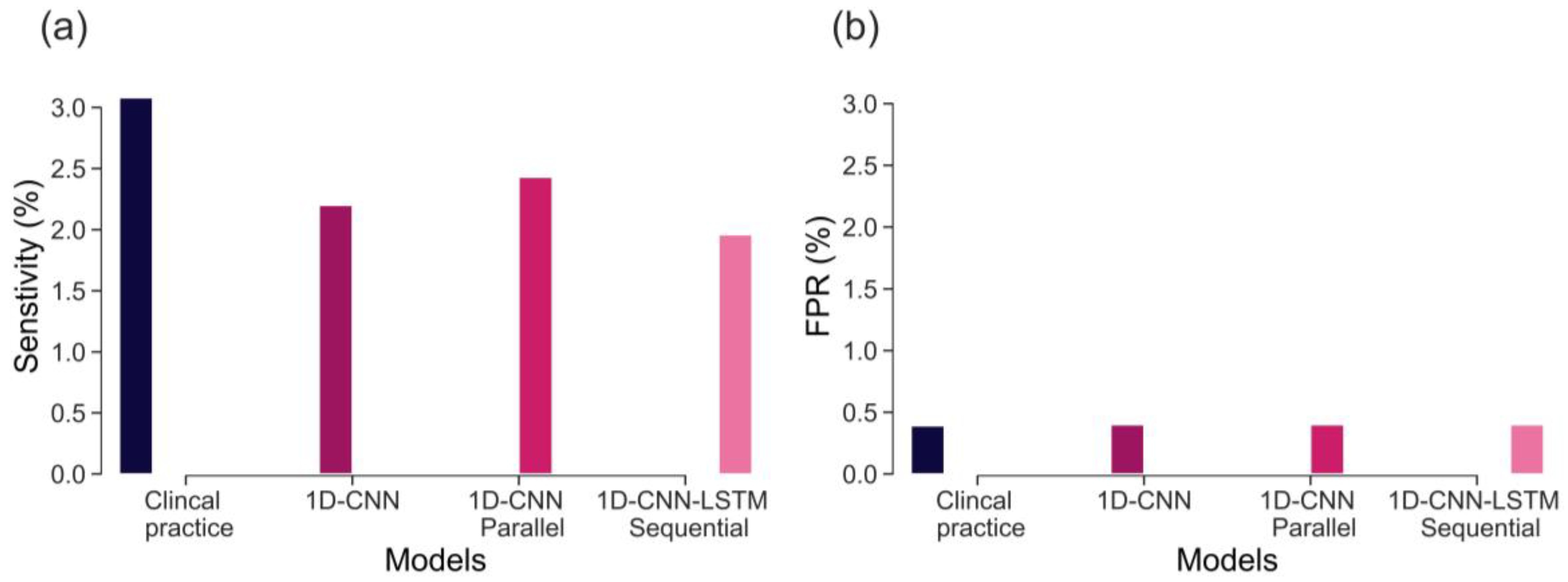
The sensitivity of CTG, based on initial hour in detecting severely compromised births, is not well established and there is limited evidence available. Lovers et al. [
11] reported that the sensitivity of admission CTG is approximately 3.1% at 0.4% FPR (
Figure 7). Our best model, the parallel 1D-CNN-LSTM model, achieved a slightly reduced sensitivity of 2.4% at a 0.4% FPR. This outcome is promising, particularly considering that clinical sensitivity in practice relies on evaluating the initial 2-h CTG data and incorporates various clinical risk factors. Nonetheless, the findings imply that our model has the potential to serve as a valuable aid for clinicians in identifying fetal distress and averting adverse birth outcomes.
Previous studies have also explored the potential of data-driven approaches in detecting abnormalities in CTG traces, focusing on the last hour CTG recording. For instance, Petrozziello et al., [
37], demonstrated that a 1D CNNs model that employs more than 35,000 CTGs of the last hour recording can achieve higher TPR in predicting birth acidemia (pH < 7.05) than the clinical diagnosis (53% vs. 31% at about 15% FPR). Other studies (12, 30, 31), using a much smaller dataset and pH < 7.15 as an abnormal outcome, also implemented 1D CNNs to classify FHR signals. However, these works have focused on detecting birth acidemia based on the last hour CTG recording. When similar outcome groups are investigated (as in this work: with and without severe compromise), the OxSys 1.5 (3), achieved slightly higher TPR (43% at 14% FPR) than the clinical diagnosis (35% at 16% FPR) and our 1D-CNN-LSTM model (35% at 16% FPR) on a dataset of more than 22,000 CTGs. Nevertheless, this relatively higher accuracy results from analysing the entire FHR trace (in our case, it is based on the first 20 min only).
The main contributions of our work are: proposing and implementing DL models, based on uniquely large and detailed dataset allowing their successful training, validation, and testing; the clinically relevant definition of a rare severe compromise; and the focus on the first 20 min of the FHR, seeking an early warning for those fetuses that are unlikely to sustain the stress of labour due to pre-existing vulnerability. We capped the false positive rate to 5% and achieved sensitivity of 20%—an encouraging result given that most infants who would sustain severe compromise, are expected to do so later in labour. Also, given the fact that the false positive rate cannot be precisely defined, due to the routine nature of our data, which includes high rates of clinical intervention and censuring the data. The achieved performance, as compared to the clinical benchmark (as shown in
Figure 7), is highly encouraging. This is particularly noteworthy because predicting adverse outcomes in clinical practice relies not only on CTG patterns but also on various risk factors such as abnormal fetal growth, antepartum hemorrhage, prolonged rupture of membranes, and meconium staining of the amniotic fluid [
9]. Consequently, a model that provides an objective assessment of CTG, without imposing a significant computational burden (with trace prediction in under a second with the ready trained model), can serve as an integral part of a clinical decision support tool. By doing so, it could contribute to optimizing the allocation of clinical resources, allowing clinicians to focus on other crucial responsibilities. Finally, in our future work, we expect to further improve the model accuracy by incorporating clinical risk factors into the analysis.
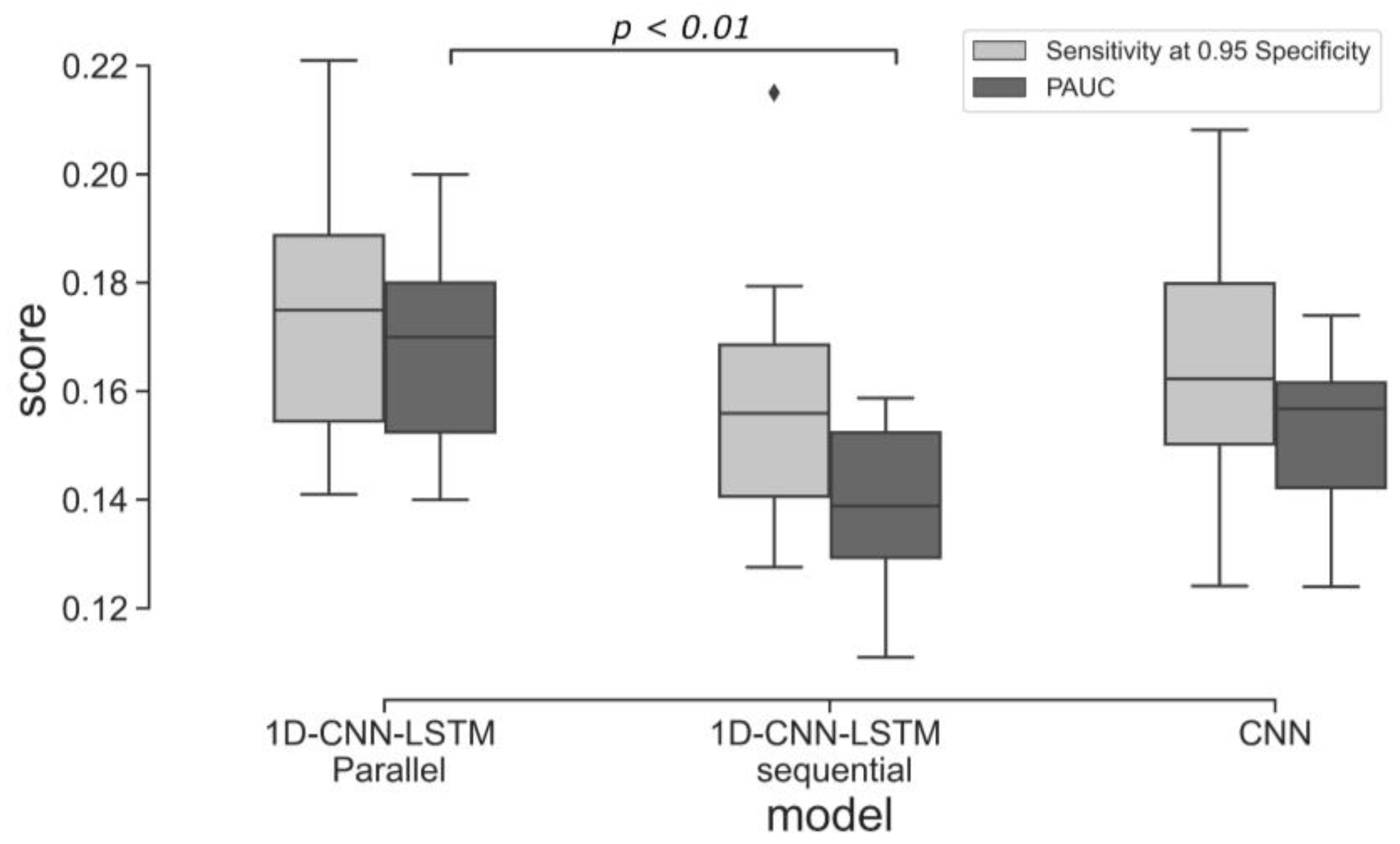
Some limitations of our approach are also worth noting. While data augmentation has demonstrated some effectiveness in addressing label imbalance and reducing model overfitting, it is important to consider the potential risk of amplifying label noise within the dataset. Thus, it is necessary to acknowledge that data augmentation alone may not offer a complete solution to the challenges associated with learning from imbalanced datasets. This limitation is evident in the variance of the ten cross-validated models, as depicted in
Figure 5. Future work should address this by employing other techniques, perhaps creating synthetic data using generative adversarial networks [
53]. The classification performance should also be improved by analysing longer traces and incorporating uterine contraction signals and clinical risk factors (such as fetal gestation and maternal co-morbidities) into the model. Finally, our approach does not explain which segment of the input leads to a particular prediction. Therefore, future work will consider applying an attention layer to provide better explainability [
54].
5. Conclusions
We developed and evaluated three different deep neural network architectures to classify a 20-min FHR segment, recorded around the onset of labour, to investigate their potential in providing very early warning and triage women in labour into high or low-risk groups for further monitoring and/or review. We achieved superior performance using the proposed 1D-CNN-LSTM parallel architecture: the best model achieved a sensitivity of 20% at 95% specificity. The results are clinically encouraging, considering the fact that the majority of the compromised babies are not expected to have demonstrated problems, and if any, they are challenging to detect at the onset of labour. It is important to note that there is also room to improve the model classification performance by analysing the entire FHR trace and incorporating clinical risk factors.
Although the proposed DL architecture achieved encouraging results on the holdout test set, it could also be tested on an external dataset to further validate its generalisation performance. In addition, the investigated models do lack explainability, and future work will incorporate an attention mechanism that will introduce it.