Exploiting Patch Sizes and Resolutions for Multi-Scale Deep Learning in Mammogram Image Classification
Abstract
1. Introduction
1.1. 2D Mammography Image Classification
1.2. Contributions
- The impact of the patch size is studied, both on the patch classifier and on the whole image classifier. For the patch-classifier, the patch size effect on lesions of different sizes is analysed;
- The impact of decreasing the input image resolution on the two classifiers is studied, as well as its effect on lesions of different sizes;
- A multi-patch size and a multi-resolution approach for classifying whole images are proposed, that leverage patch classifiers adapted to different lesion sizes. These multi-scale models are shown to outperform single patch-sized, single resolution classifiers.
2. Materials and Methods
2.1. Datasets
2.2. Patch Extraction
2.3. Patch Classifier
2.4. Base Whole Image Classifier
2.5. Multi-Resolution & Multi-Patch Size Whole Image Classifier
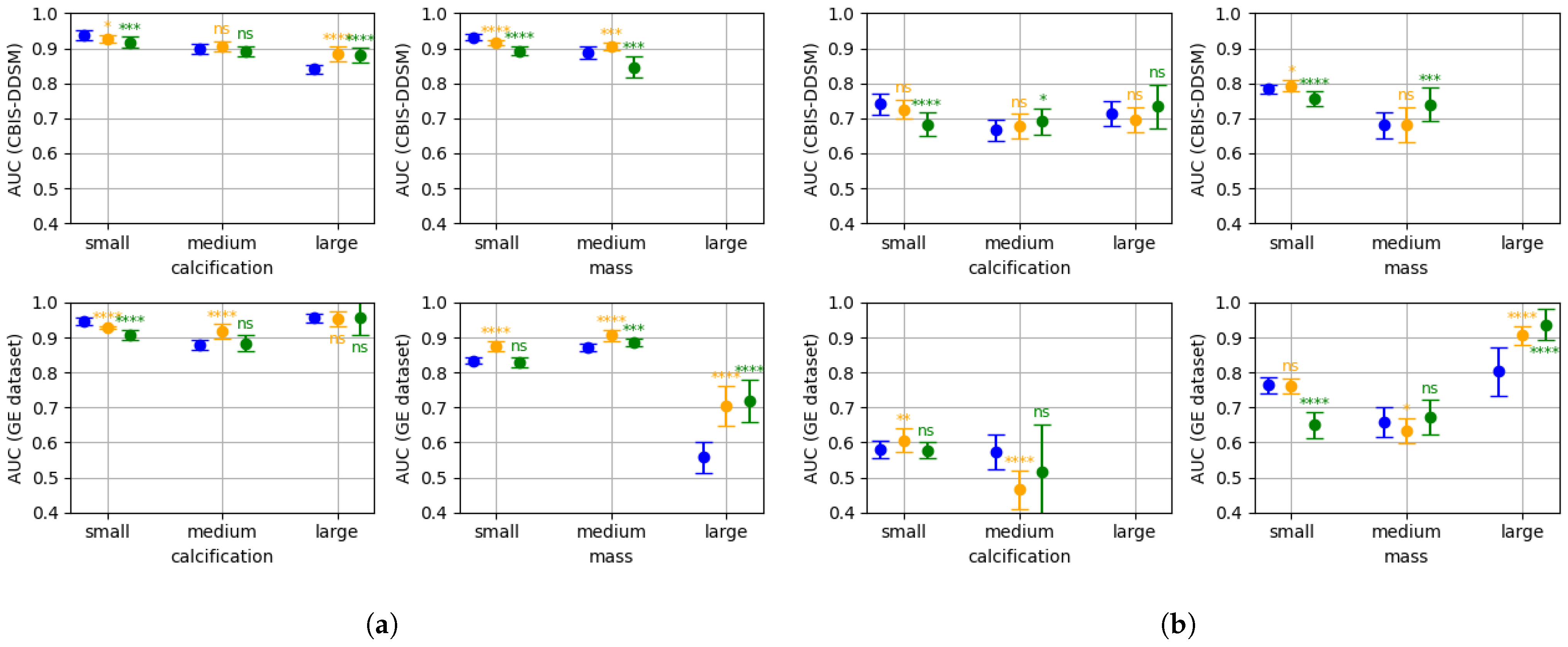
3. Results
3.1. Patch Classifier
3.2. Base Whole Image Classifier
3.3. Multi-Resolution & Multi-Patch Size Whole Image Classifier
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global Cancer Statistics 2020: GLOBOCAN Estimates of Incidence and Mortality Worldwide for 36 Cancers in 185 Countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2016. CA Cancer J. Clin. 2016, 66, 7–30. [Google Scholar] [CrossRef] [PubMed]
- Mandelblatt, J.S.; Cronin, K.A.; Bailey, S.; Berry, D.A.; De Koning, H.J.; Draisma, G.; Huang, H.; Lee, S.J.; Munsell, M.; Plevritis, S.K. Effects of mammography screening under different screening schedules: Model estimates of potential benefits and harms. Ann. Intern. Med. 2009, 151, 738–747. [Google Scholar] [CrossRef] [PubMed]
- Kolb, T.M.; Lichy, J.; Newhouse, J.H. Comparison of the performance of screening mammography, physical examination, and breast US and evaluation of factors that influence them: An analysis of 27,825 patient evaluations. Radiology 2002, 225, 165–175. [Google Scholar] [CrossRef]
- Michell, M.J. Breast screening review—A radiologist’s perspective. Br. J. Radiol. 2012, 85, 845–847. [Google Scholar] [CrossRef] [PubMed]
- Grabler, P.; Sighoko, D.; Wang, L.; Allgood, K.; Ansell, D. Recall and Cancer Detection Rates for Screening Mammography: Finding the Sweet Spot. AJR Am. J. Roentgenol. 2017, 208, 208–213. [Google Scholar] [CrossRef]
- Katzen, J.; Dodelzon, K. A review of computer aided detection in mammography. Clin. Imaging 2018, 52, 305–309. [Google Scholar] [CrossRef]
- Taylor, P.; Potts, H. Computer aids and human second reading as interventions in screening mammography: Two systematic reviews to compare effects on cancer detection and recall rate. Eur. J. Cancer 2008, 44, 798–807. [Google Scholar] [CrossRef]
- Bahl, M. Detecting Breast Cancers with Mammography: Will AI Succeed Where Traditional CAD Failed? Radiology 2019, 290, 315–316. [Google Scholar] [CrossRef]
- Baker, J.; Rosen, E.; Lo, J.; Gimenez, E.; Walsh, R.; Soo, M. Computer-Aided Detection (CAD) in Screening Mammography: Sensitivity of Commercial CAD Systems for Detecting Architectural Distortion. AJR. Am J. Roentgenol. 2003, 181, 1083–1088. [Google Scholar] [CrossRef]
- Rodriguez-Ruiz, A.; Lång, K.; Gubern-Mérida, A.; Broeders, M.; Gennaro, G.; Clauser, P.; Helbich, T.; Chevalier, M.; Tan, T.; Mertelmeier, T.; et al. Stand-Alone Artificial Intelligence for Breast Cancer Detection in Mammography: Comparison With 101 Radiologists. J. Natl. Cancer Inst. 2019, 111, 916–922. [Google Scholar] [CrossRef]
- McKinney, S.; Sieniek, M.; Godbole, V.; Godwin, J.; Antropova, N.; Ashrafian, H.; Back, T.; Chesus, M.; Corrado, G.; Darzi, A.; et al. International evaluation of an AI system for breast cancer screening. Nature 2020, 577, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Yala, A.; Lehman, C.; Schuster, T.; Portnoi, T.; Barzilay, R. A Deep Learning Mammography-based Model for Improved Breast Cancer Risk Prediction. Radiology 2019, 292, 182716. [Google Scholar] [CrossRef] [PubMed]
- Geras, K.J.; Mann, R.M.; Moy, L. Artificial Intelligence for Mammography and Digital Breast Tomosynthesis: Current Concepts and Future Perspectives. Radiology 2019, 293, 246–259. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.; Phang, J.; Park, J.; Shen, Y.; Huang, Z.; Zorin, M.; Jastrzębski, S.; Févry, T.; Katsnelson, J.; Kim, E.; et al. Deep Neural Networks Improve Radiologists’ Performance in Breast Cancer Screening. IEEE Trans. Med. Imaging 2019, 39, 1184–1194. [Google Scholar] [CrossRef] [PubMed]
- Chorev, M.; Shoshan, Y.; Spiro, A.; Naor, S.; Hazan, A.; Barros, V.; Weinstein, I.; Herzel, E.; Shalev, V.; Guindy, M.; et al. The Case of Missed Cancers: Applying AI as a Radiologist’s Safety Net. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2020; Springer: Cham, Switzerland, 2020; pp. 220–229. [Google Scholar]
- Leibig, C.; Brehmer, M.; Bunk, S.; Byng, D.; Pinker, K.; Umutlu, L. Combining the strengths of radiologists and AI for breast cancer screening: A retrospective analysis. Lancet Digit. Health 2022, 4, e507–e519. [Google Scholar] [CrossRef]
- Shen, L.; Margolies, L.R.; Rothstein, J.H.; Fluder, E.; McBride, R.; Sieh, W. Deep Learning to Improve Breast Cancer Detection on Screening Mammography. Sci. Rep. 2019, 9, 12495. [Google Scholar] [CrossRef]
- Petrini, D.G.P.; Shimizu, C.; Roela, R.A.; Valente, G.V.; Folgueira, M.A.A.K.; Kim, H.Y. Breast Cancer Diagnosis in Two-View Mammography Using End-to-End Trained EfficientNet-Based Convolutional Network. IEEE Access 2021, 10, 77723–77731. [Google Scholar] [CrossRef]
- Bakalo, R.; Ben-Ari, R.; Goldberger, J. Classification and Detection in Mammograms with Weak Supervision via Dual Branch Deep Neural Net. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019. [Google Scholar] [CrossRef]
- Gong, X.; Xia, X.; Zhu, W.; Zhang, B.; Doermann, D.S.; Zhuo, L. Deformable Gabor Feature Networks for Biomedical Image Classification. arXiv 2020, arXiv:2012.04109. [Google Scholar]
- Zhu, W.; Lou, Q.; Vang, Y.S.; Xie, X. Deep Multi-instance Networks with Sparse Label Assignment for Whole Mammogram Classification. arXiv 2016, arXiv:1612.05968. [Google Scholar]
- Arora, R.; Rai, P.K.; Raman, B. Deep feature-based automatic classification of mammograms. Med. Biol. Eng. Comput. 2020, 58, 1199–1211. [Google Scholar] [CrossRef]
- Nasir Khan, H.; Shahid, A.; Raza, B.; Dar, A.; Alquhayz, H. Multi-View Feature Fusion Based Four Views Model for Mammogram Classification Using Convolutional Neural Network. IEEE Access 2019, 7, 165724–165733. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, J.; Niu, J.; D, L. New convolutional neural network model for screening and diagnosis of mammograms. PLoS ONE 2020, 15, e0237674. [Google Scholar] [CrossRef]
- Van Tulder, G.; Tong, Y.; Marchiori, E. Multi-view Analysis of Unregistered Medical Images Using Cross-View Transformers. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2021; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 104–113. [Google Scholar] [CrossRef]
- Zhao, X.; Yu, L.; Wang, X. Cross-View Attention Network for Breast Cancer Screening from Multi-View Mammograms. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1050–1054. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv 2014, arXiv:1409.4842. [Google Scholar] [CrossRef]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. Neural Photo Editing with Introspective Adversarial Networks. arXiv 2016, arXiv:1609.07093. [Google Scholar] [CrossRef]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. arXiv 2016, arXiv:1612.03144. [Google Scholar] [CrossRef]
- Yun, D.; Ryu, J.; Lim, J. Dual aggregated feature pyramid network for multi label classification. Pattern Recognit. Lett. 2021, 144, 75–81. [Google Scholar] [CrossRef]
- Rahimzadeh, M.; Attar, A.; Sakhaei, S.M. A fully automated deep learning-based network for detecting COVID-19 from a new and large lung CT scan dataset. Biomed. Signal Process. Control 2021, 68, 102588. [Google Scholar] [CrossRef] [PubMed]
- Shu, X.; Zhang, L.; Wang, Z.; Lv, Q.; Yi, Z. Deep Neural Networks With Region-Based Pooling Structures for Mammographic Image Classification. IEEE Trans. Med. Imaging 2020, 39, 2246–2255. [Google Scholar] [CrossRef]
- Lee, R.; Gimenez, F.; Hoogi, A.; Miyake, K.; Gorovoy, M.; Rubin, D. A curated mammography data set for use in computer-aided detection and diagnosis research. Sci. Data 2017, 4, 170177. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. arXiv 2016, arXiv:1608.06993. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Lehman, C.D.; Arao, R.F.; Sprague, B.L.; Lee, J.M.; Buist, D.S.M.; Kerlikowske, K.; Henderson, L.M.; Onega, T.; Tosteson, A.N.A.; Rauscher, G.H.; et al. National Performance Benchmarks for Modern Screening Digital Mammography: Update from the Breast Cancer Surveillance Consortium. Radiology 2017, 283, 49–58. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Das, A.; Vedantam, R.; Cogswell, M.; Parikh, D.; Batra, D. Grad-CAM: Why did you say that? Visual Explanations from Deep Networks via Gradient-based Localization. arXiv 2016, arXiv:1610.02391. [Google Scholar]
- Wei, T.; Aviles-Rivero, A.I.; Wang, S.; Huang, Y.; Gilbert, F.J.; Schönlieb, C.B.; Chen, C.W. Beyond Fine-tuning: Classifying High Resolution Mammograms using Function-Preserving Transformations. arXiv 2021, arXiv:2101.07945. [Google Scholar] [CrossRef] [PubMed]
- Almeida, R.; Chen, D.; Silva-Filho, A.; Brandão, W. Machine Learning Algorithms for Breast Cancer Detection in Mammography Images: A Comparative Study. In Proceedings of the 23rd International Conference on Enterprise Information Systems (ICEIS 2021), Online, 26–28 April 2021. [Google Scholar] [CrossRef]
- Glenn, J. ultralytics/yolov5: V6.0—YOLOv5n `Nano’ Models, Roboflow Integration, TensorFlow Export, OpenCV DNN Support; Zenodo: Honolulu, HI, USA, 2021. [Google Scholar] [CrossRef]
- Calderón-Ramírez, S.; Murillo-Hernández, D.; Rojas-Salazar, K.; Calvo-Valverd, L.A.; Yang, S.; Moemeni, A.; Elizondo, D.; López-Rubio, E.; Molina-Cabello, M.A. Improving Uncertainty Estimations for Mammogram Classification using Semi-Supervised Learning. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Calderon-Ramirez, S.; Murillo-Hernandez, D.; Rojas-Salazar, K.; Elizondo, D.; Yang, S.; Molina-Cabello, M. A Real Use Case of Semi-Supervised Learning for Mammogram Classification in a Local Clinic of Costa Rica. arXiv 2021, arXiv:2107.11696. [Google Scholar] [CrossRef] [PubMed]
- Berthelot, D.; Carlini, N.; Goodfellow, I.J.; Papernot, N.; Oliver, A.; Raffel, C. MixMatch: A Holistic Approach to Semi-Supervised Learning. arXiv 2019, arXiv:1905.02249. [Google Scholar]
- Liu, H.; Li, H.; Habes, M.; Li, Y.; Boimel, P.; Janopaul-Naylor, J.; Xiao, Y.; Ben-Josef, E.; Fan, Y. Robust Collaborative Clustering of Subjects and Radiomic Features for Cancer Prognosis. IEEE Trans. Biomed. Eng. 2020, 67, 2735–2744. [Google Scholar] [CrossRef]




| AUC | Sp (with Se = 0.75) | Acc (with Se = 0.75) | |
|---|---|---|---|
| patch size 256 | 0.784 ± 0.002 (n.a.) | 0.656 ± 0.013 (n.a.) | 0.703 ± 0.014 (n.a.) |
| patch size 512 * | 0.764 ± 0.005 (<0.001) | 0.627 ± 0.029 (<0.05) | 0.689 ± 0.024 (n.s.) |
| patch size 768 | 0.776 ± 0.010 (<0.1) | 0.656 ± 0.023 (n.s.) | 0.703 ± 0.02 (n.s.) |
| multi-patch size | 0.809 ± 0.005 (<0.001) | 0.710 ± 0.020 (<0.001) | 0.730 ± 0.019 (<0.05) |
| resolution 100 * | 0.764 ± 0.005 (n.a.) | 0.627 ±0.029 (n.a.) | 0.689 ± 0.024 (n.a.) |
| resolution 150 | 0.744 ± 0.005 (<0.001) | 0.588 ± 0.013 (<0.05) | 0.669 ± 0.009 (<0.1) |
| resolution 200 | 0.736 ± 0.005 (<0.001) | 0.548 ± 0.029 (<0.005) | 0.649 ± 0.023 (<0.05) |
| multi-resolution | 0.789 ± 0.005 (<0.001) | 0.670 ± 0.005 (<0.05) | 0.710 ± 0.006 (<0.1) |
| FPN | 0.788 ± 0.003 (n.a.) | 0.685 ± 0.004 (n.a.) | 0.717 ± 0.004 (n.a.) |
| multi-resolution | 0.789 ± 0.005 (n.s.) | 0.670 ± 0.005 (<0.001) | 0.710 ± 0.006 (<0.05) |
| multi-patch size | 0.809 ± 0.005 (<0.001) | 0.710 ± 0.020 (<0.05) | 0.730 ± 0.019 (<0.1) |
| AUC | Sp (with Se = 0.75) | Acc (with Se = 0.75) | |
|---|---|---|---|
| patch size 256 | 0.685 ± 0.012 (n.s.) | 0.487 ± 0.023 (n.s.) | 0.619 ± 0.038 (n.s.) |
| patch size 512 * | 0.688 ± 0.011 (n.a.) | 0.470 ± 0.048 (n.a.) | 0.610 ± 0.041 (n.a.) |
| patch size 768 | 0.673 ± 0.010 (<0.05) | 0.430 ± 0.032 (<0.1) | 0.590 ± 0.033 (n.s.) |
| multi-patch size | 0.722 ± 0.012 (<0.005) | 0.552 ± 0.054 (<0.05) | 0.651 ± 0.042 (<0.1) |
| resolution 100 * | 0.688 ± 0.011 (n.a.) | 0.470 ± 0.048 (n.a.) | 0.610 ± 0.041 (n.a.) |
| resolution 150 | 0.628 ± 0.017 (<0.001) | 0.333 ± 0.057 (<0.005) | 0.542 ± 0.053 (<0.05) |
| resolution 200 | 0.583 ± 0.036 (<0.001) | 0.333 ± 0.065 (<0.005) | 0.542 ± 0.067 (<0.05) |
| multi-resolution | 0.709 ± 0.010 (<0.01) | 0.466 ± 0.032 (n.s.) | 0.608 ± 0.032 (n.s.) |
| FPN | 0.697 ± 0.017 (n.a.) | 0.487 ± 0.095 (n.a.) | 0.619 ± 0.061 (n.a.) |
| multi-resolution | 0.709 ± 0.010 (<0.1) | 0.466 ± 0.032 (n.s.) | 0.608 ± 0.032 (n.s.) |
| multi-patch size | 0.722 ± 0.012 (<0.05) | 0.552 ± 0.054 (<0.1) | 0.651 ± 0.042 (<0.1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintana, G.I.; Li, Z.; Vancamberg, L.; Mougeot, M.; Desolneux, A.; Muller, S. Exploiting Patch Sizes and Resolutions for Multi-Scale Deep Learning in Mammogram Image Classification. Bioengineering 2023, 10, 534. https://doi.org/10.3390/bioengineering10050534
Quintana GI, Li Z, Vancamberg L, Mougeot M, Desolneux A, Muller S. Exploiting Patch Sizes and Resolutions for Multi-Scale Deep Learning in Mammogram Image Classification. Bioengineering. 2023; 10(5):534. https://doi.org/10.3390/bioengineering10050534
Chicago/Turabian StyleQuintana, Gonzalo Iñaki, Zhijin Li, Laurence Vancamberg, Mathilde Mougeot, Agnès Desolneux, and Serge Muller. 2023. "Exploiting Patch Sizes and Resolutions for Multi-Scale Deep Learning in Mammogram Image Classification" Bioengineering 10, no. 5: 534. https://doi.org/10.3390/bioengineering10050534
APA StyleQuintana, G. I., Li, Z., Vancamberg, L., Mougeot, M., Desolneux, A., & Muller, S. (2023). Exploiting Patch Sizes and Resolutions for Multi-Scale Deep Learning in Mammogram Image Classification. Bioengineering, 10(5), 534. https://doi.org/10.3390/bioengineering10050534







