Improving the Segmentation Accuracy of Ovarian-Tumor Ultrasound Images Using Image Inpainting
Abstract
1. Introduction
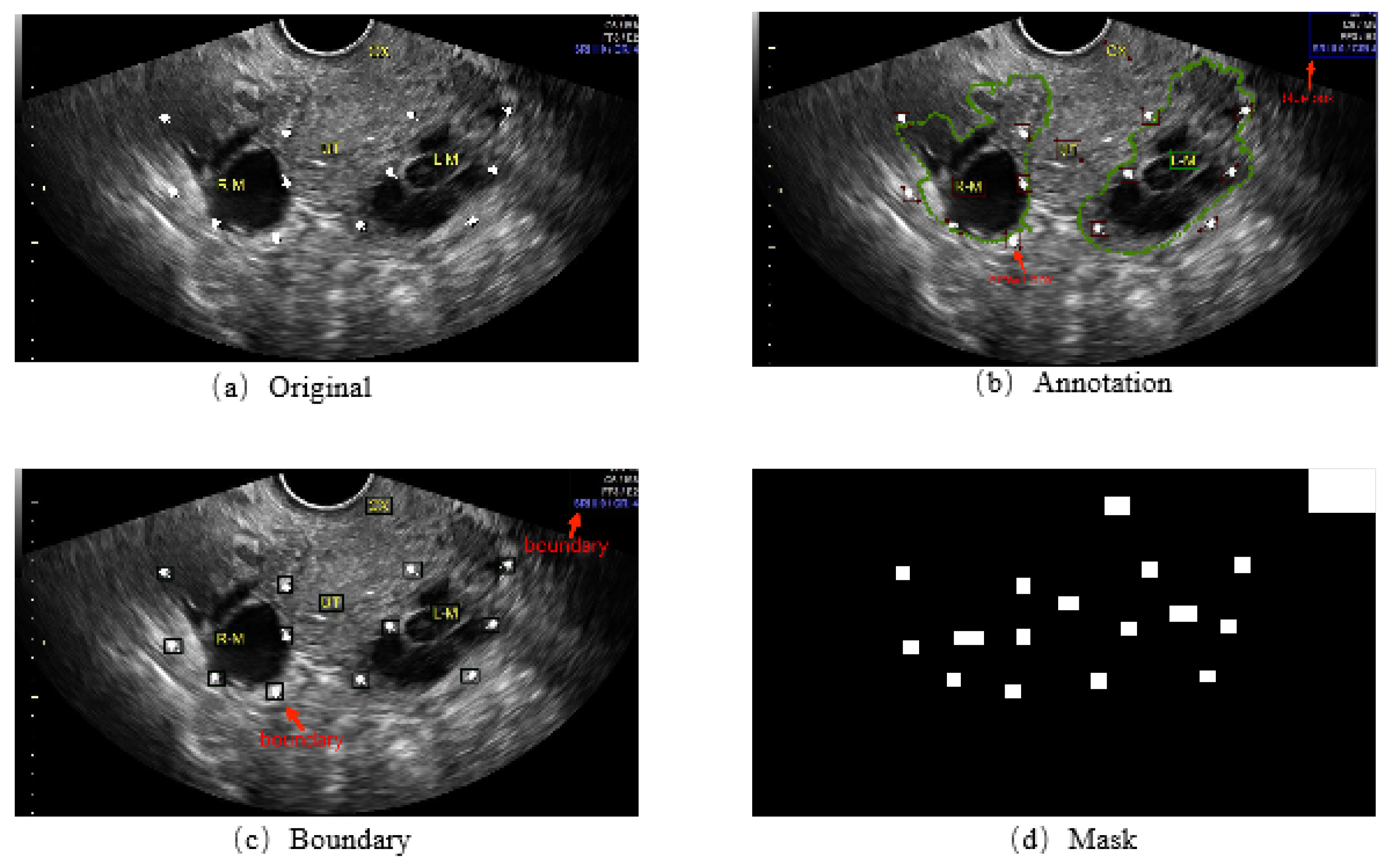
- We refined 1469 2D ovarian-tumor ultrasound images for irregular symbols and obtained binary masks to establish a 2D ovarian-tumor ultrasound image inpainting dataset.
- We introduced fast Fourier convolution to enhance the model’s global perceptual field and a channel attention mechanism to enhance the model’s attention to significant features, and the model uses global features and significant channel features to fill the holes.
- Our model achieved better results both subjectively and objectively compared to existing models while for the first time performing image inpainting without clean images.
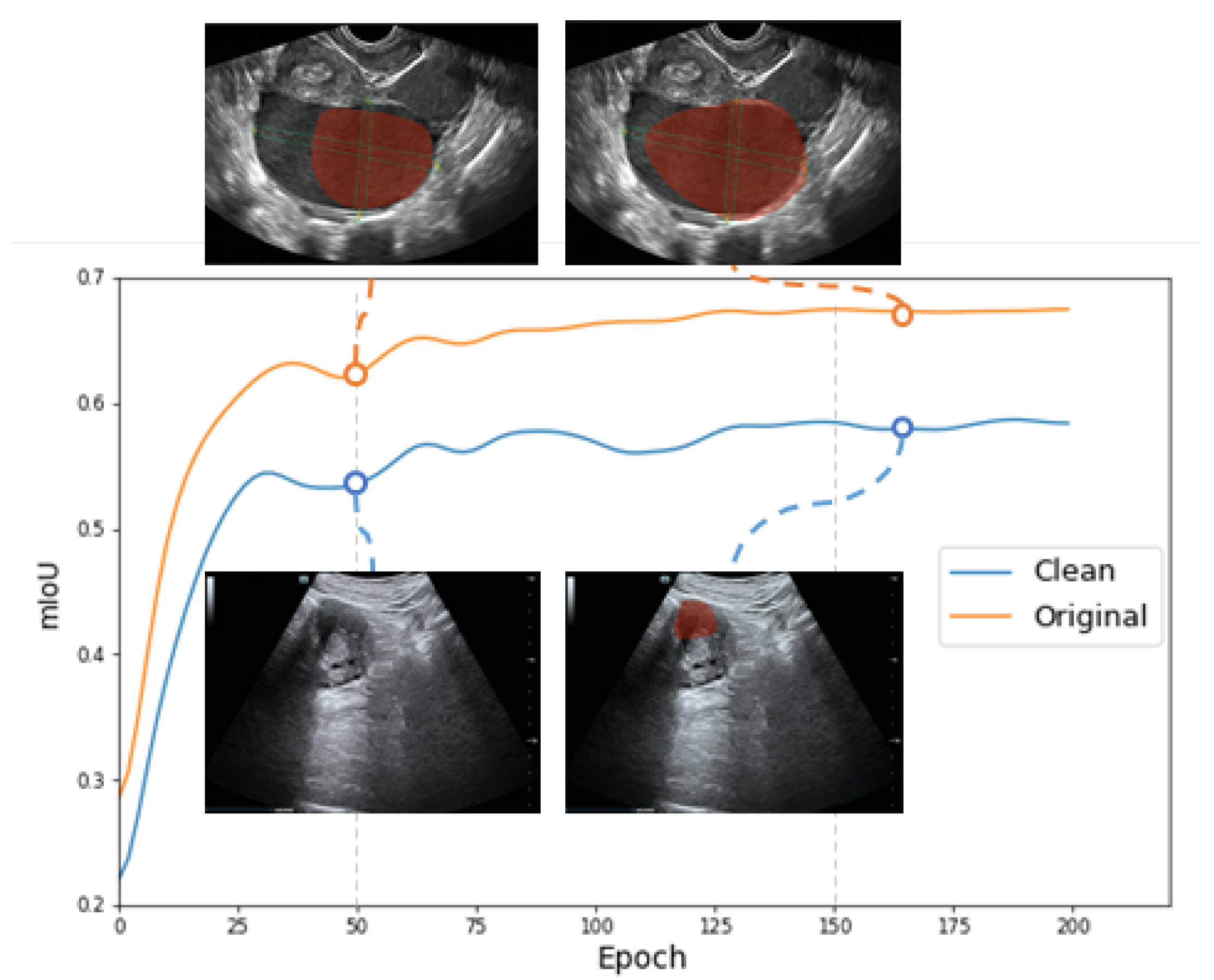
- We use the restoration images for segmentation training, which significantly enhances the accuracy of the classification and segmentation of clean images.
2. Methodology
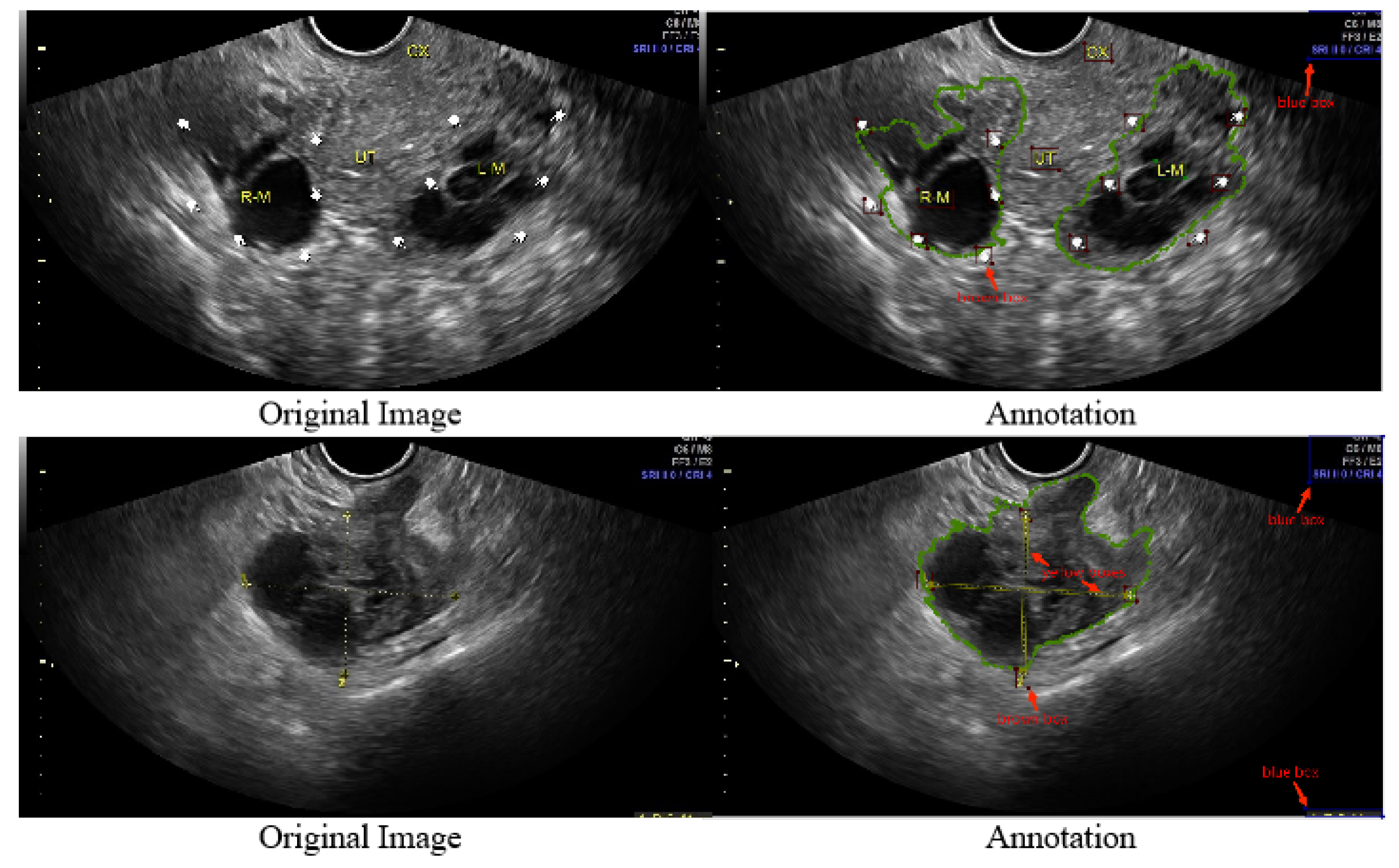
2.1. Dataset
2.2. Implementation Details
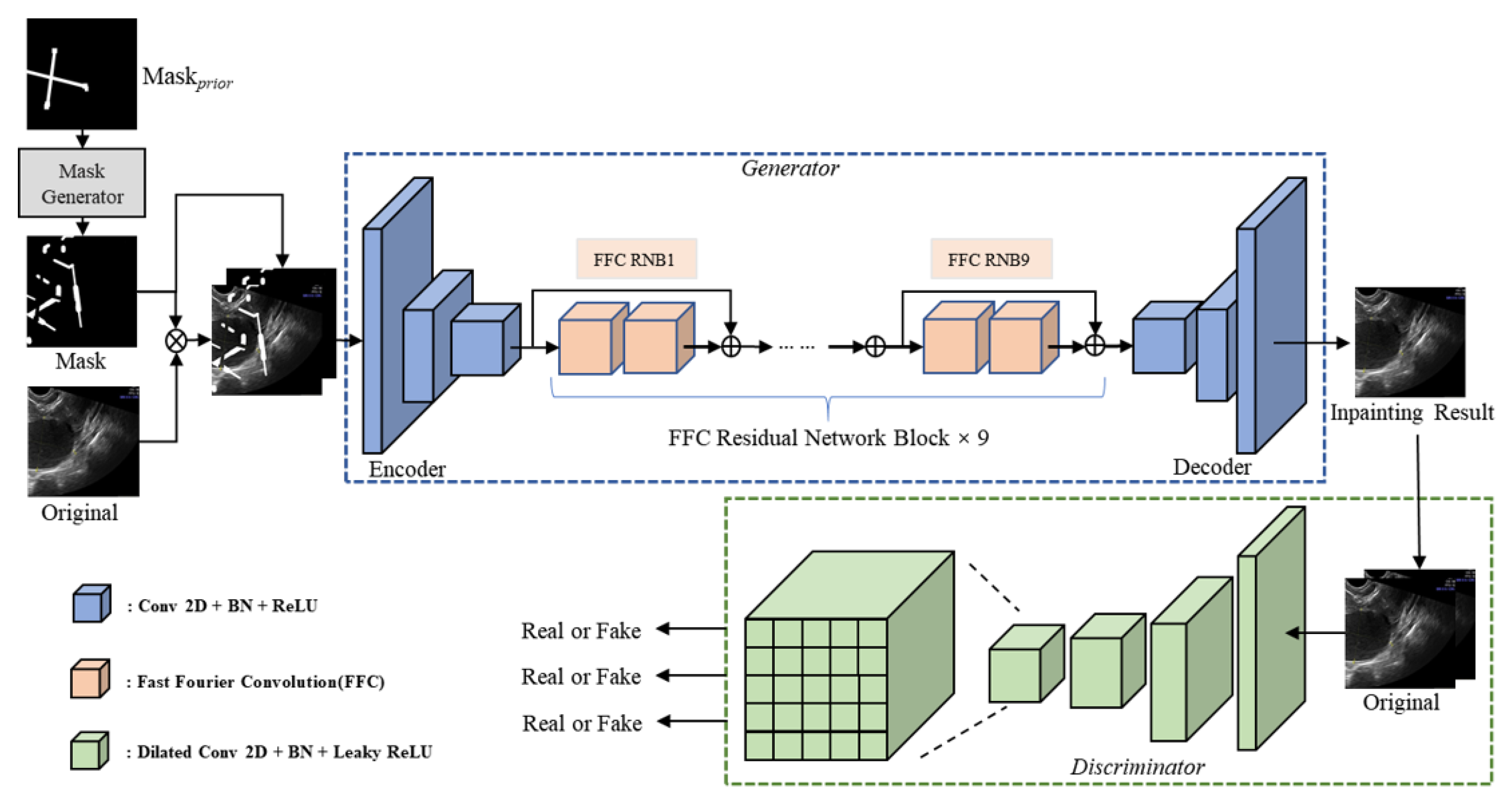
2.3. Proposed Methods
2.3.1. Network Architecture
2.3.2. Fast Fourier Convolution Block
- Transforming the input tensor to the frequency domain using the real fast Fourier transform: .
- Concatenating the real and imaginary parts in the frequency domain: .
- Obtaining convolution results in the frequency domain through the ReLU layer, BatchNorm layer, and 1 × 1 convolution layer: .
- Separating the result of frequency domain convolution into real and imaginary parts: .
- Recovering its spatial structure using Fourier inverse transform: .
2.3.3. Generation of Masks during Training
2.4. Loss Function
2.5. Evaluation Criterion
3. Experiments and Results
3.1. Results
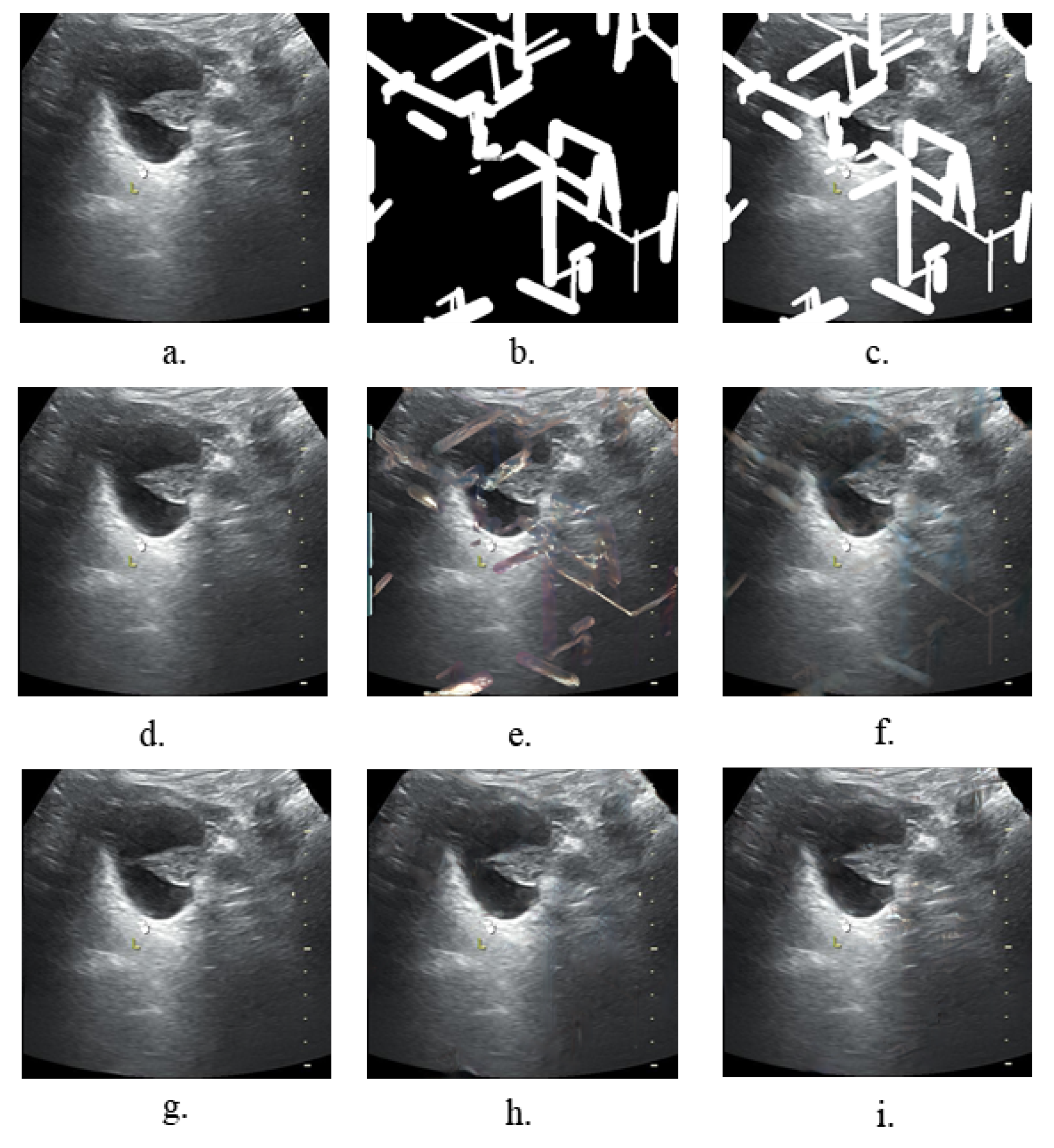
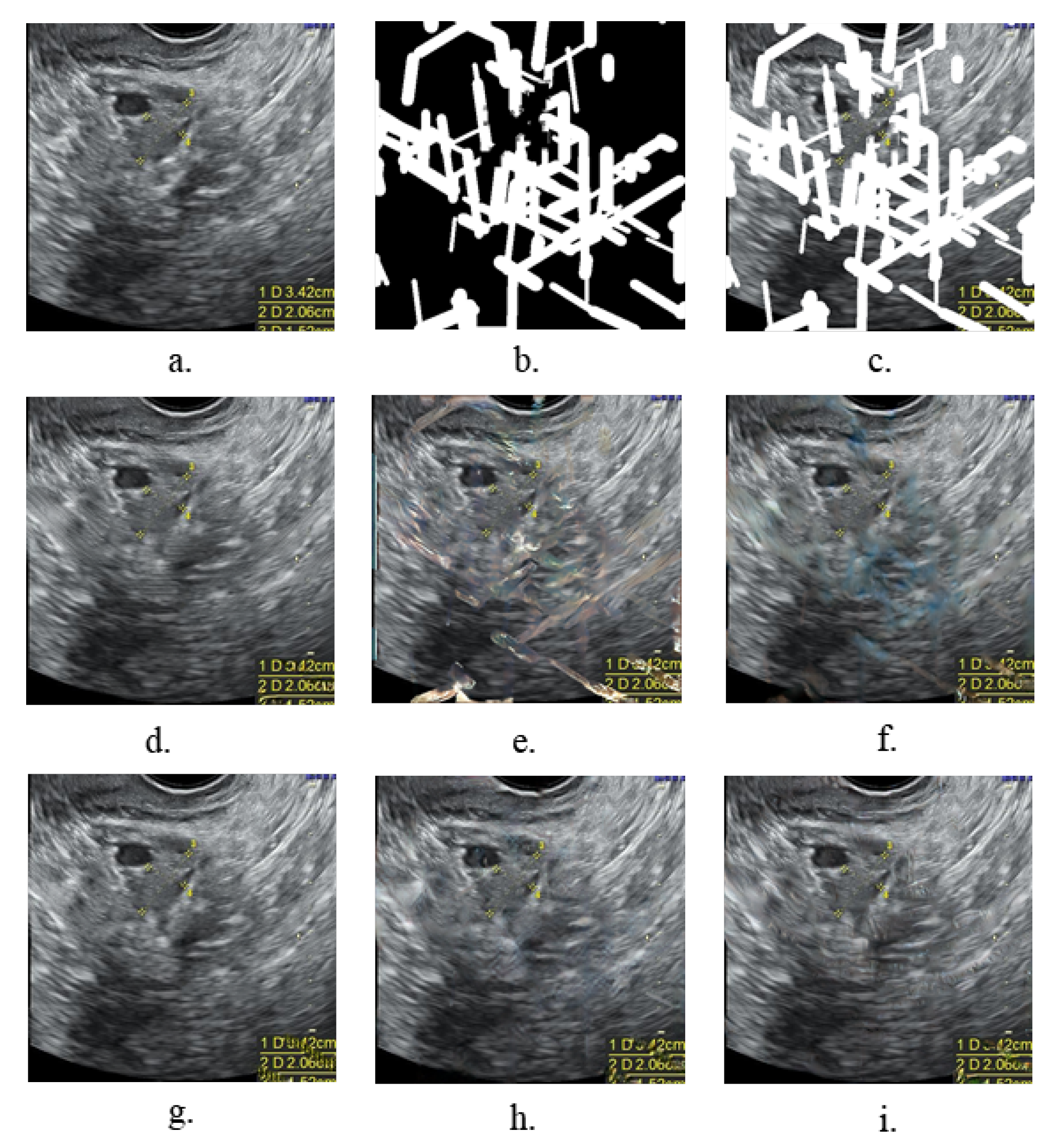
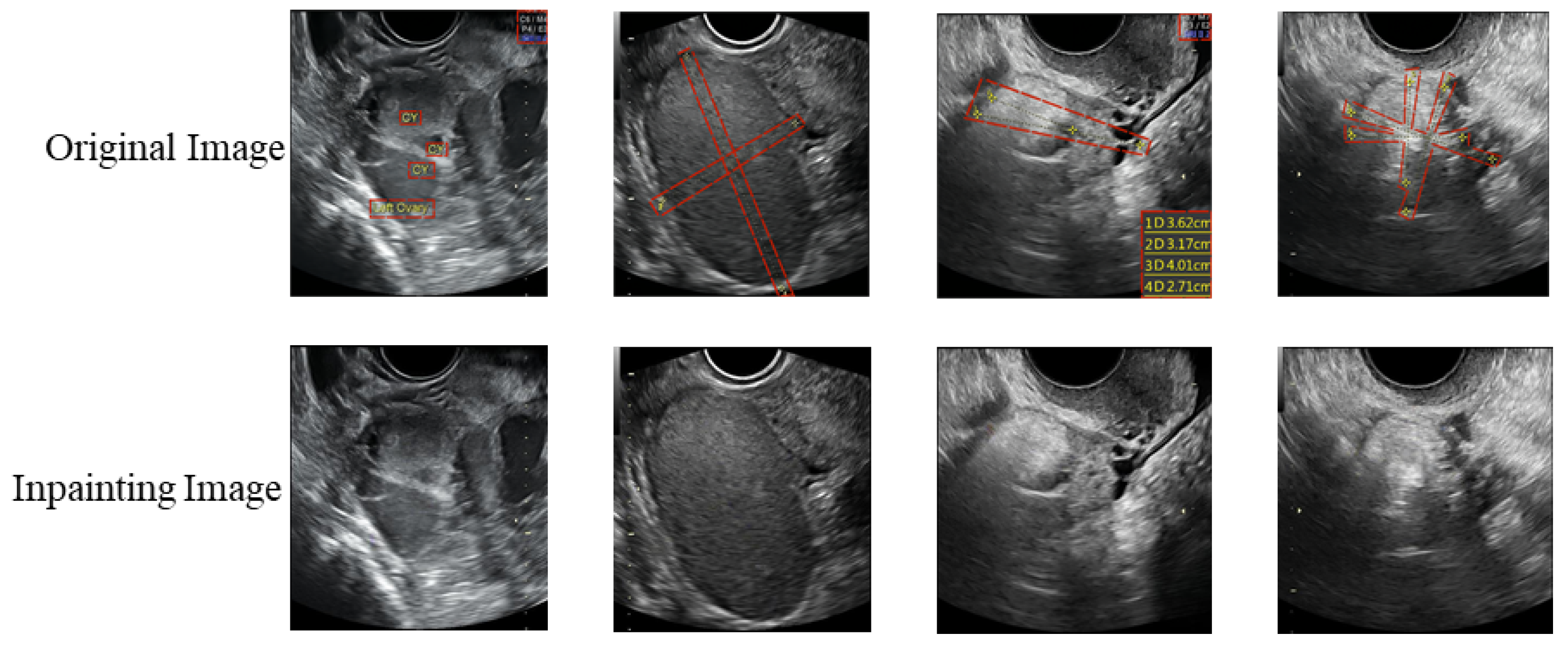
3.1.1. Experiments on the Image Inpainting
3.1.2. Ablation Experiments
- FFCsFast Fourier convolutions have a larger and more effective field of repetition, which can effectively enhance the field of repetition of our model and improve its capability. We performed quantitative experiments on fast Fourier convolution, dilated convolution, and regular convolution. The convolution kernel size was set to 3 × 3, and the expansion rate of the dilated convolution was set to 3. Table 4 shows the scores of different types of convolution. FFC performed the best, and dilated convolution was second only to FFC; however, dilated convolution depends on the resolution of the image and has poor generalization.
- Mask generationThe types, sizes, and positions of the mask during training impact the generative and generalization capabilities of the model. In our task, we focused on exploring the effect of mask generation location on the model. Regular, irregularly shaped masks will overlap with a variety of symbols in the image, and this part of the region was devoid of realistic background for a realistic inpainting quality assessment. Additionally, we avoided network learning to use the features of these symbols. We compare our mask generation approach with the conventional method, and Table 5 and Table 6 show that our method effectively improves the SSIM, LPIPS, and FID.
- Attention mechanismFor the network to attenuate the focus on symbolic features in the image and enhance the focus on other features in the real background, we introduced the SE layer. By introducing the channel attention mechanism, our model pays more attention to the features of non-symbolic regions rather than the features of symbolic regions and chooses useful features. By this method, the restored image is more similar to the original image in terms of content and no yellow pixels show up in the restoration region. Table 5 and Table 6 show the effects of the experiments.
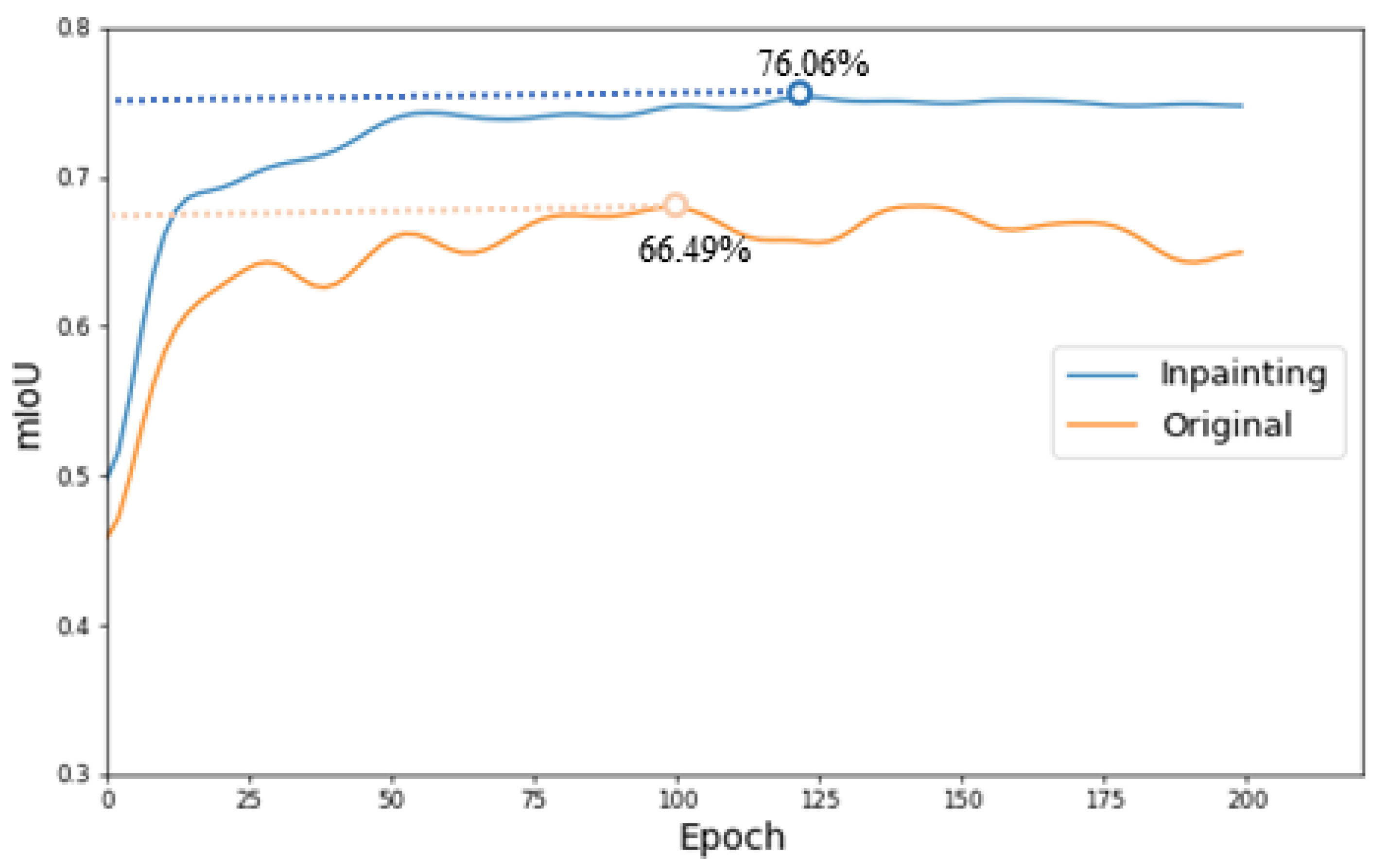
3.1.3. Experiments on the Lesion Segmentation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Al-Dhabyani, W.; Gomaa, M.; Khaled, H.; Fahmy, A. Dataset of breast ultrasound images. Data Brief 2020, 28, 104863. [Google Scholar] [CrossRef]
- George, M.; Anita, H. Analysis of kidney ultrasound images using deep learning and machine learning techniques: A review. Pervasive Comput. Soc. Netw. 2022, 317, 183–199. [Google Scholar]
- Savaş, S.; Topaloğlu, N.; Kazcı, Ö.; Koşar, P.N. Classification of carotid artery intima media thickness ultrasound images with deep learning. J. Med. Syst. 2019, 43, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Weng, J.; Shi, Y.; Gu, W.; Mao, Y.; Wang, Y.; Liu, W.; Zhang, J. An improved deep learning approach for detection of thyroid papillary cancer in ultrasound images. Sci. Rep. 2018, 8, 1–12. [Google Scholar] [CrossRef]
- Karimi, D.; Zeng, Q.; Mathur, P.; Avinash, A.; Mahdavi, S.; Spadinger, I.; Abolmaesumi, P.; Salcudean, S.E. Accurate and robust deep learning-based segmentation of the prostate clinical target volume in ultrasound images. Med Image Anal. 2019, 57, 186–196. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, Y.; Lyu, S.; Chen, L. Embedded self-distillation in compact multibranch ensemble network for remote sensing scene classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Zhao, Q.; Lyu, S.; Li, Y.; Ma, Y.; Chen, L. MGML: Multigranularity multilevel feature ensemble network for remote sensing scene classification. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Cai, L.; Wu, M.; Chen, L.; Bai, W.; Yang, M.; Lyu, S.; Zhao, Q. Using Guided Self-Attention with Local Information for Polyp Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention–MICCAI 2022: 25th International Conference, Singapore, 18–22 September 2022; pp. 629–638. [Google Scholar]
- Singh, A.; Sengupta, S.; Lakshminarayanan, V. Explainable deep learning models in medical image analysis. J. Imaging 2020, 6, 52. [Google Scholar] [CrossRef]
- Chouhan, V.; Singh, S.K.; Khamparia, A.; Gupta, D.; Tiwari, P.; Moreira, C.; Damaševičius, R.; De Albuquerque, V.H.C. A novel transfer learning based approach for pneumonia detection in chest X-ray images. Appl. Sci. 2020, 10, 559. [Google Scholar] [CrossRef]
- Loey, M.; Smarandache, F.M.; Khalifa, N.E. Within the lack of chest COVID-19 X-ray dataset: A novel detection model based on GAN and deep transfer learning. Symmetry 2020, 12, 651. [Google Scholar] [CrossRef]
- Frid-Adar, M.; Diamant, I.; Klang, E.; Amitai, M.; Goldberger, J.; Greenspan, H. GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification. Neurocomputing 2018, 321, 321–331. [Google Scholar] [CrossRef]
- Zhao, A.; Balakrishnan, G.; Durand, F.; Guttag, J.V.; Dalca, A.V. Data augmentation using learned transformations for one-shot medical image segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8543–8553. [Google Scholar]
- Zhao, Q.; Lyu, S.; Bai, W.; Cai, L.; Liu, B.; Wu, M.; Sang, X.; Yang, M.; Chen, L. A Multi-Modality Ovarian Tumor Ultrasound Image Dataset for Unsupervised Cross-Domain Semantic Segmentation. arXiv 2022, arXiv:2207.06799. [Google Scholar]
- Yao, S.; Yan, J.; Wu, M.; Yang, X.; Zhang, W.; Lu, H.; Qian, B. Texture synthesis based thyroid nodule detection from medical ultrasound images: Interpreting and suppressing the adversarial effect of in-place manual annotation. Front. Bioeng. Biotechnol. 2020, 8, 599. [Google Scholar] [CrossRef]
- Armanious, K.; Mecky, Y.; Gatidis, S.; Yang, B. Adversarial inpainting of medical image modalities. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 3267–3271. [Google Scholar]
- Xie, E.; Ni, P.; Zhang, R.; Li, X. Limited-Angle CT Reconstruction with Generative Adversarial Network Sinogram Inpainting and Unsupervised Artifact Removal. Appl. Sci. 2022, 12, 6268. [Google Scholar] [CrossRef]
- Kwon, H.J.; Lee, S.H. A Two-Step Learning Model for the Diagnosis of Coronavirus Disease-19 Based on Chest X-ray Images with 3D Rotational Augmentation. Appl. Sci. 2022, 12, 8668. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Alsalamah, M.; Amin, S. Medical image inpainting with RBF interpolation technique. Int. J. Adv. Comput. Sci. Appl. 2016, 7. [Google Scholar] [CrossRef]
- Guizard, N.; Nakamura, K.; Coupé, P.; Fonov, V.S.; Arnold, D.L.; Collins, D.L. Non-local means inpainting of MS lesions in longitudinal image processing. Front. Neurosci. 2015, 9, 456. [Google Scholar] [CrossRef]
- Vlanek, P. Fuzzy image inpainting aimed to medical imagesl. In Proceedings of the International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, Prague, Czech Republic, 27 February 2018. [Google Scholar] [CrossRef]
- Arnold, M.; Ghosh, A.; Ameling, S.; Lacey, G. Automatic segmentation and inpainting of specular highlights for endoscopic imaging. EURASIP J. Image Video Process. 2010, 2010, 1–12. [Google Scholar] [CrossRef]
- Nazeri, K.; Ng, E.; Joseph, T.; Qureshi, F.; Ebrahimi, M. Edgeconnect: Structure guided image inpainting using edge prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Republic of Korea, 27–28 October 2019; pp. 3265–3274. [Google Scholar]
- Wang, Q.; Chen, Y.; Zhang, N.; Gu, Y. Medical image inpainting with edge and structure priors. Measurement 2021, 185, 110027. [Google Scholar] [CrossRef]
- Wei, Y.; Gan, Z.; Li, W.; Lyu, S.; Chang, M.C.; Zhang, L.; Gao, J.; Zhang, P. MagGAN: High-Resolution Face Attribute Editing with Mask-Guided Generative Adversarial Network. In Proceedings of the Asian Conference on Computer Vision (ACCV), Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Zeng, Y.; Fu, J.; Chao, H.; Guo, B. Learning Pyramid-Context Encoder Network for High-Quality Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Yi, Z.; Tang, Q.; Azizi, S.; Jang, D.; Xu, Z. Contextual Residual Aggregation for Ultra High-Resolution Image Inpainting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Yan, Z.; Li, X.; Li, M.; Zuo, W.; Shan, S. Shift-net: Image inpainting via deep feature rearrangement. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 1–17. [Google Scholar]
- Wu, C.; Wang, Y.; Wang, F. Deep learning for ovarian tumor classification with ultrasound images. In Proceedings of the Pacific Rim Conference on Multimedia, Hefei, China, 21–22 September 2018; Proceedings, Part III; 2018. pp. 395–406. [Google Scholar]
- Christiansen, F.; Epstein, E.; Smedberg, E.; Åkerlund, M.; Smith, K.; Epstein, E. Ultrasound image analysis using deep neural networks for discriminating between benign and malignant ovarian tumors: Comparison with expert subjective assessment. Ultrasound Obstet. Gynecol. 2021, 57, 155–163. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, Y. Detection of ovarian tumors in obstetric ultrasound imaging using logistic regression classifier with an advanced machine learning approach. IEEE Access 2020, 8, 44999–45008. [Google Scholar] [CrossRef]
- Jin, J.; Zhu, H.; Zhang, J.; Ai, Y.; Zhang, J.; Teng, Y.; Xie, C.; Jin, X. Multiple U-Net-based automatic segmentations and radiomics feature stability on ultrasound images for patients with ovarian cancer. Front. Oncol. 2021, 10, 614201. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Ballari, India, 23–24 April 2016; pp. 770–778. [Google Scholar]
- Chi, L.; Jiang, B.; Mu, Y. Fast fourier convolution. Adv. Neural Inf. Process. Syst. 2020, 33, 4479–4488. [Google Scholar]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Generative image inpainting with contextual attention. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5505–5514. [Google Scholar]
- Iizuka, S.; Simo-Serra, E.; Ishikawa, H. Globally and locally consistent image completion. ACM Trans. Graph. (ToG) 2017, 36, 1–14. [Google Scholar] [CrossRef]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.C.; Tao, A.; Catanzaro, B. Image inpainting for irregular holes using partial convolutions. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 85–100. [Google Scholar]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Free-form image inpainting with gated convolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4471–4480. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 694–711. [Google Scholar]
- Suvorov, R.; Logacheva, E.; Mashikhin, A.; Remizova, A.; Ashukha, A.; Silvestrov, A.; Kong, N.; Goka, H.; Park, K.; Lempitsky, V. Resolution-robust large mask inpainting with fourier convolutions. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 2149–2159. [Google Scholar]
- Wang, T.C.; Liu, M.Y.; Zhu, J.Y.; Tao, A.; Kautz, J.; Catanzaro, B. High-resolution image synthesis and semantic manipulation with conditional gans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8798–8807. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]





| Model | SSIM | FID | LPIPS |
|---|---|---|---|
| PC [39] | 0.6847 | 79.42 | 0.13550 |
| GL [38] | 0.3026 | 170.69 | 0.29589 |
| DF 1 [37] | 0.6578 | 81.74 | 0.14090 |
| Df 2 [40] | 0.8932 | 54.38 | 0.10150 |
| LaMa [42] | 0.9209 | 25.54 | 0.08215 |
| Ours |
| Model | SSIM | FID | LPIPS |
|---|---|---|---|
| PC [39] | 1.47 × 10−5 | 0.2755 | 4.5 × 10−8 |
| GL [38] | 1.81 × 10−5 | 0.4878 | 9.7 × 10−8 |
| DF 1 [37] | 1.39 × 10−5 | 0.2801 | 4.3 × 10−8 |
| Df 2 [40] | 1.10 × 10−5 | 0.2311 | 2.1 × 10−8 |
| LaMa [42] | 9.90 × 10−6 | 0.1777 | 1.1 × 10−8 |
| Ours | 9.10 × 10−6 | 8.1 × 10−9 |
| Model | SSIM | FID | LPIPS |
|---|---|---|---|
| PC [39] | (0.6771, 0.6923) | (78.17, 80.67) | (0.13510, 0.13590) |
| GL [38] | (0.2939, 0.3111) | (169.81, 171.57) | (0.29556, 0.29622) |
| DF 1 [37] | (0.6502, 0.6654) | (80.57, 82.40) | (0.14050, 0.14130) |
| Df 2 [40] | (0.8860, 0.9004) | (53.46, 55.30) | (0.10122, 0.10178) |
| LaMa [42] | (0.9145, 0.9273) | (24.72, 26.36) | (0.08195, 0.08235) |
| Ours |
| Convs | LPIPS | FID |
|---|---|---|
| Regular | 0.92230 | 30.84 |
| Dilated | 0.08447 | 26.77 |
| Fast Fourier |
| Model | SSIM | FID | LPIPS |
|---|---|---|---|
| Base (only FFCs) | 0.9209 | 25.54 | 0.08215 |
| Base + Mask | 0.9240 | 23.08 | 0.08044 |
| Base + SE-Layer | 0.9238 | 23.02 | 0.07987 |
| Base + Mask + SE-Laye |
| Model | SSIM | FID | LPIPS |
|---|---|---|---|
| Base (only FFCs) | 0.9170 | 28.58 | 0.08939 |
| Base + Mask | 0.9189 | 27.15 | 0.08842 |
| Base + SE-Layer | 0.9102 | 26.89 | 0.08769 |
| Base + Mask + SE-Layer |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Qiao, C.; Wu, M.; Cai, L.; Yin, C.; Yang, M.; Sang, X.; Bai, W. Improving the Segmentation Accuracy of Ovarian-Tumor Ultrasound Images Using Image Inpainting. Bioengineering 2023, 10, 184. https://doi.org/10.3390/bioengineering10020184
Chen L, Qiao C, Wu M, Cai L, Yin C, Yang M, Sang X, Bai W. Improving the Segmentation Accuracy of Ovarian-Tumor Ultrasound Images Using Image Inpainting. Bioengineering. 2023; 10(2):184. https://doi.org/10.3390/bioengineering10020184
Chicago/Turabian StyleChen, Lijiang, Changkun Qiao, Meijing Wu, Linghan Cai, Cong Yin, Mukun Yang, Xiubo Sang, and Wenpei Bai. 2023. "Improving the Segmentation Accuracy of Ovarian-Tumor Ultrasound Images Using Image Inpainting" Bioengineering 10, no. 2: 184. https://doi.org/10.3390/bioengineering10020184
APA StyleChen, L., Qiao, C., Wu, M., Cai, L., Yin, C., Yang, M., Sang, X., & Bai, W. (2023). Improving the Segmentation Accuracy of Ovarian-Tumor Ultrasound Images Using Image Inpainting. Bioengineering, 10(2), 184. https://doi.org/10.3390/bioengineering10020184









