RCKD: Response-Based Cross-Task Knowledge Distillation for Pathological Image Analysis
Abstract
:1. Introduction
1.1. Background
1.2. Related Work
1.2.1. Self-Supervised Learning for Pathological Image Analysis
1.2.2. Knowledge Distillation
1.2.3. Efficient Network Architectures for Image Analysis
1.2.4. Visual Attention
1.3. Research Objective
2. Materials and Methods
2.1. Datasets
2.1.1. Pretraining Dataset
2.1.2. Downstream Tasks and Datasets
- The breast cancer histology images (BACH) microscopy dataset contains 400 hematoxylin and eosin (H&E) stained microscopy image patches categorized into four classes: normal, benign, in situ carcinoma, and invasive carcinoma. Each class has 100 training image patches. The average patch size is pixels.
- The colorectal cancer (CRC) dataset was collected for the classification of tissue areas from H&E stained WSIs of colorectal adenocarcinoma patients. It includes a total of 100,000 non-overlapping image patches in the training dataset extracted from 86 WSIs of cancer and normal tissues. The average patch size is pixels. The patches were manually labeled by pathologists into nine tissue classes: adipose (ADI), background (BACK), debris (DEB), lymphocytes (LYM), mucus (MUC), smooth muscle (MUS), normal colon mucosa (NORM), cancer-associated stroma (STR), and colorectal adenocarcinoma epithelium (TUM). The validation dataset includes 7180 image patches extracted from 50 colorectal adenocarcinoma patients.
- The breast cancer histopathological (BreakHis) dataset was collected for binary breast cancer classification. It contains a total of 7909 breast tumor tissue image patches from 82 patients, consisting of 2480 benign and 5429 malignant tumor patches. BreakHis includes four types of benign tumors: adenosis, fibroadenoma, phyllodes tumor, and tubular adenoma, as well as four types of malignant tumors: ductal carcinoma, lobular carcinoma, mucinous carcinoma, and papillary carcinoma. The average patch size is pixels.
- The Lymph dataset was collected for the classification of malignant lymph node cancer. It provides a total of 374 training image patches, with 113 image patches of chronic lymphocytic leukemia (CLL), 139 image patches of follicular lymphoma (FL), and 122 image patches of mantle cell lymphoma (MCL). The average patch size is pixels.
- The BACH WSI dataset consists of 10 WSIs with an average size of scanned at a resolution of 0.467 µ/pixel. It includes pixel-wise annotations in four region categories (normal, benign, in situ carcinoma, and invasive carcinoma). In this study, we cut the WSIs into 4,453 non-overlapping patches of size at magnification.
- The gland segmentation in colon histology images (GlaS) dataset is the benchmark dataset for the Gland Segmentation Challenge Contest at MICCAI in 2015. It consists of 165 image patches derived from 16 H&E stained histological sections of stage T3 or T42 colorectal adenocarcinoma. Each section originates from a different patient. The WSIs were digitized at a pixel resolution of 0.465 µm. The GlaS dataset consists of 74 benign and 91 malignant gland image patches, each with pixel-wise annotations. The average patch size is pixels.
2.1.3. General Image Dataset
2.2. Response-Based Cross-Task Knowledge Distillation
2.2.1. Pretraining from Unlabeled Pathological Images
| Algorithm 1 Pretraining Procedure | |
| 1: W | ▹ WSI in pretraining dataset (TCGA) |
| 2: | ▹ Knowledge distillation |
| 3: | ▹ Teacher model |
| 4: | ▹ Student model |
| 5: | ▹ Magnification ratio of WSI |
| 6: | ▹ Patch size |
| 7: | ▹ Number of samples for pretraining |
| 8: procedure Pretrain() | |
| 9: | ▹ Get patches from a WSI |
| 10: | ▹ Discard background patches |
| 11: | ▹ Select patches for pretraining |
| 12: for all x in D do | |
| 13: | ▹ Make pseudo label |
| 14: | ▹ Knowledge distillation |
| 15: | |
| 16: return | |
| * In this study, , , and . | |
2.2.2. Fine-Tuning for Pathological Image Analysis Tasks
| Algorithm 2 Fine-tuning Procedure | |
| 1: | ▹ Pretrained student model |
| 2: D | ▹ Target dataset |
| 3: | ▹ Total number of folds |
| 4: | ▹ Total number of training epochs |
| 5: | ▹ Patience number for early stopping |
| 6: procedure Fine-tune() | |
| 7: for fold in range [1, ] do | |
| 8: = LoadData() | |
| 9: for in range [1, ] do | |
| 10: for i in range [1, ] do | |
| 11: | |
| 12: Backpropagate | |
| 13: | |
| 14: CheckForEarlyStopping() | |
| 15: Accuracy | |
| 16: = | |
| 17: return | |
| * In this study, , , and . | |
2.3. Convolutional Neural Network with Spatial Attention by Transformer
2.3.1. Overall Structure
2.3.2. SAT Block
2.3.3. Spatial Attention by Transformer (SAT) Module
2.4. Evaluation Metrics and Experimental Environments
3. Results
3.1. Hyperparameter Search for Downstream Tasks
3.2. Performance in Downstream Tasks by Pretraining Method
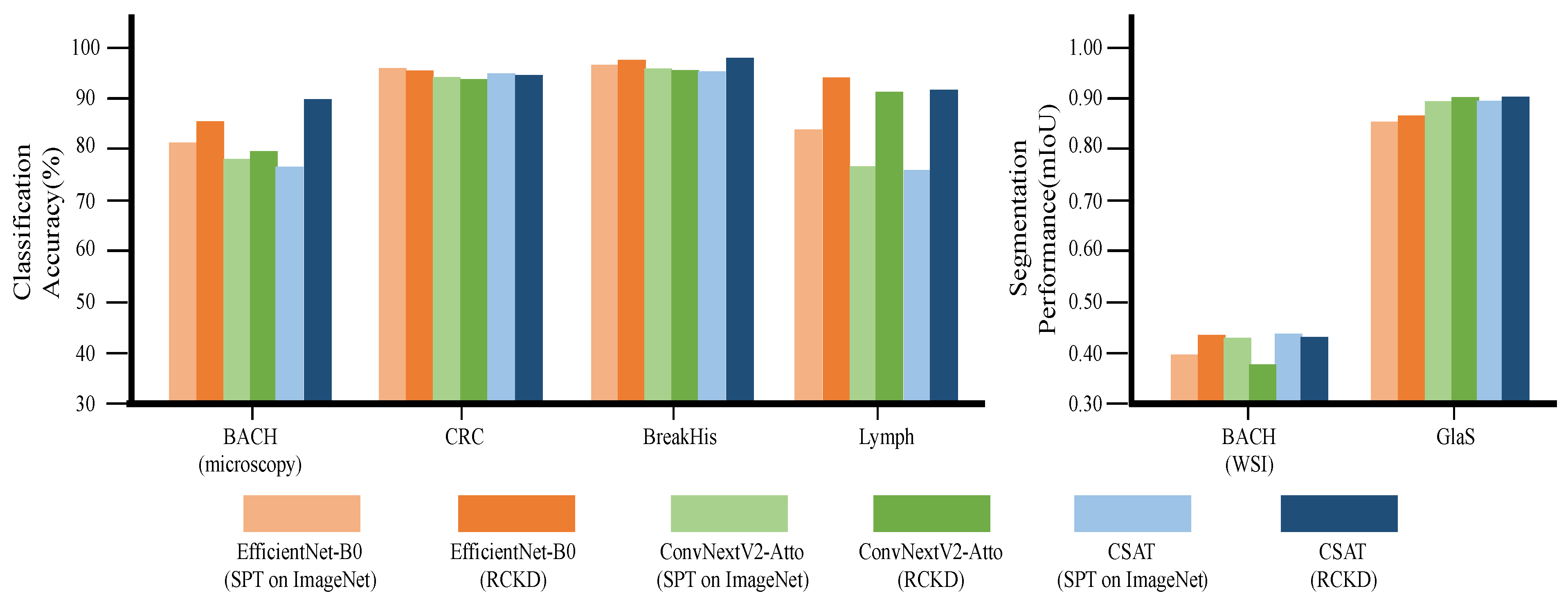
3.3. Performance in Downstream Tasks by Model Architecture
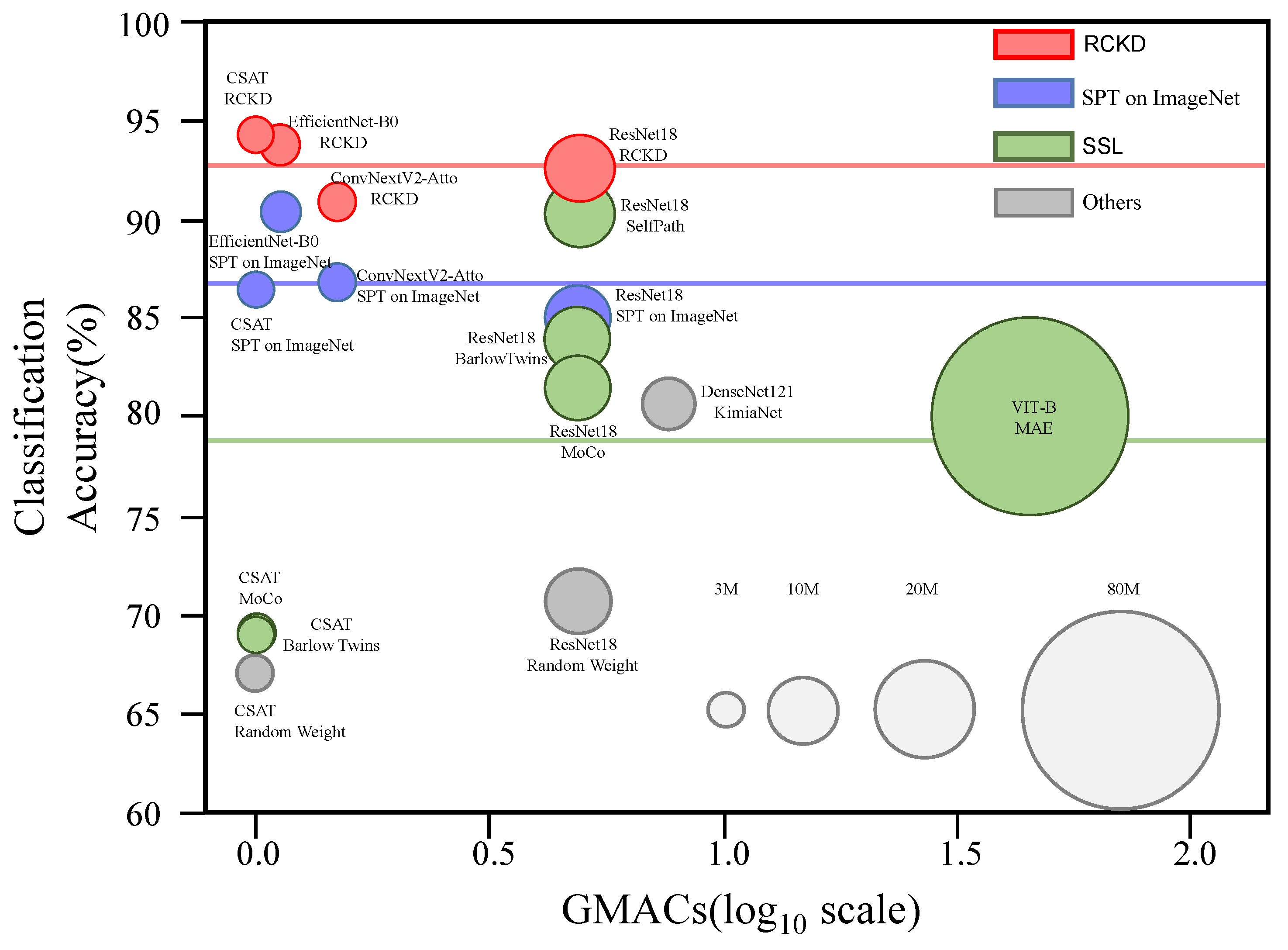
3.4. Comparison with Previous Studies on Pathological Image Analysis
3.5. Evaluation of CSAT on ImageNet
3.6. Accuracy vs. Efficiency
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSAT | Convolutional neural network with Spatial Attention by Transformer |
| CFC | Channel-wise Fully Connected |
| GRN | Global Response Normalization |
| KD | Knowledge Distillation |
| MAC | Multiply ACcumulate |
| MAE | Masked Auto Encoder |
| RCKD | Response based Cross task Knowledge Distillation |
| PEG | Position Encoding Generator |
| RKD | Response-based Knowledge Distillation |
| SAT | Spatial Attntion by Transformer |
| SGD | Stochastic Gradient Descent |
| SOTA | State Of The Art |
| SPT | Supervised PreTraining |
| SSL | Self Supervised Learning |
| USI | Unified Scheme for ImageNet |
| ViT | Vision Transformer |
| WSI | Whole Slide Imaging |
Appendix A
Appendix A.1. Detail of the TCGA Dataset
| Study Abbreviation | Study Name | WSI | # of Patches | Magnification |
|---|---|---|---|---|
| ACC | Adrenocortical carcinoma | 227 | 246781 | |
| BLCA | Bladder Urothelial Carcinoma | 458 | 457819 | |
| BRCA | Breast invasive carcinoma | 1129 | 769008 | |
| CESC | Cervical squamous cell carcinoma and endocervical adenocarcinoma | 278 | 180447 | |
| CHOL | Cholangiocarcinoma | 39 | 47288 | |
| COAD | Colon adenocarcinoma | 441 | 243863 | |
| DLBC | Lymphoid Neoplasm Diffuse Large B-cell Lymphoma | 44 | 27435 | |
| ESCA | Esophageal carcinoma | 158 | 119497 | |
| GBM | Glioblastoma multiforme | 860 | 518580 | |
| HNSC | Head and Neck squamous cell carcinoma | 468 | 326319 | |
| KICH | Kidney Chromophobe | 121 | 107381 | |
| KIRC | Kidney renal clear cell carcinoma | 519 | 454207 | |
| KIRP | Kidney renal papillary cell carcinoma | 297 | 226632 | |
| LGG | Brain Lower Grade Glioma | 843 | 549297 | |
| LIHC | Liver hepatocellular carcinoma | 372 | 320796 | |
| LUAD | Lung adenocarcinoma | 531 | 397341 | |
| LUSC | Lung squamous cell carcinoma | 512 | 394099 | |
| MESO | Mesothelioma | 79 | 52186 | |
| OV | Ovarian serous cystadenocarcinoma | 107 | 98306 | |
| PAAD | Pancreatic adenocarcinoma | 209 | 170715 | |
| PCPG | Pheochromocytoma and Paraganglioma | 194 | 182398 | |
| PRAD | Prostate adenocarcinoma | 450 | 365360 | |
| READ | Rectum adenocarcinoma | 157 | 67092 | |
| SARC | Sarcoma | 726 | 661662 | |
| SKCM | Skin Cutaneous Melanoma | 476 | 396349 | |
| STAD | Stomach adenocarcinoma | 400 | 297018 | |
| TGCT | Testicular Germ Cell Tumors | 211 | 207681 | |
| THCA | Thyroid carcinoma | 518 | 445611 | |
| THYM | Thymoma | 180 | 173342 | |
| UCEC | Uterine Corpus Endometrial Carcinoma | 545 | 585862 | |
| UCS | Uterine Carcinosarcoma | 87 | 94565 | |
| UVM | Uveal Melanoma | 80 | 44387 |
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Cireşan, D.; Giusti, A.; Gambardella, L.; Schmidhuber, J. Mitosis detection in breast cancer histology images with deep neural networks. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2013: 16th International Conference, Nagoya, Japan, 22–26 September 2013, Proceedings, Part II 16; Springer: Berlin/Heidelberg, Germany, 2013; pp. 411–418. [Google Scholar]
- Veta, M.; Van Diest, P.J.; Willems, S.M.; Wang, H.; Madabhushi, A.; Cruz-Roa, A.; Gonzalez, F.; Larsen, A.B.L.; Vestergaard, J.S.; Dahl, A.B.; et al. Assessment of algorithms for mitosis detection in breast cancer histopathology images. Med. Image Anal. 2015, 20, 237–248. [Google Scholar] [CrossRef] [PubMed]
- Araújo, T.; Aresta, G.; Castro, E.; Rouco, J.; Aguiar, P.; Eloy, C.; Polónia, A.; Campilho, A. Classification of breast cancer histology images using convolutional neural networks. PLoS ONE 2017, 12, e0177544. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Qi, X.; Yu, L.; Heng, P. DCAN: Deep contour-aware networks for accurate gland segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2487–2496. [Google Scholar]
- Serag, A.; Ion-Margineanu, A.; Qureshi, H.; McMillan, R.; Saint Martin, M.; Diamond, J.; O’Reilly, P.; Hamilton, P. Translational AI and deep learning in diagnostic pathology. Front. Med. 2019, 6, 185. [Google Scholar] [CrossRef]
- Deng, S.; Zhang, X.; Yan, W.; Chang, E.; Fan, Y.L.M.; Xu, Y. Deep learning in digital pathology image analysis: A survey. Front. Med. 2020, 14, 470–487. [Google Scholar] [CrossRef]
- Khan, S.; Islam, N.; Jan, Z.; Din, I.; Rodrigues, J. A novel deep learning based framework for the detection and classification of breast cancer using transfer learning. Pattern Recognit. Lett. 2019, 125, 1–6. [Google Scholar] [CrossRef]
- Mormont, R.; Geurts, P.; Marée, R. Comparison of deep transfer learning strategies for digital pathology. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2262–2271. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 248–255. [Google Scholar]
- Boyd, J.; Liashuha, M.; Deutsch, E.; Paragios, N.; Christodoulidis, S.; Vakalopoulou, M. Self-supervised representation learning using visual field expansion on digital pathology. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 639–647. [Google Scholar]
- Ciga, O.; Xu, T.; Martel, A. Self supervised contrastive learning for digital histopathology. Mach. Learn. Appl. 2022, 7, 100198. [Google Scholar] [CrossRef]
- Dehaene, O.; Camara, A.; Moindrot, O.; de Lavergne, A.; Courtiol, P. Self-supervision closes the gap between weak and strong supervision in histology. arXiv 2020, arXiv:2012.03583. [Google Scholar]
- Zhang, L.; Amgad, M.; Cooper, L. A Histopathology Study Comparing Contrastive Semi-Supervised and Fully Supervised Learning. arXiv 2021, arXiv:2111.05882. [Google Scholar]
- Li, J.; Lin, T.; Xu, Y. Sslp: Spatial guided self-supervised learning on pathological images. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, 27 September–1 October 2021, Proceedings, Part II 24; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 3–12. [Google Scholar]
- Koohbanani, N.; Unnikrishnan, B.; Khurram, S.; Krishnaswamy, P.; Rajpoot, N. Self-path: Self-supervision for classification of pathology images with limited annotations. IEEE Trans. Med. Imaging 2021, 40, 2845–2856. [Google Scholar] [CrossRef]
- Lin, T.; Yu, Z.; Xu, Z.; Hu, H.; Xu, Y.; Chen, C. SGCL: Spatial guided contrastive learning on whole-slide pathological images. Med. Image Anal. 2023, 89, 102845. [Google Scholar] [CrossRef] [PubMed]
- Tomasev, N.; Bica, I.; McWilliams, B.; Buesing, L.; Pascanu, R.; Blundell, C.; Mitrovic, J. Pushing the limits of self-supervised ResNets: Can we outperform supervised learning without labels on ImageNet? In Proceedings of the First Workshop on Pre-Training: Perspectives, Pitfalls, and Paths Forward at ICML, Baltimore, MD, USA, 23 July 2022. [Google Scholar]
- Weinstein, J.; Collisson, E.; Mills, G.; Shaw, K.; Ozenberger, B.; Ellrott, K.; Shmulevich, I.; Sander, C.; Stuart, J. The cancer genome atlas pan-cancer analysis project. Nat. Genet. 2013, 45, 1113–1120. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, Virtual Event, 12–18 July 2020; pp. 1597–1607. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Improved baselines with momentum contrastive learning. arXiv 2020, arXiv:2003.04297. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Adriana, R.; Nicolas, B.; Ebrahimi, K.; Antoine, C.; Carlo, G.; Yoshua, B. Fitnets: Hints for thin deep nets. Proc. ICLR 2015, 2, 3. [Google Scholar]
- Gou, J.; Yu, B.; Maybank, S.; Tao, D. Knowledge distillation: A survey. Int. J. Comput. Vis. 2021, 129, 1789–1819. [Google Scholar] [CrossRef]
- Li, D.; Wu, A.; Han, Y.; Tian, Q. Prototype-guided Cross-task Knowledge Distillation for Large-scale Models. arXiv 2022, arXiv:2212.13180. [Google Scholar]
- DiPalma, J.; Suriawinata, A.; Tafe, L.; Torresani, L.; Hassanpour, S. Resolution-based distillation for efficient histology image classification. Artif. Intell. Med. 2021, 119, 102136. [Google Scholar] [CrossRef]
- Javed, S.; Mahmood, A.; Qaiser, T.; Werghi, N. Knowledge Distillation in Histology Landscape by Multi-Layer Features Supervision. IEEE J. Biomed. Health Inform. 2023, 27, 2037–2046. [Google Scholar] [CrossRef]
- Zhang, R.; Zhu, J.; Yang, S.; Hosseini, M.; Genovese, A.; Chen, L.; Rowsell, C.; Damaskinos, S.; Varma, S.; Plataniotis, K. HistoKT: Cross Knowledge Transfer in Computational Pathology. In Proceedings of the ICASSP 2022–2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1276–1280. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- Iandola, F.; Han, S.; Moskewicz, M.; Ashraf, K.; Dally, W.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017; pp. 207–212. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Howard, A.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Tan, M.; Le, Q. Efficientnetv2: Smaller models and faster training. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual Event, 18–24 July 2021; pp. 10096–10106. [Google Scholar]
- Dai, Z.; Liu, H.; Le, Q.; Tan, M. Coatnet: Marrying convolution and attention for all data sizes. Adv. Neural Inf. Process. Syst. 2021, 34, 3965–3977. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.; Feichtenhofer, C.; Darrell, T.; Xie, S. A convnet for the 2020s. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11976–11986. [Google Scholar]
- Woo, S.; Debnath, S.; Hu, R.; Chen, X.; Liu, Z.; Kweon, I.; Xie, S. ConvNeXt V2: Co-designing and Scaling ConvNets with Masked Autoencoders. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 16133–16142. [Google Scholar]
- Li, Y.; Yuan, G.; Wen, Y.; Hu, J.; Evangelidis, G.; Tulyakov, S.; Wang, Y.; Ren, J. Efficientformer: Vision transformers at mobilenet speed. Adv. Neural Inf. Process. Syst. 2022, 35, 12934–12949. [Google Scholar]
- Li, Y.; Hu, J.; Wen, Y.; Evangelidis, G.; Salahi, K.; Wang, Y.; Tulyakov, S.; Ren, J. Rethinking Vision Transformers for MobileNet Size and Speed. In Proceedings of the IEEE International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 16889–16900. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Chen, L.; Zhang, H.; Xiao, J.; Nie, L.; Shao, J.; Liu, W.; Chua, T. Sca-cnn: Spatial and channel-wise attention in convolutional networks for image captioning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5659–5667. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Gao, Z.; Xie, J.; Wang, Q.; Li, P. Global second-order pooling convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 3024–3033. [Google Scholar]
- Lee, H.; Kim, H.; Nam, H. Srm: A style-based recalibration module for convolutional neural networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1854–1862. [Google Scholar]
- Park, J.; Woo, S.; Lee, J.; Kweon, I. Bam: Bottleneck attention module. In Proceedings of the British Machine Vision Conference (BMVC), Newcastle, UK, 3–6 September 2018; p. 147. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.; Kweon, I. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7794–7803. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. In Proceedings of the International Conference on Learning Representations, Virtual Event, 3–7 May 2021. [Google Scholar] [CrossRef]
- Aresta, G.; Araújo, T.; Kwok, S.; Chennamsetty, S.; Safwan, M.; Alex, V.; Marami, B.; Prastawa, M.; Chan, M.; Donovan, M.; et al. Bach: Grand challenge on breast cancer histology images. Med. Image Anal. 2019, 56, 122–139. [Google Scholar] [CrossRef]
- Kather, J.; Halama, N.; Marx, A. 100,000 histological images of human colorectal cancer and healthy tissue. Zenodo 2018, 10, 5281. [Google Scholar]
- Spanhol, F.; Oliveira, L.; Petitjean, C.; Heutte, L. A dataset for breast cancer histopathological image classification. IEEE Trans. Biomed. Eng. 2015, 63, 1455–1462. [Google Scholar] [CrossRef]
- Orlov, N.; Chen, W.; Eckley, D.; Macura, T.; Shamir, L.; Jaffe, E.; Goldberg, I. Automatic classification of lymphoma images with transform-based global features. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 1003–1013. [Google Scholar] [CrossRef]
- Sirinukunwattana, K.; Pluim, J.; Chen, H.; Qi, X.; Heng, P.; Guo, Y.; Wang, L.; Matuszewski, B.; Bruni, E.; Sanchez, U.; et al. Gland segmentation in colon histology images: The glas challenge contest. Med. Image Anal. 2017, 35, 489–502. [Google Scholar] [CrossRef]
- Mason, K.; Losos, J.; Singer, S.; Raven, P.; Johnson, G. Biology; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Schmidt, U.; Weigert, M.; Broaddus, C.; Myers, G. Cell detection with star-convex polygons. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2018: 21st International Conference, Granada, Spain, 16–20 September 2018, Proceedings, Part II 11; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 265–273. [Google Scholar]
- Kumar, N.; Verma, R.; Anand, D.; Zhou, Y.; Onder, O.; Tsougenis, E.; Chen, H.; Heng, P.; Li, J.; Hu, Z.; et al. A multi-organ nucleus segmentation challenge. IEEE Trans. Med. Imaging 2019, 39, 1380–1391. [Google Scholar] [CrossRef]
- Naylor, P.; Laé, M.; Reyal, F.; Walter, T. Segmentation of nuclei in histopathology images by deep regression of the distance map. IEEE Trans. Med. Imaging 2018, 38, 448–459. [Google Scholar] [CrossRef]
- Graham, S.; Jahanifar, M.; Vu, Q.; Hadjigeorghiou, G.; Leech, T.; Snead, D.; Raza, S.; Minhas, F.; Rajpoot, N. Conic: Colon nuclei identification and counting challenge 2022. arXiv 2021, arXiv:2111.14485. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015, Proceedings, Part III 18; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Ridnik, T.; Lawen, H.; Ben-Baruch, E.; Noy, A. Solving imagenet: A unified scheme for training any backbone to top results. arXiv 2022, arXiv:2204.03475. [Google Scholar]
- You, Y.; Gitman, I.; Ginsburg, B. Large batch training of convolutional networks. arXiv 2017, arXiv:1708.03888. [Google Scholar]
- Lin, T.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Park, N.; Kim, S. How do vision transformers work? In Proceedings of the International Conference on Learning Representations, Virtual Event, 25–29 April 2022. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wang, F.; Jiang, M.; Qian, C.; Yang, S.; Li, C.; Zhang, H.; Wang, X.; Tang, X. Residual attention network for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3156–3164. [Google Scholar]
- Chu, X.; Tian, Z.; Zhang, B.; Wang, X.; Wei, X.; Xia, H.; Shen, C. Conditional positional encodings for vision transformers. In Proceedings of the ICLR 2023, Kigali, Rwanda, 1–5 May 2023. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. NIPS-W. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- THOP: PyTorch-OpCounter. Available online: https://github.com/Lyken17/pytorch-OpCounter (accessed on 3 August 2023).
- Riasatian, A.; Babaie, M.; Maleki, D.; Kalra, S.; Valipour, M.; Hemati, S.; Zaveri, M.; Safarpoor, A.; Shafiei, S.; Afshari, M.; et al. Fine-tuning and training of densenet for histopathology image representation using tcga diagnostic slides. Med. Image Anal. 2021, 70, 102032. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 16000–16009. [Google Scholar]
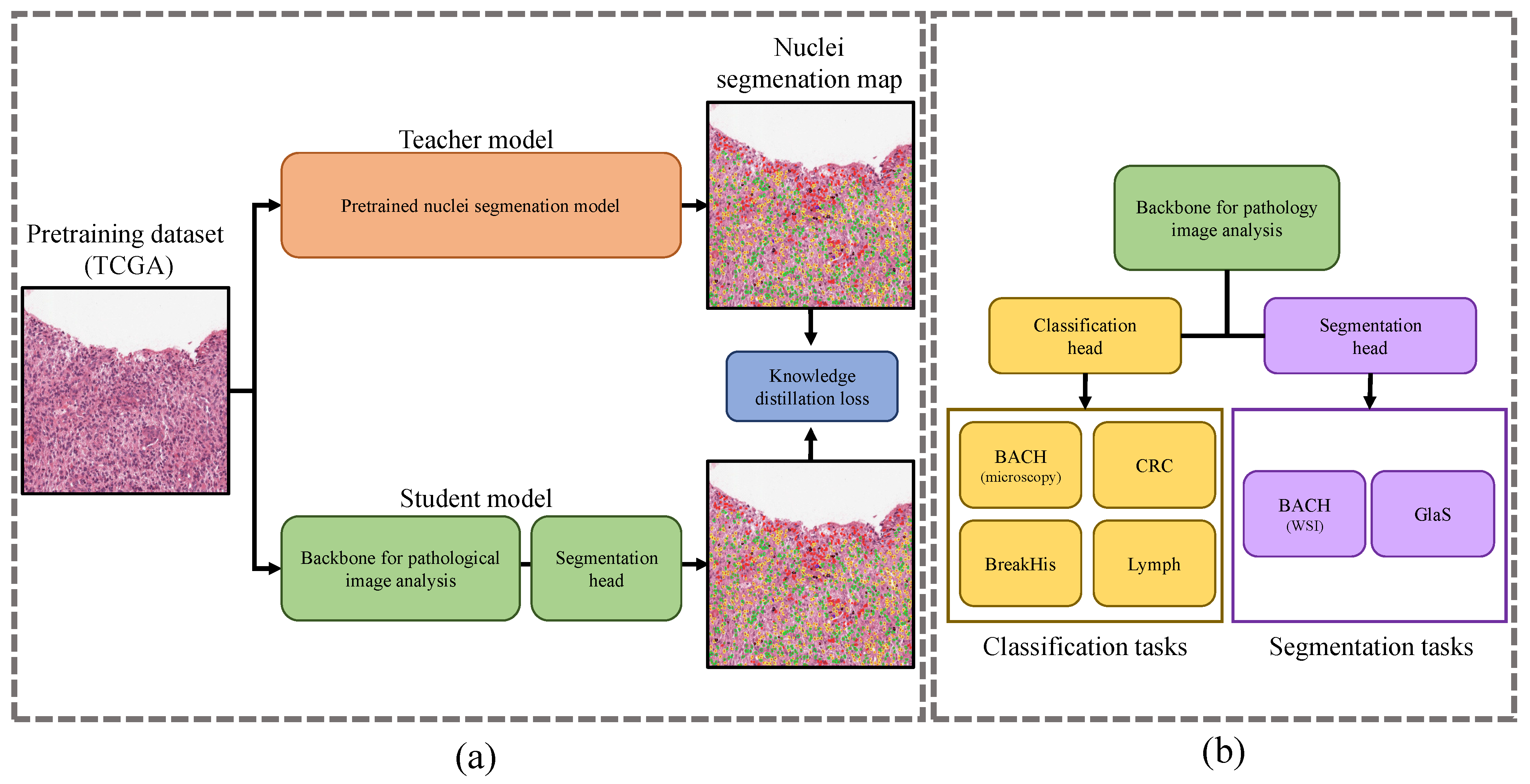
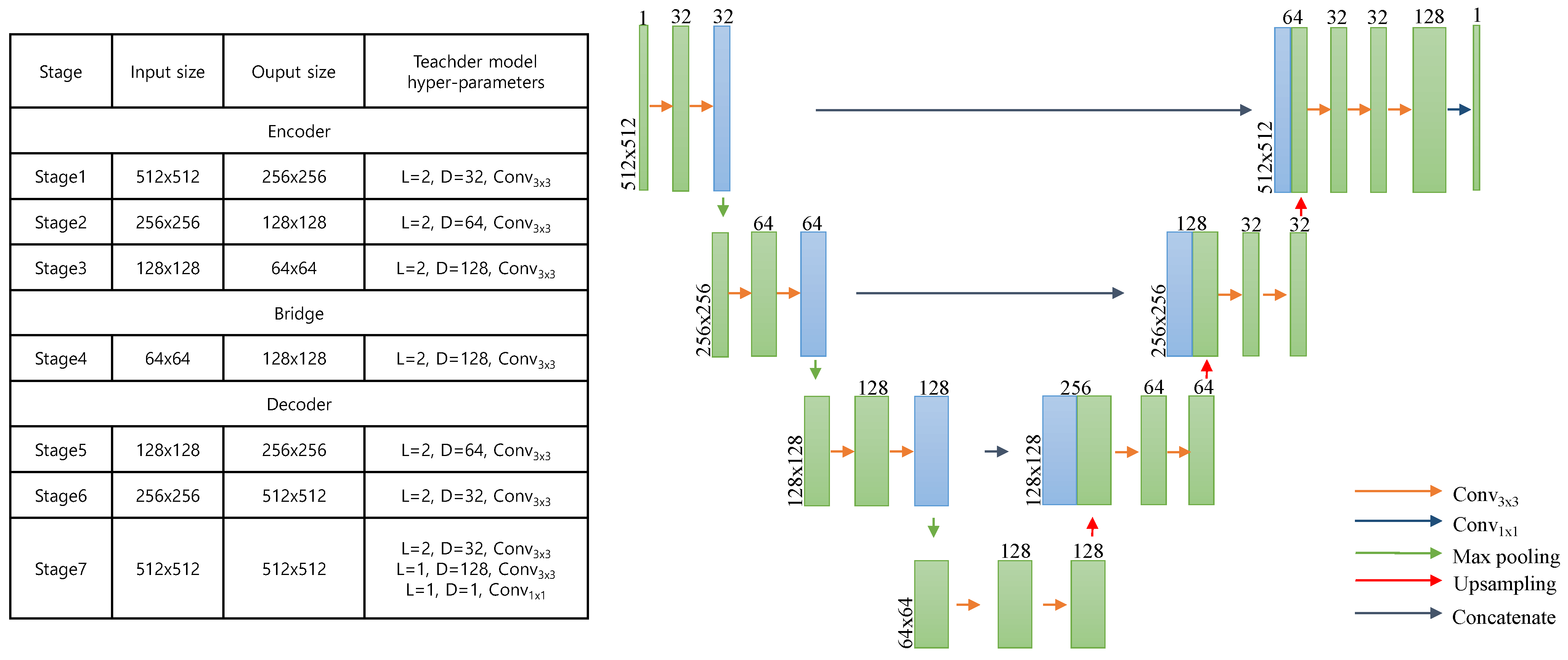
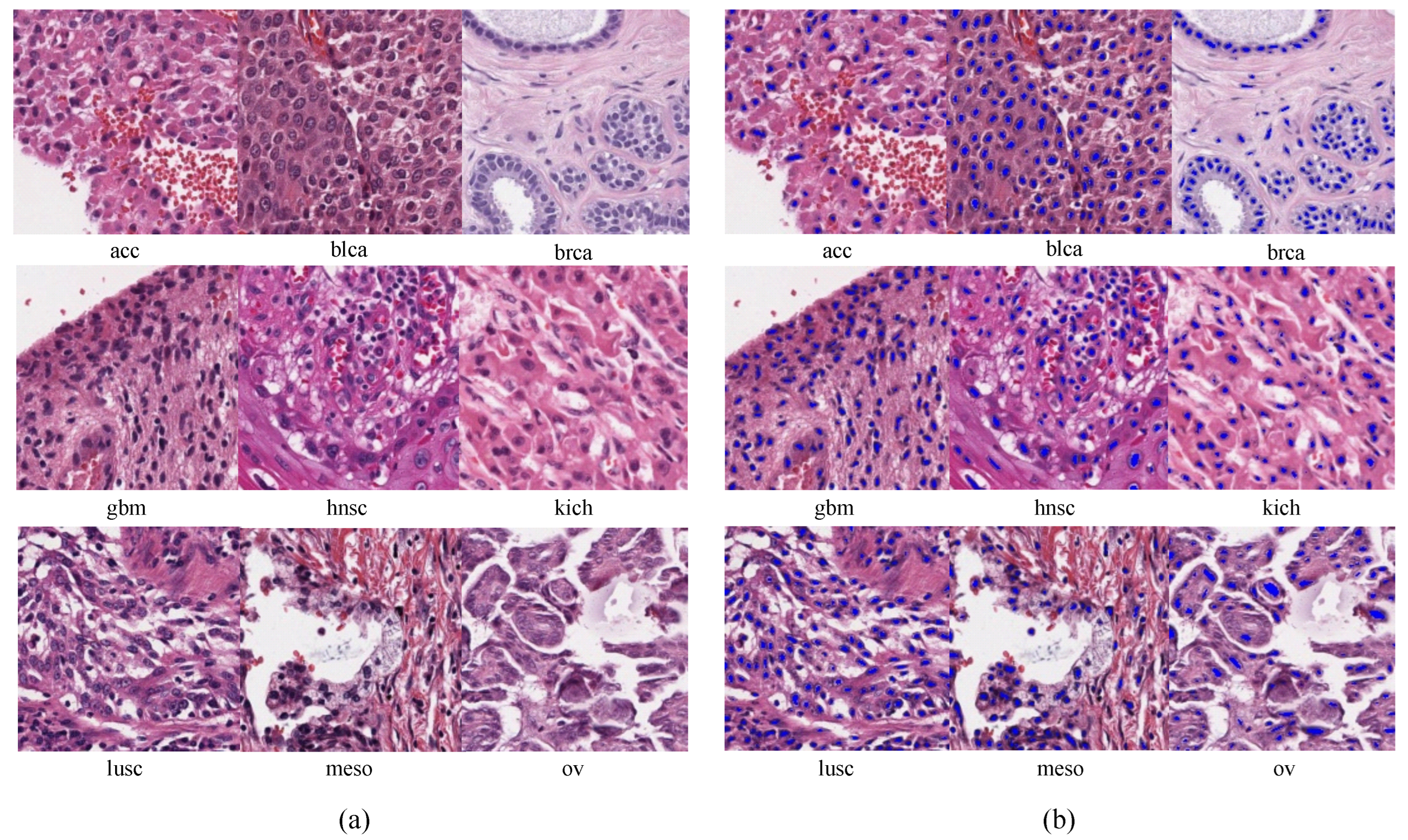
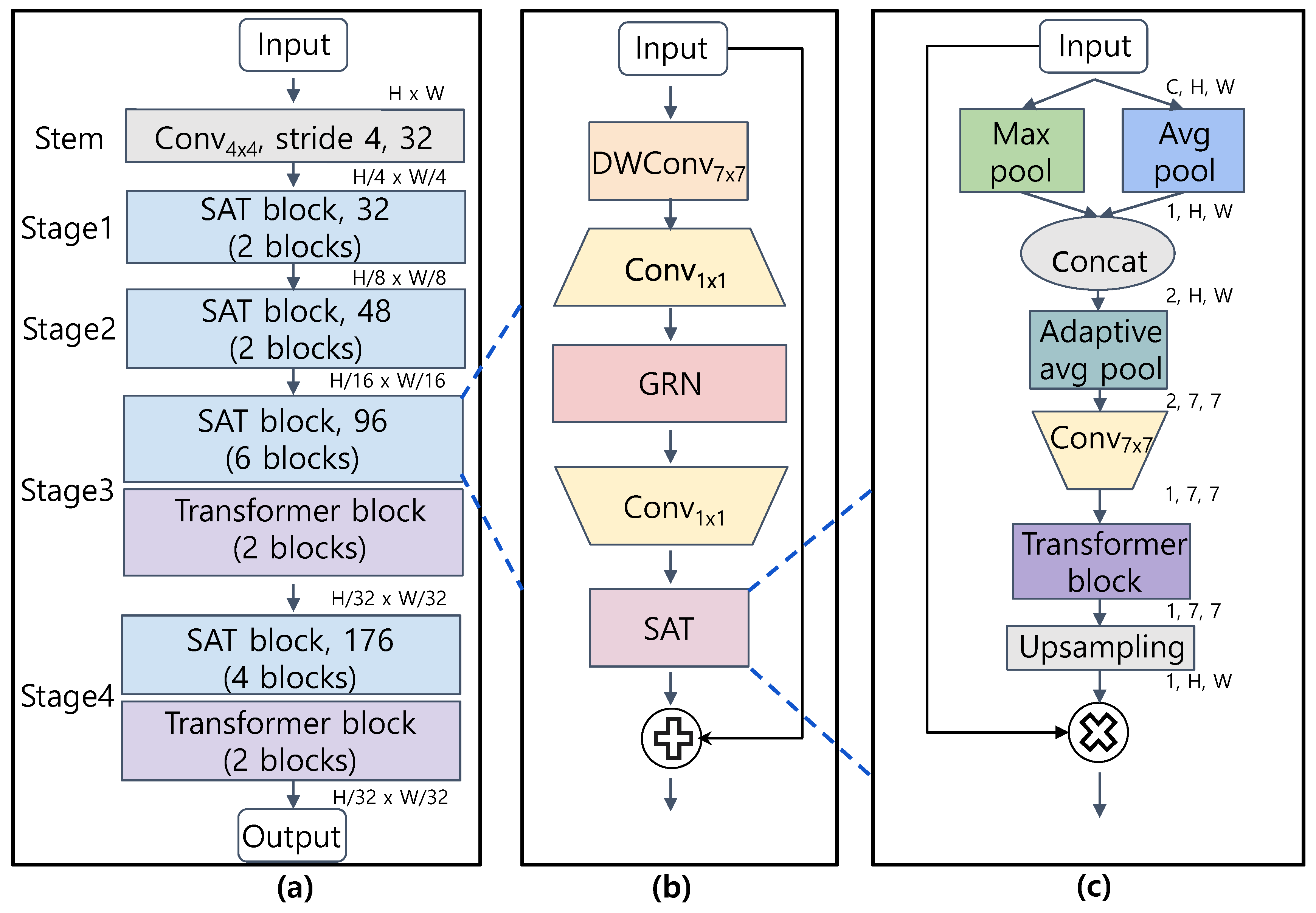
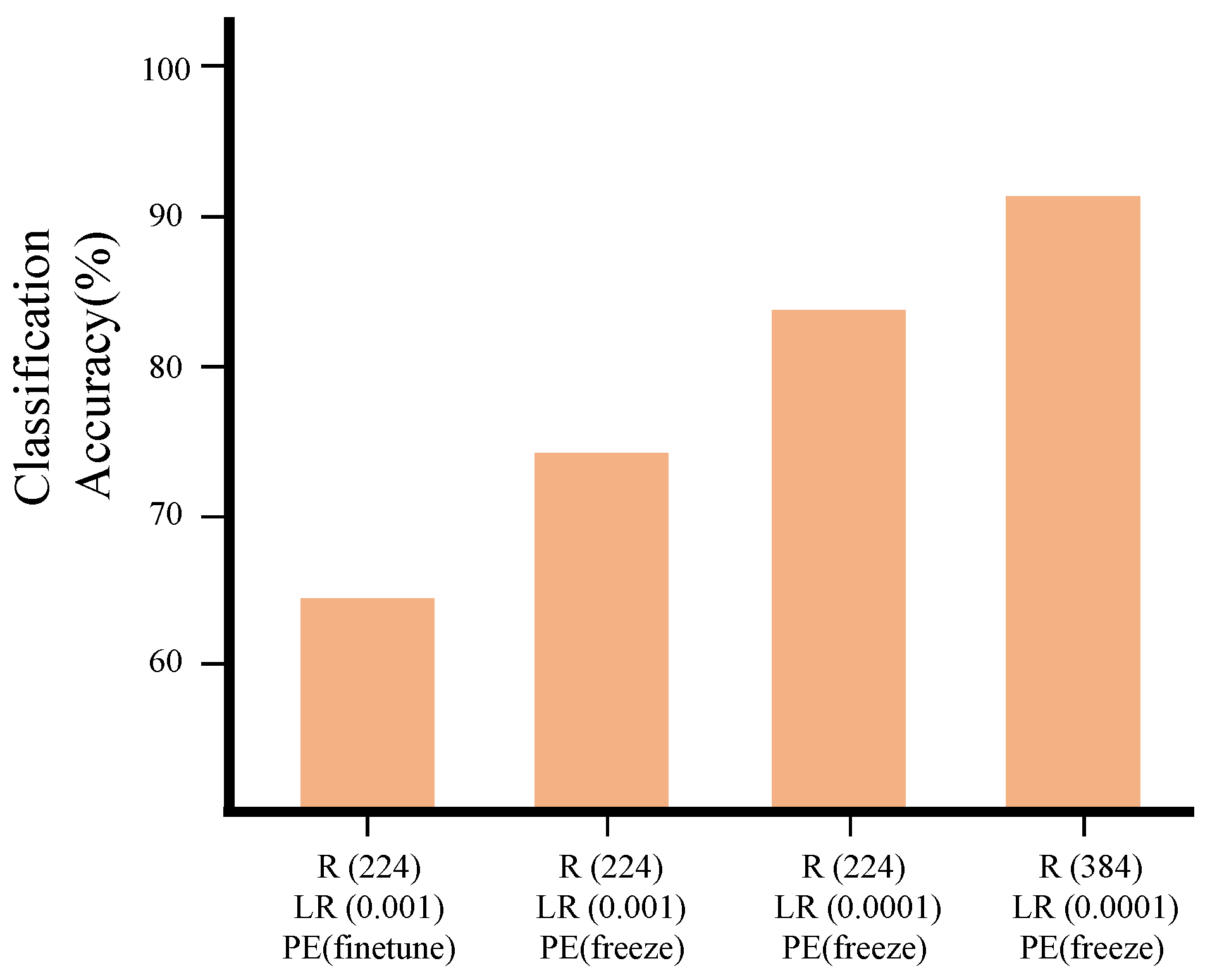
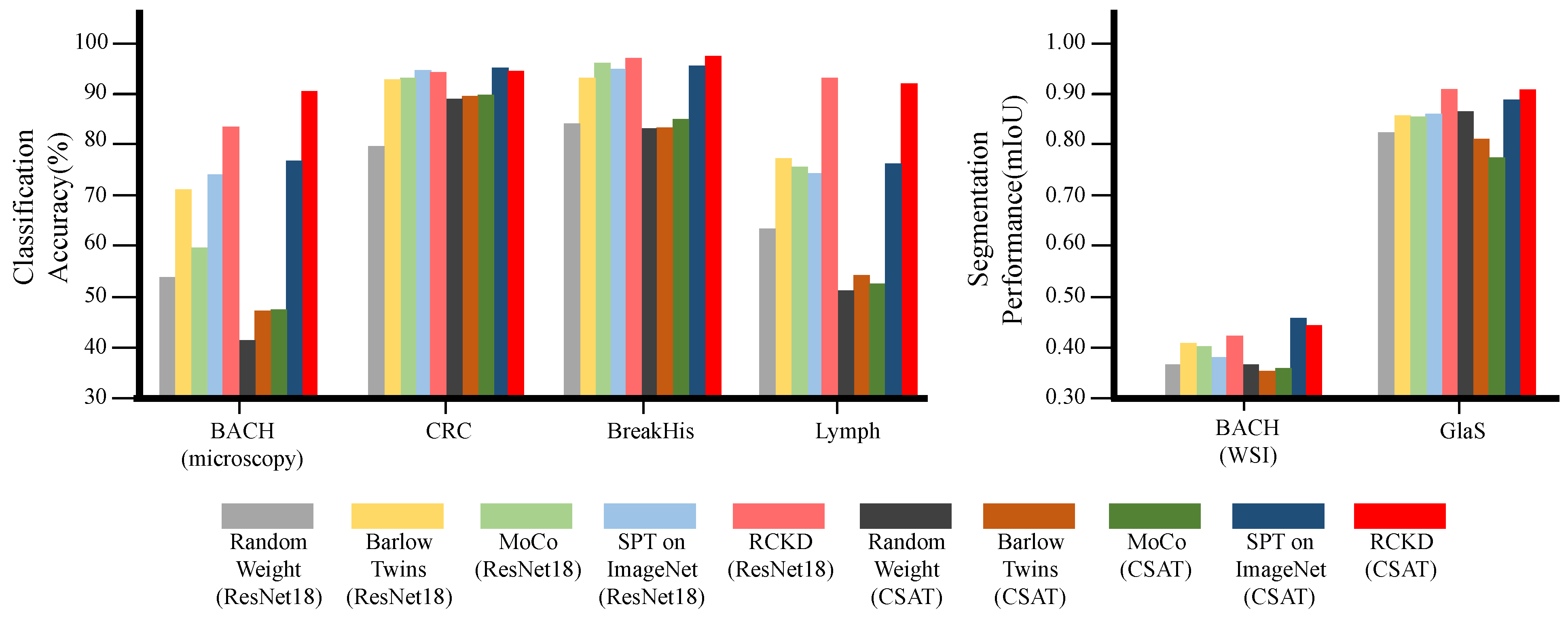
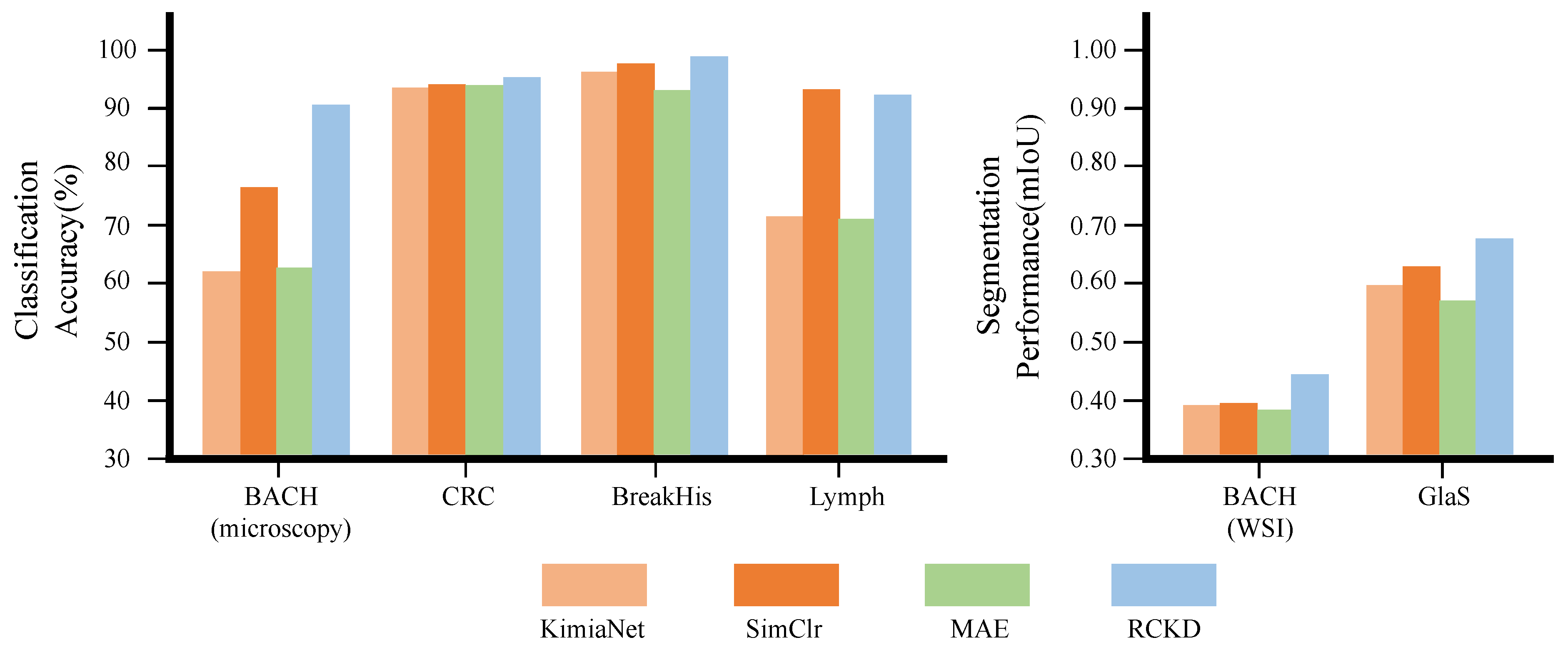
| Datasets | Tasks | Classes | Data Size | Number of Patches [Train, Validation, Test] | Magnification/ Patch Size |
|---|---|---|---|---|---|
| BACH [50] (microscopy) | Breast cancer subtype classification | Normal, Benign, In situ carcinoma, Invasive carcinoma | 400 patches | 400 [240, 80, 80] | / 2048 × 1536 |
| CRC [51] | Colorectal cancer and normal tissue classification | Adipose, Background, Debris, Lymphocytes, Mucus, Smooth muscle, Normal colon mucosa, Cancer-associated stroma, Colorectal adenocarcinoma epithelium | 107,180 patches | 107,180 [80,000, 20,000, 7180] | / 224 × 224 |
| BreakHis [52] | Malignant and benign tissue classification in breast cancer | Benign tumors, Malignant tumors | 7909 patches | 7909 [4745, 1582, 1582] | , , , / 700 × 460 |
| Lymph [53] | Malignant lymph node cancer classification | Chronic lymphocytic leukemia, Follicular lymphoma, Mantle cell lymphoma | 374 patches | 374 [224, 75, 75] | / 1388 × 1040 |
| BACH [50] (WSI) | Breast cancer subtype segmentation | Normal, Benign, In situ carcinoma, Invasive carcinoma | 10 WSIs | 4483 [2388, 1214, 881] | / 1024 × 1024 |
| GlaS [54] | Gland segmentation | Benign gland, Malignant gland | 165 patches | 165 [68, 17, 80] | / 775 × 522 |
| Stages | Input Size | Output Size | CSAT Hyper-Parameters |
|---|---|---|---|
| Stem | H, W | H/4, W/4 | L = 1, D = 32, Convolution block |
| Stage1 | H/4, W/4 | H/8, W/8 | L = 2, D = 32, SAT block |
| Stage2 | H/8, W/8 | H/16, W/16 | L = 2, D = 48, SAT block |
| Stage3 | H/16, W/16 | H/32, W/32 | L = 6, D = 96, SAT block L = 2, D = 96, Transformer block |
| Stage4 | H/32, W/32 | H/32, W/32 | L = 4, D = 176, SAT block L = 2, D = 176, Transformer block |
| Model | Params | GMAC | Pretraining Methods | Classification Accuracy (%) | Segmentation Performance (mIoU) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
BACH
(Microscopy) | CRC | BreakHis | Lymph |
Average
Accuracy |
BACH
(WSI) | GlaS |
Average
mIoU | ||||
| ResNet18 | 10.6 M | 5.35 | Random Weight | 53.7 | 80.2 | 85.0 | 63.7 | 70.6 | 0.355 | 0.83 | 0.592 |
| 10.6 M | 5.35 | Barlow Twins | 71.4 | 93.7 | 93.8 | 77.8 | 84.1 | 0.40 | 0.861 | 0.630 | |
| 10.6 M | 5.35 | MoCo | 59.7 | 93.8 | 96.9 | 76.0 | 81.6 | 0.391 | 0.864 | 0.627 | |
| 10.6 M | 5.35 | SPT on ImageNet | 74.4 | 95.5 | 95.5 | 74.6 | 85 | 0.373 | 0.866 | 0.619 | |
| 10.6 M | 5.35 | RCKD | 83.9 | 95.0 | 98.0 | 93.8 | 92.6 | 0.415 | 0.915 | 0.665 | |
| CSAT | 2.8 M | 1.08 | Random Weight | 41.3 | 89.6 | 83.7 | 51.4 | 66.5 | 0.355 | 0.872 | 0.613 |
| 2.8 M | 1.08 | Barlow Twins | 47.0 | 90.2 | 83.7 | 53.9 | 68.7 | 0.342 | 0.81 | 0.576 | |
| 2.8 M | 1.08 | MoCo | 47.1 | 90.6 | 85.5 | 52.6 | 68.9 | 0.35 | 0.783 | 0.566 | |
| 2.8 M | 1.08 | SPT on ImageNet | 77.0 | 95.8 | 96.1 | 76.5 | 86.3 | 0.441 | 0.902 | 0.671 | |
| 2.8 M | 1.08 | RCKD | 90.6 | 95.3 | 98.6 | 92.5 | 94.2 | 0.435 | 0.912 | 0.673 | |
| Model | Params | GMAC | Pretraining Methods | Classification Accuracy (%) | Segmentation Performance (mIoU) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
BACH
(Microscopy) | CRC | BreakHis | Lymph |
Average
Accuracy |
BACH
(WSI) | GlaS |
Average
mIoU | ||||
| EfficientNet-B0 | 3.8 M | 1.21 | SPT on ImageNet | 82.2 | 96.8 | 97.4 | 84.7 | 90.2 | 0.399 | 0.861 | 0.630 |
| EfficientNet-B0 | 3.8 M | 1.21 | RCKD | 85.9 | 96.2 | 98.3 | 94.9 | 93.8 | 0.438 | 0.873 | 0.655 |
| ConvNextV2-Atto | 3.2 M | 1.60 | SPT on ImageNet | 78.6 | 95.1 | 96.6 | 77.2 | 86.8 | 0.434 | 0.901 | 0.667 |
| ConvNextV2-Atto | 3.2 M | 1.60 | RCKD | 80.4 | 94.9 | 96.4 | 91.9 | 90.9 | 0.38 | 0.91 | 0.645 |
| CSAT | 2.8 M | 1.08 | SPT on ImageNet | 77.0 | 95.8 | 96.1 | 76.5 | 86.3 | 0.441 | 0.902 | 0.671 |
| CSAT | 2.8 M | 1.08 | RCKD | 90.6 | 95.3 | 98.6 | 92.5 | 94.2 | 0.435 | 0.912 | 0.673 |
| Pretraining Methods | Model | Params | GMAC | Classification Accuracy (%) | Segmentation Performance (mIoU) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
BACH
(Microscopy) | CRC | BreakHis | Lymph |
Average
Accuracy |
BACH
(WSI) | GlaS |
Average
mIoU | ||||
| KimiaNet [70] | DensNet121 | 6.6M | 8.51 | 61.3 | 93.8 | 96.3 | 71.5 | 80.7 | 0.385 | 0.804 | 0.594 |
| SimCLR [12] | ResNet18 | 10.6M | 5.35 | 76.2 | 94.2 | 97.7 | 93.3 | 90.3 | 0.386 | 0.866 | 0.626 |
| MAE [71] | ViT-B | 81.6M | 49.3 | 62.3 | 94.1 | 93.1 | 71.3 | 80.2 | 0.378 | 0.763 | 0.570 |
| RCKD | CSAT | 2.8M | 1.08 | 90.6 | 95.3 | 98.6 | 92.5 | 94.2 | 0.435 | 0.912 | 0.673 |
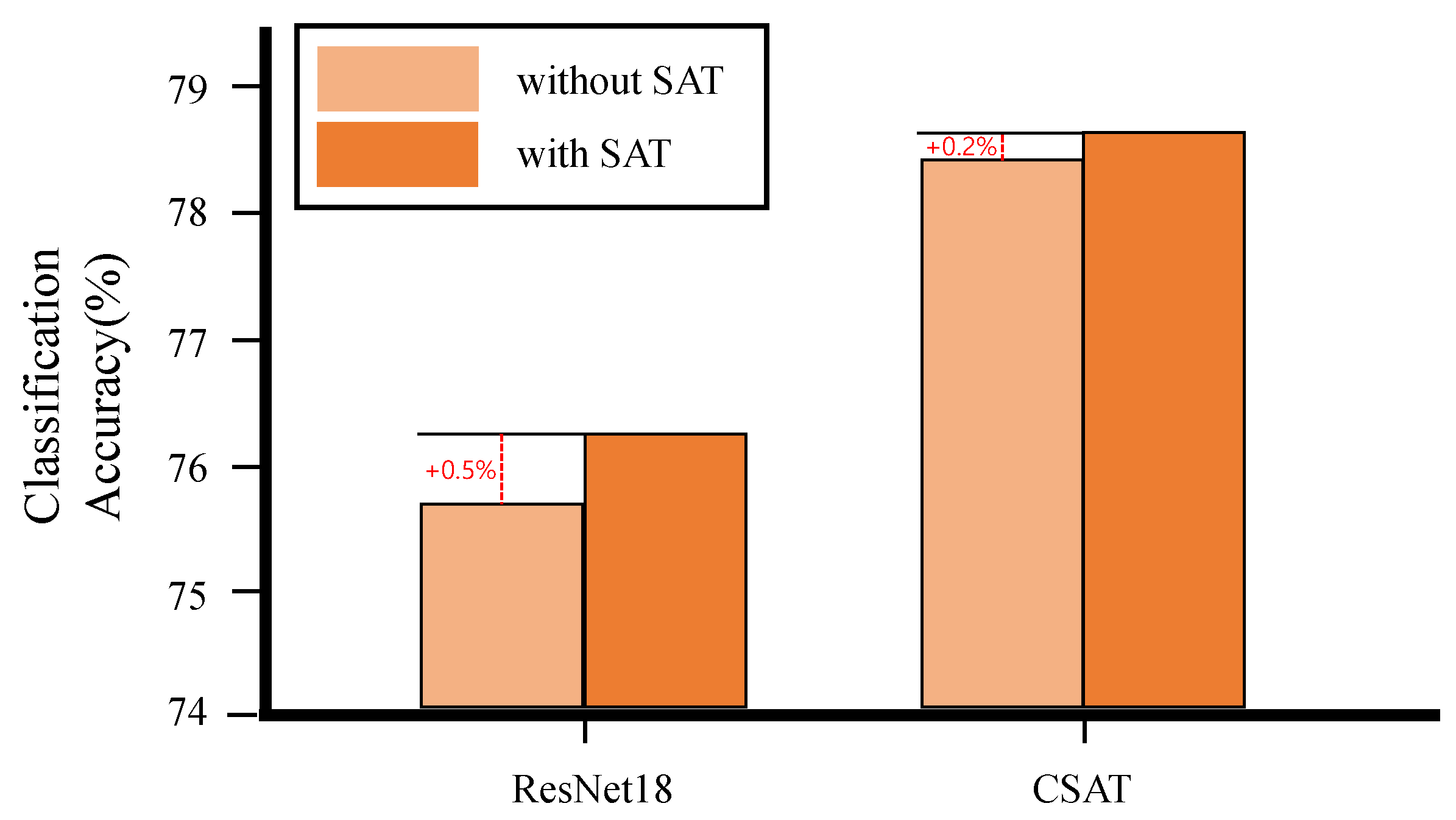
| Model | SAT Module | Params | GMAC | Classification Accuracy (%) |
|---|---|---|---|---|
| ResNet18 | X | 11,689,512 | 5.35 | 75.7 |
| ResNet18 | O | 11,690,544 | 5.35 | 76.2 |
| CSAT | X | 3,063,272 | 1.08 | 78.4 |
| CSAT | O | 3,065,078 | 1.08 | 78.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Kwak, T.-Y.; Chang, H.; Kim, S.W.; Kim, I. RCKD: Response-Based Cross-Task Knowledge Distillation for Pathological Image Analysis. Bioengineering 2023, 10, 1279. https://doi.org/10.3390/bioengineering10111279
Kim H, Kwak T-Y, Chang H, Kim SW, Kim I. RCKD: Response-Based Cross-Task Knowledge Distillation for Pathological Image Analysis. Bioengineering. 2023; 10(11):1279. https://doi.org/10.3390/bioengineering10111279
Chicago/Turabian StyleKim, Hyunil, Tae-Yeong Kwak, Hyeyoon Chang, Sun Woo Kim, and Injung Kim. 2023. "RCKD: Response-Based Cross-Task Knowledge Distillation for Pathological Image Analysis" Bioengineering 10, no. 11: 1279. https://doi.org/10.3390/bioengineering10111279
APA StyleKim, H., Kwak, T.-Y., Chang, H., Kim, S. W., & Kim, I. (2023). RCKD: Response-Based Cross-Task Knowledge Distillation for Pathological Image Analysis. Bioengineering, 10(11), 1279. https://doi.org/10.3390/bioengineering10111279









