Author Contributions
Conceptualization, N.N. and T.S.; methodology, N.N.; software, N.N.; validation, N.N.; formal analysis, N.N.; investigation, N.N.; resources, N.N.; data curation, N.N. and T.S.; writing—original draft preparation, N.N.; writing—review and editing, N.N. and T.S.; visualization, N.N.; supervision, N.N.; project administration, N.N.; funding acquisition, N.N. and T.S. All authors have read and agreed to the published version of the manuscript.
Figure 1.
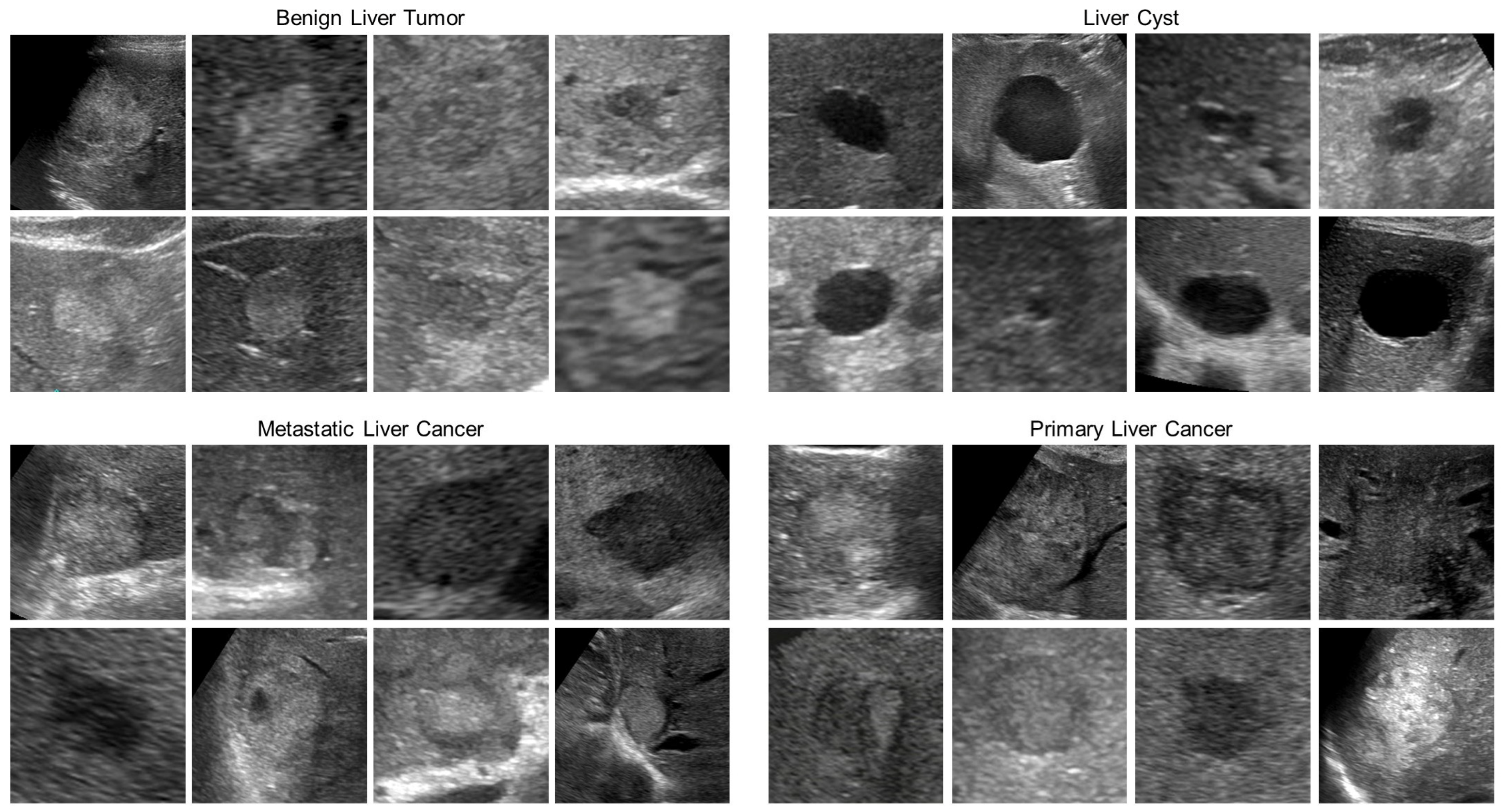
Example of test images. Each B-mode ultrasound image is a grayscale image of 256 × 256 pixels.
Figure 1.
Example of test images. Each B-mode ultrasound image is a grayscale image of 256 × 256 pixels.
Figure 2.
A schematic of training and tests of 16 CNNs.
Figure 2.
A schematic of training and tests of 16 CNNs.
Figure 3.
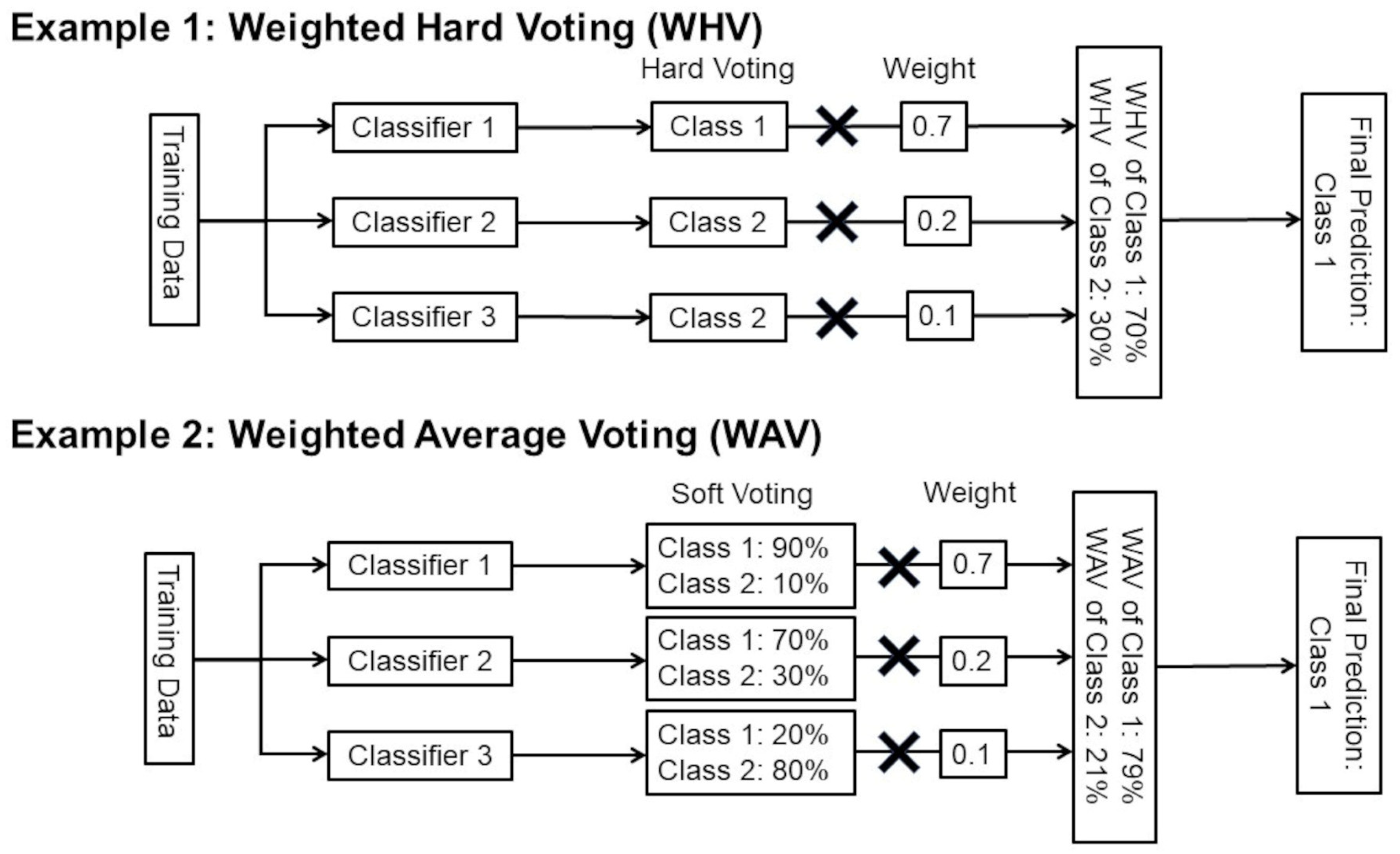
Examples of WHV and WAV. This figure shows examples of WHV and WAV with three different classifiers and two class classifications. In this study, 16 different classifiers and 4 class classifications were used.
Figure 3.
Examples of WHV and WAV. This figure shows examples of WHV and WAV with three different classifiers and two class classifications. In this study, 16 different classifiers and 4 class classifications were used.
Figure 4.
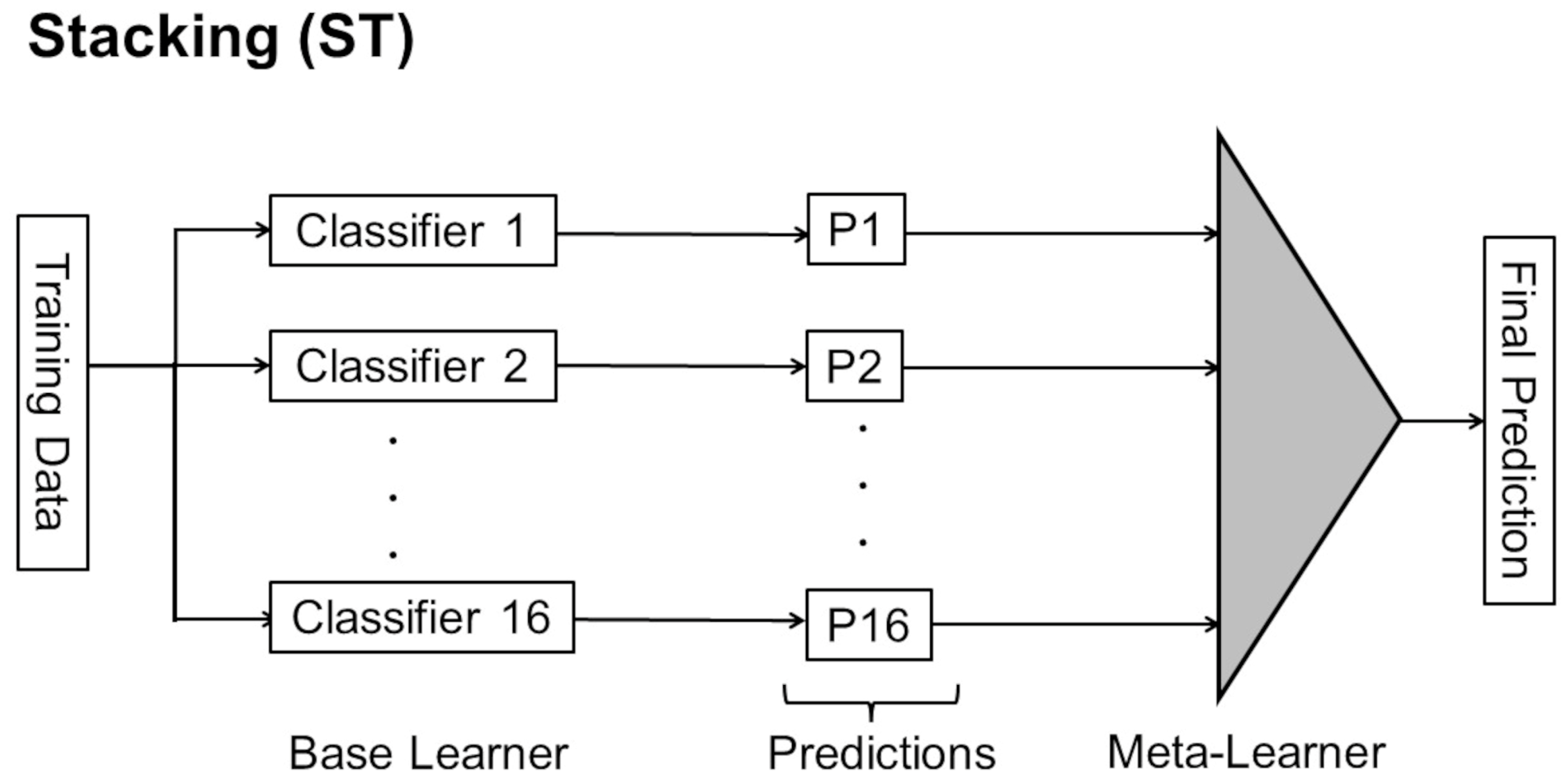
Description of ST. 16 different CNNs as base learner and LightGBM as meta-learner were used in this study.
Figure 4.
Description of ST. 16 different CNNs as base learner and LightGBM as meta-learner were used in this study.
Figure 5.
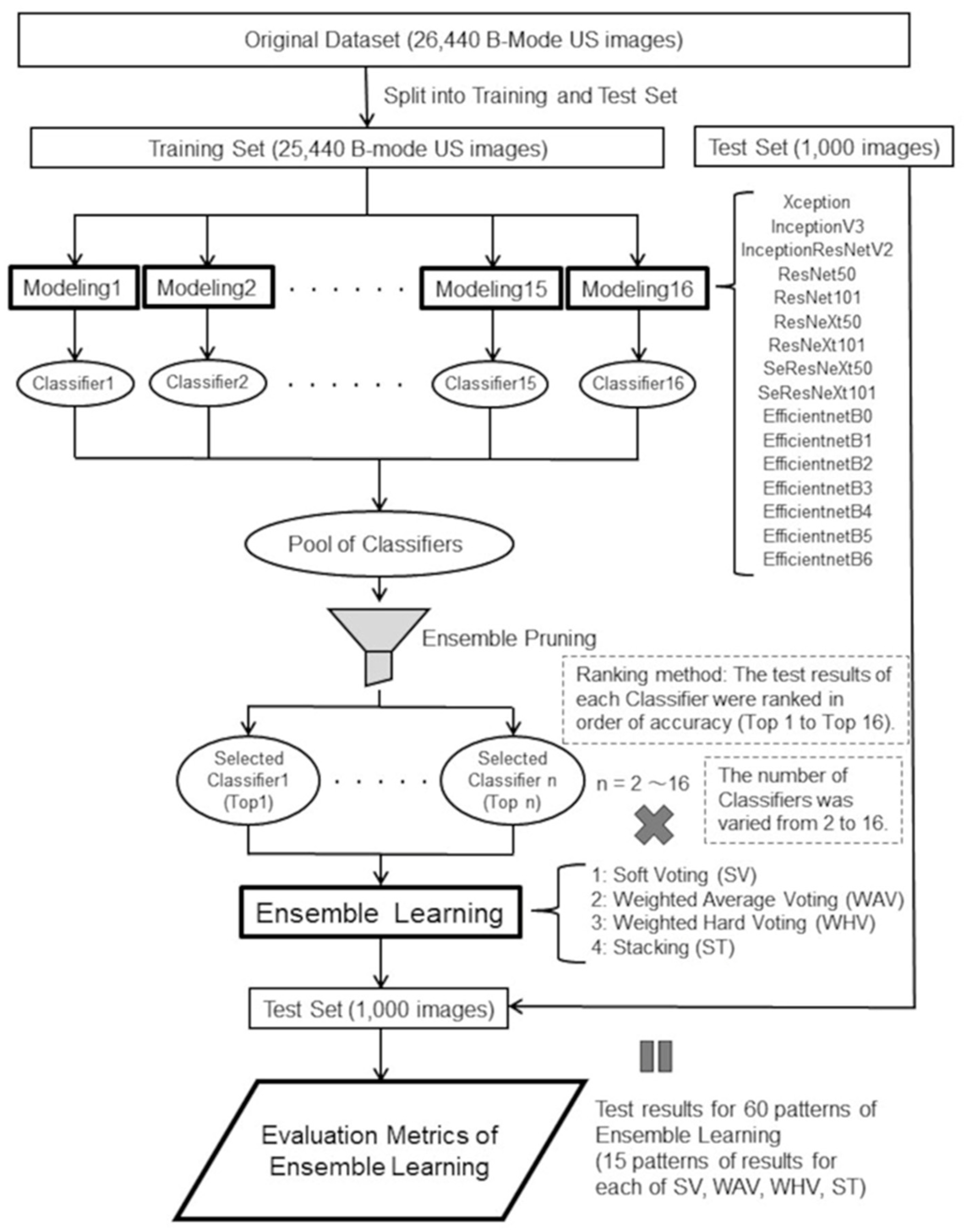
A schematic of ensemble pruning and evaluation metrics.
Figure 5.
A schematic of ensemble pruning and evaluation metrics.
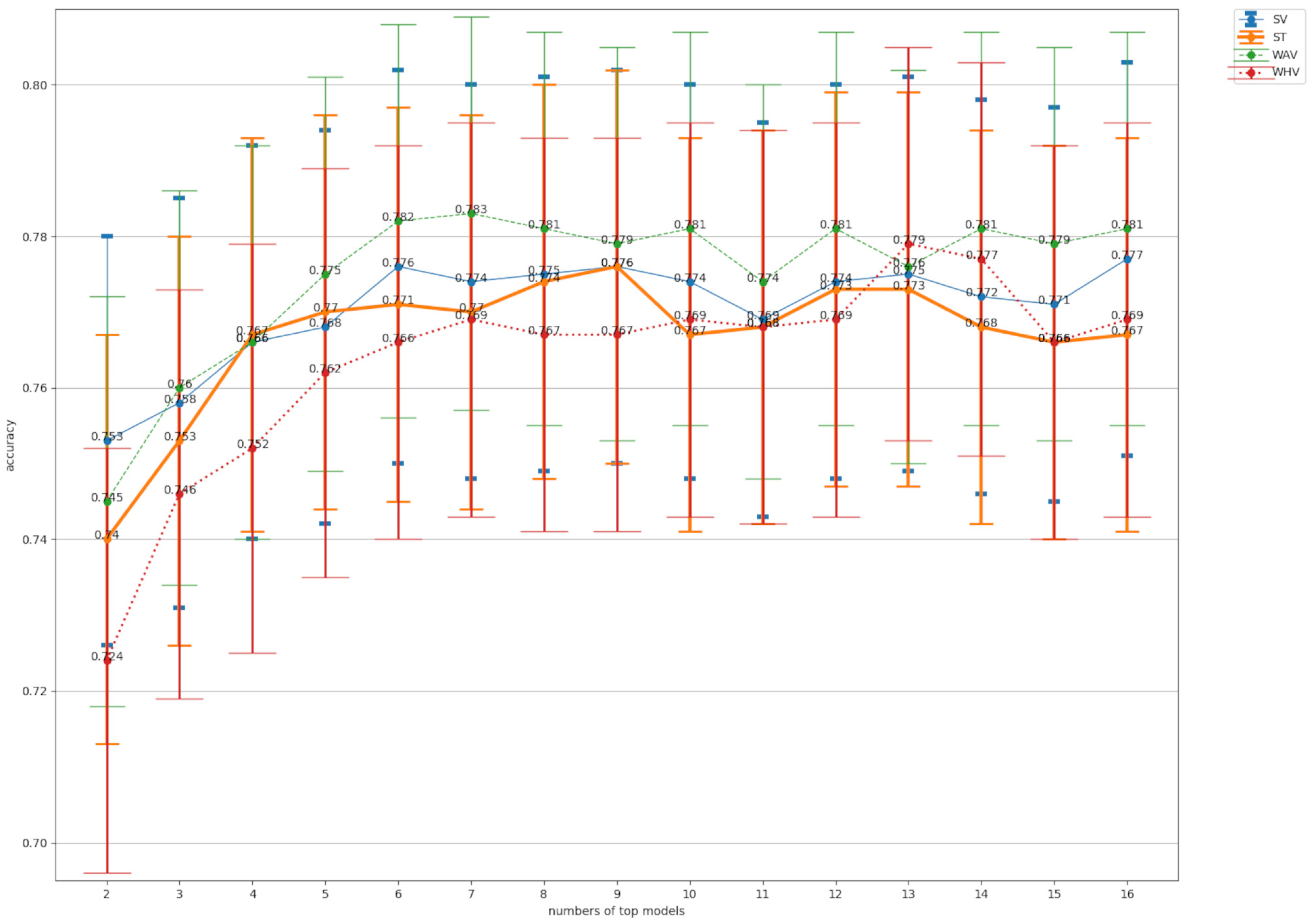
Figure 6.
A comparison of the accuracy values for ensemble pruning. SV: soft voting, ST: stacking. WAV: weighted average voting, WHV: weighted hard voting. Numbers of top models represents the number of classifiers used for ensemble training from top 2 to top 16 in accuracy. The bars in the graph are 95% confidence intervals.
Figure 6.
A comparison of the accuracy values for ensemble pruning. SV: soft voting, ST: stacking. WAV: weighted average voting, WHV: weighted hard voting. Numbers of top models represents the number of classifiers used for ensemble training from top 2 to top 16 in accuracy. The bars in the graph are 95% confidence intervals.
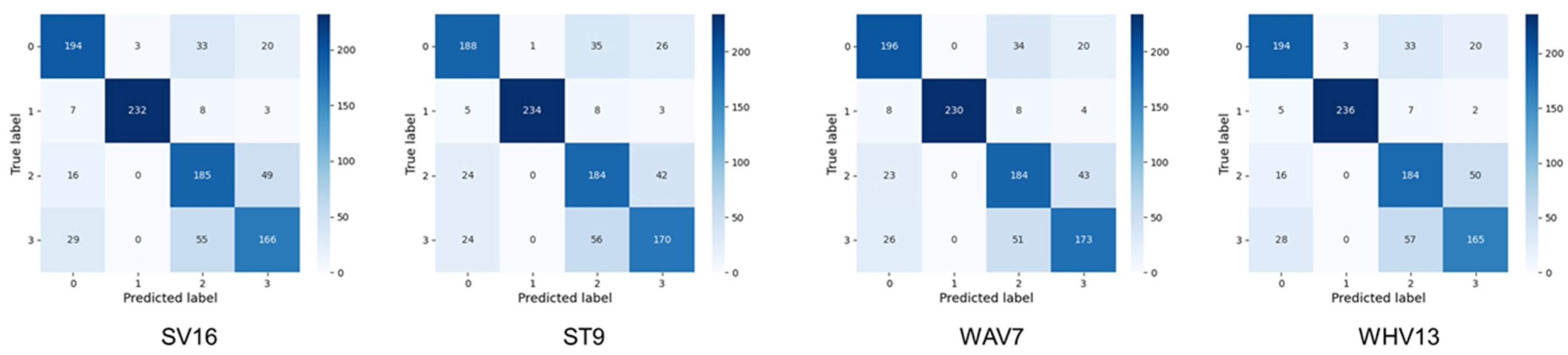
Figure 7.
Four-class confusion matrix of the models with the highest accuracy by pruning in each of the four types of ensemble learning. The classes indicated by the numbers of the labels on the x- and y-axes of each confusion matrix are as follows. 0: Benign Liver Tumor, 1: Liver Cyst, 2: Metastatic Liver Cancer, 3: Primary Liver Cancer, SV16: top16 was used for soft voting, ST9: top9 was used for stacking, WAV7: top7 was used for weighted average voting, WHV13: top13 was used for weighted hard voting.
Figure 7.
Four-class confusion matrix of the models with the highest accuracy by pruning in each of the four types of ensemble learning. The classes indicated by the numbers of the labels on the x- and y-axes of each confusion matrix are as follows. 0: Benign Liver Tumor, 1: Liver Cyst, 2: Metastatic Liver Cancer, 3: Primary Liver Cancer, SV16: top16 was used for soft voting, ST9: top9 was used for stacking, WAV7: top7 was used for weighted average voting, WHV13: top13 was used for weighted hard voting.
Table 1.
Confusion matrix for multiclass classification. Actual values are the correct values of the ultrasound images of the test set. Prediction values are the predictions of the ultrasound images of the test set by the classifier. BLT: benign liver tumor, LCY: liver cyst, MLC: metastatic liver cancer, PLC: primary liver cancer.
Table 1.
Confusion matrix for multiclass classification. Actual values are the correct values of the ultrasound images of the test set. Prediction values are the predictions of the ultrasound images of the test set by the classifier. BLT: benign liver tumor, LCY: liver cyst, MLC: metastatic liver cancer, PLC: primary liver cancer.
| | | Predicted Values |
|---|
| | | BLT | LCY | MLC | PLC |
| Actual Values | BLT |
cell1
|
cell2
|
cell3
|
cell4
|
|
LCY
|
cell5
|
cell6
|
cell7
|
cell8
|
|
MLC
|
cell9
|
cell10
|
cell11
|
cell12
|
|
PLC
|
cell13
|
cell14
|
cell15
|
cell16
|
Table 2.
Contingency table used for the McNemar’s test to compare two classifiers. n00: number of items classified correctly by both Classifier 1 and Classifier 2, n01: number of items classified correctly by Classifier 1 but not by Classifier 2, n10: number of items classified correctly by Classifier 2 but not by Classifier 1, n11: number of items misclassified by both Classifier 1 and Classifier 2. Null hypothesis: n01 = n10.
Table 2.
Contingency table used for the McNemar’s test to compare two classifiers. n00: number of items classified correctly by both Classifier 1 and Classifier 2, n01: number of items classified correctly by Classifier 1 but not by Classifier 2, n10: number of items classified correctly by Classifier 2 but not by Classifier 1, n11: number of items misclassified by both Classifier 1 and Classifier 2. Null hypothesis: n01 = n10.
| Contingency Table |
|---|
| |
Classifier 2
Correct
|
Classifier 2
Incorrect
|
Classifier 1
Correct
|
n00
|
n01
|
Classifier 1
Incorrect
|
n10
|
n11
|
Table 3.
True positive, false positive, false negative, and true negative values for 4-class classification in 16CNNs. BLT: benign liver tumor, LCY: liver cyst, MLC: metastatic liver cancer, PLC: primary liver cancer, TP: true positive, FP: false positive, FN: false negative, TN: true negative.
Table 3.
True positive, false positive, false negative, and true negative values for 4-class classification in 16CNNs. BLT: benign liver tumor, LCY: liver cyst, MLC: metastatic liver cancer, PLC: primary liver cancer, TP: true positive, FP: false positive, FN: false negative, TN: true negative.
| | | Xception | InceptionV3 | InceptionResNetV2 | ResNet50 | ResNet101 | ResNeXt50 | ResNeXt101 | SeResNeXt50 | SeResNeXt101 | EfficientNetB0 | EfficientNetB1 | EfficientNetB2 | EfficientNetB3 | EfficientNetB4 | EfficientNetB5 | EfficientNetB6 |
|---|
|
BLT
|
TP
| 180 | 156 | 169 | 170 | 167 | 173 | 172 | 194 | 190 | 165 | 153 | 179 | 151 | 134 | 148 | 156 |
|
FP
| 58 | 52 | 67 | 74 | 70 | 62 | 59 | 116 | 105 | 61 | 100 | 114 | 75 | 84 | 64 | 79 |
|
FN
| 70 | 94 | 81 | 80 | 83 | 77 | 78 | 56 | 60 | 85 | 97 | 71 | 99 | 116 | 102 | 94 |
|
TN
| 692 | 698 | 683 | 676 | 680 | 688 | 691 | 634 | 645 | 689 | 650 | 636 | 675 | 666 | 686 | 671 |
|
LCY
|
TP
| 217 | 196 | 204 | 225 | 225 | 219 | 226 | 221 | 222 | 207 | 194 | 208 | 209 | 207 | 218 | 213 |
|
FP
| 8 | 6 | 1 | 8 | 10 | 3 | 2 | 4 | 2 | 2 | 11 | 10 | 9 | 7 | 6 | 14 |
|
FN
| 33 | 54 | 46 | 25 | 25 | 31 | 24 | 29 | 28 | 43 | 56 | 42 | 41 | 43 | 32 | 37 |
|
TN
| 742 | 744 | 749 | 742 | 740 | 747 | 748 | 746 | 748 | 748 | 739 | 740 | 741 | 743 | 744 | 736 |
|
MLC
|
TP
| 166 | 169 | 164 | 184 | 183 | 156 | 166 | 160 | 146 | 161 | 144 | 124 | 165 | 126 | 151 | 159 |
|
FP
| 129 | 123 | 123 | 162 | 159 | 132 | 127 | 110 | 103 | 114 | 142 | 98 | 162 | 145 | 129 | 147 |
|
FN
| 84 | 81 | 86 | 66 | 67 | 94 | 84 | 90 | 104 | 89 | 106 | 126 | 85 | 124 | 99 | 91 |
|
TN
| 621 | 627 | 627 | 588 | 591 | 618 | 623 | 640 | 647 | 636 | 608 | 652 | 588 | 605 | 621 | 603 |
|
PLC
|
TP
| 152 | 155 | 163 | 105 | 111 | 147 | 155 | 124 | 132 | 161 | 137 | 153 | 136 | 150 | 145 | 132 |
|
FP
| 90 | 143 | 109 | 72 | 75 | 108 | 93 | 71 | 100 | 129 | 119 | 114 | 93 | 147 | 139 | 100 |
|
FN
| 98 | 95 | 87 | 145 | 139 | 103 | 95 | 126 | 118 | 89 | 113 | 97 | 114 | 100 | 105 | 118 |
|
TN
| 660 | 607 | 641 | 678 | 675 | 642 | 657 | 679 | 650 | 621 | 631 | 636 | 657 | 603 | 611 | 650 |
Table 4.
The evaluation metrics for each of the 16 CNNs.
Table 4.
The evaluation metrics for each of the 16 CNNs.
| Model | Precision *, ** | Sensitivity *, ** | Specificity *, ** | Accuracy ** | Ranking of Accuracy |
|---|
|
ResNeXt101
| 0.731 (0.778, 0.686) | 0.719 (0.772, 0.666) | 0.906 (0.925, 0.888) | 0.719 (0.747, 0.691) | 1 |
|
Xception
| 0.728 (0.777, 0.679) | 0.715 (0.769, 0.661) | 0.905 (0.924, 0.886) | 0.715 (0.743, 0.687) | 2 |
|
InceptionResNetV2
| 0.720 (0.766, 0.675) | 0.700 (0.756, 0.644) | 0.900 (0.919, 0.881) | 0.700 (0.728, 0.672) | 3 |
|
SeResNeXt50
| 0.709 (0.758, 0.660) | 0.699 (0.752, 0.646) | 0.900 (0.919, 0.880) | 0.699 (0.727, 0.671) | 4 |
|
ResNeXt50
| 0.710 (0.758, 0.663) | 0.695 (0.750, 0.640) | 0.898 (0.917, 0.879) | 0.695 (0.724, 0.666) | 5 |
|
EfficientNetB0
| 0.715 (0.762, 0.669) | 0.694 (0.750, 0.638) | 0.898 (0.917, 0.879) | 0.694 (0.723, 0.665) | 6 |
|
SeResNeXt101
| 0.698 (0.746, 0.650) | 0.690 (0.744, 0.636) | 0.897 (0.916, 0.877) | 0.690 (0.719, 0.661) | 7 |
|
ResNet101
| 0.698 (0.750, 0.647) | 0.686 (0.739, 0.633) | 0.895 (0.915, 0.875) | 0.686 (0.715, 0.657) | 8 |
|
ResNet50
| 0.697 (0.748, 0.645) | 0.684 (0.737, 0.631) | 0.895 (0.914, 0.875) | 0.684 (0.713, 0.655) | 9 |
|
InceptionV3
| 0.705 (0.754, 0.656) | 0.676 (0.733, 0.619) | 0.892 (0.912, 0.872) | 0.676 (0.705, 0.647) | 10 |
|
EfficientNetB2
| 0.674 (0.725, 0.621) | 0.664 (0.719, 0.607) | 0.888 (0.909, 0.867) | 0.664 (0.692, 0.634) | 11 |
|
EfficientNetB5
| 0.680 (0.730, 0.630) | 0.662 (0.718, 0.606) | 0.887 (0.908, 0.867) | 0.662 (0.691, 0.633) | 12 |
|
EfficientNetB3
| 0.681 (0.733, 0.630) | 0.661 (0.718, 0.604) | 0.886 (0.908, 0.866) | 0.661 (0.690, 0.632) | 13 |
|
EfficientNetB6
| 0.673 (0.726, 0.620) | 0.660 (0.716, 0.604) | 0.887 (0.908, 0.866) | 0.660 (0.689, 0.631) | 14 |
|
EfficientNetB1
| 0.647 (0.700, 0.595) | 0.628 (0.687, 0.569) | 0.876 (0.898, 0.854) | 0.628 (0.658, 0.598) | 15 |
|
EfficientNetB4
| 0.638 (0.689, 0.588) | 0.617 (0.675, 0.559) | 0.872 (0.894, 0.851) | 0.617 (0.647, 0.587) | 16 |
Table 5.
The evaluation metrics for each of the 16 CNNs (
Table 4 continued) and.significant difference test between ResNeXt101(top1) and 15 other models.
Table 5.
The evaluation metrics for each of the 16 CNNs (
Table 4 continued) and.significant difference test between ResNeXt101(top1) and 15 other models.
| Model | F1 Score * | ROC Macro AUC | Ranking of Accuracy | p-Value ** |
|---|
|
ResNeXt101
| 0.724 | 0.902 | 1 | – |
|
Xception
| 0.720 | 0.900 | 2 | 0.882 |
|
InceptionResNetV2
| 0.707 | 0.880 | 3 | 0.377 |
|
SeResNeXt50
| 0.699 | 0.874 | 4 | 0.341 |
|
ResNeXt50
| 0.701 | 0.903 | 5 | 0.238 |
|
EfficientNetB0
| 0.701 | 0.866 | 6 | 0.224 |
|
SeResNeXt101
| 0.692 | 0.870 | 7 | 0.148 |
|
ResNet101
| 0.685 | 0.887 | 8 | 0.107 |
|
ResNet50
| 0.682 | 0.888 | 9 | 0.081 |
|
InceptionV3
| 0.684 | 0.859 | 10 | 0.037 |
|
EfficientNetB2
| 0.666 | 0.868 | 11 | 0.006 |
|
EfficientNetB5
| 0.668 | 0.890 | 12 | 0.005 |
|
EfficientNetB3
| 0.667 | 0.867 | 13 | 0.006 |
|
EfficientNetB6
| 0.664 | 0.877 | 14 | 0.004 |
|
EfficientNetB1
| 0.635 | 0.852 | 15 | <0.001 |
|
EfficientNetB4
| 0.624 | 0.856 | 16 | <0.001 |
Table 6.
Correlation matrix for each of the 16 CNN test results.
Table 6.
Correlation matrix for each of the 16 CNN test results.
| ResNeXt101 | 1.000 | | | | | | | | | | | | | | | |
|
Xception
| 0.585 | 1.000 | | | | | | | | | | | | | | |
|
InceptionResNetV2
| 0.536 | 0.584 | 1.000 | | | | | | | | | | | | | |
|
SeResNeXt50
| 0.599 | 0.519 | 0.462 | 1.000 | | | | | | | | | | | | |
|
ResNeXt50
| 0.627 | 0.534 | 0.529 | 0.583 | 1.000 | | | | | | | | | | | |
|
EfficientNetB0
| 0.503 | 0.542 | 0.543 | 0.409 | 0.487 | 1.000 | | | | | | | | | | |
|
SeResNeXt101
| 0.541 | 0.509 | 0.483 | 0.630 | 0.528 | 0.388 | 1.000 | | | | | | | | | |
|
ResNet101
| 0.558 | 0.530 | 0.505 | 0.569 | 0.556 | 0.442 | 0.532 | 1.000 | | | | | | | | |
|
ResNet50
| 0.576 | 0.520 | 0.502 | 0.572 | 0.596 | 0.437 | 0.550 | 0.746 | 1.000 | | | | | | | |
|
InceptionV3
| 0.505 | 0.558 | 0.593 | 0.356 | 0.464 | 0.594 | 0.404 | 0.448 | 0.436 | 1.000 | | | | | | |
|
EfficientnetB2
| 0.492 | 0.511 | 0.424 | 0.559 | 0.499 | 0.412 | 0.496 | 0.563 | 0.548 | 0.359 | 1.000 | | | | | |
|
EfficientnetB5
| 0.496 | 0.488 | 0.486 | 0.409 | 0.480 | 0.469 | 0.373 | 0.473 | 0.474 | 0.482 | 0.513 | 1.000 | | | | |
|
EfficientnetB3
| 0.539 | 0.518 | 0.523 | 0.515 | 0.503 | 0.493 | 0.471 | 0.477 | 0.519 | 0.435 | 0.574 | 0.568 | 1.000 | | | |
|
EfficinetnetB6
| 0.524 | 0.515 | 0.429 | 0.462 | 0.480 | 0.427 | 0.420 | 0.512 | 0.491 | 0.450 | 0.548 | 0.613 | 0.506 | 1.000 | | |
|
EfficientnetB1
| 0.447 | 0.484 | 0.424 | 0.434 | 0.414 | 0.424 | 0.371 | 0.464 | 0.470 | 0.381 | 0.485 | 0.414 | 0.522 | 0.414 | 1.000 | |
|
EfficientnetB4
| 0.465 | 0.467 | 0.436 | 0.400 | 0.435 | 0.438 | 0.328 | 0.433 | 0.445 | 0.431 | 0.466 | 0.578 | 0.538 | 0.581 | 0.415 | 1.000 |
| |
ResNeXt101
|
Xception
|
InceptionResNetV2
|
SeResNeXt50
|
ResNeXt50
|
EfficientNetB0
|
SeResNeXt101
|
ResNet101
|
ResNet50
|
InceptionV3
|
EfficientnetB2
|
EfficientnetB5
|
EfficientnetB3
|
EfficinetnetB6
|
EfficientnetB1
|
EfficientnetB4
|
Table 7.
True positive, false positive, false negative, and true negative values for 4-class classification in the models with the highest accuracy by pruning in each of the four types of ensemble learning. BLT: benign liver tumor, LCY: liver cyst, MLC: metastatic liver cancer, PLC: primary liver cancer, TP: true positive, FP: false positive, FN: false negative, TN: true negative, SV16: top16 was used for soft voting, ST9: top9 was used for stacking, WAV7: top7 was used for weighted average voting, WHV13: top13 was used for weighted hard voting.
Table 7.
True positive, false positive, false negative, and true negative values for 4-class classification in the models with the highest accuracy by pruning in each of the four types of ensemble learning. BLT: benign liver tumor, LCY: liver cyst, MLC: metastatic liver cancer, PLC: primary liver cancer, TP: true positive, FP: false positive, FN: false negative, TN: true negative, SV16: top16 was used for soft voting, ST9: top9 was used for stacking, WAV7: top7 was used for weighted average voting, WHV13: top13 was used for weighted hard voting.
| | | SV16 | ST9 | WAV7 | WHV13 |
|---|
|
BLT
|
TP
| 194 | 188 | 196 | 194 |
| |
FP
| 52 | 53 | 57 | 49 |
| |
FN
| 56 | 62 | 54 | 56 |
| |
TN
| 698 | 697 | 693 | 701 |
|
LCY
|
TP
| 232 | 234 | 230 | 236 |
| |
FP
| 3 | 1 | 0 | 3 |
| |
FN
| 18 | 16 | 20 | 14 |
| |
TN
| 747 | 749 | 750 | 747 |
|
MLC
|
TP
| 185 | 184 | 184 | 184 |
| |
FP
| 96 | 99 | 93 | 97 |
| |
FN
| 65 | 66 | 66 | 66 |
| |
TN
| 654 | 651 | 657 | 653 |
|
PLC
|
TP
| 166 | 170 | 173 | 165 |
| |
FP
| 72 | 71 | 67 | 72 |
| |
FN
| 84 | 80 | 77 | 85 |
| |
TN
| 678 | 679 | 683 | 678 |
Table 8.
Evaluation metrics for the models with the highest accuracy by pruning in each of the four ensemble learning methods. SV16: top16 was used for soft voting, ST9: top9 was used for stacking, WAV7: top7 was used for weighted average voting, WHV13: top13 was used for weighted hard voting.
Table 8.
Evaluation metrics for the models with the highest accuracy by pruning in each of the four ensemble learning methods. SV16: top16 was used for soft voting, ST9: top9 was used for stacking, WAV7: top7 was used for weighted average voting, WHV13: top13 was used for weighted hard voting.
| Model | Precision *,** | Sensitivity *,** | Specificity *,** | F1 Score * | ROC Macro AUC | Accuracy ** |
|---|
| SV16 | 0.783 (0.824, 0.733) | 0.777(0.822, 0.724) | 0.926 (0.941, 0.906) | 0.779 | 0.94 | 0.777 (0.802, 0.750) |
| ST9 | 0.783 (0.822, 0.734) | 0.776 (0.821, 0.723) | 0.925 (0.940, 0.906) | 0.778 | 0.924 | 0.776 (0.801, 0.749) |
| WAV7 | 0.790 (0.831, 0.749) | 0.783 (0.832, 0.734) | 0.928 (0.943, 0.912) | 0.786 | 0.935 | 0.783 (0.809, 0.757) |
| WHV13 | 0.784 (0.829, 0.740) | 0.779 (0.827, 0.731) | 0.926 (0.943, 0.910) | 0.781 | – | 0.779 (0.805, 0.753) |
Table 9.
p-values of McNemar test between the single CNN model with the highest value of accuracy (ResNeXt101) and WAV from top2 to top16. WAV: weighted average voting.
Table 9.
p-values of McNemar test between the single CNN model with the highest value of accuracy (ResNeXt101) and WAV from top2 to top16. WAV: weighted average voting.
| p-Value | WAV2 | WAV3 | WAV4 | WAV5 | WAV6 | WAV7 | WAV8 | WAV9 | WAV10 | WAV11 | WAV12 | WAV13 | WAV14 | WAV15 | WAV16 |
|---|
| ResNeXt101 | 0.192 | 0.037 | 0.014 | 0.003 | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 | 0.004 | 0.001 | 0.003 | 0.001 | 0.001 | 0.001 |
Table 10.
Metrics of 4 different liver masses for ResNeXt101, the model with the highest accuracy among 16 CNNs, and WAV7 (top7 was used for weighted average voting), the model with the highest accuracy among all models of ensemble learning. BLT: benign liver tumor, LCY: liver cyst, MLC: metastatic liver cancer, PLC: primary liver cancer.
Table 10.
Metrics of 4 different liver masses for ResNeXt101, the model with the highest accuracy among 16 CNNs, and WAV7 (top7 was used for weighted average voting), the model with the highest accuracy among all models of ensemble learning. BLT: benign liver tumor, LCY: liver cyst, MLC: metastatic liver cancer, PLC: primary liver cancer.
| ResNeXt101 | Precision * | Sensitivity * | Specificity * | F1-Score | ROC AUC |
|---|
| BLT | 0.745 (0.797, 0.685) | 0.688 (0.742, 0.628) | 0.921 (0.900, 0.939) | 0.715 | 0.915 |
| LCY | 0.991 (1.000, 0.979) | 0.904 (0.941, 0.867) | 0.997 (1.000, 0.994) | 0.946 | 0.994 |
| MLC | 0.567 (0.623, 0.510) | 0.664 (0.723, 0.605) | 0.831 (0.858, 0.804) | 0.611 | 0.843 |
| PLC | 0.625 (0.685, 0.565) | 0.620 (0.680, 0.560) | 0.876 (0.900, 0.852) | 0.622 | 0.854 |
| WAV7 | | | | | |
| BLT | 0.775 (0.826, 0.723) | 0.784 (0.835, 0.733) | 0.924 (0.943, 0.905) | 0.779 | 0.944 |
| LCY | 1.000 (1.000, 1.000) | 0.920 (0.954, 0.886) | 1.000 (1.000, 1.000) | 0.958 | 0.999 |
| MLC | 0.664 (0.720, 0.609) | 0.736 (0.791, 0.681) | 0.876 (0.900, 0.852) | 0.698 | 0.891 |
| PLC | 0.721 (0.778, 0.664) | 0.692 (0.749, 0.635) | 0.911 (0.931, 0.890) | 0.706 | 0.903 |