Hydrological and Hydraulic Modeling Applied to Flash Flood Events in a Small Urban Stream
Abstract
1. Introduction
2. Materials and Methods
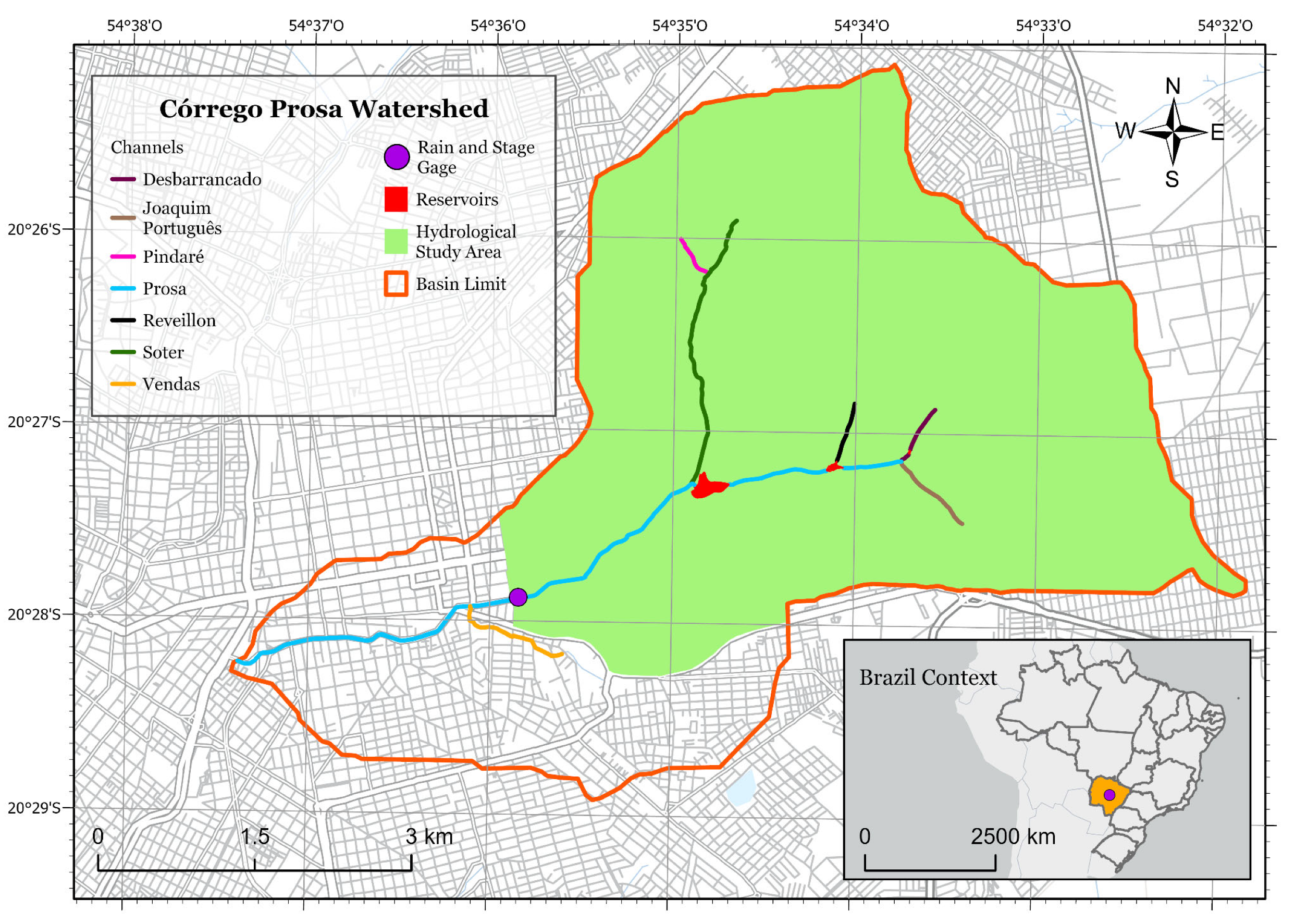
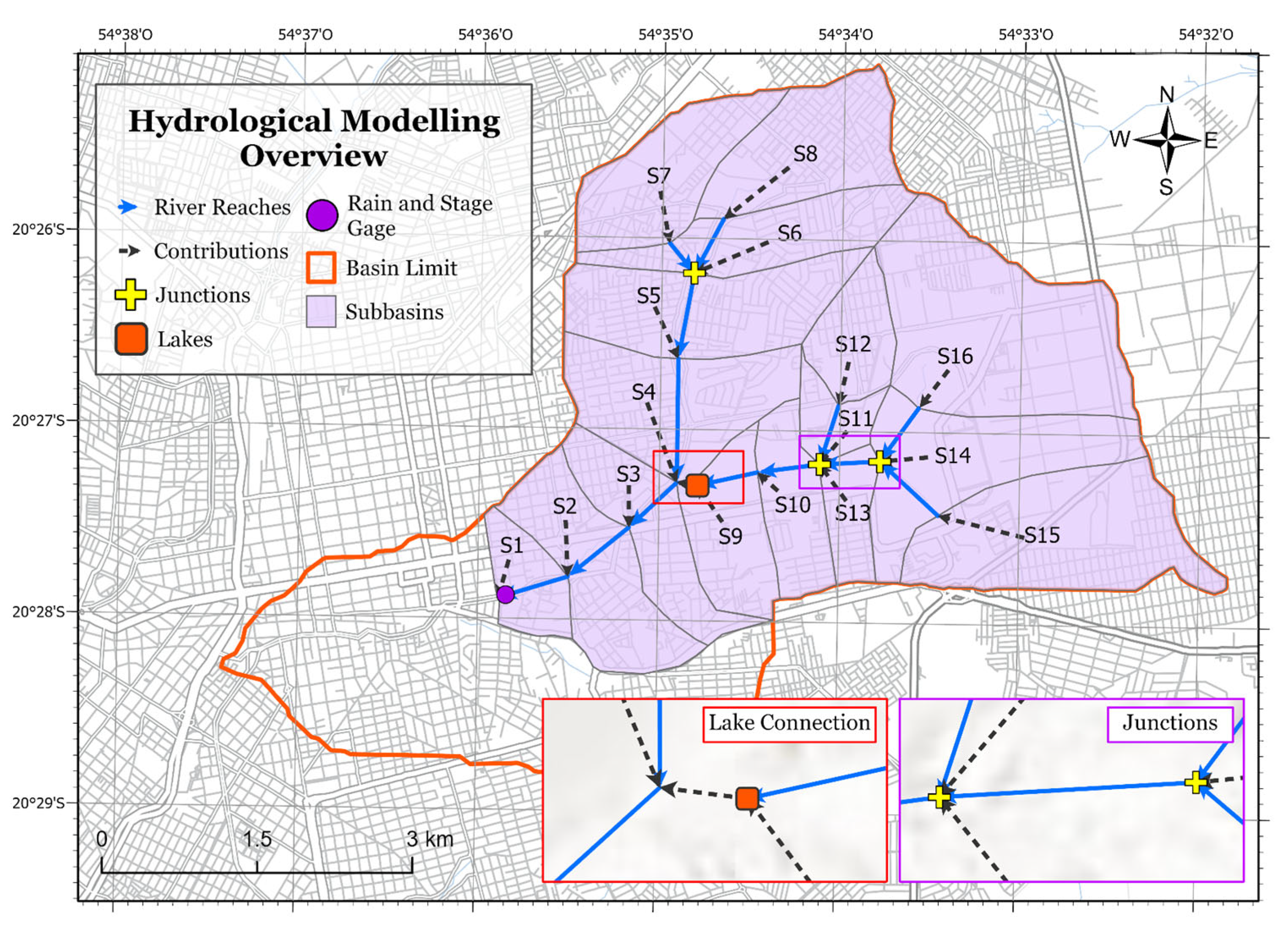
2.1. Study Area
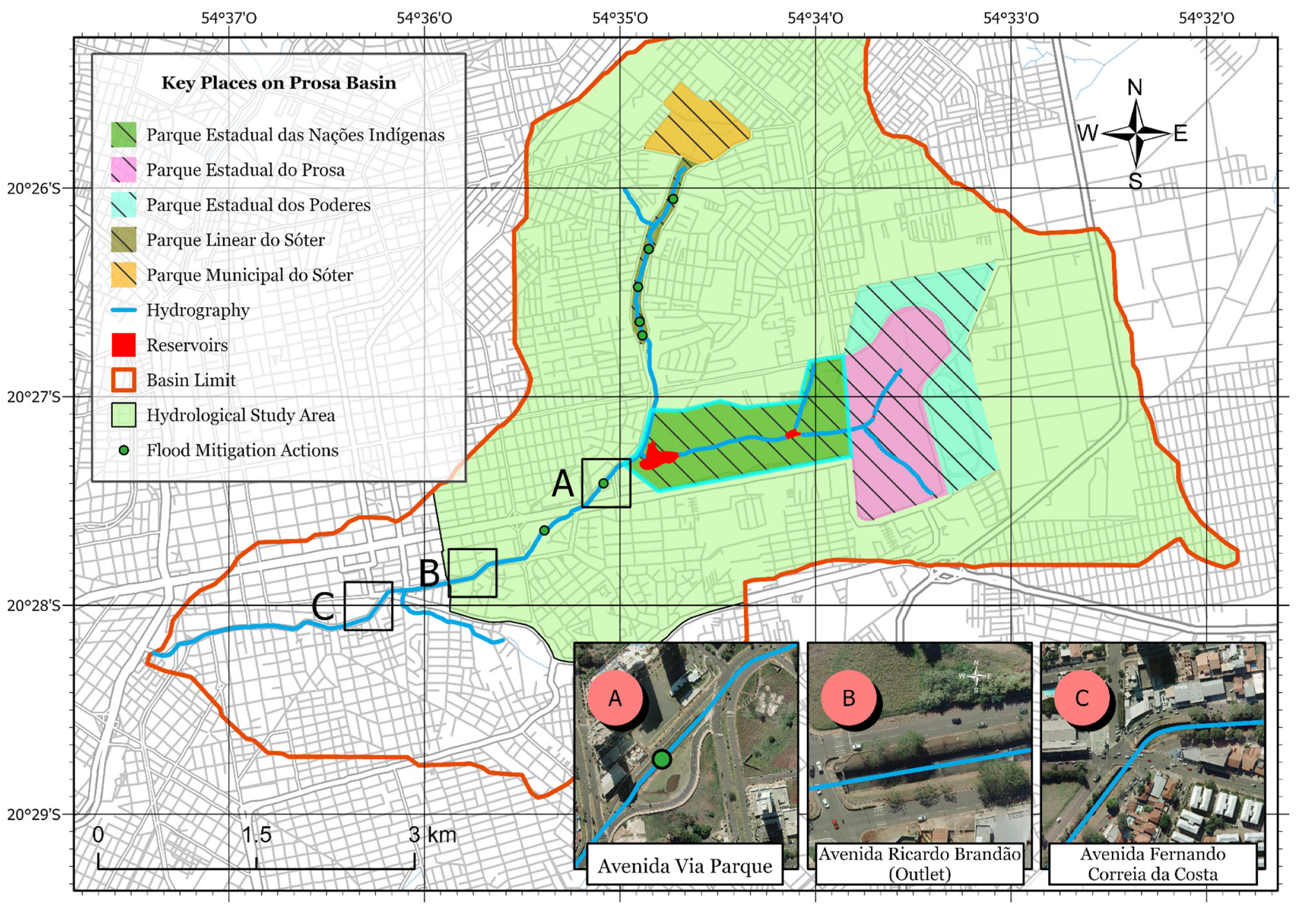
2.2. Flood Problem in Prosa Basin
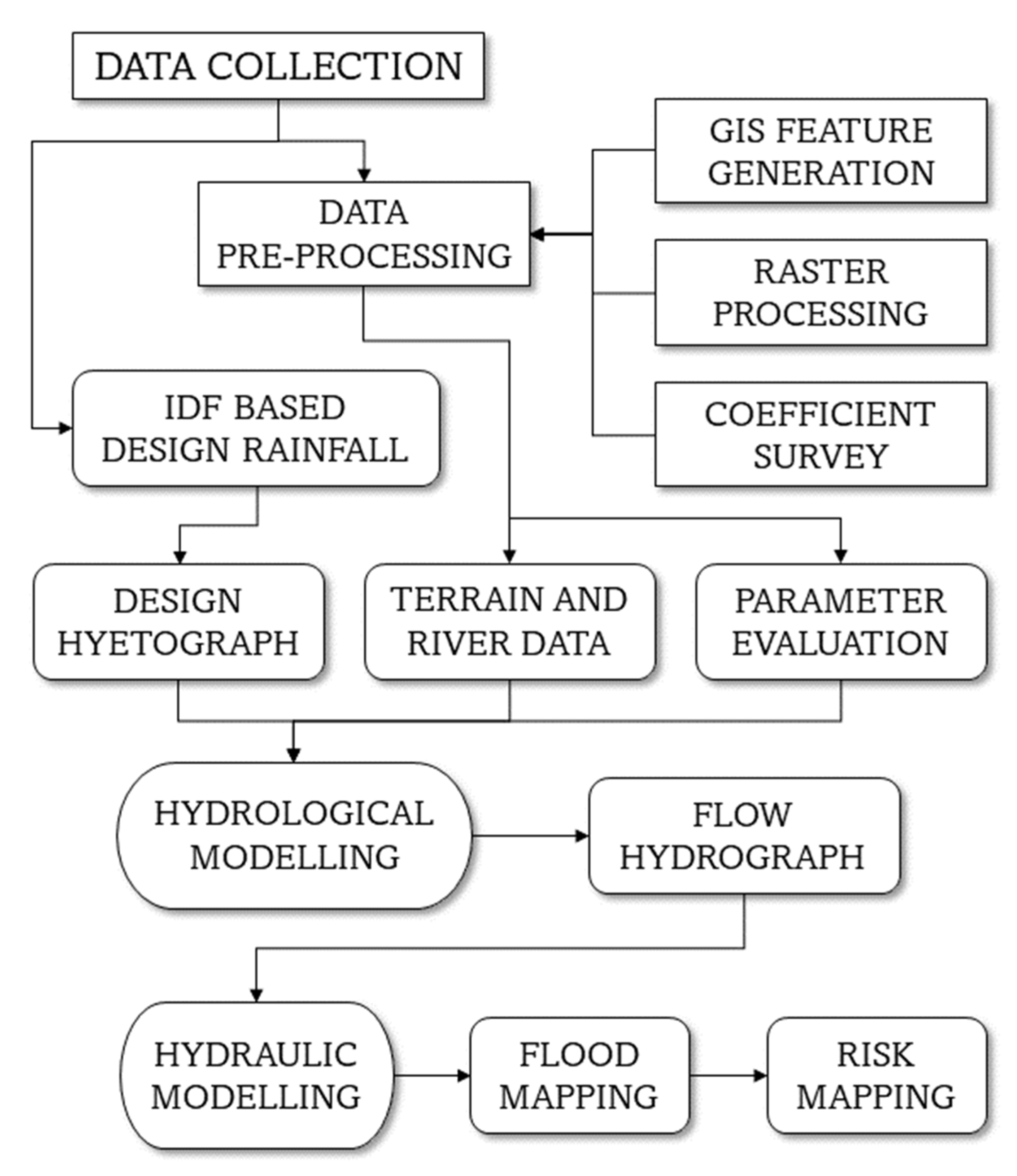
2.3. Study Workflow
2.4. Study Data
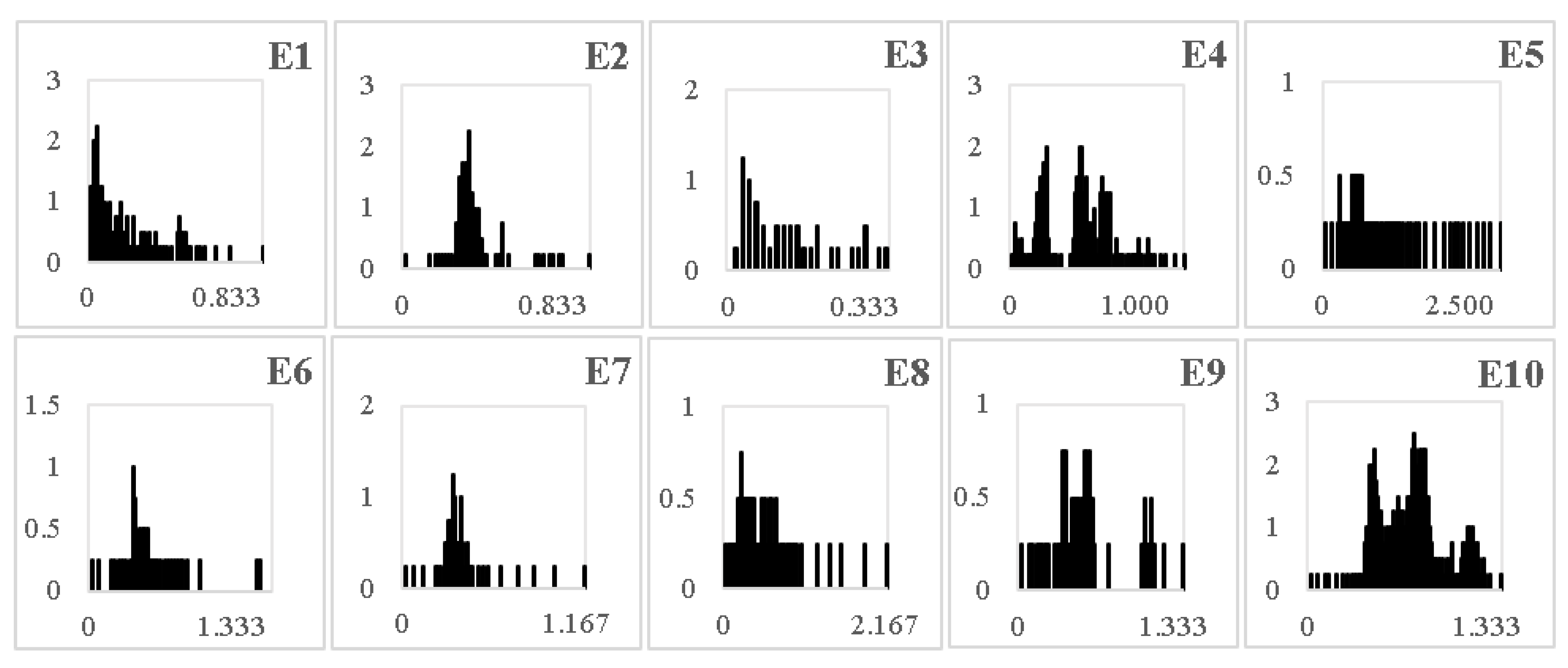
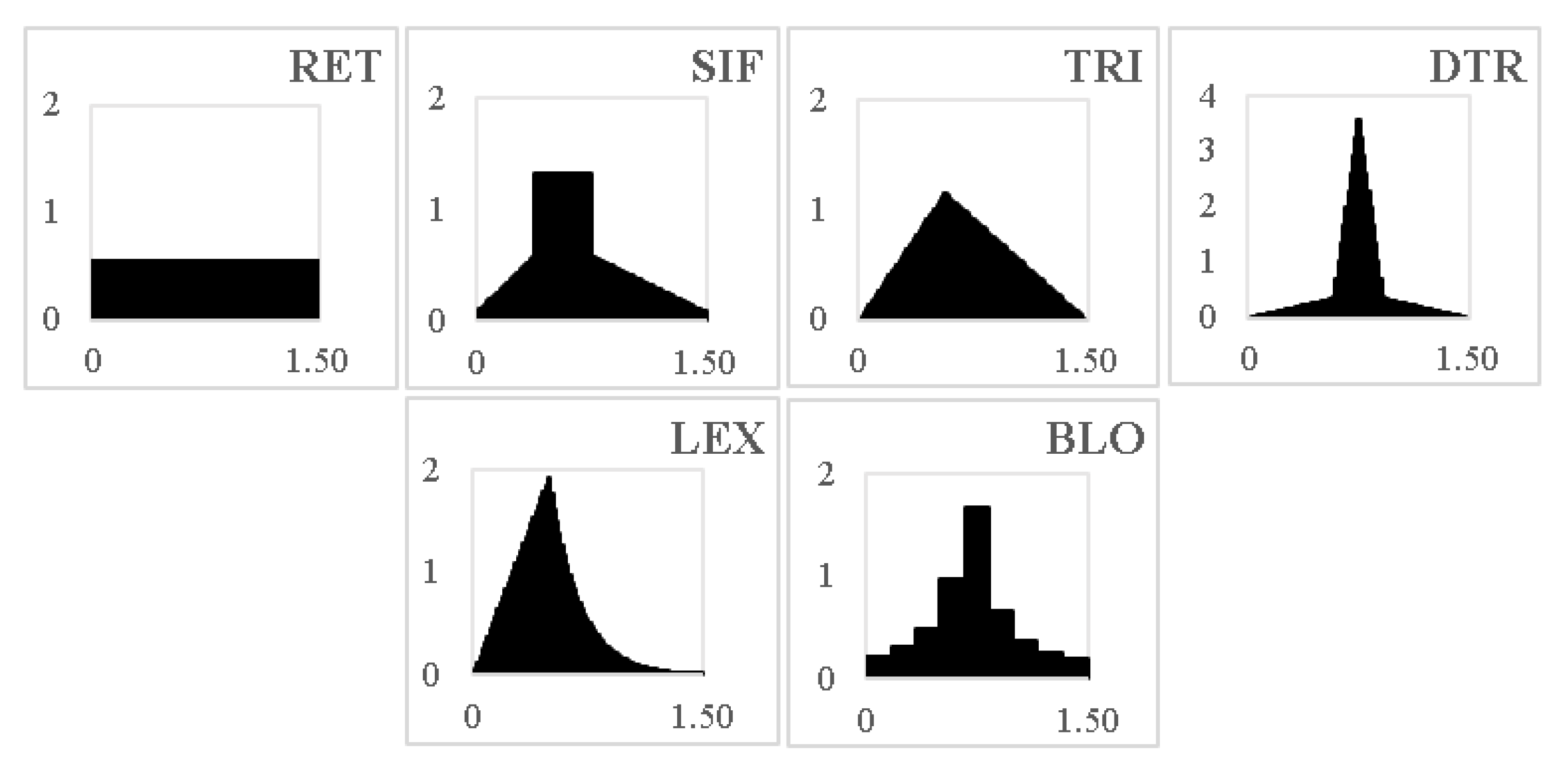
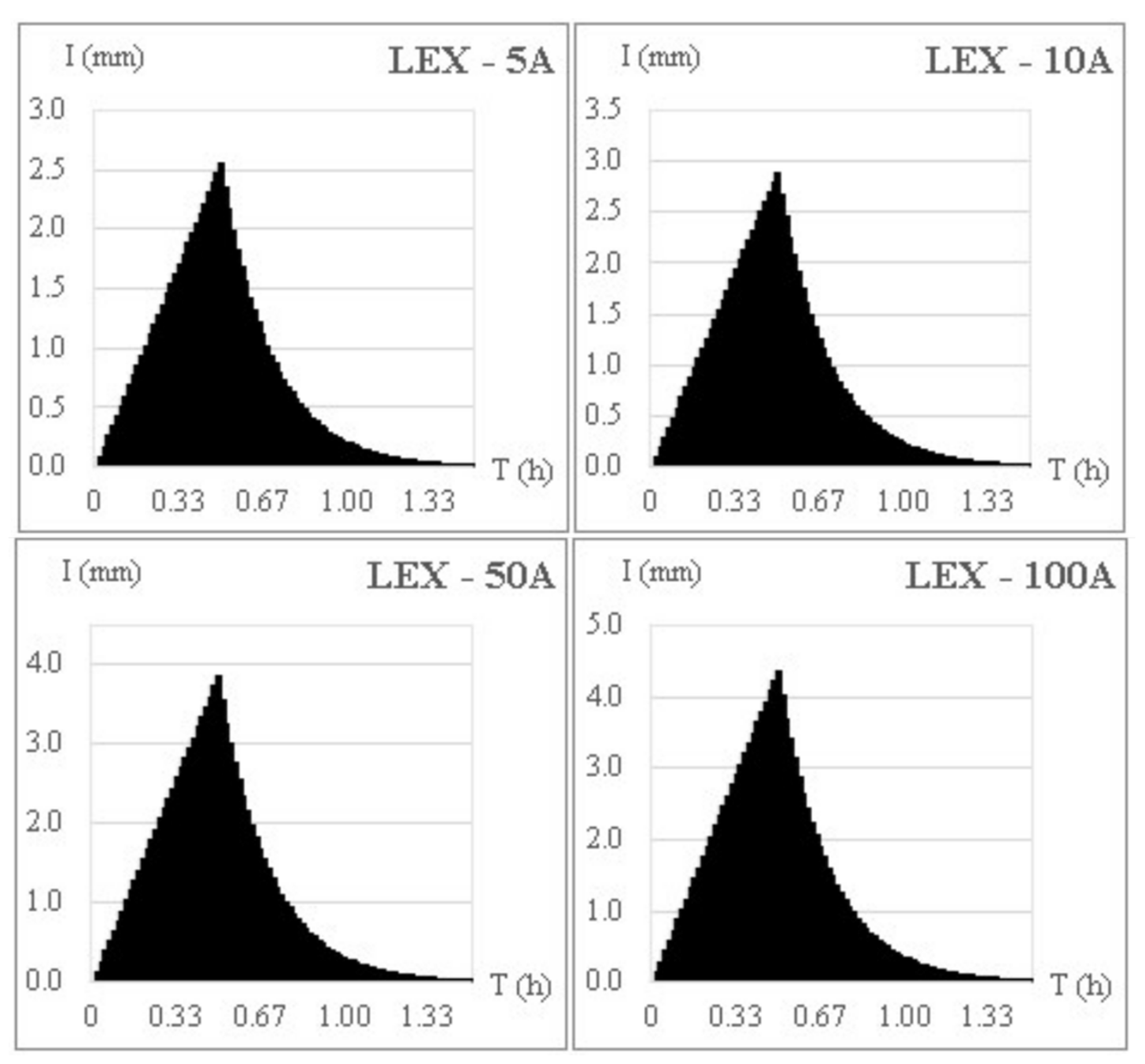
2.5. Design Rainfall
2.6. Hydrological Modelling
2.7. Hydraulic Modelling
- Equation (8): Continuity equation (conservation of mass). This form is under the assumption of fluid incompressibility. In it, t represents time, u,v the Cartesian components of velocity, x,y the Cartesian directions, h is the height of the water column in the plane fraction studied, and q is the term for the flow source [41].
- Equations (9) and (10): Equations of conservation of linear momentum. This form is under the assumption that the dimensions of the scales of the plane are much larger than the vertical, justifying that the vertical forces cut down to hydrostatic pressure. If the fluid density is constant and without the action of other vertical forces on the fluid, we can neglect the velocity and vertical inertial terms of the Navier-Stokes equation, obtaining the described equations. In these, g is the acceleration of gravity, u,v the Cartesian components of velocity, x,y the Cartesian directions, v_xx and v_yy are the coefficients of turbulent viscosity in the x and y directions, c_f is the term for the coefficient of background friction, τ_s is the wind surface shear stress, h is the water depth, and f is the Coriolis force parameter [41].
3. Results
3.1. Design Rainfall
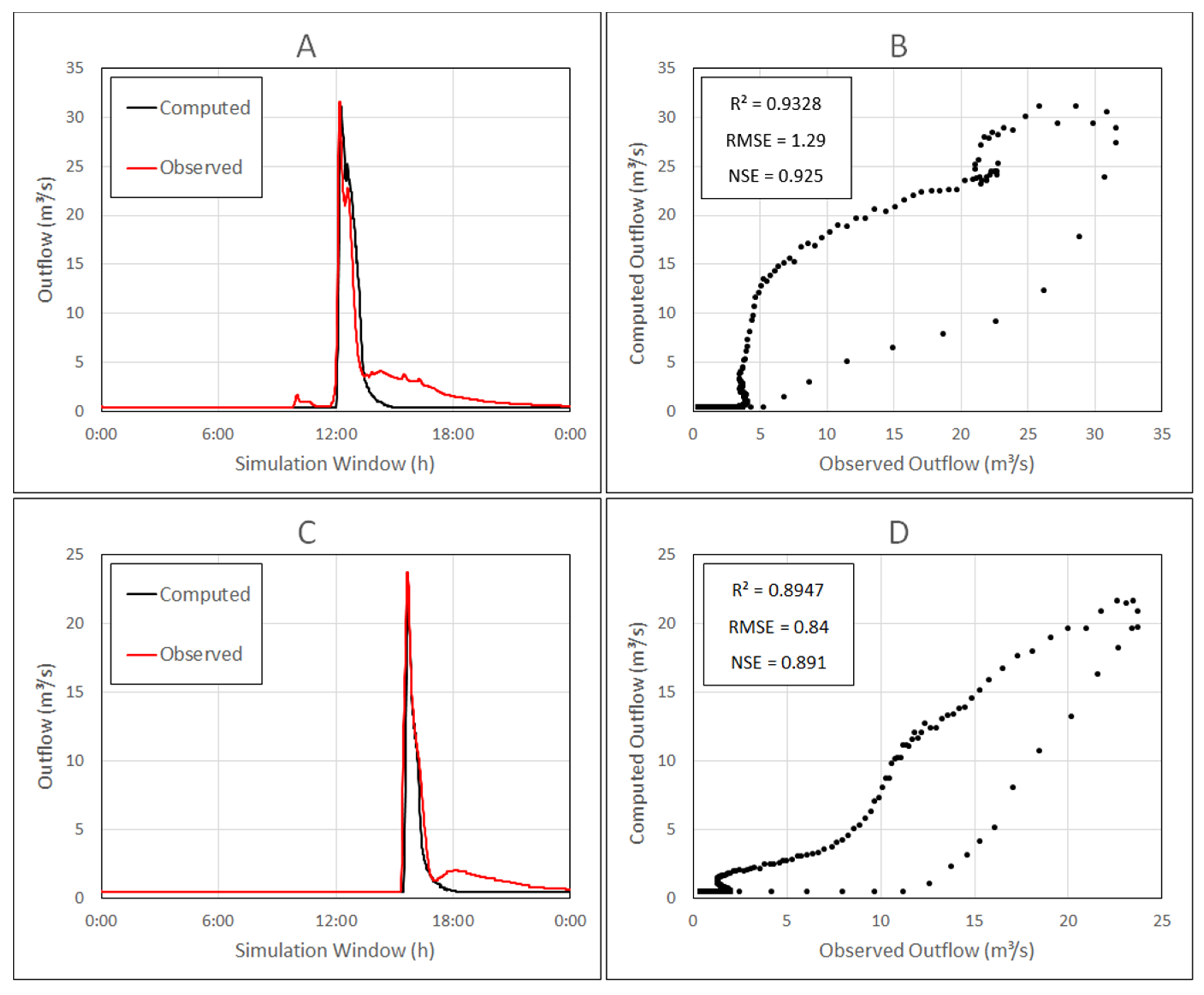
3.2. Rainfall-Runoff Model
3.3. Hydraulic Modelling
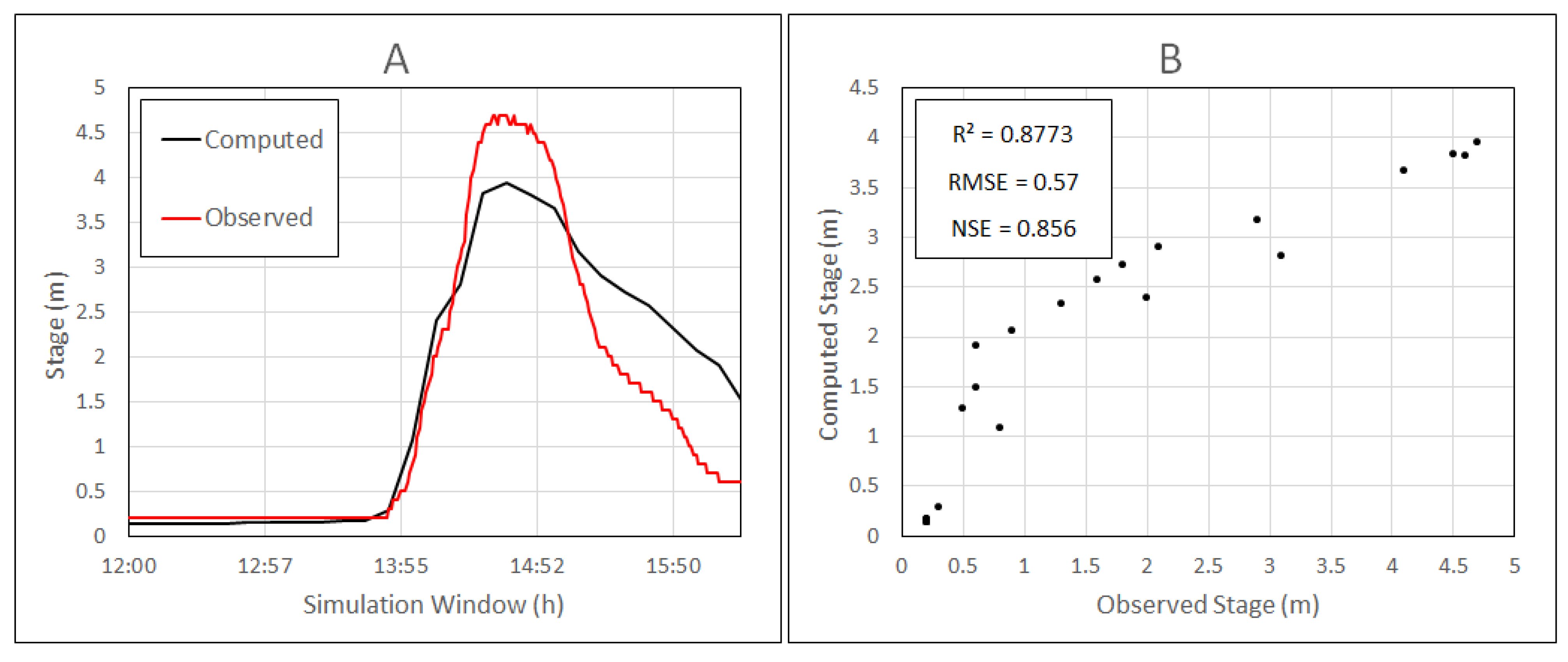
3.3.1. Model Stability
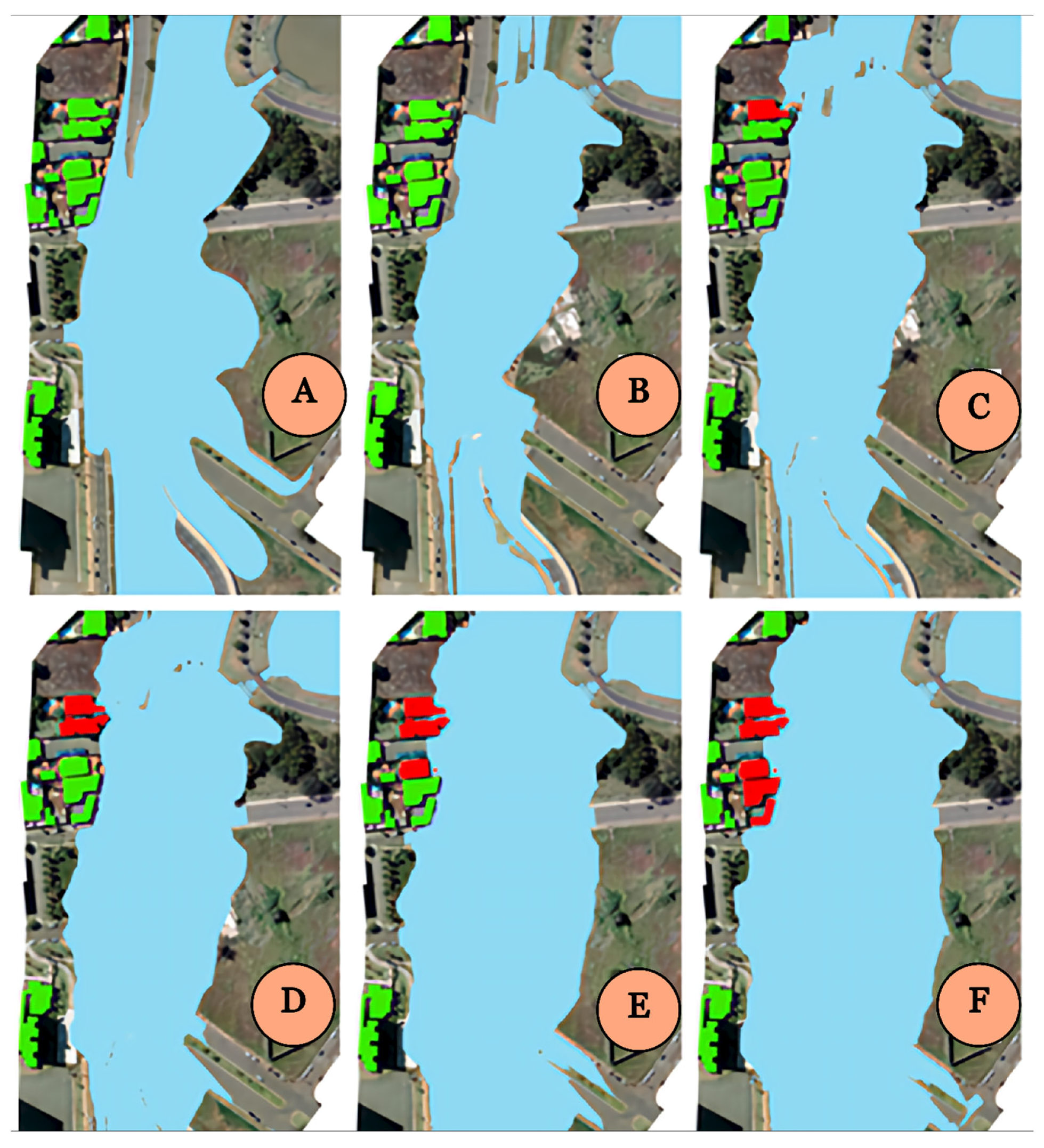
3.3.2. Flood Mapping: Via Parque Avenue
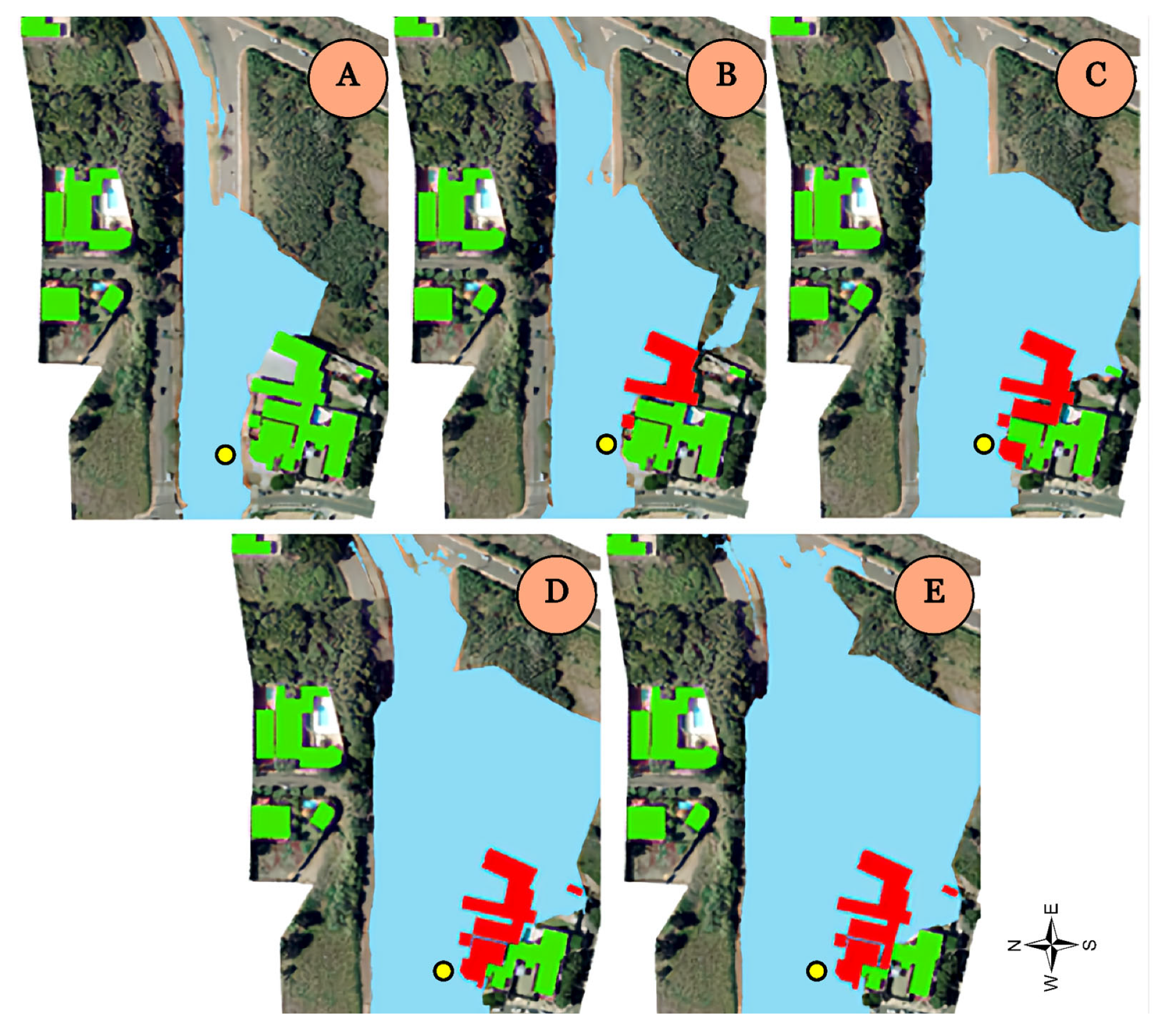
3.3.3. Flood Mapping: Ricardo Brandão Avenue
3.3.4. Flow Velocity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, W.; Sun, Y.; Nijhuis, S.; Wang, Z. Scenario-Based Flood Risk Assessment for Urbanizing Deltas Using Future Land-Use Simulation (FLUS): Guangzhou Metropolitan Area as a Case Study. Sci. Total Environ. 2020, 739, 139899. [Google Scholar] [CrossRef] [PubMed]
- Shao, M.; Zhao, G.; Kao, S.C.; Cuo, L.; Rankin, C.; Gao, H. Quantifying the Effects of Urbanization on Floods in a Changing Environment to Promote Water Security—A Case Study of Two Adjacent Basins in Texas. J. Hydrol. 2020, 589, 125154. [Google Scholar] [CrossRef]
- Pérez-Morales, A.; Gil-Guirado, S.; Olcina-Cantos, J. Housing Bubbles and the Increase of Flood Exposure. Failures in Flood Risk Management on the Spanish South-Eastern Coast (1975–2013). J. Flood Risk Manag. 2018, 11, S302–S313. [Google Scholar] [CrossRef]
- Zhou, Q.; Mikkelsen, P.S.; Halsnæs, K.; Arnbjerg-Nielsen, K. Framework for Economic Pluvial Flood Risk Assessment Considering Climate Change Effects and Adaptation Benefits. J. Hydrol. 2012, 414–415, 539–549. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood Inundation Modelling: A Review of Methods, Recent Advances and Uncertainty Analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Mourato, S.; Fernandez, P.; Marques, F.; Rocha, A.; Pereira, L. An Interactive Web-GIS Fluvial Flood Forecast and Alert System in Operation in Portugal. Int. J. Disaster Risk Reduct. 2021, 58, 102201. [Google Scholar] [CrossRef]
- Pathak, S.; Liu, M.; Jato-Espino, D.; Zevenbergen, C. Social, Economic and Environmental Assessment of Urban Sub-Catchment Flood Risks Using a Multi-Criteria Approach: A Case Study in Mumbai City, India. J. Hydrol. 2020, 591, 125216. [Google Scholar] [CrossRef]
- Elmoustafa, A.M.; Saad, N.Y.; Fattouh, E.M. Defining the Degree of Flood Hazard Using a Hydrodynamic Approach, a Case Study: Wind Turbines Field at West of Suez Gulf. Ain Shams Eng. J. 2020, 11, 741–749. [Google Scholar] [CrossRef]
- Zope, P.E.; Eldho, T.I.; Jothiprakash, V. Impacts of Land Use–Land Cover Change and Urbanization on Flooding: A Case Study of Oshiwara River Basin in Mumbai, India. Catena 2016, 145, 142–154. [Google Scholar] [CrossRef]
- Nithila Devi, N.; Sridharan, B.; Kuiry, S.N. Impact of Urban Sprawl on Future Flooding in Chennai City, India. J. Hydrol. 2019, 574, 486–496. [Google Scholar] [CrossRef]
- Rosas, M.A.; Vanacker, V.; Viveen, W.; Gutierrez, R.R.; Huggel, C. The Potential Impact of Climate Variability on Siltation of Andean Reservoirs. J. Hydrol. 2020, 581, 124396. [Google Scholar] [CrossRef]
- Guo, K.; Guan, M.; Yu, D. Urban Surface Water Flood Modelling-a Comprehensive Review of Current Models and Future Challenges. Hydrol. Earth Syst. Sci. 2021, 25, 2843–2860. [Google Scholar] [CrossRef]
- Merwade, V.; Olivera, F.; Arabi, M.; Edleman, S. Uncertainty in Flood Inundation Mapping: Current Issues and Future Directions. J. Hydrol. Eng. 2008, 13, 608–620. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, B.; Ren, S.; Zhang, R.; Zhang, W.; Ren, J.; Chen, Y. Large-Scale 3D Numerical Modelling of Flood Propagation and Sediment Transport and Operational Strategy in the Three Gorges Reservoir, China. J. Hydro-Environ. Res. 2021, 36, 33–49. [Google Scholar] [CrossRef]
- Gomes Calixto, K.; Wendland, E.C.; Melo, D.d.C.D. Hydrologic Performance Assessment of Regulated and Alternative Strategies for Flood Mitigation: A Case Study in São Paulo, Brazil. Urban Water J. 2020, 17, 481–489. [Google Scholar] [CrossRef]
- dos Santos, M.F.N.; Barbassa, A.P.; Vasconcelos, A.F. Low Impact Development Strategies for a Low-Income Settlement: Balancing Flood Protection and Life Cycle Costs in Brazil. Sustain. Cities Soc. 2021, 65, 102650. [Google Scholar] [CrossRef]
- Zambrano, F.C.; Kobiyama, M.; Pereira, M.A.F.; Michel, G.P.; Fan, F.M. Influence of Different Sources of Topographic Data on Flood Mapping: Urban Area São Vendelino Municipality, Southern Brazil. RBRH 2020, 25. [Google Scholar] [CrossRef]
- Rangari, V.A.; Umamahesh, N.V.; Patel, A.K. Flood-Hazard Risk Classification and Mapping for Urban Catchment under Different Climate Change Scenarios: A Case Study of Hyderabad City. Urban Clim. 2021, 36, 100793. [Google Scholar] [CrossRef]
- Vasconcellos, S.M.; Kobiyama, M.; Dagostin, F.S.; Corseuil, C.W.; Castiglio, V.S. Flood Hazard Mapping in Alluvial Fans with Computational Modeling. Water Resour. Manag. 2021, 35, 1463–1478. [Google Scholar] [CrossRef]
- Speckhann, G.A.; Borges Chaffe, P.L.; Fabris Goerl, R.; de Abreu, J.J.; Altamirano Flores, J.A. Flood Hazard Mapping in Southern Brazil: A Combination of Flow Frequency Analysis and the HAND Model. Hydrol. Sci. J. 2018, 63, 87–100. [Google Scholar] [CrossRef]
- de Arruda Gomes, M.M.; de Melo Verçosa, L.F.; Cirilo, J.A. Hydrologic Models Coupled with 2D Hydrodynamic Model for High-Resolution Urban Flood Simulation. Nat. Hazards 2021, 108, 3121–3157. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Gaigher, C. Com Histórico de Inundações, Campo Grande Registra Problemas Nas Mesmas Regiões Há 10 Anos; G1: Campo Grande, MS, Brazil, 2019. [Google Scholar]
- Oliveira, V. Chuva Forte Alaga Casas No Dalva de Oliveira e Assusta Moradores; Veja Vídeo; Campo Grande News: Campo Grande, MS, Brazil, 2012. [Google Scholar]
- Rodrigues, N.; Vasconcelos, N. Córrego Transborda e Carro Quase é Levado Pela Água Na Ricardo Brandão; Campo Grande News: Campo Grande, MS, Brazil, 2013. [Google Scholar]
- Dias, A.M.; dos Santos, A.; Prado, F. Córrego Prosa Transborda, Alaga Avenidas e Bloqueia Trânsito Da Capital; Campo Grande News: Campo Grande, MS, Brazil, 2014. [Google Scholar]
- Maciulevicius, P. Córrego Prosa Alaga Pontos e Assusta Na Avenida Ricardo Brandão; Campo Grande News: Campo Grande, MS, Brazil, 2015. [Google Scholar]
- Oliveira, V. Chuva Na Madrugada Enche Córregos, Alaga Casas e Causa Destruição; Campo Grande News: Campo Grande, MS, Brazil, 2016. [Google Scholar]
- Frias, S. Temporal Provocou Alagamentos Em Toda a Extensão Do Córrego Prosa; Campo Grande News: Campo Grande, MS, Brazil, 2019. [Google Scholar]
- Mattos, T.S. Improving Urban Flood Resilience; Federal University of Mato Grosso do Sul: Campo Grande, MS, Brazil, 2021. [Google Scholar]
- PMCG–Prefeitura Municipal de Campo Grande. Plano Diretor de Drenagem Urbana–Consolidado; DIOGRANDE—Diário oficial de Campo Grande: Campo Grande, MS, Brazil, 2015. [Google Scholar]
- Balbastre-Soldevila, R.; García-Bartual, R.; Andrés-Doménech, I. A Comparison of Design Storms for Urban Drainage System Applications. Water 2019, 11, 757. [Google Scholar] [CrossRef]
- Na, W.; Yoo, C. Evaluation of Rainfall Temporal Distribution Models with Annual Maximum Rainfall Events in Seoul, Korea. Water 2018, 10, 1468. [Google Scholar] [CrossRef]
- Scharffenberg, W. Hydrologic Modeling System HEC-HMS User’s Manual; USACE—United States Corps of Engineers: Davis, CA, USA, 2016; p. 612.
- Azam, M.; Kim, H.S.; Maeng, S.J. Development of Flood Alert Application in Mushim Stream Watershed Korea. Int. J. Disaster Risk Reduct. 2017, 21, 11–26. [Google Scholar] [CrossRef]
- Bhadoriya, U.P.S.; Mishra, A.; Singh, R.; Chatterjee, C. Implications of Climate Change on Water Storage and Filling Time of a Multipurpose Reservoir in India. J. Hydrol. 2020, 590, 125542. [Google Scholar] [CrossRef]
- Kaffas, K.; Hrissanthou, V.; Sevastas, S. Modeling Hydromorphological Processes in a Mountainous Basin Using a Composite Mathematical Model and ArcSWAT. Catena 2018, 162, 108–129. [Google Scholar] [CrossRef]
- USDA–United States Department of Agriculture. Urban Hydrology for Small Watersheds. In Technical Report 55; NRCS—Natural Resources Conservation Service: Washington, DC, USA, 1986. [Google Scholar]
- Spence, C. On the Relation between Dynamic Storage and Runoff: A Discussion on Thresholds, Efficiency, and Function. Water Resour. Res. 2007, 43, W12416. [Google Scholar] [CrossRef]
- Feldman, A.D. Hydrologic Modeling System HEC-HMS: Technical Reference Manual; USACE—United States Corps of Engineers: Davis, CA, USA, 2000; p. 157.
- Brunner, G.W. HEC RAS: River Analysis System—Hydraulic Reference Manual; USACE—United States Corps of Engineers: Davis, CA, USA, 2020; p. 520.
- Arrighi, C.; Campo, L. Effects of Digital Terrain Model Uncertainties on High-Resolution Urban Flood Damage Assessment. J. Flood Risk Manag. 2019, 12, e12530. [Google Scholar] [CrossRef]
- Yalcin, E. Assessing the Impact of Topography and Land Cover Data Resolutions on Two-Dimensional HEC-RAS Hydrodynamic Model Simulations for Urban Flood Hazard Analysis. Nat. Hazards 2020, 101, 995–1017. [Google Scholar] [CrossRef]
- Brunner, G.W. HEC-RAS River Analysis System User’s Manual; USACE—United States Corps of Engineers: Davis, CA, USA, 2016; p. 962.
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the Calibration of Effective Roughness Parameters in HEC-RAS Using Inundation and Downstream Level Observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Neto, O.C.L.; Neto, A.R.; Alves, F.H.B.; Cirilo, J.A. Sub-Daily Hydrological-Hydrodynamic Simulation in Flash Flood Basins: Una River (Pernambuco/Brazil). Rev. Ambient. Água 2020, 15, 1–13. [Google Scholar] [CrossRef]
- Kreibich, H.; Piroth, K.; Seifert, I.; Maiwald, H.; Kunert, U.; Schwarz, J.; Merz, B.; Thieken, A.H. Is Flow Velocity a Significant Parameter in Flood Damage Modelling? Nat. Hazards Earth Syst. Sci. 2009, 9, 1679–1692. [Google Scholar] [CrossRef]
- Lakzian, E.; Saghi, H.; Kooshki, O. Numerical Simulation of Sediment Deposition and Trapping Efficiency Estimation in Settling Basins, Considering Secondary Flows. Int. J. Sediment Res. 2020, 35, 347–354. [Google Scholar] [CrossRef]


| ID | Data | Duration (h) | Total Rainfall (mm) | Peak (mm/h) | Peak Time (h) | Relative Peak | Centroid (h) | Relative Centroid |
|---|---|---|---|---|---|---|---|---|
| 1 | 17 April 2015 | 1.050 | 24.500 | 2.25 | 0.050 | 0.048 | 0.25833 | 0.24603 |
| 2 | 27 May 2015 | 1.033 | 17.750 | 2.25 | 0.367 | 0.355 | 0.42171 | 0.40811 |
| 3 | 9 November 2015 | 0.383 | 9.000 | 1.25 | 0.033 | 0.087 | 0.15694 | 0.40942 |
| 4 | 5 December 2015 | 1.383 | 42.000 | 2 | 0.283 | 0.205 | 0.55863 | 0.40383 |
| 5 | 25 December 2015 | 3.217 | 20.500 | 0.5 | 0.567 | 0.176 | 1.03110 | 0.32055 |
| 6 | 6 January 2016 | 1.700 | 11.250 | 1 | 0.400 | 0.235 | 0.56222 | 0.33072 |
| 7 | 6 January 2016 | 1.217 | 11.000 | 1.25 | 0.333 | 0.274 | 0.41288 | 0.33926 |
| 8 | 8 January 2016 | 2.183 | 18.500 | 0.75 | 0.233 | 0.107 | 0.53401 | 0.24458 |
| 9 | 15 February 2016 | 1.417 | 16.000 | 0.75 | 0.583 | 0.412 | 0.55052 | 0.38860 |
| 10 | 2 March 2016 | 1.433 | 63.000 | 2.5 | 0.783 | 0.547 | 0.76786 | 0.53571 |
| Mean | 1.450 | 0.363 | 0.244 | 0.525 | 0.363 |
| Hydrological | ||||||
|---|---|---|---|---|---|---|
| Sub-Basin | Loss | Transform | Baseflow | |||
| C.N. | % Paved | Concentration Time (h) | Storage Coefficient | Limit Flow (m3·s−1) | K | |
| S1 | 81 | 21.086 | 0.89278 | 1.8437 | 0.02 | 0.85 |
| S2 | 71 | 19.752 | 1.3428 | 1.7359 | 0.02 | 0.85 |
| S3 | 70 | 7.417 | 1.0096 | 1.6599 | 0.02 | 0.85 |
| S4 | 62 | 33.443 | 0.95144 | 2.344 | 0.03 | 0.85 |
| S5 | 72 | 35.126 | 0.28813 | 2.325 | 0.1 | 0.85 |
| S6 | 47 | 22.833 | 0.72277 | 2.3528 | 0.03 | 0.85 |
| S7 | 58 | 33.229 | 0.30685 | 2.285 | 0.1 | 0.85 |
| S8 | 51 | 29.68 | 0.30513 | 2.2645 | 0.1 | 0.85 |
| S9 | 81 | 46.385 | 0.66934 | 0.0911 | 0.01 | 0.85 |
| S10 | 82 | 46.347 | 0.69225 | 0.09159 | 0.01 | 0.85 |
| S11 | 80 | 48.626 | 0.7246 | 0.10687 | 0.01 | 0.85 |
| S12 | 77 | 53.114 | 0.2 | 0.1 | 0 | 0.85 |
| S13 | 74 | 49.814 | 0.22 | 0.1 | 0 | 0.85 |
| S14 | 69 | 54.649 | 0.09 | 0.1 | 0 | 0.85 |
| S15 | 67 | 52.564 | 0.08 | 0.1 | 0 | 0.85 |
| S16 | 72 | 49.825 | 0.09 | 0.1 | 0 | 0.85 |
| Routing | |||
|---|---|---|---|
| Reach | Channel (Manning’s ‘n’) | ||
| Left ‘n’ | Center ‘n’ | Right ‘n’ | |
| D1 | 0.1 | 0.048 | 0.1 |
| JP1 | 0.1 | 0.048 | 0.1 |
| P6 | 0.065 | 0.2 | 0.065 |
| R1 | 0.08 | 0.048 | 0.08 |
| P5 | 0.055 | 0.04 | 0.055 |
| P4 | 0.055 | 0.04 | 0.055 |
| ST3 | 0.06 | 0.045 | 0.06 |
| PD1 | 0.055 | 0.04 | 0.054 |
| ST2 | 0.055 | 0.04 | 0.055 |
| ST1 | 0.035 | 0.02 | 0.035 |
| P3 | 0.035 | 0.015 | 0.035 |
| P2 | 0.05 | 0.04 | 0.05 |
| P1 | 0.02 | 0.015 | 0.02 |
| Variable | Value | Unity | Observation |
|---|---|---|---|
| 2D Cells Count | 110,252 | - | Squared shape |
| Cell Area (mean) | 7.88 | m2 | Variable |
| Time Step | 1 | seg | It can be split up to 4 times (0.25 s) or doubled up to 3 times (8 s), based on Courant condition |
| Weighting Factor Θ | 1 | - | Ref. [45] found no significant advantages in adopting values below 1. |
| Mapping Interval | 5 | min | - |
| Hydrograph Interval | 5 | min | - |
| Maximum Number of Iterations | 40 | - | - |
| Water Elevation Error | 0.003 | m | - |
| Solver | Pardiso | - | All CPUs. |
| Function | Rel. Peak | Rel. Centroid | Rel. Peak Time | Δ Rel. Centroid | Δ Rel. Peak Time | Δ Rel. Peak |
|---|---|---|---|---|---|---|
| Rectangular | 0.3001 | 0.4944 | 0.5000 | 36.33% | −79.30% | 104.52% |
| Sifalda | 0.6902 | 0.4502 | 0.3750 | 24.12% | −52.40% | 53.39% |
| Triangular | 0.6002 | 0.4500 | 0.3750 | 24.08% | −58.61% | 53.39% |
| Double Triangle | 1.8560 | 0.4944 | 0.5000 | 36.33% | 28.00% | 104.52% |
| Linear Exponential | 1.0033 | 0.3230 | 0.3333 | −10.94% | −30.81% | 36.35% |
| Alternated Blocks | 0.8788 | 0.4736 | 0.4889 | 30.57% | −39.39% | 99.98% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruno, L.S.; Mattos, T.S.; Oliveira, P.T.S.; Almagro, A.; Rodrigues, D.B.B. Hydrological and Hydraulic Modeling Applied to Flash Flood Events in a Small Urban Stream. Hydrology 2022, 9, 223. https://doi.org/10.3390/hydrology9120223
Bruno LS, Mattos TS, Oliveira PTS, Almagro A, Rodrigues DBB. Hydrological and Hydraulic Modeling Applied to Flash Flood Events in a Small Urban Stream. Hydrology. 2022; 9(12):223. https://doi.org/10.3390/hydrology9120223
Chicago/Turabian StyleBruno, Leonardo Souza, Tiago Souza Mattos, Paulo Tarso Sanches Oliveira, André Almagro, and Dulce Buchala Bicca Rodrigues. 2022. "Hydrological and Hydraulic Modeling Applied to Flash Flood Events in a Small Urban Stream" Hydrology 9, no. 12: 223. https://doi.org/10.3390/hydrology9120223
APA StyleBruno, L. S., Mattos, T. S., Oliveira, P. T. S., Almagro, A., & Rodrigues, D. B. B. (2022). Hydrological and Hydraulic Modeling Applied to Flash Flood Events in a Small Urban Stream. Hydrology, 9(12), 223. https://doi.org/10.3390/hydrology9120223






