Next Article in Journal
Impact of Climate Change on the Hydrology of the Upper Awash River Basin, Ethiopia
Next Article in Special Issue
Impacts of Climate Change and Variability on Precipitation and Maximum Flows in Devil’s Creek, Tacna, Peru
Previous Article in Journal
Russian Rivers Streamflow Forecasting Using Hydrograph Extrapolation Method
Previous Article in Special Issue
Improving Operational Short- to Medium-Range (SR2MR) Streamflow Forecasts in the Upper Zambezi Basin and Its Sub-Basins Using Variational Ensemble Forecasting
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Hydrology
Volume 9
Issue 1
10.3390/hydrology9010002
hydrology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Spatiotemporal Trend Analysis of Temperature and Rainfall over Ziway Lake Basin, Ethiopia

by
Aster Tesfaye Hordofa
1,2,*,
Olkeba Tolessa Leta
3,
Tane Alamirew
4 and
Abebe Demissie Chukalla
5
1
Africa Centre of Excellence for Water Management, Addis Ababa University, Addis Ababa 1176, Ethiopia
2
Faculty of Water Resources and Irrigation Engineering, Arba Minch University Water Technology Institute (AWTI), Arba Minch 4400, Ethiopia
3
Bureau of Watershed Management and Modeling, St. Johns River Water Management District, 4049 Reid Street, Palatka, FL 32177, USA
4
Ethiopian Institute of Water Resources, Addis Ababa University, Addis Ababa 1176, Ethiopia
5
The Department of Land and Water Management, IHE Delft Institute for Water Education, 2611 AX Delft, The Netherlands
*
Author to whom correspondence should be addressed.
Hydrology 2022, 9(1), 2; https://doi.org/10.3390/hydrology9010002
Submission received: 3 November 2021 / Revised: 6 December 2021 / Accepted: 16 December 2021 / Published: 22 December 2021
(This article belongs to the Special Issue Advances in Flow Modeling for Water Resources and Hydrological Engineering)
Browse Figures
Versions Notes

Abstract

:
Rainfall and temperature trends detection is vital for water resources management and decision support systems in agro-hydrology. This study assessed the historical (1983–2005) and future (2026–2100) rainfall, maximum temperature (Tmax), and minimum temperature (Tmin) trends of the Ziway Lake Basin (Ethiopia). The daily observed rainfall and temperature data at eleven stations were obtained from the National Meteorological Agency (NMA) of Ethiopia, while simulated historical and future climate data were obtained from the Coupled Model Intercomparison Project 5 (CMIP5) datasets under Representative Concentration Pathways (RCP) of 4.5 and 8.5. The CMIP5 datasets were statistically downscaled by using the climate model data for hydrologic modeling (CMhyd) tool and bias corrected using the distribution mapping method available in the CMhyd tool. The performance of simulated rainfall, Tmax, and Tmin of the CMIP5 models were statistically evaluated using observation datasets at eleven stations. The results showed that the selected CMIP5 models can reasonably simulate the monthly rainfall, Tmax, and Tmin at the majority of the stations. Modified Mann–Kendall trend test were applied to estimate the trends of annual rainfall, Tmax, and Tmin in the historical and future periods. We found that rainfall experienced no clear trends, while Tmax, and Tmin showed consistently significant increasing trends under both RCP 4.5 and 8.5 scenarios. However, the warming is expected to be greater under RCP 8.5 than RCP 4.5 by the end of the 21st century, resulting in an increasing trend of Tmax and Tmin at all stations. The greatest warming occurred in the central part of the basin, with statistically significant increases largely seen by the end of the 21st century, which is expected to exacerbate the evapotranspiration demand of the area that could negatively affect the freshwater availability within the basin. This study increases our understanding of historic trends and projected future change effects on rainfall- and evapotranspiration-related climate variables, which can be used to inform adaptive water resource management strategies.

1. Introduction

Climate change may have significant consequences on temperature and rainfall patterns, which are the most vital climatic elements used in the decision-making process for integrated water resources management [1,2]. For example, integrated water resources management models utilize temperature and rainfall as important input data for assessing freshwater availability [3]. The evidence of rapid global climate change includes an overall increase in temperature and decrease in rainfall that could result in declining freshwater availability [4,5,6], shrinking ice sheets, and rising sea level, among others [7,8]. Climate change impacts are more prominent in the African continent, especially countries that are predominantly dependent on a rain-fed agricultural system [9]. For example, several studies on temperature and rainfall changes have shown that most African countries have experienced warmer temperatures by more than 1 °C, frequent heat waves, and an increase in the number of hot days since 1901 [10]. In addition, both seasonal and annual rainfall conditions of the African countries are highly variable [11,12].
Ethiopia, located in the eastern part of the African horn, strongly depends on rain-fed agriculture that in turn contributes a large portion to the country’s economy. However, due to climate change and limited water resources availability, the country’s rain-fed and irrigated agricultural productivities are probably at risk, leading to negative consequences on food security [13,14]. This is projected to be accelerated in the future, as reported in many studies [15,16,17,18].
The Central Rift Valley (CRV) Lakes Basin of Ethiopia, located in the eastern part of the country, has experienced considerable seasonal and annual rainfall variability, with a prominent increase in temperature [19]. Some studies have already documented the hydroclimate conditions and climate change impacts in the CRV, including partially in the Ziway Basin (Meki and Katar sub-basins, the two major sub-basins draining into the Ziway Lake) [20,21]. For example, Musie et al. [21] have reported climate variability has negatively impacted the monthly streamflow of the Ziway Lake Basin (ZLB). Abraham et al. [20] indicated future annual decrement in runoff depth from the Katar and Maki rivers. They also documented that reduction in runoff has been caused by decrease in rainfall and increase in temperature. Furthermore, other studies found that an annual decline in Ziway Lake water level is due to a decrease in runoff from both the Katar and Meki rivers, including increase in evapotranspiration from the basin [20,21]. These studies show that water resources of the ZLB are highly exposed to a rapidly changing global climate [22]. The changes in rainfall and temperature in particular are important drivers affecting the runoff and evapotranspiration and thus the lake water level [23]. A good description and understanding of rainfall and temperature trends is thus crucial for many studies related to irrigation (agriculture), climatology, and hydrology. Long-term trend analyses in rainfall and temperature are also important for rain-fed and irrigated agricultural areas, particularly for the ZLB, which is dominated by agricultural land [24]. It has been reported that both rainfall and temperature can impact water availability (Ziway Lake water level), irrigation water demand, water use efficiency, and productivity of the ZLB [25,26,27,28].
Previous studies have documented hydrological responses of the ZLB to climate change with some studies based on only the historical period [21] and others based on projected areal rainfall and temperature over the large area [20]. While the previous studies focused on impact of climate change on hydrological responses of the basin [20,21,24], rainfall and temperature trends of the basin have not been analyzed in-depth. Therefore, in-depth characterization, understanding, and trend analysis of rainfall and temperature both spatially and temporally are a vital procedure in assessing climate change impacts on freshwater resources availability, irrigation water uses, and water resources planning [29,30,31,32,33,34,35,36]. This study conducted detailed rainfall and temperature trends analysis at spatial and temporal explicit scale, which is important for the ZLB with its significant topography and experiences with climate variations. The current study also introduced climate model selection criteria relevant to the case study that includes availability of the most commonly used RCP 4.5 and 8.5 scenarios, availability of high spatial resolution and ensemble models, and recommendations from the past studies [37,38]. The study further evaluated the performance of the selected climate models and identified the best performing models for the study area.
The primary aim of this study was to analyze the spatial pattern and temporal trends in annual rainfall and temperature for historical (1983–2005) and future (2026–2100) periods. The future period was split into near-term (2026–2049), middle-term (2050–2072), and far-term (2073–2100) time series. The study utilized rainfall, maximum temperature (Tmax), and minimum temperature (Tmin) from eleven stations together with Coupled Model Intercomparison Project 5 (CMIP5) under two representative concentration pathways (RCP 4.5 and RCP 8.5). In this study, we first selected some CMIP5 models based on the abovementioned selection criteria and downscaled and bias corrected the climate variables of the selected CMIP5 models. We then evaluated the performance of the CMIP5 models’ data against observations at eleven stations that are spatially fairly distributed over the ZLB. Finally, we analyzed the annual trends of historical and future temperature and rainfall datasets.

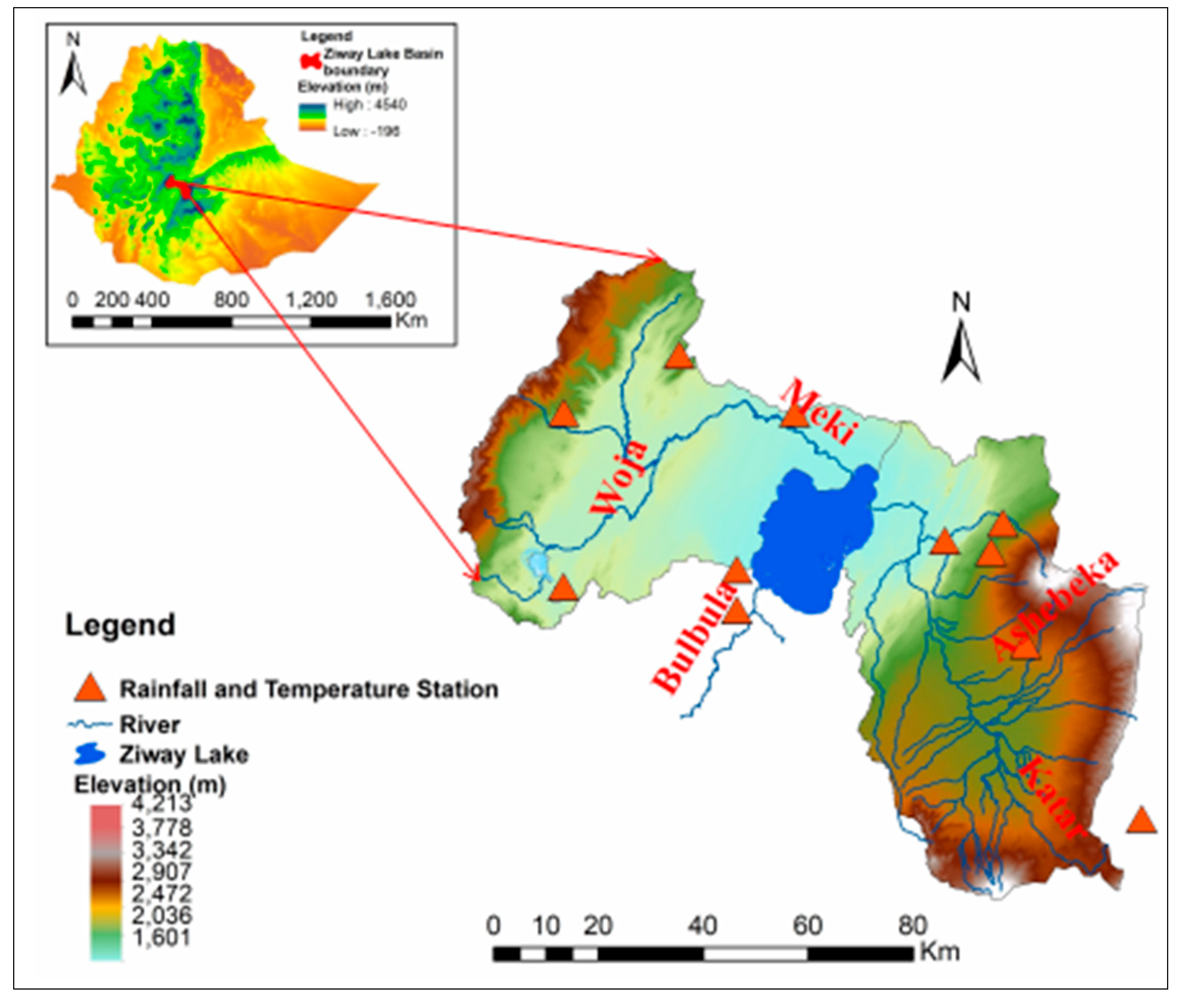
2. Study Area Description

The Ziway Lake Basin (ZLB) is located within 38°00′–39°30′ East and 7°00′–8°30′ North in the Adami Tullu–Jiddo Kombolcha Woreda of the East Shewa Zone, Oromia region, Ethiopia. The basin is about 150 km south of the capital city, Addis Ababa. The town of Ziway (recently named Batu) is situated on the lake’s western shore. The altitude of Ziway Lake is approximately 1636 m above mean sea level (amsl), and has a maximum water depth of 4 m, a total basin drainage area of about 7300 km2 (Figure 1), and a lake volume of 1.5 million cubic meters [29]. Most of the basin is characterized by low to moderately undulating topography but bounded by a steep slope and abrupt faults in the eastern and southeastern escarpments, ranging from 4200 to 1600 m (Figure 1). ZLB experiences a monsoon agro-climate and has a tropical climate with no uniform spatial and temporal climatic conditions. The rainfall patterns are generally affected by the annual oscillation of the intertropical convergence zone that forms a wet summer from June to September [30]. The mean annual rainfall of the basin spatially varies from 417 to 1012 mm, with a noticeable temporal variation at a monthly time scale. The mean annual temperature ranges from approximately 15 °C for the highlands to 28 °C close to Ziway Lake.

3. Data and Methods

3.1. Observed Data

Daily maximum and minimum temperature (Tmax and Tmin) and rainfall (RF) data of the gauged stations, which were used for historical and future climate downscaling and bias correction, were obtained from the National Meteorological Agency (NMA) of Ethiopia. The dataset was obtained from eleven climate stations distributed over the Ziway Lake Basin for the period from 1983 to 2005.

3.2. Historical and Future Climate Data

We accessed the CMPI5 model data through the four Earth System Gird Federation (ESGF) gateways that manage, analyze, and distribute the model output and observation data [31]. At the time of this study, the CMIP5 version is the most up-to-date set of widely used climate models [31]. In addition, compared to CMIP3, the updated CMIP5 models produce higher resolution projections and use an updated set of greenhouse gas emission scenarios [32]. Among the four representative concentration pathways (RCPs), this study selected the two most commonly used emission scenarios of the future climate, RCP 4.5 and RCP 8.5, which are, respectively, an intermediate and a very high greenhouse gas (GHG) emission [32] scenario. We obtained the CMIP5 (RCP 4.5 and RCP 8.5) data from https://esgf-node.llnl.gov/search/cmip5/ (accessed from 10 January 2021 to 18 January 2021). The CMIP5 output provides global climate metadata that stores the data in the form of network command data form (NetCDF).

3.3. CMIP5 Selection Criteria

A range of Global Climate Models (GCMs) are available to access the future minimum and maximum temperature and rainfall data [33,34,35,36]. Three criteria were set to select suitable GCMs that capture climate of the stations in the study area [33]. The criteria are RCP 4.5 and 8.5 scenario availability, model resolutions and ensemble, and past studies in the study area [21,37,38]. Based on these criteria, three CMIP5 GCMs were selected and their corresponding output data, such as rainfall, maximum temperature (Tmax), and minimum temperature (Tmin) were downloaded under the two RCP 4.5 and RCP 8.5 scenarios. Table 1 summarizes the characteristics of the selected GCM.

3.4. Data Extraction, Downscaling, and Bias Correction

Downscaling the GCM–CMIP5 outputs to finer spatial resolutions is necessary for a reliable assessment of the regional impact of climate change on rainfall and temperature. The statistical downscaling method, which is the most widely used due to its quick and effective assessments of local climate change impacts [39,40], is applied to downscale and generate GCM-CMIP5 data (rainfall and temperature) at individual stations. We extracted the large-scale climate variables obtained from CMPI5 model for historical, RCP 4.5 and 8.5 scenarios and downscaled using the climate model data for hydrologic modeling (CMhyd) tool [41]. We made a bias correction of the rainfall and temperature data using the distribution mapping method, which is recommended in the previous studies, and also available in the CMhyd software [38]. We used the eleven stations’ observed temperature and rainfall data for the bias correction and downscaling of the climate data from the three selected GCM–CMIP5 models (Table 1).

3.5. Climate Models Performance Evaluation

We evaluated the performance of the downscaled and bias-corrected CMIP5 models over the Ziway Lake Basin using monthly observations of rainfall, minimum temperature, and maximum temperature from 1983 to 2005 at eleven stations. We applied three statistical evaluation metrics that include percent bias (PBIAS), root mean square error (RMSE), and correlation coefficient (r) [42].

3.6. Rainfall and Temperature Trend Analysis

3.6.1. Mann–Kendall Test

The foremost measures of time series data including climate change are trend analysis, which identifies the general increasing or decreasing tendencies of the climate variables [43]. There are two main standard types of trend analysis: nonparametric and parametric methods. Parametric analysis is the most preferred method, but it is applicable for stationarity and normally distributed and serial-independent data, which is not possible in most hydroclimatological time series records [44]. In contrast, the nonparametric trend test requires time series data that are independent and less sensitive to outliers [45]. In this study, we used the nonparametric methods of Mann–Kendall (MK) to detect the rainfall and temperature trends for both historical and future periods: historical (1985–2005), near-term (2026–2049), middle-term (2050–2072), and far-term (2073–2100) time series. Because of its reliability for detecting monotonic trends in climate time series data, the nonparametric method of MK has been widely applied to discovering trends in hydrometeorological time series [45,46,47,48].
For comparison purpose, we also produced the spatial distribution maps for both mean annual temperature (Tmax and Tmin) and rainfall. For this, we used the known-distance-based interpolation method called inverse distance weighting [49]. Then, we applied ArcGIS technique to generate maps showing the spatial distribution for rainfall and temperature (Tmax and Tmin) over the ZLB.

3.6.2. Modified Mann–Kendall Test

The Mann–Kendall trend (MK) test is a nonparametric test used to reliably estimate trends of time series data. The original Mann–Kendall trend test does not consider serial correlation and seasonality effect [48]. In the actual world, the time series data are autocorrelated and this autocorrelation produces a misconception of trend test results [50,51]. To solve this problem, researchers and scholars proposed the modified Mann–Kendall tests, such as the Hamed and Rao modified MK Test [51], Yue and Wang modified MK Test [45], and modified MK test using the whitening method [52]. The modified MK (MMK) test, as proposed by Hamed and Rao [51] considers all the significant autocorrelation coefficients in a time series. Consequently, in this study, we used the widely applied MMK method [51]. We identified the trends of the selected variables (Tmax, Tmin, and rainfall) using the MMK and the Sen’s slope test for annual time scales. We performed the analyses using the Python package called PyMannKendall in Jupyter Notebook [53]. The presence of a statistically significant trend is determined using the MK value. This statistic is used to test the null hypothesis of no trend exists against the alternative hypothesis that a trend does exist. A positive MK value indicates an increasing trend in the time series, while a negative MK value indicates a decreasing trend. The MMK trend test uses a two-tailed test method for evaluating and determining trend significance by simultaneously running three confidence intervals (90%, 95%, and 99%) [54].

4. Results and Discussion

4.1. Performance Evaluation of CMIP5 Models

The three CMIP5 models (CNMR-CM5, MIP-ESM, and CSIRO-MK3.6) show a positive correlation coefficient for monthly observed rainfall with r values ranging from 0.4 to 1 at the eleven stations (Table A1, Appendix A). The CNMR-CM5 model showed the highest r-value of 1 at three stations (Kulumsa, Meraro, and Sagure) and a medium r-value of 0.6 at Bui station, suggesting higher (medium) agreements with the observed dataset. On average, the spatial correlation coefficients of the selected models range from 0.5 to 0.73. The results suggest that from the three models, the CNRM-CM5 model showed relatively a good agreement with the observed data at all stations (0.73). This may be due to its high horizontal spatial resolution compared to the other models, including its resolution improvements that increased both in the atmosphere (from 2.8° to 1.4°) and in the ocean (from 2° to 1°) [55,56,57].
All models showed good performance in simulating the monthly Tmax with r values ranging from 0.5 to 0.7, which indicates acceptable agreement against the observed data (Table A2, Appendix A). In addition, all models showed lower magnitude of RMSE (0.3 to 1.6 °C), indicating the simulated monthly Tmax values have good agreement with the observed monthly Tmax values of the eleven stations in the basin. The PBIAS values are in the range −15.5% to 40.1% for Tmax, which indicates that the selected models showed both underestimation and overestimation of the observed Tmax values.
Similar to Tmax, r values of the three models for the Tmin range from 0.5 to 0.7, while the RMSE values range from 0.8 to 1.6 °C (Table A3, Appendix A). This indicates that the monthly simulated Tmin values by the three climate models reasonably represented the observed Tmin values at all stations. The values of PBIAS are in the range −10.8% to 37.3% for Tmin, confirming the selected models both underestimated and overestimated Tmin at different stations. Overall, the selected CMIP5 models can reasonably simulate the monthly rainfall and temperature (Tmax and Tmin) at the majority of the eleven stations (see Table A1, Table A2 and Table A3, Appendix A).

4.2. Historical Annual Rainfall and Temperature Trends

4.2.1. Temporal Trends of Annual Historical Rainfall and Temperature

The modified Mann–Kendall trend test and Sen’s slope estimators for historical annual rainfall are presented in Table 2. The table shows increasing trends in rainfall for some stations while the other stations show decreasing trends under certain conditions of the three selected climate models (CNMR-CM5, CSIRO-MK3.6, and MIP-ESM-LR). The results generally indicate insignificant increasing or decreasing trends at almost all stations and for all the three models, which in turn highlights that rainfall trends varied spatially over the study area. However, a significant increasing trend in annual rainfall is shown at Arata, at 5% significance level for CNRM-CM5 model output.
Table A4 in Appendix A summarizes the modified Mann–Kendall test results for Tmax. The table clearly indicates that historical (model simulated) Tmax data have experienced statistically significant upward trends.
Table A5 of Appendix A summarizes the modified Mann–Kendall trend test results for Tmin. Similar to Tmax, the table indicates that historical (simulated) Tmin data have also experienced statistically significant upward trends. Results show that there are significant warming trends for annual Tmax and Tmin from 1983 to 2005 for all stations at different significance levels (see Table A4 and Table A5, Appendix A). Overall, both stations and GCM-CMIP5 datasets showed similar upward slopes, highlighting the suitability of downscaled Tmax and Tmin data for trend analysis.

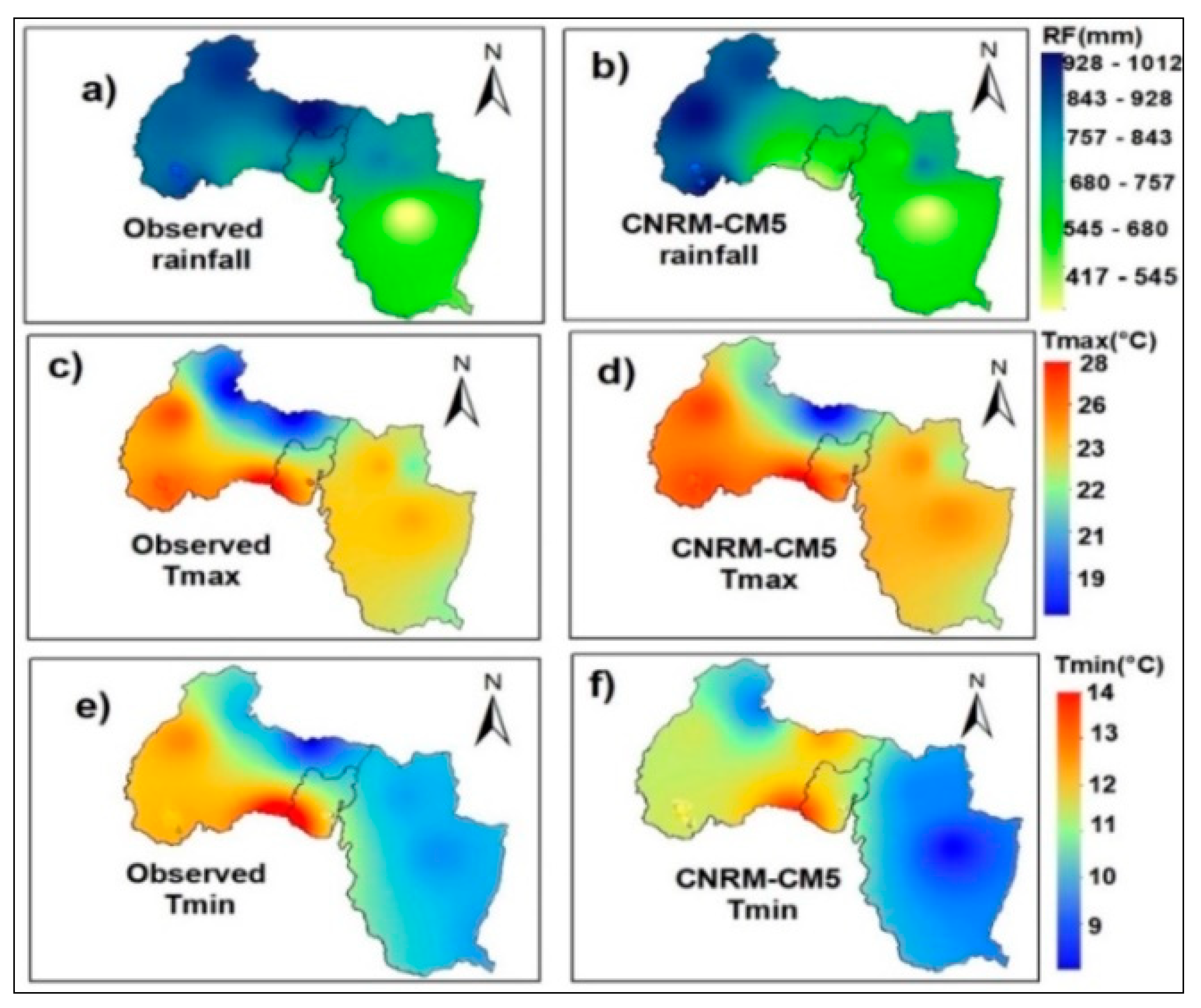
4.2.2. Spatial Distribution of Historical Mean Annual Rainfall and Temperature

Although this study conducted historical spatial trend analysis for the three selected GCM-CMIP5 models, we only present graphical results for CNMR-CM5 model that showed the best performance with observed data as compared to the other models. However, the statistical performance of the other models is summarized in Appendix A. The spatial distribution of mean annual rainfall and temperature over the Ziway Lake Basin for the period 1983 to 2005 are shown in Figure 2 for both observed (stations) and historical (GCM-CMIP5 simulated) data. The spatial distribution of stations (observed) and historical (simulated) mean annual rainfall and temperature over ZLB showed similar patterns. Figure 2a clearly shows that the western part of Ziway Lake Basin (in the part of Meki River) had received more rainfall than the eastern part of the Basin (in the part of Katar River), which is consistent with model simulation outputs (Figure 2b).
Figure 2 also shows the spatial distribution of mean annual Tmax and Tmin over ZLB for the period from 1983 to 2005. Both observed and simulated temperatures over the study area indicated similar spatial distribution; Tmax ranges from 28 to 19 °C (Figure 2c,d) and Tmin ranges from 14 to 9 °C (Figure 2e,f).

4.3. Future Annual Rainfall and Temperature Trends

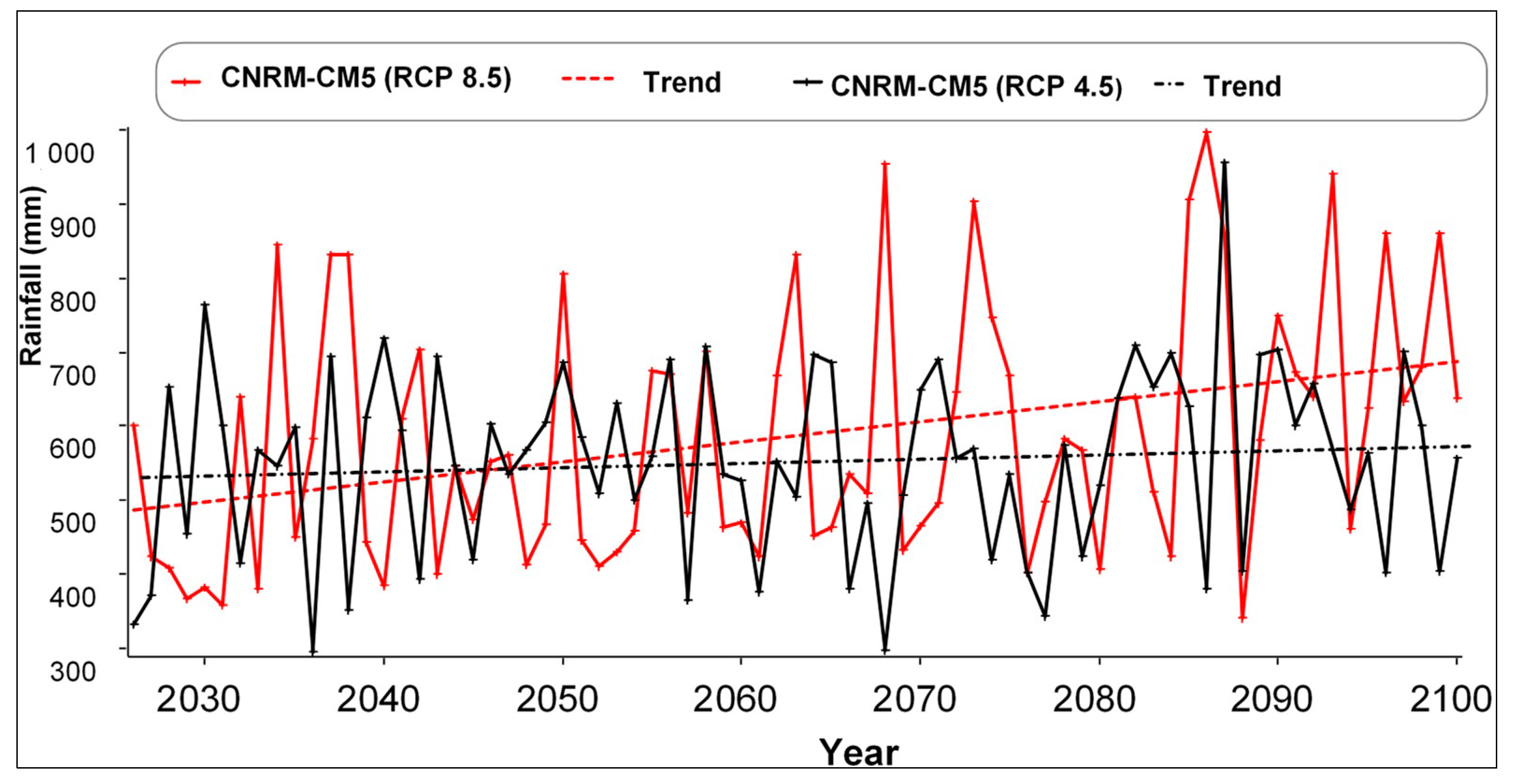
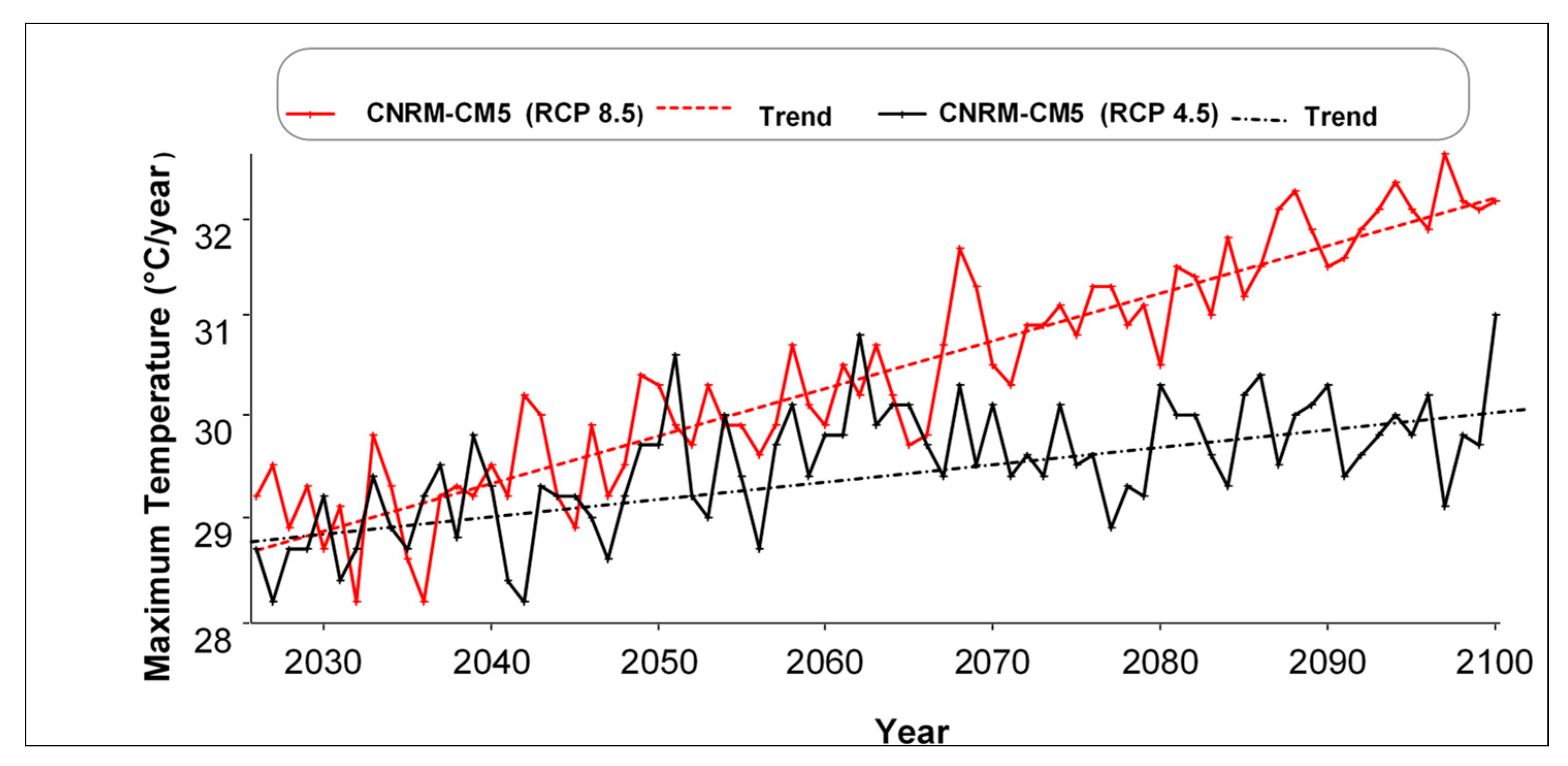
4.3.1. Temporal Trends of Annual Future Rainfall and Temperature

Annual Rainfall Trend

Table 3 shows the rainfall trend analysis for the future period (2026–2049) under RCP 4.5 and RCP 8.5 scenarios. The annual average rainfall showed nonsignificant decreasing trends under the RCP 4.5 emission scenario at most of the stations. However, under the RCP 8.5 emission scenario, annual rainfall data showed insignificant increasing or decreasing trends except at Meki and Arata stations, which showed significantly increasing trends at 5% significance level.
During the mid-term period (2050–2072), the annual rainfall is expected to show increasing trends at Bui and Tora stations at the 5% significance level under the RCP 8.5 scenario for the CNRM-CM5 model, including the Ziway station under the MIP-ESM-LR model (Table A6, Appendix A). Significant increasing trends are also projected at Arata, Meki, and Ziway stations under the RCP 4.5 for the CSIRO-MK3.6 model. During the far-term period (2073–2100), the annual rainfall under the RCP 8.5 scenario is projected to have insignificant positive trends for all models (Table A7). In general, the projected rainfall showed insignificant increase and decrease trends during the entire 21st century under both RCP 4.5 and RCP 8.5 (Figure 3).
The Intergovernmental Panel on Climate Change (IPCC) [58] reported frequent and intensive occurrence of extreme events such as droughts, under both RCP 4.5 and RCP 8.5. For example, IPCC [58] forecasted (with 66% certainty) that droughts will become more frequent, longer, and intensive by the end of the twenty-first century due to an overall decrease in rainfall amounts and increase in temperature. However, our findings indicate that the general trend in rainfall is unpredictable for the Ziway Lake Basin (ZLB), which may cause an increase or decrease in water availability that could potentially affect the farming practices in the ZLB. The results of prior studies on hydrological responses to climate change also illustrated fluctuation in rainfall [20,21]. Such trends are expected to affect the agricultural production and irrigation water requirements in the basin [59,60,61].

Annual Future Maximum Temperature (Tmax) and Minimum Temperature (Tmin) Trends

Table 4 presents the near-term (2026–2049) Tmax Mann–Kendall trend analysis for the three selected models (CNRM-CM, CSIRO-MK3.6. and MIP-ESM-LR) for both RCP 4.5 and RCP 8.5 scenarios. Maximum temperature showed significantly increasing trends at 0.1%, 1%, and 5% significance levels under both RCP 4.5 and 8.5 scenarios. However, each model indicated a slightly different increasing level of maximum temperature.
As shown in Table A8, regardless of the applied scenarios, the mid-term (2050–2072) maximum temperature is expected to be higher than the near-term (2026–2049). In addition, as it should be expected, the RCP 8.5 scenario is projected to cause more warming than the RCP 4.5 scenario by the end of this century (Figure 4). We noticed a significant increasing trend of 0.02 to 0.03 °C/year using the CNRM-CM5 model. The CSIRO-MK3.6 model showed a larger significant increasing rate of 0.08 to 0.09 °C/year within the basin (Table A9).
Overall, the annual maximum temperature at the eleven stations of the basin is generally projected to increase at an increasing rate (Figure 4). More importantly, the RCP 8.5 scenario is expected to cause a higher increase in maximum temperature as compared to the RCP 4.5 scenario (Figure 4). This could be due to a continuous increase in radiative forcing emissions under the RCP 8.5 scenario [45].
Similar to the maximum temperature, the minimum temperature is expected to increase at increasing rate at all stations for both RCP 4.5 and 8.5 scenarios (Table A10, Table A11 and Table A12, Appendix A). As compared to the RCP 4.5 scenario, the RCP 8.5 scenario is predicted to cause more warming by the end of the 21st century. For example, the majority of the stations showed a significant annual minimum temperature change of 0.1 degree by the end of this century under RCP 8.5 and CSIROM-MK3.6 model (Table A12).
In general, irrespective of the two RCP 4.5 and 8.5 scenarios, the future annual mean temperatures (Tmax and Tmin) have shown increasing trends relative to the historical trends. This indicates a warmer temperature in the near-, mid-, and far-terms [62]. In addition, RCP 8.5 is predicted to cause a larger increase in temperature than that of RCP 4.5 at all stations, especially by the end of the 21st century. This is consistent with the conclusions drawn by the IPCC Fifth Assessment Report (AR5) [62], which indicates an increase in evapotranspiration within the area and crop water demand [63,64]. Additionally, the increase in an increasing rate of future temperature will likely lead to a negative effect on freshwater availability, crop production, and the phenological days for crops [13,14,65,66].

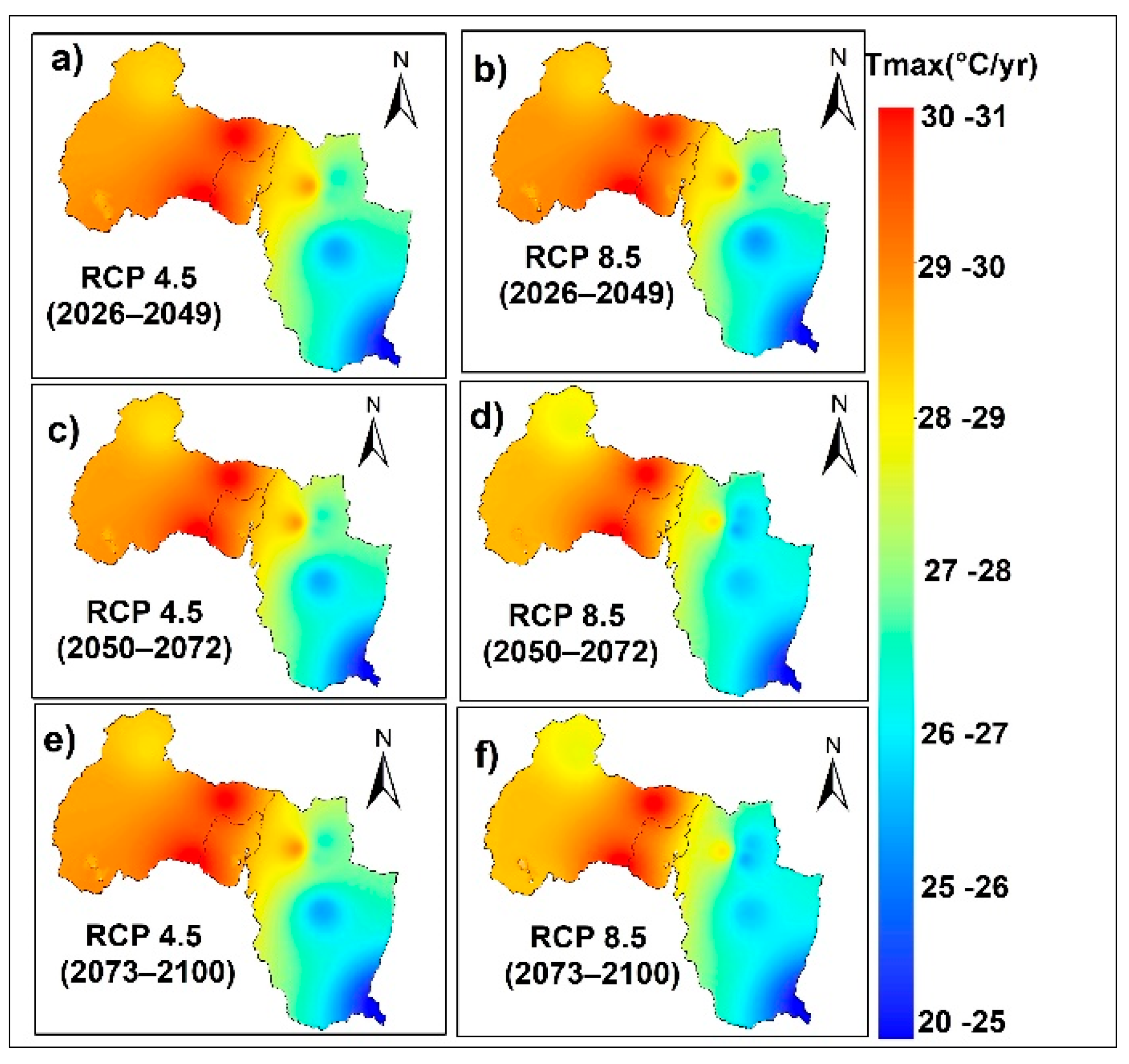
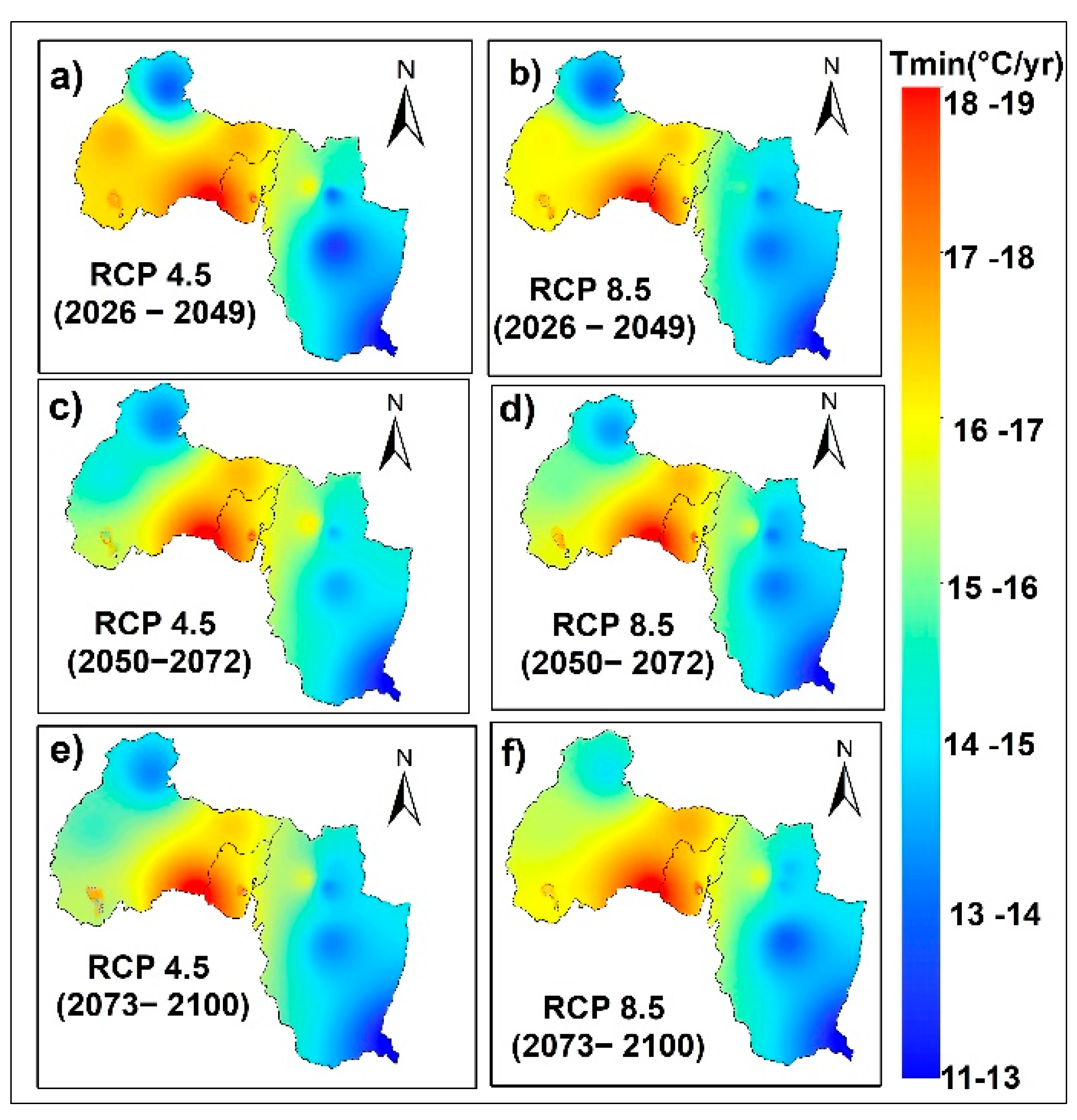
4.3.2. Spatial Distribution of Future Mean Annual Rainfall and Temperature

Figure 5 shows the spatial distribution of projected mean annual rainfall using the CNRM-CM5 model under both RCP 4.5 and 8.5 scenarios within the ZLB. The figure depicts a slight difference in rainfall distribution when compared to the spatial distribution of historical rainfall (see Figure 2). The future rainfall projections indicate wetter conditions over the basin under both RCP 4.5 and 8.5 scenarios except during the near-term of RCP 4.5 and mid-term of RCP 8.5 scenario (Figure 5a,d), which exhibit lower annual rainfall related to the other periods.
The rainfall pattern is unevenly distributed. The distribution showed lower values of rainfall corresponding to the lower elevation (in the central part of the basin) and higher values corresponding to the higher elevations, particularly, in the southern part. The average rainfall depth at each gauge station during the analyzed period of 2026–2049, 2050–2072, and 2073–2100 under both scenarios exhibit different distribution, which may be due to change in climatic conditions and topographic and physiographic factors.
The rainfall pattern shows a slight decrease within the major parts of the basin (west, north, and east) under both RCP 4.5 and 8.5 scenarios of the near-term (Figure 5a) and mid-term (Figure 5d), respectively. The eastern and central parts of the ZLB are expected to receive lower rainfall values as compared with the western part of the basin (Figure 5). Overall, as compared to the RCP 4.5 scenario, the RCP 8.5 scenario is expected to cause a larger decrease in rainfall amounts by the end of the 21st century (Figure 5f).
The spatial distributions of projected mean annual Tmax and Tmin of CNRM-CM5 for the two RCP (4.5 and 8.5) scenarios are shown in Figure 6 and Figure 7, respectively. The future minimum and maximum temperatures appear to have similar spatial distribution with the historical (1983–2005) temperature (see Figure 2). However, relative to the historical values, both the future Tmax and Tmin values are predicted to be noticeably increasing over the basin under both RCP 4.5 and 8.5 scenarios.
The central part of the basin will experience higher Tmax and Tmin values that range from 20 to 31 °C (Figure 6) and 11 to 19 °C (Figure 7), respectively. Apart from the western (in the part of Meki River) and central (around Ziway Lake), some small portions of the eastern part (in the part of Katar River) are expected to experience a cooler temperature.

5. Conclusions

Understanding spatial and temporal trends in annual rainfall and temperature is of interest in a basin’s water resource management and decision-making processes. Such studies are more important in basins where agricultural development is strongly dependent on rain-fed agriculture and irrigation, such as the Ziway Lake Basin (ZLB), Ethiopia. This study analyzed the historical (1983 to 2005) and future (2026–2100) trends of annual rainfall, minimum temperature (Tmin), and maximum temperature (Tmax) for the ZLB under RCP 4.5 and RCP 8.5 scenarios.
The results in this study revealed that the climate models reproduced well the spatial and temporal patterns of the annual mean rainfall and temperature of the study area.
The annual rainfall at the eleven stations of the ZLB showed both negative and positive insignificant trend. As the agriculture system of the basin highly depends on rain-fed agriculture and extensive irrigation, future climate change may have negative implications on the freshwater availability and agricultural productivity of the basin. We found that annual Tmax and Tmin of the ZLB are projected to increase at an increasing rate for both RCP 4.5 and 8.5. However, the RCP 8.5 is predicted to cause higher warming by the end of the 21st century. Such change is expected to increase the evapotranspiration of the basin, the key component of the hydrologic cycle, and thus negatively affects the freshwater availability and ecosystem functioning of the basin. The increase in temperature further increases the crop water requirement, which exacerbate the water supply–demand gap.
The findings of this study offer in-depth and useful information for better understanding and managing water resources and implementing mitigation measures to climate change in the Ziway Lake Basin. In addition, policy makers and relevant stakeholders such as farmer unions in the basin could also benefit from this study to minimize the negative impacts of climate change on freshwater availability and agricultural productivity.
As this study analyzed the annual rainfall and temperature trends only, future research work focuses on analyzing the spatiotemporal trends of seasonal rainfall and temperature. Furthermore, future studies should also compare the CMIP5 and CMIP6 models datasets and assess their ability to simulate the spatiotemporal distribution of rainfall and temperature.

Author Contributions

Conceptualization, A.T.H., O.T.L. and A.D.C.; data curation and analysis, A.T.H.; formula analysis and methodology, A.T.H.; writing—original draft, A.T.H.; literature review, A.T.H.; editing, A.T.H., O.T.L. and A.D.C.; supervision O.T.L., T.A. and A.D.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work was financially supported by the Africa Center of Excellence for Water Management, Addis Ababa University, Ethiopia.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used in this study are available at the World Climate Research Program (WCRP) Climate Explorer https://esgf-node.llnl.gov/search/cmip5/ (accessed from 10 January 2021 to 18 January 2021), daily CMIP5 project data of historical and future precipitation and maximum and minimum temperature under RCP 4.5 and RCP 8.5 emission scenarios.

Acknowledgments

The authors would like to thank the National Meteorological Agency (NMA) of Ethiopia for providing the gauged climate data. We would also like to express our sincere gratitude to the Africa Center of Excellence for Water Management, Addis Ababa University, for the support to conduct this research.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table
Table A1. Statistical performance indices of the GCMs–CMIP5 for monthly rainfall of 1983 to 2005.
Table A1. Statistical performance indices of the GCMs–CMIP5 for monthly rainfall of 1983 to 2005.
Model→CNMR-CM5CSIRO-MK3.6MIP-ESM-LR
StationRMSE (mm)PBIAS (%)rRMSE (mm)PBIAS (%)rRMSE (mm)PBIAS (%)r
Ziway27.411.20.822.029.90.440.729.60.5
Meki27.92.80.831.212.50.528.212.80.6
Arata31.8−10.80.940.6−11.60.537.2−20.30.6
Butajira39.735.00.728.4−3.50.443.85.30.5
Tora33.51.50.839.0−1.20.446.3−2.30.5
Bui38.2−4.20.634.62.80.532.42.40.6
Kulumsa9.1−9.01.016.1−1.60.444.9−2.80.5
Assela26.17.80.927.412.30.547.512.00.5
Sagure16.912.21.010.612.21.039.615.00.6
Merero8.515.81.019.216.70.523.433.10.6
Adamitulu16.20.00.948.6−9.70.435.8−9.50.5
Table
Table A2. Statistical indices values of GCMs–CMIP5 output monthly maximum temperature during 1983–2005 over Ziway Lake Basin.
Table A2. Statistical indices values of GCMs–CMIP5 output monthly maximum temperature during 1983–2005 over Ziway Lake Basin.
ModelCNMR-CM5CSIRO-MK3.6MIP-ESM-LR
StationRSME (C°)PBIAS (%)rRSME (C°)PBIAS (%)rRSME (C°)PBIAS (%)r
Ziway1.00.30.71.10.40.71.20.40.6
Meki1.340.10.61.328.00.61.250.20.6
Arata1.022.30.71.122.40.71.022.30.7
Butajira0.9−1.70.61.0−1.60.61.0−1.60.5
Tora0.90.80.71.00.80.71.00.80.6
Bui0.915.10.60.31.00.61.110.70.6
Kulumsa1.1−0.90.61.1−0.80.61.2−0.90.5
Assela1.1−8.80.71.1−8.80.71.2−8.80.6
Sagure1.3−8.60.71.0−22.90.61.4−15.60.5
Merero1.0−15.50.71.1−7.40.71.1−15.50.6
Adamitulu1.20.00.71.26.70.71.20.00.6
Table
Table A3. Statistical indices values of GCMs–CMIP5 output monthly minimum temperature during 1983–2005 over Ziway Lake Basin.
Table A3. Statistical indices values of GCMs–CMIP5 output monthly minimum temperature during 1983–2005 over Ziway Lake Basin.
CNRM-CM5CSIRO-MK3.6MIP-ESM-LR
Station↓
Test→		MK TrendSen’s SlopeMK TrendSen’s SlopeMK TrendSen’s Slope
Ziway2.01 *0.032.15 *0.032.32 **0.04
Meki2.21 *0.032.07 *0.032.32 **0.03
Arata2.31 *0.032.29 *0.032.43 **0.03
Butajira2.1 *0.032.20 *0.022.69 **0.05
Tora1.560.022.12 *0.022.69 **0.05
Bui2.20 *0.032.15 *0.022.27 **0.03
Kulumsa2.20 *0.032.91 **0.052.32 **0.03
Assela2.9 **0.052.05 *0.022.38 **0.03
Sagure2.65 **0.042.07 *0.022.27 **0.03
Merero2.80 **0.052.16 *0.022.51 **0.03
Adamitulu2.50 **0.052.20 *0.022.32 **0.03
Table
Table A4. Mann–Kendall trend and Sen’s slope estimator value for annual baseline and historical Tmax at Ziway Lake Basin from 1983 to 2005.
Table A4. Mann–Kendall trend and Sen’s slope estimator value for annual baseline and historical Tmax at Ziway Lake Basin from 1983 to 2005.
Model→CNMR-CM5CSIRO-MK3.6MIP-ESM-LR
StationRSME (C°)PBIAS (%)rRSME (C°)PBIAS (%)rRSME (C°)PBIAS (%)r
Ziway1.121.30.81.321.30.71.221.30.7
Meki1.437.30.71.537.10.61.812.20.4
Arata1.2−2.10.71.2−2.10.61.0−2.10.7
Butajira0.9−7.80.60.8−18.30.71.0−18.30.6
Tora0.82.20.70.82.20.71.02.20.4
Bui1.2−2.30.70.82.20.71.0−2.20.7
Kulumsa1.1−10.80.61.5−7.40.51.112.10.7
Assela1.01.10.71.0−20.40.71.2−11.80.8
Sagure0.9−7.40.71.5−43.90.51.0−27.10.6
Merero0.9−3.20.71.4−44.60.61.0−44.80.6
Adamitulu1.00.00.81.00.00.81.10.00.6
Table
Table A5. Mann–Kendall trend and Sen’s slope estimator value for annual baseline and historical Tmin at Ziway Lake Basin from 1983 to 2005.
Table A5. Mann–Kendall trend and Sen’s slope estimator value for annual baseline and historical Tmin at Ziway Lake Basin from 1983 to 2005.
CNRM-CM5CSIRO-MK3.6MIP-ESM-LR
Station↓
Test→		MK TrendSen’s SlopeMK TrendSen’s SlopeMK TrendSen’s Slope
Ziway2.85 **0.022.01 *0.032.32 *0.03
Meki1.740.021.950.022.17 *0.03
Arata2.32 *0.032.11 *0.022.3 *0.03
Butajira2.93 **0.023.16 **0.042.75 **0.04
Tora2.48 *0.022.69 **0.032.67 **0.04
Bui2.48 *0.023.06 **0.042.43 *0.03
Kulumsa1.690.012.01 *0.021.420.01
Assela1.580.012.11 *0.022.34 *0.03
Sagure1.690.012.91 **0.042.32 *0.03
Merero1.740.012.64 **0.032.32 *0.03
Adamitulu1.850.012.06 *0.032.32 *0.03
Table
Table A6. Projected Mann–Kendall trend and Sen’s slope estimator results average rainfall for 11 stations over Ziway Lake Basin from the period 2050–2072.
Table A6. Projected Mann–Kendall trend and Sen’s slope estimator results average rainfall for 11 stations over Ziway Lake Basin from the period 2050–2072.
Model→CNMR-CM5CSIRO-MK3.6MIP-ESM-LR
Station↓
Test→		MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5
Ziway0.680.351.560.382.69 **2.161.421.91−0.32−0.082.17 *0.51
Meki0.300.461.700.712.59 **2.331.473.29−1.17−0.270.820.53
Arata0.490.471.610.642.64 **2.731.141.56−0.87−0.191.100.64
Butajira0.350.431.470.482.17 *1.741.191.05−0.77−0.231.000.46
Tora−0.12−0.102.17 *1.061.891.751.651.98−1.17−0.260.630.33
Bui−0.07−0.232.03 *1.041.993.601.331.54−0.82−0.300.580.53
Kulumsa−0.30−0.301.750.762.17 *2.231.241.23−0.77−0.170.720.34
Assela0.300.411.331.202.36 *1.891.191.20−1.41−0.360.720.45
Sagure0.160.261.330.552.17 *1.760.820.44−0.92−0.251.191.20
Meraro0.300.201.280.301.891.331.331.37−1.27−0.220.820.46
Adamitulu0.210.160.490.362.73 **1.86−0.03−0.01−0.07−0.050.860.55
Table
Table A7. Projected Mann–Kendall trend and Sen’s slope estimator results of annual average rainfall for 11 stations over Ziway Lake Basin from the period 2073–2100.
Table A7. Projected Mann–Kendall trend and Sen’s slope estimator results of annual average rainfall for 11 stations over Ziway Lake Basin from the period 2073–2100.
Model→CNMR-CM5CSIROM-MK3.6MIP-ESM-LR
Station↓
Test→		MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5
Ziway−1.45−1.031.280.581.280.910.621.120.350.071.500.40
Meki−1.63−1.511.060.710.881.021.152.52−0.93−0.331.630.88
Arata−1.50−1.861.100.961.372.770.620.760.090.051.590.99
Butajira−1.32−1.081.230.521.191.061.852.140.350.101.720.81
Tora−1.45−2.060.930.681.541.121.632.66−0.40−0.151.161.03
Bui−1.81−3.140.840.651.762.270.621.00−2.47−1.101.450.99
Kulumsa−1.90−2.530.750.580.880.720.480.73−2.60−0.921.670.85
Assela−0.79−0.570.840.441.901.080.350.410.020.011.630.76
Sagure−0.97−0.791.280.631.280.950.040.03−0.79−0.250.350.41
Meraro−0.66−0.371.060.460.620.411.370.93−0.88−0.261.320.52
Adamitulu −0.93−0.330.110.121.681.380.01−0.01−0.71−0.150.040.03
Table
Table A8. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmax for 11 stations over Ziway Lake Basin from the period 2050–2072.
Table A8. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmax for 11 stations over Ziway Lake Basin from the period 2050–2072.
Model→CNMR-CM5 CSIROM-MK3.6MIP-ESM-LR
Station↓
Test→		MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5
Ziway2.45 *0.042.15 *0.034.52 ***0.094.28 ***0.090.020.013.00 **0.04
Meki2.07 *0.032.07 *0.034.56 ***0.094.09 ***0.090.030.012.91 **0.04
Arata2.08 *0.032.29 *0.034.54 ***0.094.27 ***0.090.030.012.95 **0.04
Butajira2.08 *0.032.20 *0.024.57 ***0.094.27 ***0.090.020.013.04 **0.04
Tora2.36 *0.042.12 *0.024.67 ***0.084.40 ***0.080.020.012.86 **0.04
Bui2.07 *0.032.15 *0.024.63 ***0.084.4 ***0.080.020.012.73 **0.03
Kulumsa2.08 *0.032.91 **0.034.52 **0.094.28 ***0.090.020.012.87 **0.04
Assela4.09 ***0.052.05 *0.024.50 **0.094.27 ***0.090.020.013.04 **0.04
Sagure4.09 ***0.052.07 *0.024.32 ***0.084.26 ***0.090.020.012.95 **0.04
Meraro4.09 ***0.042.16 *0.024.40 ***0.094.28 ***0.090.020.013.09 **0.04
Adamitulu4.13 ***0.052.20 *0.024.63 ***0.094.14 ***0.080.010.013.37 ***0.07
Table
Table A9. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmax for 11 stations over Ziway Lake Basin from the period 2073–2100.
Table A9. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmax for 11 stations over Ziway Lake Basin from the period 2073–2100.
Model→CNMR-CM5CSIROM-MK3.6MIP-ESM-LR
Station↓
Test→		MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5
Ziway3.67 ***0.072.78 **0.034.63 ***0.074.63 ***0.071.510.021.900.03
Meki3.62 ***0.072.73 **0.034.63 ***0.074.63 ***0.071.510.031.900.03
Arata3.71 ***0.072.5 *0.034.63 ***0.074.63 ***0.071.560.031.810.03
Butajira3.71 ***0.062.47 *0.034.63 ***0.074.63 ***0.071.560.021.850.03
Tora3.20 ***0.063.17 **0.045.47 ***0.064.72 ***0.071.660.022.250.04
Bui3.29 ***0.053.31 ***0.045.47 ***0.074.63 ***0.071.710.022.200.03
Kulumsa3.34 ***0.063.22 **0.044.63 ***0.074.63 ***0.071.510.021.980.03
Assela3.67 ***0.062.30 *0.034.63 ***0.074.63 ***0.071.510.021.900.03
Sagure3.67 ***0.062.47 *0.034.63 ***0.074.63 ***0.071.560.021.850.03
Meraro3.62 ***0.072.78 **0.034.63 ***0.074.38 ***0.061.610.020.170.00
Adamitulu3.62 ***0.083.57 ***0.054.38 ***0.064.47 **0.070.870.012.42*0.05
Table
Table A10. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmin for 11 stations over Ziway Lake Basin from the period 2026–2049.
Table A10. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmin for 11 stations over Ziway Lake Basin from the period 2026–2049.
Model→CNMR-CM5CSIROM-MK3.6MIP-ESM-LR
Station↓
Test→		MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5
Ziway3.89 ***0.073.45 ***0.054.14 ***0.084.14 ***0.082.46 *0.041.960.04
Meki4.29 ***0.073.89 ***0.064.12 ***0.084.14 ***0.082.36 *0.041.960.04
Arata2.26 *0.042.85 **0.034.14 ***0.084.09 ***0.082.31 *0.042.01 *0.04
Butajira1.510.031.170.024.14 ***0.084.14 ***0.082.36 *0.042.01 *0.04
Tora0.070.002.00 *0.014.78 ***0.074.79 ***0.072.86 **0.041.710.04
Bui0.050.001.170.014.78 ***0.074.09 ***0.082.80 **0.041.760.04
Kulumsa1.610.042.41 *0.024.14 ***0.084.14 ***0.082.46 *0.041.910.04
Assela1.120.022.80 **0.024.14 ***0.084.14 ***0.082.41 *0.041.960.04
Sagure1.170.032.65 **0.024.09 ***0.084.14 ***0.082.42 *0.042.01 *0.04
Meraro1.120.022.80 **0.034.14 ***0.084.39 ***0.072.31 *0.041.280.04
Adamitulu2.25 *0.053.25 **0.044.39 ***0.074.79 ***0.073.20 **0.062.21 *0.06
Table
Table A11. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmin for 11 stations over Ziway Lake Basin from the period 2050–2072.
Table A11. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmin for 11 stations over Ziway Lake Basin from the period 2050–2072.
Model→CNMR-CM5CSIROM-MK3.6MIP-ESM-LR
Station↓
Test→		MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5
Ziway1.280.024.12 ***0.024.58 ***0.104.20 ***0.091.140.023.61 ***0.05
Meki1.000.024.30 ***0.024.63 ***0.104.6 ***0.101.140.023.60 ***0.05
Arata1.030.024.52 ***0.024.65 ***0.094.18 ***0.091.120.023.53 ***0.05
Butajira1.000.024.54 ***0.024.56 ***0.104.18 ***0.091.050.013.57 ***0.05
Tora1.470.034.24 ***0.024.14 ***0.094.14 ***0.090.720.013.26 **0.05
Bui0.980.024.14 ***0.024.14 ***0.094.14 ***0.090.820.013.35 ***0.05
Kulumsa1.030.024.46 ***0.034.56 ***0.104.18 ***0.091.140.013.48 ***0.04
Assela1.750.034.58 ***0.024.58 ***0.104.19 ***0.091.100.013.61 ***0.04
Sagure1.750.034.09 **0.024.09 **0.084.17 ***0.091.100.023.57 ***0.04
Meraro1.700.034.54 ***0.024.54 ***0.104.18 ***0.091.100.013.61 ***0.05
Adamitulu1.560.034.62 ***0.024.62 ***0.104.06 ***0.081.560.024.18 ***0.05
Table
Table A12. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmin for 11 stations over Ziway Lake Basin from the period 2073–2100.
Table A12. Projected Mann–Kendall trend and Sen’s slope estimator results of annual mean Tmin for 11 stations over Ziway Lake Basin from the period 2073–2100.
Model→CNMR-CM5CSIROM-MK3.6MIP-ESM-LR
Station↓
Test→		MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5
Ziway2.63 **0.082.59 **0.064.43 ***0.034.76 ***0.101.510.022.78 **0.05
Meki2.63 **0.082.59 **0.063.95 ***0.054.76 ***0.101.510.032.78 **0.05
Arata2.57 *0.082.64 **0.063.45 ***0.074.76 ***0.101.560.032.73 **0.05
Butajira2.63 **0.082.69 **0.063.20 **0.044.76 ***0.101.560.022.68 **0.04
Tora2.69 **0.092.36 *0.061.560.024.89 ***0.091.660.022.82 **0.06
Bui2.69 **0.072.31 *0.051.600.014.76 ***0.101.710.022.60 **0.05
Kulumsa2.63 **0.092.31 *0.062.90 **0.044.76 ***0.101.510.022.73 **0.05
Assela2.6 **0.082.69 **0.063.1 **0.054.76 ***0.101.510.022.60 **0.04
Sagure2.6 **0.082.69 **0.063.62 ***0.074.76 ***0.101.560.022.64 **0.04
Meraro2.6 **0.082.64 **0.063.37 ***0.044.98 ***0.081.610.021.030.00
Adamitulu2.63 **0.102.540.072.52 **0.044.89 ***0.090.870.013.44 ***0.07
Mann–Kendall test of significance levels: 90% (*), 95% (**), 99% (***).

References

  1. Wilby, R.L.; Dawson, C.W.; Barrow, E.M. SDSM—A decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 145–157. [Google Scholar] [CrossRef]
  2. Bonebrake, T.C.; Mastrandrea, M.D. Tolerance adaptation and precipitation changes complicate latitudinal patterns of climate change impacts. Proc. Natl. Acad. Sci. USA 2010, 107, 12581–12586. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Hanjra, M.A.; Ferede, T.; Gutta, D.G. Reducing poverty in sub-Saharan Africa through investments in water and other priorities. Agric. Water Manag. 2009, 96, 1062–1070. [Google Scholar] [CrossRef]
  4. Carpenter, S.R.; Fisher, S.G.; Grimm, N.B.; Kitchell, J.F. Global Change and Freshwater Ecosystems. Annu. Rev. Ecol. Syst. 1992, 23, 119–139. [Google Scholar] [CrossRef]
  5. Kundzewicz, Z.W.; Mata, L.J.; Arnell, N.W.; Döll, P.; Jimenez, B.; Miller, K.; Oki, T.; Şen, Z.; Shiklomanov, I. The implications of projected climate change for freshwater resources and their management. Hydrol. Sci. J. 2008, 53, 3–10. [Google Scholar] [CrossRef]
  6. Leta, O.T.; El-Kadi, A.I.; Dulai, H. Implications of Climate Change on Water Budgets and Reservoir Water Harvesting of Nuuanu Area Watersheds, Oahu, Hawaii. J. Water Resour. Plan. Manag. 2017, 143, 05017013. [Google Scholar] [CrossRef]
  7. Kundu, A.; Dwivedi, S.; Chandra, V. Precipitation Trend Analysis over Eastern Region of India Using Cmip5 Based Climatic Models. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-8, 1437–1442. [Google Scholar] [CrossRef] [Green Version]
  8. Bamber, J.L.; Oppenheimer, M.; Kopp, R.E.; Aspinall, W.P.; Cooke, R.M. Ice sheet contributions to future sea-level rise from structured expert judgment. Proc. Natl. Acad. Sci. USA 2019, 116, 11195–11200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  9. Schilling, J.; Hertig, E.; Tramblay, Y.; Scheffran, J. Climate change vulnerability, water resources and social implications in North Africa. Reg. Environ. Chang. 2020, 20, 15. [Google Scholar] [CrossRef] [Green Version]
  10. Kotir, J.H. Climate change and variability in Sub-Saharan Africa: A review of current and future trends and impacts on agriculture and food security. Environ. Dev. Sustain. 2010, 13, 587–605. [Google Scholar] [CrossRef]
  11. Challinor, A.; Wheeler, T.; Garforth, C.; Craufurd, P.; Kassam, A. Assessing the vulnerability of food crop systems in Africa to climate change. Clim. Chang. 2007, 83, 381–399. [Google Scholar] [CrossRef]
  12. Collins, J.M. Temperature Variability over Africa. J. Clim. 2011, 24, 3649–3666. [Google Scholar] [CrossRef] [Green Version]
  13. Alemayehu, A.; Bewket, W. Local climate variability and crop production in the central highlands of Ethiopia. Environ. Dev. 2016, 19, 36–48. [Google Scholar] [CrossRef]
  14. Block, P.J.; Strzepek, K.; Rosegrant, M.W.; Diao, X. Impacts of considering climate variability on investment decisions in Ethiopia. Agric. Econ. 2008, 39, 171–181. [Google Scholar] [CrossRef]
  15. Evangelista, P.; Young, N.; Burnett, J. How will climate change spatially affect agriculture production in Ethiopia? Case studies of important cereal crops. Clim. Chang. 2013, 119, 855–873. [Google Scholar] [CrossRef]
  16. Baker, T.J.; Miller, S.N. Using the Soil and Water Assessment Tool (SWAT) to assess land use impact on water resources in an East African watershed. J. Hydrol. 2013, 486, 100–111. [Google Scholar] [CrossRef]
  17. Gummadi, S.; Rao, K.P.C.; Seid, J.; Legesse, G.; Kadiyala, M.D.M.; Takele, R.; Amede, T.; Whitbread, A. Spatio-temporal variability and trends of precipitation and extreme rainfall events in Ethiopia in 1980–2010. Theor. Appl. Clim. 2018, 134, 1315–1328. [Google Scholar] [CrossRef] [Green Version]
  18. Esayas, B.; Simane, B.; Teferi, E.; Ongoma, V.; Tefera, N. Trends in Extreme Climate Events over Three Agroecological Zones of Southern Ethiopia. Adv. Meteorol. 2018, 2018, 7354157. [Google Scholar] [CrossRef]
  19. Wagesho, N.; Jain, M.K.; Goel, N.K. Effect of Climate Change on Runoff Generation: Application to Rift Valley Lakes Basin of Ethiopia. J. Hydrol. Eng. 2013, 18, 1048–1063. [Google Scholar] [CrossRef]
  20. Abraham, A.T.; Woldemicheala, A.; Muluneha, A.; Abateb, B. Hydrological Responses of Climate Change on Lake Ziway Catchment, Central Rift Valley of Ethiopia. J. Earth Sci. Clim. Change 2018, 9, 6. [Google Scholar] [CrossRef]
  21. Musie, M.; Sen, S.; Chaubey, I. Hydrologic Responses to Climate Variability and Human Activities in Lake Ziway Basin, Ethiopia. Water 2020, 12, 164. [Google Scholar] [CrossRef] [Green Version]
  22. Belihu, M.; Abate, B.; Tekleab, S.; Bewket, W. Hydro-meteorological trends in the Gidabo catchment of the Rift Valley Lakes Basin of Ethiopia. Phys. Chem. Earth, Parts A/B/C 2018, 104, 84–101. [Google Scholar] [CrossRef]
  23. Rosa, L.; Chiarelli, D.D.; Rulli, M.C.; Dell’Angelo, J.; D’Odorico, P. Global agricultural economic water scarcity. Sci. Adv. 2020, 6, eaaz6031. [Google Scholar] [CrossRef] [PubMed]
  24. Musie, M.; Momblanch, A.; Sen, S. Exploring future global change-induced water imbalances in the Central Rift Valley Basin, Ethiopia. Clim. Chang. 2021, 164, 47. [Google Scholar] [CrossRef]
  25. Fernández García, I.; Lecina, S.; Ruiz-Sánchez, M.C.; Vera, J.; Conejero, W.; Conesa, M.R.; Domínguez, A.; Pardo, J.J.; Léllis, B.C.; Montesinos, P. Trends and Challenges in Irrigation Scheduling in the Semi-Arid Area of Spain. Water 2020, 12, 785. [Google Scholar] [CrossRef] [Green Version]
  26. Greaves, G.E.; Wang, Y.-M. Effect of regulated deficit irrigation scheduling on water use of corn in southern Taiwan tropical environment. Agric. Water Manag. 2017, 188, 115–125. [Google Scholar] [CrossRef]
  27. Cancela, J.J.; Trigo-Córdoba, E.; Martínez, E.M.; Rey, B.J.; Bouzas-Cid, Y.; Fandiño, M.; Mirás-Avalos, J.M. Effects of climate variability on irrigation scheduling in white varieties of Vitis vinifera (L.) of NW Spain. Agric. Water Manag. 2016, 170, 99–109. [Google Scholar] [CrossRef]
  28. Eshete, D.G.; Sinshaw, B.G.; Legesse, K.G. Critical review on improving irrigation water use efficiency: Advances, challenges, and opportunities in the Ethiopia context. Water-Energy Nexus 2020, 3, 143–154. [Google Scholar] [CrossRef]
  29. Legesse, D.; Ayenew, T. Effect of improper water and land resource utilization on the central Main Ethiopian Rift lakes. Quat. Int. 2006, 148, 8–18. [Google Scholar] [CrossRef]
  30. Alhamshry, A.; Fenta, A.A.; Yasuda, H.; Kimura, R.; Shimizu, K. Seasonal Rainfall Variability in Ethiopia and Its Long-Term Link to Global Sea Surface Temperatures. Water 2020, 12, 55. [Google Scholar] [CrossRef] [Green Version]
  31. Abdulla, G.M. Annual Earth System Grid Federation 2019 Progress Report; Lawrence Livermore National Lab. (LLNL): Livermore, CA, USA, 2019. [Google Scholar] [CrossRef]
  32. Lamarque, J.-F.; Kyle, G.P.; Meinshausen, M.; Riahi, K.; Smith, S.J.; van Vuuren, D.P.; Conley, A.J.; Vitt, F. Global and regional evolution of short-lived radiatively-active gases and aerosols in the Representative Concentration Pathways. Clim. Change 2011, 109, 191–212. [Google Scholar] [CrossRef]
  33. Basheer, A.K.; Lu, H.; Omer, A.; Ali, A.B.; Abdelgader, A.M.S. Impacts of climate change under CMIP5 RCP scenarios on the streamflow in the Dinder River and ecosystem habitats in Dinder National Park, Sudan. Hydrol. Earth Syst. Sci. 2016, 20, 1331–1353. [Google Scholar] [CrossRef] [Green Version]
  34. McSweeney, C.F.; Jones, R.G.; Lee, R.W.; Rowell, D.P. Selecting CMIP5 GCMs for downscaling over multiple regions. Climate Dynamics. 2015, 44, 3237–3260. [Google Scholar] [CrossRef] [Green Version]
  35. Lutz, A.F.; ter Maat, H.W.; Biemans, H.; Shrestha, A.B.; Wester, P.; Immerzeel, W.W. Selecting representative climate models for climate change impact studies: An advanced envelope-based selection approach. Int. J. Climatol. 2016, 36, 3988–4005. [Google Scholar] [CrossRef] [Green Version]
  36. Emami, F.; Koch, M. Agricultural Water Productivity-Based Hydro-Economic Modeling for Optimal Crop Pattern and Water Resources Planning in the Zarrine River Basin, Iran, in the Wake of Climate Change. Sustainability 2018, 10, 3953. [Google Scholar] [CrossRef] [Green Version]
  37. Abraham, T.; Abate, B.; Woldemicheal, A.; Muluneh, A. Impacts of Climate Change under CMIP5 RCP Scenarios on the Hydrology of Lake Ziway Catchment, Central Rift Valley of Ethiopia. J. Environ. Earth Sci. 2018, 8, 81–90. [Google Scholar]
  38. Musie, M.; Sen, S.; Srivastava, P. Application of CORDEX-AFRICA and NEX-GDDP datasets for hydrologic projections under climate change in Lake Ziway sub-basin, Ethiopia. J. Hydrol. Reg. Stud. 2020, 31, 100721. [Google Scholar] [CrossRef]
  39. Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Downscaling RCM precipitation to the station scale using statistical transformations—a comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef] [Green Version]
  40. Smid, M.; Costa, A.C. Climate projections and downscaling techniques: A discussion for impact studies in urban systems. Int. J. Urban Sci. 2018, 22, 277–307. [Google Scholar] [CrossRef] [Green Version]
  41. Rathjens, H.; Bieger, K.; Srinivasan, R.; Chaubey, I.; Arnold, J.G. CMhyd User Manual: Documentation for Preparing Simulated Climate Change Data for Hydrologic Impact Studies; SWAT: Garland, TX, USA, 2016; Available online: https://swat.tamu.edu/media/115265/bias_cor_man.pdf (accessed on 2 November 2021).
  42. Hordofa, A.T.; Leta, O.T.; Alamirew, T.; Kawo, N.S.; Chukalla, A.D. Performance Evaluation and Comparison of Satellite-Derived Rainfall Datasets over the Ziway Lake Basin, Ethiopia. Climate 2021, 9, 113. [Google Scholar] [CrossRef]
  43. Hoffmann, P.; Spekat, A. Identification of possible dynamical drivers for long-term changes in temperature and rainfall patterns over Europe. Theor. Appl. Clim. 2021, 143, 177–191. [Google Scholar] [CrossRef]
  44. Mohorji, A.M.; Şen, Z.; Almazroui, M. Trend Analyses Revision and Global Monthly Temperature Innovative Multi-Duration Analysis. Earth Syst. Environ. 2017, 1, 9. [Google Scholar] [CrossRef] [Green Version]
  45. Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
  46. Mann, H.B. Nonparametric tests against trend. Econometrica J. Econom. Soc. 1945, 1, 245–259. [Google Scholar] [CrossRef]
  47. Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
  48. Bari, S.H.; Rahman, M.T.U.; Hoque, M.A.; Hussain, M.M. Analysis of seasonal and annual rainfall trends in the northern region of Bangladesh. Atmospheric Res. 2016, 176–177, 148–158. [Google Scholar] [CrossRef]
  49. De Lima, M.I.P.; Carvalho, S.; De Lima, J.L.M.P.; Coelho, M.F.E.S. Trends in precipitation: Analysis of long annual and monthly time series from mainland Portugal. Adv. Geosci. 2010, 25, 155–160. [Google Scholar] [CrossRef] [Green Version]
  50. Hu, Y.; Maskey, S.; Uhlenbrook, S. Expected changes in future temperature extremes and their elevation dependency over the Yellow River source region. Hydrol. Earth Syst. Sci. 2013, 17, 2501–2514. [Google Scholar] [CrossRef] [Green Version]
  51. Hu, Y.; Maskey, S.; Uhlenbrook, S.; Zhao, H. Streamflow trends and climate linkages in the source region of the Yellow River, China. Hydrol. Process. 2011, 25, 3399–3411. [Google Scholar] [CrossRef]
  52. Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
  53. Hussain, M.M.; Mahmud, I. pyMannKendall: A python package for non-parametric Mann Kendall family of trend tests. J. Open Source Softw. 2019, 4, 1556. [Google Scholar] [CrossRef]
  54. Cox, D.R.; Stuart, A. Some Quick Sign Tests for Trend in Location and Dispersion. Biometrika 1955, 42, 80–95. [Google Scholar] [CrossRef] [Green Version]
  55. Tehrani, E.N.; Sahour, H.; Booij, M.J. Trend analysis of hydro-climatic variables in the north of Iran. Theor. Appl. Clim. 2019, 136, 85–97. [Google Scholar] [CrossRef]
  56. Kamworapan, S.; Surussavadee, C. Evaluation of CMIP5 Global Climate Models for Simulating Climatological Temperature and Precipitation for Southeast Asia. Adv. Meteorol. 2019, 2019, 1067365. [Google Scholar] [CrossRef]
  57. Voldoire, A.; Sanchezgomez, E.; Mélia, D.S.Y.; Decharme, B.; Cassou, C.; Senesi, S.; Valcke, S.; Beau, I.; Alias, A.; Chevallier, M.; et al. The CNRM-CM5.1 global climate model: Description and basic evaluation. Clim. Dyn. 2013, 40, 2091–2121. [Google Scholar] [CrossRef] [Green Version]
  58. Rogelj, J.; Meinshausen, M.; Knutti, R. Global warming under old and new scenarios using IPCC climate sensitivity range estimates. Nat. Clim. Change 2012, 2, 248–253. [Google Scholar] [CrossRef]
  59. Gurara, M.A.; Jilo, N.B.; Tolche, A.D. Impact of climate change on potential evapotranspiration and crop water requirement in Upper Wabe Bridge watershed, Wabe Shebele River Basin, Ethiopia. J. Afr. Earth Sci. 2021, 180, 104223. [Google Scholar] [CrossRef]
  60. Deressa, T.T.; Hassan, R.M. Economic Impact of Climate Change on Crop Production in Ethiopia: Evidence from Cross-section Measures. J. Afr. Econ. 2009, 18, 529–554. [Google Scholar] [CrossRef]
  61. Gadissa, T.; Nyadawa, M.; Behulu, F.; Mutua, B. The Effect of Climate Change on Loss of Lake Volume: Case of Sedimentation in Central Rift Valley Basin, Ethiopia. Hydrology 2018, 5, 67. [Google Scholar] [CrossRef] [Green Version]
  62. Intergovernmental Panel on Climate Change (IPCC). Summary for Policymakers. Climate Change 2014: Part of the Working Group III Contribution to the Fifth Assessment Report of the IPCC, Geneva, Switzerland. Available online: http://pure.iiasa.ac.at/11125 (accessed on 14 September 2021).
  63. Asare-Nuamah, P.; Botchway, E. Understanding climate variability and change: Analysis of temperature and rainfall across agroecological zones in Ghana. Heliyon 2019, 5, e02654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  64. Kelkar, S.M.; Kulkarni, A.; Rao, K.K. Impact of Climate Variability and Change on Crop Production in Maharashtra, India. Curr. Sci. 2020, 118, 1235–1245. [Google Scholar] [CrossRef]
  65. Gebrehiwot, T.; van der Veen, A. Assessing the evidence of climate variability in the northern part of Ethiopia. J. Dev. Agric. Econ. 2013, 5, 104–119. [Google Scholar] [CrossRef] [Green Version]
  66. Tesfaye, K.; Aggarwal, P.K.; Mequanint, F.; Shirsath, P.B.; Stirling, C.M.; Khatri-Chhetri, A.; Rahut, D.B. Climate Variability and Change in Bihar, India: Challenges and Opportunities for Sustainable Crop Production. Sustainability 2017, 9, 1998. [Google Scholar] [CrossRef] [Green Version]
Hydrology 09 00002 g001 550
Figure 1. Topographic map of the Ziway Lake Basin.
Figure 1. Topographic map of the Ziway Lake Basin.
Hydrology 09 00002 g001
Hydrology 09 00002 g002 550
Figure 2. Spatial distribution of observed and CNRM-CM5 model annual mean rainfall (mm/year) and annual mean temperatures (Tmax and Tmin (°C)) for (a) observed and (b) CNRM-CM5 rainfall (c) observed Tmax, (d) CNRM-CM5 Tmax, (e) observed Tmin, and (f) CNRM-CM5 Tmin over the ZLB (1983–2005).
Figure 2. Spatial distribution of observed and CNRM-CM5 model annual mean rainfall (mm/year) and annual mean temperatures (Tmax and Tmin (°C)) for (a) observed and (b) CNRM-CM5 rainfall (c) observed Tmax, (d) CNRM-CM5 Tmax, (e) observed Tmin, and (f) CNRM-CM5 Tmin over the ZLB (1983–2005).
Hydrology 09 00002 g002
Hydrology 09 00002 g003 550
Figure 3. The annual rainfall from 2026 to 2100 for CNRM-CM5 model under RCP 4.5 and 8.5 scenarios.
Figure 3. The annual rainfall from 2026 to 2100 for CNRM-CM5 model under RCP 4.5 and 8.5 scenarios.
Hydrology 09 00002 g003
Hydrology 09 00002 g004 550
Figure 4. Annual average Tmax trends from 2026 to 2100 under RCP (4.5 and 8.5) for CNRM-CM5.
Figure 4. Annual average Tmax trends from 2026 to 2100 under RCP (4.5 and 8.5) for CNRM-CM5.
Hydrology 09 00002 g004
Hydrology 09 00002 g005 550
Figure 5. Spatial distribution of CNRM-CM5 model mean annual rainfall (mm/year) within the ZLB for RCP 4.5 and 8.5 scenarios and three future periods: (a) near-term RCP 4.5, (b) near-term RCP 8.5, (c) mid-term RCP 4.5, (d) mid-term RCP 8.5, (e) far-term RCP 4.5, and (f) far-term RCP 8.5.
Figure 5. Spatial distribution of CNRM-CM5 model mean annual rainfall (mm/year) within the ZLB for RCP 4.5 and 8.5 scenarios and three future periods: (a) near-term RCP 4.5, (b) near-term RCP 8.5, (c) mid-term RCP 4.5, (d) mid-term RCP 8.5, (e) far-term RCP 4.5, and (f) far-term RCP 8.5.
Hydrology 09 00002 g005
Hydrology 09 00002 g006 550
Figure 6. Spatial distribution of CNRM-CM5 model mean annual Tmax (°C) within the ZLB for RCP 4.5 and 8.5 scenarios and three future periods: (a) near-term RCP 4.5, (b) near-term RCP 8.5, (c) mid-term RCP 4.5, (d) mid-term RCP 8.5, (e) far-term RCP 4.5, and (f) far-term RCP 8.5.
Figure 6. Spatial distribution of CNRM-CM5 model mean annual Tmax (°C) within the ZLB for RCP 4.5 and 8.5 scenarios and three future periods: (a) near-term RCP 4.5, (b) near-term RCP 8.5, (c) mid-term RCP 4.5, (d) mid-term RCP 8.5, (e) far-term RCP 4.5, and (f) far-term RCP 8.5.
Hydrology 09 00002 g006
Hydrology 09 00002 g007 550
Figure 7. Spatial distribution of CNRM-CM5 model mean annual Tmin (°C) within the ZLB for RCP 4.5 and 8.5 scenarios and three future periods: (a) near-term RCP 4.5, (b) near-term RCP 8.5, (c) mid-term RCP 4.5, (d) mid-term RCP 8.5, (e) far-term RCP 4.5, and (f) far-term RCP 8.5.
Figure 7. Spatial distribution of CNRM-CM5 model mean annual Tmin (°C) within the ZLB for RCP 4.5 and 8.5 scenarios and three future periods: (a) near-term RCP 4.5, (b) near-term RCP 8.5, (c) mid-term RCP 4.5, (d) mid-term RCP 8.5, (e) far-term RCP 4.5, and (f) far-term RCP 8.5.
Hydrology 09 00002 g007
Table
Table 1. CMIP5 global climate models considered in this study.
Table 1. CMIP5 global climate models considered in this study.
Modeling CenterModelResolution in DegreesInstituteReference
CNRM-CERFACSCNRM-CM51.4 × 1.4Centre National de Recherches Meteorologiques/Centre Europeen de Recherche et Formation Avancees en Calcul Scientifique[24,38]
MPI-MMPI-ESM-LR1.9 × 1.9Max Planck Institute for Meteorology
(MPI-M)		[33,34,38]
CSIRO-QCCCECSIRO-MK3.61.8 × 1.8Commonwealth Scientific and Industrial Research Organization in collaboration with the Queensland Climate Change Centre of Excellence[37,38]
Table
Table 2. Mann–Kendall trend and Sen’s slope estimator value for annual baseline (observed) and historical rainfall within the Ziway Lake Basin from 1983–2005.
Table 2. Mann–Kendall trend and Sen’s slope estimator value for annual baseline (observed) and historical rainfall within the Ziway Lake Basin from 1983–2005.
CNMR-CM5CSIRO-MK3.6MIP-ESM-LR
Station↓
Test→		MK TrendSen’s SlopeMK TrendSen’s SlopeMK TrendSen’s Slope
Ziway−2.14−0.520.160.080.790.33
Meki0.420.100.010.060.790.34
Arata2.17 *0.56−0.02−0.02−0.42−0.14
Butajira−1.21−0.310.630.270.630.23
Tora−0.50−0.19−0.26−0.19−0.58−0.30
Bui−0.66−0.230.630.290.630.31
Kulumsa0.900.37−0.53−0.070.050.07
Assela0.850.37−0.16−0.030.050.10
Sagure1.060.360.480.181.020.01
Meraro0.480.18−0.90−0.42−0.58−0.21
Adamitulu1.110.350.110.050.900.20
Table
Table 3. Projected Mann–Kendall trend and Sen’s slope estimator results average rainfall for eleven stations within the Ziway Lake Basin for the period 2026–2049.
Table 3. Projected Mann–Kendall trend and Sen’s slope estimator results average rainfall for eleven stations within the Ziway Lake Basin for the period 2026–2049.
Model→CNMR-CM5CSIRO-MK3.6MIP-ESM-LR
Station↓ Test→MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5
Ziway0.710.520.380.230.940.061.611.34−0.550.22−1.41−2.35
Meki−0.54−0.111.070.290.120.242.06 *2.370.38−0.030.070.04
Arata−0.53−0.091.410.530.020.142.01 *1.350.240.12−0.27−0.15
Butajira0.480.080.570.20−0.02−0.121.461.53−0.380.08−0.05−0.01
Tora0.280.050.070.040.670.531.611.92−0.34−0.02−0.12−0.10
Bui0.170.030.370.150.620.601.360.930.05−0.100.070.02
Kulumsa−0.42−0.070.470.25−0.07−0.051.601.14−0.55−0.010.220.05
Assela−0.53−0.070.622.90−0.02−0.131.701.05−0.250.060.320.07
Sagure−0.18−0.030.570.15−0.07−0.231.510.69−0.67−0.061.661.05
Meraro−0.34−0.050.520.07−0.27−0.191.310.71−0.38−0.080.170.08
Adamitulu−0.54−0.090.390.231.070.41−0.06−0.010.700.03−0.17−0.16
Table
Table 4. Projected Mann–Kendall trend and Sen’s slope estimator results for annual mean Tmax for eleven stations within the Ziway Lake Basin for the period 2026–2049.
Table 4. Projected Mann–Kendall trend and Sen’s slope estimator results for annual mean Tmax for eleven stations within the Ziway Lake Basin for the period 2026–2049.
Model→CNMR-CM5CSIRO-MK3.6MIP-ESM-LR
Station↓
Test→		MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5MK RCP 4.5Sen’s RCP 4.5MK RCP 8.5Sen’s RCP 8.5
Ziway2.00 *0.041.860.032.43 *0.033.35 ***0.051.510.022.66 **0.03
Meki2.21 *0.042.51 *0.052.95 **0.054.14 ***0.051.510.031.710.03
Arata2.21 *0.042.85 **0.073.35 ***0.073.35 ***0.051.560.031.660.03
Butajira2.21 *0.041.170.023.20 ***0.043.34 ***0.051.560.021.660.02
Tora1.560.032.00 *0.041.560.023.64 ***0.061.660.022.98 **0.03
Bui2.20 *0.040.570.010.600.013.69 ***0.062.71 **0.022.01 *0.03
Kulumsa2.20 *0.042.41 *0.042.90 **0.043.35 ***0.051.510.021.610.02
Assela2.9 **0.042.80 **0.043.17 ***0.053.34 ***0.052.32 *0.021.690.03
Sagure2.65 **0.042.65 **0.043.62 ***0.073.35 **0.051.560.023.66 **0.02
Meraro2.800.052.80 **0.053.37 ***0.043.32 ***0.051.610.021.710.03
Adamitulu2.50 **0.073.25 **0.073.52 ***0.042.12 *0.040.870.013.96 **0.02
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Hordofa, A.T.; Leta, O.T.; Alamirew, T.; Chukalla, A.D. Spatiotemporal Trend Analysis of Temperature and Rainfall over Ziway Lake Basin, Ethiopia. Hydrology 2022, 9, 2. https://doi.org/10.3390/hydrology9010002

AMA Style

Hordofa AT, Leta OT, Alamirew T, Chukalla AD. Spatiotemporal Trend Analysis of Temperature and Rainfall over Ziway Lake Basin, Ethiopia. Hydrology. 2022; 9(1):2. https://doi.org/10.3390/hydrology9010002

Chicago/Turabian Style

Hordofa, Aster Tesfaye, Olkeba Tolessa Leta, Tane Alamirew, and Abebe Demissie Chukalla. 2022. "Spatiotemporal Trend Analysis of Temperature and Rainfall over Ziway Lake Basin, Ethiopia" Hydrology 9, no. 1: 2. https://doi.org/10.3390/hydrology9010002

APA Style

Hordofa, A. T., Leta, O. T., Alamirew, T., & Chukalla, A. D. (2022). Spatiotemporal Trend Analysis of Temperature and Rainfall over Ziway Lake Basin, Ethiopia. Hydrology, 9(1), 2. https://doi.org/10.3390/hydrology9010002

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop