Abstract
In ungauged watersheds, the estimation of the time of concentration (Tc) is always a challenging task due to the intrinsic uncertainty involved when making assumptions. Given that Tc is one of the main inputs in a hydrological analysis for the design of hydraulic structures for stormwater management, ten equations (including one proposed in several local studies) and two Tc methodologies (overland flow time plus channel flow time) were used to compute the Tc in fifteen urban ungauged watersheds, located in Cartagena de Indias (Colombia), with different area sizes and slopes to statistically assess their performance against the value obtained via the Natural Resources Conservation Service (NRCS) velocity method (assumed to be the true value). According to the Nash–Sutcliffe efficiency index, none of the equations proved to be reliable in all watersheds as only four equations predicted the Tc value in 53% of the cases. In addition, based on the percent bias, all equations tended to significantly over- or underestimate the Tc, which affects the quantification of the runoff volume necessary for, among others, the implementation of best management practices for watershed management (e.g., conventional and/or sustainable drainage system design), flood-prone area delineation and flood risk analyses, urban planning, and stream restoration.
1. Introduction
Hydrological analysis in ungauged watersheds might be challenging as several assumptions have to be made that could introduce uncertainties into the estimation of the design runoff via rainfall-runoff models, in which rainfall is one of the main inputs. This is particularly true in ungauged watersheds where, typically, rainfall data are only available from nearby gauges. In the absence of data from pluviographs that help with the understanding of rainfall duration and distribution over time, the Tc becomes a variable of paramount relevance in determining the design rainfall. The time of concentration has been defined differently [1,2,3,4,5,6,7,8,9,10] and multiple empirical equations have been derived for its estimation that can be found throughout the available literature on hydrology, in different types of stormwater management and design of drainage structure manuals/guidelines [3,11,12,13,14], embedded in software programs for hydrologic-hydraulic modeling such as Win TR-20 [15], Win TR-55 [16], HydroCAD® [17], Autodesk® [18], Storm Water Management Model (SWMM) [19], Hydrologic Engineering Center-Hydrologic Modeling System HEC-HMS [20], SewerCAD® [21], and StormCAD® [22], in freely available Tc online calculators such as Vlab [23], or as an input in rainfall-runoff models such as the rational method. These equations have considered different variables that range from rainfall and surface direct runoff to watershed morphological parameters (e.g., area, slope, length of flow path, and outlet elevation), land use/land cover (LULC) conditions, and channel characteristics.
The development of an equation based on local or regional data is always preferable. Manoj and Fang [24], Yoo et al. [25], De Almeida et al. [26], Sandoval-Erazo et al. [27], Michailidi et al. [9], and Perdikaris et al. [10] are examples of studies conducted to derive equations based on local available information. Unfortunately, in ungauged areas, there is no other option but to use existing empirical Tc equations. On this basis, the existence of numerous equations might become a hindrance when it comes to deciding which is best for a given area, especially when the person using a particular equation is not familiar with how it was derived and/or its advantages and intrinsic limitations. Various studies [1,2,5,6,7,8,28,29,30,31,32,33,34,35,36] performed in different locations around the world have resulted in large differences among the Tc values estimated by means of multiple equations, which contributes to (a) highlighting the need for assessing the performance of existing Tc equations prior to their use, (b) realizing that the equations cannot be randomly used, and (c) understanding and quantifying the impact on the subsequent computation of the design runoff.
Given the large amount of ungauged areas around the world, water-related professionals are accustomed to the use of empirical Tc equations for hydrological analyses. For instance, in Ireland [37] and Colombia [38,39,40], some estimate Tc as the average of Tc values from selected equations, while others prefer to eliminate the outliers before calculating the average. In the case of Colombia, this seems to be the reason that Invías [41] (pp. 22–28) and MinVivienda [42,43] recommend, respectively, fifteen (Kirpich, Témez, Williams, Johnstone–Cross, Giandotti, California culvert practice, Ventura–Heras, V.T. Chow, Kerby–Hathaway, Izzard, U.S. Federal Aviation Administration (FAA), kinematic wave, NRCS lag equation, George Rivero, and NRCS velocity method for shallow concentrated flow) and three empirical equations (Kerby–Hathaway, FAA, and NRCS velocity method for shallow concentrated flow). Whereas this practice might give the user a range of Tc values to choose from, it also raises doubts as to whether the selection of such an array of equations was indeed the result of an assessment of their performance. Furthermore, based on the authors’ experience and the scarce literature on Tc equation assessment in Colombia, the reasons behind such practice when computing the Tc are unclear. The bottom line is that averaging, per se, does not suffice when it comes to assessing the performance of such equations. Indeed, few studies [44,45] have either addressed this matter (though both studies used averaging as well) or developed local/regional Tc equations based on observed data [46,47].
The inherent degree of uncertainty involved in the computation of Tc in ungauged areas should be minimized by performing an assessment of the equation(s) to be utilized [48] (pp. 9.16). Therefore, this study intends to help with this task by assessing the performance of ten empirical equations (and two Tc methodologies that combine two different equations) in fifteen small urban ungauged watersheds located in Cartagena de Indias (Colombia) by comparing the Tc values with the value obtained via NRCS velocity method [3,49], which was assumed to be the “true” value owing to (a) the absence of hyetographs and hydrographs from which Tc could have been derived, (b) the conceptual robustness behind the method [6,10,11] that permits it, to a certain extent, to make up for the lack of data, and (c) in urban areas, it is recommendable to estimate Tc as the result of length over velocity [48]. The assessment consisted of measuring accuracy, bias, the model’s prediction power, and true simulated values’ linear correlation through, respectively, pre-established performance categories [50,51,52,53,54] for the statistical indicators of ratio of root mean square error and standard deviation (RSR), percent bias (PBIAS), Nash–Sutcliffe efficiency (NSE), and coefficient of determination (R2). The assessment also took into account the performance of the Tc equations when (a) applying the empirical formulas to the average slope and total length (original approach), (b) applying the empirical formulas to each of the identified flow types and then adding them up, and (c) utilizing both the 2-year, 24 h rainfall (P2) under stationary (SC) and non-stationary (NSC) conditions for the NRCS velocity method sheet flow formula owing to the findings of González-Álvarez et al. [55], who concluded that a non-stationary frequency analysis better fitted the 24 h rainfall time series at Aeropuerto (Apto.) Rafael Núñez rain gauge.
2. Study Area and Data
Cartagena de Indias, a city located within the Caribbean Colombian region, has a total area of approximately 623 km2, with an average total annual rainfall ranging between 1000 and 1500 mm [56], a rainy season during the months of April–June and August–November [57], and reported values of daily maximum rainfall of up to 222 mm (reported in 2 October 2016 at the Rafael Núñez Airport rain gauge). Despite the fact that 87.8% of its territory is rural, more than 90% of its population (around 925,860 people) lives in the urban area [58]. This exacerbates the flooding problems that the city experiences every year during the rainy season, chiefly caused by, among others, increasing rainfall and obsolete and/or deficiently designed hydraulic structures for stormwater management [55].
The selected urban watersheds’ areas range from 29.2 to 72.8 ha and discharge into either Las Quintas Swamp or Bazurto and Juan Angola Bayous (Figure 1 and Table 1), which are the water bodies that have undergone the largest anthropogenic pressure among the six water bodies that compose the city’s internal estuarine bayous and lagoons system [59].
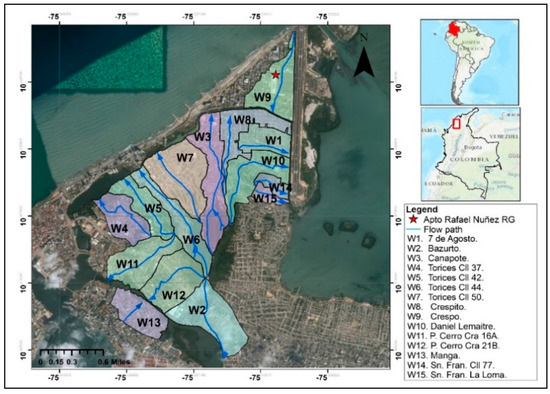
Figure 1.
Study area selected watersheds. Source: adapted from Establecimiento Público Ambiental de Cartagena (EPA-Cartagena) and Universidad de Cartagena (UDC) [59].

Table 1.
Selected urban watersheds.
Some of the data used in this study include the P2 value of the Apto. Rafael Núñez rain gauge (study area’s nearest rain gauge), estimated by González-Álvarez et al. [55], who concluded that a non-stationary frequency analysis better fitted the 24 h rainfall time series. Thus, both stationary and non-stationary P2 values (89 and 128 mm, respectively) were used as some of the inputs for the NRCS velocity method sheet flow formula to test whether it might bring any improvement in the performance of the Tc equations. The derivation of the remaining variables (length, slope, runoff coefficient, curve number, imperviousness and conveyance factors, and Manning coefficient) needed for the different Tc equations used is explained in the following sections as they (the variables) are all dependent on the watershed’s characteristics.
3. Methodology
The proposed methodology (Figure 2) consisted of four basic tasks: (a) the watershed delineation, (b) selection of Tc equations and estimation of relevant watershed morphometric parameters and Tc equations related variables, (c) Tc computation, and (d) Tc equation performance assessment via statistical analysis. Each of these stages are detailed in the following subsections.

Figure 2.
Methodology’s flowchart.
3.1. Watershed Delineation, Morphometric Parameters, and Flow Types
The delineation of the fifteen watersheds, initial identification of the flow paths, and flow length and slope computation were conducted via ArcGIS (Version 10.6.1, ESRI Inc., Redlands, CA, USA [60]) using the 30-m National Aeronautics and Space Administration (NASA) Digital Elevation Model (DEM) [61]. Field work was also performed to (a) corroborate watersheds divide, (b) identify multiple flow paths and types of flows (sheet, shallow concentrated, and channel) within each watershed, and (c) obtain channel dimensions in watersheds where channel flow was identified.
Table 2 summarizes the different flow paths and flow types identified as well as their total length, average slope, and shallow concentrated flow as a percentage of the total flow. It might be observed that this type of flow corresponds to 46% to 100% of the total watershed identified flow types. Most of the empirical Tc equations have the slope as one of their main inputs, which greatly impacts the Tc estimation [10,62]. As a result, in this study, the slope estimation for each identified flow type and the entire watershed’s flow path was carried out by carefully observing the elevation longitudinal profiles of each of the identified flow paths. This avoids incurring any possible error by omitting relevant elevation differences along them (the flow paths).

Table 2.
Identified flow types within selected watersheds.
It is also noteworthy to point out that, in Colombia, contrary to selecting the longest travel time of all possible flow paths within a watershed, it is a common practice among hydrologists to select the shorter time of concentration (with a minimum possible value of 15 min), arguing that it helps to be on the safe side because a shorter Tc value will lead to a larger rainfall (or rainfall intensity) [41] (pp. 2–8). However, this omits the fact that peak discharge occurs when all parts of a watershed are contributing to the runoff, which is assumed to occur at the time of concentration [9,11,63]. In this study, the longest travel time is used as the watershed’s time of concentration. Table 2 presents the paths with the longest travel time of all identified flow paths within each of the fifteen urban watersheds (Table S1). Figure 3 shows the flow paths identified in some of the selected watersheds of this study.
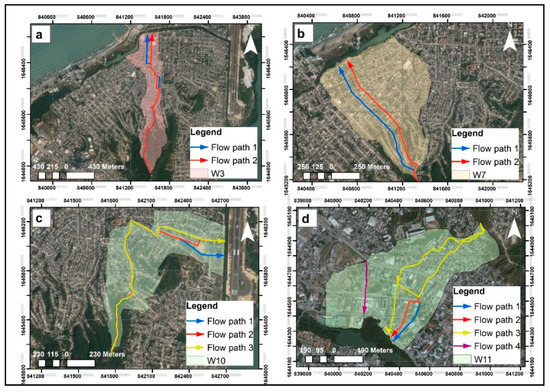
Figure 3.
Watersheds’ identified flow paths. (a) Canapote (W3); (b) Torices Calle 50 (W7); (c) Daniel Lemaitre (W10); (d) Pie del Cerro Cra 16A (W11).
3.2. Selected Tc Equations
A total of ten empirical equations used for different types of flow and two additional methodologies that involve the combination of some of these ten equations were selected for the computation of the Tc: Miller [64,65], U.S. Federal Aviation Agency (FAA) [66], Espey-Winslow (E-W) [67], Kerby-Hathaway (with and without slope adjustment) [65,68], NRCS lag equation [11], Kirpich-Tennessee (with and without slope adjustment) [65,69], Bransby-Williams (B-W) [70], Johnstone-Cross (J-C) [71], Sheridan [72], NRCS velocity method for shallow concentrated flow with a local/regional coefficient for Cartagena proposed by Cartagena’s Stormwater Management Master Plan (PMDPC in Spanish) [73], the Kerby-Kirpich (K-K) methodology with and without slope adjustment [14,65,74], and the Tc methodology proposed by MinVivienda [42]. A brief description of all equations and methodologies is provided in Tables S7–S10.
For performance assessment purposes, Tc values were computed by means of the NRCS velocity method [3,11], which were assumed to be the “true” (or reference) values owing to (a) the absence of observed rainfall and runoff data (ungauged watersheds) from which Tc could have been derived and (b) the methodology’s robustness. The NRCS velocity method defines three types of flow, namely sheet, shallow concentrated, and channel. The time of concentration is the sum of the travel times of each identified flow type (Equation (1)). The travel time for sheet flow is estimated via Equation (2), while for shallow concentrated and channel flows, it is necessary to first calculate the velocities. Sheet flow velocity is estimated via either plot (or their corresponding equations [3,11]) if the flow path slope and soil cover type are known. Channel flow velocity is estimated through Equation (3). Finally, travel times for shallow concentrated and channel flow are estimated via Equation (4).
where Tsheet is sheet flow travel time (h), n0 is the roughness coefficient, L is the flow path length (m), P2 is the 2-year, 24 h rainfall (mm), and S is the slope (m/m).
where VChannel is the channel water velocity (m/s), R is the hydraulic radius (m), S is the channel slope (m/m), and n is the Manning’s coefficient.
where Tt (h), L (m), and V (m/s) are the travel time, flow path length, and velocity for either shallow concentrated (TShallow Conc) or channel (TChannel) flows.
Additionally, in order to test how using a given equation for a type of flow for which it was not intended could introduce errors, each of the ten equations was applied to (a) each of the identified flow types within a watershed (sheet, shallow concentrated, and channel flow), and the total time of concentration was estimated as the sum of the times of concentration computed individually for each of the flow types (named each flow, E.F.), and (b) to the flow path as a whole, irrespective of the identified flow types (named total length, T.L.). Both results were compared to that of the NRCS velocity method (using P2 under SC and NSC). For instance, if the Kirpich equation was to be used in a watershed where shallow concentrated and channel flows have been identified, then the time of concentration was estimated both ways by applying the equation to (a) each of the identified flows, and adding both results, and (b) the total length, as the original methodology that is typically used (and derived for). For the two additional Tc methodologies used in this study (Kerby-Kirpich and MinVivienda), the sheet and shallow concentrated flows were considered as one. Additionally, these methodologies were not used for the total length scenario given the nature of the methodologies that establishes the separation of two flows to be applied.
3.3. Determination of Tc Equation Variables
Variables related to LULC, such as composite runoff coefficient (C) [75], composite curve number (CN) [3,11], and percentage of impervious area (ip) [67], were estimated by means of satellite imagery analysis (LandSat imagery processed via ENVI®.(Version 5.1, Harris Geospatial Solutions Inc, Boulder, CO, USA [76])) (Table S2). The Espey-Winslow channelization factor (φ) and roughness (n0) and Manning (n) coefficients were determined based on the channel soil cover observed during field visits. (Table S2). Descriptions of all variables used in the different selected Tc equations are given in Tables S7–S10.
3.4. Tc Equations Performance Assessment
The equations’ performance was assessed by means of the coefficient of determination (R2) (Equation (5)), the ratio of root mean square error and standard deviation (RSR) (Equation (6)), percent bias (PBIAS) (Equation (7)), and Nash–Sutcliffe efficiency (NSE) (Equation (8)) [50,51,52,77,78,79]. In Equations (5) through (8), , , , and are, respectively, the values of the observed (true value obtained from NRCS velocity method), simulated (from each of the ten empirical Tc equations and two additional Tc methodologies), average observed, and average simulated values.
The coefficient of determination indicates the association (and goodness-of-fit) between the true and the simulated values through a linear correlation and has a range of values from zero (no correlation) to one (optimal value or perfect fit). RSR is a standardized form of the root mean square (RMSE) that measures the error of a model, with an optimal value of zero (no error). PBIAS, with an optimal value of zero, shows the model’s tendency to under- or overestimate when compared with the true value, where a negative PBIAS indicates that the simulated value is greater than the observed one (overestimation), while positive denotes underestimation. NSE permits us to assess the model’s prediction power; it ranges from −∞ to one (optimal value). If negative values of NSE are obtained, then the true values’ average is a better predictor than the simulated values. When NSE equals zero (or close to zero), either the average of true values or the simulated values could be used. Details of the theory and limitations/advantages of these statistical indices for model performance assessment can be widely found in the literature.
In order to better assess the equations’ performance, various categories were established for each of the four statistical indices used based on their corresponding range of values, as per Moriasi et al. [51,52] (Table 3). The color bar helps with the visualization and identification of such categories.

Table 3.
Statistical variables performance categories.
4. Results and Discussion
Tables S11–S14 show the watersheds’ estimated Tc values for all equations and methodologies used for each flow and total length with P2 values under stationary and non-stationary conditions.
Values of R2 are presented in Table S5. The range of R2 values under stationary conditions for each flow and total length ranged, respectively, from 0.03 (Kerby-Kirpich with slope adjusted) to 0.8 (PMDPC). For the total length under stationary conditions, the R2 range of values was between 0.02 (Miller) and 0.82 (Kirpich). Under non-stationary conditions, the R2 values oscillated between 0.002 (Miller) and 0.84 (PMDPC) for each flow and between 0.005 (Miller) and 0.86 (Kirpich) for total length.
The assessment of the Tc equations through the R2 revealed, as expected, that empirical formulas perform best when applied to the total length. The coefficient of determination values increased in all cases, except for the Sheridan equation, which had a decrease of 0.01 for stationary and non-stationary conditions when the equation was applied to each flow and total length. The equations’ performance improvement was also noted from the reduction in the standard deviation values in almost all equations (Tables S3 and S4). The Kirpich slope-adjusted equation had the largest R2 increases in both stationary and non-stationary conditions (+0.18) when each flow and total length were compared (Table S5). However, the slope adjustment did not bring major improvements when compared to other equations such as FAA, unadjusted Kirpich, Johnstone-Cross, NRCS lag equation, PMDPC, or the MinVivienda methodology (with FAA and NRCS lag equation). Despite the fact that shallow concentrated flow was mostly present in all fifteen watersheds (shallow concentrated flow as a percentage of the total flow had values ranging between 58% and 100%, Table 2), channel flow equations (except for the Sheridan equation), in general, had higher R2 values, the Kirpich equation being the one with the highest R2 values (0.82 and 0.86 for total length under stationary and non-stationary conditions, respectively). The use of P2 under non-stationary conditions in the NRCS velocity method sheet flow equation made R2 values increase, which might suggest not only that NSC are more representative of Cartagena’s rainfall behavior [55] but also that the NRCS velocity method sheet flow equation might work best whenever NSC are recommended after a frequency analysis has been conducted.
Regarding the assessment with respect to NSE, the equations of Kerby, NRCS lag equation, Johnstone-Cross, and PMDPC, as well as the Kerby-Kirpich slope-adjusted and MinVivienda with Kerby equation methods, showed eight watersheds (out of 15) with values within the 0.75 to 1.0 range (or very good category) when applied to total length flow and P2 under stationary conditions (Table S15). FAA, Kirpich (adjusted and unadjusted), Kirpich-Kerby (unadjusted), MinVivienda with FAA, and MinVivienda with NRCS shallow concentrated flow followed, with seven watersheds within the very good category. The Espey-Winslow, Sheridan, and Bransby-Williams equations performed poorly, with, respectively, zero, two, and five watersheds exhibiting NSE values within the very good category. Based on these results, Espey-Winslow is not recommended. On the other hand, the Sheridan equation, despite its poor performance, demonstrated that indeed it works best when used on watersheds with low slope. The two watersheds (7 de Agosto and Manga) where the equation had high NSE values had slopes of 0.13% and 0.05%. It is important to point out that the Sheridan equation did not perform well in the Crespo watershed, despite having a slope of 0.01%. A look at other watersheds’ physical parameters permitted us to notice that the Crespo watershed was the least urbanized of the three (Table S2), which could partially explain its performance, with negative NSE, high RSR, and negative PBIAS (this denotes overestimation) (Tables S15 and S16). Overall, the poor performance of Espey–Winslow and Sheridan were in line with the findings of Gericke and Smithers [8,29].
The slope adjustment for both Kerby and Kirpich equations and the Kerby-Kirpich methodology was performed in watersheds Crespo, Pie del Cerro Cra 16A, and Manga (the only ones that complied with the adjustment conditions), aiming towards better results. Apropos the Kerby equation, however, the adjustment did not bring any improvement judging by the NSE values obtained under stationary conditions (Table S15) in either case (each flow and total length). As for the Kirpich equation, the adjustment made the NSE values decline, except for Pie del Cerro Cra 16A, where NSE increased from 0.62 to 0.72 when the equation was applied to each flow (Table S15). For the Kerby-Kirpich methodology, only the Pie del Cerro Cra 16A watershed presented improvement, with NSE values increasing from 0.68 (unadjusted) to 0.76 (slope adjusted). Based on the results and considering the watersheds’ types of flow (Crespo and Manga with shallow concentrated flow and Pie del Cerro Cra 16A with all three flows), the slope adjustment seemed to work best for the channel flow (Kirpich equation).
When P2 under NSC was used (Table S16), it was observed that the Kerby equation’s performance slightly worsened when compared to that obtained with P2 under SC. It moved from eight watersheds with NSE values within the very good category to seven. Similarly, the MinVivienda with Kerby equation and Kerby-Kirpich slope-adjusted method experienced the same setback: the first decreased from eight watersheds to seven and the latter from eight to six. On the other hand, the NRCS lag equation increased from eight to nine watersheds, PMDPC remained constant with eight watersheds, and MinVivienda with the NRCS equation (for shallow concentrated flow) moved from seven to nine watersheds (the NSE values of watersheds Bazurto and San Francisco La Loma increased from 0.7 to 1.0 and from 0.48 to 0.75, respectively).
All Tc equations applied to the total length performed better than when applied to the each length approach, corroborating the notion that their use should be limited to what they were designed for. As for the use of P2 under SC or NSC, NSE results indicated that, under SC, more Tc equations ended up having up to eight watersheds (8 out of 15, or 53.3%) within the very good category. On the other hand, under NSC, more watersheds (9 out of 15, or 60%) lay within the same category despite having only two Tc equations with that result (NRCS lag equation and MinVivienda with NRCS velocity method equation for shallow concentrated flow). This could be also an indicator of the local rainfall behavior’s non-stationarity, as previously mentioned. Nonetheless, further investigation is recommended.
In terms of both the error (RSR) and bias (PBIAS) performance (Tables S15 and S16), Tc equations with NSE values in the range of 0.75 to 1.0 had also low values of RSR (within the very good category, 0.0 to 0.5) in either case of P2 under SC or NSC. Tc equations applied to total flow performed better than each flow, which was also previously noticed. Notwithstanding, most of the equations presented bias, with values greater than or equal to ±25% (unsatisfactory). With either P2 under SC or NSC, there was a tendency for all equations to overestimate (negative PBIAS) with the each flow approach, whereas the opposite was true for the total flow approach. Kirpich was the equation with more watersheds (four) with PBIAS the under very good category (PBIAS < ±10%) under stationary conditions, followed by the FAA equation and MinVivienda methodology (with Kerby and FAA equations) with three, and the Kerby, NRCS lag equation, J-C, and Sheridan, with two watersheds. Under non-stationary conditions, the number of watersheds under the very good category dropped by one unit in some of the equations: Kirpich (from 4 to 3), Kerby and J-C (from 2 to 1), J-C (from 1 to 0), and MinVivienda with Kerby equation (from 3 to 2). However, this was a slight performance diminishment as all those watersheds fell into the following category (±10% ≤ PBIAS < ±15%, or “good” category), except for the MinVivienda with Kerby equation.
The concernment of the obtained PBIAS results lies chiefly in the fact that, in ungauged watersheds, where the computation of the design flow for a given return period is mostly performed via rainfall-runoff models, the Tc plays a key role since the duration of design rainfall depends on it. This is particularly true, for instance, when using the rational method for peak flow estimation in small urban watersheds (area < 80 ha) [14,42,43]. In this rainfall-runoff model, rainfall intensity is obtained from Intensity-Duration-Frequency (IDF) curves, whose main input is the rainfall duration, which is assumed to be equal to the Tc. As a result, any tendency to over- or underestimate the Tc will affect the design runoff and the inherent implications of this on the design of hydraulic structures, which might lead to life, infrastructure, and economic losses [80,81]. As a result, efforts to reduce possible errors when computing Tc should be made by minimizing any source of uncertainty, such as the estimation of the variables associated with a particular equation (rainfall, slope, area, land cover, flow path length, etc.) [5,10,82]. The more input variables a model has, there more chances there are to introduce errors, especially in hydrology, where the watershed’s morphometric parameter estimation depends on map scales and imagery interpretation. For instance, a closer look at watersheds Pie del Cerro Cra. 16A and Pie del Cerro Cra. 21B, which have similar area sizes (52.85 ha and 56.58 ha) and flow path lengths (1233 m and 1480 m) (Table 2), revealed the following:
- (a)
- Equations with two and three variables outperformed Espey–Winslow despite having two additional variables related to land cover (channelization factor and impervious area percentage), which did not bring any advantage, especially in the case of the channelization factor (Table 4 and Tables S7–S10). In fact, Espey–Winslow was the equation with the poorest performance of all (Tables S15 and S16).
 Table 4. Variables in each Tc Equation.
Table 4. Variables in each Tc Equation. - (b)
- The slope and length of each of the different flow types seems to affect the equations’ performance. Their average slope is different, with values of 9.2% and 15.2%, respectively. Additionally, Pie del Cerro Cra 21B has 91% (versus 58% of Pie del Cerro Cra 16A) of its total flow path corresponding to shallow concentrated flow, with a slope of 14.8% (Table 2). In this sense, watershed area and total urbanized area appear to also play a role in the equations’ performance given that the NRCS lag equation and Bransby–Williams performed well in the Bazurto watershed, despite having an average slope of 18.8% (larger than Pie del Cerro Cra 21B), 82% of its total flow path as shallow concentrated flow with a slope of 15.1% (similar to Pie del Cerro Cra 21B), and an area of 66.05 ha (Table 2). These two equations did not perform well in Pie del Cerro Cra 16A and Cra 21B even though the watersheds have similar area sizes and urbanized areas.
The authors also estimated the average Tc from equations Miller, FAA, Kerby, E-W, NRCS lag equation, Kirpich, Bransby-Williams, Johnstone–Cross, Sheridan, and PMDPC so as to mimic the procedure practiced by some hydrologists (none of the Tc methodologies assessed herein were included as they are not typically used to estimate Tc). Outliers were first identified (and excluded) by means of box plots. The resulting Tc average values were compared with those from the NRCS velocity method for each of the watersheds. The average Tc approach also showed poor agreement, with a tendency to underestimate in nine and ten watersheds for the each flow and total length approaches, respectively, under SC or NSC (gray cells in Table S6). The underestimation was less evident under non-stationary conditions.
All Tc equations (and Tc estimation methodologies) evaluated in this study showed setbacks, including those recommended by the Colombian drainage manuals MinVivienda [42] and Invías [41]. Inasmuch as these two manuals are used by many as almost indisputable references for hydrological analyses in the case of Colombia, the findings herein reaffirm the necessity of assessing the suitability of a given equation prior to its application, especially in ungauged areas. In the context of Cartagena de Indias, this becomes particularly relevant due to the use of an ad hoc Tc equation (PMDPC) to design eight concrete open channels for the first phase of the city’s Stormwater Management Master Plan, one of which (7 m by 1.0 m and 400 m long channel, which was built less than two years ago) is overflowed every year during the rainy season (Figure 4). The PMDPC’s performance was no better than that of the other equations, despite featuring a so-called regional constant (Table S9, K = 4.47) not validated by any study. Furthermore, the PMDPC equation has been utilized irrespective of the watershed’s flow type, regardless of the fact that the value of K is the same for all channel surfaces. Using an equation originally developed for shallow concentrated flows for watersheds that also have sheet and/or channel flows seems, then, counterintuitive to the nature of the NRCS velocity method since it implies that all watersheds only have shallow concentrated flows. Likewise, the PMDPC’s PBIAS poor performance indicated that the equation tended to overestimate in 60% of the selected watersheds, which leads to both smaller design rainfall intensity and peak flow values.

Figure 4.
Emiliano Alcalá channel during (a) dry season and (b) rainy season.
Adjustment factors have been proposed (Table 5) for those empirical equations that showed R2 values within the good and very good categories in Table S5. The adjustment factors are the inverse of the slope of the trend line equations obtained when Tc-simulated (empirical equations) and Tc-true (NRCS velocity method) values were scatter-plotted (trend line equations are summarized in Table S5), which makes the time of concentration values closer to the 1:1 line. This can be observed in Figure 5, where the majority of the time of concentration values obtained by means of the FAA and Kirpich equations before and after the proposed adjustment factors for the fifteen selected watersheds tended to follow the 1:1 line (black dashed line). Despite the improvement observed, the use of these adjustment factors is only recommended for the selected watersheds and/or for watersheds exhibiting similar characteristics.

Table 5.
Proposed adjustment factors.
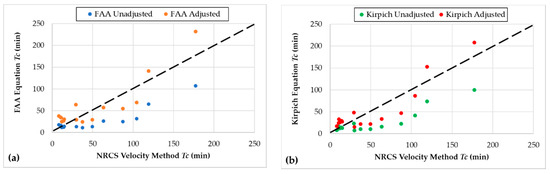
Figure 5.
Time of concentration values before and after proposed adjustment factors. (a) FAA equation and (b) Kirpich equation.
Finally, the findings of this study are in line with other aforementioned studies with respect to the broad range of Tc values that designers have to typically deal with when performing a hydrological analysis. Based on the results herein and in the absence of measured rainfall and flow data, the authors recommend the estimation of Tc by means of the NRCS velocity method given the methodology’s conceptual robustness and the availability of data of the methodology’s variables.
5. Conclusions
Estimating the design rainfall and its associated runoff values for a given return period in ungauged watersheds can become daunting as it depends on various assumptions, such as the Tc computation among a large array of available empirical equations with different results. Thus, this task should be always accompanied by the best engineering judgement, which also involves an assessment of equations. Hydrologic and hydraulic (H&H) analysis for stormwater management such as dam-breach analyses; flood-prone area delineation and flood risk analyses; stream restoration; erosion, sediment, and contaminant load estimation, and conventional and sustainable drainage system design must be as accurate as possible when estimating all variables [10,80,81,83,84,85,86]. This includes the estimation of the Tc, which becomes relevant when using rainfall-runoff models and software programs requiring such input for the design runoff computation (e.g., rational method, HEC-HMS, WinTR-55, WinTR-20, StormCAD®/SewerCAD®). In this context, the results of this study shed light on the following: (a) the fact that selecting a given equation cannot be taken as a random process in a hydrological analysis, which implies being aware of the equation’s background and limitations; (b) the identification of suitable equations for the area of study to start ruling out those that definitely do not perform well; (c) the need to implement, in any given location, a robust network of flow and rain gauges so as to have a better understanding of the local hydrology, which should include the derivation of local Tc equations for rural and urban areas given that none of equations utilized in this study performed well in all of the fifteen selected watersheds, and (d) conduct these types of studies in both urban and rural areas given the different hydrological and hydraulic behavior of their watersheds and water courses. Finally, in the absence of measured rainfall and runoff data in a particular site, the authors recommend the use of the NRCS velocity method for Tc estimation, which, despite its own limitations [3], has proven to be reliable over the years since its inception. Validation of the resulting design runoff derived from the Tc estimation, whenever possible, should be performed via (a) hydraulic simulation using available water marks and/or (b) hydrologic simulation by means of software programs such as SWMM, which does not require the Tc as an input.
Supplementary Materials
The following are available online at https://www.mdpi.com/2306-5338/7/3/47/s1. Table S1: Identified flow paths information at each watershed within the study area, Table S2: Watersheds’ additional variables used for Tc estimation, Table S3: Tc minimum, maximum, average, and standard deviation with P2 under stationary conditions, Table S4: Tc minimum, maximum, average, and standard deviation with P2 under non-stationary conditions, Table S5: Linear trend line equations between simulated and true Tc values, Table S6. Comparison between NRCS velocity method and Tc average, Table S7. Sheet flow equations, Table S8. Shallow concentrated flow equations, Table S9. Channel flow equations, Table S10. Additional Tc estimation methodologies, Table S11. Estimated Tc (min) values for each flow for P2 under stationary conditions, Table S12. Estimated Tc (min) values for total length flow for P2 under stationary conditions, Table S13. Estimated Tc (min) values for each flow for P2 under non-stationary conditions, Table S14. Estimated Tc (min) values for total length flow for P2 under stationary conditions, Table S15. Results of statistical variables with P2 under stationary conditions, Table S16. Results of statistical variables with P2 under non-stationary conditions.
Author Contributions
GIS and data collection and analysis, J.M.P., B.M.-Z., and O.M.V.-M.; analysis, writing and review, K.T. and J.A.M.-B.; writing—original draft preparation, supervision, and analysis, Á.G.-Á. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors express no acknowledgement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McCuen, R.H.; Wong, S.L.; Rawls, W.J. Estimating Urban Time of Concentration. J. Hydraul. Eng. 1984, 110, 887–904. [Google Scholar] [CrossRef]
- McCuen, R.H.; Wong, S.L.; Rawls, W.J. Closure to “Estimating Urban Time of Concentration”. J. Hydraul. Eng. 1987, 113, 127–128. [Google Scholar] [CrossRef]
- U.S. Department of Agriculture Natural Resources Conservation Service (USDA-NRSC), C.E.D. Urban. Hydrology for Small Watersheds, Technical Release 55 (TR-55); U.S. Department of Agriculture Natural Resources Conservation Service (USDA-NRSC), C.E.D.: Washington, DC, USA, 1986.
- Huber, W.C. Discussion of “Estimating Urban. Time of Concentration”. J. Hydraul. Eng. 1987, 113, 122–124. [Google Scholar] [CrossRef]
- McCuen, R.H. Uncertainty Analyses of Watershed Time Parameters. J. Hydrol. Eng. 2009, 14, 490–498. [Google Scholar] [CrossRef]
- Sharifi, S.; Hosseini, S.M. Methodology for Identifying the Best Equations for Estimating the Time of Concentration of Watersheds in a Particular Region. J. Irrig. Drain. Eng. 2011, 137, 712–719. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Tauro, F.; Porfiri, M. Temps de concentration: Un paradoxe dans l’hydrologie moderne. Hydrol. Sci. J. 2012, 57, 217–228. [Google Scholar] [CrossRef]
- Gericke, O.J.; Smithers, J.C. Review of methods used to estimate catchment response time for the purpose of peak discharge estimation. Hydrol. Sci. J. 2014, 59, 1935–1971. [Google Scholar] [CrossRef]
- Michailidi, E.M.; Antoniadi, S.; Koukouvinos, A.; Bacchi, B.; Efstratiadis, A. Timing the time of concentration: Shedding light on a paradox. Hydrol. Sci. J. 2018, 63, 721–740. [Google Scholar] [CrossRef]
- Perdikaris, J.; Gharabaghi, B.; Rudra, R. Reference Time of Concentration Estimation for Ungauged Catchments. Earth Sci. Res. 2018, 7, 58. [Google Scholar] [CrossRef]
- U.S. Department of Agriculture Natural Resources Conservation Service (USDA-NRCS). Time of Concetration. In National Engineering Handbook (NEH); U.S. Department of Agriculture Natural Resources Conservation Service (USDA-NRCS): Washington, DC, USA, 2010; p. 29. [Google Scholar]
- Ontario Ministry of Transportation (OMTO). Drainage Management Manual; Ontario Ministry of Transportation (OMTO): Toronto, ON, Canada, 1997.
- U.S. Department of Transportation Federal Highway Administration (USDOT-FHWA). Hydraulic Engineering Circular No. 22 (HEC-22) . In Urban Drainage Design Manual, 3rd ed.; U.S. Department of Transportation Federal Highway Administration (USDOT-FHWA): Washington, DC, USA, 2009. [Google Scholar]
- Texas Department of Transportation (TxDOT). Hydraulic Design Manual (Revised); Texas Department of Transportation (TxDOT): Austin, TX, USA, 2019.
- U.S. Department of Agriculture Natural Resources Conservation Service (USDA-NRCS). Conservation Engineering Division WinTR-20 User Guide; U.S. Department of Agriculture Natural Resources Conservation Service (USDA-NRCS): Washington, DC, USA, 2006.
- WinTR-55; (Version 1.00.10); U.S. Department of Agriculture Natural Resources Conservation Service (USDA-NRSC): Washington, DC, USA, 2017.
- HydroCAD Stormwater; (Version 10.1); Modeling System; HydroCAD Software Solutions LLC: Chocorua, NH, USA, 2020.
- Autodesk Storm and Sanitary Analysis; (Version 2019); Autodesk Inc.: San Rafael, CA, USA, 2019.
- Storm Water Management Model (SWMM); (Version 5.1); United States Environmental Agency (USEPA): Washington, DC, USA, 2020.
- Hydrologic Modeling System (HEC-HMS); (Version 4.4.1); U.S. Army Corps of Engineers: Washington, DC, USA, 2018.
- SewerCAD; (Version 10.02.00.55); Bentley Systems: Exton, PA, USA, 2019.
- StormCAD; (Version 10.02.00.55); Bentley Systems: Exton, PA, USA, 2019.
- San Diego State University (SDTU). Online Time of Concentration: Time of Concentration of Small Watersheds. Available online: http://ponce.sdsu.edu/onlinetimeofconcentration.php (accessed on 16 March 2020).
- Manoj, K.C.; Fang, X. Estimating Time of Concentration of Overland Flow on Impervious Surface using Particle Tracking Model. In Proceedings of the World Environmental and Water Resources Congress 2014, Oregon, Portland, 1–5 June 2014; Volume 0300, pp. 30–37. [Google Scholar]
- Yoo, C.; Lee, J.; Park, C.; Jun, C. Method for Estimating Concentration Time and Storage Coefficient of the Clark Model Using Rainfall-Runoff Measurements. J. Hydrol. Eng. 2014, 19, 626–634. [Google Scholar] [CrossRef]
- De Almeida, I.K.; Almeida, A.K.; Steffen, J.L.; Alves Sobrinho, T. Model for Estimating the Time of Concentration in Watersheds. Water Resour. Manag. 2016, 30, 4083–4096. [Google Scholar] [CrossRef]
- Sandoval-Erazo, W.; Toulkeridis, T.; Rodriguez-Espinosa, F.; Mora, M.J.M. Velocity and time of concentration of a basin-A renewed approach applied in the Rio Grande Basin, Ecuador. IOP Conf. Ser. Earth Environ. Sci. 2018, 191. [Google Scholar] [CrossRef]
- Vahabzadeh, G.; Saleh, I.; Safari, A.; Khosravi, K. Determination of the best method of estimating the time of concentration in pasture watersheds (case study: Banadak Sadat and Siazakh Watersheds, Iran). J. Biodivers. Environ. Sci. 2013, 3, 150–159. [Google Scholar]
- Gericke, O.J.; Smithers, J.C. Are estimates of catchment response time inconsistent as used in current flood hydrology practice in South Africa? J. S. Afr. Inst. Civ. Eng. 2016, 58, 2–15. [Google Scholar] [CrossRef]
- De Almeida, I.K.; Almeida, A.K.; Anache, J.A.A.; Steffen, J.L.; Alves Sobrinho, T. Estimation on time of concentration of overland flow in watersheds: A review. Geociencias 2014, 33, 661–671. [Google Scholar]
- Kaufmann de Almeida, I.; Kaufmann Almeida, A.; Garcia Gabas, S.; Alves Sobrinho, T. Performance of methods for estimating the time of concentration in a watershed of a tropical region. Hydrol. Sci. J. 2017, 62, 2406–2414. [Google Scholar] [CrossRef]
- Salimi, E.T.; Nohegar, A.; Malekian, A.; Hoseini, M.; Holisaz, A. Estimating time of concentration in large watersheds. Paddy Water Environ. 2017, 15, 123–132. [Google Scholar] [CrossRef]
- Wong, T.S.W.; Asce, F. Assessment of Time of Concentration Formulas for Overland Flow. J. Irrig. Drain. Eng. 2005, 131, 383–387. [Google Scholar] [CrossRef]
- Fang, X.; Thompson, D.B.; Cleveland, T.G.; Pradhan, P.; Malla, R. Time of Concentration Estimated Using Watershed Parameters Determined by Automated and Manual Methods. J. Irrig. Drain. Eng. 2008, 134, 202–211. [Google Scholar] [CrossRef]
- Wong, T. Evolution of Kinematic Wave Time of Concentration Formulas for Overland Flow. J. Hydrol. Eng. 2009, 14, 739–744. [Google Scholar] [CrossRef]
- Manoj, K.C.; Fang, X.; Yi, Y.J.; Li, M.H.; Cleveland, T.G.; Thompson, D.B. Estimating time of concentration on low-slope planes using diffusion hydrodynamic model. In Proceedings of the World Environmental And Water Resources Congress 2012, Albuquerque, NM, USA, 20–24 May 2012; pp. 360–371. [Google Scholar] [CrossRef]
- Longo, E.; Rooney, J. Development of a General Protocol to Enhance the Hydrological Analysis Techniques for Urban Catchments in Ireland. Geosciences 2018, 8, 252. [Google Scholar] [CrossRef]
- Aristizábal, V.; Hernández, B.; Vélez, J. Manual de Hidrología para Obras Viales Basado en el Uso de Sistemas de Información Geográfica; Universidad Nacional de Colombia: Manizales, Colombia, 2012. [Google Scholar]
- Otálvaro, M. Consideraciones Generales para Realizar el Diseño Hidrológico e Hidráulico de Obras de Drenaje para Vías de Bajos Volúmenes de Tránsito. Caso de Estudio Pista de Prueba Urrao-Antioquia; Universidad de Medellín: Medellín, Colombia, 2016. [Google Scholar]
- Ochoa, T. Hidrología Hidráulica y Socavación en Puentes; ECOE Ediciones Ltda: Bogota, Colombia, 2017. [Google Scholar]
- Instituto Nacional de Vías de Colombia (Invías). Manual de Drenajes para Carreteras (Road Drainage Manual); Ministerio de Transporte de Colombia: Bogotá, Colombia, 2009.
- Ministry of Housing, City, and Territory (MinVivienda), R. of C. Technical Regulations for the Sector of Drinking Water and Basic Sanitation (RAS), Title D, Domestic Wastewater and Stormwater Collection Systems; Ministerio de Vivienda de Colombia: Bogotá, Colombia, 2016.
- Ministry of Housing, City, and Territoty (MinVivienda), R. of C. Resolution 0330 of 8 June 2017, Technical Guidelines for the Sector of Potable Water and Basic Sanitation (RAS); Ministerio de Vivienda de Colombia: Bogotá, Colombia, 2017.
- Vélez, J.J.; Gutiérrez, A. Estimación del Tiempo de Concentración y tiempo de rezago en la Cuenca Experimental Urbana De La Quebrada San Luis, Manizales. Dyna 2011, 78, 58–71. [Google Scholar]
- Torres, J.A.; Ordoñez, J.I.; Duque, R. Análisis de incertidumbre del tiempo de concentración en la modelación de eventos de tormenta en la cuenca alta del Río Magdalena. In Proceedings of the XXV Congreso Latinoamericano de Hidráulica, San José, Costa Rica, 9–12 September 2012. [Google Scholar]
- Montoya, J.; Patiño, J. Estudio Hidrometereológico y Geomorfológico de Diez Quebradas del Valle de Aburrá; Universidad EAFIT: Medellín, Colombia, 2001. [Google Scholar]
- Avila, L.; AÁvila, H.; Sisa, A. A reactive early warning model for urban flash flood management. World Environ. Water Resour. Congr. 2017, 372–382. [Google Scholar] [CrossRef]
- Maidment, D.R. Handbook of Hydrology; MacGraw Hill: New York, NY, USA, 1993. [Google Scholar]
- Welle, P.I.; Woodward, D. Technical Note No. N4, Time of concentration (Revised); U.S. Department of Agriculture National Resources Conservation Service (USDA-NRCS): Chester, PA, USA, 2003.
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological modeling of the Iroquois River watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines. 2007; Volume 50, pp. 885–900. Available online: https://www.researchgate.net/publication/43261199_Model_Evaluation_Guidelines_for_Systematic_Quantification_of_Accuracy_in_Watershed_Simulations (accessed on 8 May 2020). [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Boskidis, I.; Gikas, G.D.; Sylaios, G.K.; Tsihrintzis, V.A. Hydrologic and Water Quality Modeling of Lower Nestos River Basin. Water Resour. Manag. 2012, 26, 3023–3051. [Google Scholar] [CrossRef]
- Rauf, A.; Ghumman, A. Impact Assessment of Rainfall-Runoff Simulations on the Flow Duration Curve of the Upper Indus River—A Comparison of Data-Driven and Hydrologic Models. Water 2018, 10, 876. [Google Scholar] [CrossRef]
- González-Álvarez, Á.; Coronado-Hernández, O.; Fuertes-Miquel, V.; Ramos, H. Effect of the Non-Stationarity of Rainfall Events on the Design of Hydraulic Structures for Runoff Management and Its Applications to a Case Study at Gordo Creek Watershed in Cartagena de Indias, Colombia. Fluids 2018, 3, 27. [Google Scholar] [CrossRef]
- Instituto de Hidrología Meteorología y Estudios Ambientales (IDEAM) Atlas Climatológico de Colombia 1981–2010. Available online: http://atlas.ideam.gov.co/visorAtlasClimatologico.html (accessed on 8 May 2020).
- Centro de Investigaciones Oceanográficas e Hidrográficas (CIOH). General Circulation of the Atmosphere in Colombia; CIOH: Cartagena de Indias, Colombia, 2010. [Google Scholar]
- Perez, G.; Salazar, I. La Pobreza en Cartagena: Un Análisis por barrios; Banco de La República: Cartagena de Indias, Colombia, 2007; Volume 94. [Google Scholar]
- EPA-Cartagena & UDC. Diseño del sistema inteligente de monitoreo de la calidad ambiental del distrito de Cartagena. Estud. Integr. La Calid. Ambient. Del Sist. Caños Y Lagos 2015, 2. [Google Scholar]
- ArcGIS, (version 10.6.1); Esri Inc.: Redlands, CA, USA, 2019.
- Crippen, R.; Buckley, S.; Agram, P.; Belz, E.; Gurrola, E.; Hensley, S.; Kobrick, M.; Lavalle, M.; Martin, J.; Neumann, M.; et al. NASADEM Global Elevation Model: Methods and Progress. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B4, 125–128. [Google Scholar] [CrossRef]
- Azizian, A. Uncertainty Analysis of Time of Concentration Equations based on First-Order-Analysis (FOA) Method. Am. J. Eng. Appl. Sci. 2018, 11, 327–341. [Google Scholar] [CrossRef]
- Iowa State University’s Institute for Transportation (InTrans). Iowa Statewide Urban Design and Specifications Program Urban Hydrology and Runoff (2B-3 Time of Concentration). In SUDAS Design Manual; Iowa State University: Ames, IA, USA, 2020. [Google Scholar]
- Miller, W.C. Evolving a shortcut for design of storm sewers. Munic. Util. 1951, 89, 42–59. [Google Scholar]
- Cleveland, T.G.; Thompson, D.B.; Ming-Han Li, X.F. Guidance for Estimation of Time of Concentration in Texas for Low-Slope Conditions (Report # 0-6382-P1); Texas Department of Transportation: Austin, TX, USA, 2012.
- Federal Aviation Agency (FAA). Airport Drainage; Department of Transport Advisory Circular: Washington, DC, USA, 1970.
- Espey, W.H.; Winslow, D.E. The Effects of Urbanisation on Unit Hydrographs for Small Watersheds; Tracor Incorporated: Houston, Austin, TX, USA, 1968; Report No. 68/ 975U and 1006/U. [Google Scholar]
- Kerby, W. Time of concentration for overland flow. Civ. Eng. 1959, 29, 174. [Google Scholar]
- Kirpich, Z. Time of concentration of small agricultural watersheds. Civ. Eng. 1940, 10, 362. [Google Scholar]
- Williams, G.B. Flood discharges and the dimensions of spillways in India. Engineering 1922, 134–321. [Google Scholar]
- Johnstone, D.; Cross, W.P. Elements of Applied Hydrology; Ronald Press: New York, NY, USA, 1949. [Google Scholar]
- Sheridan, J.M. Hydrograph Time Parameters for Flatland Watersheds. Trans. ASAE 1994, 37, 103–113. [Google Scholar] [CrossRef]
- Alcaldía Mayor de Cartagena de Indias (AMCI). Estudios y Diseños del Plan. Maestro de Drenajes Pluviales del Distrito de Cartagena; Consorcio Consultores Cartageneros: Cartagena de Indias, Colombia, 2009. [Google Scholar]
- Roussel, M.C.; Thompson, D.B.; Fang, X.; Cleveland, T.G.; Garcia, C.A. Time-Parameter Estimation for Applicable Texas Watersheds; Texas Department of Transportation: Beaumont, TX, USA, 2005.
- Te Chow, T.; Maidment, D.R.; Mays, L.W. Applied Hydrology, 1st ed.; McGraw-Hill: New York, NY, USA, 1988; ISBN 0-07-010810-2. [Google Scholar]
- ENVI, (version 5.1); Harris Geospatial Solutions Inc.: Boulder, CO, USA, 2019.
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Legates David, R.; McCabe, G.J., Jr. Evaluating the use of goodness-of-fit measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- González-Álvarez, Á.; Viloria-Marimón, O.M.; Coronado-Hernández, Ó.E.; Vélez-Pereira, A.M.; Tesfagiorgis, K.; Coronado-Hernández, J.R. Isohyetal maps of daily maximum rainfall for different return periods for the Colombian Caribbean Region. Water 2019, 11, 358. [Google Scholar] [CrossRef]
- Duan, W.; Takara, K.; He, B.; Luo, P.; Nover, D.; Yamashiki, Y. Spatial and temporal trends in estimates of nutrient and suspended sediment loads in the Ishikari River, Japan, 1985 to 2010. Sci. Total Environ. 2013, 461–462, 499–508. [Google Scholar] [CrossRef]
- Duan, W.; He, B.; Nover, D.; Fan, J.; Yang, G.; Chen, W.; Meng, H.; Liu, C. Floods and associated socioeconomic damages in China over the last century. Nat. Hazards 2016, 82, 401–413. [Google Scholar] [CrossRef]
- Martins, L.; Diéz-Herrero, A.; Bodoque, J.; Bateira, C. Time of Concentration equations: The role of morphometric uncertainties in flood risk analysis and management. In Proceedings of the EGUGA, Vienna, Austria, 17–22 April 2016. EPSC2016-15660. [Google Scholar]
- Hoogestraat, G.K. Flood hydrology and dam-breach hydraulic analyses of four reservoirs in the Black Hills, South. Dakota: U.S. In Geological Survey Scientific Investigations Report 2011–5011; U.S. Geological Survey (USGS): Reston, VA, USA, 2011. [Google Scholar]
- Poleto, C.; Rutinéia, T. Sustainable Urban Drainage Systems. In Drainage Systems; IntechOpen: London, UK, 2012; ISBN 978-953-51-0243-4. [Google Scholar]
- Jiang, X.; Yang, L.; Tatano, H. Assessing Spatial Flood Risk from Multiple Flood Sources in a Small River Basin: A Method Based on Multivariate Design Rainfall. Water 2019, 11, 1031. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA). Guidance for Flood Risk Analysis and Mapping. In Hydrology: Rainfall-Runoff Analysis; U.S. Department of Homeland Security: Washington, DC, USA, 2019. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).