Next Article in Journal
Evaluating SWAT Model Performance for Runoff, Percolation, and Sediment Loss Estimation in Low-Gradient Watersheds of the Atlantic Coastal Plain
Previous Article in Journal
Potential Impacts of Climate Change on Extreme Weather Events in the Niger Delta Part of Nigeria
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Hydrology
Volume 7
Issue 2
10.3390/hydrology7020020
hydrology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

On the Ability of LIDAR Snow Depth Measurements to Determine or Evaluate the HRU Discretization in a Land Surface Model

by
Michael Weber
1,*,
Moritz Feigl
2,
Karsten Schulz
2 and
Matthias Bernhardt
2
1
Department of Geography, University of Munich, Luisenstraße 37, 80333 Munich, Germany
2
Institute for Hydrology and Water Management, University of Natural Resources and Life Sciences, Muthgasse 18, 1190 Vienna, Austria
*
Author to whom correspondence should be addressed.
Hydrology 2020, 7(2), 20; https://doi.org/10.3390/hydrology7020020
Submission received: 21 February 2020 / Revised: 26 March 2020 / Accepted: 27 March 2020 / Published: 29 March 2020
Browse Figures
Versions Notes

Abstract

:
To find the adequate spatial model discretization scheme, which balances the models capabilities and the demand for representing key features in reality, is a challenging task. It becomes even more challenging in high alpine catchments, where the variability of topography and meteorology over short distances strongly influences the distribution of snow cover, the dominant component in the alpine water cycle. For the high alpine Research Catchment Zugspitze (RCZ) a new method for objective delineation of hydrological response units (HRUs) using a time series of high resolution LIDAR derived snow depth maps and the physiographic properties of the RCZ is introduced. Via principle component analysis (PCA) of these maps, a dominant snow depth pattern, that turned out to be largely defined during the (winter) accumulation period was identified. This dominant pattern serves as a reference for HRU delineations on the basis of cluster analyses of the catchment’s physiographic properties. The method guarantees for an appropriate, objective, spatial discretization scheme, which allows for a reliable and meaningful reproduction of snow cover variability with the Cold Regions Hydrological Model—at the same time avoiding significant increase of computational demands. Different HRU schemes were evaluated with measured snow depth and the comparison of their model results identified significant differences in model output and best performance of the scheme which best represents measured snow depth distribution.

1. Introduction

Alpine catchments are characterized by changes in topography and meteorology over short distances. Hence, hydrological processes and storages are highly variable in space and time. Since runoff regimes of alpine catchments are largely influenced by snow accumulation and ablation patterns, their heterogeneity has major influence on the observed runoff during the ablation period [1]. Hydrological models applied in alpine catchments need to account for snow cover variability in order to produce meaningful and reliable results. This has to be reflected in the model formulations as well as in the spatial model discretization. Both factors are in general dependent on each other as a high model resolution does only lead to a surplus in the achieved information content if the model formulations are able to reflect processes, which are active at the chosen spatial resolution [2,3]. If this is not the case, more spatial elements will not lead to enhanced information content. The difficult task now is to identify the most adequate spatial model discretization scheme to achieve the optimal information content without increasing the computational demands by introducing too many model elements. The usual way for guaranteeing the coverage of all hydrological key features is the application of a high resolution yet computationally demanding, raster based discretization [4]. This approach is used e.g., by the Water balance Simulation Model (WaSiM) [5], ALPINE3D [6] or the mesoscale hydrologic model (mHM) [7]. However, this approach does not make use of any information about the characteristics of the investigated area itself. As a result, there is a chance that the spatial resolution in general is by far too high for large parts of the area of interest just for covering some specific features, which are only relevant in certain parts of the model domain. A solution, which tries to omit this effect and which makes use of catchment specific information is the concept of hydrological response units (HRUs). HRUs are defined as “distributed, heterogeneously structured entities having a common climate, land use and underlying pedo-topo-geological associations controlling their hydrological dynamics” [8]. Prominent representatives of HRU based models are the Precipitation-Runoff Modeling System/Modular Modeling System (PRMS/MMS) [8,9], the Soil and Water Assessment Tool (SWAT) [10], or the Cold Regions Hydrological Model (CRHM) [11]. A shortcoming of HRUs is that their delineation often dependents on the operator. The resulting HRU scheme is therefore neither objective nor reproducible by other scientists. Approaches to objectively delineate HRUs usually use surface and subsurface characteristics (e.g., geology, soil type, vegetation, slope, aspect) that are known to influence hydrological processes [8,12,13,14]. Yet, the disadvantage of these approaches is that they do not directly represent the hydrologically dominant component or processes of the water cycle. The heterogeneity of key hydrological processes in alpine catchments makes a meaningful and reproducible delineation of HRUs that accounts for the dominant hydrological component even more challenging. Therefore, the key question in this study is: Is it possible, to objectively delineate HRUs in the high alpine Research Catchment Zugspitze (RCZ)? In order to achieve such delineation, a cluster analysis which is based on the physiographic properties of the catchment was performed. The assumption is that land surface properties influence the meteorological situation and thus snow cover distribution [15,16,17,18]. Therefore, the focus of this study is on snow cover distribution. In contrast to the low land snow cover, a mountain snow cover shows pronounced heterogeneity resulting from the complex terrain in combination with the meteorological situation that is highly variable, too [1,18,19]. In addition, in high alpine catchments the snow cover is the dominant component of the water cycle [20,21,22,23]. This has to be considered in hydrological models, which are used to predict the alpine water cycle. Prasch et al. [24], Stahl et al. [25], Verbunt et al. [26], Engelhardt et al. [27] and Wulf et al. [28] demonstrated the importance of snow melt as a runoff component in catchments, which are partly or entirely high alpine such as the upper Danube river basin (where the RCZ is part of), the Rhine basin and further high alpine catchments in Norway, Switzerland and the Himalayas. The question that arises from that is: How is it possible to validate the clustering results or, respectively, is it possible to map possible patterns in the snow cover of the RCZ using the physiographic properties?
The solution presented in this study is to use a series of high-resolution snow depth maps derived from a terrestrial LIDAR and to use dominant patterns in snow depth distribution—in case of existence—as a reference for HRU delineation by means of a cluster analysis of the catchment’s physiographic properties. LIDAR measurements have become a well-established method for spatially distributed snow cover monitoring and allow for a spatially and temporally distributed detection of snow depth patterns [29,30,31,32,33]. To detect patterns, a principle component analysis (PCA) which is a common tool for identifying dominant structures in remote sensing data [34,35,36], was applied to the available stack of LIDAR derived snow depth maps. The PCA revealed the clearest and most pronounced snow depth pattern in the accumulation period. Therefore this pattern was used as a reference for HRUs derived by cluster analysis. The presented approach of delineating HRUs is the first that directly links the physiographic properties to the snow cover as the dominant water cycle component of a high alpine catchment. In contrast, previously presented approaches only make use of surface and subsurface information [8,12,13,14]. A similar approach has been presented for a low land catchment using remotely sensed land surface temperature [36]. In order to answer the questions whether the method for HRU delineation produces meaningful results and how different HRU schemes influence model results, model runs with three cluster derived HRU schemes and one with the simpler scheme from [37] that follows elevation bands were performed. The model’s sensitivity was evaluated by a comparison of simulated snow cover and runoff of different HRU schemes and with measured snow depth data. Thereby huge differences were identified and the strong influence the model user has on model output by defining HRUs could be demonstrated. This underpins the necessity of an objective method for HRU delineation.

2. Study Area

The high-alpine RCZ (center coordinates: UTM 5250416 N 653692 E, Figure 1) is located in the Northern Calcareous Alps and is part of the Zugspitze massif. The highest elevated point of the 12 km2 catchment is represented by Mount Zugspitze (2962 m a.s.l.) and its runoff is gauged at 1365 m a.s.l. at the Partnach spring. The environmental research station UFS Schneefernerhaus is located at 2650 m a.s.l. in the RCZ (Figure 1) and provided us with logistical support during the field work for this study. Annual mean temperature measured at Mount Zugspitze is −4.5 °C (1981–2010) while the annual mean precipitation for the same period is 2080 mm a−1 (own calculations from data provided by the station of the German Weather Service (DWD) at Mt. Zugspitze). The Zugspitzplatt, which represents most of RCZ is largely free of vegetation, except from some sparse alpine meadows and pioneer plants. Apart from knee wood in the lower parts (<2000 m a.s.l.) of the catchment, vegetation on the Zugspitzplatt is considered to be insignificant for snow cover development. Due to the geological situation and glacial processes during the Little Ice Age (1550–1850) in the upper part of the catchment and during the Pleistocene in the entire catchment, the terrain of the RCZ is characterized by both, karst and glacial features, forming a rugged surface. This surface shows great heterogeneity in slope angle, exposition and curvature, which leads to complex meteorological conditions in combination with the catchment’s altitudinal gradient of almost 1600 m. There are two meteorological stations, one operated by DWD and one by the Bavarian Avalanche Service (LWD), which provide long term recordings of meteorological parameters and snow depth. DWD automatically records meteorological parameters close to the summit of Mt. Zugspitze, whereas snow depth is measured daily with a snow stake at 2600 m a.s.l. on the Zugspitzplatt. At the lower LWD station (2420 m a.s.l.) all parameters are recorded automatically including snow depth and snow water equivalent (SWE). Snow depth at the LWD station is measured with a Sommer USH-8 ultrasound device from 5m above ground with a beam angle of 12 ° and allows for continuous automatic recordings. At the same time a Sommer SSG snow gauge with a measurement area of 2.4 × 2.8 m records SWE. The device was constructed to minimize ice bridging effects and thus provides highly accurate data. This SWE data are used to correct the snow precipitation measurements, which are conducted with a NIWA/MED-K505 precipitation gauge with a 500 cm2 catching surface and an automatic scale. The precipitation gauge is mounted at 5m above ground. Data from DWD serves as model input whereas LWD data is used for validation. An overview of the RCZ as well as the locations of the weather stations and measured parameters is given in Figure 1 and Table 1. For more detailed information on the physiography of the RCZ, it is referred to [37,38,39,40]. Since the catchment’s snow cover is largely influenced by ski slopes and the goal is to investigate the natural snow depth distribution, a specific field of interest (FOI) was identified which is rather untouched by human activities (Figure 1). The surface of the FOI is very undulant with depressions and ridges of various sizes, and can be regarded as representative for large parts of the Zugspitzplatt, which show a very similar structure.

3. Materials and Methods

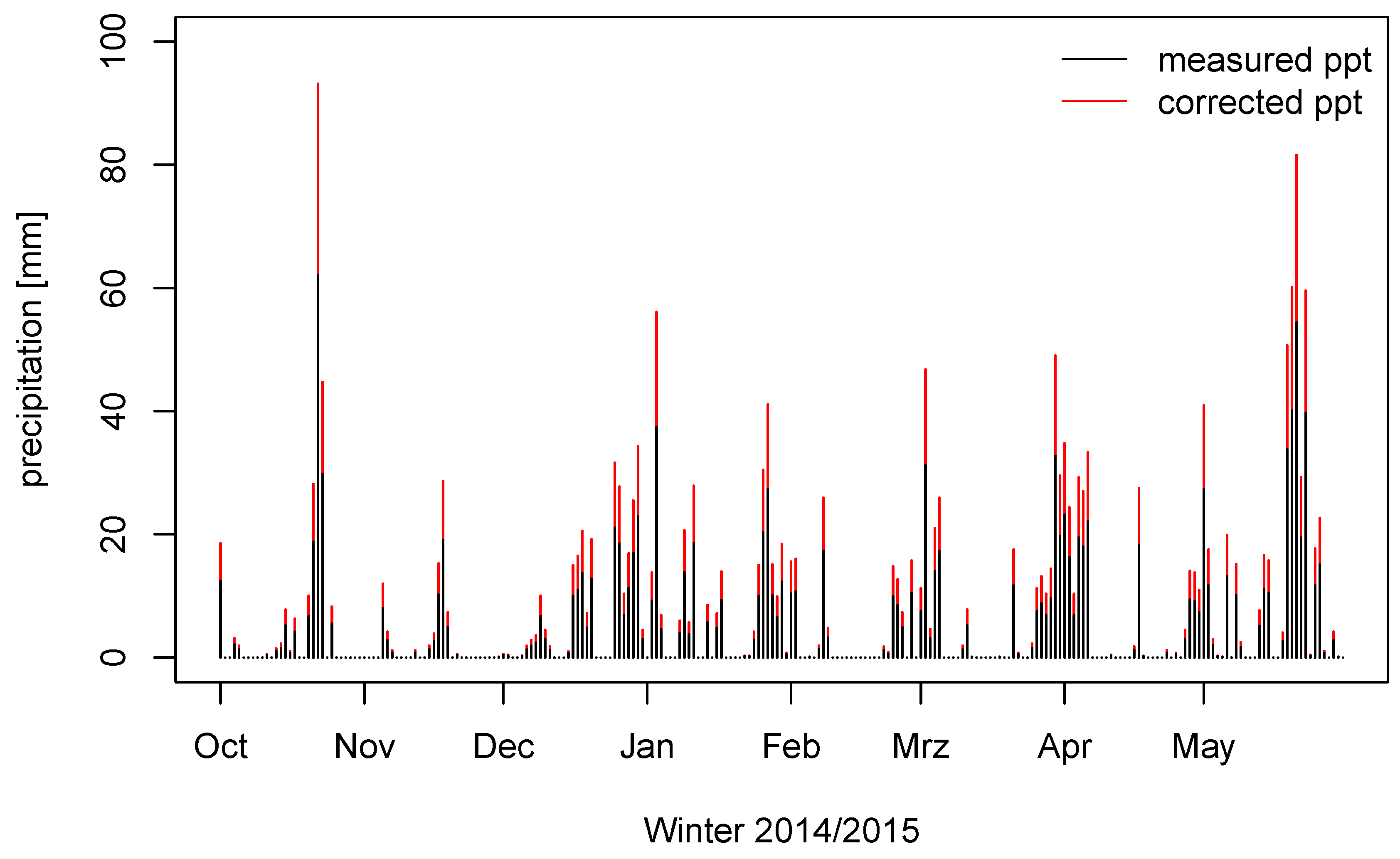
3.1. Hydrological Modelling

CRHM is used to model the hydrology of the RCZ. CRHM was especially designed to model hydrological processes in cold environments and in small-to-medium sized catchments like the RCZ and successfully simulated hydrological processes in various environments such as prairies, forests, arctic, and alpine regions, including the RCZ [37,41,42,43,44,45,46,47]. A detailed description of CRHM, its components, and the implemented processes can be found in [11]. For means of comparability, the parameterization and modules of [37] were chosen as basis for the hydrological modeling in the present study. CRHM is driven by hourly meteorological data, which are provided by the Wetterhütte Zugspitze of the DWD (Figure 1, Table 1) for the period 1998–2016. The data is preprocessed in the same way like in [37], which includes the detection and elimination of measurement errors and the interpolation of gaps according to the procedure proposed by [48]. Due to large data gaps, the measurements of the LWD station (Figure 1, Table 1) were not used as model input. However, the snow water equivalent (SWE) and precipitation data from the station were used to assess the underestimation in snow precipitation measurements. Therefore, we compared winter sums of positive daily SWE change (only snowfall events are considered) and sums of winter precipitation (only snow) from 2012–2017 (SWE available since 2012). Winter was defined as the period from October to May, which is the main accumulation period in RCZ. To be sure that only snow precipitation is included in the analysis all SWE and precipitation values at temperatures higher than 0 °C were excluded. Basis for this threshold value is the study from [49]. They identified that the threshold in the Northern Hemisphere is within a range of −0.4–2.4 °C in 95% of the precipitation events. Moreover, they found out that the Alps have a slightly higher average threshold value than the Northern Hemisphere. The measured accumulated SWE is 5295 mm, whereas only 3544 mm accumulated precipitation was recorded. The offset of nearly 50% at the LWD station goes in line with findings from [50,51]. Over the years the station operated, it has been shown to be largely unaffected by snow redistribution processes, unlike other stations that have recently been set up in RCZ and are heavily affected by snow redistribution. It is therefore valid to use the data of the LWD station to evaluate the under catch in precipitation measurements in RCZ. According to this, precipitation data of the DWD station was corrected at temperatures <=0 °C by multiplication with a factor of 1.5. Figure 2 shows measured and corrected daily precipitation data for winter 2014/2015 as an example.
In CRHM, the spatial discretization, which is the main topic in course of this paper, is on the basis of HRUs which contain information about the surface properties. Process-specific cascades like blowing snow transport or the runoff components serve as connection between HRUs. Since the HRU scheme defines surface properties like altitude, aspect, slope, vegetation height, etc. for CRHM, it has great influence on the model routines which depend on these properties. Via its influence on temperature, altitude significantly controls the development of a snow cover in CRHM. Mean altitude of HRUs and the proportion of high altitude HRUs in a HRU scheme are therefore highly relevant for the onset of snow accumulation, the amount of accumulated snow and the onset of melt in the simulated catchment. In the model setups, the threshold temperatures for snow and rain are defined as 0 °C (below all precipitation is snow) and 2 °C (above or equal all precipitation is rain). This range is supported by findings from [49]. Therefore, the HRU-altitude-dependent air temperature controls the amount of liquid and solid precipitation. Snow melt is described by the energy balance model SnobalCRHM [52,53]. In addition to air temperature, SnobalCRHM uses the shortwave radiation, which depends very much on the HRU slope and aspect. The HRU slope and aspect specific correction of shortwave incoming radiation is done by an approach developed by [54]. A further crucial factor for snowmelt is albedo, which is calculated by a procedure by [55] and serves as input for SnobalCRHM. The approach of albedo calculation uses HRU specific values of temperature, SWE and net snow precipitation. The CRHM modules just described are the most important for snow cover development and are highly dependent on HRU specific values surface properties. Therefore, significant variations on model output according to the HRU scheme are expected.

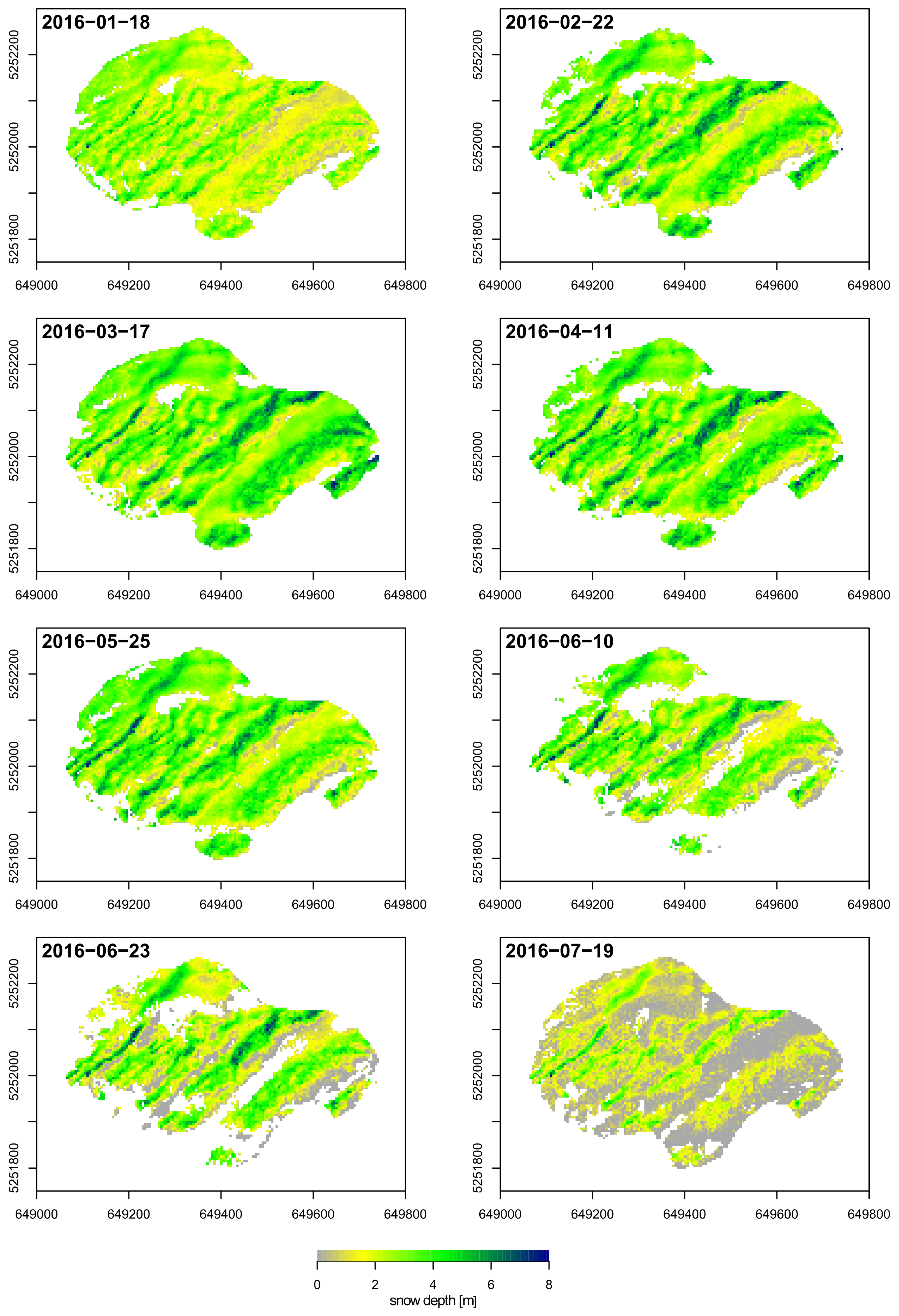
3.2. LIDAR Snow Depth Measurements and Its Analysis

Obtaining spatially distributed snow depth data using terrestrial LIDAR systems has become a well-established approach [1,29,30,31,32,33]. Since snow cover is largely dominating the hydrology of the RCZ, the aim is to detect dominant snow depth patterns by means of LIDAR data, which can serve as reference for HRU delineation. Since a possible temporal variation in dominant snow depth patterns should also be examined, 15 measurement campaigns during the snow accumulation, ablation and settlement periods from June 2015 to July 2017 were conducted with the logistical support of UFS Schneefernerhaus. The campaigns were carried out with an OPTECH ILRIS-LR LIDAR system (Table 2) which is based on the time-of-light principle and has a range of more than 3000 m. The LIDAR’s long range enables a setup on the visitor terrace close to the peak of Mt. Zugspitze. This position is ideal to measure snow depth of the FOI (Figure 1) at an average distance of 1900 m—it guarantees a minimum of shadows, the same position at each scan for means of comparability, optimal measurement geometry, easy accessibility, which is important due to time constraints and the weight of the LIDAR as well as power supply for the device. In addition to being largely free of human influence, the FOI was chosen since the backscatter of LIDAR is high here compared to the more distant parts of the RCZ.
Before the measurement campaigns, the appropriate scan resolution needs to be selected. It needs to allow for a time efficient execution of the scans and at the same time it needs to be high enough for the purpose of detecting dominant snow depth patterns. Time played an important role during the campaigns since it was necessary to scan a much larger area than the FOI in order to record enough unchanging structures to appropriately co-register the scans. Snow depth variations due to redistribution processes have been shown to be mostly larger than 0.3 m [56]. Based on this information and to assess the system’s maximum resolution capacity, steps of 1 m, 0.5 m, 0.25 m, 0.1 m, 0.05 m and 0.01 m height (Figure 3c) were dug into the snow and scanned from a distance of 1400 m (Figure 3a). Scans were carried out with 1 μ rad and 5 μ rad resolution. Figure 3d shows that it is possible to clearly identify steps up to 0.05 m height with the highest resolution. Steps >= 0.25 m can be resolved with the 5 μ rad resolution (Figure 3e). The achieved accuracy in the 5 μ rad mode is sufficient for identifying dominant patterns and allows for a time efficient implementation of the measurement campaigns. Moreover, snow depth obtained from LIDAR at the chosen 5 μ rad resolution was compared with snow depth measured by the ultrasound device of the LWD station, which is 1600 m away from the scanner position. The mean difference between the two measurement techniques is 0.04 m.
Error detection and correction is performed with the JRC 3D Reconstructor 3 software [57] automatically and manually. The co-registration of point clouds on the basis of unchanging structures like ropeway stations and other buildings shows an accuracy of 0.04 m with a standard deviation of 0.01 m and is thus accurate enough for pattern detection. The 5 μ rad scan resolution allowed calculating gridded maps with a horizontal resolution of 5 m, which is high enough to detect major, larger scale (>10 m) snow depth patterns. Based on these maps, which represent snow DEMs (digital elevation model), difference maps were calculated, showing the snow depth for each time step. The difference was calculated by subtracting a LIDAR derived bare ground DEM from the LIDAR derived snow DEM. For the year 2016 those snow depth maps are presented in Figure A1 in the Appendix A showing snow depth development. In a further step, the difference between the measurement dates was calculated to obtain snow depth changes. These difference maps are the basis for further processing. Since during snow accumulation, ablation and settlement, different snow processes are predominant, scans were classified into these periods and a PCA was applied. The main purpose of PCA is to reduce redundancy in data and thus the detection of dominant structures [58]. For a mathematical description of PCA it is referred to [59]. Results from PCA in the FOI serve as a benchmark for the following HRU delineation for the entire catchment.

3.3. Cluster Analysis

The delineation of HRUs for the entire RCZ is achieved by applying a cluster analysis. Cluster analyses have been successfully performed in numerous studies, mainly to investigate hydrological similarity between catchments and on meso- to large-scale catchments [60,61,62,63,64]. In contrast, in this study it is applied to a small headwater catchment. The used input parameters are vegetation cover, altitude, slope, aspect, and the wind sheltering index (Sx), that was developed by [17]. Calculation of Sx requires the prevailing wind direction in addition to the DEM and is a measure whether a pixel is exposed to wind or sheltered, i.e., whether a pixel is subject to wind driven snow deposition or snow erosion. To get an overview of the physiographic characteristics of the area, slope, aspect, Sx and the vegetation cover of the RCZ are displayed in Figure 4. Elevation is presented in Figure 1.
The cluster analysis is based on the assumption that the dominant patterns in snow depth distribution are controlled by physiographic properties in combination with the meteorological conditions, mainly wind [18,65]. Apart from vegetation cover, which is available as a classification map all parameters were calculated on the basis of a 5 m DEM. Due to the size and the mixed data type (continuous and discontinuous) of the input data the k-prototype algorithm [66], a modification of the k-means algorithm [67] for large mixed type data sets, was used for clustering. While the k-means algorithm is based on grouping around cluster means, k-prototype uses grouping around cluster prototypes, which are representative vectors for each cluster. K-prototype uses a cost function, which is a combined similarity measure for numerical and categorical attributes. The similarity measure for numerical attributes remains the Euclidean distance; the similarity measure for the categorical attributes is the number of mismatches between objects and prototype. Before clustering, all continuous input variables (altitude, slope, aspect, Sx) were standardized by subtraction of the mean and division by the standard deviation since k-prototype is not scale invariant. The clustering was performed iteratively for a range of different numbers of clusters to identify the clustering, which best represents, the dominant, and PCA derived patterns in the FOI. This clustering is chosen as HRU delineation. In order to represent their individuality, glaciated areas in the catchment were excluded from clustering and are assigned to a separate HRU. Glaciated areas encompass the glaciers Nördlicher and Südlicher Schneeferner, which are characterized by a homogeneous surface and little variation in altitude.

4. Results and Discussion

4.1. PCA Derived Patterns in Snow Cover

One of the main goals in course of this study was to identify dominant snow depth patterns, in case of existence, in the periods of snow accumulation, ablation and settlement. These patterns serve as a reference for the cluster based HRU delineation. For that purpose 15 LIDAR snow depth maps were analyzed via PCA. The obtained PCs for the accumulation, ablation and settlement period are summarized in Table 3. Figure 5 illustrates the component values of the 1., 2., and 3.PC of the respective period in the FOI. The relatively large areas of no data values in the ablation images compared to the accumulation and settlement images can be traced back to the very wet snow cover during measurements in the ablation period, which significantly decreases LIDAR backscatter. As explained in Section 3.2 the PCA was conducted with maps showing snow depth change. The most distinct pattern can be observed in the 1.PC of the accumulation period (Figure 5a), followed by the 1.PC of the ablation period (Figure 5d) and the 2.PC of the accumulation period (Figure 5b). The other PCs show hardly any pattern but mainly noise (Figure 5c,e–i). The strong pattern in the 1.PC of the accumulation (Figure 5a) shows clear small scale variations (5–20 m) which resemble the snow free surface. Here, the negative component values indicate areas with an increase in snow depth (troughs) while the positive component values indicate areas with little change (ridges). In contrast, the 2.PC of the accumulation period (Figure 5b) slightly reflects variations on a scale of 20–100 m. This can be attributed to the slight increase in elevation from north-east to south-west (almost 100 m)—positive component values indicate positive changes in snow depth while negative values indicate little change on a larger scale. The 1.PC of the ablation period reveals a similar pattern like the 1.PC of the accumulation period. However, it is less pronounced and not as small-scale. The positive component values are related to areas that are subject to negative changes in snow depth due to melt and positive values indicate little change. The results from the visual interpretation of Figure 5 are supported by the semivariograms of the PCs (Figure 6). The 1.PC of the accumulation period has the largest semivariance, which increases with increasing lag (Figure 6a). The curve of the semivariances of 1.PC of the ablation period is very similar but with generally lower values compared to the 1.PC of the accumulation period (Figure 6b). This means that the differences between the component values are smaller than in the 1.PC of the accumulation period. The almost constant semivariances in the other PCs as well as in all PCs of the settlement period (Figure 6c) indicate that there is almost no lag dependent variation in component values that means, there is mainly noise. This also applies to the 2.PC of the accumulation period where a purely visual interpretation suggests the previously described pattern.
Based on the PCA results and the semivariograms of the PCs it can be concluded that snow depth distribution is largely defined by processes during accumulation and that processes during ablation or settlement have only limited influence on it. On the one hand, this was to be expected since at steep angles of incidence of the solar rays there is hardly any shading in the FOI, which limits the effect of solar radiation on the development of snow depth patterns. Nonetheless there are differences in the radiation balance due to variations in aspect and slope angle. These are reflected in the snow depletion pattern of the 1.PC of the ablation period. On the other hand, the identified importance of the accumulation period for snow depth distribution goes in line with findings from [68,69,70,71] who identified snow fall events accompanied by strong winds in combination with the roughness of the snow free surface as the main drivers for snow depth distribution in the Alps. Analysis of wind and gust speed at the LWD-station, which is in close vicinity to the test area, revealed that wind and gust speed are on an average 25% and 26% higher during snow fall events than in periods without snow fall. This analysis is based on data from November 2014–May 2016 and includes the months October, November, December, January, February, March, April, and May, which are most relevant for snow cover development in the RCZ and in which LIDAR measurements were carried out. The result of the wind analysis underpins the greater importance of wind during snow accumulation than during settlement or during ablation. Moreover, the dominant, small scale snow depth pattern which was identified during accumulation season is essential for snow ablation dynamics in complex terrain [56], such as RCZ. Features, which remain snow free at the end of accumulation or melt out early, are most important for melt dynamics and subsequently the distribution of melt induced snow depletion. These features provide a source for long-wave radiation, the most important source for melt [72]. In addition, the heterogeneous surface causes local advection of warm air from the snow free ground to snow and thus enhances melt [56,73]. As a result, a snow cover as shown in Figure 7, which represents a typical sequence of snow cover depletion during the ablation period in the FOI, was observed. Starting with spots which are still snow free at snow depth maximum, melt processes create a particular pattern which resembles PC1 of ablation. In summary, it can be noticed that snow depth distribution is largely defined during accumulation, which becomes visible in the dominant pattern in PC1 of the accumulation period. This pattern also influences melt dynamics and subsequently snow depth distribution during ablation. Thus, the pattern in PC1 of the ablation period resembles the one in the accumulation period but less distinct. For this reasons, the pattern of the 1.PC of the accumulation period was chosen as benchmark for HRU delineation via cluster analysis.

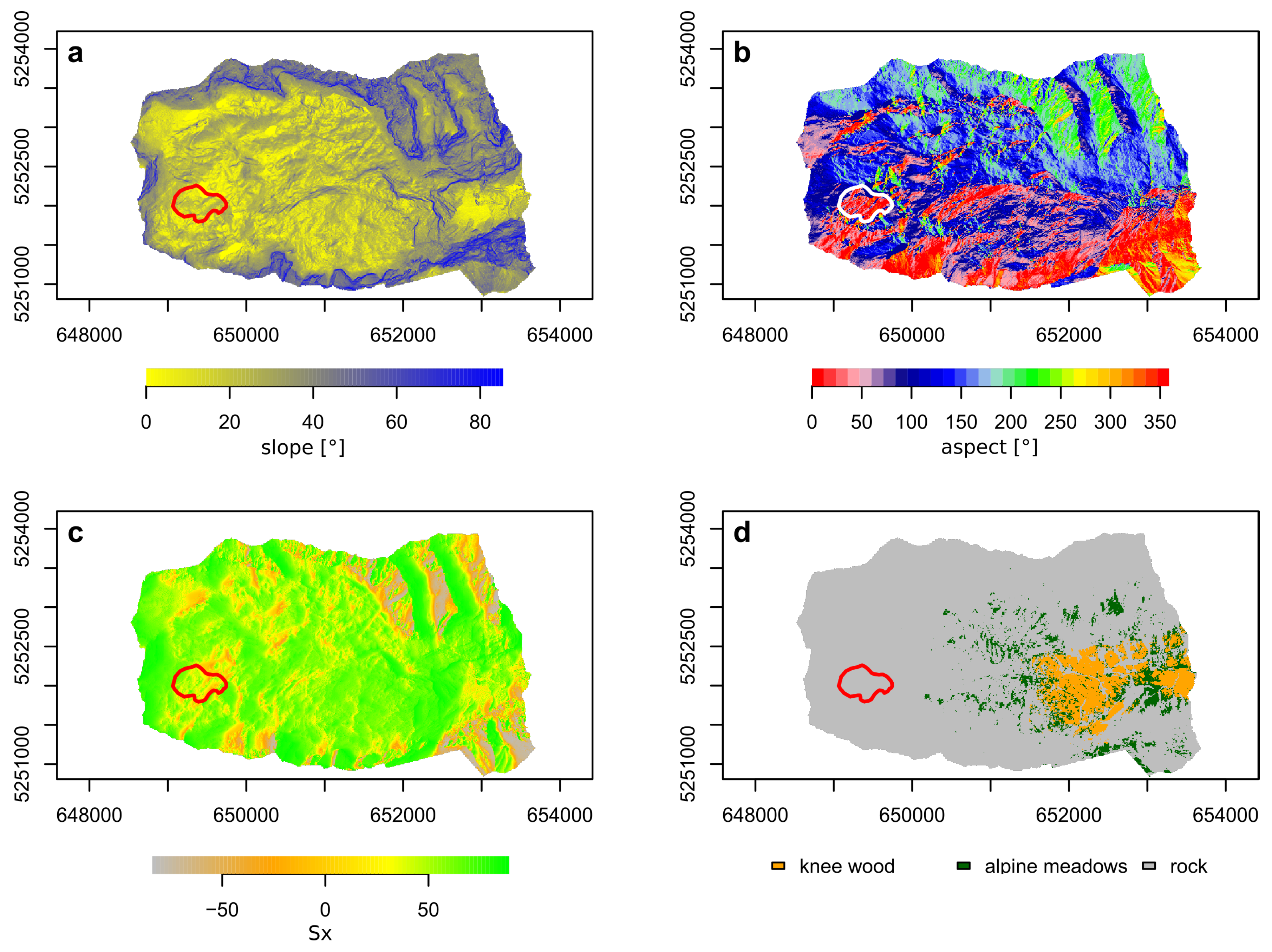
4.2. Cluster Analysis Results and HRU Delineation

To benchmark the cluster derived HRU schemes, they are compared with LIDAR derived snow depth patterns as described previously. It turned out that 10 HRUs (9 clusters plus one glacier HRU) are optimal as the comparison of the cluster results with the 1.PC of the accumulation period in Figure 8 shows. In addition to the visual interpretation and the semivariograms that suggest choosing the 1.PC of the accumulation period as a reference for cluster evaluation, the density distribution of the component values of the 1.PCs of the accumulation and ablation period (Figure 9) in the clusters was analyzed. While in the ablation period (Figure 9b) the density distributions are very similar in each cluster, in the accumulation period (Figure 9a) they differ more and clusters can be separated according this distributions. This underpins the validity of the 1.PC of the accumulation period as a reference for cluster evaluation. The comparison of clusters and PCA results (Figure 8) shows, that small scale patterns in the western part of the FOI are clearly reproduced by the clusters. Also larger scale patterns in the eastern part, which can also be observed in the 1.PC of the ablation period (Figure 5b), are represented satisfactory. Even areas, which have no data in the PCs because of shadowing effects during LIDAR measurements (south exposed parts of deeper troughs) (Figure 8a) are precisely attributed to a cluster (Figure 8b). All three clusters also occur outside the FOI and account for 40% of the RCZ, which highlights that the FOI is representative for large parts of the catchment. The chosen clustering thus represent the delineation of HRUs. The main parameters of the resulting 10 HRUs are given in Table 4. Despite the comparison of the clustering results with 12 clusters (Figure 8e) shows an equally good representation of snow patterns like the one with 10 clusters, the latter was chosen as the “best-fit” scheme. This is justified in the goal of the HRU classification to identify as many HRUs as necessary—and not more—to ensure a high computational efficiency of the model setup. Both HRU schemes and another cluster analysis derived scheme with 8 clusters (Figure 8d) are used for modelling in order to evaluate the model’s sensitivity to various HRU schemes. It could be argued that the FOI of which snow depth patterns serve for evaluation of the clustering results only represents a small part of the RCZ. However, its terrain can be regarded as representative for large parts of the catchment, as it has ridges and depressions of various sizes typical of the catchment. These terrain features have been shown to be controlling snow depth distribution in combination with wind in numerous studies [17,65,70,74]. In the clustering, the wind effect is represented by the wind sheltering index Sx (see Section 3.3) [17]. Of course, it would have been beneficial if snow cover patterns of larger parts or even the entire catchment could have been obtained to validate the clustering results. However, for logistical reasons, this was not feasible in this study.

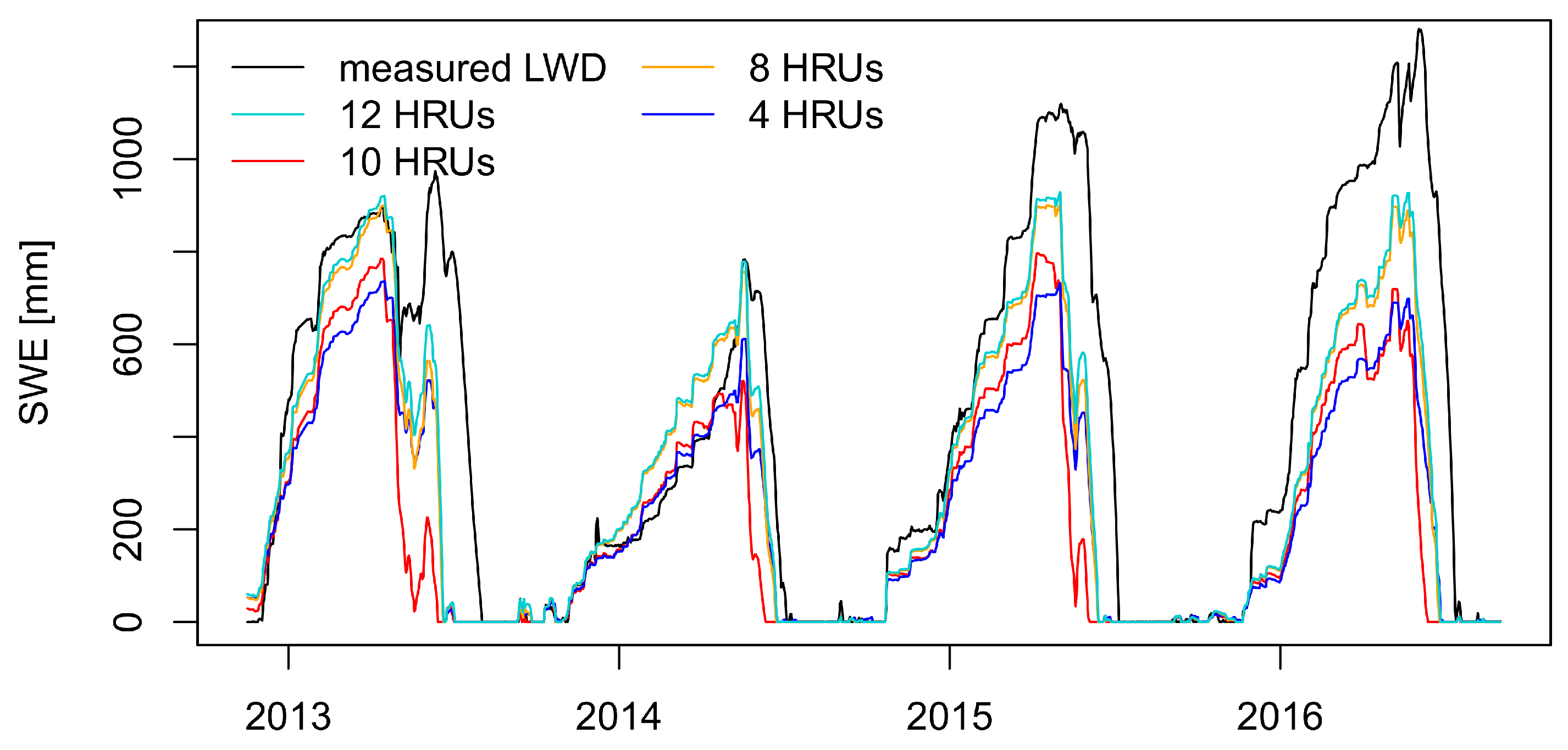
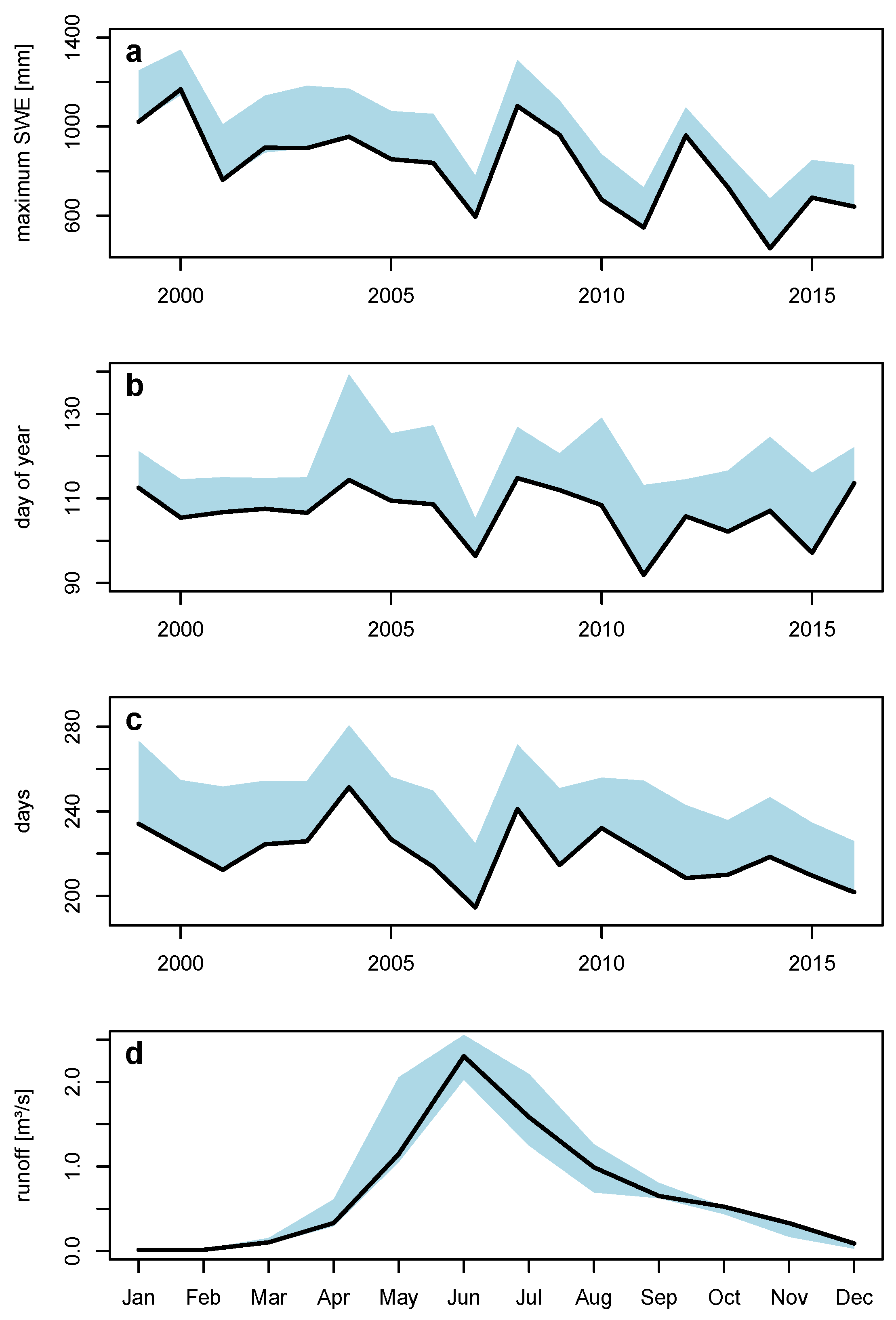
4.3. Evaluation of HRU Schemes with Station Measurement Data and Effects on Snow Parameters and Runoff

The presented method of HRU delineation was evaluated by a comparison of snow depth, modeled by CRHM and measured data from DWD and LWD stations. Moreover, the HRU schemes were compared with the rather subjective, elevation dependent scheme from [37] in order to analyze the effects on modeled snow parameters and runoff. Figure 10 displays modeled snow depth of the “best-fit” HRU scheme in comparison to DWD and LWD measurements, which are available for the period 1998–2016. It can be seen that CRHM is able to well reproduce snow accumulation and ablation at both stations. This results in a NSE (Nash-Sutcliffe Efficiency) [75] of 0.76 when comparing modeled with measured values of DWD and 0.70 for the LWD station (Table 5). Table 5 also shows NSE values of the discretization schemes with 4, 8 and 12 HRUs. The comparison reveals that the “best-fit” scheme and the one with 8 HRUs produce the best simulation results at the measurement stations while the non-cluster based scheme with 4 HRUs performs worst. Moreover, the simulation results were compared to measured SWE from the LWD station (Figure 11). In contrast to snow depth, SWE data is only available from Winter 2012/2013–2016. Figure 11 shows that in all schemes SWE is underestimated at the measurement site, in particular in the 10 HRU scheme. A similar underestimation in this scheme can also be observed in snow depth simulations for the same period, resulting in a lower NSE value (0.47) compared to the NSE value for the 1998–2016 period. Moreover it can be seen that the scheme with 10 HRUs exhibits greater underestimation in SWE simulation than the schemes with 8 and 12 HRUs. The same applies for modeled snow depth in the 2012/2013–2016 period, resulting in better NSEs than for the 10 HRU scheme (0.80 (12 HRU), 0.76 (8 HRU)). However, the comparison of these results with the previous snow depth analyses should be differentiated, especially with regard to the model quality. First, the analyzed time periods are different (18 vs. 4 years) and second, the comparatively weaker performance of the 10 HRU scheme in SWE modeling is due to the generally more massive snow cover modeled in the 12 and 8 HRU schemes, as the following analyses show.
In addition to evaluate the model performance of the relatively short period with measurement data, the robustness of the HRU schemes for long term simulation was tested. Therefore, the period 1961–2016 (Figure 10c,d) was simulated. In the highest elevated HRU of the 8 and 12 HRU scheme, snow never melts completely during summer, which leads to a continuously growing snow pack over the years (Figure 10c). Figure 10c is also exemplary for the situation in the highest HRU in the scheme with 12 HRUs. Such a snow cover development was never observed in nature. A similar unrealistic snow cover development can be observed in two further HRUs of the scheme with 12 and 8 HRUs but never in the 10 HRU scheme. Moreover, the setup with 12 HRUs shows an unrealistic snow cover simulation for one HRU even in the shorter period 1998–2016. Due to this and due to the fact that the 10 HRU scheme performs equally well in simulating snow depth at the two measurement sites, it is legitimate to label it as “best-fit”. The analysis of the 1961–2016 period indicates, that more HRUs do not necessarily mean better simulation results. Rather, good simulation results depend on whether the HRUs describe the catchment realistically. A surplus in HRUs can cause that catchment characteristics are described that do not occur in reality and so does a too coarse discretization. The partly unrealistic snow depth simulations described, illustrate CRHM’s sensitivity to HRU discretization. It is in particular remarkable, that the severest differences could be observed when simulating longer time periods. As a consequence, an adequate HRU discretization is highly relevant when it comes to simulations of future climate change effects on the hydrology, since these projections are usually calculated for periods of at least 30 years.
To investigate the effects of the various HRU schemes on model output, the snow hydrological indices MSWE (maximum snow water equivalent), day of MSWE, and snow cover duration are compared for the setups with 12, 10 (“best-fit”), 8 and 4 HRUs. The indices, which are displayed in Figure 12, are mean values for the entire RCZ, weighted by HRU areas. In addition Table 5 provides the 18-year (1998–2016) areal means of the indices. MSWE (Figure 12a, Table 5) is modeled highest with the 12 HRU scheme and lowest with the “best-fit” scheme. MSWE results achieved with the other schemes are in between. The comparison of the day of the MSWE (Figure 12b, Table 5) shows an earlier occurrence of MSWE in the setup with 10 HRUs. Regarding the 18-year mean, peak snow storage represented by MSWE, is 10–12 days earlier in the “best-fit” scheme. Great differences between the setups can also be observed in snow cover duration (Figure 12c), which is on the 18-year average 25–30 days shorter in the “best-fit” scheme (Table 5). Based on the comparison of these indices it can be concluded that there is a significant influence of the HRU scheme on simulation of snow cover in the RCZ. The significance of the parameters in Table 5 was tested with a Welch two sided t-test, α = 0.05 . The generally higher values and the later day of MSWE in the elevation zone oriented 4 HRU scheme can be explained by the lesser variability in exposition, altitude, and slope among HRUs in comparison to the physiographic property based HRU setups, which result in more diverse conditions for snow accumulation and ablation. The reason for the lower values in MSWE, DoMSWE and snow cover duration in the “best-fit” scheme compared to the other cluster derived schemes lies in the unrealistic simulation of snow cover development in some HRUs, which influences the mean values.
Although runoff is measured at the karst spring, the data was not used for the evaluation of the different HRU schemes. One reason are large data gaps due to avalanche and flood damage. Other reason are changes in the channel cross section and varying bed load coverage which leads to a limited validity of the water level-discharge relationship. Moreover, a flood event lead to changes in the karst system, which made measurements before and after this event incomparable. Thus, statements regarding the quality of simulated runoff with the various HRU schemes are not possible. Consequently, in following only the differences in the runoff responses of the various HRU schemes are presented. The differences in snow depth development that were identified due to different HRU schemes resulted in great variations in runoff development in the simulations. Figure 12d illustrates this and depicts the range of the 18-year mean monthly catchment runoff for simulations with 12, 10 (“best-fit”), 8 and 4 HRUs. The general regime with a runoff maximum in June is similarly modeled with each discretization. However, the amount of runoff greatly varies. For example, this could be of particular importance, if a HRU based model is used for runoff simulations in order to estimate e.g., hydropower potential. The runoff simulation results give a good overview of the effects different HRU schemes and subsequently different snow cover developments have on the runoff regime of RCZ.
Both, the results for snow cover development and the results for runoff illustrate the model’s sensitivity to different HRU schemes. Moreover, the results show how model outcomes can be influenced by the user if HRUs are delineated without an objective, user independent method. Furthermore, the presented method for an objective delineation of HRUs for the RCZ has proven to produce the best results of modeled snow depth development. Nevertheless, it would be helpful to have a consistent time series of runoff data that would allow a comprehensive analysis of the modeled and measured components of the water cycle. This is especially true with regard to the available SWE measurements and would allow a deeper analysis of the relatively weaker performance of the 10 HRU setup in SWE modeling at the LWD station.

5. Conclusions and Outlook

The goal of the study was to introduce a method for an objective model discretization that guarantees computational efficiency and an adequate representation of dominant hydrological processes in the high alpine, snow dominated RCZ. To achieve this a method for HRU delineation was developed that makes use of a time series of LIDAR derived snow depth maps. The analysis of this data by PCA allows for identification of dominant snow depth patterns in the FOI, serving as a reference for the following physiographic property based HRU delineation. Before analyzing the LIDAR data, the accuracy of the data was assessed. This was done by a field experiment, where snow steps of defined size were measured with the LIDAR. In addition, LIDAR snow depth measurements were compared with LWD operated ultrasound measurements. The results show that the accuracy of LIDAR measurements varies according to the angle of incidence on the target, the distance of the target to the LIDAR and the snow conditions. However, the obtained accuracy, which is in a range of 0.05–0.35 m is sufficiently high to detect the dominant seasonal snow depth pattern where changes in snow depth of tens of centimeters to meters occur over distances of more than 5 m. Results of the PCA of the time series of LIDAR snow depth maps show that seasonal snow cover distribution is largely defined during snow fall events and that processes during settlement and ablation play a minor role in the RCZ which confirms findings from [69,71] for other regions in the Alps. PCA identified patterns of snow depth of the FOI serve as a benchmark for the following cluster analysis on basis of the physiographic properties of RCZ. The iteratively performed cluster analysis allows for delineation of HRUs for the entire catchment. The clustering that best fits the PCA identified dominant snow depth pattern of the accumulation period was chosen as HRU delineation. The resulting HRU delineation could be successfully evaluated by comparing modeled snow depth with snow depth measured by DWD and LWD. So far, the presented method enables to objectively delineate HRUs in consideration of dominant snow depth patterns. In addition to that, it was analyzed how different HRU schemes influence model results, i.e., how the user may influence model results due to the choice of HRUs. Therefore model results of the “best-fit” HRU scheme were compared to results of the model setup from [37], in which HRUs are delineated according to vegetation zones as well as to further cluster analysis derived HRU schemes. The cluster derived HRU schemes performed better in simulating snow cover dynamics at the measurement sites of LWD and DWD than the vegetation zone oriented HRU scheme. Moreover, the scheme with 12 HRUs, which represents PCA derived snow cover patterns equally well like the “best-fit” scheme, shows unrealistic snow cover simulations in one HRU. This underpins the presented approach of delineating only as many HRUs as necessary, as too many spatial units may lead non-existent surface characteristics that negatively influence model quality. Furthermore, this guarantees computational efficiency without reducing the model quality. This agrees with [76] who conclude that a limited amount of functional units, which were identified by clustering, does not mean a substantial loss in model performance. Analysis of simulated mean snow cover development of the entire RCZ revealed huge differences between the used HRU schemes. This becomes evident in snow storage, temporal dynamics of the snow cover and the hydrograph, particularly in long term simulations. The results stress the necessity of an adequate and objective discretization approach in alpine catchments, that reflects dominant snow depth patterns and thus allows for an appropriate representation of key processes in the used model to gain optimal simulation results. Unlike previously presented concepts for an objective HRU delineation [8,12,13,14], the here presented approach directly links the HRU delineation to the snow cover as an internal state of alpine hydrology. The presented method makes use of terrestrial LIDAR data. However, to acquire this data is not trivial for a few reasons that are the costs of the LIDAR, the power supply in remote areas, an adequate location for the setup and necessary logistics due to the instrument weight. All these reasons hamper a resource effective application of a terrestrial LIDAR. Moreover, with a terrestrial LIDAR it is impossible to cover an entire catchment. Thus it is also impossible to derive an HRU discretization solely based on LIDAR snow cover data. Nevertheless, there have been recent developments in remote sensing [29,30,77,78] and in particular in the field of unmanned aerial vehicles [79] that allow for a more comfortable and cost effective generation of high resolution snow cover maps. These methods are applicable to larger areas and are thus predestined to be applied for future studies on spatial model discretization in alpine catchments.

Author Contributions

Conceptualization, methodology, software, writing—original draft preparation, investigation, formal analysis, M.W.; software, formal analysis, M.F.; writing—review and editing, supervision, K.S.; conceptualization, methodology, supervision, funding acquisition, writing—review and editing, M.B. All authors have read and agreed to the published version of the manuscript.

Funding

The study was funded by the Bavarian State Ministry for the Environment and Consumer Protection as part of the project “Expansion and Internationalization of the Virtual Alpine Observatory (VAO-II)”.

Acknowledgments

The authors thank the University of Natural Resources and Life Sciences (BOKU), Vienna, for its support during the study and Benjamin Müller from the Department of Geography, University of Munich for technical support. The authors also thank the staff of the UFS Schneefernerhaus for logistical support during the field work and for their great hospitality. Many thanks to Stefan Härer for the help during the field work.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
SWEsnow water equivalent
MSWEmaximum snow water equivalent
DoMSWEday of maximum snow water equivalent
NSENash-Sucliffe efficiency
CRHMCold Regions Hydrological Model
HRUhydrological response unit
DWDDeutscher Wetterdienst (Germen Weather Service)
LWDLawinenwarndienst Bayern (Bavarian Avalanche Service)
RCZResearch Catchment Zugspitze
PCAprinciple component analysis
FOIfield of interest
DEMdigital elevation model
Sxwind sheltering index
LIDARlight detection and ranging

Appendix A

Hydrology 07 00020 g0a1 550
Figure A1. LIDAR derived snow depth maps of the FOI for 2016.
Figure A1. LIDAR derived snow depth maps of the FOI for 2016.
Hydrology 07 00020 g0a1

References

  1. Grünewald, T.; Schirmer, M.; Mott, R.; Lehning, M. Spatial and temporal variability of snow depth and ablation rates in a small mountain catchment. Cryosphere 2010, 4, 215–225. [Google Scholar] [CrossRef] [Green Version]
  2. Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef] [Green Version]
  3. Klemeš, V. The modelling of mountain hydrology: The ultimate challenge. In Hydrology of Mountain Areas; IAHS Publisher: Wallingford, UK, 1990; pp. 29–43. [Google Scholar]
  4. Dehotin, J.; Braud, I. Which spatial discretization for distributed hydrological models? Proposition of a methodology and illustration for medium to large-scale catchments. Hydrol. Earth Syst. Sci. 2008, 12, 769–796. [Google Scholar] [CrossRef] [Green Version]
  5. Schulla, J. Model Description WaSiM.Zürich Hydrology Software Consulting. Available online: http://www.wasim.ch/en/products/wasim_description.htm (accessed on 9 February 2020).
  6. Lehning, M.; Völksch, I.; Gustafsson, D.; Nguyen, T.A.; Stähli, M.; Zappa, M. ALPINE3D: A detailed model of mountain surface processes and its application to snow hydrology. Hydrol. Process. 2006, 20, 2111–2128. [Google Scholar] [CrossRef]
  7. Samaniego, L.; Kumar, R.; Jackisch, C. Predictions in a data-sparse region using a regionalized grid-based hydrologic model driven by remotely sensed data. Hydrol. Res. 2011, 42, 338–355. [Google Scholar] [CrossRef]
  8. Flügel, W. Delineating hydrological response units by geographical information system analyses for regional hydrological modelling using PRMS/MMS in the drainage basin of the River Bröl, Germany. Hydrol. Process. 1995, 1995, 423–436. [Google Scholar] [CrossRef]
  9. Leavesley, G.H.; Lichty, R.W.; Troutman, B.M.; Saindon, L.G. Precipitation-Runoff Modeling System; User’s Manual; U.S. Geological Survey, Water Resources Division: Reston, VA, USA, 1983. [Google Scholar] [CrossRef] [Green Version]
  10. Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool, SWAT 2009. Theoretical Documentation. Available online: http://swat.tamu.edu/media/99192/swat2009-theory.pdf (accessed on 9 February 2020).
  11. Pomeroy, J.W.; Gray, D.M.; Brown, T.; Hedstrom, N.R.; Quinton, W.L.; Granger, R.J.; Carey, S.K. The cold regions hydrological model: A platform for basing process representation and model structure on physical evidence. Hydrol. Process. 2007, 21, 2650–2667. [Google Scholar] [CrossRef]
  12. Zehe, E.; Ehret, U.; Pfister, L.; Blume, T.; Schröder, B.; Westhoff, M.; Jackisch, C.; Schymanski, S.J.; Weiler, M.; Schulz, K.; et al. HESS Opinions: From response units to functional units: A thermodynamic reinterpretation of the HRU concept to link spatial organization and functioning of intermediate scale catchments. Hydrol. Earth Syst. Sci. 2014, 18, 4635–4655. [Google Scholar] [CrossRef] [Green Version]
  13. Savvidou, E.; Efstratiadis, A.; Koussis, A.D.; Koukouvinos, A.; Skarlatos, D. A curve number approach to formulate hydrological response units within distributed hydrological modelling. Hydrol. Earth Syst. Sci. Discuss. 2016, 12, 1–34. [Google Scholar] [CrossRef]
  14. Savvidou, E.; Efstratiadis, A.; Koussis, A.; Koukouvinos, A.; Skarlatos, D. The Curve Number Concept as a Driver for Delineating Hydrological Response Units. Water 2018, 10, 194. [Google Scholar] [CrossRef] [Green Version]
  15. Balk, B.; Elder, K. Combining binary decision tree and geostatistical methods to estimate snow distribution in a mountain watershed. Water Resour. Res. 2000, 36, 13–26. [Google Scholar] [CrossRef]
  16. Liston, G.E. Representing Subgrid Snow Cover Heterogeneities in Regional and Global Models. J. Clim. 2004, 17, 1381–1397. [Google Scholar] [CrossRef]
  17. Winstral, A.; Elder, K.; Davis, R.E. Spatial Snow Modeling of Wind-Redistributed Snow Using Terrain-Based Parameters. J. Hydrometeorol. 2002, 3, 524–538. [Google Scholar] [CrossRef]
  18. Winstral, A.; Marks, D. Long-term snow distribution observations in a mountain catchment: Assessing variability, time stability, and the representativeness of an index site. Water Resour. Res. 2014, 50, 293–305. [Google Scholar] [CrossRef]
  19. Gampe, D.; Ludwig, R. Evaluation of Gridded Precipitation Data Products for Hydrological Applications in Complex Topography. Hydrology 2017, 4, 53. [Google Scholar] [CrossRef] [Green Version]
  20. Burlando, P.; Pellicciotti, F.; Strasser, U. Modelling Mountainous Water Systems Between Learning and Speculating Looking for Challenges. Hydrol. Res. 2002, 33, 47–74. [Google Scholar] [CrossRef]
  21. DeBeer, C.M.; Pomeroy, J.W. Simulation of the snowmelt runoff contributing area in a small alpine basin. Hydrol. Earth Syst. Sc. 2010, 14, 1205–1219. [Google Scholar] [CrossRef] [Green Version]
  22. DeBeer, C.M.; Pomeroy, J.W. Influence of snowpack and melt energy heterogeneity on snow cover depletion and snowmelt runoff simulation in a cold mountain environment. J. Hydrol. 2017, 553, 199–213. [Google Scholar] [CrossRef]
  23. Strasser, U.; Kunstmann, H. Tackling complexity in modelling mountain hydrology: Where do we stand, where do we go? In Cold and Mountain Region Hydrological Systems Under Climate Change: Towards Improved Projections; IAHS Publisher: Wallingford, UK, 2013; pp. 3–12. [Google Scholar]
  24. Prasch, M.; Mauser, W.; Weber, M. Quantifying present and future glacier melt-water contribution to runoff in a central Himalayan river basin. Cryosphere 2013, 7, 889–904. [Google Scholar] [CrossRef] [Green Version]
  25. Stahl, K.; Weiler, M.; Kohn, I.; Freudiger, D.; Seibert, J.; Vis, M.; Gerlinger, K.; Böhm, M. The Snow and Glacier Melt Components of Streamflow of the River Rhine and Its Tributaries Considering the Influence of Climate Change; Vol. Nr. 25, Report KHR. 1; Internationale Kommission für die Hydrologie des Rheingebietes (KHR/CHR): Lelystad, The Netherlands, 2016. [Google Scholar]
  26. Verbunt, M.; Gurtz, J.; Jasper, K.; Lang, H.; Warmerdam, P.; Zappa, M. The hydrological role of snow and glaciers in alpine river basins and their distributed modeling. J. Hydrol. 2003, 282, 36–55. [Google Scholar] [CrossRef]
  27. Engelhardt, M.; Schuler, T.V.; Andreassen, L.M. Contribution of snow and glacier melt to discharge for highly glacierised catchments in Norway. Hydrol. Earth Syst. Sci. 2014, 18, 511–523. [Google Scholar] [CrossRef] [Green Version]
  28. Wulf, H.; Bookhagen, B.; Scherler, D. Differentiating between rain, snow, and glacier contributions to river discharge in the western Himalaya using remote-sensing data and distributed hydrological modeling. Adv. Water Resour. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
  29. Currier, W.R.; Pflug, J.; Mazzotti, G.; Jonas, T.; Deems, J.S.; Bormann, K.J.; Painter, T.H.; Hiemstra, C.A.; Gelvin, A.; Uhlmann, Z.; et al. Comparing Aerial Lidar Observations With Terrestrial Lidar and Snow–Probe Transects From NASA’s 2017 SnowEx Campaign. Water Resour. Res. 2019, 55, 6285–6294. [Google Scholar] [CrossRef] [Green Version]
  30. Deems, J.S.; Painter, T.H.; Finnegan, D.C. Lidar measurement of snow depth: A review. J. Glaciol. 2013, 59, 467–479. [Google Scholar] [CrossRef] [Green Version]
  31. Egli, L.; Jonas, T.; Grünewald, T.; Schirmer, M.; Burlando, P. Dynamics of snow ablation in a small Alpine catchment observed by repeated terrestrial laser scans. Hydrol. Process. 2012, 26, 1574–1585. [Google Scholar] [CrossRef]
  32. Prokop, A. Assessing the applicability of terrestrial laser scanning for spatial snow depth measurements. Cold Reg. Sci. Technol. 2008, 54, 155–163. [Google Scholar] [CrossRef]
  33. Schön, P.; Prokop, A.; Vionnet, V.; Guyomarc’h, G.; Naaim-Bouvet, F.; Heiser, M. Improving a terrain-based parameter for the assessment of snow depths with TLS data in the Col du Lac Blanc area. Cold Reg. Sci. Technol. 2015, 114, 15–26. [Google Scholar] [CrossRef]
  34. de Almeida, T.I.R.; Penatti, N.C.; Ferreira, L.G.; Arantes, A.E.; do Amaral, C.H. Principal component analysis applied to a time series of MODIS images: The spatio-temporal variability of the Pantanal wetland, Brazil. Wetl. Ecol. Manag. 2015, 23, 737–748. [Google Scholar] [CrossRef]
  35. Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B.; Lambin, E. Digitalchange detection methods in ecosystem monitoring: A review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
  36. Müller, B.; Bernhardt, M.; Schulz, K. Identification of catchment functional units by time series of thermal remote sensing images. Hydrol. Earth Syst. Sci. 2014, 18, 5345–5359. [Google Scholar] [CrossRef] [Green Version]
  37. Weber, M.; Bernhardt, M.; Pomeroy, J.W.; Fang, X.; Härer, S.; Schulz, K. Description of current and future snow processes in a small basin in the Bavarian Alps. Environ. Earth Sci. 2016, 75, 962. [Google Scholar] [CrossRef]
  38. Friedmann, A.; Korch, O. Die Vegetation des Zugspitzplatts (Wettersteingebirge, Bayerische Alpen): Aktueller Zustand und Dynamik. Berichte der Reinhold-Tüxen-Gesellschaft 2010, 22, 114–128. [Google Scholar]
  39. Rappl, A.; Wetzel, K.F.; Büttner, G.; Scholz, M. Tracerhydrolgische Untersuchungen am Partnach-Ursprung: Dye tracer investigation at the Partnach Spring (German Alps). Hydrol. Wasserbewirtsch. 2010, 54, 220–230. [Google Scholar]
  40. Wetzel, K.F. On the Hydrology of the Partnach Area in the Wetterstein Mountains (Bavarian Alps). Erdkunde 2004, 58, 172–186. [Google Scholar] [CrossRef]
  41. Dornes, P.F.; Pomeroy, J.W.; Pietroniro, A.; Carey, S.K.; Quinton, W.L. Influence of landscape aggregation in modelling snow-cover ablation and snowmelt runoff in a sub-arctic mountainous environment. Hydrolog. Sci. J. 2008, 53, 725–740. [Google Scholar] [CrossRef] [Green Version]
  42. Ellis, C.R.; Pomeroy, J.W.; Brown, T.; MacDonald, J. Simulations of snow accumulation and melt in needleleaf forest environments. Hydrol. Earth Syst. Sci. 2010, 14, 925–940. [Google Scholar] [CrossRef] [Green Version]
  43. Essery, R.; Rutter, N.; Pomeroy, J.W.; Baxter, R.; Stähli, M.; Gustafsson, D.; Barr, A.; Bartlett, P.; Elder, K. SNOWMIP2: An Evaluation of Forest Snow Process Simulations. Am. Meteorol. Soc. 2009, 90, 1120–1135. [Google Scholar] [CrossRef] [Green Version]
  44. Fang, X.; Pomeroy, J.W. Impact of antecedent conditions on simulations of a flood in a mountain headwater basin. Hydrol. Process. 2016, 30, 2754–2772. [Google Scholar] [CrossRef]
  45. López-Moreno, J.I.; Pomeroy, J.W.; Revuelto, J.; Vicente-Serrano, S.M. Response of snow processes to climate change: Spatial variability in a small basin in the Spanish Pyrenees. Hydrol. Process. 2013, 27, 2637–2650. [Google Scholar] [CrossRef]
  46. Pomeroy, J.W.; Gray, D.M.; Landine, P.G. The Prairie Blowing Snow Model: Characteristics, validation, operation. J. Hydrol. 1993, 144, 165–192. [Google Scholar] [CrossRef]
  47. Pomeroy, J.W.; Stewart, R.E.; Whitfield, P.H. The 2013 flood event in the South Saskatchewan and Elk River basins: Causes, assessment and damages. Can. Water Resour. J. / Rev. Can. Des Ressour. Hydr. 2016, 41, 105–117. [Google Scholar] [CrossRef]
  48. Liston, G.E.; Elder, K. A Meteorological Distribution System for High-Resolution Terrestrial Modeling (MicroMet). J. Hydrometeorol. 2006, 7, 217–234. [Google Scholar] [CrossRef] [Green Version]
  49. Jennings, K.S.; Winchell, T.S.; Livneh, B.; Molotch, N.P. Spatial variation of the rain-snow temperature threshold across the Northern Hemisphere. Nat. Commun. 2018, 9, 1148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  50. WMO. Technical Regulations: Basic Documents No. 2: Volume I—General Meteorological Standards and Recommended Practices, 2010 ed.; World Meteorological Organization: Geneva, Switzerland, 2011. [Google Scholar]
  51. Grossi, G.; Lendvai, A.; Peretti, G.; Ranzi, R. Snow Precipitation Measured by Gauges: Systematic Error Estimation and Data Series Correction in the Central Italian Alps. Water 2017, 9, 461. [Google Scholar] [CrossRef] [Green Version]
  52. MacDonald, M.K.; Pomeroy, J.W.; Pietroniro, A. Hydrological response unit-based blowing snow modelling over an alpine ridge. Hydrol. Earth Syst. Sci. 2010, 2010, 1167–1208. [Google Scholar] [CrossRef] [Green Version]
  53. Marks, D.; Domingo, J.; Susong, D.; Link, T.; Garen, D. A spatially distributed energy balance snowmelt model for application in mountain basins. Hydrol. Process. 1999, 13, 1935–1959. [Google Scholar]
  54. Garnier, B.J.; Ohmura, A. The evaluation of surface variations in solar radiation income. Sol. Energy 1970, 13, 21–34. [Google Scholar] [CrossRef]
  55. Essery, R.; Etchevers, P. Parameter sensitivity in simulations of snowmelt. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
  56. Mott, R.; Egli, L.; Grünewald, T.; Dawes, N.; Manes, C.; Bavay, M.; Lehning, M. Micrometeorological processes driving snow ablation in an Alpine catchment. Cryosphere 2011, 5, 1083–1098. [Google Scholar] [CrossRef] [Green Version]
  57. Campanella, M.; Rossi, G.; Ruggiero, G. JRC 3D Reconstructor User Manual 2014: For An Easy Learning of JRC 3D Reconstructor Tools. Available online: www.gexcel.homeip.net/Reconstructor/R_Manual/R_ManualEN.pdf (accessed on 9 February 2020).
  58. Crósta, A.P.; de Souza Filho, C.R.; Azevedo, F.; Brodie, C. Targeting key alteration minerals in epithermal deposits in Patagonia, Argentina, using ASTER imagery and principal component analysis. Int. J. Remote Sens. 2003, 24, 4233–4240. [Google Scholar] [CrossRef]
  59. Richards, J.A. Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
  60. Rao, A.R.; Srinivas, V.V. Regionalization of watersheds by fuzzy cluster analysis. J. Hydrol. 2006, 318, 57–79. [Google Scholar] [CrossRef]
  61. Rao, A.R.; Srinivas, V.V. Regionalization of watersheds by hybrid-cluster analysis. J. Hydrol. 2006, 318, 37–56. [Google Scholar] [CrossRef]
  62. Sawicz, K.; Wagener, T.; Sivapalan, M.; Troch, P.A.; Carrillo, G. Catchment classification: Empirical analysis of hydrologic similarity based on catchment function in the eastern USA. Hydrol. Earth Syst. Sci. 2011, 15, 2895–2911. [Google Scholar] [CrossRef] [Green Version]
  63. Li, Q.; Li, Z.; Zhu, Y.; Deng, Y.; Zhang, K.; Yao, C. Hydrological regionalisation based on available hydrological information for runoff prediction at catchment scale. Proc. Int. Assoc. Hydrol. Sci. 2018, 379, 13–19. [Google Scholar] [CrossRef] [Green Version]
  64. Nied, M.; Hundecha, Y.; Merz, B. Flood-initiating catchment conditions: A spatio-temporal analysis of large-scale soil moisture patterns in the Elbe River basin. Hydrol. Earth Syst. Sci. 2013, 17, 1401–1414. [Google Scholar] [CrossRef] [Green Version]
  65. Dadic, R.; Mott, R.; Lehning, M.; Burlando, P. Wind influence on snow depth distribution and accumulation over glaciers. Environ. Res. Lett. 2010, 115, 1064. [Google Scholar] [CrossRef] [Green Version]
  66. Huang, Z. Extensions to the k-Means Algorithm for Clustering Large Data Sets with Categorical Values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
  67. MacQueen, J.B. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; Le Cam, L.M., Neyman, J., Eds.; University of California Press: Berkeley, CA, USA, 1967. [Google Scholar]
  68. Schirmer, M.; Wirz, V.; Clifton, A.; Lehning, M. Persistence in intra-annual snow depth distribution: 1. Measurements and topographic control. Water Resour. Res. 2011, 47, 435. [Google Scholar] [CrossRef] [Green Version]
  69. Schirmer, M.; Lehning, M. Persistence in intra-annual snow depth distribution: 2. Fractal analysis of snow depth development. Water Resour. Res. 2011, 47, 2373. [Google Scholar] [CrossRef] [Green Version]
  70. Winstral, A.; Marks, D.; Gurney, R. Simulating wind-affected snow accumulations at catchment to basin scales. Adv. Water Resour. 2013, 55, 64–79. [Google Scholar] [CrossRef]
  71. Mott, R.; Scipión, D.; Schneebeli, M.; Dawes, N.; Berne, A.; Lehning, M. Orographic effects on snow deposition patterns in mountainous terrain. J. Geophys. Res. Atmos. 2014, 119, 1419–1439. [Google Scholar] [CrossRef] [Green Version]
  72. Ohmura, A. Physical Basis for the Temperature-Based Melt Index Method. J. Appl. Meteorol. 2001, 40, 753–761. [Google Scholar] [CrossRef]
  73. Marsh, P.; Pomeroy, J.W.; Neumann, N. Sensible heat flux and local advection over a heterogeneous landscape at an Arctic tundra site during snowmelt. Ann. Glaciol. 1997, 25, 132–136. [Google Scholar] [CrossRef] [Green Version]
  74. Dadic, R.; Mott, R.; Lehning, M.; Burlando, P. Parameterization for wind-induced preferential deposition of snow. Hydrol. Process. 2010, 24, 1994–2006. [Google Scholar] [CrossRef]
  75. Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
  76. Loritz, R.; Gupta, H.; Jackisch, C.; Westhoff, M.; Kleidon, A.; Ehret, U.; Zehe, E. On the dynamic nature of hydrological similarity. Hydrol. Earth Syst. Sci. 2018, 22, 3663–3684. [Google Scholar] [CrossRef] [Green Version]
  77. Kwok, R.; Markus, T. Potential basin-scale estimates of Arctic snow depth with sea ice freeboards from CryoSat-2 and ICESat-2: An exploratory analysis. Adv. Space Res. 2018, 62, 1243–1250. [Google Scholar] [CrossRef]
  78. Härer, S.; Bernhardt, M.; Schulz, K. PRACTISE – Photo Rectification And ClassificaTIon SoftwarE (V.2.1). Geosci. Model Dev. 2016, 9, 307–321. [Google Scholar] [CrossRef] [Green Version]
  79. Cimoli, E.; Marcer, M.; Vandecrux, B.; Bøggild, C.E.; Williams, G.; Simonsen, S.B. Application of Low-Cost UASs and Digital Photogrammetry for High-Resolution Snow Depth Mapping in the Arctic. Remote Sens. 2017, 9, 1144. [Google Scholar] [CrossRef] [Green Version]
Hydrology 07 00020 g001 550
Figure 1. Overview of the RCZ, the location of meteorological stations, the environmental research station Schneefernerhaus (UFS) and the test area (FOI (field of interest)) used for PCA.
Figure 1. Overview of the RCZ, the location of meteorological stations, the environmental research station Schneefernerhaus (UFS) and the test area (FOI (field of interest)) used for PCA.
Hydrology 07 00020 g001
Hydrology 07 00020 g002 550
Figure 2. Measured and corrected daily precipitation data at the DWD station for winter 2014/2015 (example).
Figure 2. Measured and corrected daily precipitation data at the DWD station for winter 2014/2015 (example).
Hydrology 07 00020 g002
Hydrology 07 00020 g003 550
Figure 3. Steps to assess the LIDAR accuracy. (a) LIDAR point of view. (b) Medium zoom to the LIDAR point cloud. (c) Steps and their height. (d) Near zoom to the steps of the highest possible resolution (1 μ rad) point cloud. (e) Near zoom to the steps of a high resolution (5 μ rad) point cloud.
Figure 3. Steps to assess the LIDAR accuracy. (a) LIDAR point of view. (b) Medium zoom to the LIDAR point cloud. (c) Steps and their height. (d) Near zoom to the steps of the highest possible resolution (1 μ rad) point cloud. (e) Near zoom to the steps of a high resolution (5 μ rad) point cloud.
Hydrology 07 00020 g003
Hydrology 07 00020 g004 550
Figure 4. Physiographic parameters of RCZ. (a) slope, (b) aspect, (c) Sx (negative values indicate wind exposure, positive values indicate wind shelter), (d) land cover. The red and white polygon represent the FOI.
Figure 4. Physiographic parameters of RCZ. (a) slope, (b) aspect, (c) Sx (negative values indicate wind exposure, positive values indicate wind shelter), (d) land cover. The red and white polygon represent the FOI.
Hydrology 07 00020 g004
Hydrology 07 00020 g005 550
Figure 5. Component values of the 1., 2., and 3. PC of the accumulation, ablation, and settlement period in the FOI. x- and y-axis are coordinates in UTM WGS84 Zone 32N.
Figure 5. Component values of the 1., 2., and 3. PC of the accumulation, ablation, and settlement period in the FOI. x- and y-axis are coordinates in UTM WGS84 Zone 32N.
Hydrology 07 00020 g005
Hydrology 07 00020 g006 550
Figure 6. Semivariogram of the 1., 2. and 3.PC of the (a) accumulation, (b) ablation, (c) settlement period.
Figure 6. Semivariogram of the 1., 2. and 3.PC of the (a) accumulation, (b) ablation, (c) settlement period.
Hydrology 07 00020 g006
Hydrology 07 00020 g007 550
Figure 7. Photographs of the FOI taken by an automatic camera of DWD at the peak of Mt. Zugspitze facing south. (a) Photograph recorded on 22 May 2016 shortly after the accumulation maximum. Black ellipses indicate spots which are still snow free. The red ellipse indicates the location of the LWD-station. (b) Photograph recorded on 10 June 2016. (c) Photograph recorded on 5 July 2016. All images are taken from https://www.foto-webcam.eu/webcam/zugspitze-sued/ © Deutscher Wetterdienst.
Figure 7. Photographs of the FOI taken by an automatic camera of DWD at the peak of Mt. Zugspitze facing south. (a) Photograph recorded on 22 May 2016 shortly after the accumulation maximum. Black ellipses indicate spots which are still snow free. The red ellipse indicates the location of the LWD-station. (b) Photograph recorded on 10 June 2016. (c) Photograph recorded on 5 July 2016. All images are taken from https://www.foto-webcam.eu/webcam/zugspitze-sued/ © Deutscher Wetterdienst.
Hydrology 07 00020 g007
Hydrology 07 00020 g008 550
Figure 8. (a) 1.PC of the accumulation period. (b) Result of the cluster analysis (10 clusters) for the FOI. (c) Result of the cluster analysis with 10 clusters, (d) 8 clusters and (e) 12 clusters for the entire RCZ. x- and y-axis are coordinates in UTM WGS84 Zone 32N.
Figure 8. (a) 1.PC of the accumulation period. (b) Result of the cluster analysis (10 clusters) for the FOI. (c) Result of the cluster analysis with 10 clusters, (d) 8 clusters and (e) 12 clusters for the entire RCZ. x- and y-axis are coordinates in UTM WGS84 Zone 32N.
Hydrology 07 00020 g008
Hydrology 07 00020 g009 550
Figure 9. Density distribution of the component values of the 1.PCs of the (a) accumulation and (b) ablation period in the clusters (Cl). The vertical bars at the bottom line indicate mode values of the distributions.
Figure 9. Density distribution of the component values of the 1.PCs of the (a) accumulation and (b) ablation period in the clusters (Cl). The vertical bars at the bottom line indicate mode values of the distributions.
Hydrology 07 00020 g009
Hydrology 07 00020 g010 550
Figure 10. (a) Modeled and measured snow depth of the “best-fit” scheme at the DWD station (NSE = 0.76) and (b) at the LWD station (NSE = 0.70). (c) Modeled daily SWE with the 8 HRU setup and (d) with the “best-fit” scheme for the period 1961–2016.
Figure 10. (a) Modeled and measured snow depth of the “best-fit” scheme at the DWD station (NSE = 0.76) and (b) at the LWD station (NSE = 0.70). (c) Modeled daily SWE with the 8 HRU setup and (d) with the “best-fit” scheme for the period 1961–2016.
Hydrology 07 00020 g010
Hydrology 07 00020 g011 550
Figure 11. Comparison of measured SWE from the LWD station with modeled SWE with different HRU schemes. NSE values: 0.67 (12 HRUs), 0.29 (10 HRUs), 0.63 (8 HRUs), 0.49 (4 HRUs).
Figure 11. Comparison of measured SWE from the LWD station with modeled SWE with different HRU schemes. NSE values: 0.67 (12 HRUs), 0.29 (10 HRUs), 0.63 (8 HRUs), 0.49 (4 HRUs).
Hydrology 07 00020 g011
Hydrology 07 00020 g012 550
Figure 12. (a) Range of catchment means of MSWE, (b) day of MSWE (c) and snow cover duration modeled with 12, 10, 8 and 4 HRUs. (d) Range of mean monthly catchment runoff (18–year mean) modeled with 12, 10, 8 and 4 HRUs. The bold black line represents the model setup with 10 HRUs.
Figure 12. (a) Range of catchment means of MSWE, (b) day of MSWE (c) and snow cover duration modeled with 12, 10, 8 and 4 HRUs. (d) Range of mean monthly catchment runoff (18–year mean) modeled with 12, 10, 8 and 4 HRUs. The bold black line represents the model setup with 10 HRUs.
Hydrology 07 00020 g012
Table
Table 1. Automatic weather stations and measured parameters (T = air temperature, ppt = precipitation, rh = relative humidity, u = wind speed, Qsi = shortwave incoming radiation, Qli = longwave incoming radiation, SD = snow depth, SWE = snow water equivalent).
Table 1. Automatic weather stations and measured parameters (T = air temperature, ppt = precipitation, rh = relative humidity, u = wind speed, Qsi = shortwave incoming radiation, Qli = longwave incoming radiation, SD = snow depth, SWE = snow water equivalent).
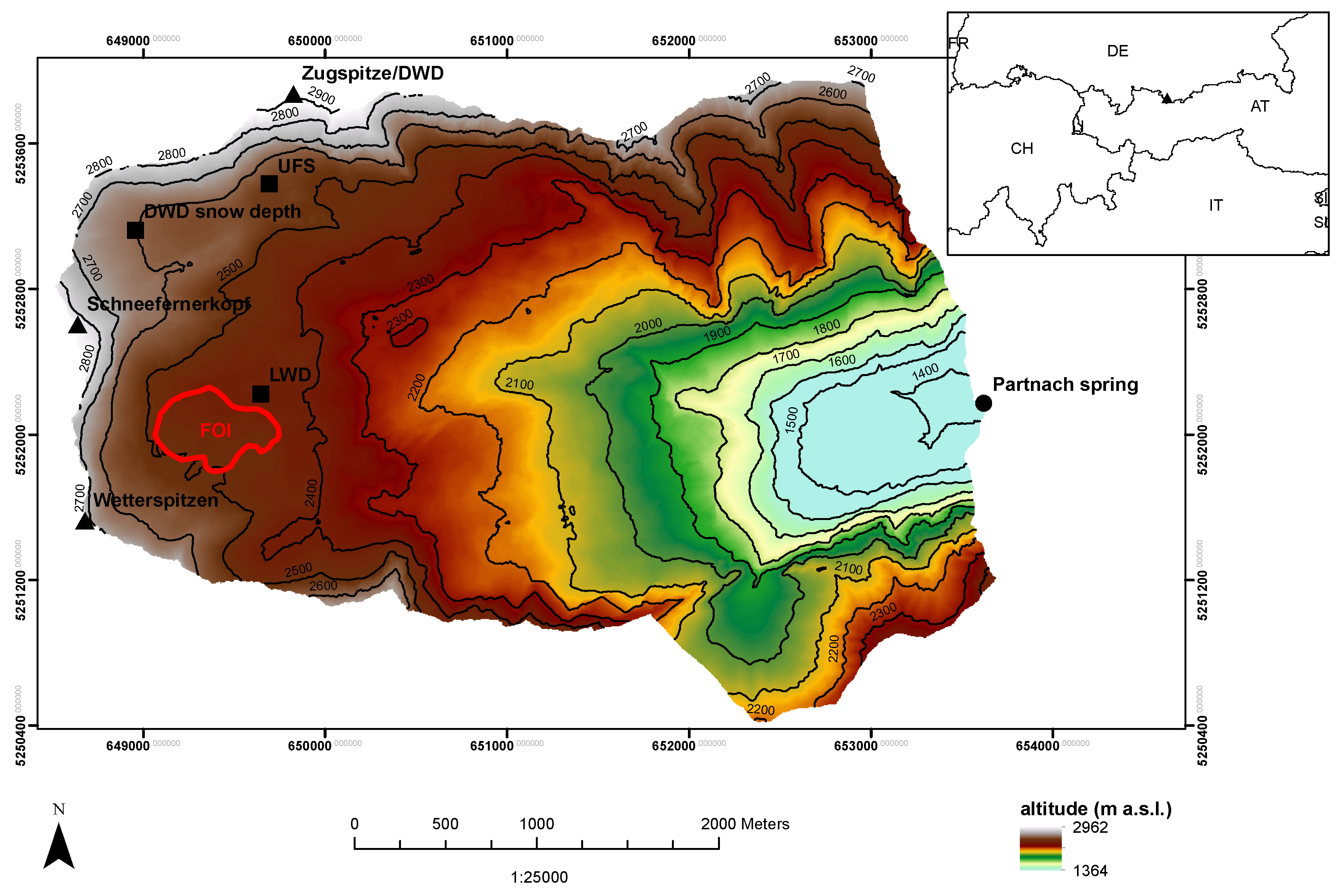
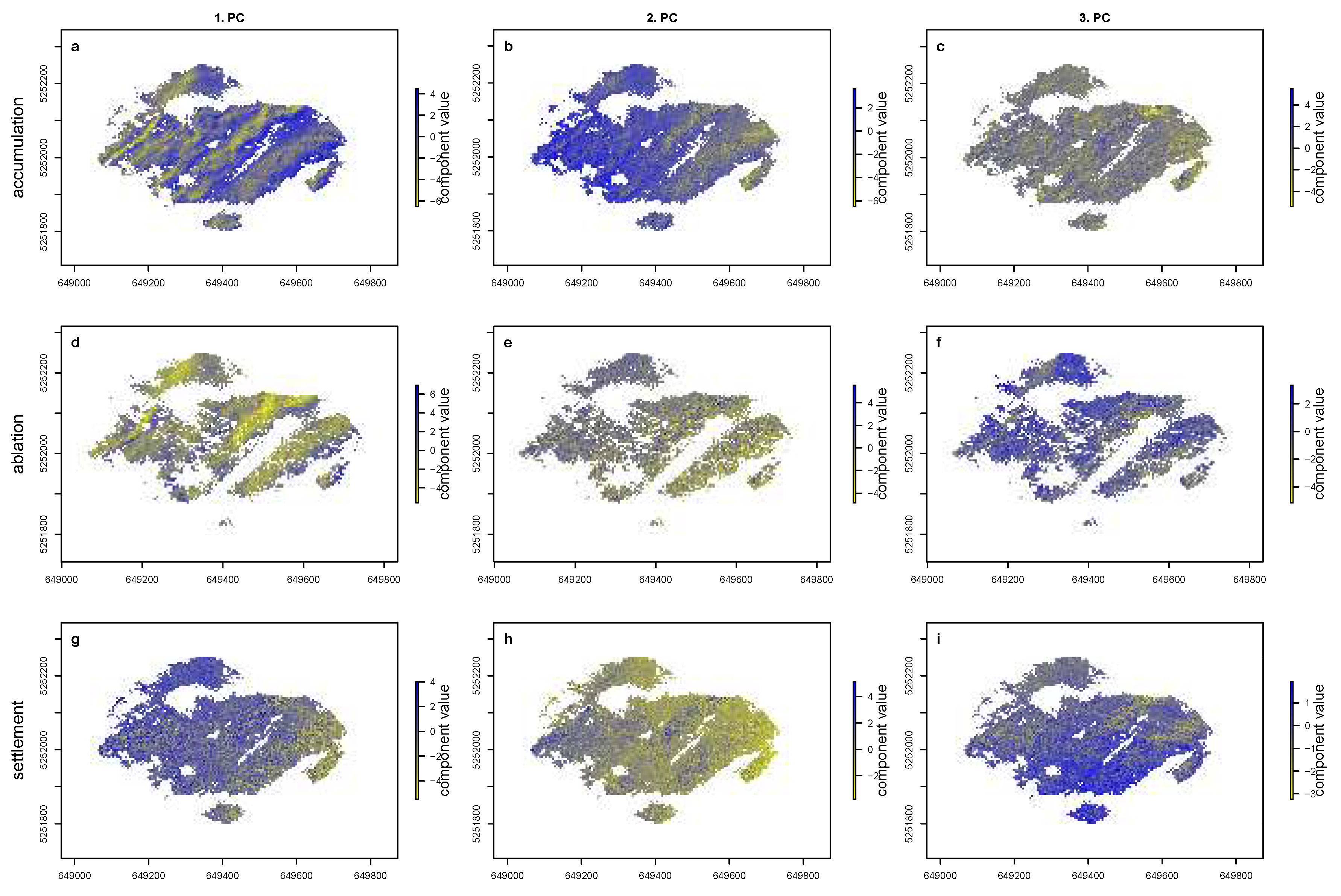
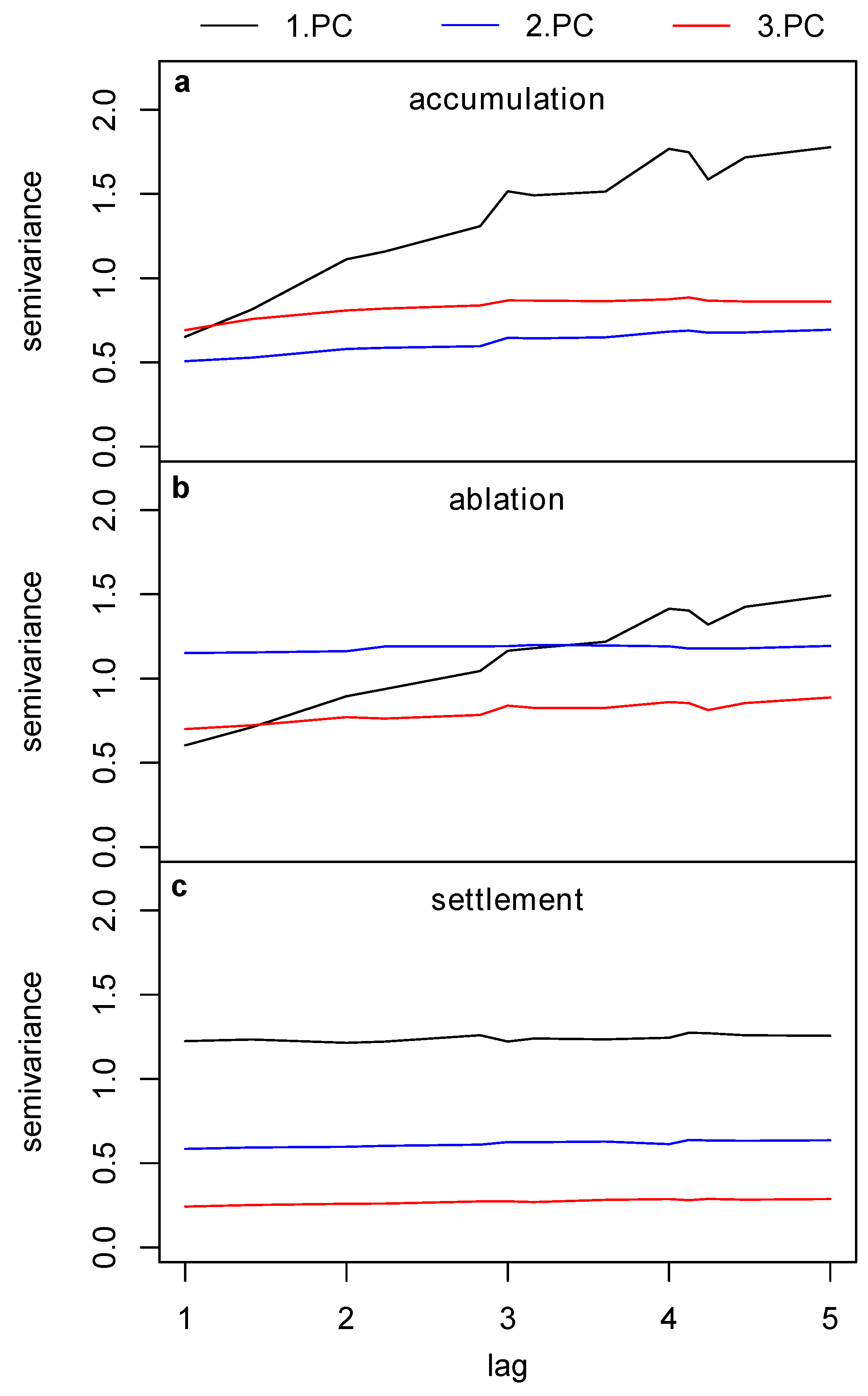
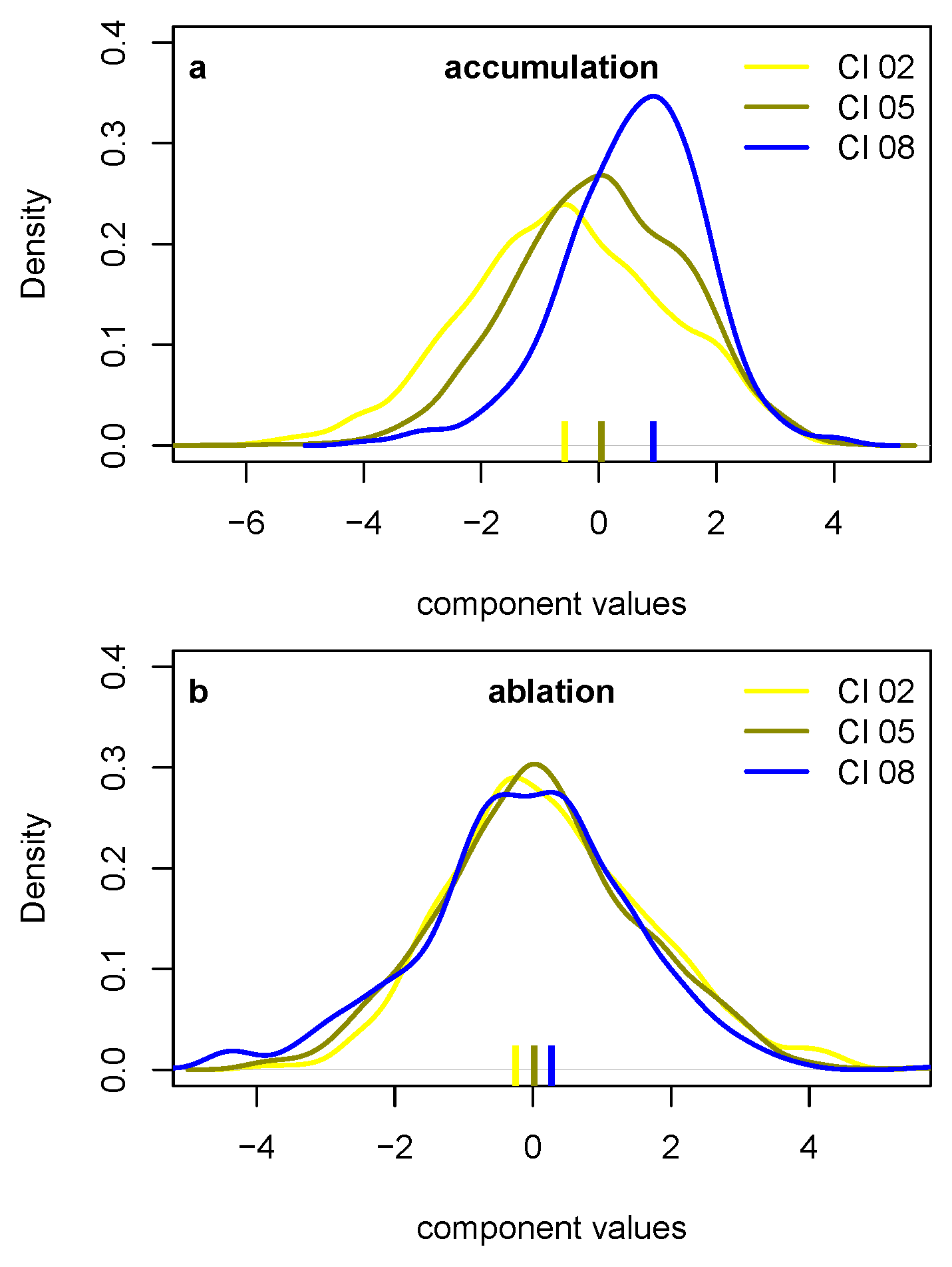
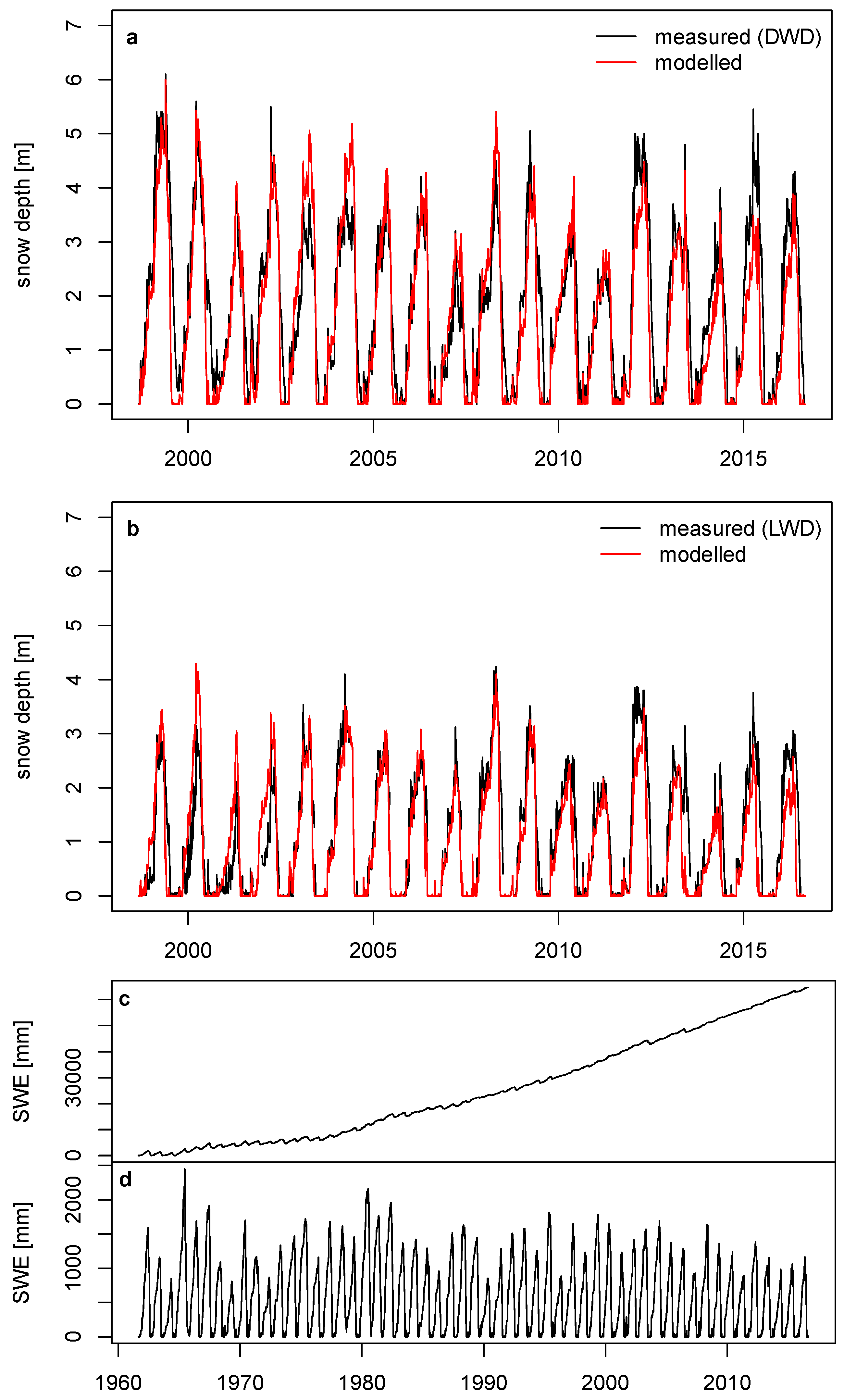
Station NameAltitude (m a.s.l.)Measured ParametersData Available Since
DWD2964, SD at 2600T, ppt, rh, u, Qsi, Qli, SD1900
LWD2420T, ppt, rh, u, SD, SWE1998
Table
Table 2. Specifications of the LIDAR system OPTECH ILRIS-LR.
Table 2. Specifications of the LIDAR system OPTECH ILRIS-LR.
Range 80% reflectivity3000+ m
Range 10% reflectivity1330+ m
Laser repetition rate10000 Hz
Raw range accuracy4 mm @ 100 m
Raw angular accuracy8 mm @ 100 m
Laser wavelength1064 nm
Beam diameter27 mm @ 100 m
Beam divergence0.014324°
Table
Table 3. Standard deviation ( σ ), proportion of variance (prop. of VAR) and cumulative proportion of variance (cum. prop.) of the principle components (PCs) in the accumulation, ablation and settlement period.
Table 3. Standard deviation ( σ ), proportion of variance (prop. of VAR) and cumulative proportion of variance (cum. prop.) of the principle components (PCs) in the accumulation, ablation and settlement period.
Accumulation
PC1PC2PC3PC4PC5PC6
σ 1.5311.1610.9750.7970.6820.506
prop. of VAR0.3840.2370.1540.1340.0810.010
cum. prop.0.3840.6210.7750.9080.9891.000
Ablation
PC1PC2PC3PC4PC5PC6
σ 1.5311.1610.9750.7970.6820.506
prop. of VAR0.3910.2250.1590.1050.0780.043
cum. prop.0.3910.6160.7740.8800.9571.000
Settlement
PC1PC2PC3
σ 1.2810.9290.704
prop. of VAR0.5470.2880.165
cum. prop.0.5470.8351.000
Table
Table 4. Main parameters of HRUs of the “best-fit” scheme.
Table 4. Main parameters of HRUs of the “best-fit” scheme.
HRU/ClusterAltitude [m a.s.l.]Aspect [°]Slope [°]Land CoverArea [km2]
1259816044rock1.30
2210432736rock0.96
3231224346rock0.97
4232117524rock1.81
522282922rock0.71
616878126knee wood1.03
7180315540knee wood1.11
8232910219rock2.71
923765951rock0.90
1026158114ice0.23
Table
Table 5. Snow parameters (18-year catchment mean) and model efficiencies of different HRU schemes at LWD and DWD snow depth measurement sites.
Table 5. Snow parameters (18-year catchment mean) and model efficiencies of different HRU schemes at LWD and DWD snow depth measurement sites.
MSWE [mm]DoMSWE [day of year]Snow Cover Duration [days]NSE (LWD)NSE (DWD)
12 HRUs10171182470.670.75
10 HRUs (“best fit”)8181072200.700.76
8 HRUs9681172450.710.76
4 HRUs8411192500.670.25

Share and Cite

MDPI and ACS Style

Weber, M.; Feigl, M.; Schulz, K.; Bernhardt, M. On the Ability of LIDAR Snow Depth Measurements to Determine or Evaluate the HRU Discretization in a Land Surface Model. Hydrology 2020, 7, 20. https://doi.org/10.3390/hydrology7020020

AMA Style

Weber M, Feigl M, Schulz K, Bernhardt M. On the Ability of LIDAR Snow Depth Measurements to Determine or Evaluate the HRU Discretization in a Land Surface Model. Hydrology. 2020; 7(2):20. https://doi.org/10.3390/hydrology7020020

Chicago/Turabian Style

Weber, Michael, Moritz Feigl, Karsten Schulz, and Matthias Bernhardt. 2020. "On the Ability of LIDAR Snow Depth Measurements to Determine or Evaluate the HRU Discretization in a Land Surface Model" Hydrology 7, no. 2: 20. https://doi.org/10.3390/hydrology7020020

APA Style

Weber, M., Feigl, M., Schulz, K., & Bernhardt, M. (2020). On the Ability of LIDAR Snow Depth Measurements to Determine or Evaluate the HRU Discretization in a Land Surface Model. Hydrology, 7(2), 20. https://doi.org/10.3390/hydrology7020020

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop