Short-Term Water Demand Forecasting Model Combining Variational Mode Decomposition and Extreme Learning Machine
Abstract
1. Introduction
2. Materials and Methods
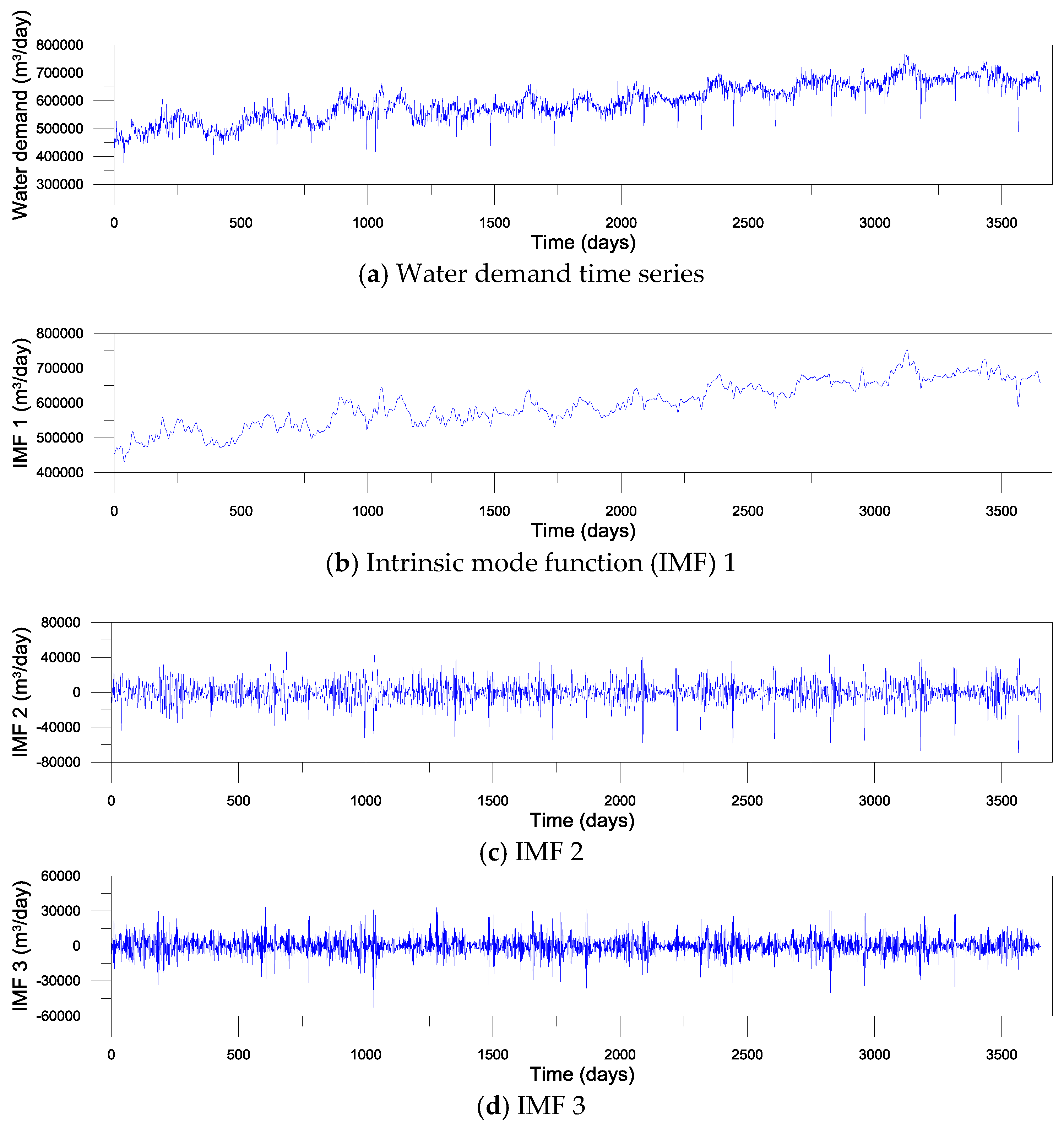
2.1. Data Used
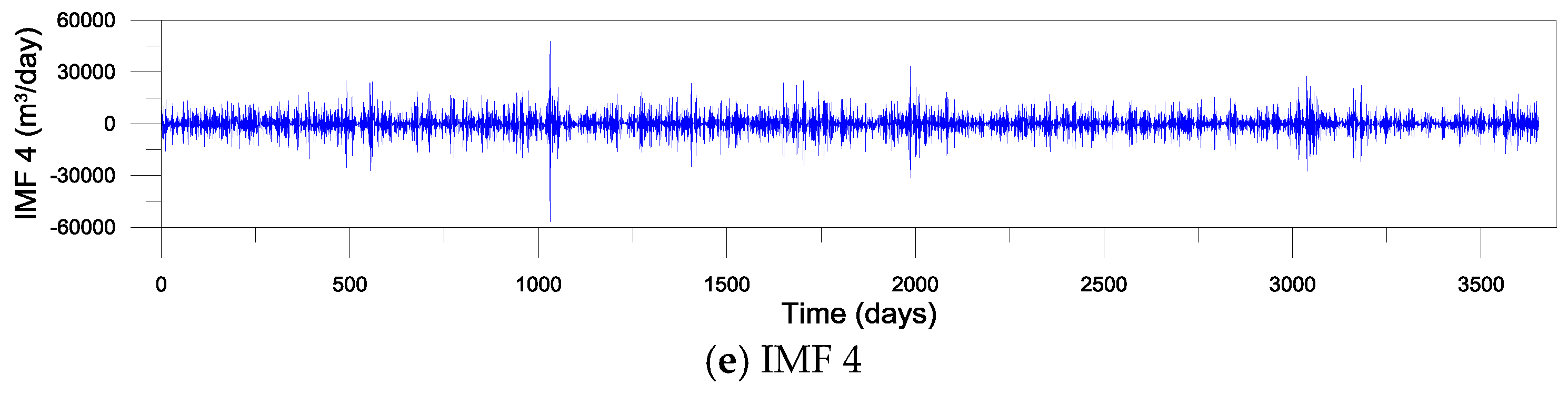
2.2. Variational Mode Decomposition (VMD)
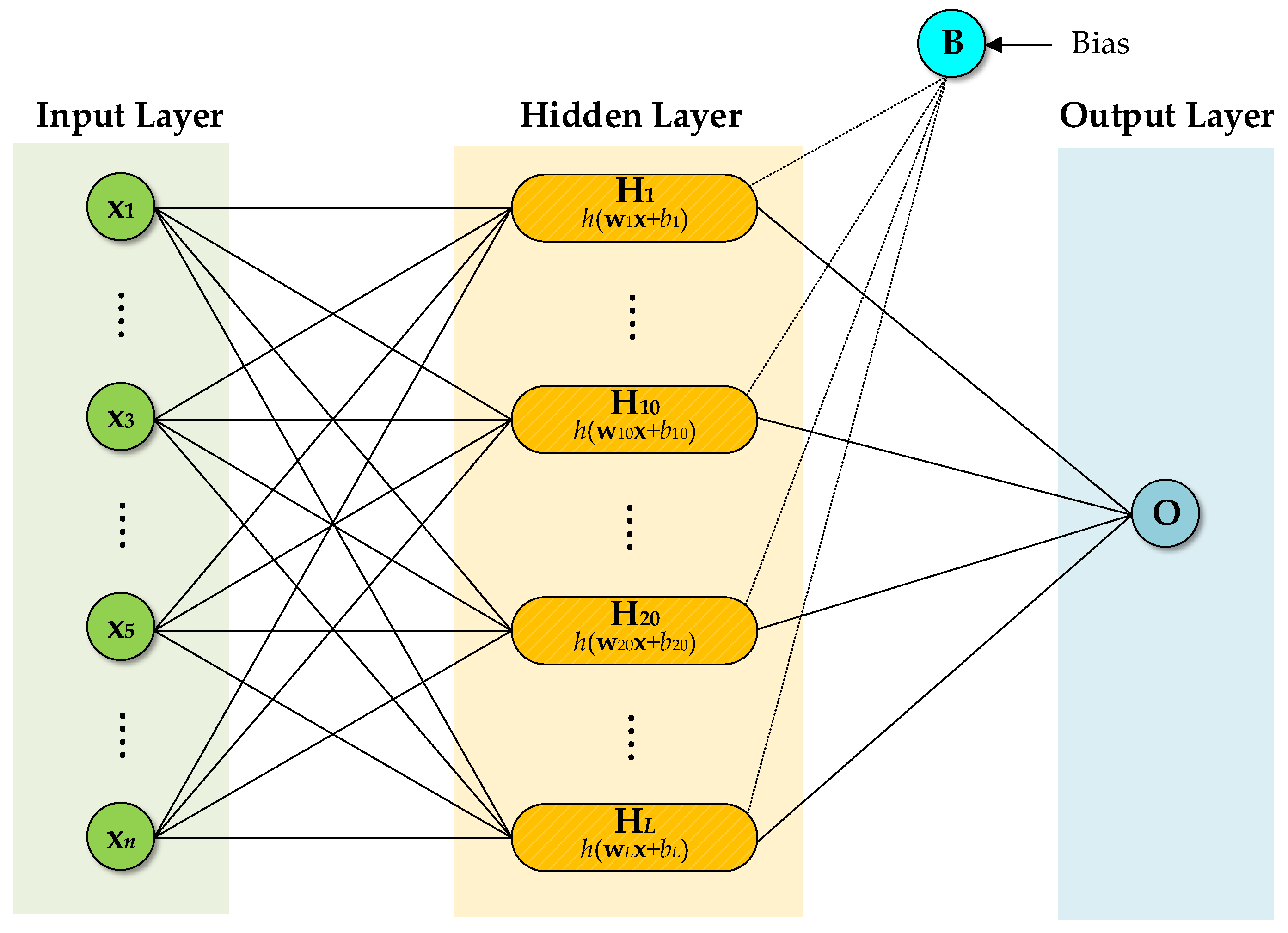
2.3. Artificial Neural Network (ANN)
2.4. Extreme Learning Machine (ELM)
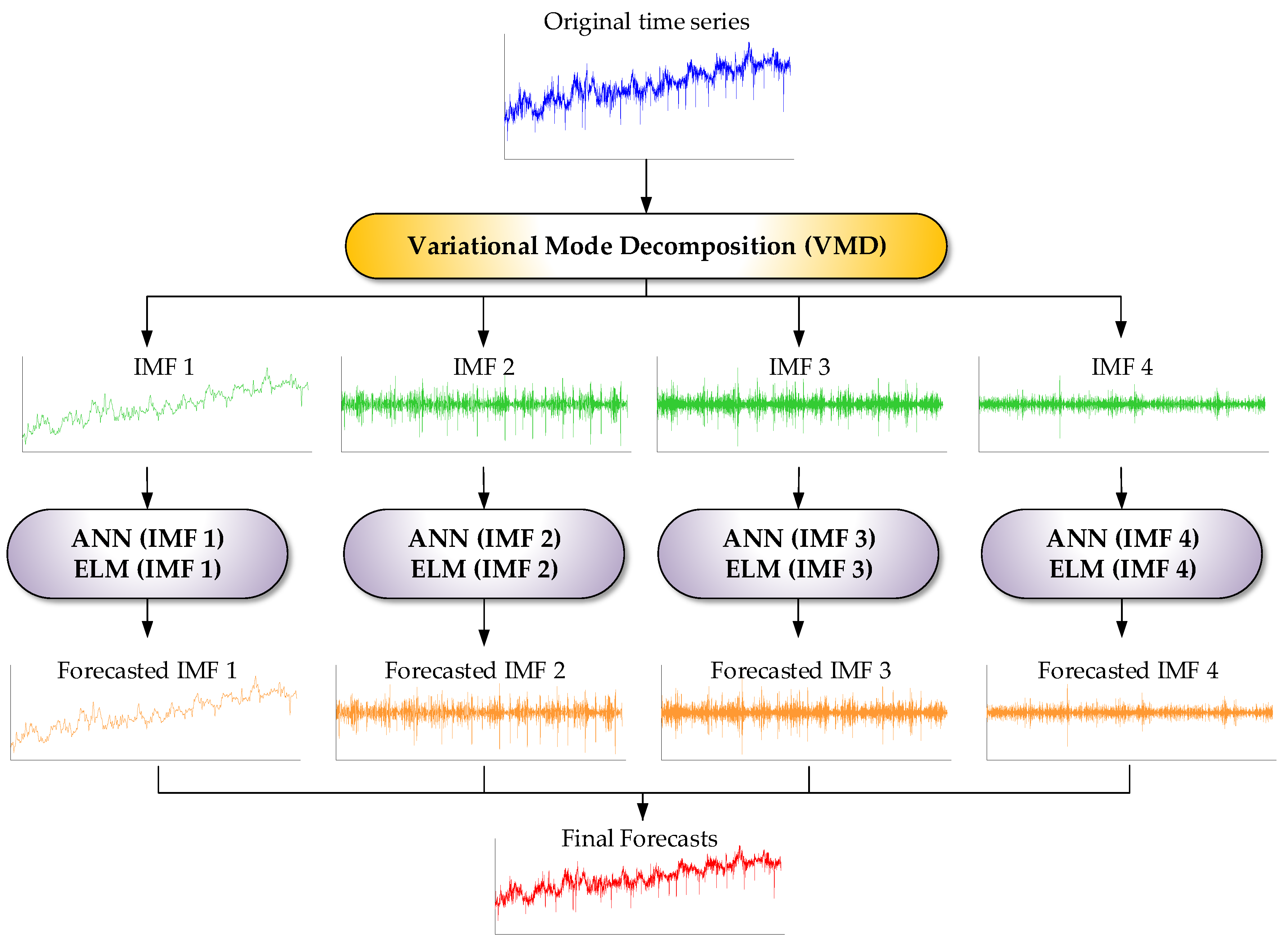
2.5. VMD-Based Water Demand Forecasting
- Step 1.
- Decomposition: Water demand time series is decomposed into IMFs using VMD.
- Step 2.
- Model learning: ANN and ELM models are learned for each IMF.
- Step 3.
- IMF forecasts: ANN and ELM models produce forecasted values for each IMF.
- Step 4.
- Final forecasts: Summing the forecasted IMFs produces the final water demand forecasts.
2.6. Performance Evaluation Indices
3. Results and Discussion
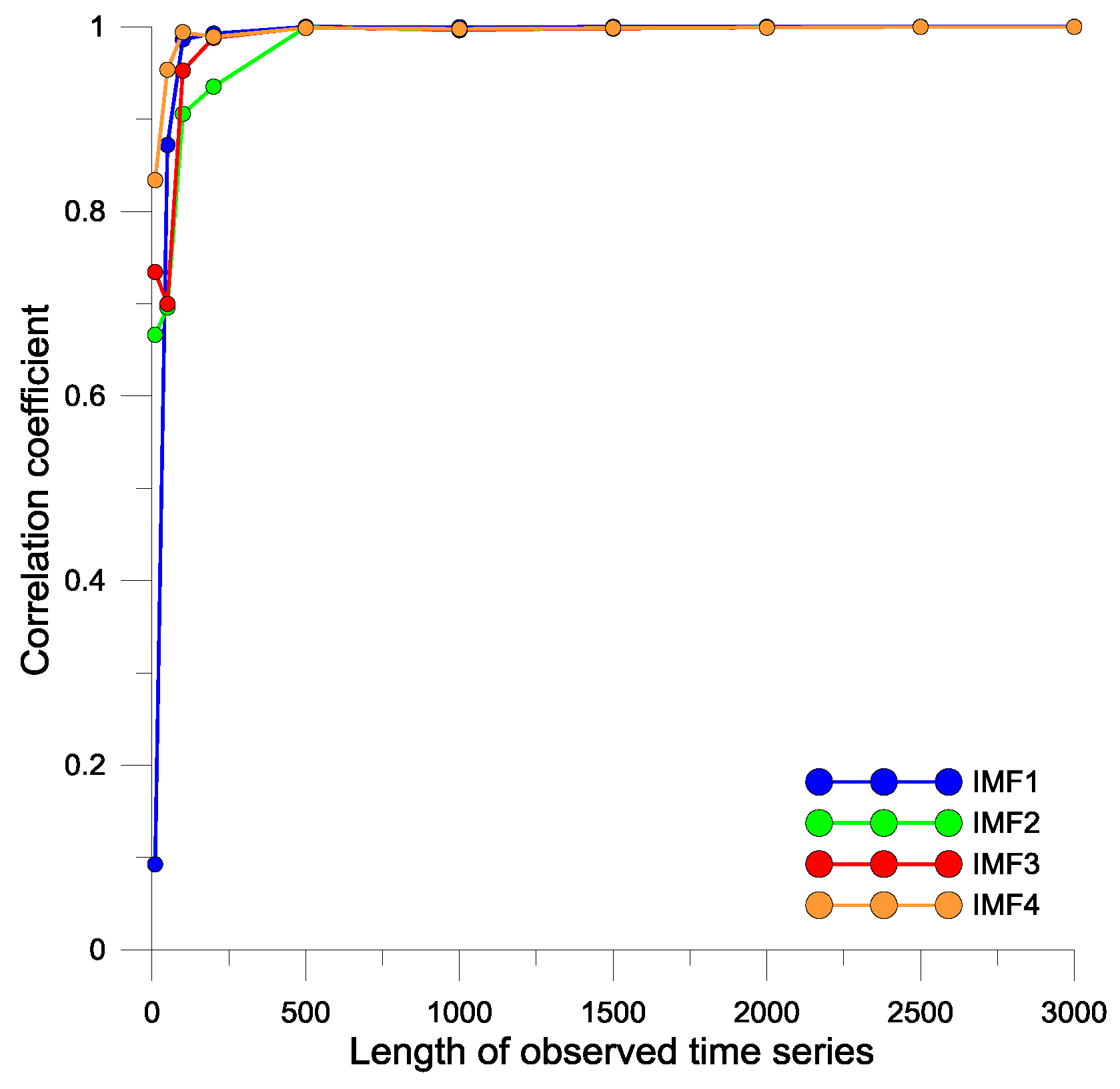
3.1. Development of Single and VMD-Based Forecasting Models
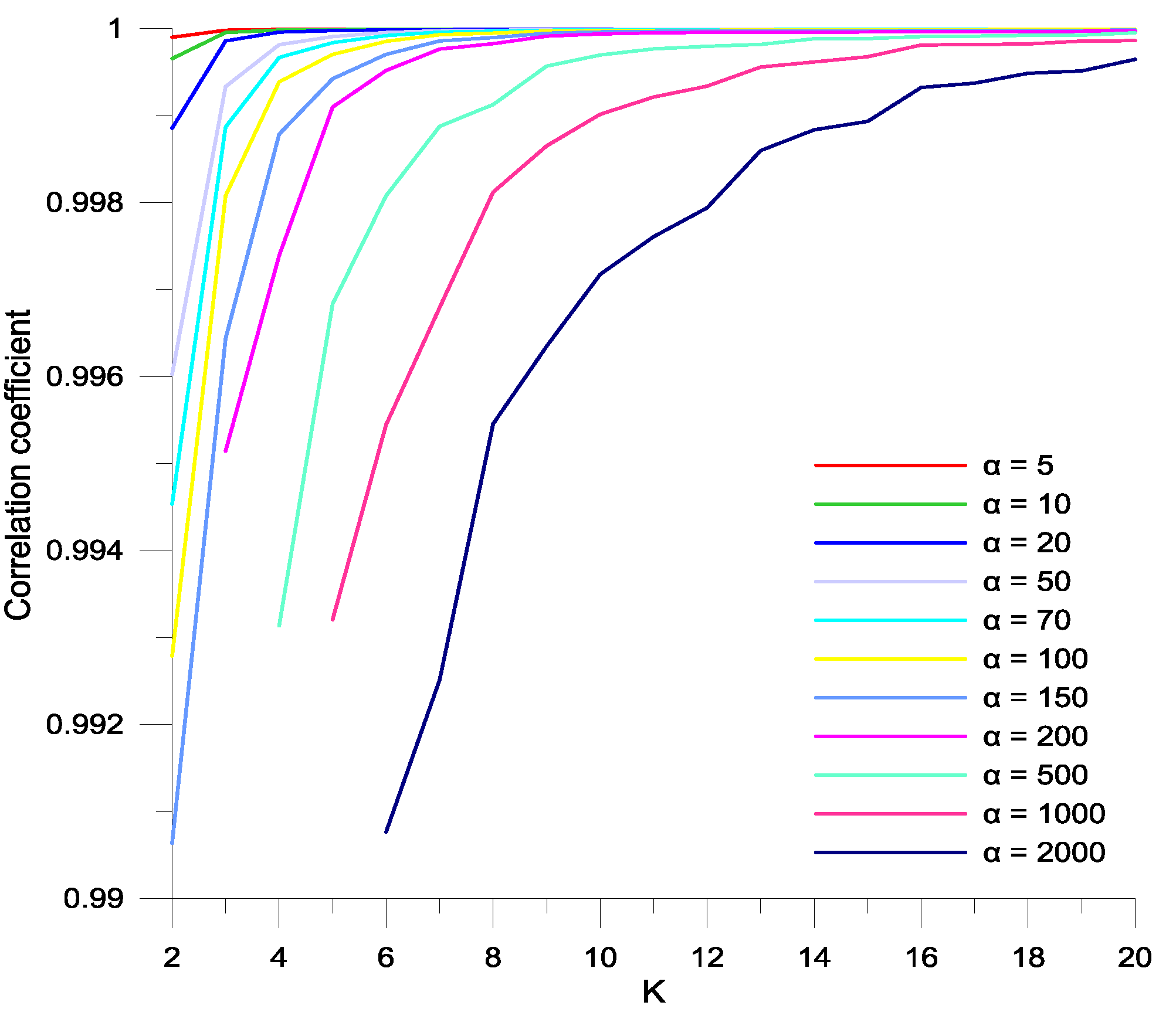
- Step 1.
- For K = {2, 3, ......, 20} and α = {5, 10, 20, 50, 70, 100, 150, 200, 500, 1000, 2000}, the corresponding IMFs are generated from water demand time series.
- Step 2.
- For each set of K and α values, the IMFs are summed to reconstruct the water demand time series.
- Step 3.
- Correlation coefficients (r) between original and reconstructed water demand time series are estimated.
- Step 4.
- The sets of K and α values corresponding to are selected.
- Step 5.
- The optimal values of K and α are selected based on the performances of VMD-based forecasting models.
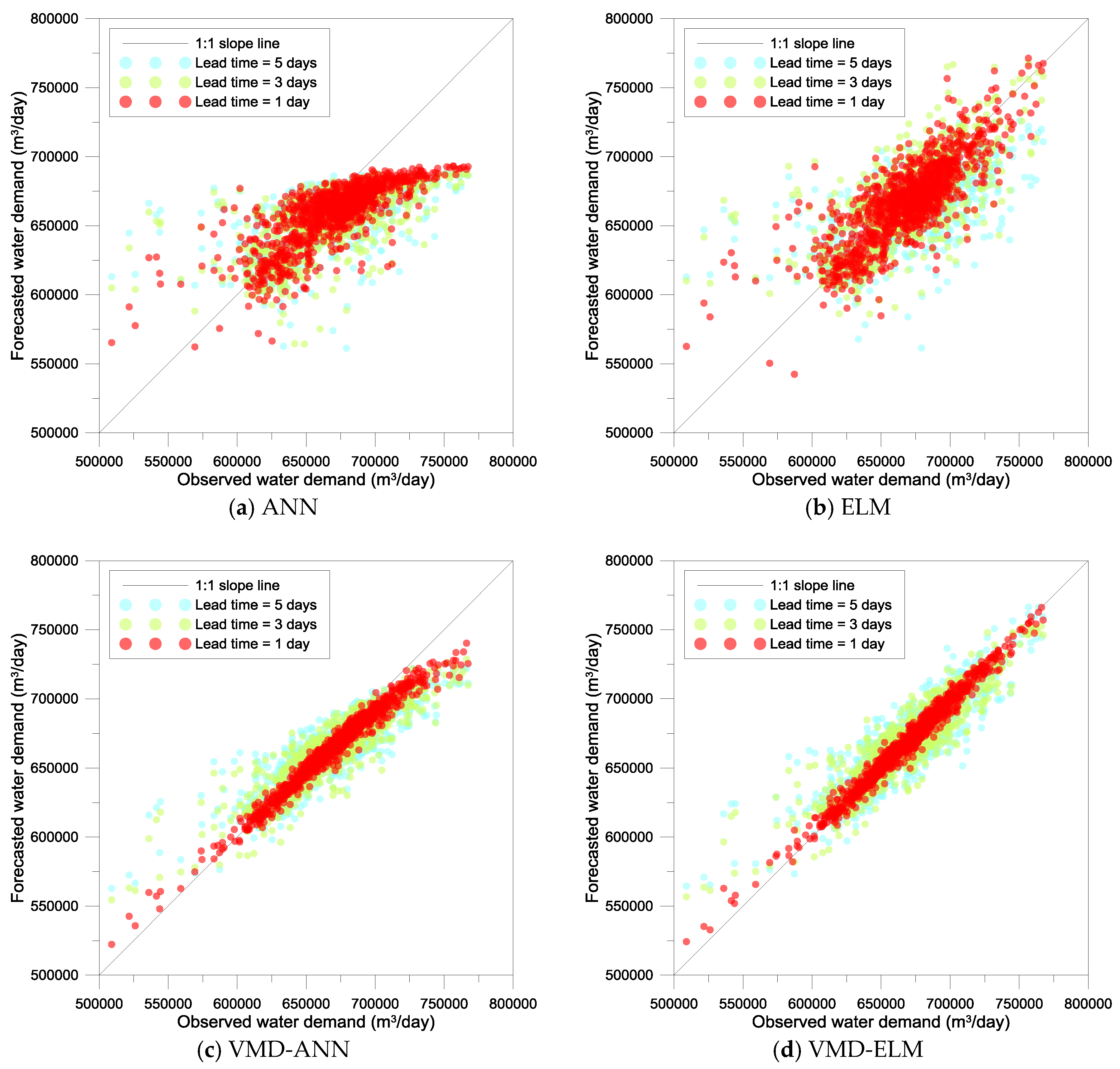
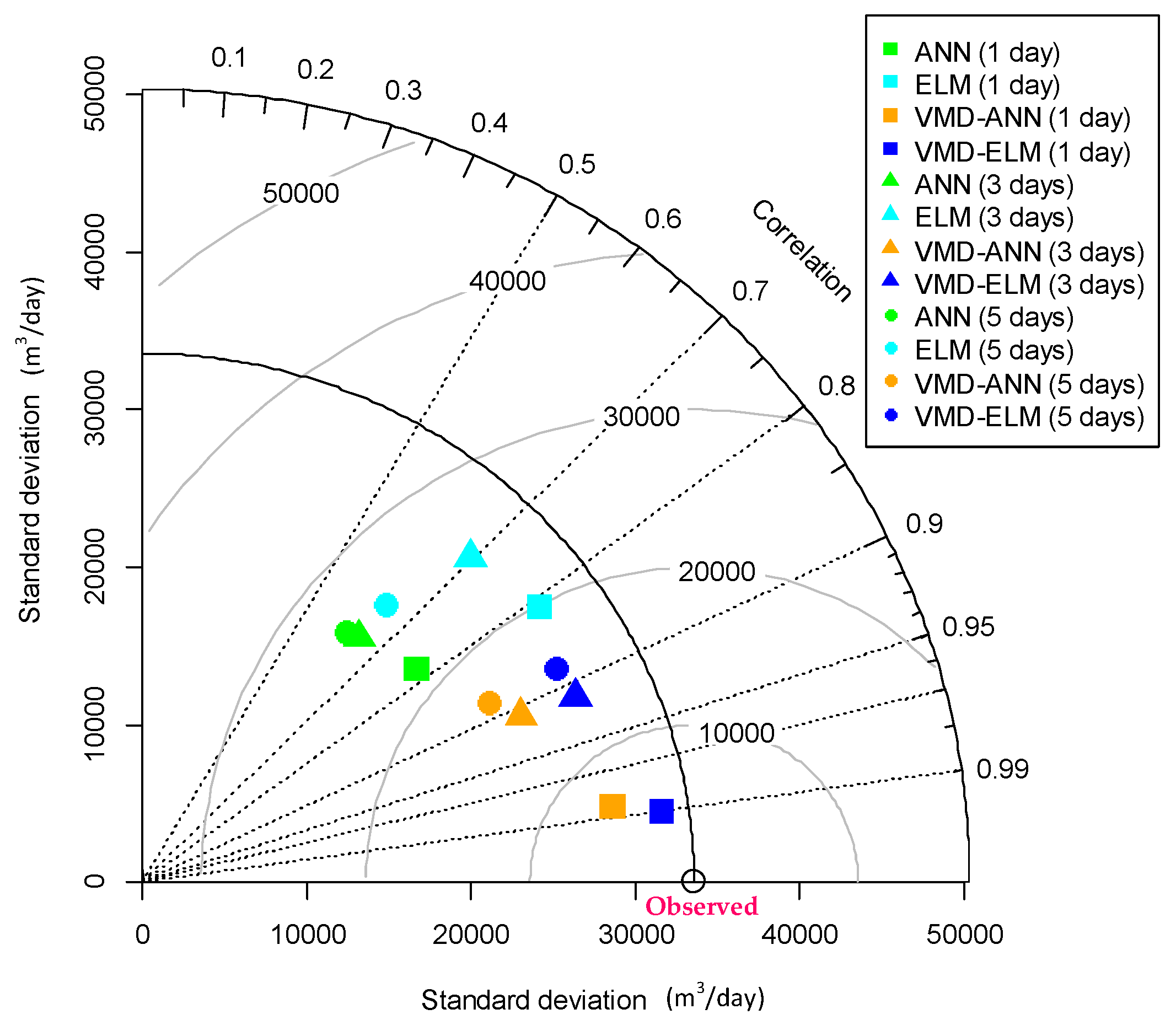
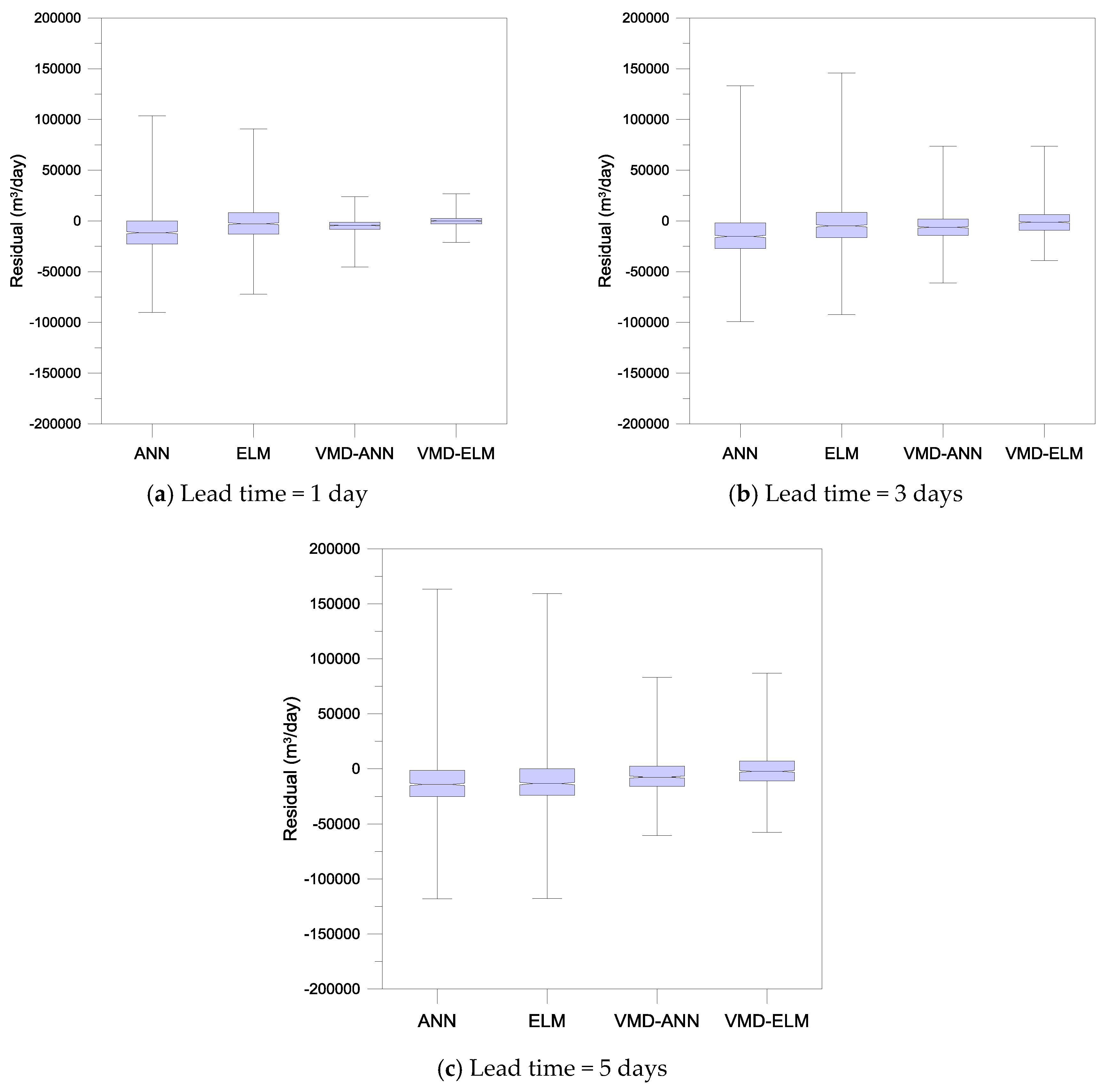
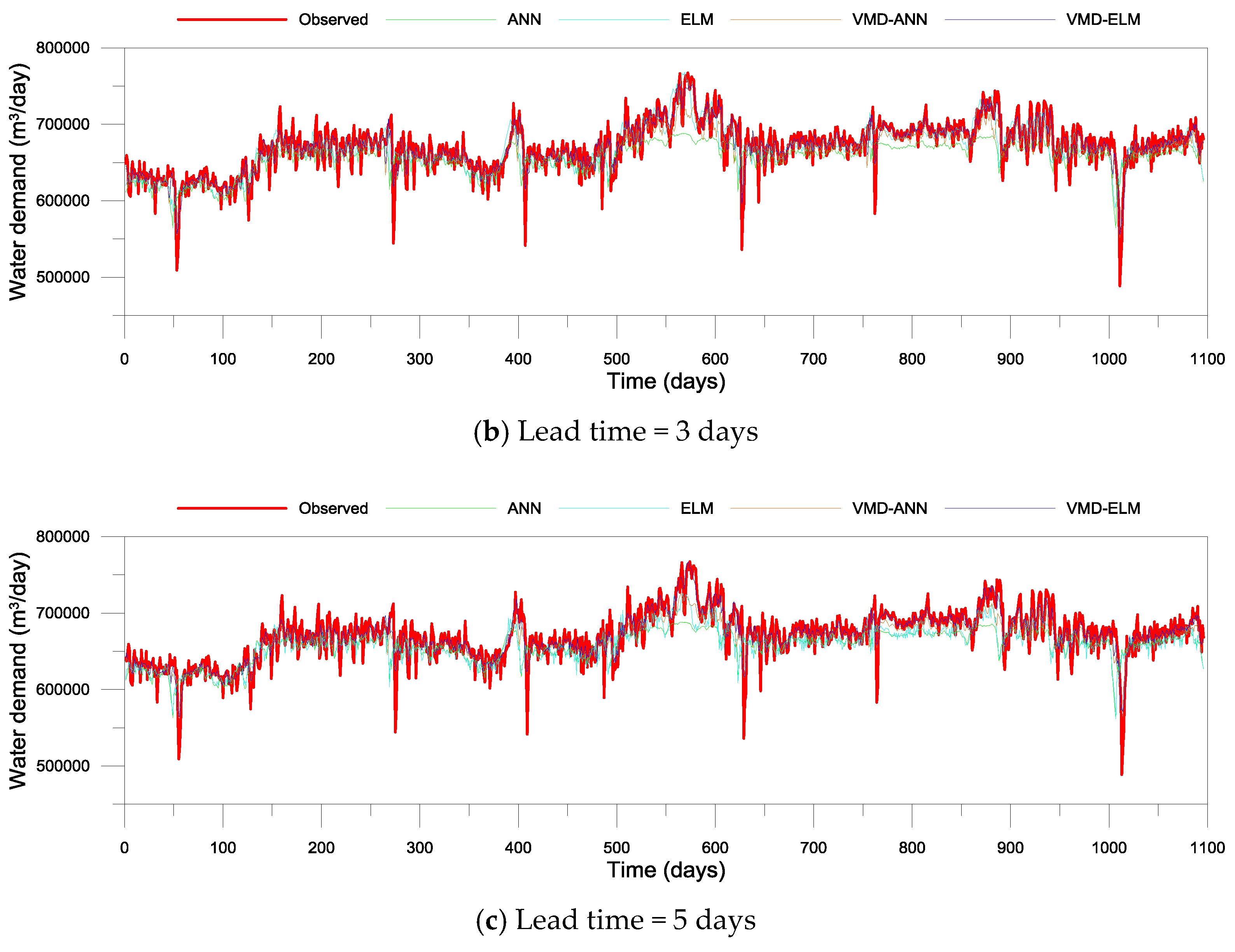
3.2. Performance Evaluation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47, W05401. [Google Scholar] [CrossRef]
- Schuetze, T.; Santiago-Fandiño, V. Quantitative assessment of water use efficiency in urban and domestic buildings. Water 2013, 5, 1172–1193. [Google Scholar] [CrossRef]
- Hao, L.; Sun, G.; Liu, Y.; Qian, H. Integrated modeling of water supply and demand under management options and climate change scenarios in Chifeng city, China. J. Am. Water Resour. Assoc. 2015, 51, 655–671. [Google Scholar] [CrossRef]
- Arsiso, B.K.; Tsidu, G.M.; Stoffberg, G.H.; Tadesse, T. Climate change and population growth impacts on surface water supply and demand of Addis Ababa, Ethiopia. Clim. Risk Manag. 2017, 18, 21–33. [Google Scholar] [CrossRef]
- Lee, J.S.; Kim, J.W. Assessing strategies for urban climate change adaptation: The case of six metropolitan cities in South Korea. Sustainability 2018, 10, 2065. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Roberson, J.A. Urban water demand forecasting: Review of methods and models. J. Water Res. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Adamowski, J. Urban water demand forecasting and uncertainty assessment using ensemble wavelet-bootstrap-neural network models. Water Resour. Res. 2013, 49, 6486–6507. [Google Scholar] [CrossRef]
- Adamowski, J.; Chan, H.F.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48, W01528. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, P.; Li, C.; Xie, J.; Wang, Y. A multi-scale relevance vector regression approach for daily urban water demand forecasting. J. Hydrol. 2014, 517, 236–245. [Google Scholar] [CrossRef]
- Brentan, B.M.; Luvizotto, E., Jr.; Herrera, M.; Izquierdo, J.; Pérez-García, R. Hybrid regression model for near real-time urban water demand forecasting. J. Comput. Appl. Math. 2017, 309, 532–541. [Google Scholar] [CrossRef]
- Arandia, E.; Ba, A.; Eck, B.; McKenna, S. Tailoring seasonal time series models to forecast shot-term water demand. J. Water Res. Plan. Manag. 2016, 142, 1–10. [Google Scholar] [CrossRef]
- Gagliardi, F.; Alvisi, S.; Kapelan, Z.; Franchini, M. A probabilistic short-term water demand forecasting model based on the Markov chain. Water 2017, 9, 507. [Google Scholar] [CrossRef]
- Pacchin, E.; Alvisi, S.; Franchini, M. A short-term water demand forecasting model using a moving window on previously observed data. Water 2017, 9, 172. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M. Assessment of predictive uncertainty within the framework of water demand forecasting using the Model Conditional Processor (MCP). Urban Water J. 2017, 14, 1–10. [Google Scholar] [CrossRef]
- Anele, A.O.; Hamam, Y.; Abu-Mahfouz, A.M.; Todini, E. Overview, comparative assessment and recommendations of forecasting models for short-term water demand prediction. Water 2017, 9, 887. [Google Scholar] [CrossRef]
- Anele, A.O.; Todini, E.; Hamam, Y.; Abu-Mahfouz, A.M. Predictive uncertainty estimation in water demand forecasting using the model conditional processor. Water 2018, 10, 475. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Singh, V.P. Comparison of different heuristic and decomposition techniques for river stage modeling. Environ. Monit. Assess. 2018, 190, 392. [Google Scholar] [CrossRef] [PubMed]
- Seo, Y.; Kim, S.; Singh, V.P. Machine learning models coupled with variational mode decomposition: A new approach for modeling daily rainfall-runoff. Atmosphere 2018, 9, 251. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Polyak, N.; Pearlman, W.A. Stationarity of the Gabor basis and derivation of Janssen’s formula. In Proceedings of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis, Victoria, BC, Canada, 4–6 October 1992. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. An extreme learning machine model for the simulation of monthly mean streamflow water level in eastern Queensland. Environ. Monit. Assess. 2016, 188, 90. [Google Scholar] [CrossRef] [PubMed]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning ling-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Brink, H.; Richards, J.W.; Fetherolf, M. Real-World Machine Learning; Manning Publications Co.: Shelter Island, NY, USA, 2017; ISBN 978-1617291920. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R.L. Hydrological modelling using artificial neural networks. Prog. Phys. Geogr. 2001, 25, 80–108. [Google Scholar] [CrossRef]
- Partal, T.; Cigizoglu, H.K. Estimation and forecasting of daily suspended sediment data using wavelet-neural networks. J. Hydrol. 2008, 358, 317–331. [Google Scholar] [CrossRef]
- Mohanta, A.; Patra, K.C.; Sahoo, B.B. Anticipate Manning’s coefficient in meandering compound channels. Hydrology 2018, 5, 47. [Google Scholar] [CrossRef]
- ASCE Task Committee. Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- Zahmatkesh, Z.; Goharian, E. Comparing machine learning and decision making approaches to forecast long lead monthly rainfall: The city of Vancouver, Canada. Hydrology 2018, 5, 10. [Google Scholar] [CrossRef]
- Lima, A.R.; Cannon, A.J.; Hsieh, W.W. Forecasting daily streamflow using online sequential extreme learning machines. J. Hydrol. 2016, 537, 431–443. [Google Scholar] [CrossRef]
- Alpaydin, E. Introduction to Machine Learning, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2010; ISBN 978-0262028189. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and application. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Yu, L.; Dai, W.; Tang, L. A novel decomposition ensemble model with extended extreme learning machine for crude oil price forecasting. Eng. Appl. Artif. Intell. 2016, 47, 110–121. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Dawson, C.W.; Abrahart, R.J.; See, L.M. HydroTest: A web-based toolbox of evaluation metrics for the standardized assessment of hydrological forecasts. Environ. Model. Softw. 2007, 22, 1034–1052. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Kisi, O.; Singh, V.P. Daily water level forecasting using wavelet decomposition and artificial neural intelligence techniques. J. Hydrol. 2015, 520, 224–243. [Google Scholar] [CrossRef]
- Zell, A.; Mamier, G.; Mache, M.V.N.; Hübner, R.; Dörin, S.; Hermann, K.U. SNNS Stuttgart Neural Network Simulator v. 4.2, User Manual. University of Stuttgart/University of Tübingen. 1998. Available online: http://www.ra.cs.uni-tuebingen.de/downloads/SNNS/SNNSv4.2.Manual.pdf (accessed on 30 June 2018).
- Dai, H.; MacBeth, C. Effects of learning parameters on learning procedure and performance of a BPNN. Neural Netw. 1997, 10, 1505–1521. [Google Scholar] [CrossRef]
- Rumelhart, D.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Pao, Y.H. Adaptive Pattern Recognition and Neural Networks; Addison-Wesley Publishing Company, Inc.: New York, NY, USA, 1988; ISBN 978-0201125849. [Google Scholar]
- Shi, P.; Yang, W. Precise feature extraction from wind turbine condition monitoring signals by using optimised variational mode decomposition. IET Renew. Power Gener. 2017, 11, 245–252. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Sun, G.; Chen, T.; Wei, Z.; Sun, Y.; Zang, H.; Chen, S. A carbon price forecasting model based on variational mode decomposition and spiking neural networks. Energies 2016, 9, 54. [Google Scholar] [CrossRef]
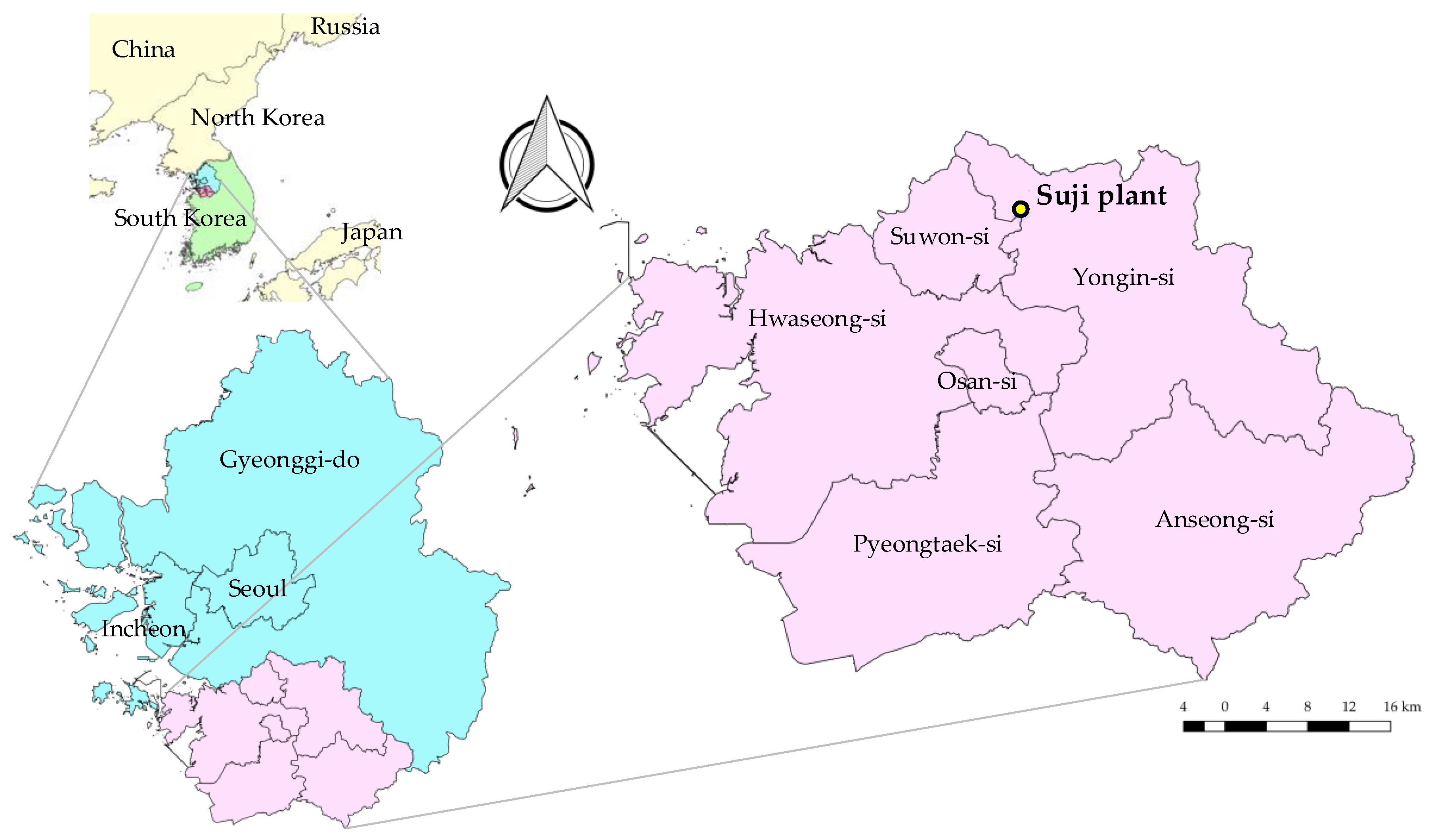


| Cities | Area (km2) | Population (People) | Population Density (People/km2) | Water Demand (103 m3/year) | |||
|---|---|---|---|---|---|---|---|
| Total | Domestic | Industrial | Agricultural | ||||
| Anseong-si | 553.39 | 182,294 | 329.4 | 245,000 | 41,353 | 17,873 | 185,774 |
| Hwaseong-si | 693.92 | 729,939 | 1051.9 | 381,375 | 96,075 | 30,260 | 255,040 |
| Pyeongtaek-si | 458.08 | 489,081 | 1067.7 | 384,013 | 80,825 | 46,221 | 256,967 |
| Osan-si | 42.73 | 218,635 | 5116.7 | 37,403 | 24,160 | 6474 | 6769 |
| Suwon-si | 121.05 | 1,203,285 | 9940.4 | 582,384 | 520,385 | 14,339 | 47,660 |
| Yongin-si | 591.34 | 1,017,673 | 1721.0 | 705,685 | 418,171 | 2733 | 284,781 |
| Performance Indices | Equations | Ranges | |
|---|---|---|---|
| Absolute errors | MAE | ||
| RMSE | |||
| R4MS4E | |||
| Relative errors | MARE | ||
| MdAPE | |||
| Dimensionless errors | MCE | with | |
| MIOA | with | ||
| Models | Lead Times (Days) | MAE (m3/day) | RMSE (m3/day) | R4MS4E (m3/day) | MARE | MdAPE | MCE1 | MIOA1 | MCE2 | MIOA2 | MCE3 | MIOA3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ANN | 1 | 18,694 | 24,366 | 34,700 | 0.028 | 2.330 | −0.141 | 0.576 | −0.284 | 0.797 | −0.422 | 0.901 |
| 2 | 21,322 | 27,658 | 39,636 | 0.032 | 2.592 | −0.362 | 0.516 | −0.831 | 0.728 | −1.533 | 0.835 | |
| 3 | 22,714 | 29,468 | 42,812 | 0.035 | 2.851 | −0.460 | 0.491 | −1.086 | 0.692 | −2.088 | 0.792 | |
| 4 | 21,924 | 29,203 | 43,984 | 0.033 | 2.616 | −0.431 | 0.498 | −1.106 | 0.688 | −2.296 | 0.775 | |
| 5 | 22,044 | 29,447 | 45,190 | 0.034 | 2.606 | −0.432 | 0.496 | −1.126 | 0.683 | −2.421 | 0.761 | |
| 6 | 23,444 | 30,669 | 45,419 | 0.036 | 2.824 | −0.514 | 0.478 | −1.282 | 0.666 | −2.610 | 0.752 | |
| 7 | 25,252 | 32,166 | 45,993 | 0.039 | 3.245 | −0.639 | 0.452 | −1.551 | 0.644 | −3.065 | 0.739 | |
| ELM | 1 | 14,620 | 19,928 | 30,446 | 0.022 | 1.622 | 0.421 | 0.693 | 0.648 | 0.894 | 0.783 | 0.961 |
| 2 | 16,703 | 23,184 | 37,696 | 0.025 | 1.849 | 0.338 | 0.643 | 0.523 | 0.846 | 0.625 | 0.920 | |
| 3 | 17,890 | 24,932 | 40,900 | 0.027 | 2.003 | 0.291 | 0.618 | 0.449 | 0.822 | 0.527 | 0.898 | |
| 4 | 19,809 | 26,841 | 42,127 | 0.030 | 2.285 | 0.216 | 0.558 | 0.361 | 0.767 | 0.452 | 0.857 | |
| 5 | 21,006 | 28,235 | 43,937 | 0.031 | 2.510 | 0.169 | 0.533 | 0.294 | 0.740 | 0.372 | 0.832 | |
| 6 | 19,585 | 27,322 | 43,623 | 0.029 | 2.161 | 0.226 | 0.594 | 0.339 | 0.793 | 0.398 | 0.875 | |
| 7 | 20,375 | 27,516 | 43,073 | 0.031 | 2.416 | 0.195 | 0.561 | 0.330 | 0.770 | 0.412 | 0.858 | |
| VMD-ANN | 1 | 6417 | 8719 | 13,455 | 0.009 | 0.717 | 0.746 | 0.864 | 0.933 | 0.981 | 0.982 | 0.997 |
| 2 | 8852 | 11,899 | 17,349 | 0.013 | 1.004 | 0.649 | 0.808 | 0.874 | 0.961 | 0.957 | 0.993 | |
| 3 | 12,166 | 16,154 | 23,847 | 0.018 | 1.432 | 0.518 | 0.728 | 0.769 | 0.923 | 0.891 | 0.978 | |
| 4 | 14,291 | 18,210 | 25,581 | 0.021 | 1.824 | 0.434 | 0.682 | 0.706 | 0.902 | 0.857 | 0.972 | |
| 5 | 13,701 | 18,046 | 26,735 | 0.020 | 1.655 | 0.458 | 0.686 | 0.711 | 0.899 | 0.849 | 0.967 | |
| 6 | 16,225 | 21,094 | 30,659 | 0.024 | 1.987 | 0.359 | 0.631 | 0.606 | 0.860 | 0.765 | 0.946 | |
| 7 | 17,058 | 23,013 | 35,325 | 0.026 | 1.945 | 0.326 | 0.609 | 0.531 | 0.827 | 0.664 | 0.916 | |
| VMD-ELM | 1 | 3637 | 4927 | 7519 | 0.005 | 0.403 | 0.856 | 0.927 | 0.978 | 0.994 | 0.997 | 0.999 |
| 2 | 6327 | 8643 | 12,999 | 0.010 | 0.696 | 0.749 | 0.868 | 0.934 | 0.981 | 0.983 | 0.997 | |
| 3 | 10,156 | 13,824 | 21,805 | 0.015 | 1.161 | 0.598 | 0.784 | 0.830 | 0.949 | 0.925 | 0.987 | |
| 4 | 10,068 | 13,691 | 21,945 | 0.015 | 1.159 | 0.601 | 0.784 | 0.834 | 0.949 | 0.926 | 0.987 | |
| 5 | 11,888 | 16,010 | 25,408 | 0.018 | 1.393 | 0.530 | 0.745 | 0.773 | 0.930 | 0.884 | 0.979 | |
| 6 | 12,836 | 17,513 | 27,604 | 0.019 | 1.460 | 0.493 | 0.728 | 0.728 | 0.917 | 0.847 | 0.972 | |
| 7 | 14,405 | 20,077 | 31,553 | 0.022 | 1.634 | 0.431 | 0.696 | 0.643 | 0.890 | 0.766 | 0.956 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, Y.; Kwon, S.; Choi, Y. Short-Term Water Demand Forecasting Model Combining Variational Mode Decomposition and Extreme Learning Machine. Hydrology 2018, 5, 54. https://doi.org/10.3390/hydrology5040054
Seo Y, Kwon S, Choi Y. Short-Term Water Demand Forecasting Model Combining Variational Mode Decomposition and Extreme Learning Machine. Hydrology. 2018; 5(4):54. https://doi.org/10.3390/hydrology5040054
Chicago/Turabian StyleSeo, Youngmin, Soonmyeong Kwon, and Yunyoung Choi. 2018. "Short-Term Water Demand Forecasting Model Combining Variational Mode Decomposition and Extreme Learning Machine" Hydrology 5, no. 4: 54. https://doi.org/10.3390/hydrology5040054
APA StyleSeo, Y., Kwon, S., & Choi, Y. (2018). Short-Term Water Demand Forecasting Model Combining Variational Mode Decomposition and Extreme Learning Machine. Hydrology, 5(4), 54. https://doi.org/10.3390/hydrology5040054





