Regional Assessment of Groundwater Recharge in the Lower Mekong Basin
Abstract
:1. Introduction
2. Study Site
2.1. Climate and Hydrology
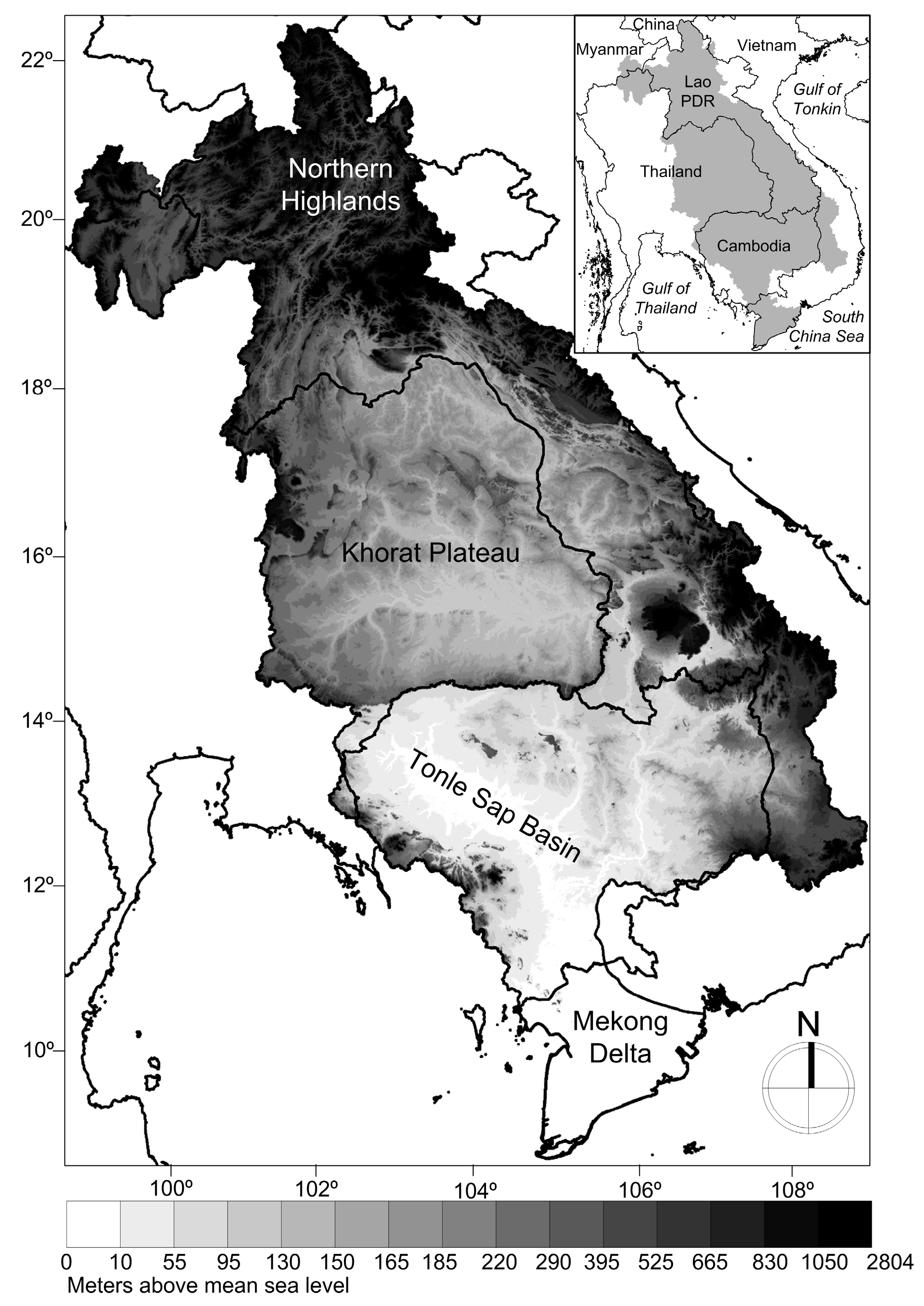
2.2. Topography
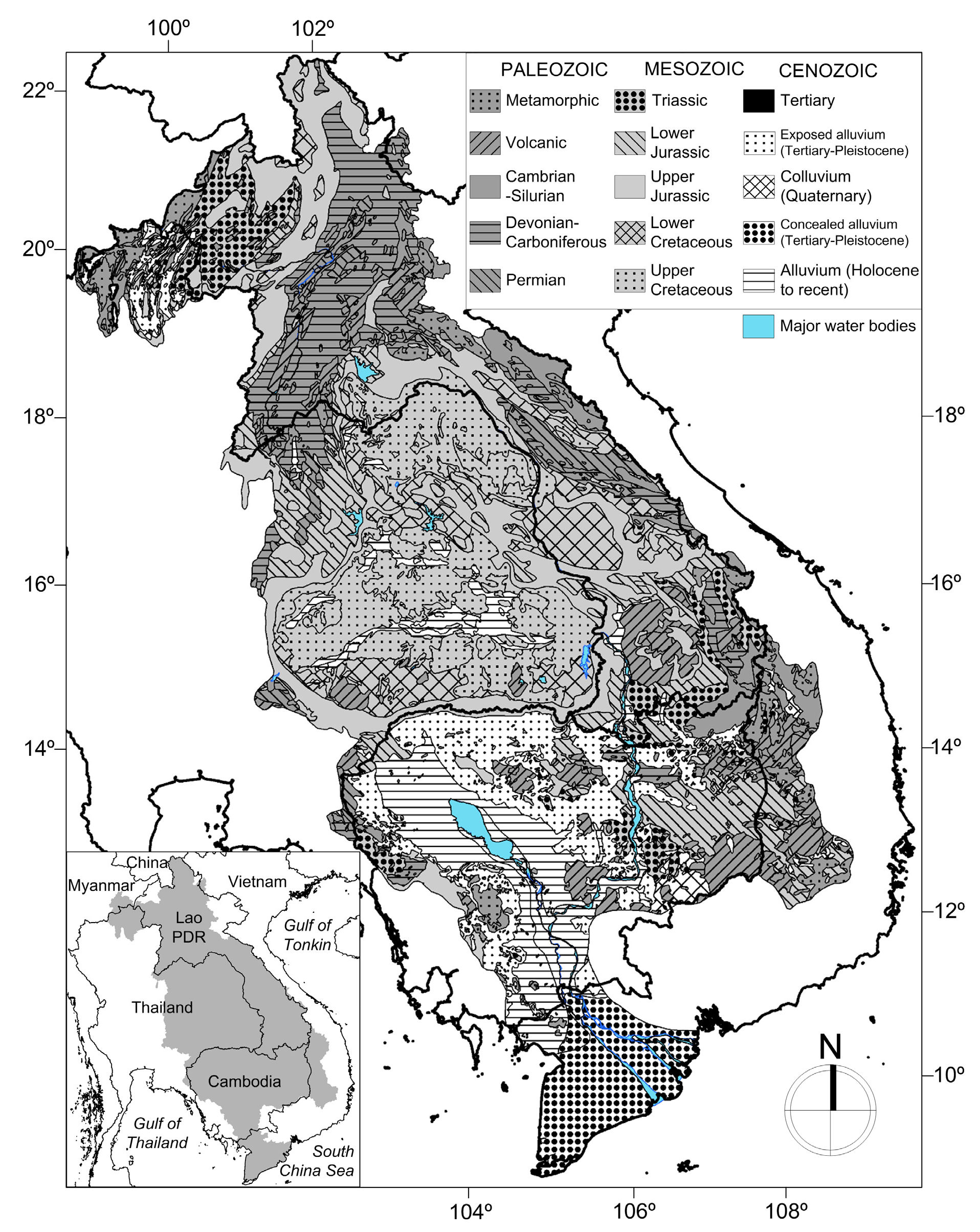
2.3. Hydrogeology
3. Materials and Methods
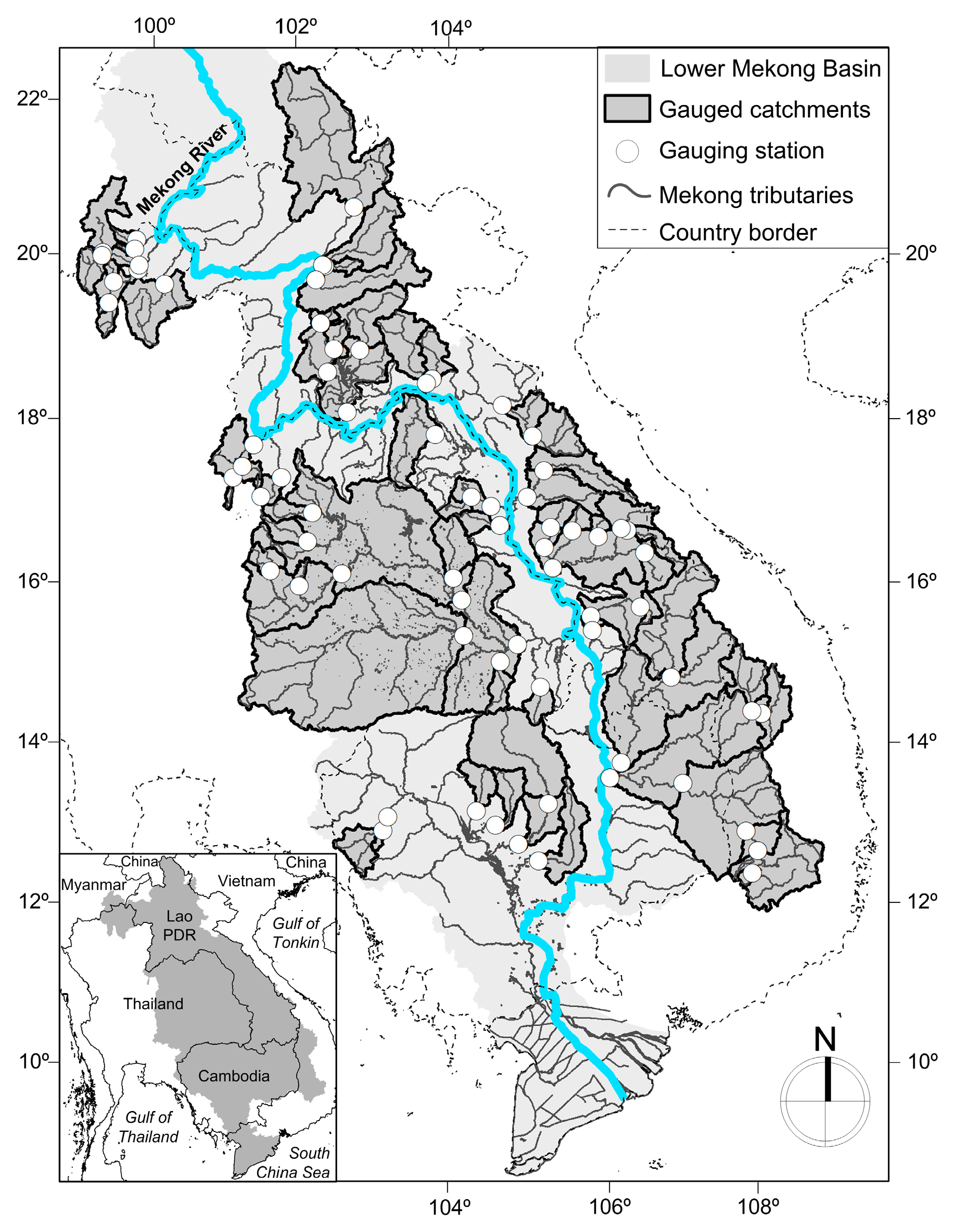
3.1. Catchment Selection and Baseflow Computation
3.2. Prediction of Baseflow Across the Lower Mekong Basin
3.3. Catchment Characteristics
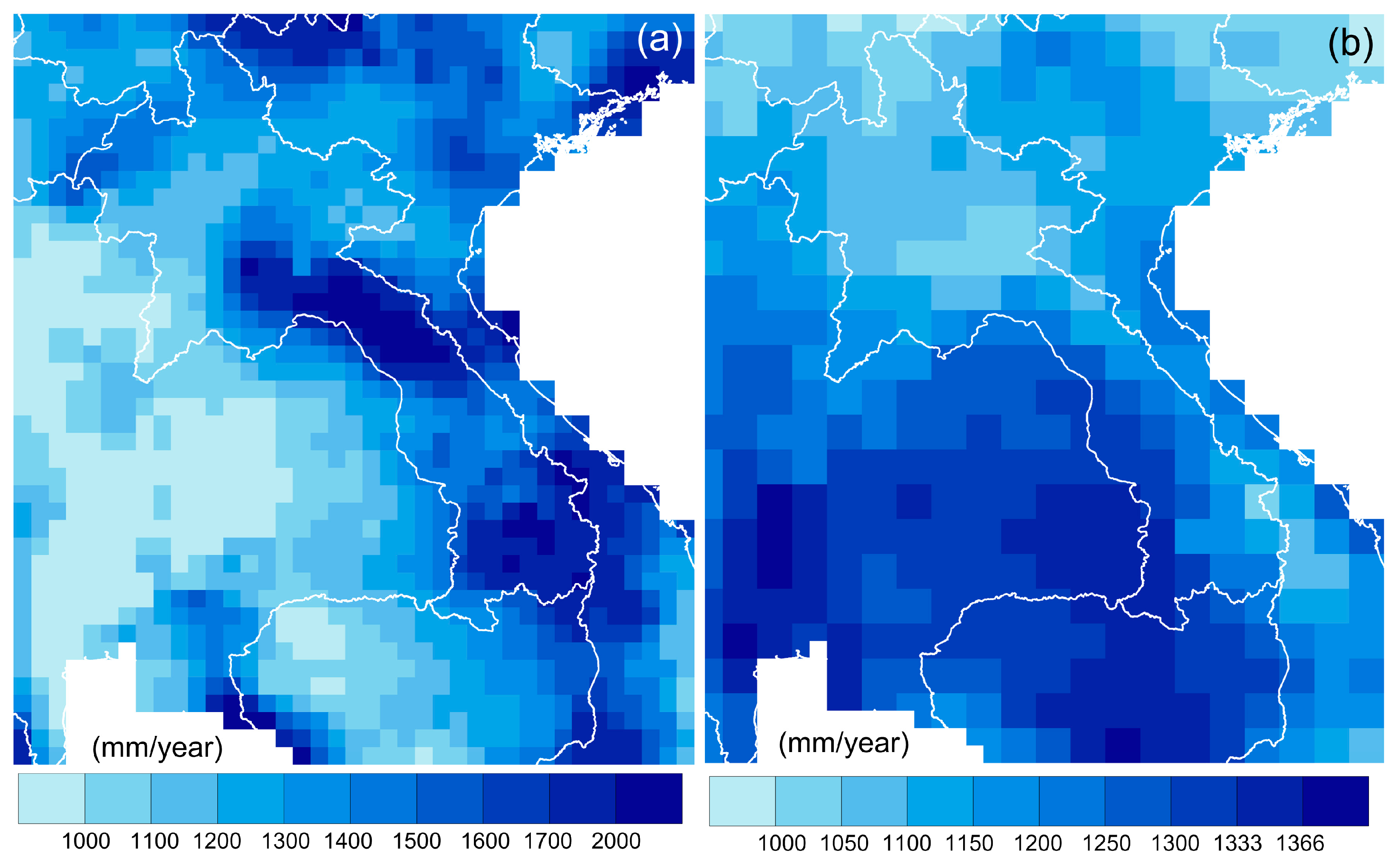
3.3.1. Climate
3.3.2. Geomorphology and Geographic Coordinates
3.3.3. Soil
3.3.4. Land Cover
4. Results
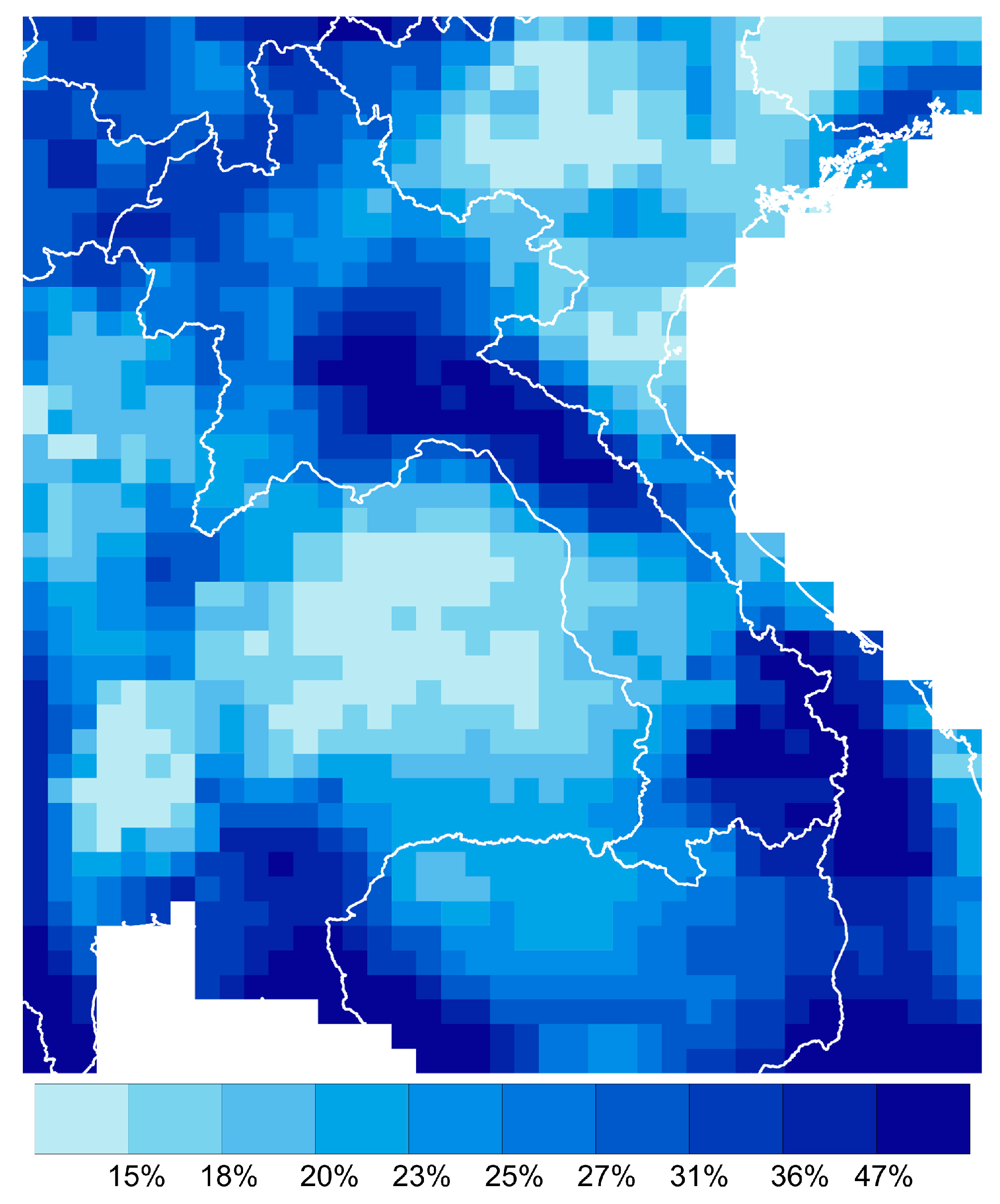
4.1. Baseflow Estimations
4.2. Multiple Regressions Analysis
4.2.1. Prediction of Groundwater Recharge
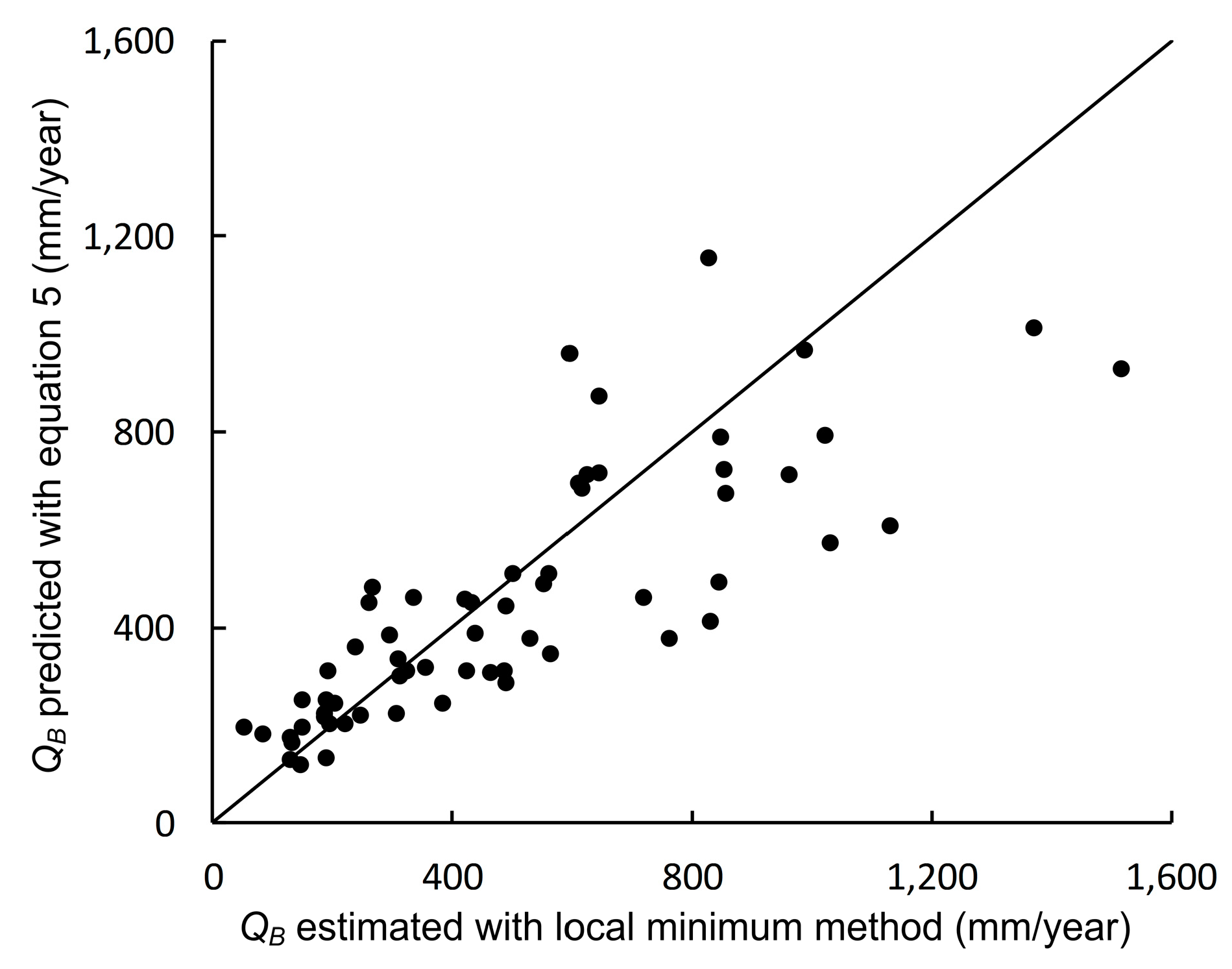
4.2.2. Model Performance
5. Discussion
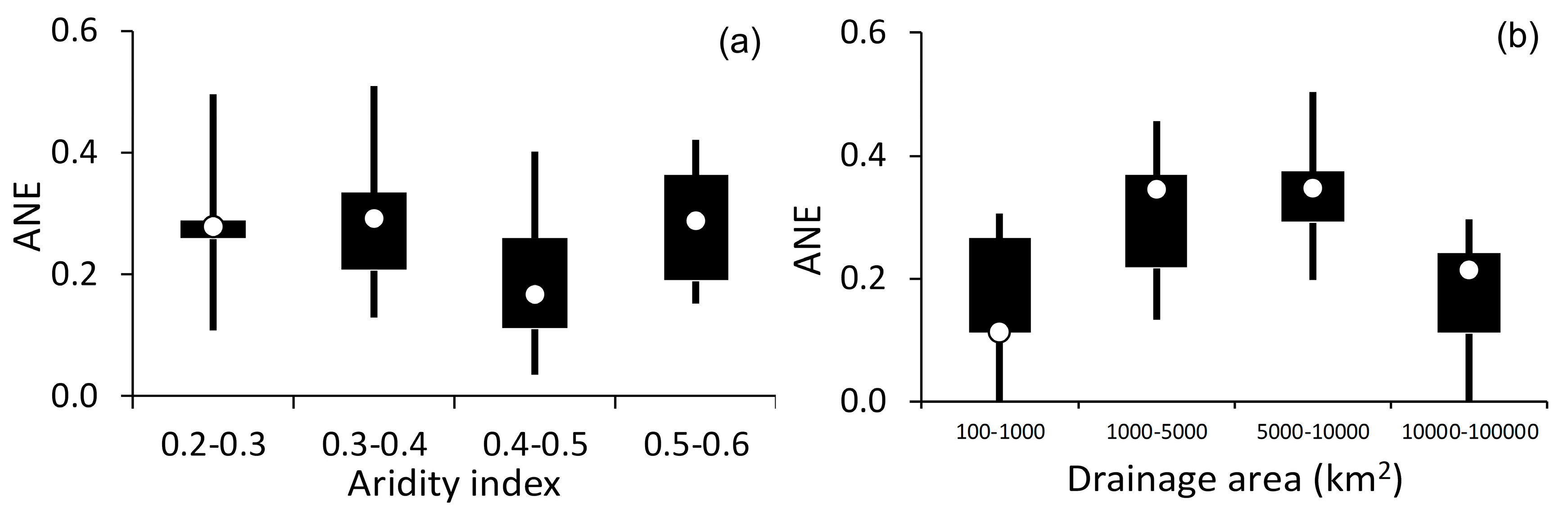
5.1. Factors Determining Groundwater Recharge
5.2. Comparison with Previous Studies
5.3. Limitations of the Study
5.4. Groundwater Potential for Irrigation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gleeson, T.; Wada, Y.; Bierkens, M.F.P.; van Beek, L.P.H. Water balance of global aquifers revealed by groundwater footprint. Nature 2012, 488, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef] [Green Version]
- Landon, M. Preliminary Compilation and Review of Current Information on Groundwater Monitoring and Resources in the Lower Mekong River Basin; U.S. Geological Survey Report to the Mekong River Commission: Vientiane, Laos, 2001.
- Vote, C.; Newby, J.; Phouyyavong, K.; Inthavong, T.; Eberbach, P. Trends and perceptions of rural household groundwater use and the implications for smallholder agriculture in rain-fed Southern Laos. Int. J. Water Resour Dev. 2015, 31, 558–574. [Google Scholar] [CrossRef]
- Döll, P.; Fiedler, K. Global-scale modelling of groundwater recharge. Hydrol. Earth Syst. Sci. 2008, 12, 863–885. [Google Scholar] [CrossRef]
- Gleeson, T.; Alley, W.M.; Allen, D.M.; Sophocleous, M.A.; Zhou, Y.X.; Taniguchi, M.; VanderSteen, J. Towards sustainable groundwater use: Setting long-term goals, backcasting, and managing adaptively. Groundwater 2012, 50, 19–26. [Google Scholar] [CrossRef] [PubMed]
- Wada, Y.; van Beek, L.P.H.; van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, L20402. [Google Scholar] [CrossRef]
- Saraphirom, P.; Wirojanagud, W.; Srisuk, K. Impact of climate change on waterlogging and salinity distributions in Huai Khamrian subwatershed, NE Thailand. Environ. Earth Sci. 2013, 70, 887–900. [Google Scholar] [CrossRef]
- Rõi, N.D. Estimation of groundwater recharge of the Holocene aquifer from rainfall by RIB method for Hưng Yên Province. VNU J. Sci. Earth Environ. Sci. 2014, 30, 49–63. [Google Scholar]
- Vinh, C.T.; Khuyen, N.M.; Hieu, N.H.; Long, D.V.; Bach, N.T.; Van, T.T.T. Assessment of Groundwater Recharge from Rainfall in the Plain of Cai Phan Rang, Vietnam. J. Environ. Sci. Eng. 2014, 3, 141–149. [Google Scholar]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Von Freyberg, J.; Moeck, C.; Schirmer, M. Estimation of groundwater recharge and drought severity with varying model complexity. J. Hydrol. 2015, 527, 844–857. [Google Scholar] [CrossRef]
- Mekong River Commission (MRC). Overview of the Hydrology of the Mekong River Basin; Mekong River Commission (MRC): Vientiane, Laos, 2005. [Google Scholar]
- Halford, K.J.; Mayer, G.C. Problems associated with estimating ground water discharge and recharge from stream discharge records. Groundwater 2000, 38, 331–342. [Google Scholar] [CrossRef]
- Nathan, R.J.; McMahon, T.A. Evaluation of automated techniques for base flow and recession analyses. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Price, K. Effects of watershed topography, soils, land use, and climate on baseflow hydrology in humid regions: A review. Prog. Phys. Geol. 2011, 35, 465–492. [Google Scholar] [CrossRef]
- Mekong River Commission (MRC). State of the Basin Report; Mekong River Commission (MRC): Vientiane, Laos, 2010. [Google Scholar]
- Johnson, J.H. Preliminary Appraisal of the Hydrogeology of the Lower Mekong Basin; Interim Mekong Committee: Vientiane, Laos, 1986; p. 147. [Google Scholar]
- Charuratna, A.; Phu, T.H. Hydrogeological Map of Lower Mekong Basin. 1:1,000,000; Mekong Secretariat, Interim Committee for Coordination of Investigations of the lower Mekong Basin: Bangkok, Thailand, 1992. [Google Scholar]
- Japan International Cooperation Agency (JICA). Basic Design Study Report on the Project for Groundwater Development in the Vientiane Province in Lao PDR; Japan International Cooperation Agency (JICA): Tokyo, Japan, 1993; p. 199.
- Perttu, N.; Wattanasen, K.; Phommasone, K.; Elming, S.A. Characterization of aquifers in the Vientiane Basin, Laos, using magnetic resonance sounding and vertical electrical sounding. J. Appl. Geophys. 2011, 73, 207–220. [Google Scholar] [CrossRef]
- Lacombe, G.; McCartney, M. Evaluating the Flow Regulating Effects of Ecosystems in the Mekong and Volta River Basins; IWMI Research Report 166; International Water Management Institute: Colombo, Sri Lanka, 2016; p. 40. [Google Scholar]
- Yermoli, C. Draft User Manual. Hydropower Project Database; Basin Development Plan Phase 2; Mekong River Commission: Vientiane, Laos, 2008; p. 27. [Google Scholar]
- WLE. Dams in the Mekong River Basin: Commissioned, under Construction and Planned Dams in April 2016; CGIAR Research Program on Water, Land and Ecosystems-Greater Mekong (WLE): Vientiane, Laos, 2016. [Google Scholar]
- Pettyjohn, W.A.; Henning, R. Preliminary Estimate of Groundwater Recharge Rates, Related Streamflow and Water Quality in Ohio; Completion Report Number 552; University Water Resources Center: Columbus, OH, USA, 1979. [Google Scholar]
- HydroOffice. BFI+ 3.0. User’s Manual by Milos Gregor; HydroOffice: Bratislava, Slovakia, 2010. [Google Scholar]
- Milnes, E.; Negro, F.; Perrochet, P. Vietnam to Produce More Coffee with Less Water—Towards a Reduction of the Blue Water Footprint in Coffee Production. Hydrogeological Study of the Basaltic Plateau in Dak Lak Province, Vietnam; Université de Neuchâtel: Neuchâtel, Switzerland, 2015. [Google Scholar]
- Linsley, R.K.; Kohler, M.A.; Paulhus, J.L.H. Hydrology for Engineers, 2nd ed.; McGraw-Hill Book Company: New York, NY, USA, 1975. [Google Scholar]
- Eckhardt, K. A comparison of baseflow indices, which were calculated with seven different baseflow separation methods. J. Hydrol. 2008, 352, 168–173. [Google Scholar] [CrossRef]
- Risser, D.W.; Gburek, W.J.; Folmar, G.J. Comparison of Methods for Estimating Ground-Water Recharge and Base Flow at a Small Watershed Underlain by Fractured Bedrock in the Eastern United States; US Geological Survey Scientific Investigations Report 2005–5038; U.S. Geological Survey: Reston, VA, USA, 2005.
- Vogel, R.M.; Wilson, I.; Daly, C. Regional regression models of annual streamflow for the United States. J. Irrig. Drain. Eng. 1999, 125, 148–157. [Google Scholar] [CrossRef]
- Homa, E.S.; Brown, C.; McGarigal, K.; Compton, B.W.; Jackson, S.D. Estimating hydrologic alteration from basin characteristics in Massachusetts. J. Hydrol. 2013, 503, 196–208. [Google Scholar] [CrossRef]
- Tasker, G.D. Hydrologic regression with weighted least squares. Water Resour. Res. 1980, 16, 1107–1113. [Google Scholar] [CrossRef]
- Cook, R.D.; Weisberg, S. Residuals and Influence in Regression; Chapman and Hall: New York, NY, USA, 1982. [Google Scholar]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; US Geological Survey: Reston, VA, USA, 2002.
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Lauri, H.; Räsänen, T.A.; Kummu, M. Using reanalysis and remotely sensed temperature and precipitation data for hydrological modeling in monsoon climate: Mekong river case study. J. Hydrometeorol. 2014, 15, 1532–1545. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRUTS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
- Ekström, M.; Jones, P.D.; Fowler, H.J.; Lenderink, G.; Buishand, T.A.; Conway, D. Regional climate model data used within the SWURVE project 1: Projected changes in seasonal patterns and estimation of PET. Hydrol. Earth Syst. Sci. 2007, 11, 1069–1083. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. HydroSHEDS Technical Documentation; World Wildlife Fund US: Washington, DC, USA, 2006. [Google Scholar]
- MRC. Planning Atlas of the Lower Mekong River Basin. Basin Development Plan Programme; Mekong River Commission (MRC): Phnom-Penh, Cambodia, 2011. [Google Scholar]
- Lacombe, G.; Douangsavanh, S.; Vogel, R.M.; McCartney, M.; Chemin, Y.; Rebelo, L.M.; Sotoukee, T. Multivariate power-law models for streamflow prediction in the Mekong Basin. J. Hydrol. Reg. Stud. 2014, 2, 35–48. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Hydrological functions of tropical forests: Not seeing the soil for the trees? Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar]
- Salinas, J.L.; Laaha, G.; Rogger, M.; Parajka, J.; Viglione, A.; Sivapalan, M.; Blöschl, G. Comparative assessment of predictions in ungauged basins—Part 2. Flood and low flow studies. Hydrol. Earth Syst. Sci. 2013, 17, 2637–2652. [Google Scholar] [CrossRef]
- Nolan, B.T.; Healy, R.W.; Taber, P.E.; Perkins, K.; Hitt, K.J.; Wolock, D.M. Factors influencing ground-water recharge in the eastern United States. J. Hydrol. 2007, 332, 187–205. [Google Scholar] [CrossRef]
- Kim, J.H.; Jackson, R.B. A global analysis of groundwater recharge for vegetation, climate, and soils. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Zomlot, Z.; Verbeiren, B.; Huysmans, M.; Batelaan, O. Spatial distribution of groundwater recharge and base flow: Assessment of controlling factors. J. Hydrol. Reg. Stud. 2015, 4, 349–368. [Google Scholar] [CrossRef]
- Kim, H.W.; Hwang, K.; Mu, Q.; Lee, S.O.; Choi, M. Validation of MODIS 16 Global Terrestrial Evapotranspiration Products in Various Climates and Land Cover Types in Asia. KSCE J. Civ. Eng. 2012, 16, 229–238. [Google Scholar] [CrossRef]
- Kornkul, J.; Chotpantarat, S. Distributed Groundwater Recharge Estimation in Phrae Province Using WetSpass. In Proceedings of the Second Environment Asia International Conference on “Human Vulnerability and Global Environmental Change”, Chonburi, Thailand, 15–17 May 2013; pp. 553–565. [Google Scholar]
- Van der Wolf, M. Effects of Land Use Change on Groundwater Recharge. A case Study in the Day River Basin, Vietnam. Master’s Thesis, Utrecht University, Utrecht, The Netherlands, 2015. [Google Scholar]
- JICA. The Study on Groundwater Development in Central Cambodia; Interim Report of the Japan International Cooperation Agency (JICA); Kokusai Kogyo Co. Ltd.: Tokyo, Japan, 2001. [Google Scholar]
- Vouillamoz, J.M.; Valois, R.; Lun, S.; Caron, D.; Arnout, L. Can groundwater secure drinking-water supply and supplementary irrigation in new settlements of North-West Cambodia? Hydrogeol. J. 2016, 24, 195–209. [Google Scholar] [CrossRef]
- Erban, L.E.; Gorelick, S.M. Closing the irrigation deficit in Cambodia: Implications for transboundary impacts on groundwater and Mekong River flow. J. Hydrol. 2016, 535, 85–92. [Google Scholar] [CrossRef]
- Pilgrim, D.H.; Cordery, I.; Baron, B.C. Effects of catchment size on runoff relationships. J. Hydrol. 1982, 58, 205–221. [Google Scholar] [CrossRef]
- Suhardiman, D.; Giordano, M.; Leebouapao, L.; Keovilignavong, O. Farmers’ strategies as building block for rethinking sustainable intensification. Agric. Hum. Values 2016, 33, 563–574. [Google Scholar] [CrossRef]
- Pavelic, P.; Smakhtin, V.; Favreau, G.; Villholth, K. Water-balance approach for assessing potential for smallholder groundwater irrigation in Sub-Saharan Africa. Water SA 2012, 38, 399–406. [Google Scholar] [CrossRef]
- Brouwer, C.; Heibloem, M. Irrigation Water Needs Irrigation Water Management Training Manual 3; Food and Agriculture Organization (FAO): Rome, Italy, 1986. [Google Scholar]
- Agricultural Statistics of Thailand 2011. Office of Agricultural Economics (OAE). Available online: http://www.oae.go.th (accessed on 9 July 2016).
- Pavelic, P.; Xayviliya, O.; Ongkeo, O. Pathways for effective groundwater governance in the least developed country context of the Lao PDR. Water Int. 2014, 39, 469–485. [Google Scholar] [CrossRef]

| Variables | Unit | Minimum | Median | Maximum |
|---|---|---|---|---|
| Climate | ||||
| Median annual rainfall | mm/year | 880 | 1416 | 2093 |
| Median annual temperature | °C | 21.0 | 24.2 | 27.4 |
| Median annual standard evapotranspiration | mm/year | 1017 | 1168 | 1338 |
| Median annual actual evapotranspiration | mm/year | 818 | 1280 | 1374 |
| Geomorphology | ||||
| Drainage area | km2 | 207 | 3278 | 106,748 |
| Drainage density | km−1 | 0.09 | 0.13 | 0.17 |
| Mean elevation | m | 84 | 562 | 1168 |
| Mean slope | % | 2 | 15 | 32 |
| Perimeter | km | 76 | 401 | 2090 |
| Geographic coordinates of catchment centroid | ||||
| Latitude | decimal degree | 12.33 | 16.70 | 20.70 |
| Longitude | 99.35 | 104.03 | 108.00 | |
| Soil | ||||
| Top-soil texture | 4-unit * scale | 0 | 2.08 | 2.91 |
| Depth | 0 | 3.07 | 4.00 | |
| Land cover | ||||
| Forest | % area | 3 | 75 | 98 |
| Rain-fed lowland paddy | 0 | 4 | 77 | |
| Soil Depth | Top Soil Texture | 4-Unit Scale |
|---|---|---|
| <30 cm | Coarse | 1 |
| 30–50 cm | Medium | 2 |
| 30–50 cm with gravel | Fine | 3 |
| >50 cm | Peat | 4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lacombe, G.; Douangsavanh, S.; Vongphachanh, S.; Pavelic, P. Regional Assessment of Groundwater Recharge in the Lower Mekong Basin. Hydrology 2017, 4, 60. https://doi.org/10.3390/hydrology4040060
Lacombe G, Douangsavanh S, Vongphachanh S, Pavelic P. Regional Assessment of Groundwater Recharge in the Lower Mekong Basin. Hydrology. 2017; 4(4):60. https://doi.org/10.3390/hydrology4040060
Chicago/Turabian StyleLacombe, Guillaume, Somphasith Douangsavanh, Sinxay Vongphachanh, and Paul Pavelic. 2017. "Regional Assessment of Groundwater Recharge in the Lower Mekong Basin" Hydrology 4, no. 4: 60. https://doi.org/10.3390/hydrology4040060
APA StyleLacombe, G., Douangsavanh, S., Vongphachanh, S., & Pavelic, P. (2017). Regional Assessment of Groundwater Recharge in the Lower Mekong Basin. Hydrology, 4(4), 60. https://doi.org/10.3390/hydrology4040060





