Spatial and Temporal Variability of Potential Evaporation across North American Forests
Abstract
:1. Introduction
2. Data and Methods
2.1. Pan Evaporation Measurements
2.2. Models of Potential Evaporation
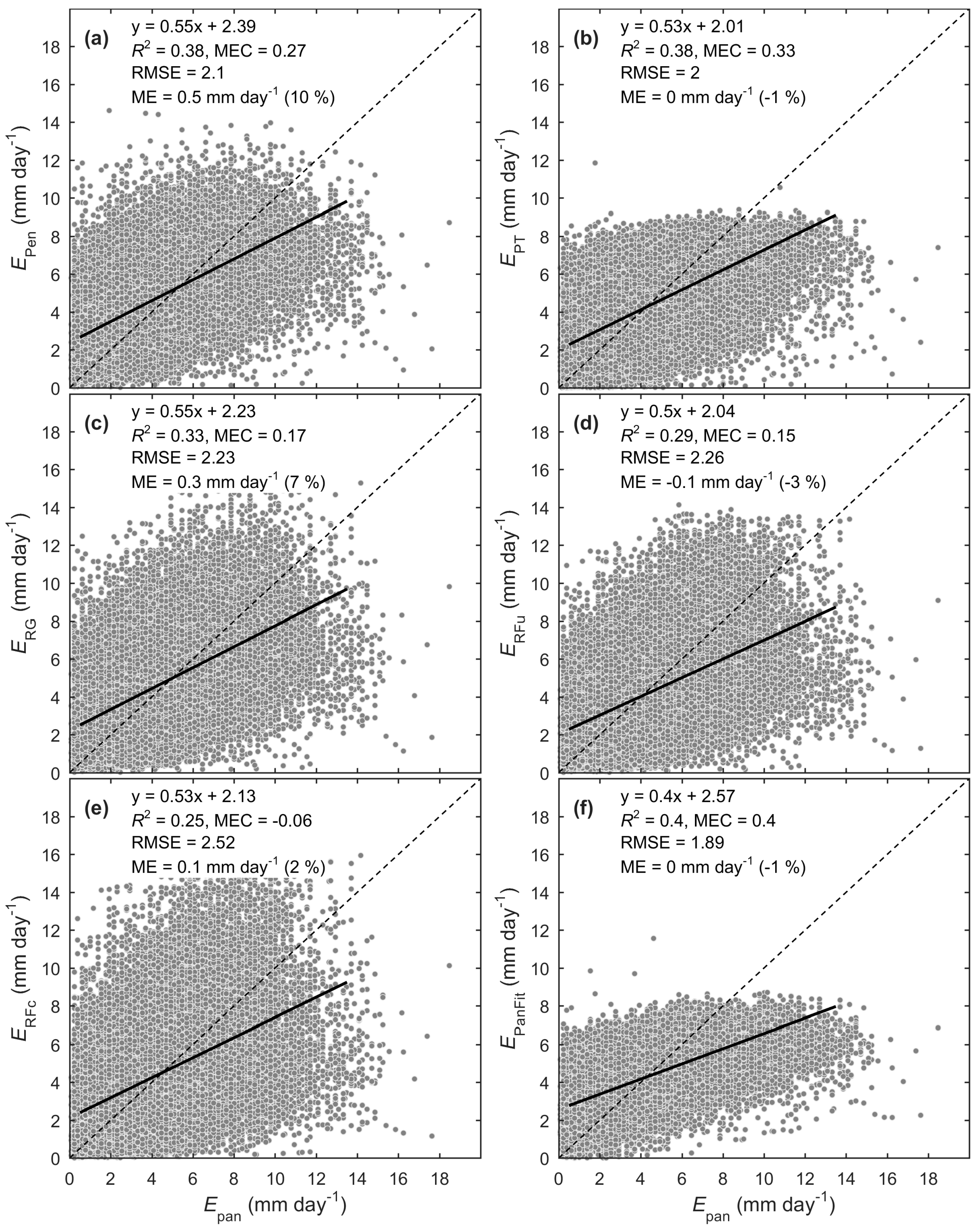
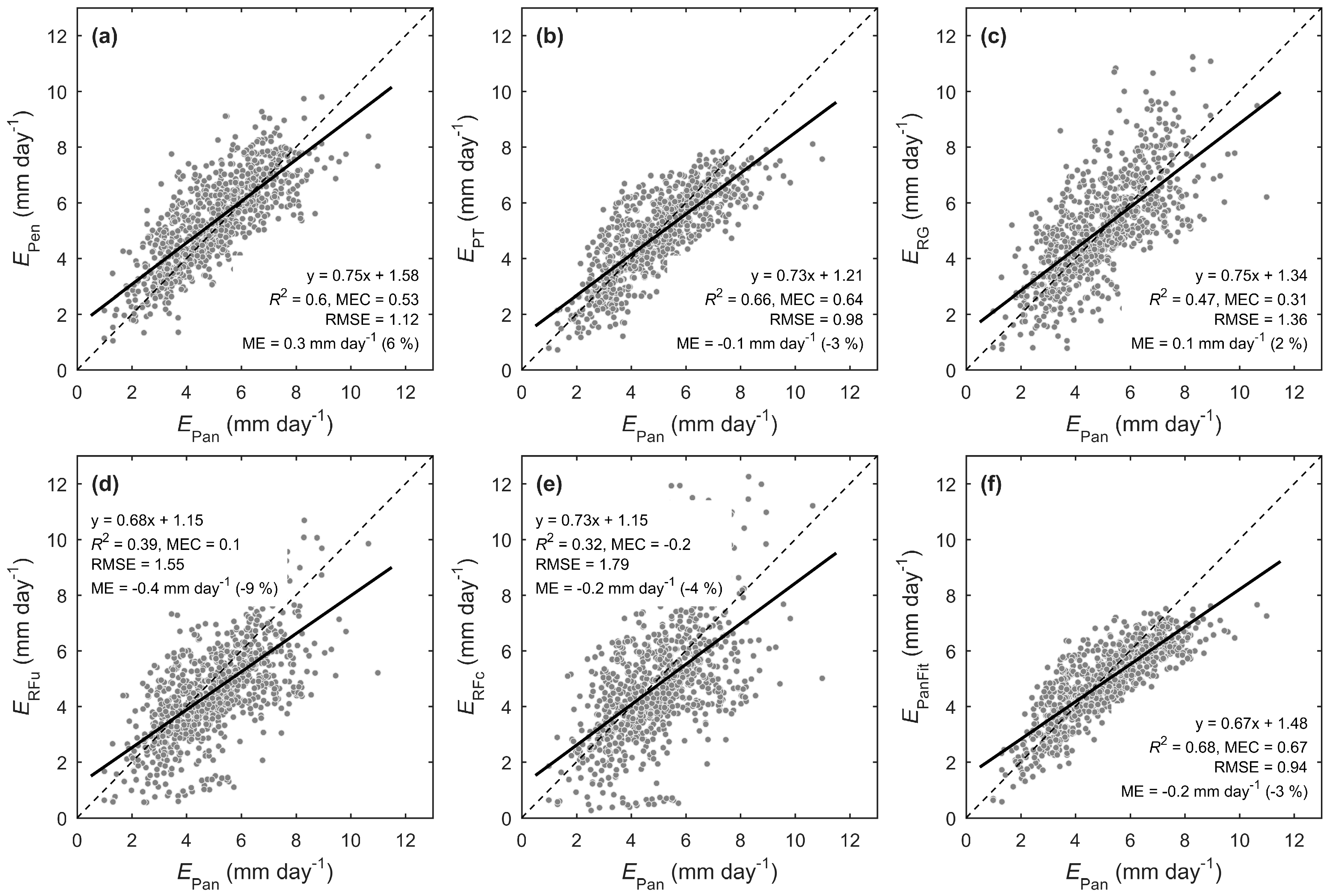
2.3. Comparison between Models and Pan Evaporation
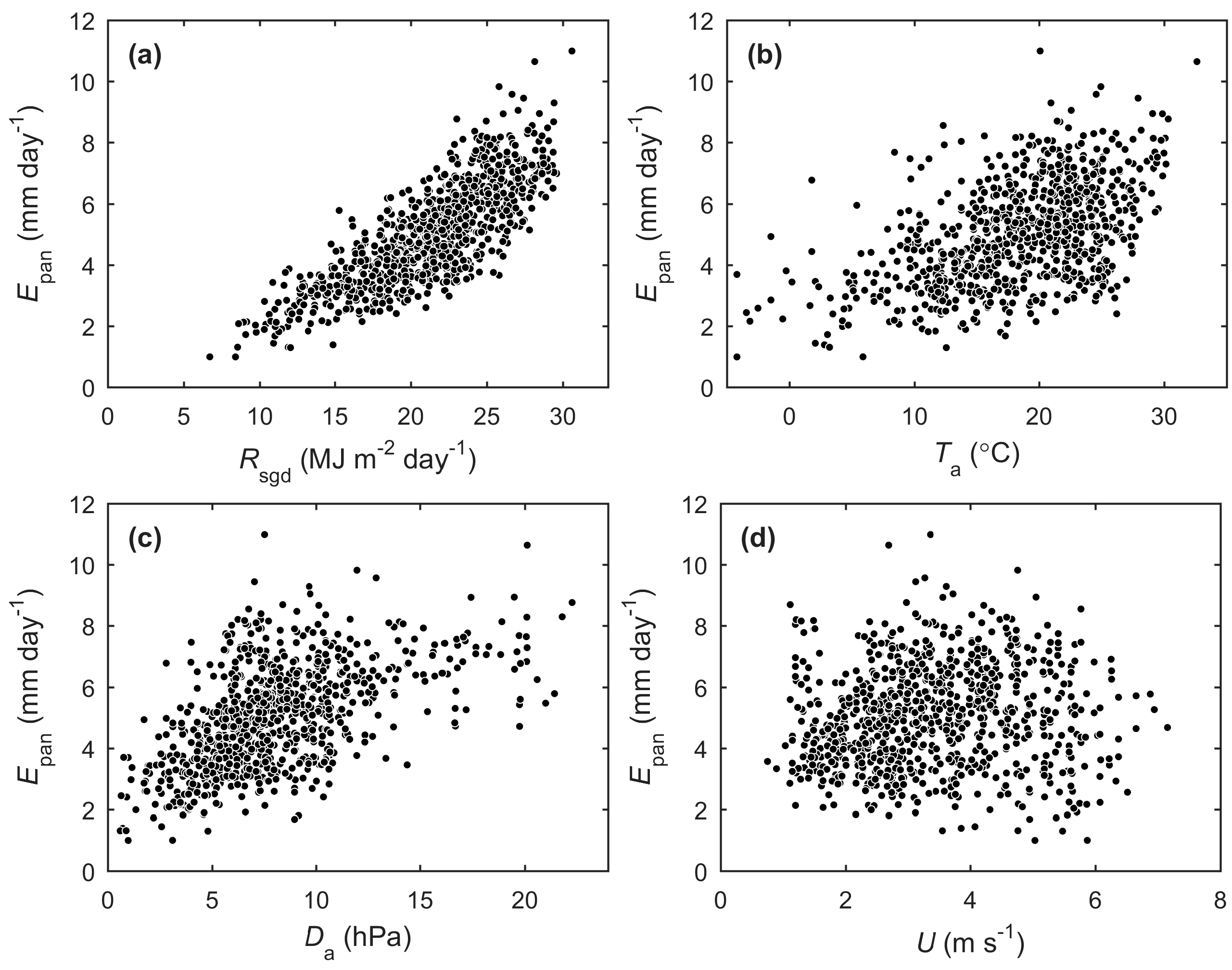
2.4. Analysis of Variance Attribution
2.5. Model Application
3. Results
3.1. Daily Model Comparison
3.2. Monthly Model Comparison
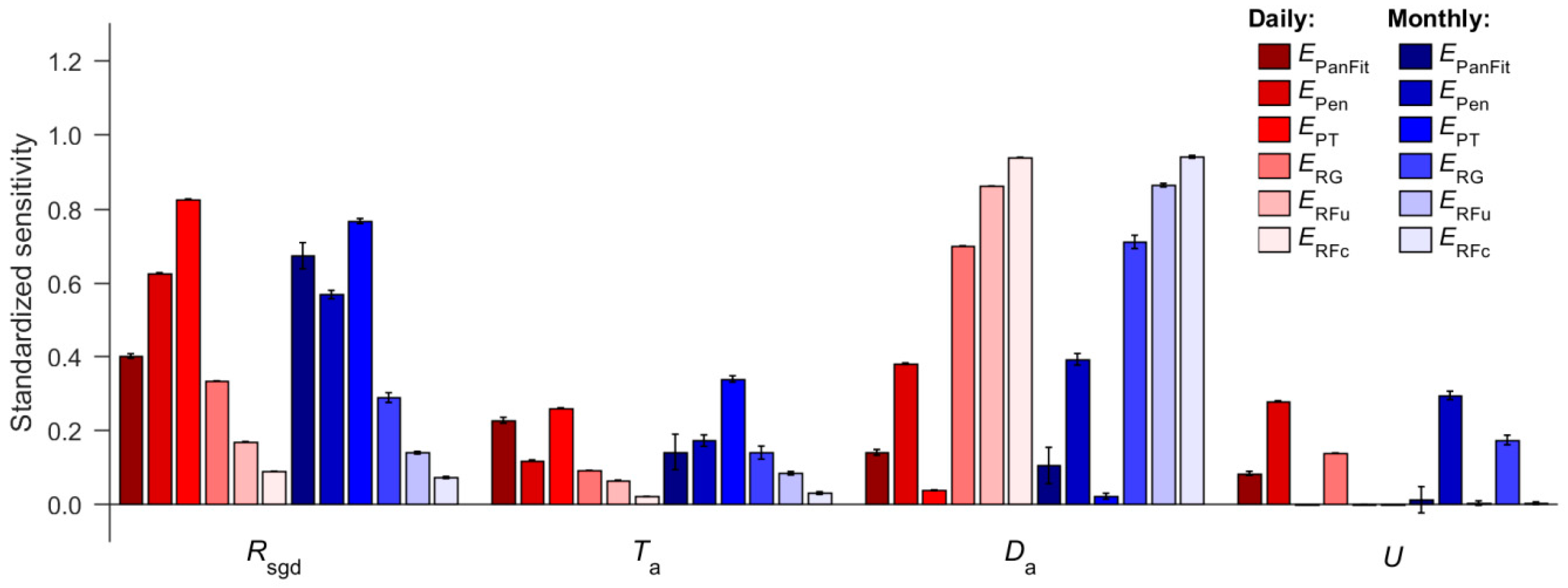
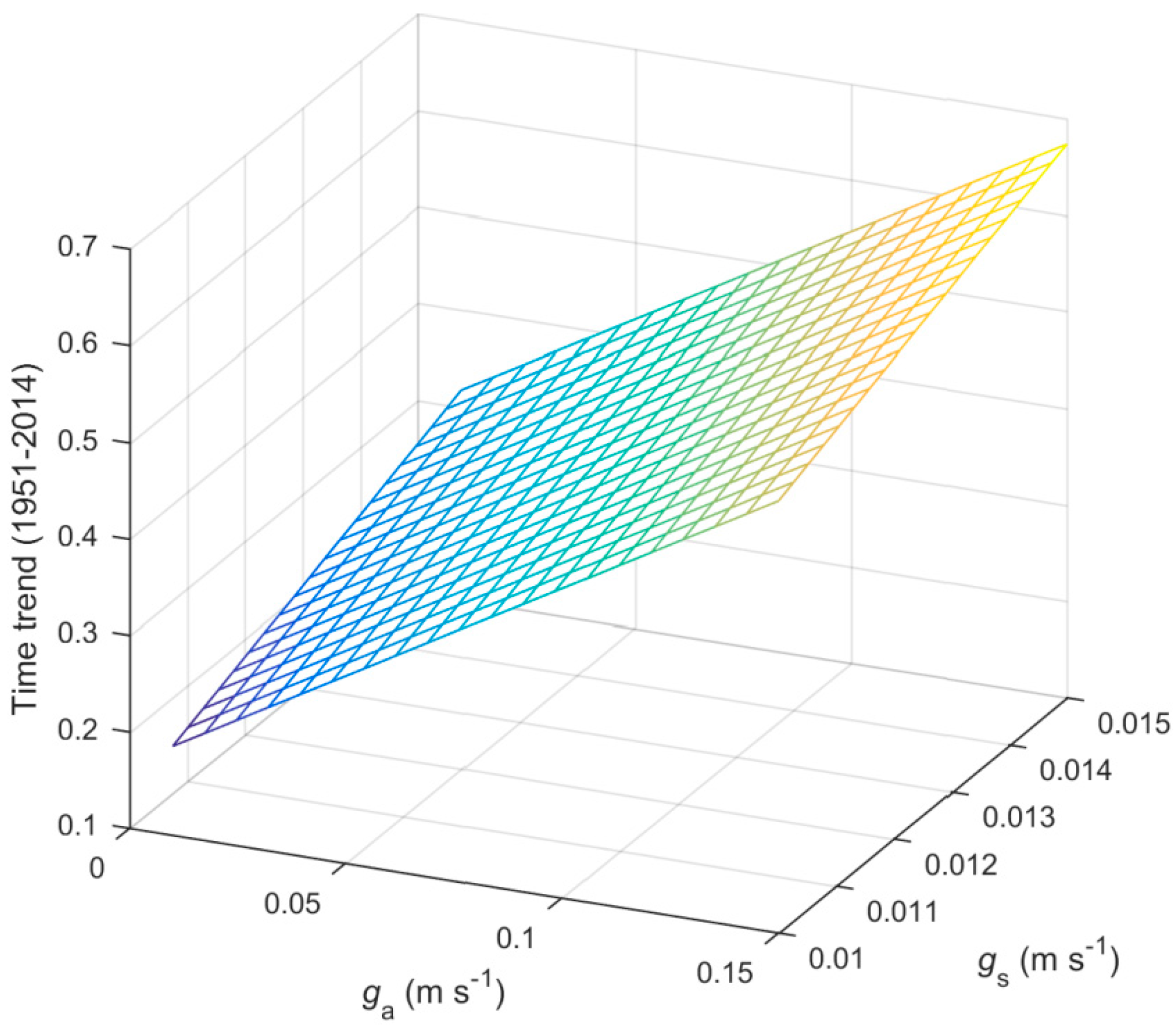
3.3. Attribution of Variance in PE to Meteorological Drivers
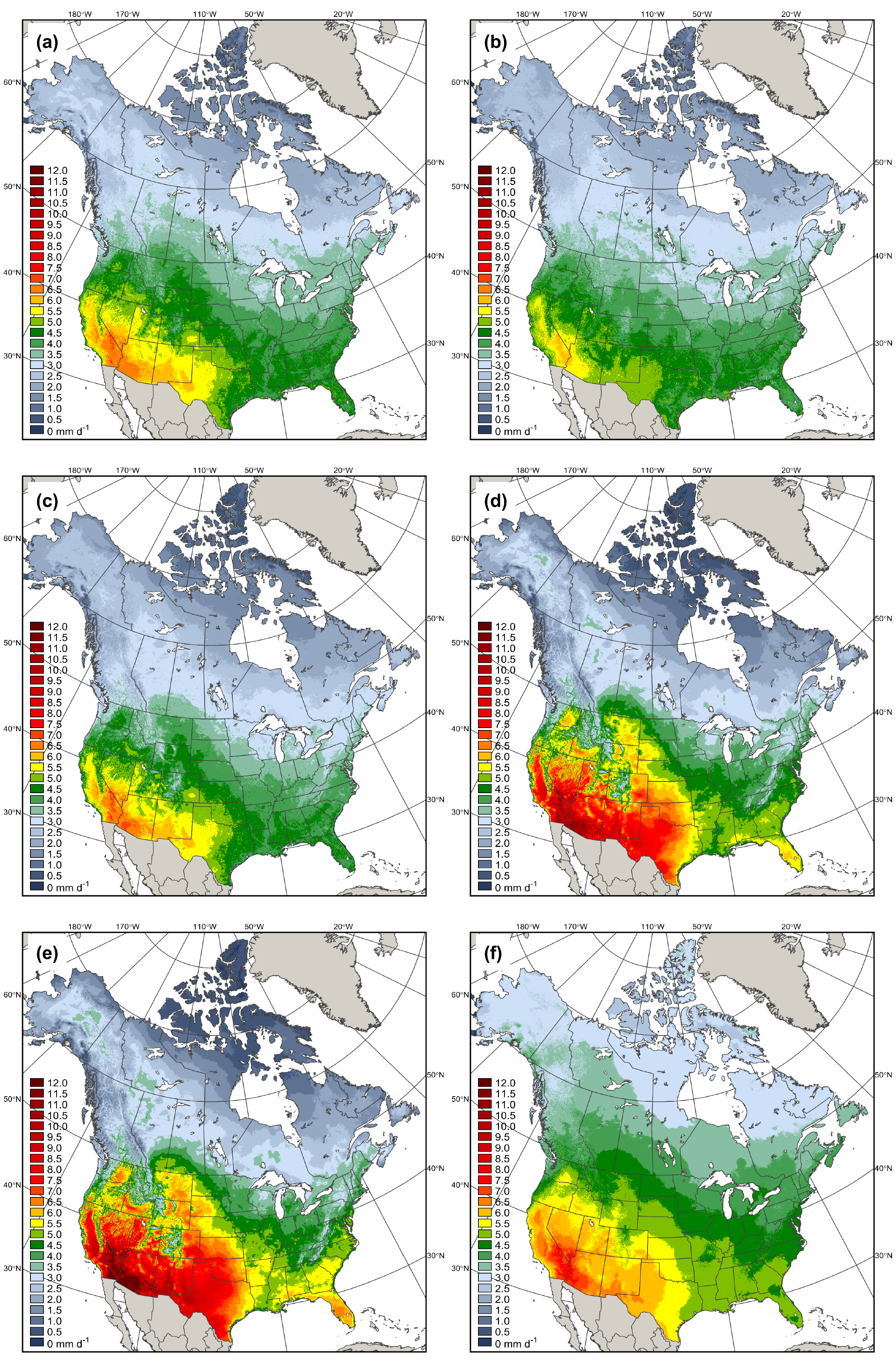
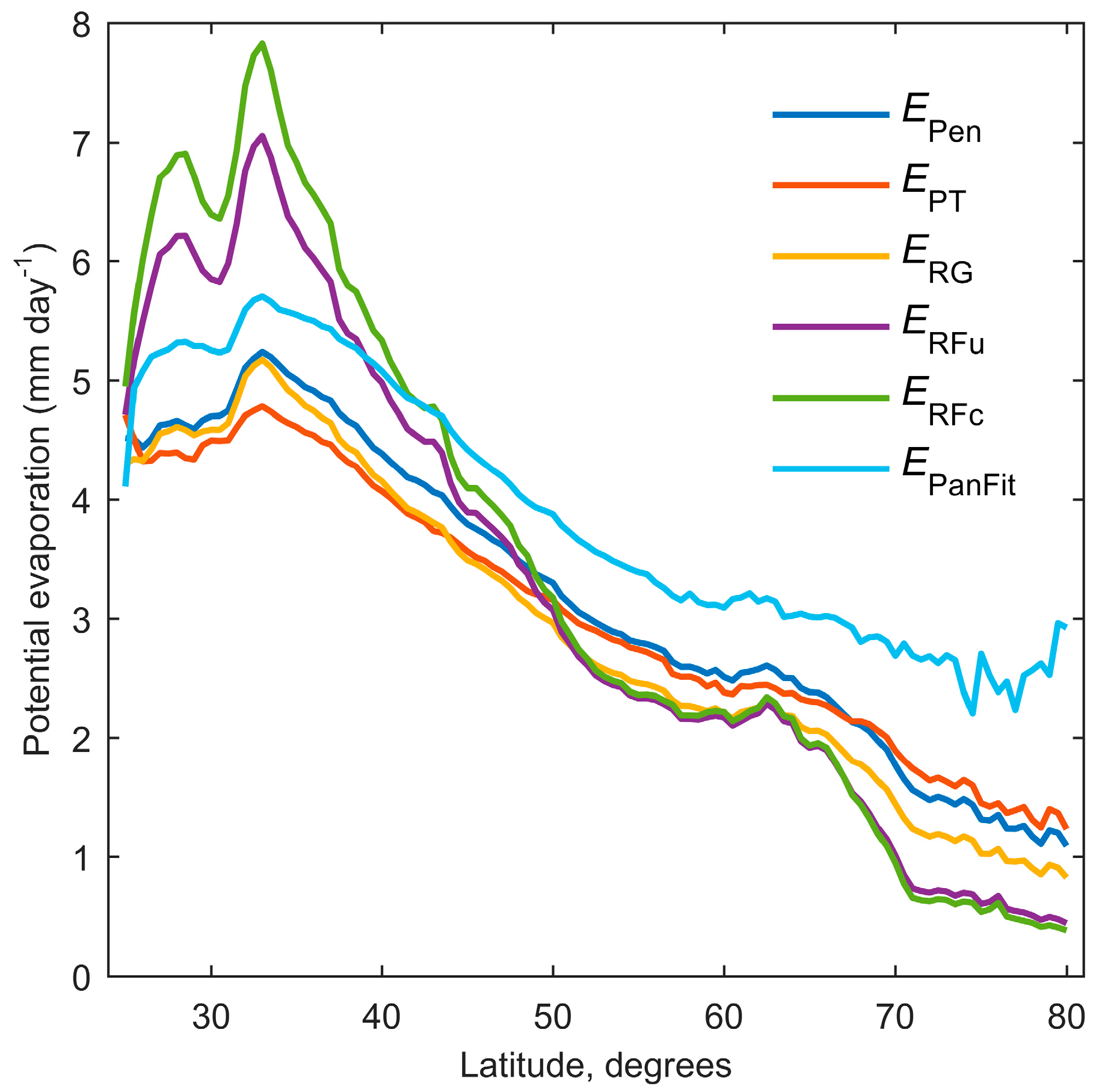
3.4. Spatial and Temporal Variability
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fisher, J.B.; Whittaker, R.J.; Malhi, Y. ET come home: Potential evapotranspiration in geographical ecology. Glob. Ecol. Biogeogr. 2011, 20, 1–18. [Google Scholar] [CrossRef]
- Webb, W.L.; Lauenroth, W.K.; Szarek, S.R.; Kinerson, R.S. Primary production and abiotic controls in forests, grasslands, and desert ecosystems in the united states. Ecology 1983, 64, 134–151. [Google Scholar] [CrossRef]
- Stephenson, N.L. Actual evapotranspiration and deficit: biologically meaningful correlates of vegetation distribution across spatial scales. J. Biogeogr. 1998, 25, 855–870. [Google Scholar] [CrossRef]
- Sperry, J.S.; Tyree, M.T. Water-stress-induced xylem embolism in three species of conifers. Plant Cell Environ. 1990, 13, 427–436. [Google Scholar] [CrossRef]
- Tyree, M.T.; Sperry, J.S. Do woody plants operate near the point of catastrophic xylem dysfunction caused by dynamic water stress? Answers from a model. Plant Physiol. 1988, 88, 574–580. [Google Scholar] [CrossRef] [PubMed]
- Choat, B.; Jansen, S.; Brodribb, T.J.; Cochard, H.; Delzon, S.; Bhaskar, R.; Bucci, S.J.; Feild, T.S.; Gleason, S.M.; Hacke, U.G.; et al. Global convergence in the vulnerability of forests to drought. Nature 2012, 491, 752–755. [Google Scholar] [CrossRef] [PubMed]
- Hember, R.A.; Kurz, W.A.; Coops, N.C. Relationships between individual-tree mortality and water-balance variables indicate positive trends in water stress-induced tree mortality across North America. Glob. Change Biol. 2016. [Google Scholar] [CrossRef] [PubMed]
- Millar, C.I.; Stephenson, N.L. Temperate forest health in an era of emerging megadisturbance. Science 2015, 349, 823–826. [Google Scholar] [CrossRef] [PubMed]
- McDowell, N.G.; Williams, A.P.; Xu, C.; Pockman, W.T.; Dickman, L.T.; Sevanto, S.; Pangle, R.; Limousin, J.; Plaut, J.; Mackay, D.S.; et al. Multi-scale predictions of massive conifer mortality due to chronic temperature rise. Nat. Clim. Change 2016, 6, 295–300. [Google Scholar] [CrossRef]
- Martínez-Vilalta, J.; Lloret, F. Drought-induced vegetation shifts in terrestrial ecosystems: The key role of regeneration dynamics. Glob. Planet. Change 2016, 144, 94–108. [Google Scholar] [CrossRef]
- Clark, J.S.; Iverson, L.; Woodall, C.W.; Allen, C.D.; Bell, D.M.; Bragg, D.C.; D’Amato, A.W.; Davis, F.W.; Hersh, M.H.; Ibanez, I.; et al. The impacts of increasing drought on forest dynamics, structure, and biodiversity in the United States. Glob. Change Biol. 2016. [Google Scholar] [CrossRef] [PubMed]
- Sucoff, E. Water potential in red pine: Soil moisture, evapotranspiration, crown position. Ecology 1972, 53, 681–686. [Google Scholar] [CrossRef]
- Sharkey, T.D. Transpiration-induced changes in the photosynthetic capacity of leaves. Planta 1984, 160, 143–150. [Google Scholar] [CrossRef] [PubMed]
- Novick, K.A.; Ficklin, D.L.; Stoy, P.C.; Williams, C.A.; Bohrer, G.; Oishi, A.C.; Papuga, S.A.; Blanken, P.D.; Noormets, A.; Sulman, B.N.; et al. The increasing importance of atmospheric demand for ecosystem water and carbon fluxes. Nat. Clim. Change 2016. [Google Scholar] [CrossRef]
- Sanderson, M. Drought in the Canadian Northwest. Geogr. Rev. 1948, 38, 289. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: Cambridge, UK, 1987. [Google Scholar]
- Rosenberg, N.; Blad, B.; Verma, S. Microclimate, the Biological Environment, 2nd ed.; Jon Wiley and Sons Inc.: Toronto, ON, Canada, 1983. [Google Scholar]
- Slatyer, R.; McIlroy, I. Practical Microclimatology. Commonw. Sci. Ind. Res. Organ. 1961. [Google Scholar] [CrossRef]
- Mather, J.R.; Ambroziak, R.A. A Search for Understanding Potential Evapotranspiration. Geogr. Rev. 1986, 76, 355–370. [Google Scholar] [CrossRef]
- Ferguson, H.L.; O’Neill, A.D.J.; Cork, H.F. Mean Evaporation over Canada. Water Resour. Res. 1970, 6, 1618–1633. [Google Scholar] [CrossRef]
- Kohler, M.A.; Nordenson, T.J.; Fox, W.E. Evaporation from Pans and Lakes; US Department of Commerce: Washington, DC, USA, 1955.
- Thornthwaite, C.W.; Mather, J.R. The Water Balance; Laboratory of Climatology: Centerton, NJ, USA, 1955. [Google Scholar]
- Hargreaves, G.H.; Allen, R.G. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Christiansen, J.E. Estimating Evaporation and Evpoatranspiration from Climate Data; Utah Water Research Laboratory, Utah State University: Logan, UT, USA, 1966. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Black, T.A. Evapotranspiration from douglas-fir stands exposed to soil-water deficits. Water Resour. Res. 1979, 15, 164–170. [Google Scholar] [CrossRef]
- Brümmer, C.; Black, T.A.; Jassal, R.S.; Grant, N.J.; Spittlehouse, D.L.; Chen, B.; Nesic, Z.; Amiro, B.D.; Arain, M.A.; Barr, A.G.; et al. How climate and vegetation type influence evapotranspiration and water use efficiency in Canadian forest, peatland and grassland ecosystems. Agric. For. Meteorol. 2012, 153, 14–30. [Google Scholar] [CrossRef]
- Greve, P.; Seneviratne, S.I. Assessment of future changes in water availability and aridity. Geophys. Res. Lett. 2015, 42. [Google Scholar] [CrossRef] [PubMed]
- Hogg, E.H. Temporal scaling of moisture and the forest-grassland boundary in western Canada. Agric. For. Meteorol. 1997, 84, 115–122. [Google Scholar] [CrossRef]
- Willmott, C.J.; Rowe, C.M.; Mintz, Y. Climatology of the terrestrial seasonal water cycle. J. Climatol. 1985, 5, 589–606. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements, FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Cleugh, H.A.; Leuning, R.; Mu, Q.Z.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Spittlehouse, D.L. Water availability, climate change and the growth of Douglas-fir in the Georgia Basin. Can. Water Resour. J. 2003, 28, 673–687. [Google Scholar] [CrossRef]
- Coops, N.; Coggins, S.; Kurz, W. Mapping the environmental limitations to growth of coastal Douglas-fir stands on Vancouver Island, British Columbia. Tree Physiol. 2007, 27, 805–815. [Google Scholar] [CrossRef] [PubMed]
- Seely, B.; Welham, C.; Scoullar, K. Application of a hybrid forest growth model to evaluate climate change impacts on productivity, nutrient cycling and mortality in a montane forest ecosystem. PLoS ONE 2015, 10, e0135034. [Google Scholar] [CrossRef] [PubMed]
- King, D.A.; Bachelet, D.M.; Symstad, A.J.; Ferschweiler, K.; Hobbins, M. Estimation of potential evapotranspiration from extraterrestrial radiation, air temperature and humidity to assess future climate change effects on the vegetation of the Northern Great Plains, USA. Ecol. Model. 2015, 297, 86–97. [Google Scholar] [CrossRef]
- Hogg, E.H.; Barr, A.G.; Black, T.A. A simple soil moisture index for representing multi-year drought impacts on aspen productivity in the western Canadian interior. Agric. For. Meteorol. 2013, 178–179, 173–182. [Google Scholar] [CrossRef]
- Wang, Y.; Hogg, E.H.; Price, D.T.; Edwards, J.; Williamson, T. Past and projected future changes in moisture conditions in the Canadian boreal forest. For. Chron. 2014, 90, 678–691. [Google Scholar] [CrossRef]
- Chattopadhyay, N.; Hulme, M. Evaporation and potential evapotranspiration in India under conditions of recent and future climate change. Agric. For. Meteorol. 1997, 87, 55–73. [Google Scholar] [CrossRef]
- Hobbins, M.; Ramirez, J.; Brown, T. Trends in pan evaporation and actual evapotranspiration across the conterminous US: Paradoxical or complementary? Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Linacre, E.T. Estimating U.S. Class A pan evaporation from few climate data. Water Int. 1994, 19, 5–14. [Google Scholar] [CrossRef]
- Hobbins, M.T.; Dai, A.; Roderick, M.L.; Farquhar, G.D. Revisiting the parameterization of potential evaporation as a driver of long-term water balance trends. Geophys. Res. Lett. 2008, 35, L12403. [Google Scholar] [CrossRef]
- Kingston, D.G.; Todd, M.C.; Taylor, R.G.; Thompson, J.R.; Arnell, N.W. Uncertainty in the estimation of potential evapotranspiration under climate change. Geophys. Res. Lett. 2009, 36, L20403. [Google Scholar] [CrossRef]
- Scheff, J.; Frierson, D.M.W. Scaling potential evapotranspiration with greenhouse warming. J. Clim. 2013, 27, 1539–1558. [Google Scholar] [CrossRef]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Change 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Dai, A. Characteristics and trends in various forms of the Palmer Drought Severity Index during 1900–2008. J. Geophys. Res. Atmospheres 2011, 116. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef] [PubMed]
- Amatya, D.; Tian, S.; Dai, Z.; Sun, G. Long-term potential and actual evapotranspiration of two different forests on the Atlantic Coastal Plain. Trans. ASABE 2016, 59, 647–660. [Google Scholar]
- Brauman, K.A.; Freyberg, D.L.; Daily, G.C. Potential evapotranspiration from forest and pasture in the tropics: A case study in Kona, Hawai‘i. J. Hydrol. 2012, 440–441, 52–61. [Google Scholar] [CrossRef]
- NREL 2013 US Department of Energy, National Renewable Energy Laboratory. National Solar Radiation Data Base. Available online: http://rredc.nrel.gov/solar/old_data/nsrdb/ (accessed on 26 April 2016).
- GSOD 2013 National Oceanic and Atmospheric Administration, Global Summary of the Day. Available online: https://data.noaa.gov/dataset/global-surface-summary-of-the-day-gsod (accessed on 31 October 2013).
- Brouwer, C.; Heibloem, M. Irrigation Water Management: Irrigation Water Needs; Food and Agriculture Orgainzation of the United Nations: Rome, Italy, 1985. [Google Scholar]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D. A comparison of six potential evapotranspiration methods for regional use in the Southeastern United States. J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Kelliher, F.; Leuning, R.; Schulze, E. Evaporation and canopy characteristics of coniferous forests and grasslands. Oecologia 1993, 95, 153–163. [Google Scholar] [CrossRef]
- Landsberg, J.; Sands, P. Physiological Ecology of Forest Production: Principles, Processes and Models, 1st ed.; Elsevier Inc.: Boston, MA, USA, 2011. [Google Scholar]
- Pereira, A.R. The Priestley–Taylor parameter and the decoupling factor for estimating reference evapotranspiration. Agric. For. Meteorol. 2004, 125, 305–313. [Google Scholar] [CrossRef]
- Bladon, K.D.; Silins, U.; Landhäusser, S.M.; Lieffers, V.J. Differential transpiration by three boreal tree species in response to increased evaporative demand after variable retention harvesting. Agric. For. Meteorol. 2006, 138, 104–119. [Google Scholar] [CrossRef]
- Humphreys, E.; Black, T.; Ethier, G.; Drewitt, G.; Spittlehouse, D.; Jork, E.; Nesic, Z.; Livingston, N. Annual and seasonal variability of sensible and latent heat fluxes above a coastal Douglas-fir forest, British Columbia, Canada. Agric. For. Meteorol. 2003, 115, 109–125. [Google Scholar] [CrossRef]
- Martin, T.A.; Hinckley, T.M.; Meinzer, F.C.; Sprugel, D.G. Boundary layer conductance, leaf temperature and transpiration of Abies amabilis branches. Tree Physiol. 1999, 19, 435–443. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, P.G.; McNaughton, K.G. Stomatal Control of Transpiration: Scaling Up from Leaf to Region. In Advances in Ecological Research; Elsevier: Amsterdam, The Netherlands, 1986; Volume 15, pp. 1–49. [Google Scholar]
- Running, S.; Coughlan, J. A General-Model of Forest Ecosystem Processes for Regional Applications. 1. Hydrologic Balance, Canopy Gas-Exchange and Primary Production Processes. Ecol. Model. 1988, 42, 125–154. [Google Scholar] [CrossRef]
- Bates, D.M. Lme4: Mixed-Effects Modeling with R; Springer: New York, NY, USA, 2010. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Schroeder, T.; Hember, R.; Coops, N.; Liang, S. Validation of solar radiation surfaces from modis and reanalysis data over topographically complex terrain. J. Appl. Meteorol. Climatol. 2009, 48, 2441–2458. [Google Scholar] [CrossRef]
- NARR 2013 National Oceanic and Atmospheric Administration, Earth System Research Laboratory. North American Regional Reanalysis. Available online: www.esrl.noaa.gov/psd/data/gridded (accessed on 18 December 2013).
- ESRI. ArcGIS 2013 ArcGIS 9.2 Desktop Help. Available online: webhelp.esri.com/arcgisdesktop/9.2/index.cfm?TopicName=Area_Solar_Radiation (accessed on 23 July 2013).
- Cogley, J.G. Greenland accumulation: An error model. J. Geophys. Res. Atmospheres 2004, 109. [Google Scholar] [CrossRef]
- Press, W.; Teukolsky, S.; Vetterling, W.; Flannery, B. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge Universiy Press: New York, NY, USA, 2007. [Google Scholar]
- Wang, T.; Hamann, A.; Spittlehouse, D.; Aitken, S. Development of scale-free climate data for western Canada for use in resource management. Int. J. Climatol. 2006, 26, 383–397. [Google Scholar] [CrossRef]
- Wang, T.; Hamann, A.; Spittlehouse, D.; Carroll, C. Locally downscaled and spatially customizable climate data for historical and future periods for north america. PLoS ONE 2016, 11, e0156720. [Google Scholar] [CrossRef] [PubMed]
- EC-NCDIA 2013 Environment Canada, National Climate Data and Information Archive. 2013. Available online: http://climate.weather.gc.ca/index_e.html (accessed on 5 January 2013).
- Menne, M.J.; Williams, C.N.; Vose, R.S. United States Historical Climatology Network (USHCN); Version 2.5 Serial Monthly Dataset; Oak Ridge National Laboratory, Carbon Dioxide Information Analysis Center: Oak Ridge, TN, USA.
- EC-AHCCD 2013 Environment Canada, Adjusted and Homogenized Canadian Climate Data. 2013. Available online: http://www.ec.gc.ca/dccha-ahccd/ (accessed on 15 July 2013).
- CRU31 2013 UK Met Office, Climate Research Unit. Climate Database, Version 3.1; Available online: http://badc.nerc.ac.uk/view/badc.nerc.ac.uk__ATOM__dataent_1256223773328276 (accessed on 25 July 2013).
- Kimball, J.; Running, S.; Nemani, R. An improved method for estimating surface humidity from daily minimum temperature. Agric. For. Meteorol. 1997, 85, 87–98. [Google Scholar] [CrossRef]
- Thornton, P.; Running, S.; White, M. Generating surfaces of daily meteorological variables over large regions of complex terrain. J. Hydrol. 1997, 190, 214–251. [Google Scholar] [CrossRef]
- USGS National Atlas of the United States. Available online: https://nationalmap.gov/small_scale/ (accessed on 13 March 2015).
- Coakley, J.A. Reflectance and albedo, surface. In Encyclopedia of the Atmospheric Sciences; Holton, J.R., Curry, J.A., Pyle, J.A., Eds.; Academic Press: Cambridge, MA, USA, 2002; pp. 1914–1923. [Google Scholar]
- Oak Ridge National Laboratory Distributed Active Archive Center (ORNL DAAC). FLUXNET Web Page; ORNL DAAC: Oak Ridge, TN, USA, 2015. [Google Scholar]
- CEC 1997 Commission for Environmental Cooperation (CEC): Ecological Regions of North America—Towards a Common Perspective. GIS Data (shapefiles, metadata and symbology). Available online: http://www.cec.org/tools-and-resources/map-files/terrestrial-ecoregions-level-i (accessed on 29 November 2009).
- Isaac, V.; van Wijngaarden, W.A. Surface water vapor pressure and temperature trends in North America during 1948–2010. J. Clim. 2012, 25, 3599–3609. [Google Scholar] [CrossRef]
- Vincent, L.A.; Zhang, X.; Brown, R.D.; Feng, Y.; Mekis, E.; Milewska, E.J.; Wan, H.; Wang, X.L. Observed Trends in Canada’s Climate and Influence of Low-Frequency Variability Modes. J. Clim. 2015, 28, 4545–4560. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Federer, C.A.; Schloss, A.L. Potential evaporation functions compared on US watersheds: Possible implications for global-scale water balance and terrestrial ecosystem modeling. J. Hydrol. 1998, 207, 147–169. [Google Scholar] [CrossRef]
- Yao, H. Long-term study of lake evaporation and evaluation of seven estimation methods: Results from Dickie Lake, south-central Ontario, Canada. J. Water Resour. Prot. 2009, 1, 59–77. [Google Scholar] [CrossRef]
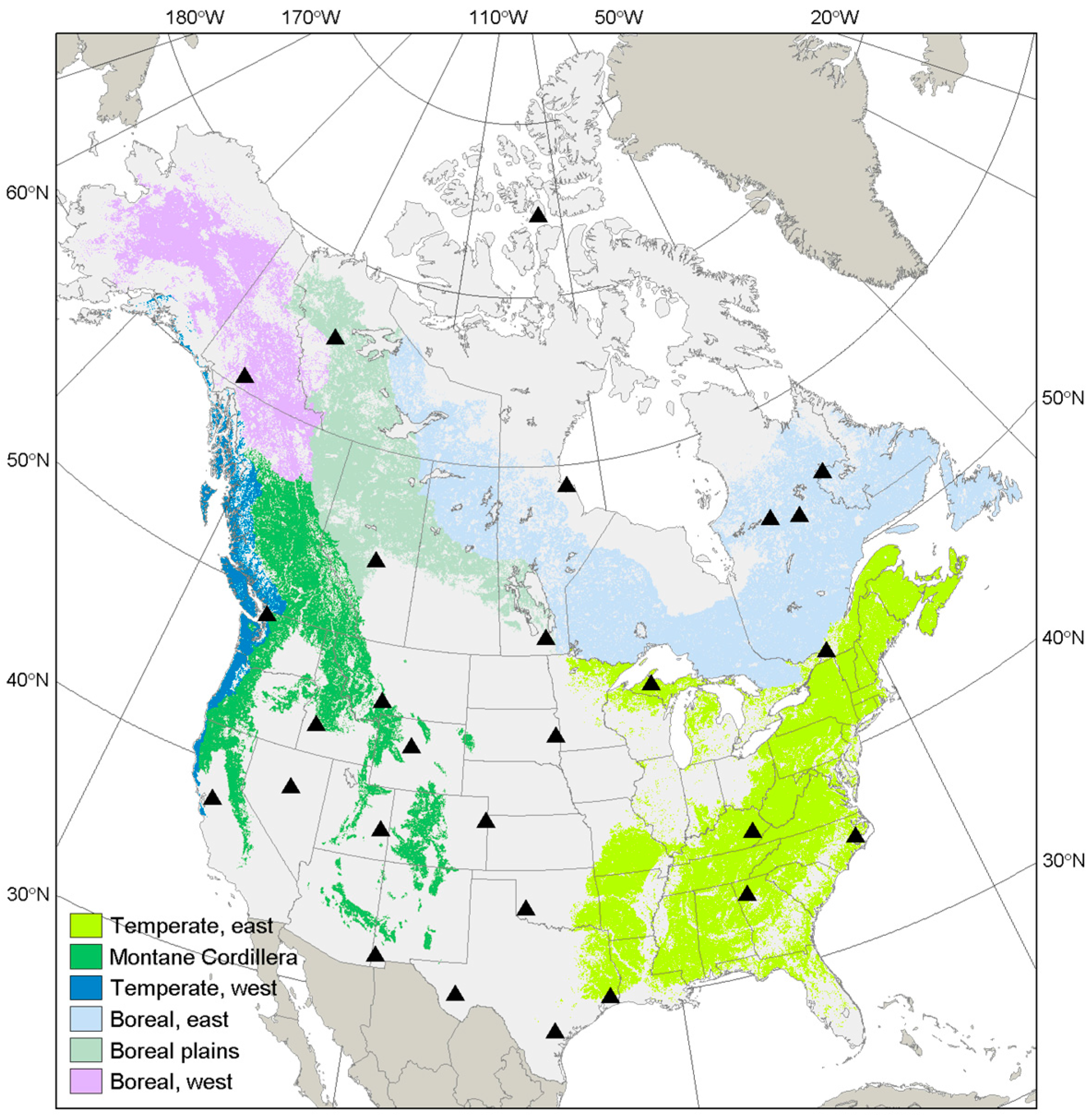

| Station ID | Station Name | Lat. (°N) | Long. (°W) | Elev. (m a.s.l.) | MAT (°C) | MAP (mm·year−1) | N (d) | Period |
|---|---|---|---|---|---|---|---|---|
| 2101300 | Whitehorse A | 60.71 | 135.07 | 706 | −0.6 | 274 | 2787 | 1974–1996 |
| 2202800 | Norman Wells | 65.28 | 126.80 | 73 | −4.6 | 294 | 2573 | 1964–1984 |
| 2403500 | Resolute Cars | 74.72 | 94.99 | 66 | −15.2 | 127 | 2231 | 1962–2004 |
| 301222F | Edmonton Stony Plain | 53.55 | 114.11 | 766 | 2.7 | 530 | 2654 | 1988–2004 |
| 5023222 | Winnipeg Richarson Int’l A | 49.92 | 97.23 | 239 | 3.2 | 545 | 5422 | 1962–1996 |
| 5060600 | Churchill A | 58.74 | 94.06 | 29 | −6.9 | 385 | 3672 | 1963–2000 |
| 7025250 | Pierre Elliott Trudau Intl A | 45.47 | 73.75 | 36 | 6.3 | 1059 | 1173 | 1987–1994 |
| 7093GJ3 | La Grande IV A | 53.76 | 73.68 | 306 | −5 | 732 | 955 | 1987–1995 |
| 7095480 | Nitchequon | 53.20 | 70.90 | 536 | −7.6 | 845 | 2261 | 1966–1985 |
| 7117825 | Schefferville A | 54.80 | 66.82 | 522 | −7.7 | 772 | 818 | 1962–1969 |
| 040232 | Antioch Pump Plant 3 | 37.98 | 121.73 | 18 | 15.7 | 346 | 7966 | 1955–1978 |
| 050834 | Bonny Dam 2 NE | 39.63 | 102.18 | 1113 | 10.8 | 466 | 7601 | 1951–2006 |
| 090181 | Allatoona Dam 2 | 34.17 | 84.73 | 299 | 16 | 1347 | 10,578 | 1952–2006 |
| 100448 | Arrowrock Dam | 43.62 | 115.92 | 988 | 8.7 | 569 | 6630 | 1951–1998 |
| 151080 | Buckhorn Lake | 37.35 | 83.38 | 287 | 13 | 1199 | 6049 | 1961–1994 |
| 200089 | Alberta Ford For Cen | 46.65 | 88.48 | 400 | 3.2 | 867 | 246 | 1969–1971 |
| 241044 | Bozeman Montana SU | 45.67 | 111.05 | 1482 | 5.9 | 487 | 3401 | 1951–1969 |
| 260800 | Beowawe 49 S U of N Ranch | 39.90 | 116.58 | 1751 | 8.4 | 263 | 2208 | 1981–1998 |
| 290417 | Animas 3 ESE | 31.95 | 108.82 | 1348 | 15.3 | 305 | 3427 | 1967–1979 |
| 310375 | Aurora 6 N | 35.38 | 76.78 | 6 | 16.3 | 1273 | 10,845 | 1973–2014 |
| 340184 | Altus Dam | 34.88 | 99.30 | 467 | 14.8 | 735 | 7927 | 1979–2014 |
| 391076 | Brookings 2 NE | 44.32 | 96.77 | 503 | 6 | 634 | 9470 | 1953–2014 |
| 410174 | Alpine | 30.35 | 103.67 | 1360 | 16.5 | 438 | 3550 | 1971–1982 |
| 410613 | Beaumont Resrch Ctr | 30.07 | 94.28 | 9 | 19.3 | 1471 | 12,181 | 1979–2014 |
| 410639 | Beeville 5 NE | 28.45 | 97.70 | 76 | 20.6 | 832 | 9254 | 1979–2014 |
| 420336 | Arches National Park HQS | 38.62 | 109.62 | 1259 | 14 | 250 | 3666 | 1980–2004 |
| 450587 | Bellingham 3 SSW | 48.72 | 122.52 | 9 | 10.3 | 964 | 4947 | 1985–2014 |
| 481000 | Boysen Dam | 43.42 | 108.20 | 1467 | 7.6 | 245 | 3772 | 1951–1976 |
| Intercept | Rsgd | Ta | Da | U | |
|---|---|---|---|---|---|
| Fixed effects | |||||
| Estimate | 0.033 | 0.402 | 0.209 | 0.156 | 0.126 |
| Standard error | 0.060 | 0.032 | 0.023 | 0.026 | 0.031 |
| Random effects | |||||
| Whitehorse A | −0.030 | −0.008 | −0.179 | 0.149 | −0.020 |
| Norman Wells | 0.295 | 0.062 | −0.046 | 0.038 | 0.263 |
| Resolute Cars | 0.230 | −0.064 | 0.013 | 0.208 | 0.029 |
| Edmonton Stony Plain | 0.406 | 0.091 | −0.059 | 0.001 | 0.434 |
| Winnipeg Richarson Int’l A | 0.299 | 0.079 | 0.039 | −0.016 | 0.211 |
| Churchill A | 0.101 | −0.093 | 0.027 | 0.156 | −0.020 |
| Pierre Elliott Trudau Intl A | −0.020 | 0.052 | 0.003 | −0.057 | −0.075 |
| La Grande IV A | 0.379 | 0.057 | 0.072 | 0.039 | 0.297 |
| Nitchequon | −0.187 | −0.036 | 0.012 | −0.032 | −0.075 |
| Schefferville A | 0.136 | 0.034 | 0.048 | 0.055 | 0.237 |
| Antioch Pump Plant 3 | 0.082 | 0.275 | −0.040 | −0.164 | −0.144 |
| Bonny Dam 2 NE | 0.394 | 0.021 | 0.096 | −0.102 | −0.006 |
| Allatoona Dam 2 | −0.632 | −0.262 | −0.034 | −0.033 | −0.031 |
| Arrowrock Dam | −0.052 | 0.105 | 0.028 | −0.208 | −0.181 |
| Buckhorn Lake | −0.565 | −0.211 | −0.069 | −0.086 | −0.035 |
| Alberta Ford For Cen | −0.611 | −0.166 | −0.028 | −0.007 | −0.111 |
| Bozeman Montana SU | −0.208 | 0.043 | −0.099 | −0.029 | −0.228 |
| Beowawe 49 S U of N Ranch | 0.049 | 0.010 | 0.161 | −0.096 | −0.011 |
| Animas 3 ESE | 0.456 | 0.376 | −0.058 | −0.124 | −0.073 |
| Aurora 6 N | −0.077 | −0.162 | 0.051 | 0.148 | 0.003 |
| Altus Dam | −0.264 | −0.268 | 0.083 | 0.219 | 0.070 |
| Brookings 2 NE | 0.136 | −0.120 | 0.106 | −0.104 | −0.110 |
| Alpine | −0.137 | −0.029 | −0.307 | 0.177 | −0.009 |
| Beaumont Resrch Ctr | 0.037 | 0.121 | −0.087 | −0.126 | −0.121 |
| Beeville 5 NE | −0.299 | −0.136 | 0.062 | 0.073 | 0.042 |
| Arches National Park HQS | 0.429 | 0.378 | −0.078 | −0.066 | −0.189 |
| Bellingham 3 SSW | −0.352 | −0.155 | 0.056 | 0.181 | 0.038 |
| Boysen Dam | 0.006 | 0.008 | 0.225 | −0.195 | −0.183 |
| Rsgd | Ta | ea | Da | EPen | EPT | ERG | ERFu | ERFc | EPanFit | |
|---|---|---|---|---|---|---|---|---|---|---|
| Boreal, west | 16.0 | 9.6 | 8.0 | 4.3 | 2.7 | 2.5 | 2.4 | 2.6 | 2.7 | 3.2 |
| Boreal Plains | 17.7 | 11.7 | 9.4 | 4.7 | 3.1 | 3.0 | 2.8 | 2.8 | 2.9 | 3.6 |
| Boreal, east | 17.2 | 11.6 | 10.4 | 3.8 | 2.9 | 2.9 | 2.5 | 2.5 | 2.4 | 3.4 |
| Temperate, west | 18.1 | 12.2 | 10.8 | 4.0 | 3.1 | 3.1 | 2.7 | 2.5 | 2.5 | 3.6 |
| Montane Cordillera | 21.4 | 11.8 | 8.0 | 6.3 | 4.0 | 3.8 | 3.6 | 3.7 | 3.9 | 4.2 |
| Temperate, east | 19.5 | 20.7 | 19.1 | 6.2 | 3.9 | 4.0 | 3.6 | 4.1 | 3.8 | 4.5 |
| Mean | 18.3 | 12.9 | 11.0 | 4.9 | 3.3 | 3.2 | 2.9 | 3.0 | 3.1 | 3.8 |
| Rsgd | Ta | ea | Da | EPen | EPT | ERG | ERFu | ERFc | EPanFit | |
|---|---|---|---|---|---|---|---|---|---|---|
| Boreal, west | 0.09 | 1.30 | 0.43 | 0.63 | 0.17 | 0.10 | 0.19 | 0.31 | 0.36 | 0.15 |
| Boreal Plains | 0.08 | 1.33 | 0.20 | 1.01 | 0.22 | 0.10 | 0.26 | 0.48 | 0.57 | 0.18 |
| Boreal, east | 0.40 | 1.49 | 0.72 | 0.65 | 0.23 | 0.18 | 0.24 | 0.34 | 0.38 | 0.21 |
| Temperate, west | 0.09 | 1.11 | 0.37 | 0.74 | 0.17 | 0.10 | 0.20 | 0.34 | 0.41 | 0.14 |
| Montane Cordillera | −0.04 | 1.14 | 0.19 | 0.95 | 0.18 | 0.09 | 0.22 | 0.43 | 0.52 | 0.14 |
| Temperate, east | −0.58 | 0.86 | 0.35 | 0.89 | 0.00 | −0.10 | 0.06 | 0.31 | 0.44 | 0.04 |
| Mean | 0.01 | 1.21 | 0.38 | 0.81 | 0.16 | 0.08 | 0.19 | 0.37 | 0.45 | 0.14 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hember, R.A.; Coops, N.C.; Spittlehouse, D.L. Spatial and Temporal Variability of Potential Evaporation across North American Forests. Hydrology 2017, 4, 5. https://doi.org/10.3390/hydrology4010005
Hember RA, Coops NC, Spittlehouse DL. Spatial and Temporal Variability of Potential Evaporation across North American Forests. Hydrology. 2017; 4(1):5. https://doi.org/10.3390/hydrology4010005
Chicago/Turabian StyleHember, Robbie A., Nicholas C. Coops, and David L. Spittlehouse. 2017. "Spatial and Temporal Variability of Potential Evaporation across North American Forests" Hydrology 4, no. 1: 5. https://doi.org/10.3390/hydrology4010005
APA StyleHember, R. A., Coops, N. C., & Spittlehouse, D. L. (2017). Spatial and Temporal Variability of Potential Evaporation across North American Forests. Hydrology, 4(1), 5. https://doi.org/10.3390/hydrology4010005







