Anthropocene Trends in Water Flow of Small and Medium-Sized Rivers in the East of the East European Plain: The Forest-Steppe and Steppe Zones

Abstract

Based on long-term series of observations of water flow of 22 small and medium-sized rivers in the forest-steppe and steppe east of the East European Plain, an analysis of its trend changes in 1961–2022, i.e., in the time interval of the Anthropocene with the most progressive climate change in the study region, was carried out. The main quantitative hydrological parameters studied were annual average water discharge, annual maximum water discharge (Q_max), minimum water discharge (Q_min-CP) during the ice-covered period of the riverbed (cold period, mainly December–March), minimum water discharge (Q_min-WP) during the ice-free period of the riverbed (warm period, mainly April–November), as well as some of their ratios, which provide a clear idea of changes in the intra-annual variability of water flow. The principal methodological toolkit used was a standard set of statistical tests applied to time series analysis. A summary of the study results showed that statistically significant trend changes in the annual water flow of most of the analyzed rivers were not observed for the specified period. At the same time, statistically significant intra-annual changes in the flow were revealed: a significant reduction in Q_max (especially in the forest-steppe zone) and a significant increase in Q_min-CP and Q_min-WP. Thus, the ratio between Q_max and Q_min-CP (Q_min-WP) decreased between the baseline climatic periods 1961–1990 and 1991–2020 by an average of 4.1 (4.0) times in the rivers of the forest-steppe zone, and by 5.2 (5.3) times in the rivers of the steppe zone. Climate change is considered the leading cause of the observed intra-annual changes in river water flow in the study region, with the main factor being an increment in annual air temperature, especially during the cold season.

1. Introduction

The scientific results presented in the Sixth Assessment Report (AR6) of the Intergovernmental Panel on Climate Change [1] allow us to state with confidence that the Earth’s atmosphere, hydrosphere, and biosphere have undergone rapid and almost ubiquitous changes. Their scales are unprecedented in many respects for many millennia, and these changes have been influenced by direct and indirect human activities. According to the World Meteorological Organization (WMO), the period 2015–2020 was the warmest six-year period on record, and 2011–2020 was the warmest decade on record [2]. The average rate of near-surface air warming during 1976–2020 was 0.18 °C/10 years globally, and during this period alone, global near-surface air temperature increased by 0.8 °C. Air temperature increased especially rapidly in the North Polar Region, where a linear increment in the annual average air temperature was about 2.64 °C over 30 years (1991–2020) [2]. Modern global warming, which is also clearly detectable in Russia, has some important features. The warming of the lowest layer of the troposphere over Russia is occurring most than twice as fast as the average on Earth’s land surface—0.51 °C per decade. Each decade since 1981–1990 has been warmer than the previous one, and 9 of the 10 warmest years were observed in the 21st century [2]. The warming in Russia has occurred and continues to occur in all seasons. However, significant interdecadal fluctuations were superimposed on seasonal trends, which were/are especially clearly evident in winter (December–February), when, after rapid warming in the period from the mid-1970s to the mid-1990s, a slight cooling occurred over most of Russia. It lasted until about 2010 and was caused by changes in the atmospheric circulation of the Atlantic-European sector [2]. Along with the noted increase in air temperature, there has been and continues to be a reduction in the duration of snow cover, observed across Russia during 1976–2020 at an average rate of 1.17 days per 10 years. However, significant descending trends were detected mainly in European Russia and also partially in Asian Russia (in the south of Western Siberia and the north of Central Siberia) [2]. At the same time, compared with the period 1966–1990 [3], the average linear trend coefficient of the maximum snow reserve grew from 2 cm/10 years to 6–8 cm/10 years, with the maximum rates of this change revealed in Western Siberia. In essence, the snow cover period tends to be shorter; the first snowfall occurs later, and spring snowmelt occurs earlier in most of Russia. However, the amount of snowfall has increased overall, particularly in the western part of Russia [4].

In Russia, the phase of active climate change in the Anthropocene (a term not yet generally accepted, denoting a hypothetical new geological epoch in which the main driving force of change on Earth is human activity, influencing geological, climatic, and biotic processes since the end of World War II) coincided with significant changes in land use. Following the collapse of the former Soviet Union at the very end of 1991, Russia experienced significant degradation of agriculture. This was manifested, first of all, in the abandonment of cultivated land, a reduction in the fleet of agricultural machinery, and unprecedented changes in livestock farming. Regional characteristics and reasons for the noted changes in the post-Soviet space have been analyzed in numerous studies [5,6,7,8,9,10,11,12]. For example, according to our estimates [5], the area of cropland in the country reduced by more than a third between 1971–1991 and 2005–2017; despite this, there has been small growth (recovery) of cropland area across the country since the mid-2000s. It has also been noted that the most significant and sustainable (beginning long before 1991) reduction in the area of cropland occurred in the administrative regions of Russia located primarily in the forest zone, which was especially evident in the European territory of the country [5,12]. Along with the noted reduction in cropland area, significant changes in crop rotation have also occurred [5].

Even this brief overview of changes in climate and human activity leaves no doubt that they could be reflected in changes in the hydrosphere objects on land in Russia, primarily in the flow of river water. Moreover, the complexity of the “mechanism” of these changes, caused by the combined influence of these two noted main factors, led to different trends in the change of annual and seasonal river water flow in various physiographic regions of the country. Thus, according to [2], during the period of active climate warming, an increase in the annual river flow occurred in Russia as a whole. However, in some rivers of the Ob River and Yenisei River basins, in the extreme northeast of Russia and in the rivers of the south of European Russia (in general, the annual runoff in European Russia has tended to rise in recent decades, associated with a general increase in the humidity of the territory [13]), a statistically significant decline in the annual flow was found. Changes in maximum water discharges for the majority of the territory of Russia were insignificant. In recent decades, a decrease in maximum water flow has been observed in the rivers of the south and southwest of European Russia. In the basins of the lower Volga River and the Don River, as well as the south part of the Oka River basin, a decrease in maximum water discharges of 40–70% has been traced on most rivers since 1979–1983 [2,13,14]. In the Don River basin and the east of the Volga River basin, the contribution of snowmelt flood water flow has reduced to 50% or less of the annual flow [14,15] (50% is a critical level for rivers of the Eastern European type of water regime). As a comparison, in the first half of the 20th century, the snowmelt flood flow in these basins averaged 60–70% and more of the annual values [16,17,18]. These processes were accompanied by changes in the timing of the onset of floods in the rivers [19]. It is noteworthy that in the western part of the forest (coniferous–broad-leaved) zone of the East European Plain, in the Baltic countries, there has also been a predominant reduction in flood runoff caused by snowmelt in recent decades [20]. At the same time, the winter low-water runoff of rivers has increased significantly. For example, in the Volga River basin, the share of this runoff in the annual water runoff has increased by up to 40–60% and more in most of the basin between the periods 1946–1977 and 1978–2010 [16]. The change in the share of summer–autumn low-water flow has also been quite significant over recent decades [14]. In the rivers of the north of European Russia, in general, no significant changes in the intra-annual distribution of runoff were detected [14].

From the above it follows that the trend variability of river water flow in recent decades has been subject, to one degree or another, to physiographical (landscape) zonality, following changes in climate and human activity. The East European, or Russian, Plain is one of the most extensive plains on Earth’s land and the largest natural-geographical region of Europe, being one of the best expressions of the latitudinal zonality of natural landscapes and their anthropogenic transformation. Previous studies have either avoided considering contemporary landscape-level directional changes in water flow or considered this issue for only one of its components (for example, the minimum or base water flow of the warm or cold seasons of the year). Below, using the example of small and medium-sized rivers in the east sector of the forest-steppe and steppe zones of the plain, we examine the transformations of their annual and extreme seasonal water flow (discharges) since the beginning of the 1960s and provide a preliminary and mostly qualitative assessment of some natural local factors that could affect these transformations. These transformations of river water flow in the indicated landscape zones are analyzed in a comparative context.

2. Materials and Methods

2.1. Study Region

The region under study is located in the east of the East European Plain and covers such large geomorphic units as the Volga Upland, Bugulma–Belebey Upland (western mega-slope), Obshchy Syrt Upland (western mega-slope), Central Russian Upland (eastern mega-slope), and the Trans-Volga Lowland. They are composed of sedimentary cover rocks of the Russian tectonic platform, which have different compositions and ages (from Late Paleozoic to Quaternary deposits) [21] (Figure 1).

Figure 1. Location of the analyzed rivers in the study region. 1, 2, …, 22—the numbering of the rivers (see Figure 1 and Table 1); I and II—the analyzed river sectors; B–B—the Bugulma–Belebey Upland. A—the location of the analyzed gauging stations on the rivers; B—some of the largest cities in the region and their names; C—seas, lakes, reservoirs, and rivers; D—forests (excluding the Caspian and Aral lowlands); E—cropland; F—grassland; G—the approximate boundary of the basins of the Volga and Don rivers within the study region (rivers with numbers 11–12 and 18, 19, 21, and 22 belong to the Don River basin; all the rest belong to the Volga River basin).

Figure 1. Location of the analyzed rivers in the study region. 1, 2, …, 22—the numbering of the rivers (see Figure 1 and Table 1); I and II—the analyzed river sectors; B–B—the Bugulma–Belebey Upland. A—the location of the analyzed gauging stations on the rivers; B—some of the largest cities in the region and their names; C—seas, lakes, reservoirs, and rivers; D—forests (excluding the Caspian and Aral lowlands); E—cropland; F—grassland; G—the approximate boundary of the basins of the Volga and Don rivers within the study region (rivers with numbers 11–12 and 18, 19, 21, and 22 belong to the Don River basin; all the rest belong to the Volga River basin).

Table 1. The analyzed rivers and some topographic, geological, and hydrological characteristics of their basins (see Figure 1).

No.	River	Gauging Station and Its Code 1		F, km2	h, m	H, m	Z	Lit
Forest-steppe zone
1	Myosha	Pestretsy	77197	3230	54.9	150	5.4	C
2	Kubnya	Chuteyevo	77164	930	77.3	153	3.8	C
3	Kichui	Utyashkino	77189	1330	51.0	185	5.3	C
4	Aktai	Karavayevo	77201	690	69.7	132	3.1	L
5	Sheshma	S.-P.	77179	3110	59.8	205	5.0	C
6	Maliy Cheremshan	Abalduyevka	77217	1230	85.3	144	3.7	L
7	Krasnaya	Krasnaya Reka	77209	311	55.0	120	2.9	L
8	Bol’shoy Cheremshan	Novocheremshansk	77212	6050	59.5	143	3.5	C
9	Tushonka	Sergeyevka	77210	309	54.2	227	4.0	C
10	Syzranka	Repyovka	77329	4380	48.0	220	3.4	Sed
11	Sosna	Yelets	78054	16,300	106.9	210	3.7	S-S
12	Vorona	Borisoglebsk	78165	13,200	84.5	ND	3.0	Ch-O
				4256	67.2	172	3.9
Steppe zone
13	Maliy Kinel’	Poludni	77298	2090	49.5	165	2.6	C
14	Bol’shoy Kinel’	Timashevo	77292	12,000	32.2	165	3.2	C
15	Chapayevka	Pod’yom Mikhailovka	77311	1480	48.0	132	1.7	Lo
16	Chagra	Novotulka	77336	2550	29.7	107	1.2	L
17	Buzuluk	Perevoznikovo	77270	4280	61.7	162	1.6	C
18	Khopyor	Balashov	78138	14,300	100.8	220	3.1	Ch-O
19	Medveditsa	Lysyye Gory	78196	7610	126.6	220	2.6	C
20	Bol’shoy Karaman	Sovetskoye	77362	3470	29.0	82	0.4	L
21	Ilovlya	Borovki	78231	8730	40.3	150	0.8	S-S
22	Chir	Oblivskaya	78252	8470	39.2	150	1.1	Lo
				6498	55.7	155	1.8

¹ According to https://gmvo.skniivh.ru (accessed on 8 February 2025); F—river basin area upstream of the corresponding gauging station; h—the absolute elevation of the zero level at the corresponding gauging station; H—the average absolute elevation of river basin upstream of the corresponding gauging station; Z—the long-term specific annual average water runoff during 1961–2022, L s⁻¹ km⁻²; Lit—lithological complexes of surface deposits: C—clays, L—loams, Lo—loess and loess-like loams, S-S—sand-shale deposits, Ch-O—chemo- and organogenic deposits, and Sed—undifferentiated sedimentary rocks; S.-P—Sloboda Petropavlovskaya. The average values for each landscape zone are underlined. Note: Data on H and Lit were obtained from [22].

Table 1. The analyzed rivers and some topographic, geological, and hydrological characteristics of their basins (see Figure 1).

No.	River	Gauging Station and Its Code 1		F, km2	h, m	H, m	Z	Lit
Forest-steppe zone
1	Myosha	Pestretsy	77197	3230	54.9	150	5.4	C
2	Kubnya	Chuteyevo	77164	930	77.3	153	3.8	C
3	Kichui	Utyashkino	77189	1330	51.0	185	5.3	C
4	Aktai	Karavayevo	77201	690	69.7	132	3.1	L
5	Sheshma	S.-P.	77179	3110	59.8	205	5.0	C
6	Maliy Cheremshan	Abalduyevka	77217	1230	85.3	144	3.7	L
7	Krasnaya	Krasnaya Reka	77209	311	55.0	120	2.9	L
8	Bol’shoy Cheremshan	Novocheremshansk	77212	6050	59.5	143	3.5	C
9	Tushonka	Sergeyevka	77210	309	54.2	227	4.0	C
10	Syzranka	Repyovka	77329	4380	48.0	220	3.4	Sed
11	Sosna	Yelets	78054	16,300	106.9	210	3.7	S-S
12	Vorona	Borisoglebsk	78165	13,200	84.5	ND	3.0	Ch-O
				4256	67.2	172	3.9
Steppe zone
13	Maliy Kinel’	Poludni	77298	2090	49.5	165	2.6	C
14	Bol’shoy Kinel’	Timashevo	77292	12,000	32.2	165	3.2	C
15	Chapayevka	Pod’yom Mikhailovka	77311	1480	48.0	132	1.7	Lo
16	Chagra	Novotulka	77336	2550	29.7	107	1.2	L
17	Buzuluk	Perevoznikovo	77270	4280	61.7	162	1.6	C
18	Khopyor	Balashov	78138	14,300	100.8	220	3.1	Ch-O
19	Medveditsa	Lysyye Gory	78196	7610	126.6	220	2.6	C
20	Bol’shoy Karaman	Sovetskoye	77362	3470	29.0	82	0.4	L
21	Ilovlya	Borovki	78231	8730	40.3	150	0.8	S-S
22	Chir	Oblivskaya	78252	8470	39.2	150	1.1	Lo
				6498	55.7	155	1.8

¹ According to https://gmvo.skniivh.ru (accessed on 8 February 2025); F—river basin area upstream of the corresponding gauging station; h—the absolute elevation of the zero level at the corresponding gauging station; H—the average absolute elevation of river basin upstream of the corresponding gauging station; Z—the long-term specific annual average water runoff during 1961–2022, L s⁻¹ km⁻²; Lit—lithological complexes of surface deposits: C—clays, L—loams, Lo—loess and loess-like loams, S-S—sand-shale deposits, Ch-O—chemo- and organogenic deposits, and Sed—undifferentiated sedimentary rocks; S.-P—Sloboda Petropavlovskaya. The average values for each landscape zone are underlined. Note: Data on H and Lit were obtained from [22].

The climate of the region is moderately continental (according to the Köppen climate classification, Dfb—cold (continental) without a dry season and with warm summers) in the northern and central parts, and continental (Dfa—cold (continental) without a dry season and with hot summers) in the south [21]. It is characterized by warmer summers and harsher winters compared with the western subregions of the plain. There is relatively often persistent dry weather and little rainfall. Climatic conditions vary from north to south, from forest-steppe to steppe. The annual precipitation in the forest-steppe is about 430–500 mm, in the steppe, about 350–430 mm.

The vegetation cover in the forest-steppe of the region is represented by a combination of forest communities consisting mainly of linden (Tilia cordata Mill., 1768) and oak (Quercus robur L., 1753) with an admixture of other broad-leaved species (especially in the Trans-Volga region) and forb-cereal meadows growing mainly on the southern subtypes of gray forest soils and northern subtypes of chernozem soils [21]. The vegetation of the steppes (in the interfluves) is represented mainly by forbs and cereal communities: mostly Stipa ucrainica P.A.Smirn. in the Pre-Volga region and the Don River basin, and predominantly Stipa zalesskii Wilensky, 1925, Stipa korshinskyi Roshev., 1916, and Stipa lessingiana Trin. and Rupr. in the Trans-Volga region [21]. The steppe herbaceous communities of the study region grow mainly on the central and southern subtypes of chernozem soils. In most of the forest-steppe and steppe zones, especially in the Pre-Volga region and the Don River basin, the soils are plowed, and natural vegetation has been replaced by agricultural crops (see Figure 1).

2.2. Study Objects

This study covers 22 small and medium-sized rivers with a total basin area (upstream of the analyzed gauging stations) of 116,050 km² (51,070 km², or 44%, in the forest-steppe zone and 64,980 km², or 56%, in the steppe zone), located in the basins of the Volga and Don rivers (see Figure 1), between 48°28′ N and 56°11′ N, and between 36°21′ E and 54°06′ E. Their basin areas vary from 311 to 16,300 km². Some topographic, geological, and hydrological characteristics of the basins of the analyzed rivers are presented in Table 1. It is noteworthy that the average elevations of the river basins in the steppe zone are somewhat lower than those in the forest-steppe zone. This fact reflects the background of a general reduction in elevation in the southeast of the East European Plain towards the Caspian Lowland. The long-term average specific water runoff (Z) in the forest-steppe river basins is more than twice as high as in the steppe river basins (see Table 1).

The highest average elevations are confined to the river basins composed on the surface of a complex of chemo-organogenic, undifferentiated sedimentary and partially clayey deposits of the uplands. The lowest average elevations are typical for the basins of the analyzed rivers of the lowland plains of the Trans-Volga region, formed on alluvial and predominantly loamy deposits of the ancient valley of the Volga River (Figure 2A).

In both the forest-steppe and steppe landscape zones, the relative maximum of specific water runoff is confined to those river basins that are composed of clayey deposits on the surface (Figure 2B). In general, there is a tendency for the runoff of the analyzed rivers (Z) to increase with increasing elevation of their basins (H). This is better and statistically reliably expressed in the steppe zone of the study region (the coefficient of linear correlation between H and Z in this zone is 0.77; in the forest-steppe zone, it is only 0.33) (Figure 2C).

2.3. Materials

The study materials were based on data from long-term observations (up to and including 2022) of the flow of water of the above-mentioned rivers (Figure 3), namely the following quantitative values: Q—annual average water discharge; Q_max—annual maximum water discharge (during the period of spring snowmelt-induced flood); Q_min-CP—annual minimum water discharge in the period of the ice-covered channel (the cold period, mainly December–March); Q_min-WP—annual minimum water discharge in the period of the ice-free channel (the warm period, mainly April–November), as well as some of their ratios (Q_max/Q, Q_max/Q_min-CP, Q_max/Q_min-WP, and Q_min-WP/Q_min-CP) (see Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7 and Figure A8 in Appendix A). For all the rivers analyzed, there are long-term series of all the specified hydrological quantities, except for the Maliy Kinel’ River, for which only long-term changes in Q, Q_max, and Q_max/Q were considered. A total of 171 series of long-term observations (1961–2022) were examined.

Where possible, the few gaps (14 units: 12 for 1 year, 1 for 2 years, 1 for 3 years) in the series of water flow in some rivers (6 units) were filled according to standard procedures using long-term series of observations either for the same hydrological parameters on adjacent rivers or within a single river between different parameters (for example, restoring the annual average water discharge based on the values of the annual maximum water discharge). When restoring the data, the main requirement was the presence of a high correlation (r > 70%) of the corresponding water discharge values between these rivers/parameters (Figure 4).

According to Figure 3 and adhering to the principle of homogeneity in the duration of the observation series, the period from 1961 to 2022 was chosen as the principal period for the subsequent examination of long-term trends in water flow of the rivers in the study region. Notably, this period fully includes two baseline (reference) periods for observing long-term climate change: the updated 30-year period of the climate norm–1991–2020 (P₂), according to the US National Oceanic and Atmospheric Administration (NOAA), and the previous baseline period 1961–1990 (P₁), which is still recommended by WMO for historical comparison and monitoring of climate change (P₂/P₁).

Data on the specified hydrological parameters were obtained from the following sources: automated information system for state monitoring of water bodies of the Federal Agency for Water Resources of the Ministry of Natural Resources and Environment of the Russian Federation (https://gmvo.skniivh.ru/, accessed on 17 January 2025); reference hydrological collections published on paper for different periods [23,24,25,26,27,28,29,30,31,32,33], and others.

2.4. Methods

The above-mentioned time series were examined for homogeneity (with the identification of points (years) of statistically significant changes in the values of water flow in the observation series), stationarity, trend (with the computation of Sen’s slope), heteroscedasticity, and the presence of outliers. The statistical tests used and the conditions for their implementation are presented below, in

Table 2. Statistical tests of the examined time series and the conditions for their implementation.

Time Series Analysis	Statistical Test	Testing Conditions
Homogeneity	Pettitt’s test	The p-value has been computed using 10,000 Monte Carlo simulations. The significance level is 5%.
	Buishand’s test
	Standard normal homogeneity test (SNHT)
Unit Root and Stationarity	KPSS test 1	The significance level is 5%.
	ADF test 2
Trend	Mann–Kendall test	A two-tailed test was used. The confidence interval is 5%. The confidence interval of Sen’s slope is 5%. Autocorrelations (Hamed–Rao method) were used with a significance level of 5%. The Seasonal Mann-Kendall test was used with a period of 12.
	Seasonal Mann–Kendall test
Heteroscedasticity	White test	The significance level is 5%.
Outliers	Grubbs test	Two-tailed tests were used. The alternative hypothesis is two-sided. The significance level is 5%.
	Dixon test

¹ Kwiatkowski–Phillips–Schmidt–Shin test; ² Augmented Dickey–Fuller test.

.

The conclusion about the homogeneity/heterogeneity of a series of observations and the presence of a point (year) of statistically significant change in the series was also made based on the prevailing test results (at least two tests out of three). However, if there was a discrepancy in all three tests, the year with the highest statistical probability was considered the main year of change (μ) for the observation series (see Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7 and Figure A8 in Appendix A). The year with the second-highest statistical probability was chosen as the additional year of change (η) in the observation series. When examining the observation series for stationarity/non-stationarity, the KPSS test was preferred because it was most consistent with the results of the Mann–Kendall trend test. The White test was used to examine some time series and relationships for heteroscedasticity/homoscedasticity. Extreme values in the observation series were considered outliers if they were confirmed by two of the two tests used. These outliers helped to detect a very few technical errors in the series associated with incorrect input of data.

This study also used descriptive statistics methods, correlation analysis (Pearson and Spearman correlations), regression analysis, two-sample t-test, as well as other auxiliary methods. All the above statistical procedures were implemented in XLSTAT 2016.02.28451 for the Microsoft Excel software program.

In addition, the following auxiliary coefficients were computed:

The coefficient K, showing the relative average “involvement” of a series of observations in trend (general and seasonal) changes:

K = [(S × 62)/Ѳ] × 100%

(1)

where Ѳ is the long-term annual average water flow (discharge) of the corresponding river; S is the value of Sen’s slope in a Q-series; 62 is the number of years in the tested period (1961–2022). Similarly, the coefficient K was computed for the parameters Q_max, Q_min-CP, and Q_min-WP using values Ѳ_max, Ѳ_min-CP, and Ѳ_min-WP, respectively. The relativity of the coefficient K allows comparing rivers with different water discharges. The higher the modular value of the coefficient (|K|), the greater (the more noticeable) the trend in their series of observations (an ascending trend when K > 0, a descending trend when K < 0).

The coefficient β, showing the relative changes in the average values of the examined hydrological parameters between the considered baseline periods (1961–1990 (P₁) and 1991–2020 (P₂)), was computed as follows:

β = [{Ѳ(P₂) − Ѳ(P₁)}/Ѳ(P₁)] × 100%

(2)

where Ѳ(P₁) and Ѳ(P₂) are the long-term annual average water discharges of the corresponding river during 1961–1990 and 1991–2020, respectively. In the same way, the coefficient β was computed for the parameters Ѳ_max, Ѳ_min-CP, Ѳ_min-WP, and their ratios.

The coefficient ΔC_v, showing the relative change in the coefficient of interannual variation C_v in the series of the main hydrological parameters computed for the baseline periods 1961–1990 (P₁) and 1991–2020 (P₂), was determined as follows:

ΔC_v = [{C_v(P₂) − C_v(P₁)}/C_v(P₁)] × 100%

(3)

where C_v(P₁) and C_v(P₂) are the coefficients of interannual variation of the values of Q (or Q_max, Q_min-CP, and Q_min-WP) in 1961–1990 and 1991–2020, respectively.

The separation of two sectors (Sector I, related to the Middle Volga physiographical region, and Sector II, related to the Lower Volga region and partly to the Don River basin, see Figure 1) is associated with the differences in their climates. From Sector I to Sector II, there is an increase in the average annual temperature and the temperature of the cold period of the year, a decrease in annual precipitation, as well as a decrease in the duration and depth of snow cover [21]. In agroclimatic terms, Sector I is characterized by both a sufficient (in the north) and an arid (in the south) growing season, while Sector II is distinguished by an arid (southern half of the Don River basin, the Pre-Volga sector of the Lower Volga region) and dry (Trans-Volga region of the Lower Volga region) growing season [21].

2.5. Limitations

The main limitations of the study are as follows:

(1)

The identified trends in water flow changes, although objectively present, are not unidirectional in some cases. This primarily concerns minimum water discharges. In this regard, the results obtained and their interpretation should be treated with caution.

(2)

Despite the fact that the study examines the main average and boundary indicators of water flow, they do not fully characterize the long-term trends in the change of seasonal flow (average flow rates, flow volume, the share in annual runoff, etc.) in the main phases of the hydrological regime of the analyzed rivers (snowmelt-induced flood runoff, winter and summer–autumn low-water runoff, and summer–autumn rainfall-induced flood runoff).

(3)

Trends over the years with various anomalies (both positive and negative) in water flow were not analyzed.

(4)

Although this study covered 22 small and medium-sized river basins, this is still not enough to carry out a comprehensive and more detailed statistical examination of the factorial determination of the identified patterns. In this regard, the analysis of the factors that caused changes in water flow (preliminary climate and human activity) is mostly descriptive, aimed at understanding the general essence.

(5)

Because the onset of the Anthropocene usually dates back to the mid- to late 1940s [34], our study of all the rivers analyzed did not cover the first 10–15 years of this era. Nevertheless, we carried out a retrospective analysis (up to 1961) of water flow changes based on some representative rivers of the study region.

3. Results

3.1. Homogeneity and Stationarity

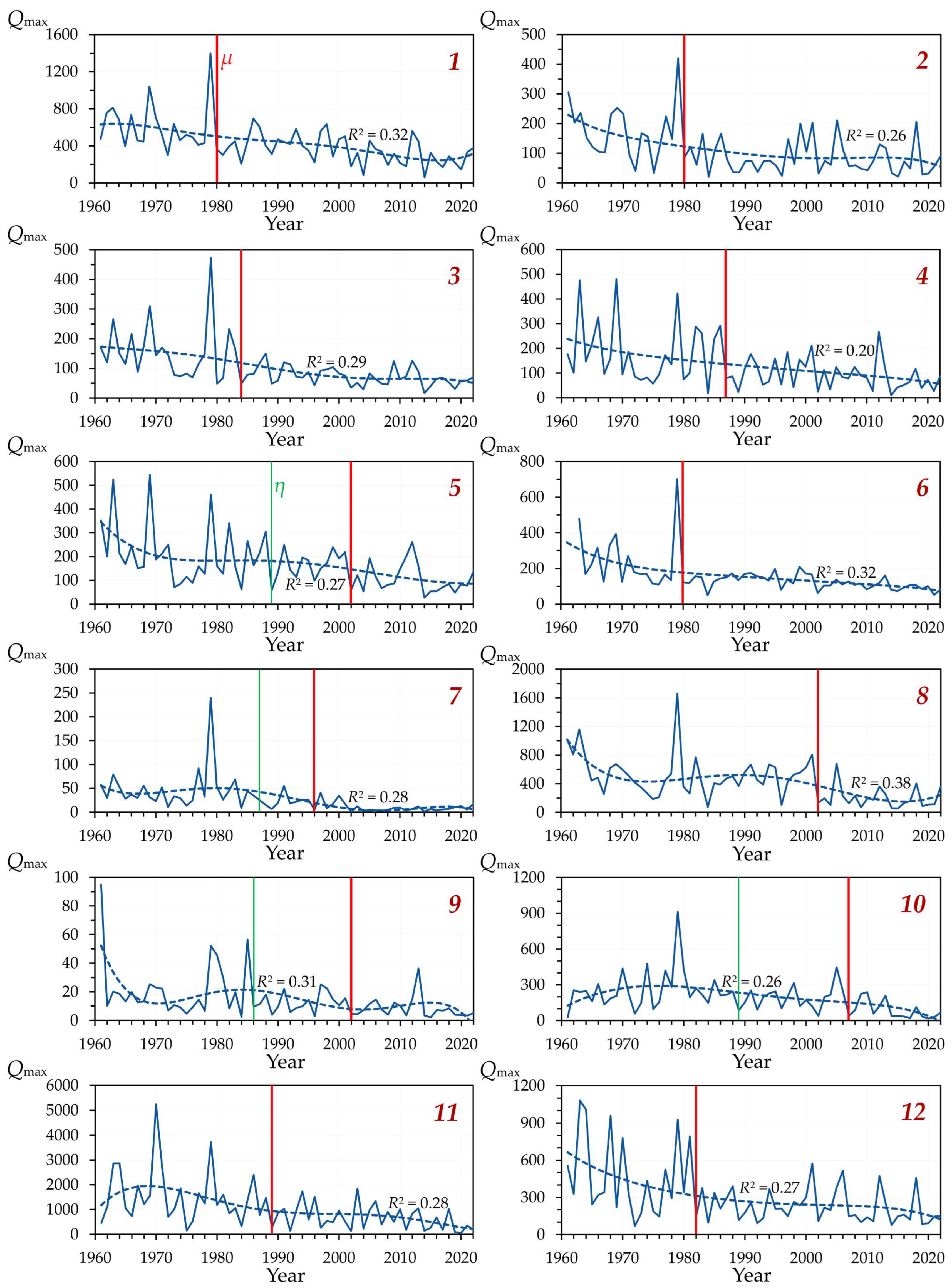
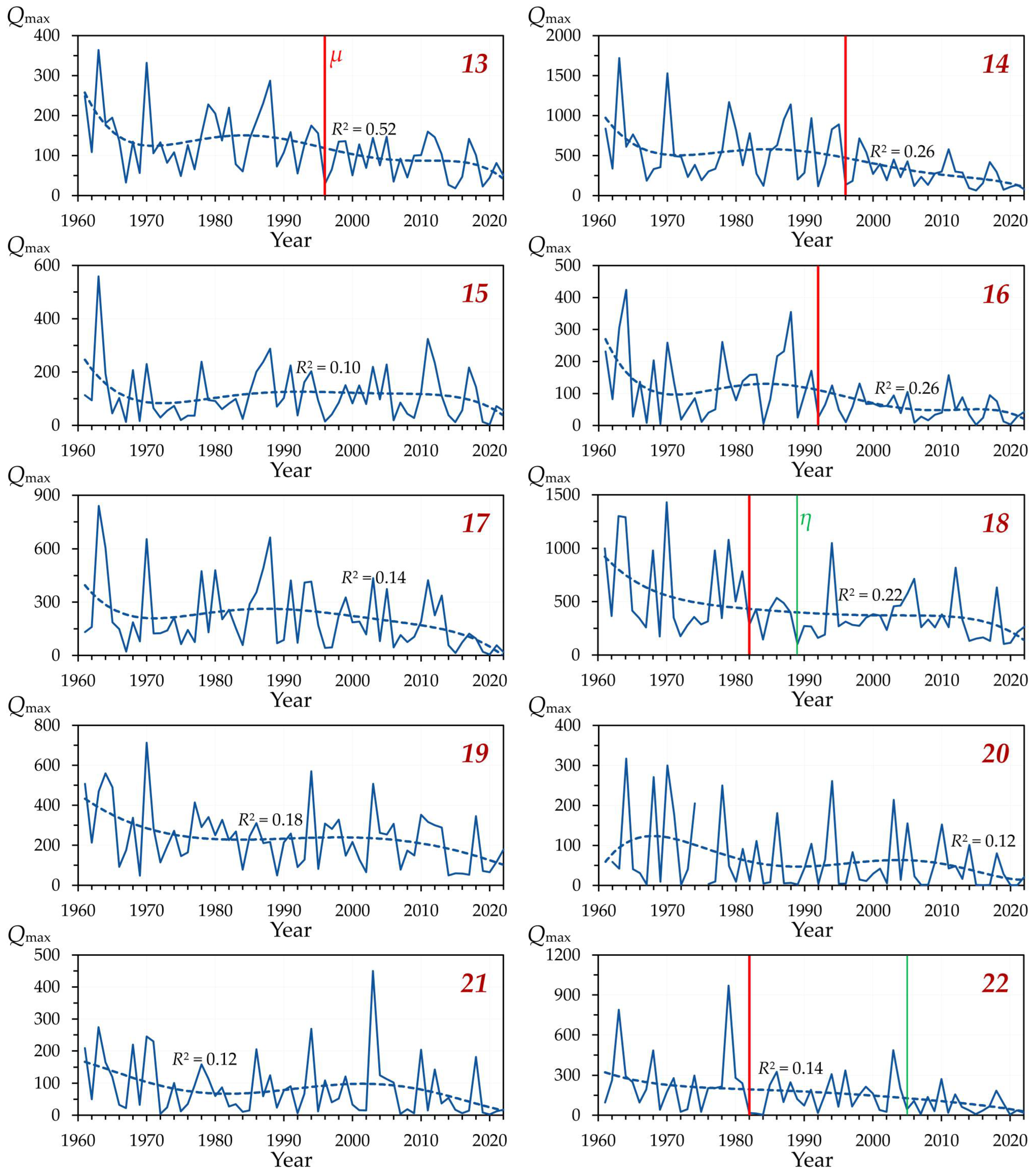
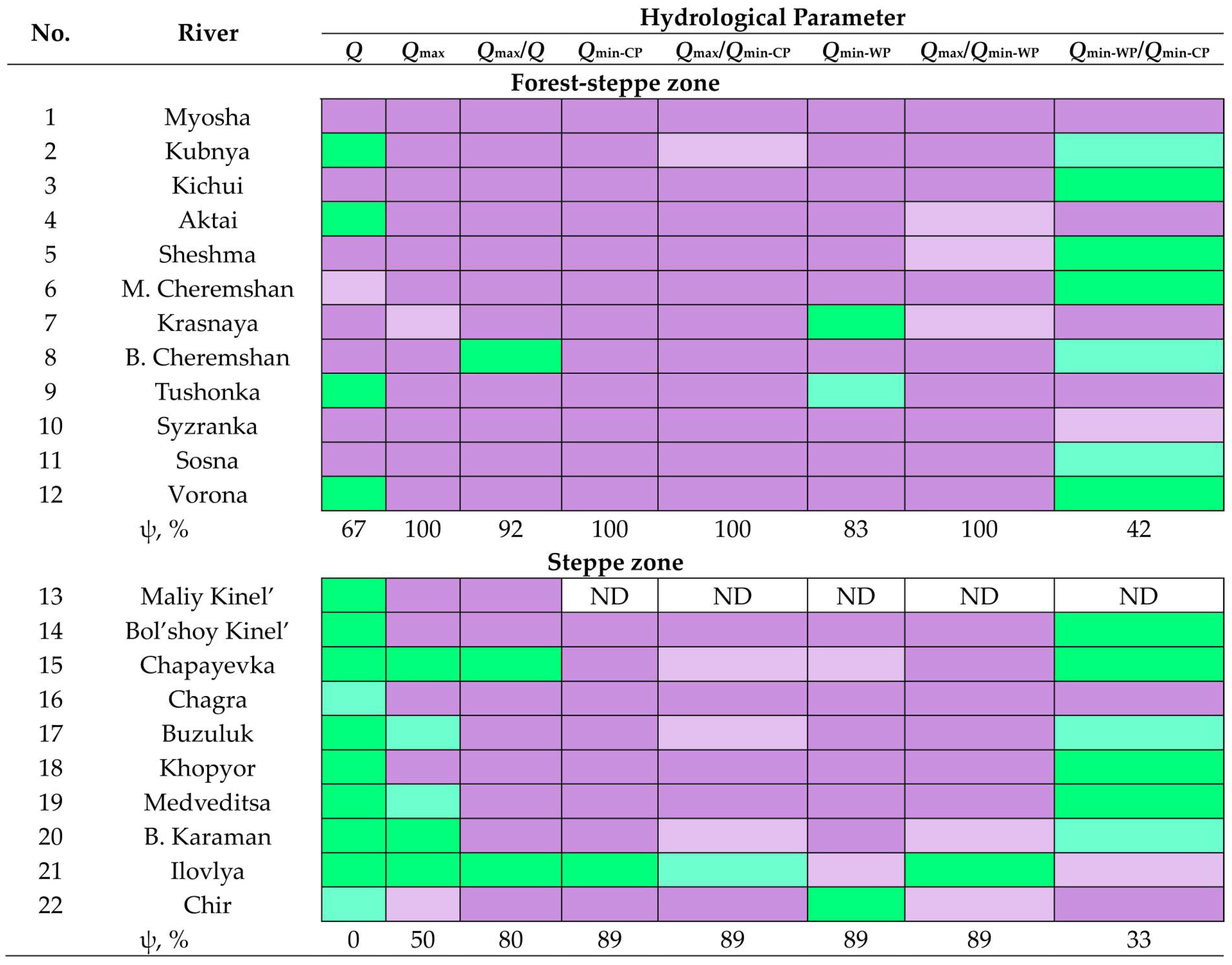
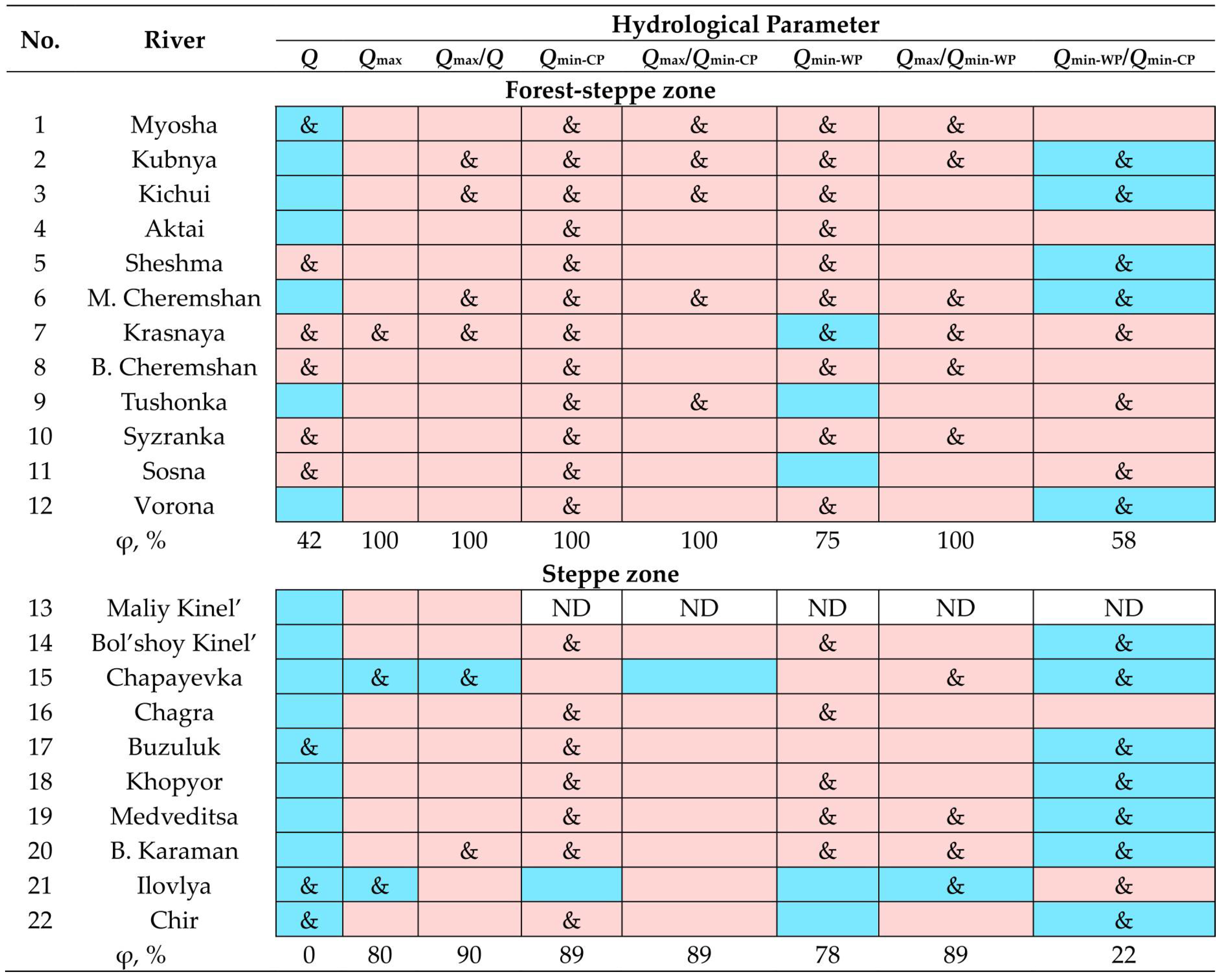
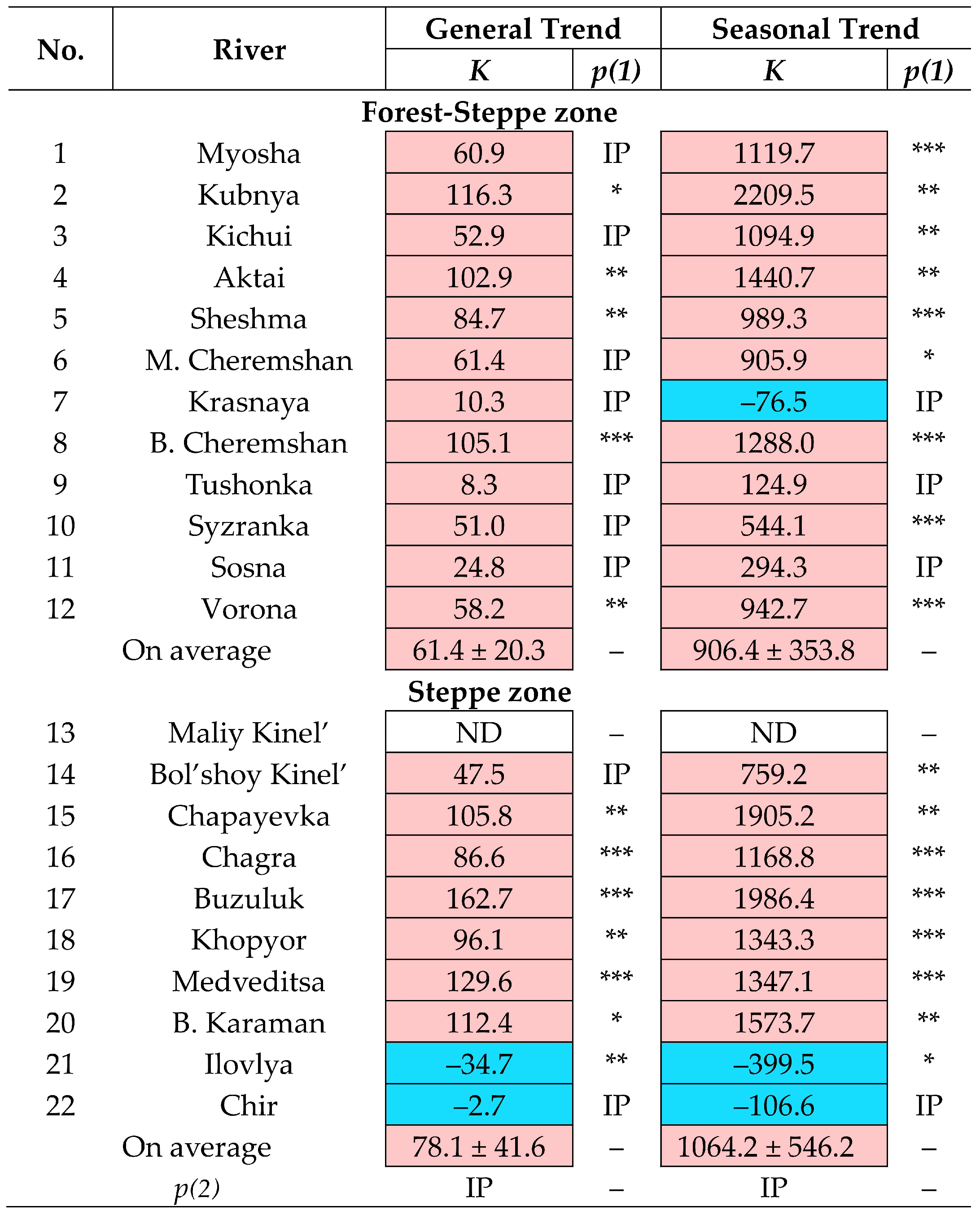
The tested series of observations are also heterogeneous in the overwhelming majority of cases, especially for rivers in the forest-steppe zone: 85% of cases in the forest-steppe zone and 64% of cases in the steppe zone (Figure 5). The relatively high proportion of homogeneous series of the parameter Q_min-WP/Q_min-CP in the two landscape zones under consideration and the 100% homogeneity of the Q-series of the analyzed rivers in the steppe zone are also noteworthy.

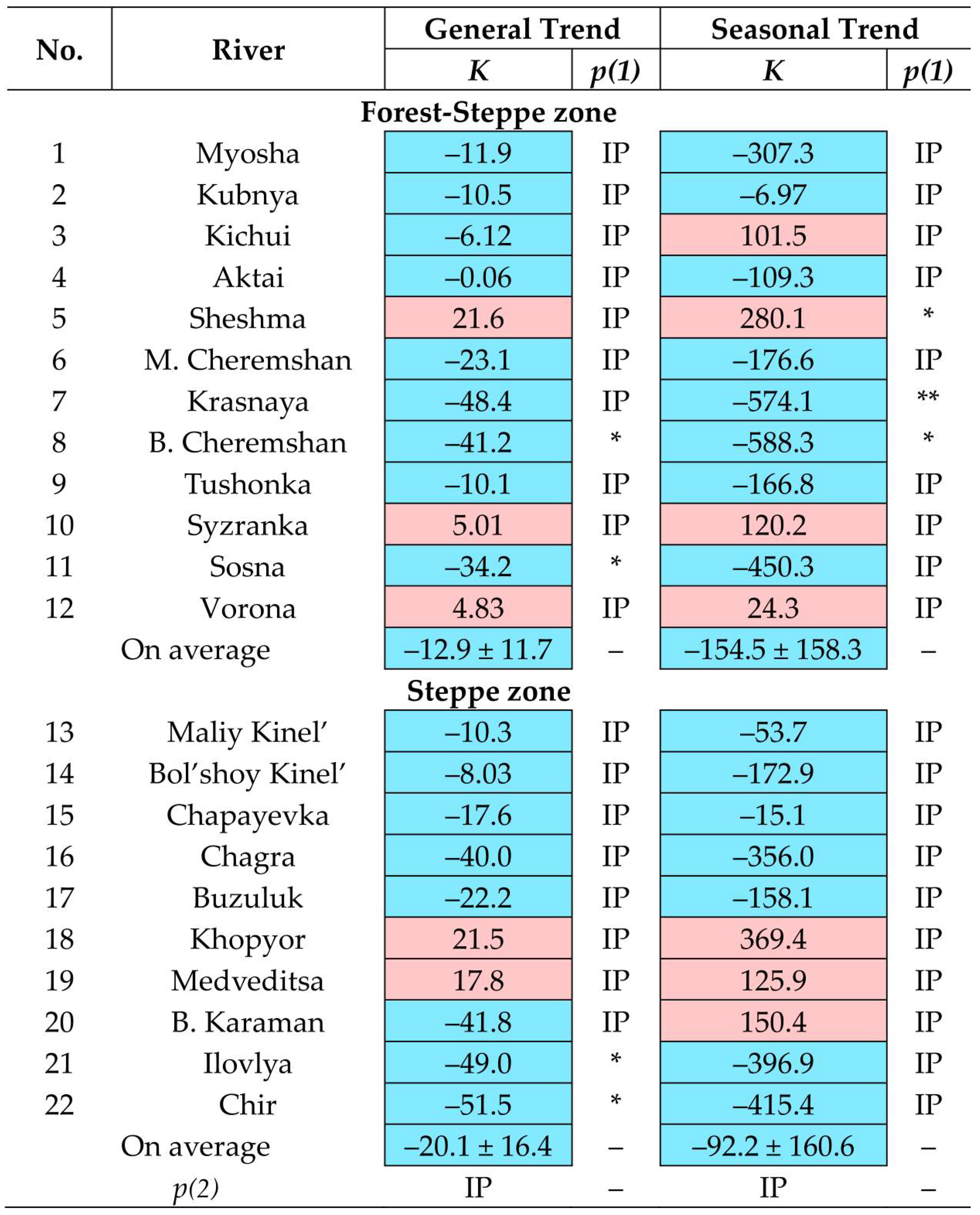
In those observation series that were characterized by heterogeneity, the main changes in intra-annual parameters Q_max, Q_min-CP, and Q_min-WP occurred, on average, around 1990 (

Table 3. The average calendar years (T_av) of the principal critical changes in the tested long-term series (1961–2022) of the main hydrological parameters, based on the data from Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7 and Figure A8 of Appendix A.

Landscape Zone	Hydrological Parameter
	Q		Qmax		Qmin-CP		Qmin-WP
	Tav	σ	Tav	σ	Tav	σ	Tav	σ
Forest-Steppe	1998	12.1 [8]	1991	10.3 [12]	1989	5.7 [12]	1987	5.3 [10]
Steppe	—	—	1990	7.1 [5]	1988	4.1 [8]	1990	3.3 [8]

σ—the standard deviation (the number of years); “—” indicates that there are no years of changes in the series. Note: The number of analyzed rivers with identified principal critical changes in the observation series is shown in square brackets.

). Moreover, in the forest-steppe zone, critical changes in the minimum runoff of the warm period (Q_min-WP) occurred, on average, earlier than changes in the minimum runoff of the cold season (Q_min-CP) and changes in the maximum runoff (Q_max). In the forest-steppe zone, critical changes in the annual average water flow (Q) happened much later (on average, in the late 1990s). Compared with the steppe zone, the rivers of the forest-steppe zone were characterized by a greater spread of years of principal changes (larger σ values), which could partly be associated with a greater number of cases of their detection than for the steppe zone rivers.

The above-mentioned significant heterogeneity of the examined long-term observation series is also manifested in their significant non-stationarity: 84% of cases in the forest-steppe zone and 67% of cases in the steppe zone (Figure 6). In the rivers of the steppe zone, the relatively high proportion of stationary series for the parameter Q_min-WP/Q_min-CP and the total statistical stationarity of the tested series for the parameter Q are also noteworthy.

3.2. Trend Changes

3.2.1. Annual Water Flow

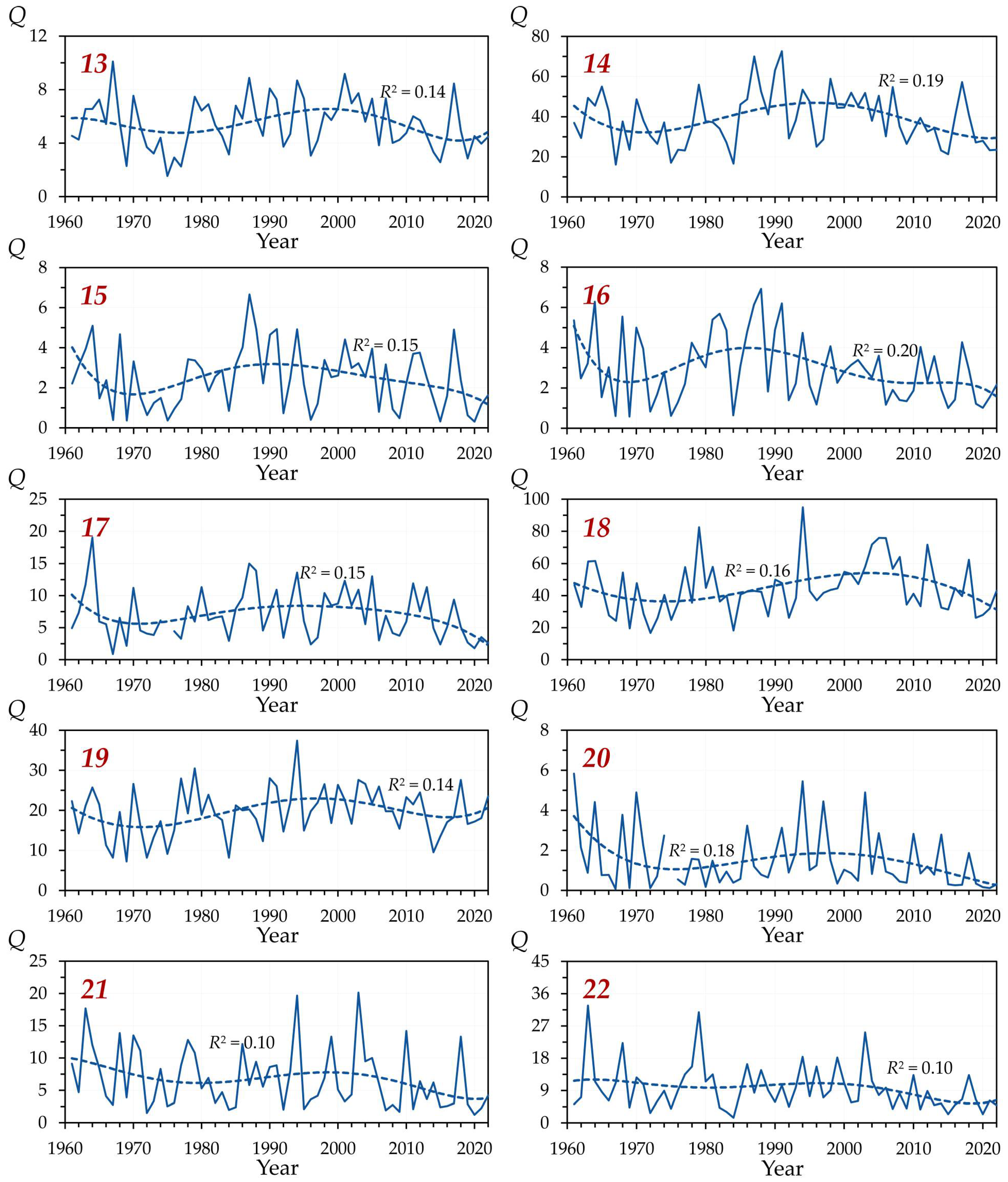
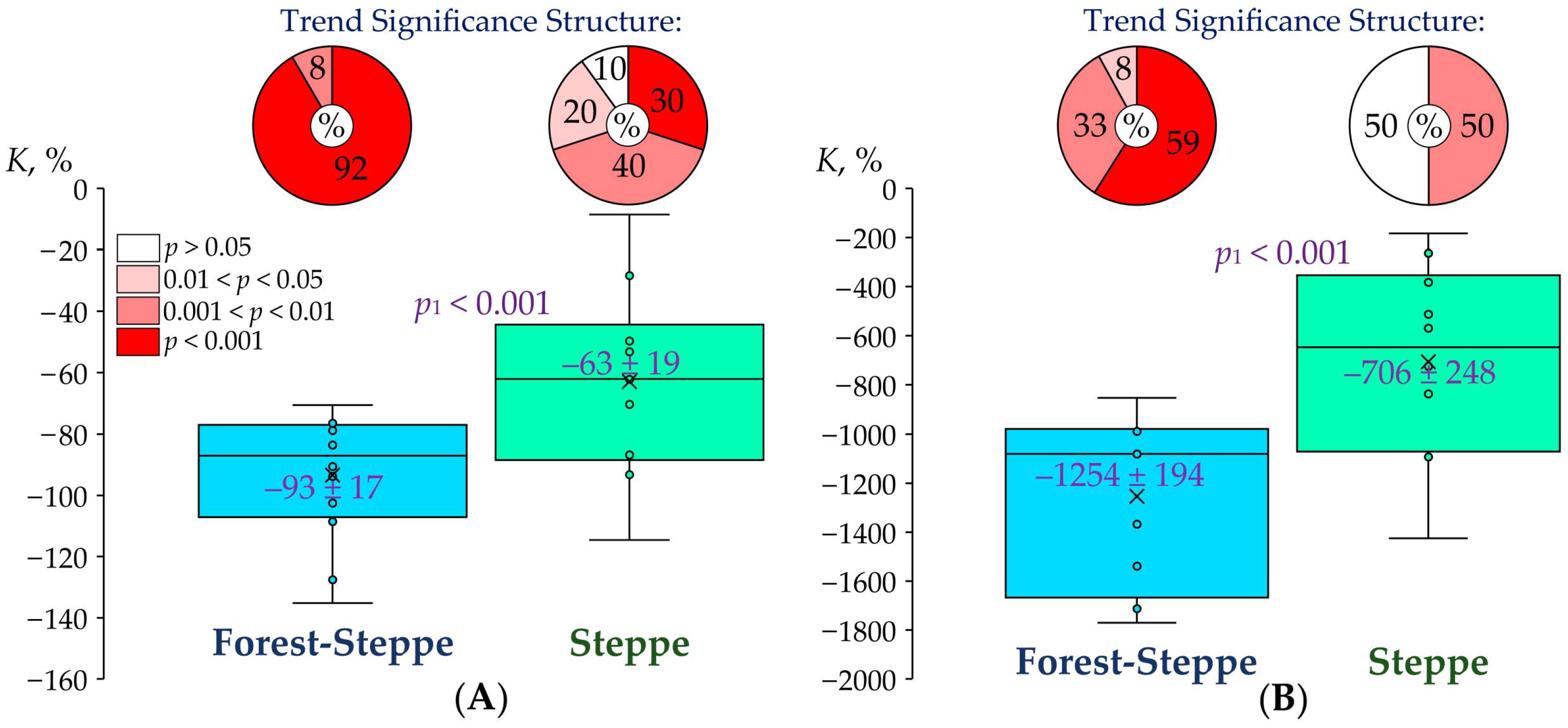
In the period from 1960 to 2022, on the vast majority of the rivers under consideration (in total for the two zones, this amounted to 77%: 75% in the forest-steppe zone and 80% in the steppe zone), a general trend of reducing annual water flow (Q) was observed. In the steppe zone, it was somewhat more significant than in the forest-steppe zone (Figure 7). At the same time, the prevalence (68%: 67% in the forest-steppe zone and 70% in the steppe zone) of a descending seasonal trend was also noted. Compared with general trends, in the forest-steppe zone, descending seasonal trends were more noticeable than in the steppe zone. However, no statistically significant differences were found in the degree of expression of either general or seasonal trends between the two landscape zones. It is fundamentally important to note that, despite the presence of prevailing tendencies towards a decline in Q throughout the region under consideration, in 82–86% of cases, these tendencies turned out to be statistically insignificant.

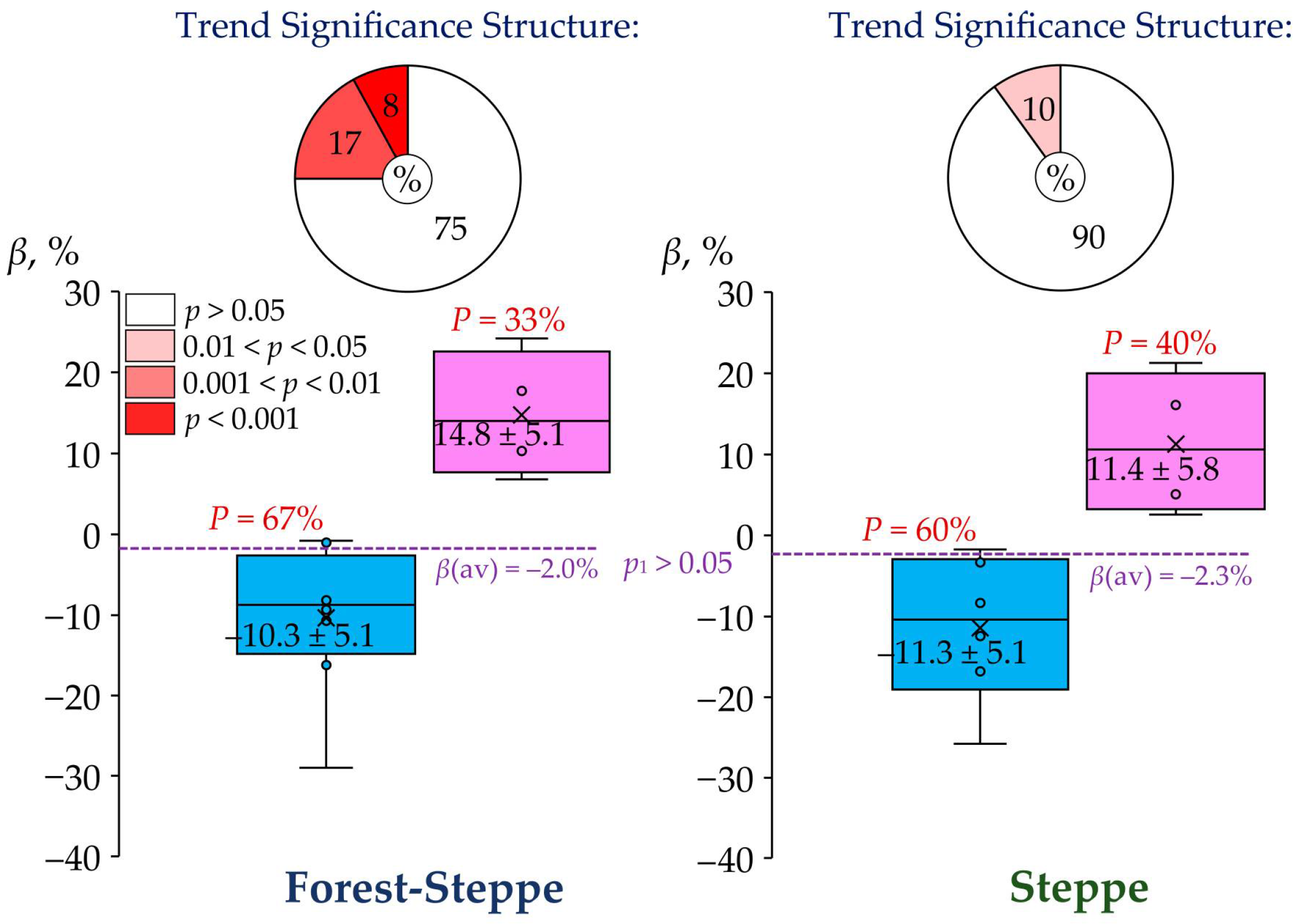
In the context of regional climate change, changes in the flow of water of small and medium-sized rivers in the east of the East European Plain are of interest when comparing the baseline periods 1961–1990 and 1991–2020. This possibility is provided by using the coefficient β (see Formula (2)). According to the coefficient β, there were no statistically significant changes in the annual average water flow (Q) across the study region. The flow reduced by only 2.0–2.3% between the baseline periods 1961–1990 and 1991–2020 (Figure 8).

Moreover, in 33–40% of cases, even an increment in Q was noted. Despite this, the dominant part (≥75%) of these trends did not have statistical significance, especially in the steppe zone (see Figure 8). Also, no statistically significant difference in the average values of Q was found between the analyzed landscape zones.

3.2.2. Annual Maximum Water Flow

In contrast to the annual average water flow (Q), the annual maximum water flow (Q_max) showed decreasing general and seasonal trends everywhere in both the forest-steppe and steppe zones. This decrease was more noticeable and mostly statistically significant (Figure 9). In the steppe zone, a statistically significant general trend of reducing Q_max was not noted only for the Chapayevka River. It should be noted that the general and seasonal decline in Q_max in the rivers of the forest-steppe zone was, on average, “deeper” (and the differences were statistically significant) compared to the rivers of the steppe zone (see Figure 9).

According to the revealed widespread descending trend (see Figure 9), the annual maximum water flow of the rivers (Q_max) in the study region reduced between the baseline periods 1961–1990 and 1991–2020 by almost 40%, and this reduction was more significant in the forest-steppe than in the steppe zone (with a statistically significant difference) (Figure 10). Moreover, if in the forest-steppe zone all decreases in Q_max were statistically significant to one degree or another, then in the steppe zone, only 60% of all cases of decrease in Q_max were considered as such.

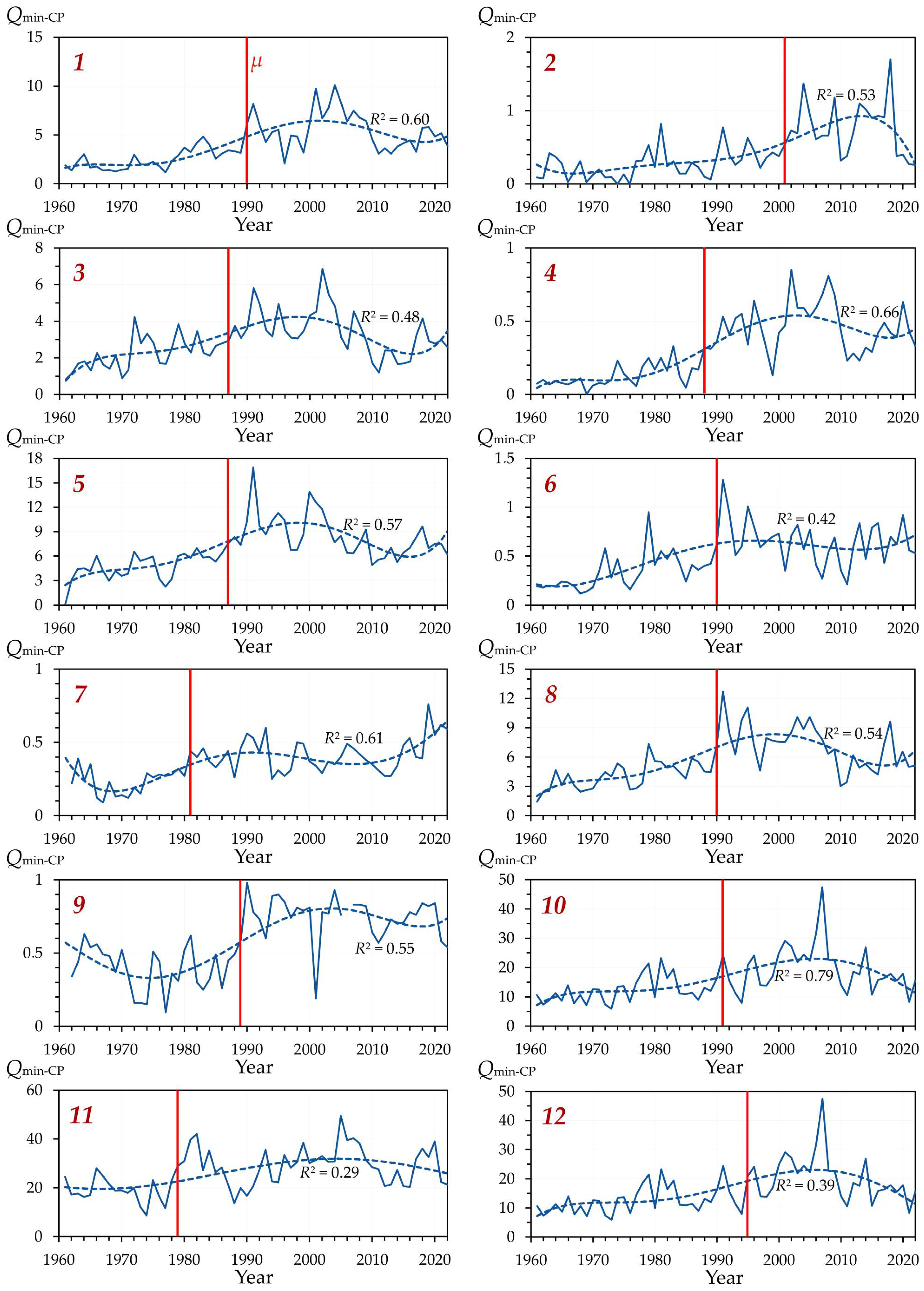
3.2.3. Annual Minimum Water Flow in the Cold Season

Analysis of changes in the annual minimum water flow in the cold (mainly winter) season of the year (Q_min-CP) revealed its general increment in 1961–2022 (Figure 11). The vast majority of these trends were statistically significant, especially in the forest-steppe zone. In the steppe zone, only in the southernmost rivers of the study region (the Ilovlya and Chir rivers), no statistical significance was found for either the general or seasonal Q_min-CP growth trend. No statistically significant differences in the degree of expression of ascending trends in Q_min-CP between the forest-steppe and steppe zones were found.

As for the minimum water flow during the cold season (Q_min-CP), in the study region, it increased significantly (on average, by 96–100%) between 1961–1990 and 1991–2020, while no statistically significant differences between the average values for the forest-steppe and steppe zones were found (Figure 12). All identified increments in Q_min-CP between the periods were statistically significant.

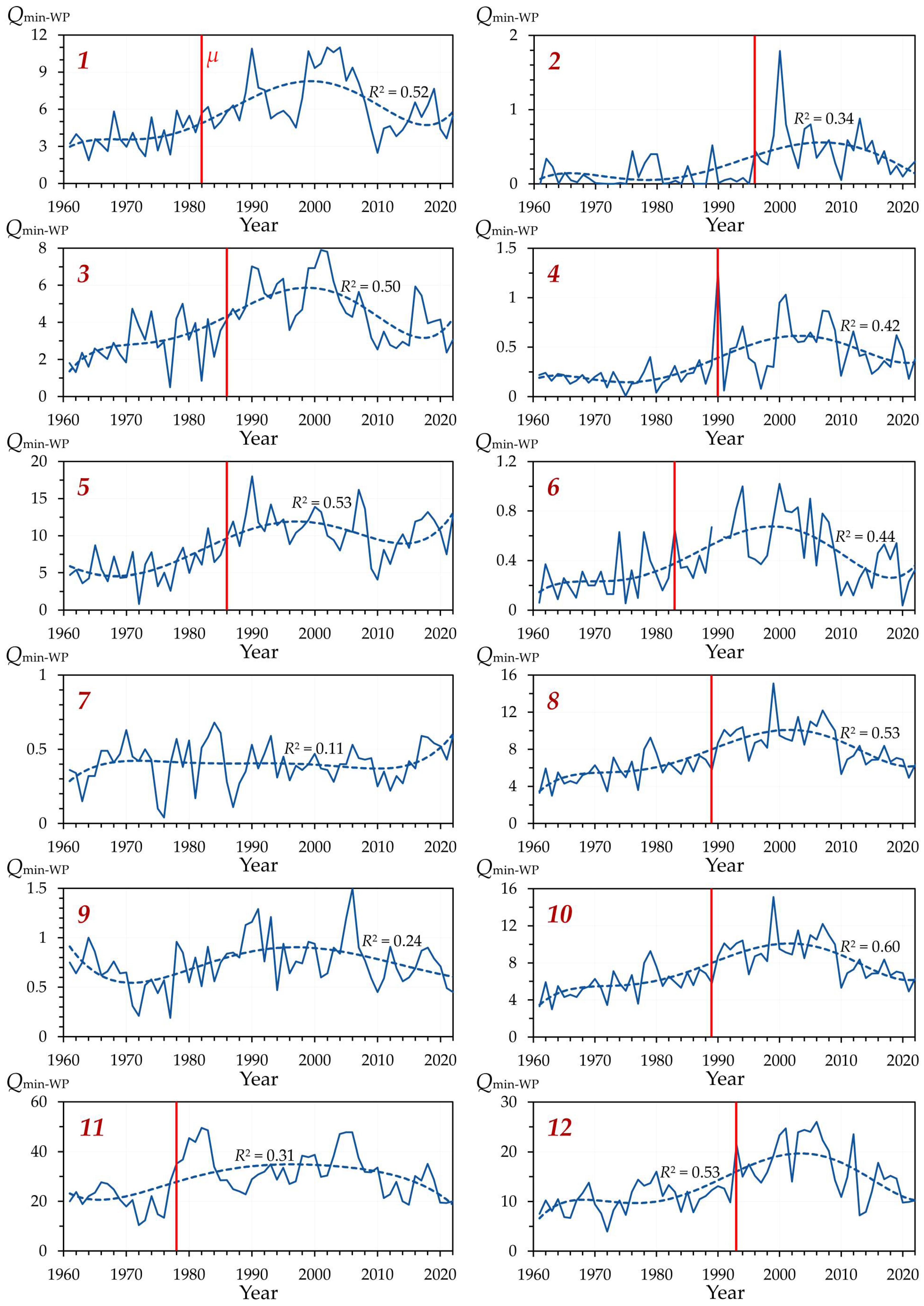
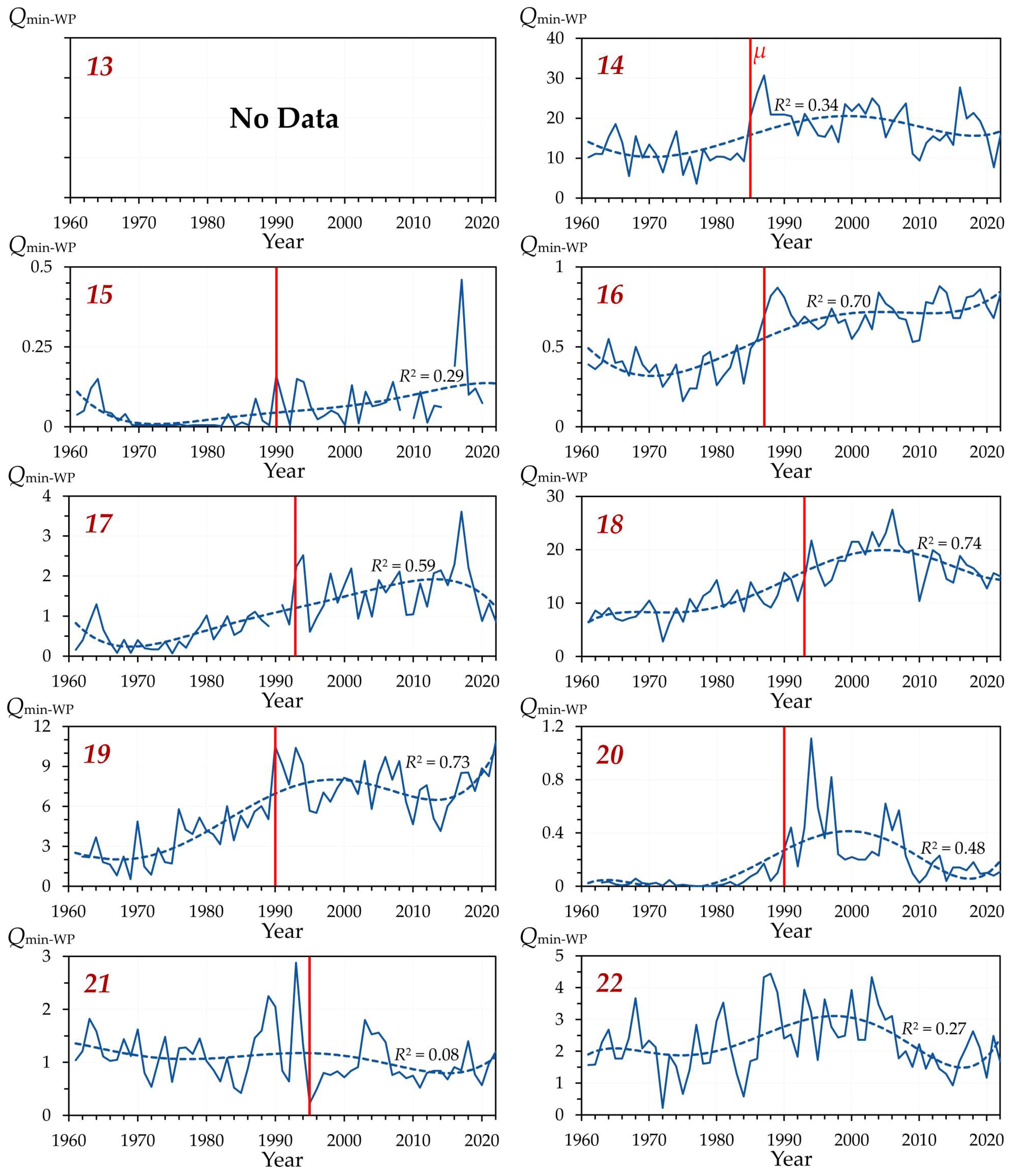
3.2.4. Annual Minimum Water Flow in the Warm Season

As with Q_min-CP, the annual minimum flow of the warm season (Q_min-WP) had a predominant increasing general and seasonal trends (in 86–90% of the analyzed rivers) during the period under consideration: in 92–100% of cases in the forest-steppe zone and 78% of cases in the steppe zone (in the latter, in the Ilovlya River, the decreasing general and seasonal trends in Q_min-WP even had statistical significance) (Figure 13). However, in contrast to Q_min-CP, the general trend of Q_min-WP growth in 1961–2022 had a predominant statistical significance only in the rivers of the steppe zone (in 78% of cases), while in the rivers of the forest-steppe zone it was detected in less than half of the cases (42%). In the seasonal trend in these landscape zones, the statistical significance was higher—89% and 75%, respectively.

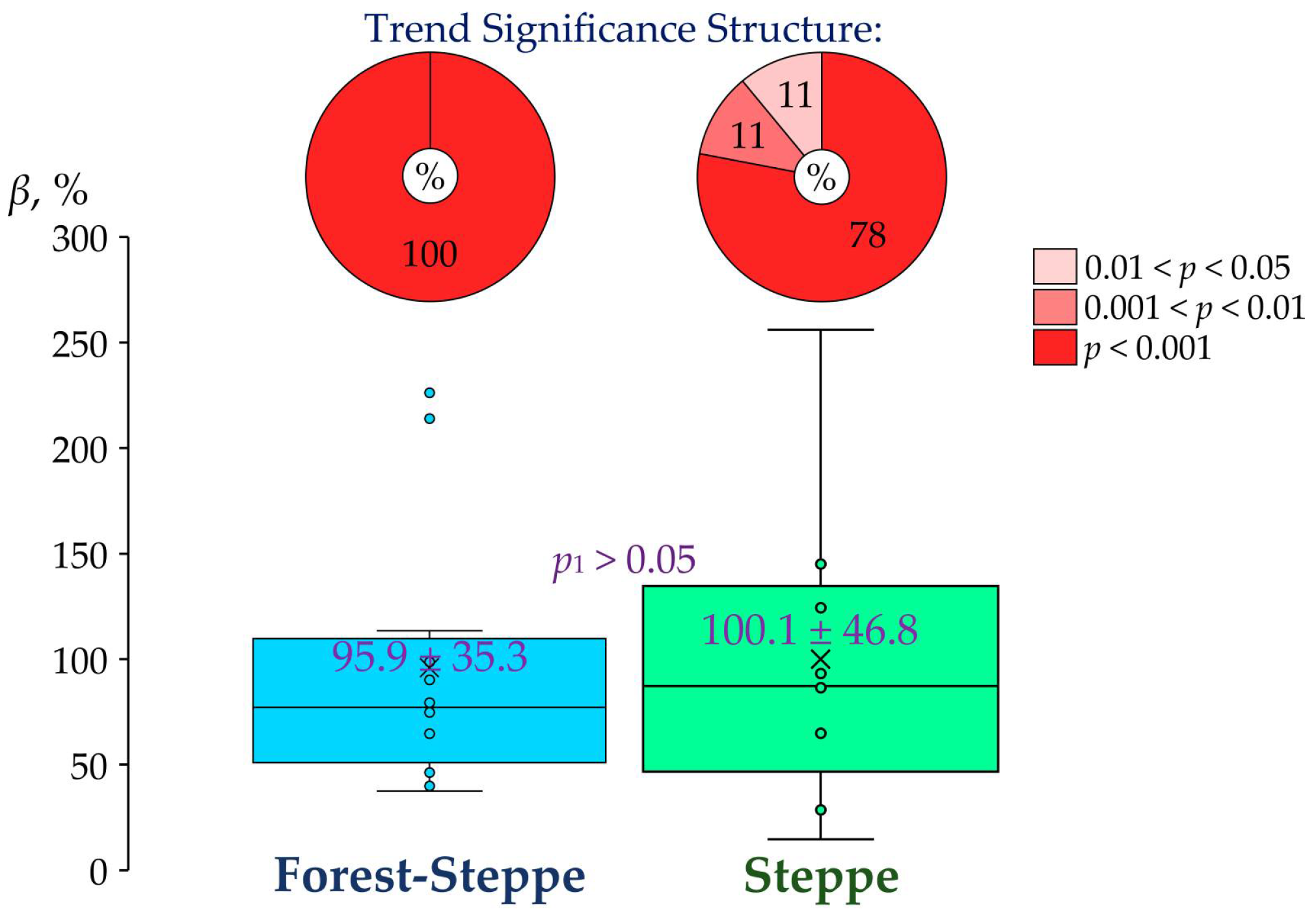
An increase in the minimum water flow during the warm period of the year (Q_min-WP) was also significant (on average, by 103%) between 1961–1990 and 1991–2020 (Figure 14).

Except for two rivers in the Middle Volga region (see Sector I in Figure 1) and two rivers in the extreme south of the region covered by the study (within the Don River basin, see Sector II in Figure 1), the identified increases in the coefficient β were statistically significant. As in the case of Q_min-CP, no statistical significance was also found in the difference of the average values of β for Q_min-WP between the forest-steppe and steppe zones.

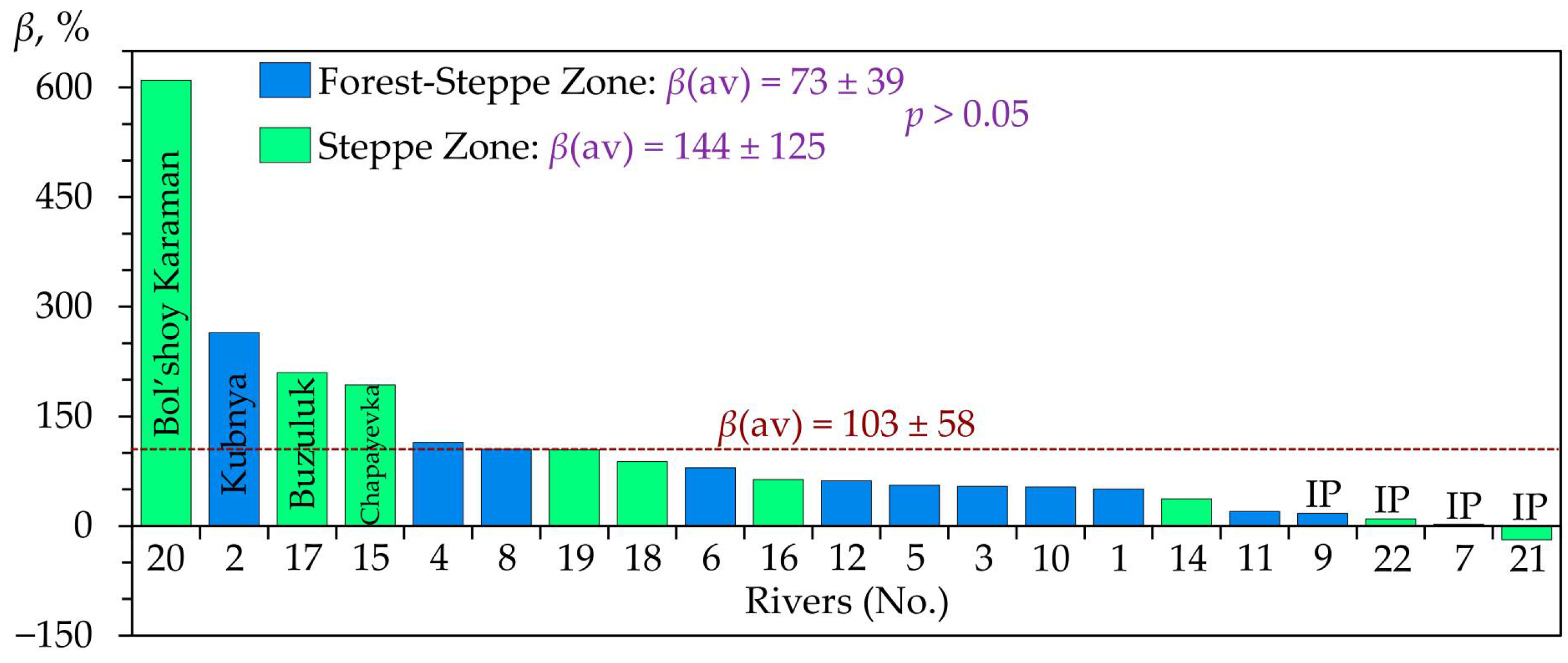
As for the ratio of values K and β for each river in the study region, their overall good comparability was revealed, which is expressed in high coefficients of their linear correlation (r). For the parameter Q, r is equal to 0.88 in magnitude and 0.77 in sign; for Q_max, 0.81 and 1.0, respectively; for Q_min-CP, 0.85 and 0.95, respectively. For Q_min-WP, the coefficient r turned out to be comparatively low—0.60 and 0.81, respectively. The reasons for these discrepancies require separate study.

3.3. Changes in Intra-Annual Variability

It is quite expected that the above-described changes in the main hydrological parameters also entailed changes in their ratios, which are one of the indicators of intra-annual variability of river water flow. The value of the coefficient β for the parameter Q_max/Q shows that, on average, across the entire region under study, this ratio declined by 40% (or 1.7 times) between the baseline periods 1961–1990 and 1991–2020 (see

Table A1. The β values computed for Q_max/Q of the analyzed rivers.

No.	River	β, Qmax/Q
		%	Times	p(1)
Forest-Steppe Zone
1	Myosha	−35.1	−1.5	***
2	Kubnya	−40.8	−1.7	***
3	Kichui	−50.4	−2.3	***
4	Aktai	−48.4	−1.9	***
5	Sheshma	−50.8	−2.0	***
6	M. Cheremshan	−33.4	−1.5	***
7	Krasnaya	−57.8	−2.4	***
8	B. Cheremshan	−33.0	−1.5	***
9	Tushonka	−45.5	−1.8	**
10	Syzranka	−50.9	−2.0	***
11	Sosna	−49.0	−2.0	***
12	Vorona	−48.2	−1.9	***
On average		−45.3 ± 4.5	−1.9 ± 0.2	–
Steppe zone
13	Maliy Kinel’	−45.2	−1.8	***
14	Bol’shoy Kinel’	−47.0	−1.9	***
15	Chapayevka	−0.3	−1.03	IP
16	Chagra	−39.4	−1.7	**
17	Buzuluk	−32.3	−1.5	**
18	Khopyor	−46.0	−1.9	***
19	Medveditsa	−36.4	−1.6	***
20	B. Karaman	−40.2	−1.7	*
21	Ilovlya	−15.1	−1.2	IP
22	Chir	−35.8	−1.6	**
On average		−33.8 ± 9.3	−1.6 ± 0.2	–
p(2)		*	*	–

p(1)—the statistical significance of β; p(2)—the statistical significance of the difference in the average β values computed for the forest-steppe and steppe zones. IP—statistically insignificant difference (p > 0.05); * 0.01 < p < 0.05; ** 0.001 < p < 0.01; *** p < 0.001.

in Appendix B). These reductions were statistically significant in 100% of cases in the forest-steppe zone and in 80% of cases in the steppe zone. Moreover, the analyzed rivers of the forest-steppe zone were characterized by a more noticeable variability reduction (statistically significant difference) in the flow, according to β, than the rivers of the steppe zone.

The reduction in Q_max/Q_min-CP and Q_max/Q_min-WP between the periods indicated turned out to be even more significant: on average, by 70–73% in the analyzed rivers of the forest-steppe zone (100% statistical significance) and by 65–68% in the steppe zone (89% statistical significance) (see

Table A2. The β values computed for Q_max/Q_min-CP, Q_max/Q_min-WP, and Q_min-WP/Q_min-CP of the analyzed rivers.

No.	River	Hydrological Parameter
		β, Qmax/Qmin-CP			β, Qmax/Qmin-WP			β, Qmin-WP/Qmin-CP
		%	Times	p(1)	%	Times	p(1)	%	Times	p(1)
Forest-Steppe Zone
1	Myosha	−74.5	−3.9	***	−60.5	−2.5	***	−31.0	−1.5	***
2	Kubnya	−87.1	−7.8	**	−91.2	−11.4	**	−28.3	−1.4	IP
3	Kichui	−66.7	−3.0	***	−74.2	−3.9	***	6.0	1.1	IP
4	Aktai	−84.2	−6.3	***	−70.1	−3.3	**	−38.6	−1.6	**
5	Sheshma	−62.3	−2.7	***	−70.8	−3.4	**	−1.5	−1.0	IP
6	M. Cheremshan	−73.0	−3.7	***	−66.1	−3.0	***	−7.1	−1.1	IP
7	Krasnaya	−80.2	−5.1	***	−77.0	−4.4	***	−42.7	−1.7	**
8	B. Cheremshan	−72.1	−3.6	***	−82.7	−5.8	***	23.2	1.2	IP
9	Tushonka	−67.4	−3.1	***	−57.3	−2.3	**	−39.5	−1.7	***
10	Syzranka	−71.1	−3.5	***	−62.2	−2.6	***	−24.7	−1.3	***
11	Sosna	−69.5	−3.3	***	−66.6	−3.0	***	−14.5	−1.2	IP
12	Vorona	−64.8	−2.8	***	−66.6	−3.0	***	−0.7	−1.0	IP
On average		−72.7	−4.1	–	−70.4	−4.0	–	−16.6	−0.93	–
Steppe zone
13	Maliy Kinel’	ND	ND	ND	ND	ND	ND	ND	ND	ND
14	Bol’shoy Kinel’	−66.6	−3.0	***	−60.5	−2.5	***	−11.3	−1.1	IP
15	Chapayevka	−69.4	−3.3	**	−74.7	−4.0	***	35.8	1.4	IP
16	Chagra	−80.5	−5.1	**	−71.6	−3.5	***	−18.8	−1.2	IP
17	Buzuluk	−75.6	−4.1	**	−78.8	−4.7	***	14.5	1.2	IP
18	Khopyor	−64.0	−2.8	***	−68.4	−3.2	***	1.9	1.0	IP
19	Medveditsa	−74.0	−3.8	***	−69.8	−3.1	***	−10.9	−1.1	IP
20	B. Karaman	−95.2	−20.9	*	−95.7	−23.4	*	42.7	1.4	IP
21	Ilovlya	−26.7	−1.4	IP	−6.3	−1.1	IP	−23.5	−1.3	*
22	Chir	−57.4	−2.3	**	−58.2	−2.4	**	−19.2	−1.2	IP
On average		−67.7	−5.2	–	−64.9	−5.3	–	1.2	0.1	–
p(2)		IP	IP	–	IP	IP	–	IP	IP	–

p(1)—the statistical significance of β; p(2)—the statistical significance of the difference in the average values of β computed for the forest-steppe and steppe zones. ND—no data; IP—statistically insignificant difference (p > 0.05); * 0.01 < p < 0.05; ** 0.001 < p < 0.01; *** p < 0.001.

in Appendix B). No statistically significant difference was detected between the average coefficients β computed for rivers in the forest-steppe and steppe zones for the two ratios under consideration.

As for the coefficient β, computed based on the ratio of two minimum water flows Q_min-WP/Q_min-CP, it revealed significant variability in both the forest-steppe and steppe zones. If we take into account the average values, we can state a slight decrement (by 16%) in this ratio only in the forest-steppe zone; however, even in this case, in almost 60% of the rivers, these changes were not statistically significant (see Table A2 in Appendix B). These changes were also statistically insignificant in 89% of the rivers in the steppe zone.

3.4. Changes in Interannual Variability

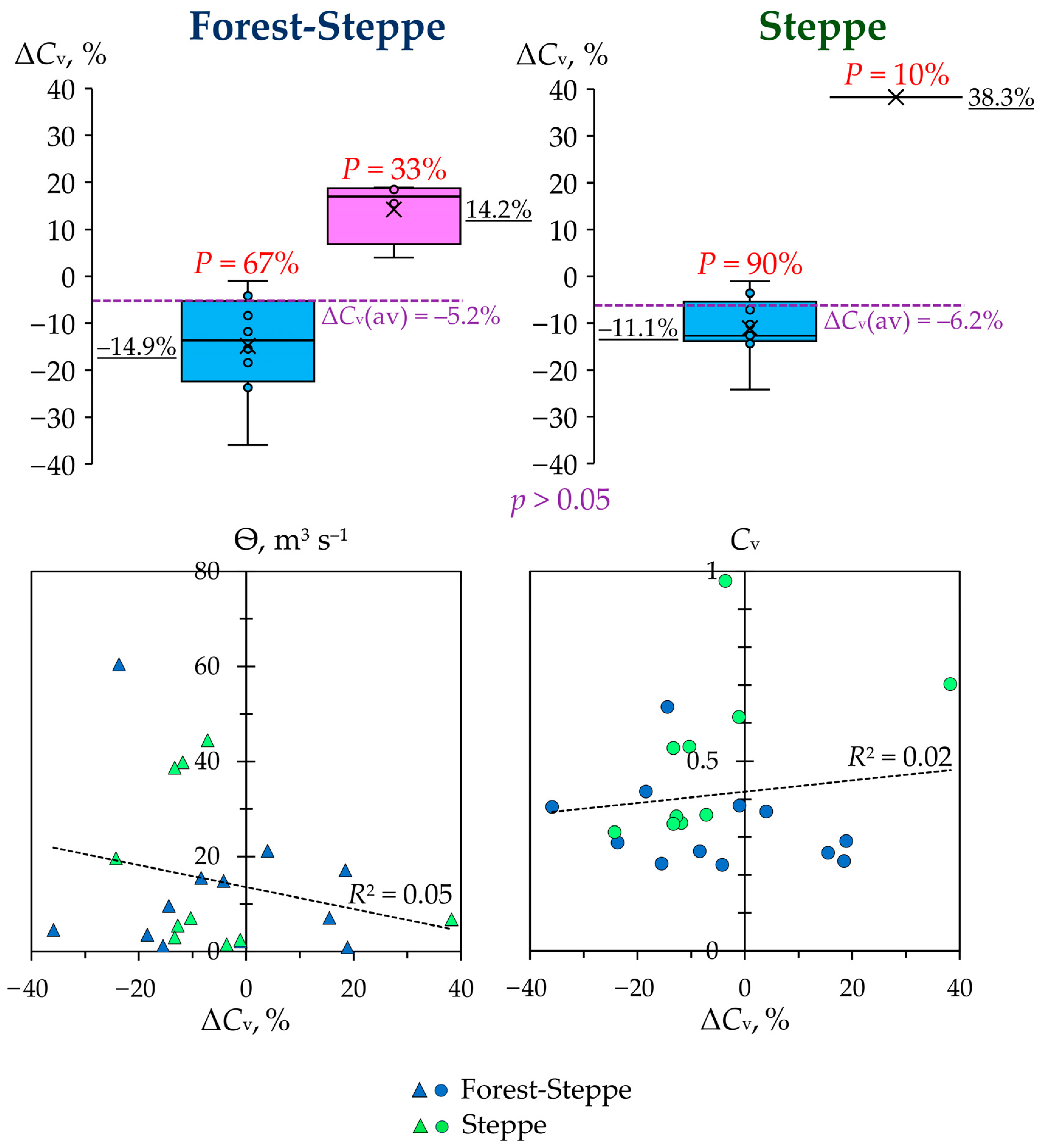
In the study region, a slight decrease (by 5–6%) in the interannual variability of the annual average water flow (Q) was noted between the baseline periods 1961–1990 and 1991–2020. This decrease was reflected in a decline in the ΔC_v coefficient (Figure 15). It is noteworthy that in 33% of the rivers of the forest-steppe zone and 10% (the Ilovlya River) of the steppe zone, an increase in the interannual variability of Q was detected. No statistically significant dependence of the coefficient ΔC_v on the long-term average Q and the long-term average variability of the flow was revealed.

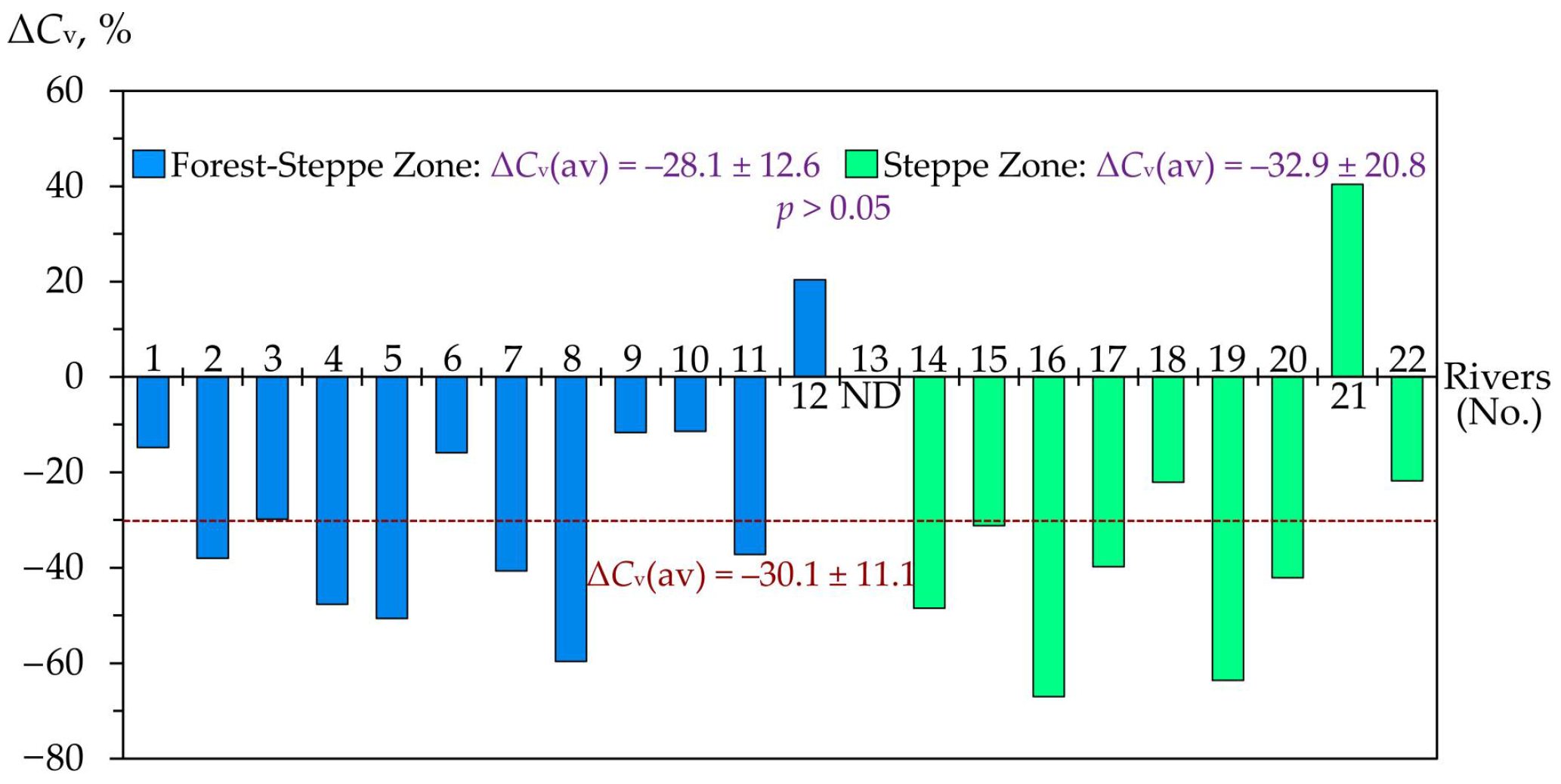
There were also changes in the interannual variability of the annual maximum water flow (Q_max), which differed in the landscape zones considered. In the forest-steppe zone of the east of the East European Plain, the tendency towards decreasing variability of Q_max generally prevailed (67% of the studied rivers, in contrast to 60% in the steppe zone), and the average zonal value of ΔC_v was −12.2%, in contrast to +1.7% in the steppe zone (with statistical significance of the difference in the average values between these zones). No statistically significant dependence of the coefficient ΔC_v on the long-term average values of Q_max and the long-term average variability of Q_max was traced.

The overall decrease in the interannual variability of the cold season minimum water flow (Q_min-CP) between the baseline periods 1961–1990 and 1991–2020 by an average of 26% in the forest-steppe and 21% in the steppe was due to the prevailing tendency to decrease the variability of this flow in 83% and 78% of the rivers in these zones, respectively. No statistically significant difference in the average values of ΔC_v was found between the rivers of the forest-steppe and the steppe. Also, no statistically significant dependence of the ΔC_v coefficient on the long-term average values of Q_min-CP and the long-term average variability of Q_min-CP was revealed.

The greatest changes occurred in the interannual variability of the minimum water flow during the warm period of the year (Q_min-WP). For all the analyzed rivers, the reduction in the coefficient of interannual Q_min-WP variation (C_v) averaged about 30% between 1961–1990 and 1991–2020 (Figure 16). No statistically significant difference in the average values of ΔC_v for Q_min-WP was found between the rivers of the forest-steppe and the steppe.

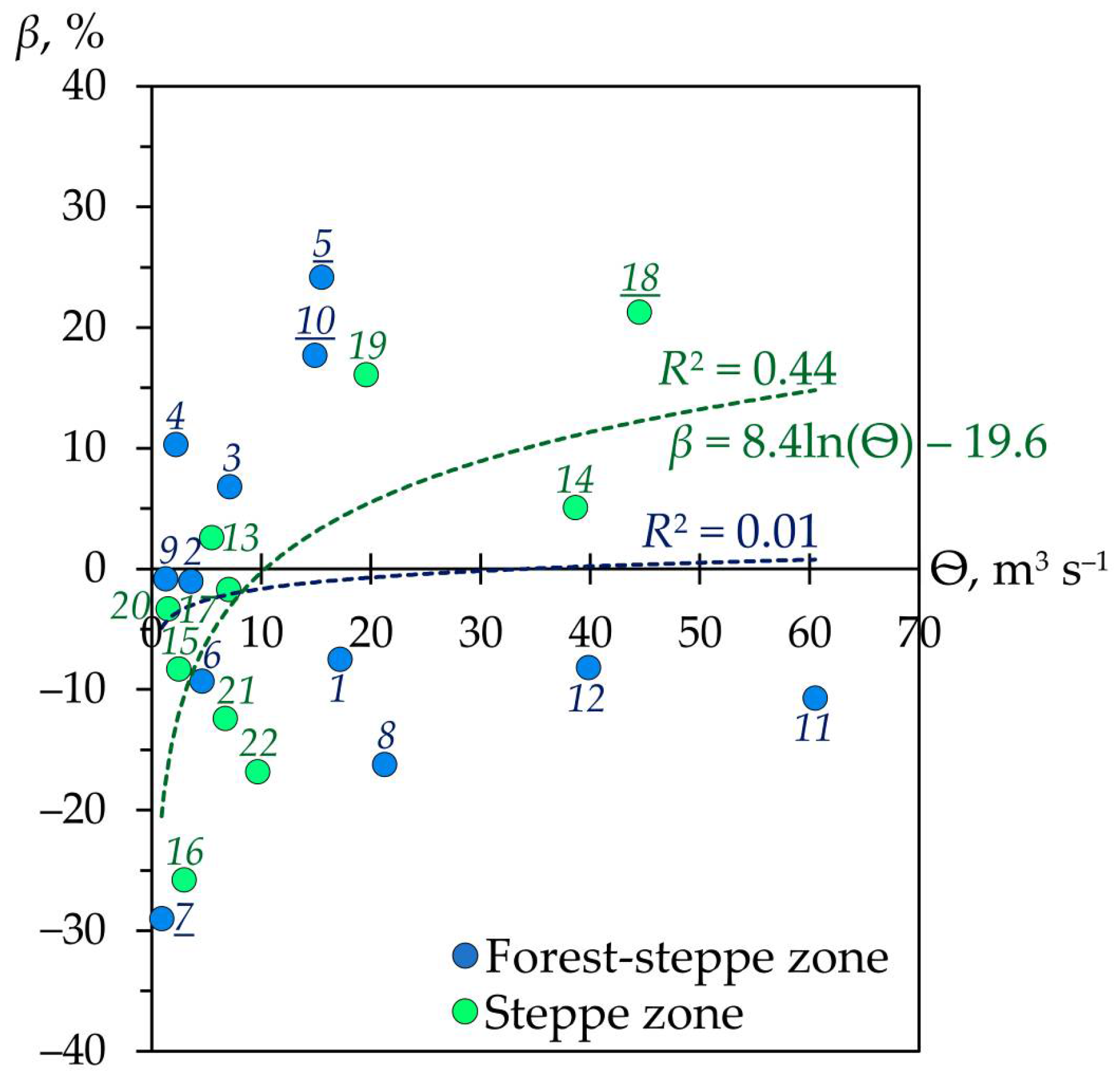
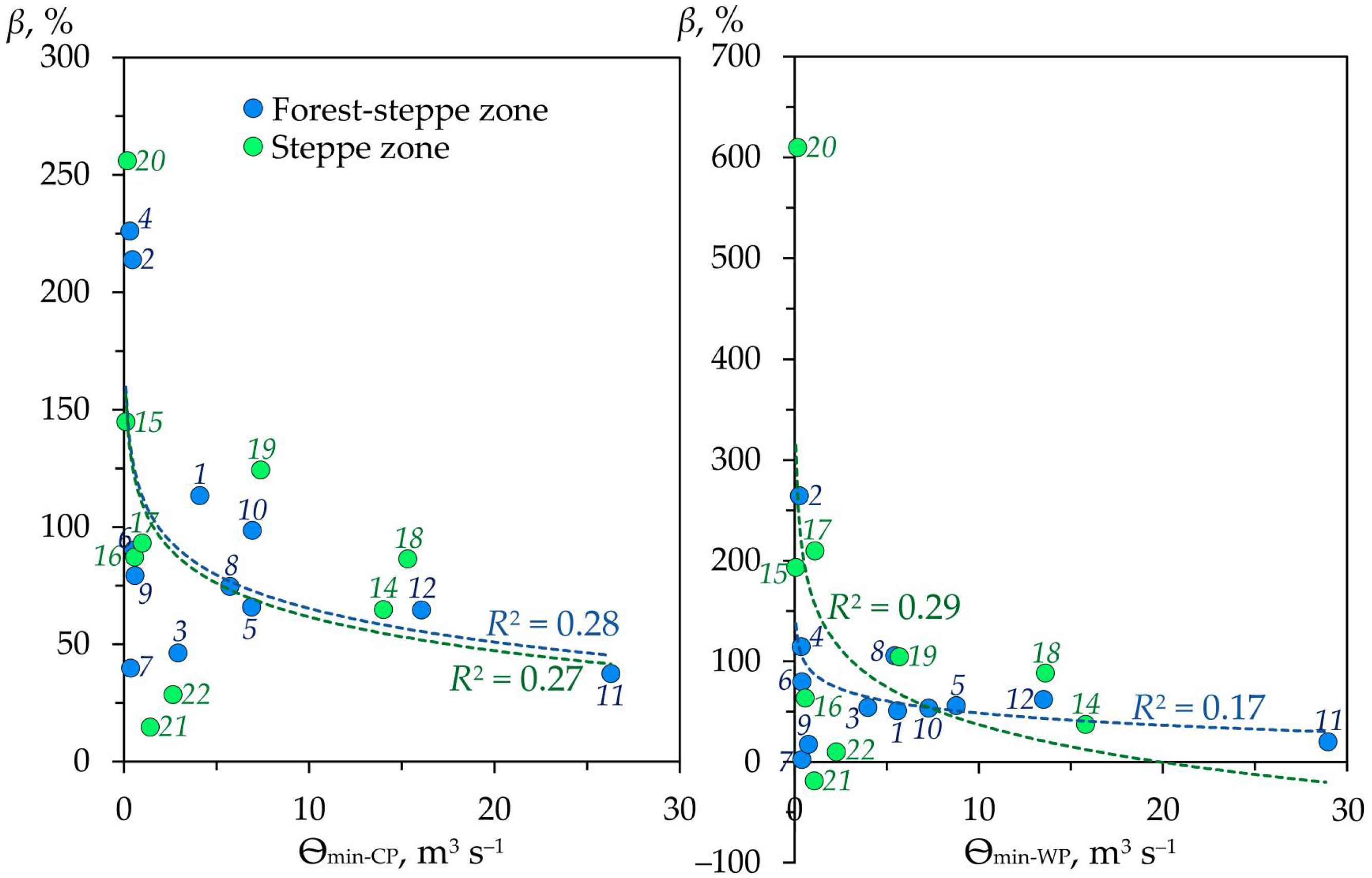
3.5. Water Flow Changes and Some Factors

An analysis of the regional distribution of trends in the change of the annual average water flow (Q) of the analyzed rivers between baseline periods (the coefficient β) revealed some dependence on the absolute elevation of their basins (Figure 17A).

This was especially clear and statistically reliable in the rivers of the steppe zone, as opposed to the forest-steppe zone. Thus, the elevation level of 160 m a.s.l. can be preliminarily called the regional topographic boundary of multidirectional trends in the change of Q (primarily for the steppe rivers) in the period from 1961 to 2020.

As for the annual maximum water flow (Q_max) in the study region, no clear and statistically significant relationships were identified between its changes and changes in the absolute elevations of the analyzed river basins (Figure 17B). However, as in the case of annual water flow, this relationship is manifested somewhat better in steppe river basins than in forest-steppe ones.

It is obvious that the specified dependence (β = f(h, or H)) reflects primarily changes in the flow of water in rivers with different long-term annual average flow volumes (Ѳ). The latter directly depends on the elevation of the river basins in given climatic conditions. In the more full-flowing rivers (with increasing Ѳ), an increase in Q (β) was observed between the baseline periods 1961–1990 and 1991–2020, and vice versa (see Figure A9 in Appendix A). This trend again turned out to be most noticeable and statistically significant in the rivers of the steppe zone.

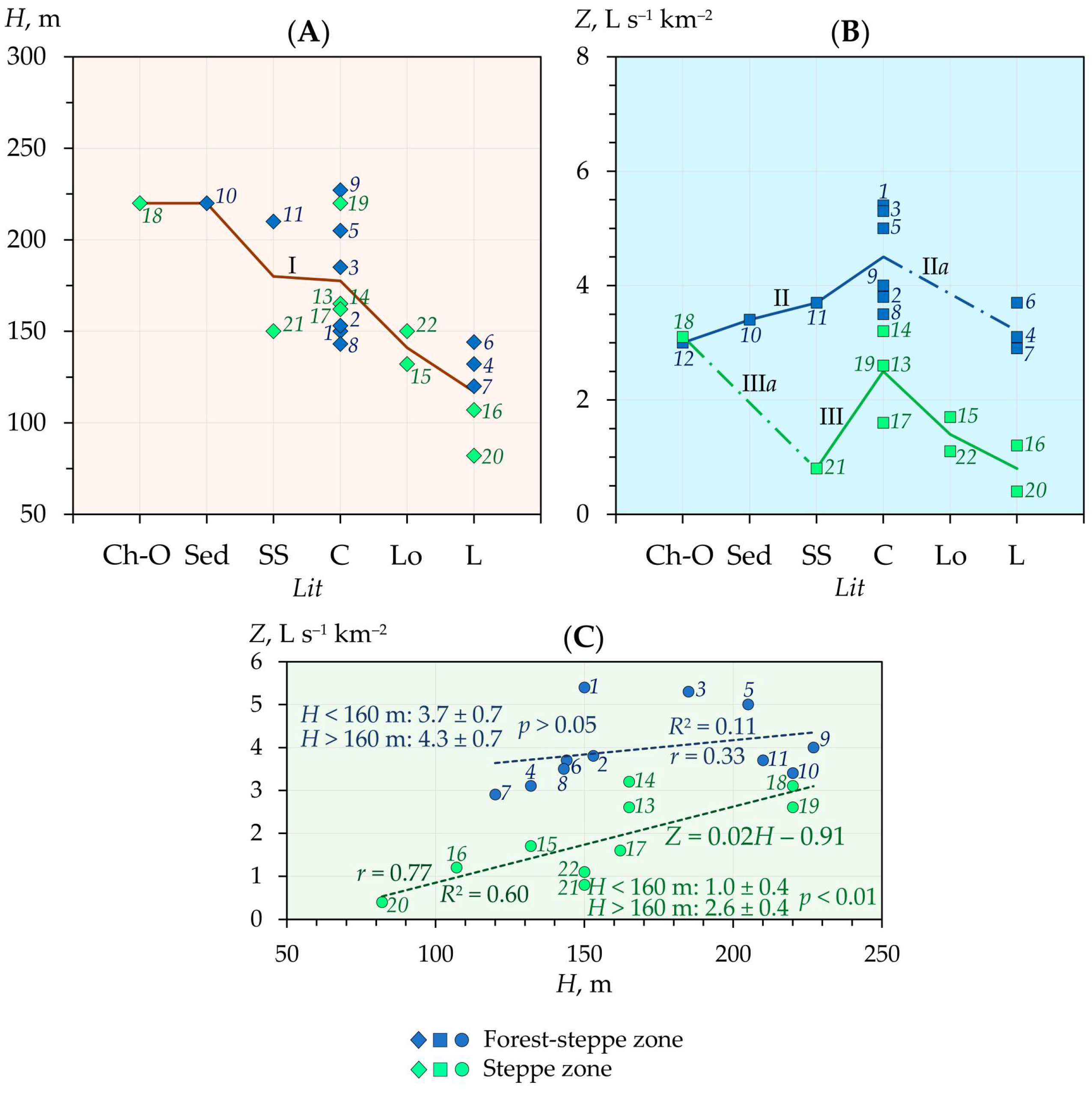
The relationship β = f(Ѳ) is manifested even better if we take into account the factor of the river basin area, that is, through the use of the value of the specific water runoff (Z, L s⁻¹ km⁻²). As can be seen from Figure 18, with an increase in Z, an increase in the coefficient β is traced. This dependence is again most clear and statistically significant for the analyzed rivers of the steppe zone, in contrast to the rivers of the forest-steppe zone.

In this regard, in the steppe zone, the value of Z equal to 2 L s^–1 km^–2 can be preliminarily considered a conditional boundary of changes in the sign of the value of β and, consequently, the direction of the trend in the change in the annual average water flow (Q) of rivers in the study region. When Z > 2 L s^–1 km^–2, the annual water runoff increased, and when Z < 2 L s^–1 km^–2, it decreased between the baseline periods 1961–1990 and 1991–2020.

For minimum water discharges during the cold and warm periods of the year, a relationship between their changes across the baseline climatological periods (β) and their long-term average values (Ѳ_min-CP and Ѳ_min-WP) was revealed (see Figure A10 in Appendix A). This dependence had an inverse logarithmic character. When the values of Ѳ_min-CP and Ѳ_min-WP are less than 8 m³ s^–1, the values of β increase as a whole, but their spread also increases, up to negative values of β (for Ѳ_min-WP). Despite this, neither in the rivers of the forest-steppe nor in the rivers of the steppe zone did the identified logarithmic dependencies have statistical significance.

3.6. Intraregional Changes

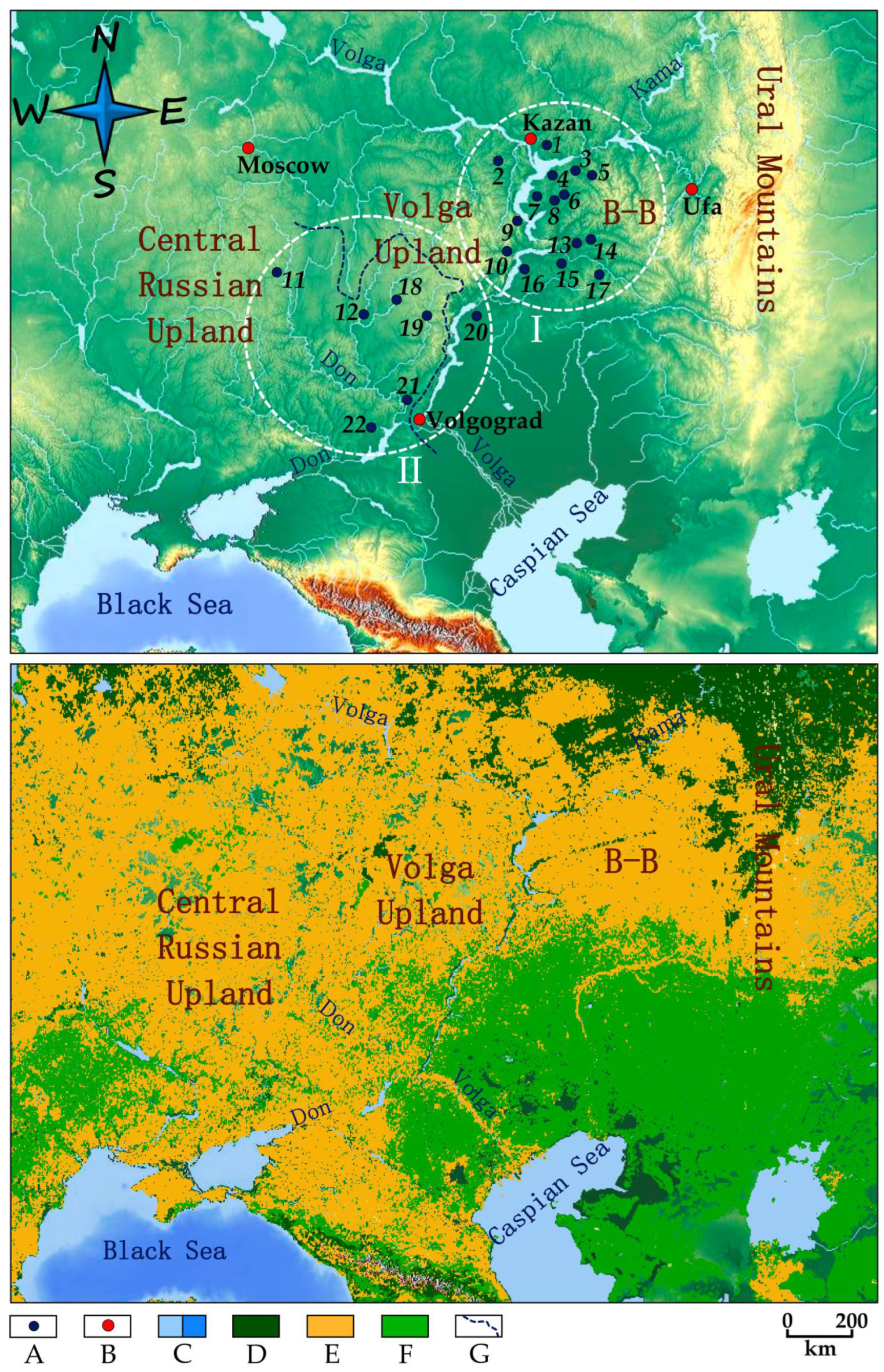
The location of the analyzed rivers in the east of the East European Plain allows them to be grouped into two relatively isolated sectors (subregions): Sector I—the Middle Volga region, and Sector II—the Lower Volga region and part of the Don River basin (see Figure 1). Analysis of changes in the main examined hydrological parameters between the baseline periods 1961–1990 and 1991–2020 (the coefficient β) did not reveal statistically significant differences between these sectors (

Table 4. The average coefficients β computed for the main hydrological parameters in the two analyzed sectors (see Figure 1).

Parameter	Sector I	Sector II	p
Q	−1.8	−2.8	p > 0.05
Qmax	−43.8	−33.0	p > 0.05
Qmin-CP	99.5	94.7	p > 0.05
Qmin-WP	85.2	133.5	p > 0.05

p—the statistical significance of the difference in the average β-values between the sectors.

).

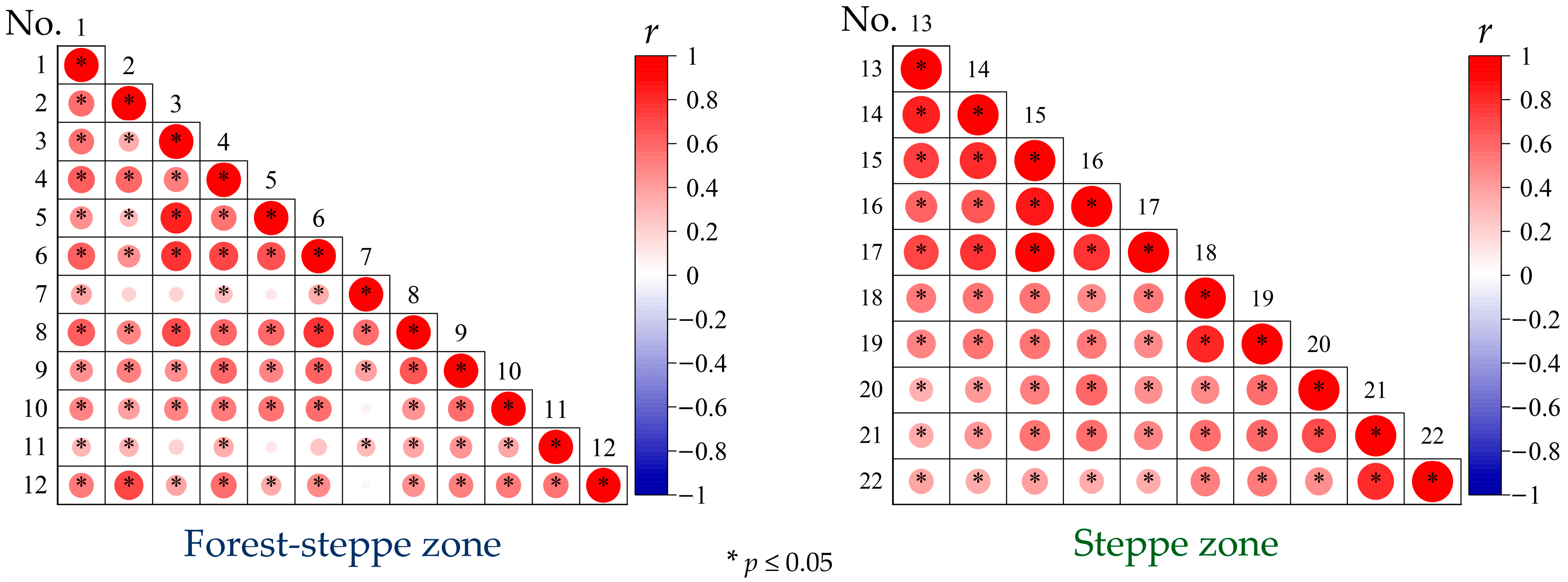
For each sector, a mutual correlation of long-term series of each of the main hydrological parameters was carried out, after which the analyzed rivers were ranked by the value of their average correlation coefficient (r) with the other rivers. The results of this work were grouped into correlation matrices. These matrices make it possible to identify in each sector both the most representative rivers (more precisely, their long-term hydrological series) (

Table 5. Three studied rivers that are the most representative (with the highest values of Spearman’s mutual correlation—r) in terms of the analyzed hydrological parameters in the corresponding sectors of the study region.

Parameter	Sector
	I	II
Q	8 [0.62], 14, 6	18 [0.61], 21, 19
Qmax	8 [0.66], 5, 14	21 [0.69], 18, 19
Qmin-CP	1 [0.70], 4, 8	18 [0.59], 19, 12
Qmin-WP	5 [0.63], 8, 1	19 [0.52], 18, 12

8, 14, 6, … are the numbers of the rivers (see Figure 1 and Table 1). Note-1: The numbers of those rivers that are represented in all four parameters are underlined. Note-2: The highest r for each sector is shown in square brackets.

), and “anomalous” rivers, the flow of water in which, due to a combination of factors, is least correlated with the water flow of the other rivers in the sectors. In the groups of the most representative rivers (the first three rivers in the ranked series for each parameter), one can single out those rivers that cover all the main examined hydrological parameters. An example of an “anomalous” river is the Krasnaya River (No. 7, Sector I), long-term changes in the hydrological parameters Q and Q_min-WP, of which were characterized by an abnormally low (r is equal to 0.28 and 0.05, respectively) similarity with the changes in these parameters of other rivers in this sector. The Ilovlya River (No. 21, Sector II) also turned out to be anomalous in terms of changes in the parameters Q_min-CP and Q_min-WP (r is equal to 0.27 and 0.07, respectively).

No statistically significant differences in the average correlation coefficients (r_av) between the two sectors for each hydrological parameter were found, except for the parameter Q_min-CP. In the latter case, r_av in the Sector I significantly exceeds its value in Sector II.

3.7. Water Flow Change Before 1961

In the representative groups for each main hydrological parameter, one river with the longest series of observations was identified (see Figure 3). This made it possible to trace changes in water flow in the period up to 1961 and their relationship with changes in water flow between the baseline periods of 1961–1990 and 1991–2020. The results of this comparison are presented in

Table 6. Changes in the analyzed hydrological parameters (HPs), averaged over the selected periods, in the most representative (and with the longest observation periods) rivers (see Table 1 and Table 5) of the analyzed sectors of the study region since the 1930s.

HPs	River (No.)	Sector I			Sector II
		Period			Period
		(…–1960)	1961–1990	1991–2020	(…–1960)	1961–1990	1991–2020
Q	Bol’shoy Kinel’ (14)	32.7 (1934–1960)	38.2 (0)	40.1 (0)	—	—	—
	Khopyor (18)	—	—	—	48.5 (1940–1960)	40.4 (0)	49.0 *
Qmax	Sheshma (5)	231.3 (1934–1960)	210.1 (0)	131.2 **	—	—	—
	Khopyor (18)	—	—	—	942.7(1940–1960)	536.6 **	348.1 *
Qmin-CP	Sheshma (5)	2.6 (1935–1960)	5.2 ***	8.6 ***	—	—	—
	Khopyor (18)	—	—	—	6.6 (1940–1960)	10.7 ***	19.9 ***
Qmin-WP	Sheshma (5)	3.1 (1934–1960)	6.8 ***	10.7 ***	—	—	—
	Medveditsa (19)	—	—	—	3.2 (1940–1960)	3.6 (0)	7.4 ***

The statistical significance of the difference in the average values between a given period and the period preceding it: ⁽⁰⁾ p > 0.05, * 0.01 < p < 0.05, ** 0.001 < p < 0.01, *** p < 0.001.

.

As can be seen from Table 6, a statistically significant trend towards growing water flow has been observed since the 1930s for the parameters Q_min-CP and Q_min-WP in Sector I and since the 1940s for the parameter Q_min-CP in Sector II. Sector II also shows a statistically significant inter-period decrement in the annual maximum river water flow since the 1940s. For other parameters, retrospective continuity of trends in water flow changes prior to 1961 was either not maintained or was statistically insignificant.

4. Discussion

4.1. Changes in Spring (Snowmelt-Induced Flood) Water Flow

As shown above, the annual maximum water flow had a decreasing trend in the period from 1961 to 2022 for all analyzed rivers in the study region. This trend was more noticeable and 100% statistically significant in the forest-steppe zone than in the steppe zone. The interzonal difference in the seasonal trend in Q_max was even more noticeable. Although these values only characterize changes in the annual maximum (peak) flow, they also clearly demonstrate the overall “degradation” of the snowmelt-induced flood flow of water in the region’s rivers. We have previously shown this “degradation” using the example of the rivers of the Middle Volga region [5], which spatially coincides with Sector I identified above. There, from 1960–1979 to 2002–2016, the share of snowmelt-induced flood runoff in the annual runoff decreased, on average, from 59% to 39%, and the average intensity of snowmelt-induced flood surface runoff in river basins decreased by an average of 43% between the noted periods [17].

The “degradation” of snowmelt-induced water flow in recent decades has also been observed within stationary runoff plots located in different parts of the study region and beyond [35,36,37]. Thus, according to data from more than 60 years of observations at the Novosilskaya Zonal Agro-Forestry Reclamation Experimental Station, located in the Oryol Oblast, an administrative region in the southwestern part of European Russia, over a 16-year period from 1959 to 1974, meltwater runoff on experimental slope sites was absent only one year, and its maximum value in other years reached 146 mm on fallow land and 186 mm on compacted cropland. Over a 23-year period from 1975 to 1997, there was no runoff for seven years, with maximum values of 40 and 50 mm, respectively; over a 25-year period from 1998 to 2022, there was no runoff for 24 years, with maximum values of 46 and 71 mm, respectively [36]. The absence of snowmelt runoff is associated with weak soil freezing or its absence, as well as with low soil moisture. This, in turn, is associated with the ratio of the timing of the onset of frosts and the formation of snow cover. If the snow cover is formed on thawed or slightly frozen (up to 50 cm) soil, then no snowmelt runoff is formed. If snow falls on deeply frozen (more than 50 cm) and highly moistened (more than 120 mm) soil, then snowmelt runoff is always formed and depends on snow reserves and soil moisture [36]. It was also noted [36] that from the late 1950s to 2016, the greatest decrease in snowmelt runoff was observed on gray forest soils in the forest-steppe (77% on fallow soil and 69% on compacted soil). This may be due to more intense climate warming during the cold season in more northern (“forest-steppe”) latitudes [2,38]. A fairly high percentage (40%) of statistically insignificant descending general trends in the annual maximum water flow in the steppe zone, according to the coefficient β (see Figure 10) (50% for seasonal trends, according to the coefficient K (see Figure 9)), may indicate a weaker winter warming in this zone [38]. Moreover, the large external transformation of the Q_max series in the forest-steppe zone is also indicated by their 100% heterogeneity over the study period compared with 50% heterogeneity in the steppe zone (see Figure 5).

One of the reasons for the current changes in spring flow in river basins is a change in meteorological conditions. This manifested primarily in a rise of air temperature in the near-surface layer of the troposphere during the cold period of the year (from November to March), especially in January–March. The depth of soil freezing in the aeration zone has reduced significantly (for example, in the area of Novosilskaya station by 2 times), and thaws have become more frequent. All this resulted in increased filtration of surface snowmelt runoff into the soil and subsoil and an increment of undersurface runoff [39]. In addition, the thaws that have become more frequent in recent decades could have led to a reduction in water reserves in the snow by the beginning of spring, i.e., before the start of the process of widespread snowmelt in the region. At the same time, the amount of precipitation for the entire cold period in the East European Plain, recorded by regional meteorological stations, has changed less clearly in recent decades [39].

Although climate change may have been the leading cause of the noted changes in snowmelt runoff, we assume that human activity may have also played some (may be an important) role during the last 40 years. This role could be primarily related to the reduction in the area of cropland and the change in crop rotations towards the expansion of perennial crops that followed in the region since the early 1990s due to the political and economic transformations associated with the collapse of the former Soviet Union (see above). According to our calculations [5], the area of cropland in the forest-steppe and steppe zones of the region decreased by approximately 30% between 1970–1987 and 1996–2017. This resulted in a proportional growth in the area of natural perennial meadows [5,7,10]. The latter, as is known, are natural regulators of surface runoff due to the high roughness of their surface, the warming effect of sod on the soil, and so on. This expansion of abandoned cropland area could contribute to the noted increased infiltration of meltwater into underground runoff, thereby also reducing peak snowmelt runoff values in the region’s rivers. The likely role of this factor (the noted reduction in cropland area) is also confirmed by the fact that the average calendar year of the principal critical change in the long-term series (1961–2022) of the parameter Q_max fell precisely on 1990/1991, the last two years of the existence of the former Soviet Union (see Table 3). This issue (hypothesis) requires further detailed study.

The detected trends fit well into the overall context of changes in snowmelt flood runoff in recent decades not only in the southern and western parts of the East European Plain [14,15,16,17,39,40,41], but also further west, in Central Europe (in most of Poland, in Lithuania, Latvia, and Estonia) [15,20], as well as in most of Fennoscandia, especially in Finland [15]. The prevailing trend of reducing snowmelt flood runoff was also noted further east, in the predominantly semi-humid and semi-arid Ural River basin (the border basin of Russia and Kazakhstan) [42], and in the steppe and semi-desert regions of northern Kazakhstan [43].

4.2. Changes in Cold Season Water Flow

The annual minimum flow of rivers in the study region is observed (especially earlier, in past decades) during the winter low water period, when the rivers are fed practically by groundwater. As shown above, the minimum cold season water flow (Q_min-CP) tended to increase in the period from 1961 to 2022 for all analyzed rivers in the study region. This trend was approximately equally noticeable in both the forest-steppe zone and the steppe zone without a statistically significant difference between them: from 1961–1990 to 1991–2020, Q_min-CP increased by an average of 96–100% with 100% statistical significance of these changes in all rivers (see Figure 12). In these zones, almost all long-term Q_min-CP-series were heterogeneous and with significant non-stationarity, again except for the steppe Ilovlya River, flowing in the extreme south of the region under study (see Figure 5 and Figure 6). It is noteworthy that a somewhat greater increment in Q_min-CP was noted in rivers with lower long-term annual average water flow.

The average years of the break (disturbance of homogeneity) of the Q_min-CP series in the region were 1988/1989. Taking into account the generally observed synchronicity of Q_min-CP fluctuations, we are dealing with a non-uniform response of river basins to changes in runoff-forming characteristics [44], as indicated by a fairly large spread of the years (on average, 4–6 years) of the break in homogeneity for each river (see Table 3).

As in the case of spring maximum water flow, the variability of winter minimum water flow reflects well the variability of winter low-water flow as a whole. The significant growth in the flow of rivers in European Russia in winter (some increase in winter runoff also occurred in the adjacent steppe and semi-desert regions of the Ural River basin and northern Kazakhstan [42,43]), characteristic of recent decades, was primarily due to climate change. As is known, the main feature of contemporary climate change is a rise in air temperature. The intensity of this rise is not the same throughout the year. In Russia, this phenomenon is most noticeable in the cold period of the year [2]. An assessment of the intensity of the increase in average air temperature during the cold period [38] showed that the most intense increment of the temperature was traced in the west of the Volga River basin and in its central part, while in the direction to the southeast, the intensity of winter warming decreases. The principal consequences of the increment of winter air temperatures were:

(1) A rise in the proportion of precipitation falling in liquid form (rainfall). According to [45], for the entire Don River basin, for example, a rise in the amount of liquid (rainfall) and solid (snowfall) precipitation of the cold period was noted with a linear trend coefficient of 15–20 mm/10 years on average. In the north of the study region (most of the Middle Volga region and the north of the Lower Volga region), the prevailing trend was towards increasing precipitation in January during 1966–2018 with an intensity of 1–9 mm/10 years, growing to the north (in the south of the forest zone) to 10–20 mm/10 years and even higher [38]. It is important to note that autumn precipitation plays a major role in the formation of groundwater, which is the main source of water for rivers during the winter low-water period. Earlier, Boglov with colleagues [46,47] analyzed changes in precipitation amounts during the autumn months (September–November) for the period from 1966 to 2010. The linear trend coefficient of this characteristic in the overwhelming majority of cases turned out to be statistically insignificant. However, in most of the Volga River basin, it was still negative and did not exceed 6 mm/10 years, while at other meteorological stations, it had small positive values. Thus, the change in precipitation was highly unlikely to be the cause of the observed increase in winter low-water runoff in the Volga River basin.

(2) An increase in the number and intensity of thaws. The increasing number of thaws was due to the increase in the average air temperature, the growth of the sum of negative and positive air temperatures during the cold period, which determined the conditions for their transition through 0 °C [18].

(3) An increase in groundwater reserves during long thaws. In the current situation, favorable conditions have developed for infiltration feeding of groundwater and an increase in its reserves in various underground horizons. As a result, there has been a tendency towards an increase in the groundwater level and, accordingly, its reserves, as well as a tendency towards a rise in the share of underground (base) flow in the feeding of rivers. This concerns primarily medium-sized rivers draining the main water horizons [48].

(4) Increased surface runoff into the river due to snow melting.

The indicated increase in the annual minimum winter water flow in particular and winter low-water flow in general in the last decades could have been influenced by human activity. On the one hand, this could be achieved indirectly, through the above-mentioned reduction in the area of cropland in the region and, accordingly, the expansion in their place of natural sod-grass associations, which better filter snowmelt surface water into underground runoff. On the other hand, the noted increase in the base winter flow could have been influenced by a decrease in water consumption observed in the region during the 1990s and 2000s in the conditions of a deep economic crisis and post-crisis associated with the collapse of the former Soviet Union. This issue also requires further study.

4.3. Changes in Warm Season Water Flow

The period under consideration (1961–2022; in the rivers of Cluster I, this trend may even date back to the 1930s) was characterized in the region by an almost universal growth in the minimum water flow (Q_min-WP) during the warm season of the year: by 100% in the forest-steppe, and by almost 80% in the steppe. Despite this, the statistical significance of linear trends, according to the coefficient K, in the forest-steppe zone was relatively low (45% in general trends and 75% in seasonal trends), compared with the steppe zone (78% and 83%, respectively) (see Figure 10). More statistically significant were the changes in Q_min-WP between 1961–1990 and 1991–2020. As shown earlier, no statistically significant differences were found between the average growth rates of Q_min-WP (the coefficient β) between the forest-steppe and steppe zones. The average years of homogeneity break in the Q_min-WP series occurred in 1987 in the forest-steppe and in 1990 in the steppe.

The main reason for the disturbance of homogeneity in the long-term Q_min-WP series on average since the end of the 1980s has also been climate change in the region. Firstly, this is the noted rise in air temperatures during the cold season of the year, which led to the replenishment of groundwater reserves due to increased filtration of snowmelt water, as described above. In turn, this annually resulted in a gradual discharge of these “excess” groundwaters into the river network and a proportional increase in the base flow of the rivers after the passage of the “wave” of flood runoff caused by the spring melting of snow. Secondly, this could be partly due to increased warm-season precipitation in recent decades, which has caused an augmentation in both baseflow and rainfall-induced flood discharges in rivers. In fairness, it should be noted that the variability of warm period precipitation in the region was quite heterogeneous both territorially and by month. According to [38], in the northern half of the region under consideration, in the period 1966–2018, a growth in monthly precipitation was observed in late spring (May) and early summer (June), while in July a slight decline prevailed (up to 4 mm/10 years, and in some places even more).

Human activities (reduction of cropland areas, changes in crop rotation structure, reduction of technical load (tractors, combines, etc.) [5,7,10]) on agricultural soils, possible reduction of water consumption in crisis and post-crisis years (1990–2000s), as in the case of Q_min-CP, could contribute to increasing trends in Q_min-WP (and the basic water flow in general) in the region’s rivers. This issue also requires a separate detailed study.

4.4. Changes in Annual Water Flow

Our analysis showed that statistical stationarity prevailed in the annual average water flow (Q) in the region during 1961–2022 in the overwhelming majority of cases. In 60% of rivers in the forest-steppe zone and 100% in the steppe zone. During the same period, in 3/4 of cases for general trends (and in 2/3 of cases for seasonal trends) in the forest-steppe zone and in 80% of cases for general trends (and in 70% of cases for seasonal trends) in the steppe zone, a decreasing linear trend prevailed. However, it was statistically significant only in 17% (25%) and 20% (0%) of cases, respectively (see Figure 7). Also, no statistically significant changes in the long-term average annual water flow were found between 1961–1990 and 1991–2020, although a reduction in the β coefficient was observed in the analyzed rivers in more than 60% of cases. However, even in this case, these changes were statistically insignificant for 75% of the rivers in the forest-steppe zone and 90% of the rivers in the steppe zone. It is noteworthy that the rivers with growing annual runoff in most cases corresponded to the basins with relatively the highest average absolute elevations and relatively the highest specific water runoff in them. On the contrary, the rivers with decreasing annual runoff corresponded predominantly to lower topographic areas in the plain, where a lower long-term average specific water runoff is traced. This was especially clearly and statistically reliably demonstrated in the rivers of the steppe zone with its semiarid-semihumid climate. However, it is not worth drawing far-reaching conclusions from this pattern, since it is based on the obtained data on the values of β, which are mostly statistically insignificant, as well as a relatively small sample. No statistically significant dependence of the change in the coefficient β of Q on the change in the area of river basins was revealed.

In the forest-steppe zone, only 1/3 of all analyzed rivers had homogeneous series for Q in the period 1961–2022; in the remaining rivers, a very large spread of critical years of homogeneous disturbance (mutation years) of the Q series was noted (see Table 3), the average value of which fell to 1998. In contrast to the forest-steppe zone, all analyzed rivers of the steppe zone had homogeneous Q series without any statistically significant critical changes in these series. Along with (and because of) the absence of statistically significant linear trends in most of the analyzed rivers, no obvious changes in the interannual variability of their annual water flow were found. Between the periods 1961–1990 and 1991–2022, this variability (the coefficient C_v) reduced on average by only 5.2–6.2% for all the rivers analyzed, and in most cases, especially in the steppe zone, trends towards decreasing the variability of the flow prevailed.

5. Conclusions

Based on the results of this study, the following main conclusions can be formulated:

(1)

In the context of progressive climate change in the European territory of Russia, our analysis did not reveal statistically significant changes in the total annual water flow in most small and medium-sized rivers of the forest-steppe and, especially, steppe zones of the region under consideration for the period 1961–2022. Nevertheless, for most of the analyzed rivers, it is possible to state a general background of a decrease in the average annual water flow and some reduction in the interannual variability of its indicators.

(2)

Against the background of statistically unexpressed in most cases trend variability of annual water flow, its internal structure underwent significant changes during the study period. This primarily affected the intra-annual variability of the flow. Thus, the ratio between the annual maximum flow (peak discharge of the snowmelt-induced flood) and the minimum flow of the cold (warm) period of the year reduced between the baseline periods 1961–1990 and 1991–2020, respectively, by an average of 4.1 (4.0) times in the rivers of the forest-steppe zone and by an average of 5.2 (5.3) times in the rivers of the steppe zone. All of these interperiod changes, except for one steppe river of Sector II of the study region, turned out to be statistically significant. The identified changes in critical (maximum and minimum) values of water flow result in a noticeable leveling of its intra-annual hydrograph.

(3)

With varying intensity of manifestation, the detected trends were widespread not only in the southern half of European Russia, but also in neighboring countries of Eastern, Central, and Northern Europe, as well as in northern Kazakhstan.