Machine Learning Approaches for Simulating Temporal Changes in Bed Profiles Around Cylindrical Bridge Pier: A Comparative Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Analysis
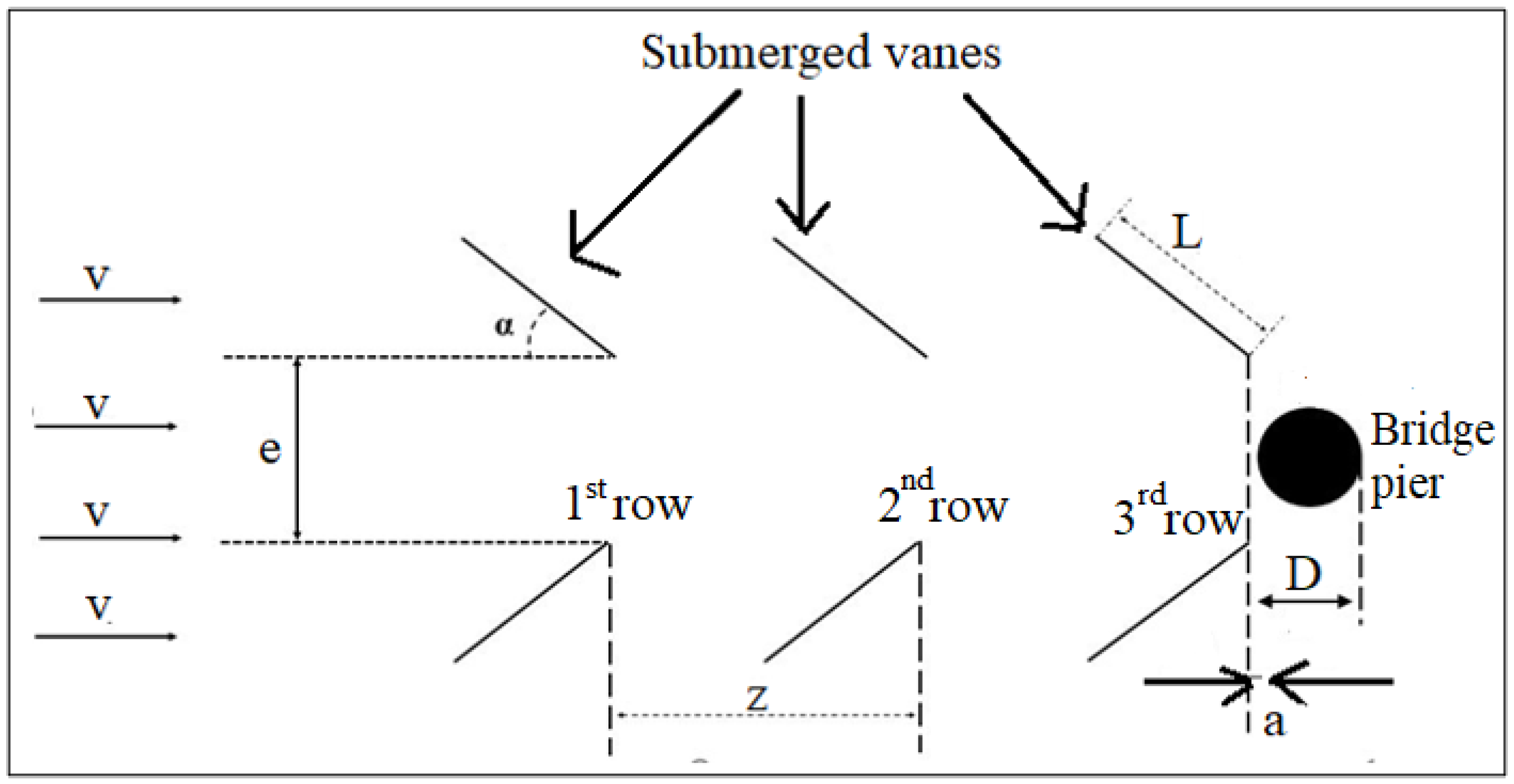
2.2. Non-Dimensional Analysis and Mathematical Formulation
2.3. Limitations and Scope
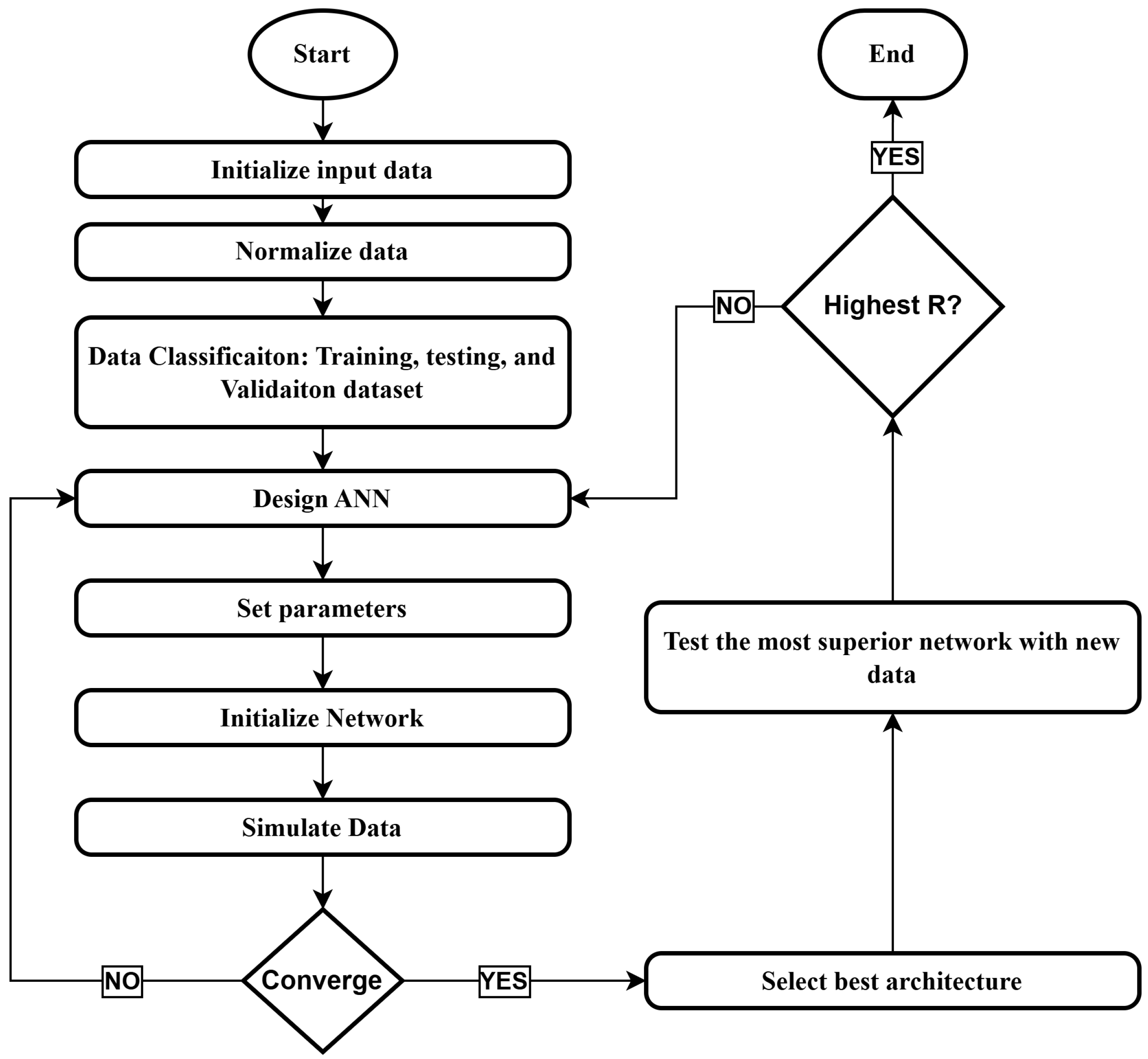
3. Model Configurations and Training Protocol
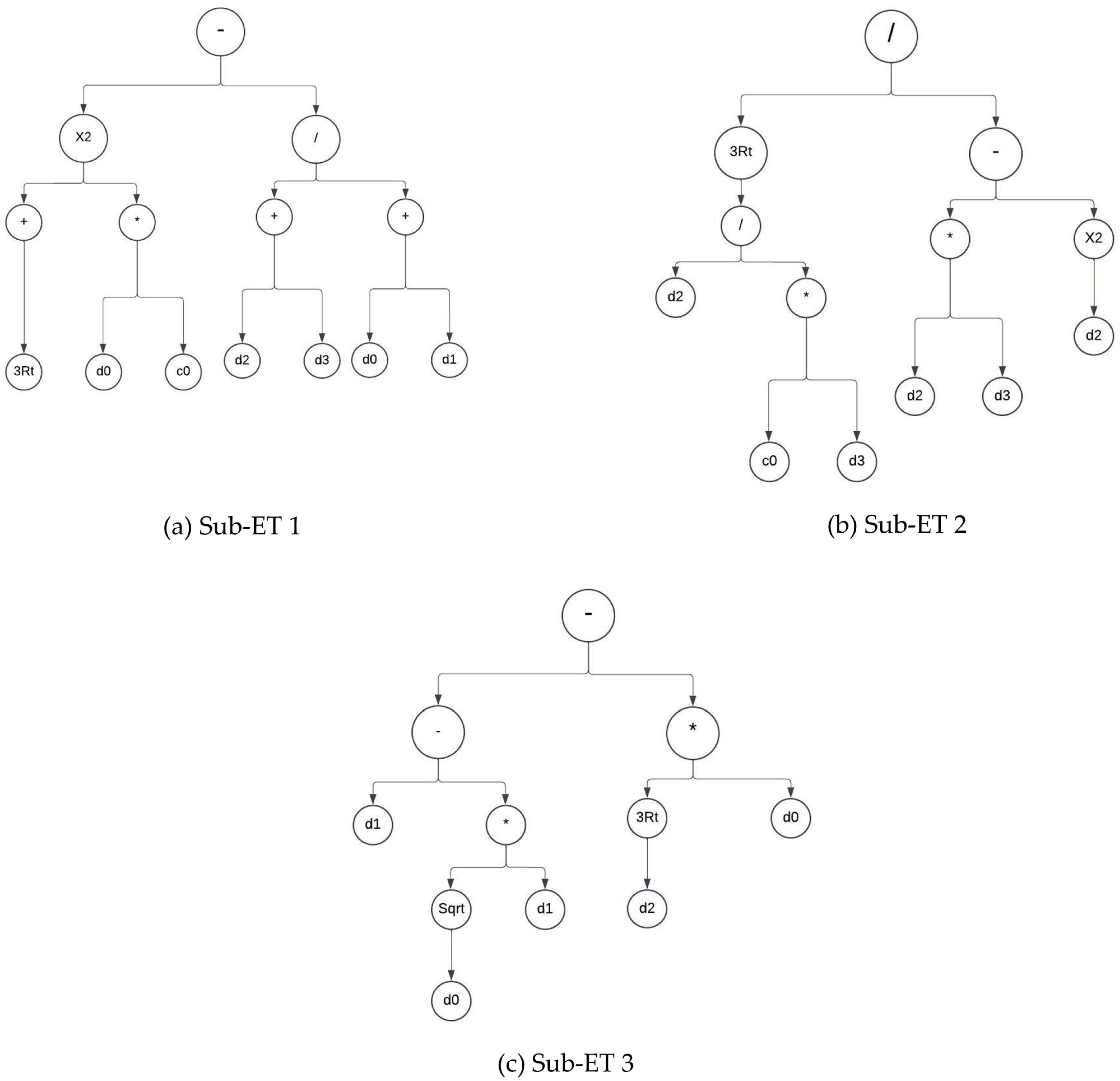
3.1. GEP Configuration
- Configuratio2 (problem-specific).
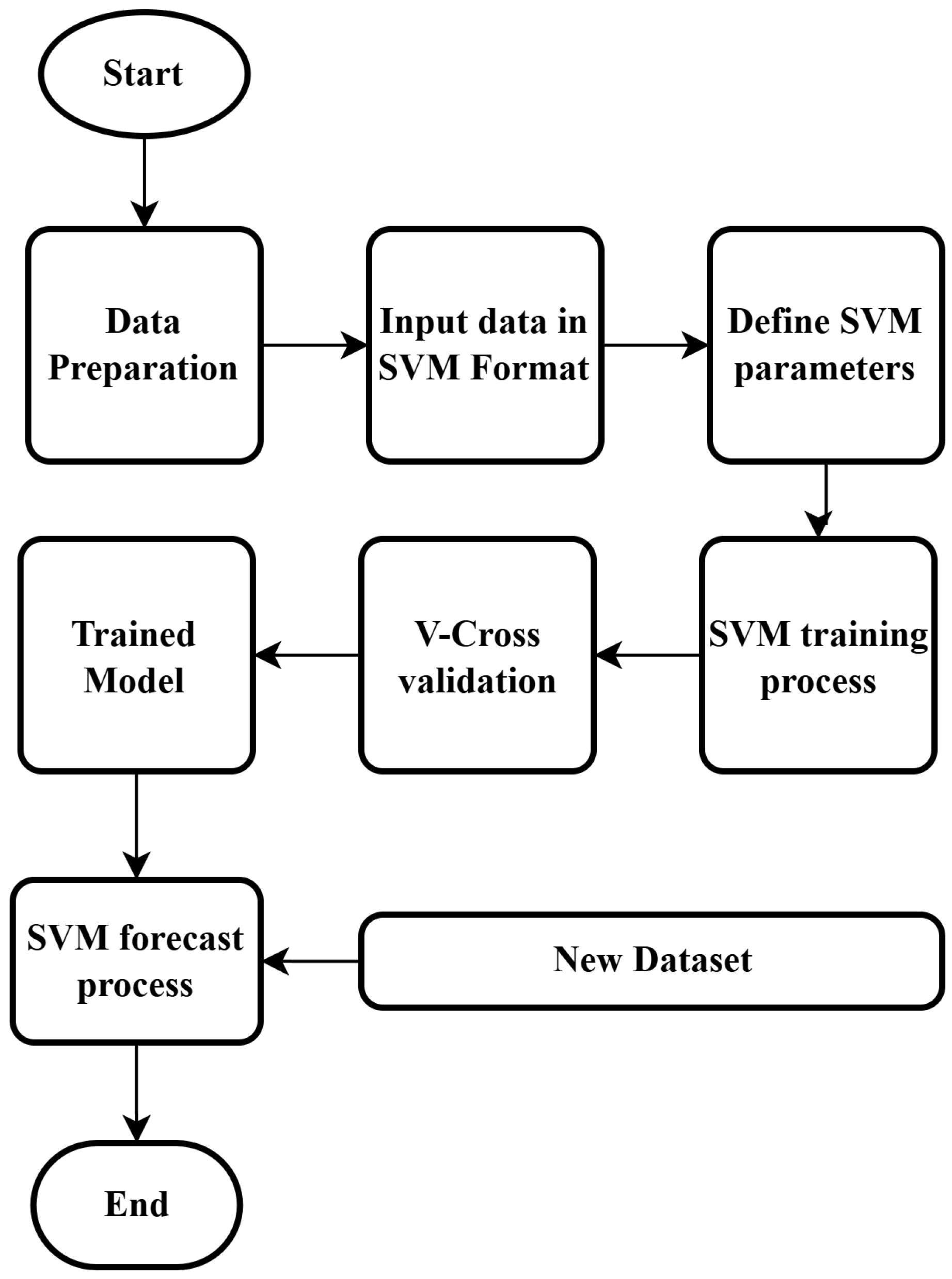
3.2. SVR Configuration
- Configuration (problem-specific).
- Notes on kernels (for context).
3.3. ANN Configuration
- Configuration (problem-specific).
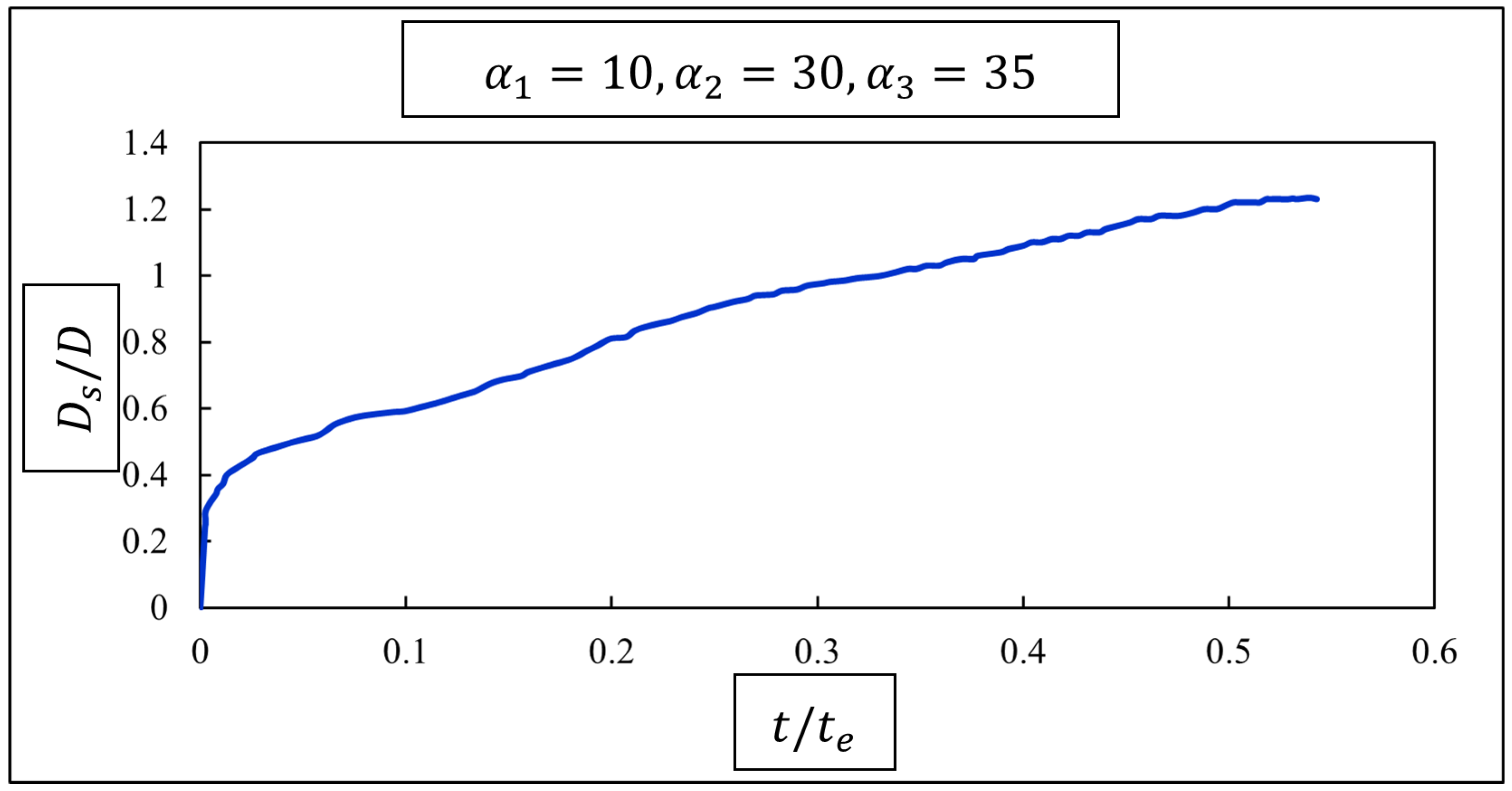
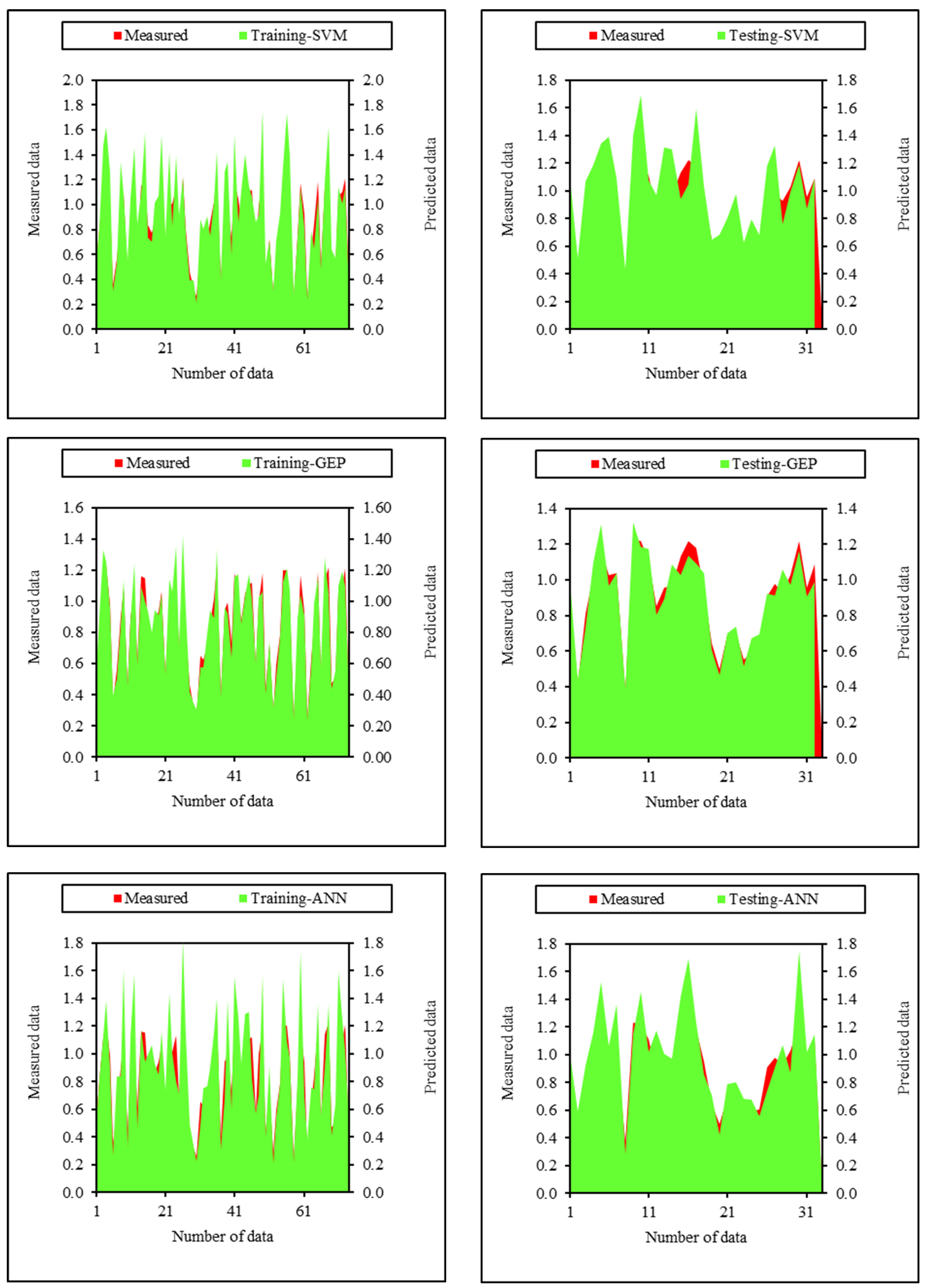
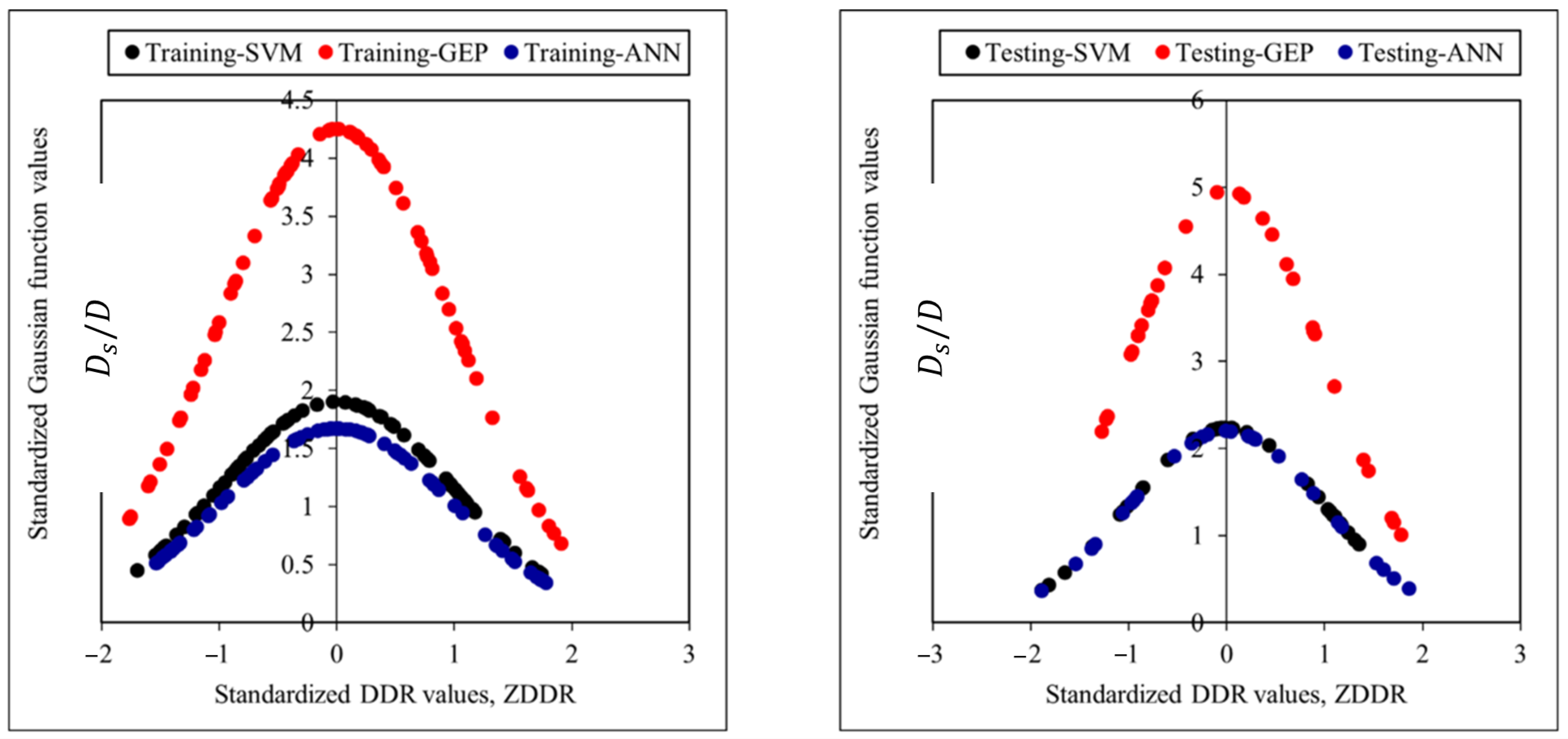
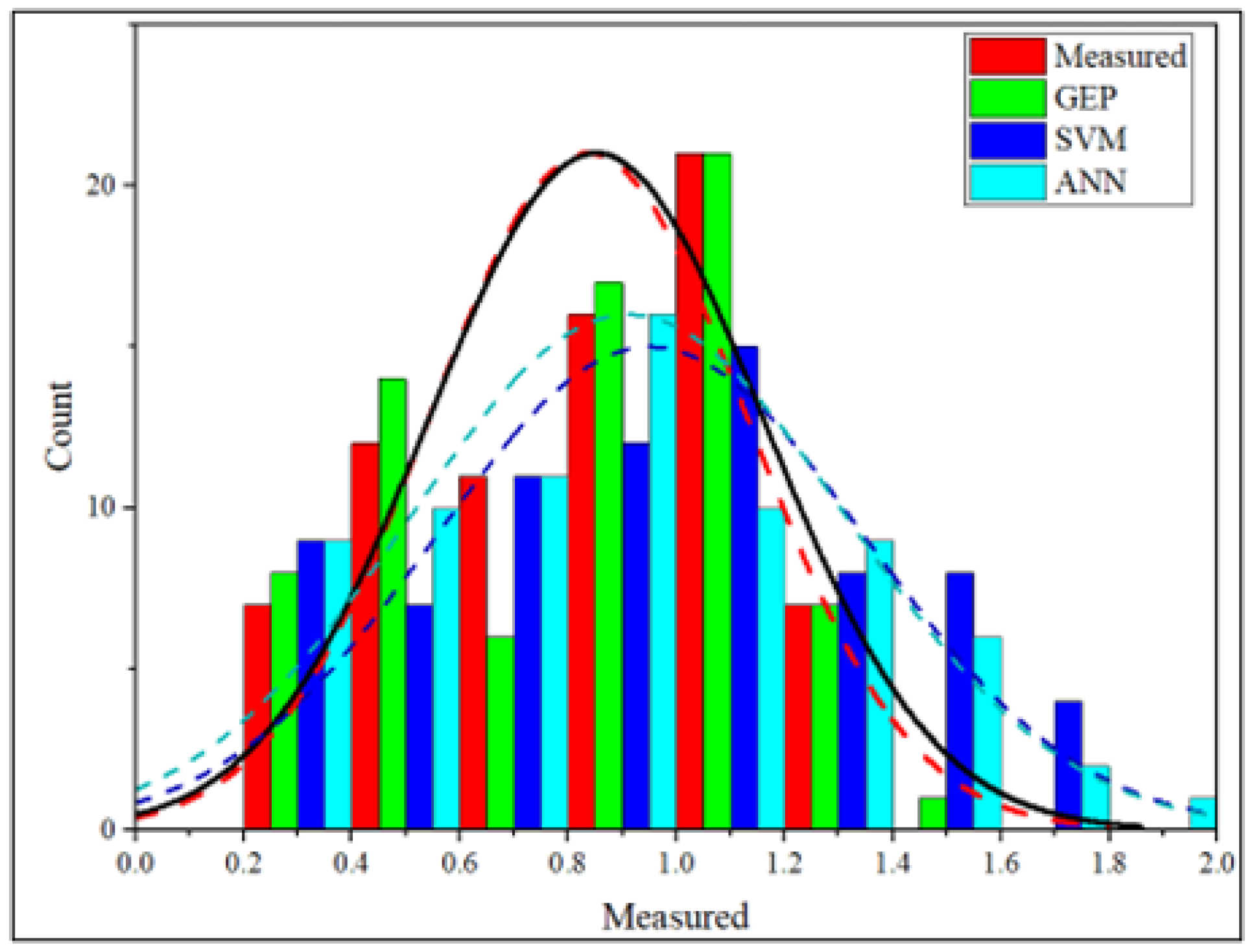
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raudkivi, A.J. Functional trends of scour at bridge piers. J. Hydraul. Eng. 1986, 112, 1–13. [Google Scholar] [CrossRef]
- Ettema, R.; Nakato, T.; Muste, M.V.I. An Illustrated Guide for Monitoring and Protecting Bridge Waterways Against Scour; Technical report; Iowa Highway Research Board Project TR-515; IIHR-Hydroscience & Engineering, University of Iowa: Iowa City, IA, USA, 2006. [Google Scholar]
- Chiew, Y.M. Scour Protection at Bridge Piers. J. Hydraul. Eng. 1992, 118, 1260–1269. [Google Scholar] [CrossRef]
- Ettema, R.; Constantinescu, G.; Melville, B.W. Flow-Field Complexity and Design Estimation of Pier-Scour Depth: Sixty Years Since Laursen and Toch. J. Hydraul. Eng. 2017, 143, 03117006. [Google Scholar] [CrossRef]
- Zarrati, A.R.; Gholami, H.; Mashahi, M.B. Application of collar to control scouring around rectangular bridge piers. J. Hydraul. Res. 2004, 42, 97–103. [Google Scholar] [CrossRef]
- Hamidi, M.; Sadeqlu, M.; Khalili, A.M. Investigating the design and arrangement of dual submerged vanes as mitigation countermeasure of bridge pier scour depth using a numerical approach. Ocean Eng. 2024, 299, 117270. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Kennedy, J.F. River-bend bank protection by submerged vanes. J. Hydraul. Eng. 1983, 109, 1161–1173. [Google Scholar]
- Ebrahimi, T.; Hamidi, M.; Rahmani Firoozjaiee, A.; Khavasi, E. Numerical investigation of scour around a cylindrical pier in laboratory scale using Euler-Lagrange approach. Amirkabir J. Mech. Eng. 2021, 53, 411–426. [Google Scholar]
- Omara, H.; Ookawara, S.; Nassar, K.A.; Masria, A.; Tawfik, A. Assessing local scour at rectangular bridge piers. Ocean Eng. 2022, 266, 112912. [Google Scholar] [CrossRef]
- Mashahir, M.; Zarrati, A.R.; Tabarestani, M.K. Evaluation of collar efficiency to prevent scouring around cylindrical bridge piers under live bed condition. J. Hydro-Environ. Res. 2024, 52, 17–25. [Google Scholar] [CrossRef]
- Mowla, Q.A.E.; Ahmari, H. Experimental Study of Flow Characteristics and Geometry of Scour Hole around Cylindrical Piers Subject to Wave and Current. J. Waterw. Port Coast. Ocean Eng. 2024, 150, 04023020. [Google Scholar] [CrossRef]
- Javidi Vahdati, V.; Ahmadi, A.; Abedini, A.; Heidarpour, M. Efficacy of the Combined Use of Bed Sill and Sacrificial Piles to Control Local Scour Around Circular Bridge Piers. Shock Vib. 2024, 2024, 5527946. [Google Scholar] [CrossRef]
- Qi, H.; Yuan, T.; Zhao, F.; Chen, G.; Tian, W.; Li, J. Local Scour Reduction around Cylindrical Piers Using Permeable Collars in Clear Water. Water 2023, 15, 897. [Google Scholar] [CrossRef]
- Salemi, F.; Ghomeshi, M.; Bahrami Yarahmadi, M. Experimental Study of Transverse Waves Effects by Obstacles on Local Scour Around Cylindrical Pier Groups of Bridge. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 2409–2421. [Google Scholar] [CrossRef]
- Farooq, R.; Azimi, A.H.; Tariq, M.A.U.R.; Ahmed, A. Effects of hooked-collar on the local scour around a lenticular bridge pier. Int. J. Sediment Res. 2023, 38, 1–11. [Google Scholar] [CrossRef]
- Valela, C.; Rennie, C.D.; Nistor, I. Improved bridge pier collar for reducing scour. Int. J. Sediment Res. 2022, 37, 37–46. [Google Scholar] [CrossRef]
- Aly, A.M.; Dougherty, E. Bridge pier geometry effects on local scour potential: A comparative study. Ocean Eng. 2021, 234, 109326. [Google Scholar] [CrossRef]
- Raeisi, N.; Ghomeshi, M. Effect of bridge pier diameter on maximum depth of scour impacts on the environment. SN Appl. Sci. 2020, 2, 1974. [Google Scholar] [CrossRef]
- Tipireddy, R.T.; Barkdoll, B.D. Scour reduction by air injection at a cylindrical bridge pier: Experimental determination of optimal configuration. J. Hydraul. Eng. 2019, 145, 06018016. [Google Scholar] [CrossRef]
- Jahangirzadeh, A.; Basser, H.; Akib, S.; Karami, H.; Naji, S.; Shamshirband, S. Experimental and numerical investigation of the effect of different shapes of collars on the reduction of scour around a single bridge pier. PLoS ONE 2014, 9, e98592. [Google Scholar] [CrossRef]
- EL-Ghorab, E.A. Reduction of scour around bridge piers using a modified method for vortex reduction. Alex. Eng. J. 2013, 52, 467–478. [Google Scholar] [CrossRef]
- Zarrati, A.R.; Chamani, M.R.; Shafaie, A.; Latifi, M. Scour countermeasures for cylindrical piers using riprap and combination of collar and riprap. Int. J. Sediment Res. 2010, 25, 313–322. [Google Scholar] [CrossRef]
- Zarrati, A.R.; Nazariha, M.; Mashahir, M.B. Reduction of local scour in the vicinity of bridge pier groups using collars and riprap. J. Hydraul. Eng. 2006, 132, 154–162. [Google Scholar] [CrossRef]
- Chiew, Y.M. Local scour and riprap stability at bridge piers in a degrading channel. J. Hydraul. Eng. 2004, 130, 218–226. [Google Scholar] [CrossRef]
- Rathod, P.; Manekar, V.L. Comprehensive approach for scour modelling using artificial intelligence. Mar. Georesour. Geotechnol. 2023, 41, 312–326. [Google Scholar] [CrossRef]
- Le, X.H. Predicting maximum scour depth at sluice outlet: A comparative study of machine learning models and empirical equations. Environ. Res. Commun. 2024, 6, 015010. [Google Scholar] [CrossRef]
- Nandi, B.; Patel, G.; Das, S. Prediction of maximum scour depth at clear water conditions: Multivariate and robust comparative analysis between empirical equations and machine learning approaches using extensive reference metadata. J. Environ. Manag. 2024, 354, 120349. [Google Scholar] [CrossRef]
- Adib, A.; Tabatabaee, S.H.; Khademalrasoul, A.; Shoushtari, M.M. Recognizing of the best different artificial intelligence method for determination of local scour depth around group piers in equilibrium time. Arab. J. Geosci. 2020, 13, 1004. [Google Scholar] [CrossRef]
- Kumar, S.; Goyal, M.K.; Deshpande, V.; Agarwal, M. Estimation of time dependent scour depth around circular bridge piers: Application of ensemble machine learning methods. Ocean Eng. 2023, 270, 113611. [Google Scholar] [CrossRef]
- Roshni, T. Application of GEP, M5-TREE, ANFIS, and MARS for Predicting Scour Depth in Live Bed Conditions Around Bridge Piers. J. Soft Comput. Civ. Eng. 2023, 7, 24–49. [Google Scholar]
- Fujail, A.K.M. Hybrid Artificial Neural Network Model for Prediction of Scour Depth Upstream of Bridge Piers. In Soft Computing: Theories and Applications: Proceedings of SoCTA 2022; Springer Nature: Singapore, 2022; pp. 741–746. [Google Scholar]
- Kumar, L.; Afzal, M.S. Estimating pier scour depth under combined waves and current using boosting machine-learning models. Acta Geophys. 2024, 72, 1895–1911. [Google Scholar] [CrossRef]
- Choudhary, A.; Das, B.S.; Devi, K.; Khuntia, J.R. ANFIS-and GEP-based model for prediction of scour depth around bridge pier in clear-water scouring and live-bed scouring conditions. J. Hydroinform. 2023, 25, 1004–1028. [Google Scholar] [CrossRef]
- Zhang, W.; Rennie, C.D.; Nistor, I. A new model developed by multigene genetic programming for the temporal evolution of bridge pier scour. Can. J. Civ. Eng. 2023, 50, 549–559. [Google Scholar] [CrossRef]
- Choi, S.U.; Choi, S. Prediction of local scour around bridge piers in the cohesive bed using support vector machines. Ksce J. Civ. Eng. 2022, 26, 2174–2182. [Google Scholar] [CrossRef]
- Chou, J.S.; Nguyen, N.M. Scour depth prediction at bridge piers using metaheuristics-optimized stacking system. Autom. Constr. 2022, 140, 104297. [Google Scholar] [CrossRef]
- Ghodsi, H.; Khanjani, M.J. Application of improved GMDH models to predict local scour depth at complex bridge piers. Civ. Eng. J. 2020, 6, 69–84. [Google Scholar] [CrossRef]
- Li, Z.; Dai, G.; Du, S.; Ouyang, H.; Hu, T.; Liu, H.; Li, Z. Local Scour Depth Prediction of Offshore Wind Power Monopile Foundation Based on GMDH Method. J. Mar. Sci. Eng. 2023, 11, 753. [Google Scholar] [CrossRef]
- Guan, D.W.; Xie, Y.X.; Chiew, Y.M.; Ding, F.; Ferradosa, T.F.; Hong, J. Estimation of local scour around monopile foundations for offshore structures using machine learning models. Ocean Eng. 2024, 296, 116951. [Google Scholar] [CrossRef]
- Fedakar, H.I.; Dinçer, A.E.; Bozkuş, Z. Developing empirical formulae for scour depth in front of Inclined bridge piers. Građevinar 2023, 75, 239–256. [Google Scholar]
- Ali, A.S.A.; Günal, M. Artificial neural network for estimation of local scour depth around bridge piers. Arch. Hydro-Eng. Environ. Mech. 2021, 68, 87–101. [Google Scholar] [CrossRef]
- Dang, N.M.; Tran Anh, D.; Dang, T.D. ANN optimized by PSO and Firefly algorithms for predicting scour depths around bridge piers. Eng. Comput. 2021, 37, 293–303. [Google Scholar] [CrossRef]
- Abdulkathum, S.; Al-Shaikhli, H.I.; Al-Abody, A.A.; Hashim, T.M. Statistical analysis approaches in scour depth of bridge piers. Civ. Eng. J. 2023, 9, 143–153. [Google Scholar] [CrossRef]
- Kitsikoudis, V.; Sidiropoulos, E.; Hrissanthou, V. Machine learning utilization for bed load transport in gravel-bed rivers. Water Resour. Manag. 2014, 28, 3727–3743. [Google Scholar] [CrossRef]
- Valyrakis, M.; Diplas, P.; Dancey, C.L. Prediction of coarse particle movement with adaptive neuro-fuzzy inference systems. Hydrol. Process. 2011, 25, 3513–3524. [Google Scholar] [CrossRef]
- Shojaee, P.; Farsadizadeh, D.; Hoseinzadeh, D.A.; Salmasi, F.; Ghorbani, M.A. Application of submerged vanes at cylindrical bridge pier as a scour countermeasure. Water Soil Sci. 2012, 22, 91–108. [Google Scholar]
- Ferreira, C. Mutation, Transposition, and Recombination: An Analysis of the Evolutionary Dynamics. In Proceedings of the Joint Conference on Information Sciences (JCIS), Research Triangle Park, NC, USA, 8–13 March 2002; pp. 614–617. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]

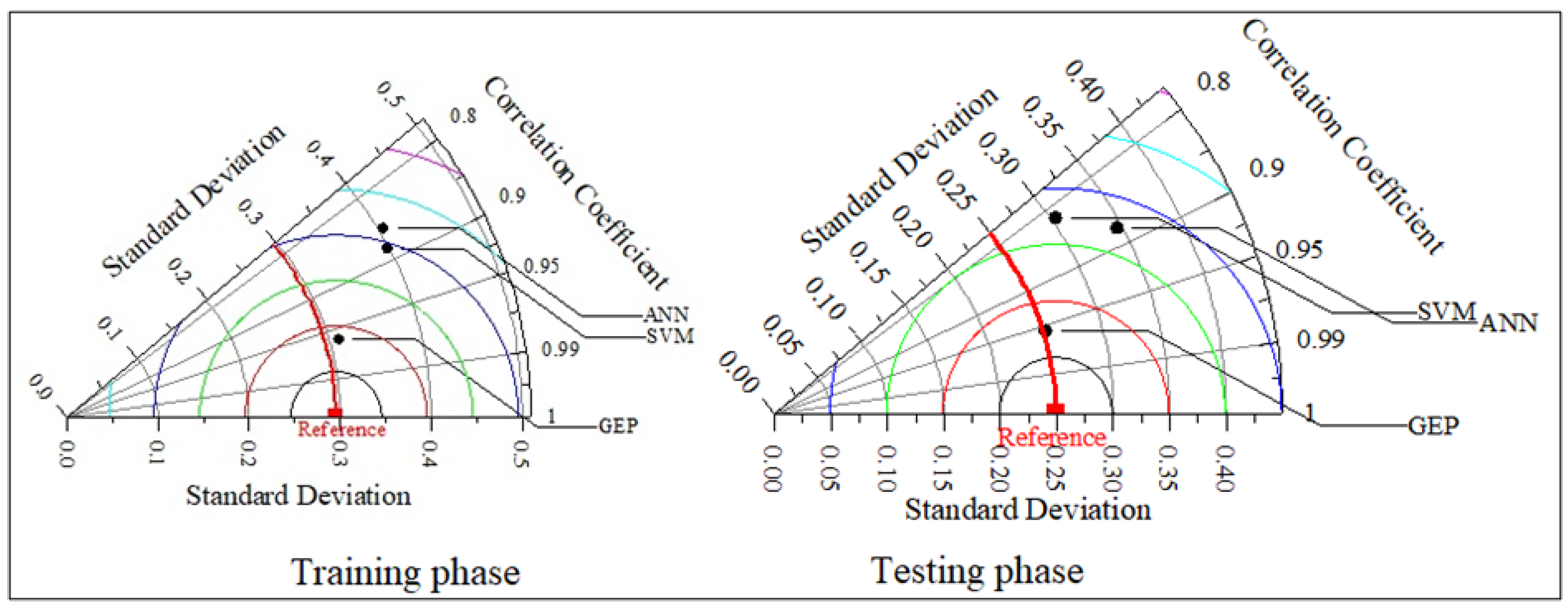

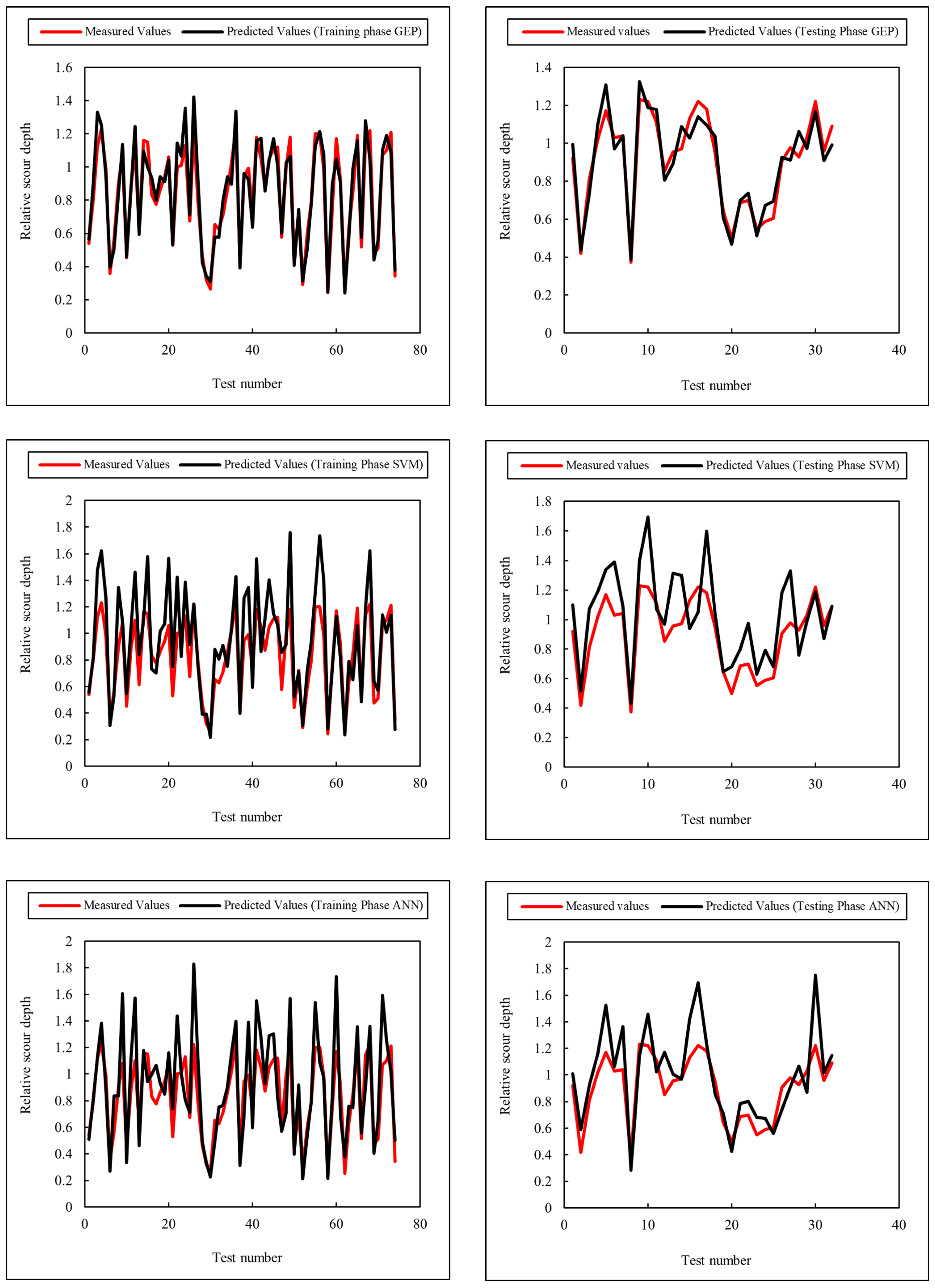
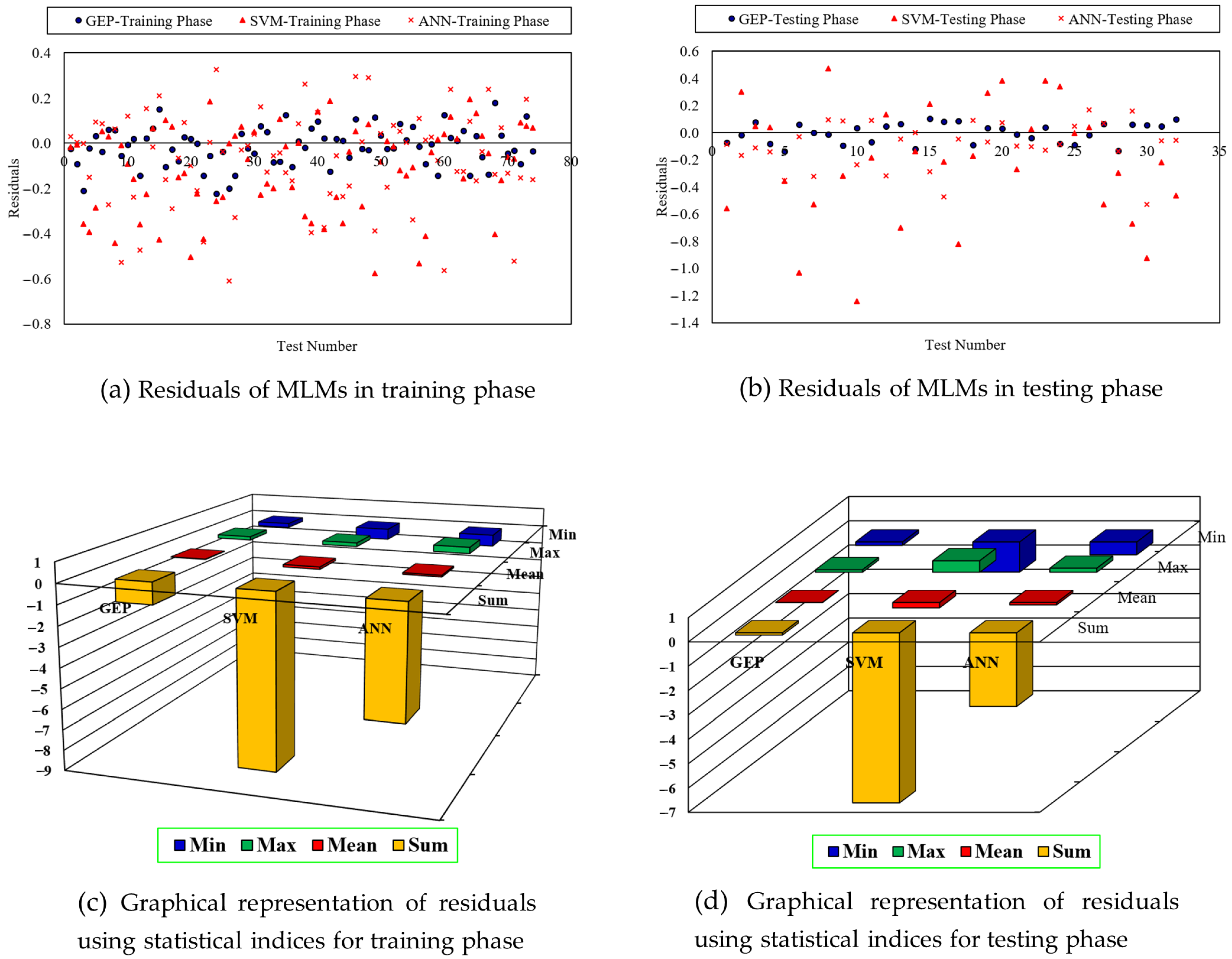
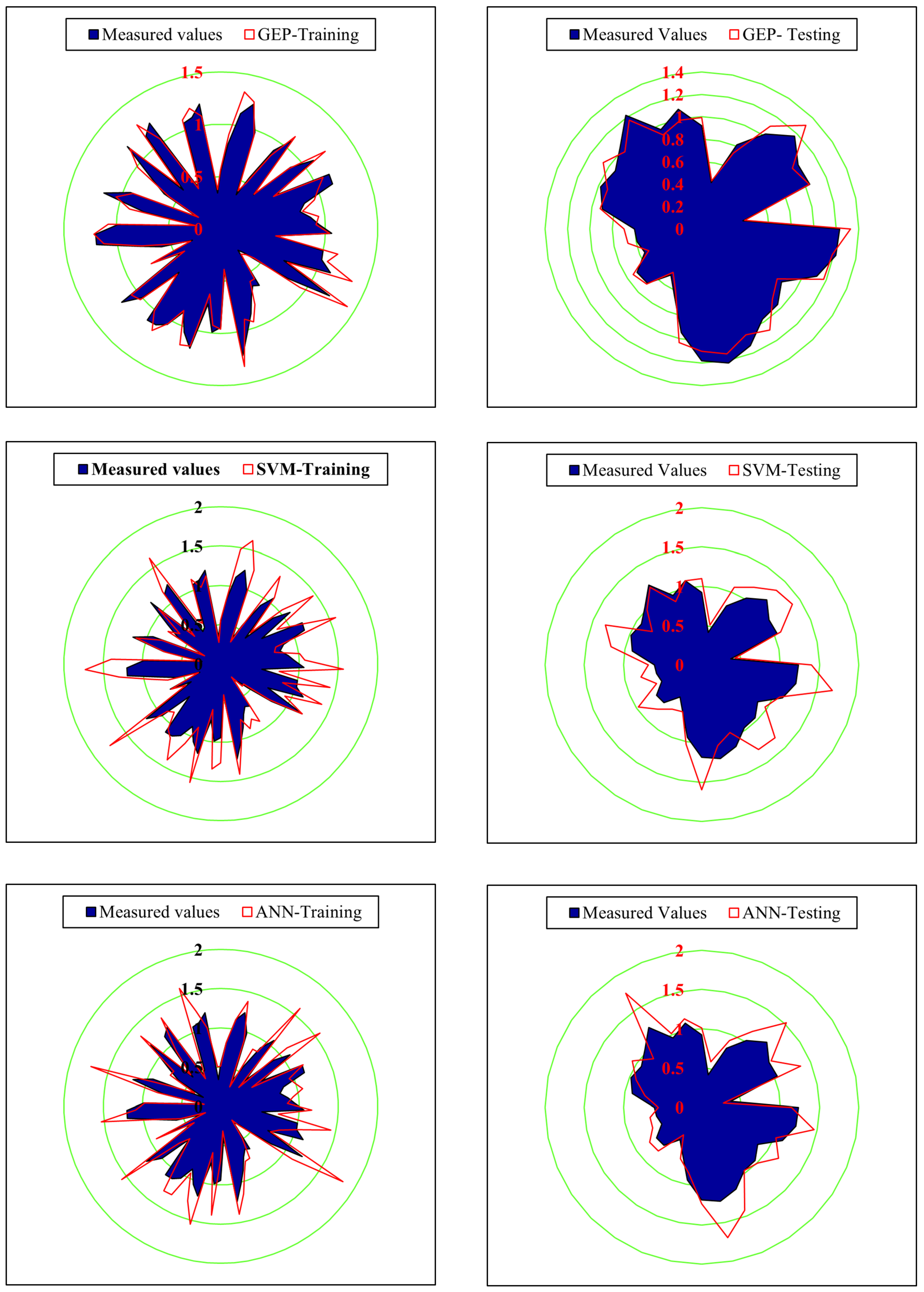
| Reference | Models Included | Case Study | Findings |
|---|---|---|---|
| [25] | ANN, ANFIS, SVM, M5P, GEP, GMDH | Scour depth of bridge pier | SVM performed better. |
| [26] | Traditional empirical equations, RID, SVM, CAT, XGB | Scour depth at sluice outlet | XGB demonstrated superiority. |
| [27] | SVR, RFR, Reptree, BRT, SGB | Scour depth of bridge pier | SGB exhibited the highest performance. |
| [28] | MLP, SVM, ANN, ANFIS | Scour depth around group piers | ANN had the most accurate outcomes. |
| [29] | Empirical models, BR, ABR, SVR | Scour depth of bridge pier | All MLMs outperformed empirical models. |
| [30] | GEP, M5-TREE, MARS, ANFIS | Scour depth of bridge pier | NFIS model was the most superior. |
| [31] | GA-ANN | Scour depth of bridge pier | GA-ANN model predicted with high accuracy. |
| [32] | AdaBoost, XGBoost, CatBoost, LightGBM | Scour depth of bridge pier | XGBoost model outperformed others. |
| [33] | ANFIS, GEP | Scour depth of bridge pier | ANFIS model was the most accurate. |
| [34] | MGGP | Scour depth of bridge pier | MGGP model had good prediction. |
| [35] | SVM, ANFIS, GEP | Scour depth of bridge pier | SVM had better outputs. |
| [36] | MOSS, FBI, LSSVR, RBFNN | Scour depth of bridge pier | MOSS exhibited fewer errors than others. |
| [37] | GMDH, GMDH-HS, GMDH-SCE | Scour depth of complex bridge pier | GMDH-SCE offered the best performance. |
| [38] | GMDH, empirical equations | Scour depth of bridge pier under wave condition | GMDH had less error. |
| [39] | BPNN, RBFNN, SVM | Scour around monopile foundations | The accurate model was the SVM. |
| [40] | MLP, RBNN, empirical equations | Scour depth in front of inclined bridge piers | MLP and RBNN had more accuracy. |
| [41] | ANN | Scour depth of bridge pier | ANN model was the superior. |
| [42] | ANN-PSO | Scour depth of bridge pier | Hybrid model outperformed traditional methods. |
| [43] | GEP, ANN, MNLR | Scour depth of bridge pier | ANN had better outputs. |
| [44] | ANN, ANFIS, RM | Bed load transport | Data-driven techniques were well trained and tested. |
| [45] | ANFIS | Coarse particle movement | – |
| Geometric Dimension | Notation | Value | Unit |
|---|---|---|---|
| Number of vanes | n | 2, 4, 6 | number |
| Collision angle of flow | 20–60 | degrees | |
| Vane distance in flow direction | z | cm | |
| Vane distance perpendicular to flow direction | e | cm | |
| Distance of the nearest vane to pier | a | cm | |
| Length of vane | L | 9 | cm |
| Height of vane | H | 18, 27 | cm |
| Kernel | Function |
|---|---|
| Linear | |
| Polynomial | |
| Radial Basis Function (RBF) | |
| Sigmoid |
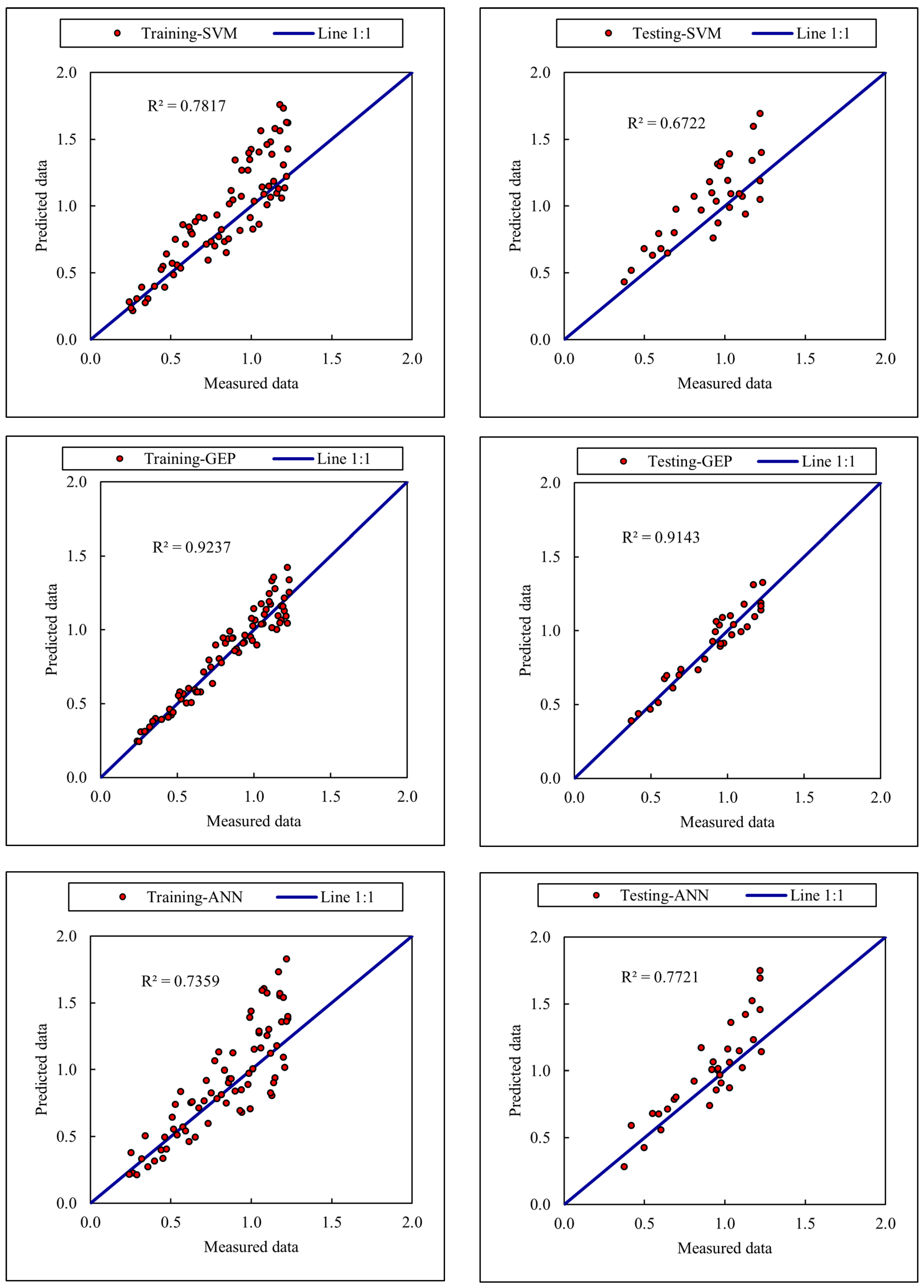
| Model | Phase | RMSE | MAE | ||
|---|---|---|---|---|---|
| SVM | Training | 0.2239 | 0.1692 | 0.7817 | 1.8964 |
| Testing | 0.2141 | 0.1743 | 0.6722 | 2.2346 | |
| GEP | Training | 0.0864 | 0.0681 | 0.9237 | 4.2501 |
| Testing | 0.0729 | 0.0641 | 0.9143 | 4.9405 | |
| ANN | Training | 0.1531 | 0.0794 | 0.7359 | 1.6720 |
| Testing | 0.1476 | 0.0852 | 0.7721 | 2.1992 |
| Parameter | Value |
|---|---|
| Head size | 8 |
| Number of chromosomes | 30 |
| Number of genes | 3 |
| Mutation rate | 0.044 |
| Inversion rate | 0.1 |
| One-point recombination rate | 0.3 |
| Two-point recombination rate | 0.3 |
| Gene recombination rate | 0.1 |
| Gene transposition rate | 0.1 |
| IS transposition rate | 0.1 |
| RIS transposition rate | 0.1 |
| Fitness function error type | RRSE |
| Linking function | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molavi, A.; Kaleybar, F.A.; Rathnayake, N.; Rathnayake, U.; Fuladipanah, M.; Azamathulla, H.M. Machine Learning Approaches for Simulating Temporal Changes in Bed Profiles Around Cylindrical Bridge Pier: A Comparative Analysis. Hydrology 2025, 12, 238. https://doi.org/10.3390/hydrology12090238
Molavi A, Kaleybar FA, Rathnayake N, Rathnayake U, Fuladipanah M, Azamathulla HM. Machine Learning Approaches for Simulating Temporal Changes in Bed Profiles Around Cylindrical Bridge Pier: A Comparative Analysis. Hydrology. 2025; 12(9):238. https://doi.org/10.3390/hydrology12090238
Chicago/Turabian StyleMolavi, Ahad, Fariborz Ahmadzadeh Kaleybar, Namal Rathnayake, Upaka Rathnayake, Mehdi Fuladipanah, and Hazi Mohammad Azamathulla. 2025. "Machine Learning Approaches for Simulating Temporal Changes in Bed Profiles Around Cylindrical Bridge Pier: A Comparative Analysis" Hydrology 12, no. 9: 238. https://doi.org/10.3390/hydrology12090238
APA StyleMolavi, A., Kaleybar, F. A., Rathnayake, N., Rathnayake, U., Fuladipanah, M., & Azamathulla, H. M. (2025). Machine Learning Approaches for Simulating Temporal Changes in Bed Profiles Around Cylindrical Bridge Pier: A Comparative Analysis. Hydrology, 12(9), 238. https://doi.org/10.3390/hydrology12090238













