Simulating the Porosity Reduction in a Permeable Reactive Barrier–Aquifer System Using THMC Software
Abstract
1. Introduction
2. Materials and Methods
2.1. Conceptual Model
2.2. Groundwater Flow Model
2.3. Reactive Transport Model
2.4. Calculate the Porosity Reduction
2.5. Sensitivity Analyses
- Mineral type: simulations were run for individual minerals and selected combinations to determine their relative influence. Groundwater ion concentrations and reaction rate coefficients applied in the simulations were based on baseline scenarios.
- Influent concentrations: the baseline groundwater composition (Table 3) was systematically varied within literature-reported ranges.
- Reaction rate coefficients: rate constants for iron corrosion (aerobic, anaerobic, nitrate-driven), microbial sulfate reduction, and mineral precipitation were varied according to reported ranges (Table 4).
| Ion in Groundwater | Baseline Scenario 1 (Molar) | Sensitivity Analyses (Molar) | Literature Review 2 (Molar) |
|---|---|---|---|
| Fe2+ | 1.0 × 10−10 | 1.0 × 10−12, 1.0 × 10−4 | <9.0 × 10−4 |
| Ca2+ | 1.0 × 10−3 | 2.5 × 10−6, 2.5 × 10−2 | 2.5 × 10−6–2.5 × 10−2 |
| Mg2+ | 1.0 × 10−3 | 4.1 × 10−6, 4.1 × 10−3 | 4.1 × 10−6–4.1 × 10−3 |
| Mn2+ | 1.0 × 10−7 | 1.0 × 10−9, 1.0 × 10−5 | <1.8 × 10−5 |
| OH− | 1.0 × 10−7 | 1.0 × 10−8, 3.2 × 10−6 | 1.0 × 10−8–3.2 × 10−6 |
| Alkalinity (HCO3−) | 1.0 × 10−3 | 1.0 × 10−5, 1.0 × 10−2 | 1.0 × 10−5–1.0 × 10−2 |
| O2 | 1.0 × 10−10 | 1.0 × 10−12, 1.0 × 10−4 | <2.5 × 10−4 |
| NO3− | 1.0 × 10−5 | 1.0 × 10−7, 1.0 × 10−3 | <1.6 × 10−3 |
| SO42− | 1.0 × 10−3 | 1.0 × 10−4, 5.0 × 10−3 | <1.0 × 10−2 |
| Reaction Terms | Units | Baseline Scenario 1 | Sensitivity Analyses | Literature Review 2 |
|---|---|---|---|---|
| Aerobic iron corrosion | m3/m2-day | 2.8 × 10−2 | 1.0 × 10−3, 1.0 × 104 | <2.8 × 104 |
| Anaerobic iron corrosion | mole/m2-day | 2.0 × 10−7 | 3.0 × 10−8, 5.4 × 10−3 | 3.0 × 10−8–5.4 × 10−3 |
| Nitrate iron corrosion | m3/m2-day | 1.0 × 10−6 | 1.8 × 10−8, 2.8 × 10−5 | 1.8 × 10−8–2.8 × 10−5 |
| Microbial sulfate reduction | M/day | 1.0 × 10−5 | 5.0 × 10−6, 5.0 × 10−3 | 5.0 × 10−6–5.0 × 10−3 |
| CaCO3 | M/day | 1.0 × 10−4 | 2.7 × 10−9, 1.4 × 10−4 | 2.7 × 10−9–1.4 × 10−4 |
| CaMg(CO3)2 | M/day | 1.0 × 10−9 | 9.0 × 10−10, 6.9 × 10−6 | 9.0 × 10−10–6.9 × 10−6 |
| MgCO3 | M/day | 1.0 × 10−4 | 1.1 × 10−8, 1.4 × 10−4 | 1.1 × 10−8–1.4 × 10−4 |
| Mg(OH)2 | M/day | 1.0 × 10−4 | 3.4 × 10−6, 2.3 × 10−3 | 3.4 × 10−6–2.3 × 10−3 |
| MnCO3 | M/day | 1.0 × 10−6 | 1.1 × 10−8, 1.4 × 10−5 | 1.1 × 10−8–1.4 × 10−5 |
| Mn(OH)2 | M/day | 1.0 × 10−4 | 1.0 × 10−5, 1.0 × 10−3 | No data |
| FeCO3 | M/day | 1.0 × 10−4 | 1.1 × 10−5, 2.7 × 10−4 | 1.1 × 10−5–2.7 × 10−4 |
| Fe(OH)2 | M/day | 1.0 × 10−4 | 1.0 × 10−3, 2.0 × 10−4 | <2.2 × 10−4 |
| FeS | M/day | 1.0 × 10−6 | 1.1 × 10−8, 2.2 × 10−5 | 1.1 × 10−8–2.2 × 10−5 |
3. Results and Discussion
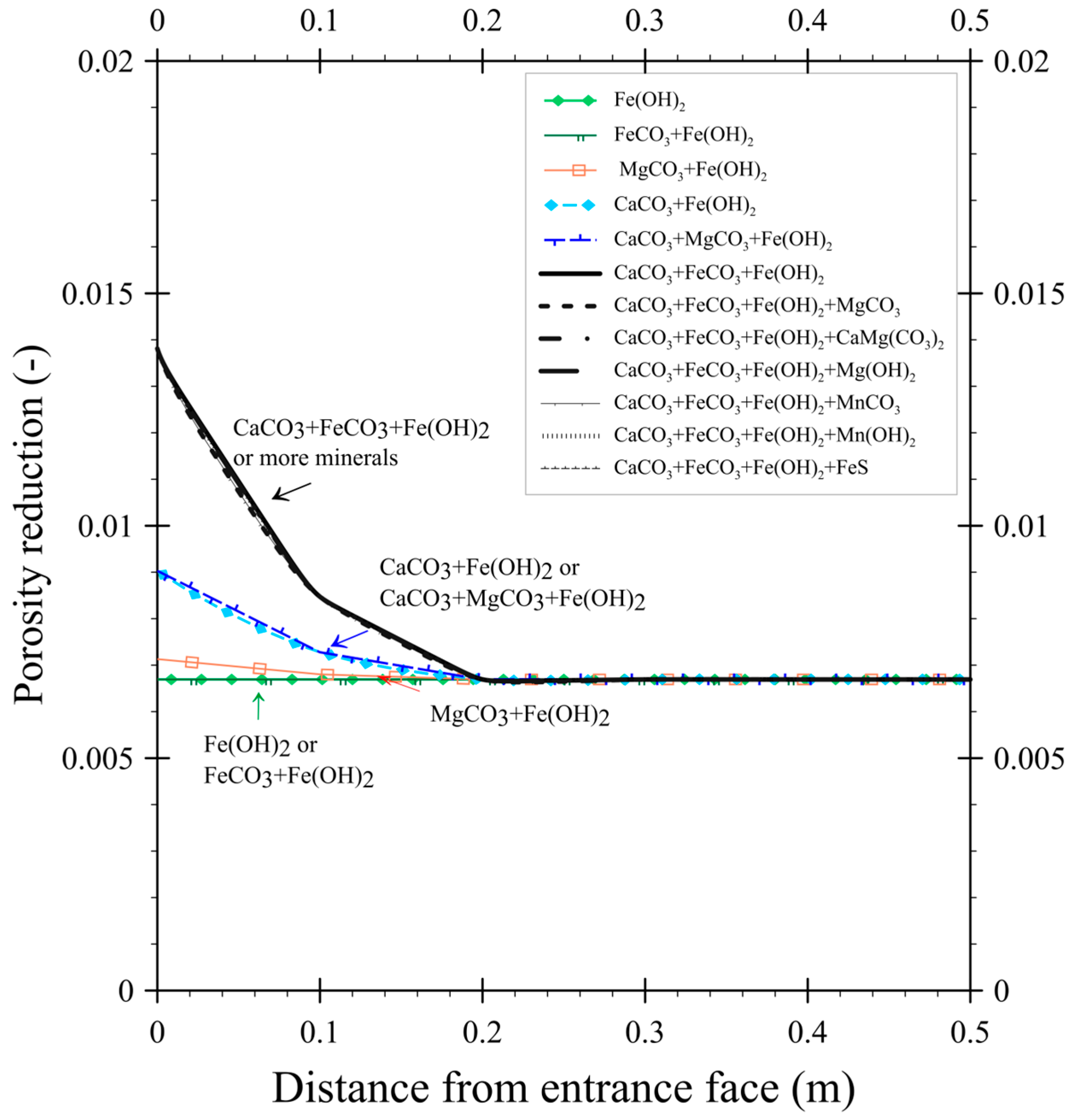
3.1. The Effect of Mineral Type on Porosity Reduction
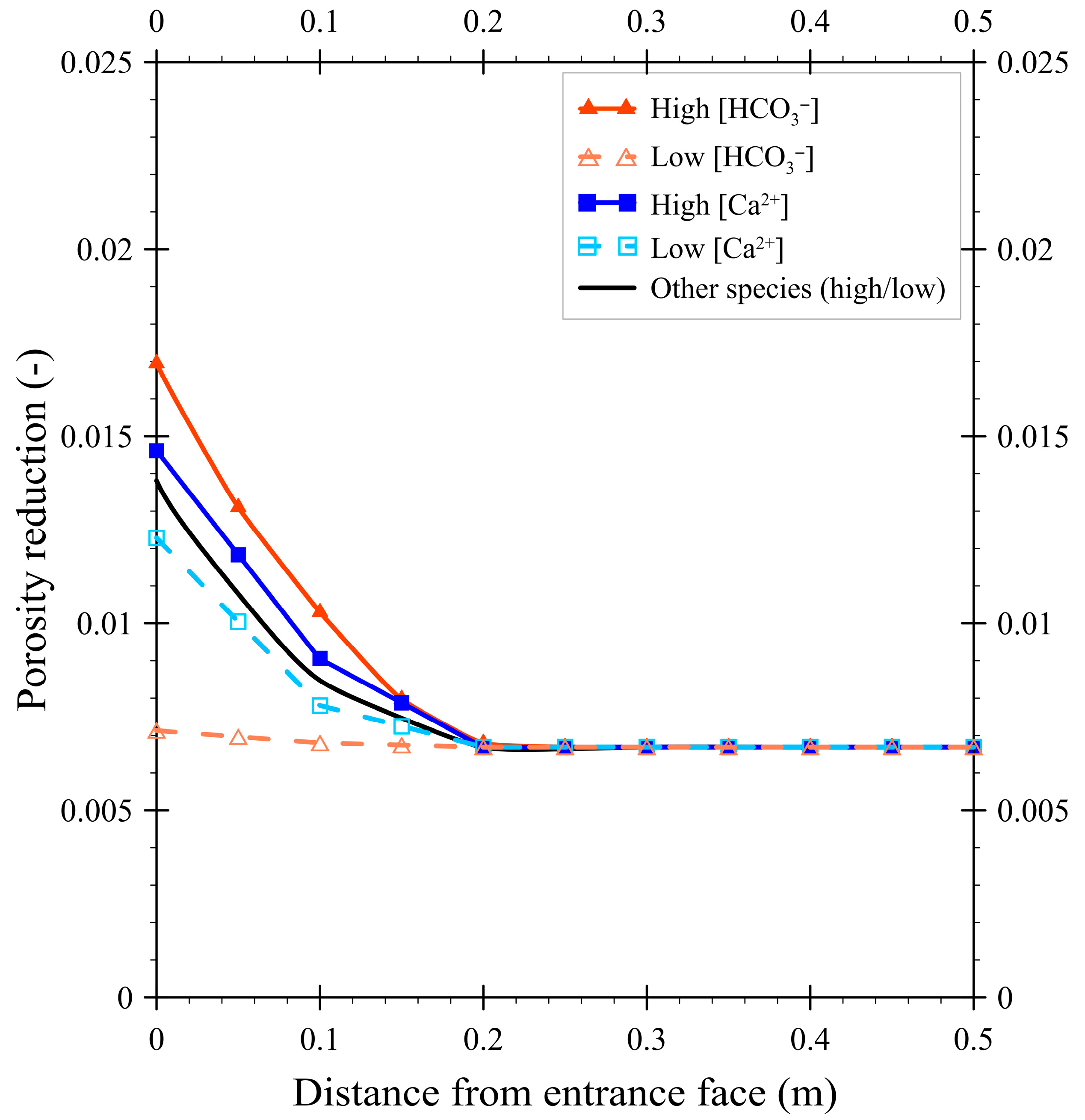
3.2. The Effect of Concentration on Porosity Reduction
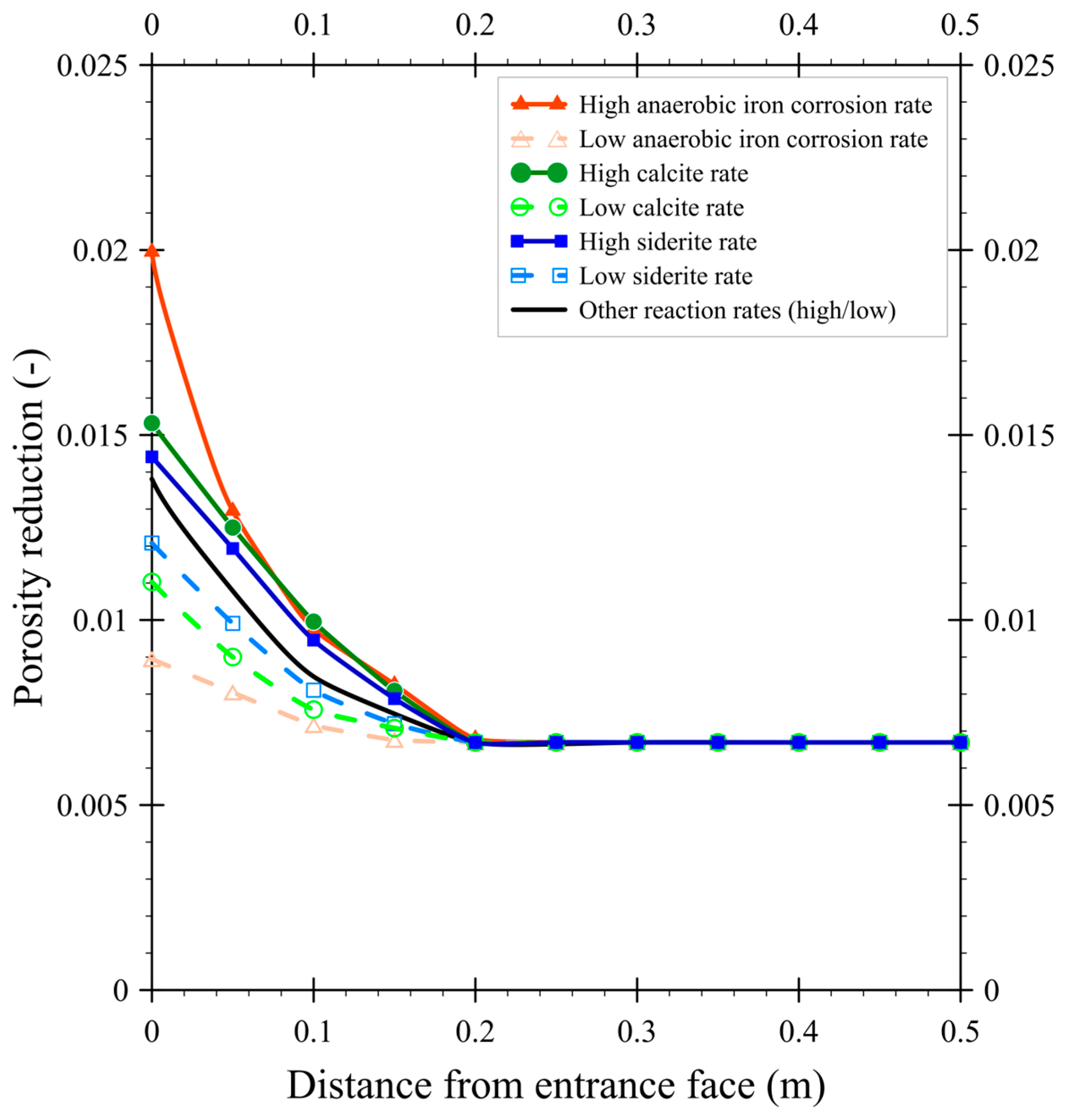
3.3. The Effect of Rate Coefficients on Porosity Reduction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Naidu, R.; Bekele, D.N.; Birke, V. Permeable reactive barriers: Cost-effective and sustainable remediation of groundwater. Sustain. Groundw. Remediat. 2014, 1, 1–2. [Google Scholar]
- Gillham, R. In Situ Remediation of VOC-Contaminated Groundwater Using Zero-Valent Iron: Long-Term Performance; Center for Groundwater Studies: Fremantle, Australia, 1999. [Google Scholar]
- O’Hannesin, S.F.; Gillham, R.W. Long-term performance of an in situ “iron wall” for remediation of VOCs. Groundwater 1998, 36, 164–170. [Google Scholar] [CrossRef]
- Phillips, D.H.; Watson, D.B.; Roh, Y.; Gu, B. Mineralogical characteristics and transformations during long-term operation of a zerovalent iron reactive barrier. J. Environ. Qual. 2003, 32, 2033–2045. [Google Scholar] [CrossRef] [PubMed]
- Richardson, J.P.; Nicklow, J.W. In situ permeable reactive barriers for groundwater contamination. Soil Sediment Contam. 2002, 11, 241–268. [Google Scholar] [CrossRef]
- Wilkin, R.T.; Puls, R.W.; Sewell, G.W. Long-Term Performance of Permeable Reactive Barriers Using Zero-Valent Iron: An Evaluation at Two Sites; Report EPA/600/S-02/001; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2002. [Google Scholar]
- Phillips, D.H.; Gu, B.; Watson, D.B.; Roh, Y.; Liang, L.; Lee, S. Performance evaluation of a zerovalent iron reactive barrier: Mineralogical characteristics. Environ. Sci. Technol. 2000, 34, 4169–4176. [Google Scholar] [CrossRef]
- Vikesland, P.J.; Klausen, J.; Zimmermann, H.; Roberts, A.L.; Ball, W.P. Longevity of granular iron in groundwater treatment processes: Changes in solute transport properties over time. J. Contam. Hydrol. 2003, 64, 3–33. [Google Scholar] [CrossRef]
- Warner, S.D.; Sorel, D. Ten Years of Permeable Reactive Barriers: Lessons Learned and Future Expectations. In Chlorinated Solvent and DNAPL Remediation: Innovative Strategies for Subsurface Cleanup; ACS Symposium Series 837; Warner, S.D., Ed.; American Chemical Society: Washington, DC, USA, 2003. [Google Scholar]
- Gavaskar, A.R.; Gupta, N.; Sass, B.; Janosy, R.; O’Sullivan, D. Permeable Barriers for Groundwater Remediation; Battelle Press: Columbus, OH, USA, 1998. [Google Scholar]
- Li, L.; Benson, C.H.; Lawson, E.M. Impact of mineral fouling on hydraulic behavior of permeable reactive barriers. Groundwater 2005, 43, 582–596. [Google Scholar] [CrossRef]
- Mayer, K.U.; Blowes, D.W.; Frind, E.O. Reactive transport modeling of an in situ reactive barrier for the treatment of hexavalent chromium and trichloroethylene in groundwater. Water Resour. Res. 2001, 37, 3091–3103. [Google Scholar] [CrossRef]
- Yabusaki, S.; Cantrell, K.; Sass, B.; Steefel, C. Multicomponent reactive transport in an in situ zero-valent iron cell. Environ. Sci. Technol. 2001, 35, 1493–1503. [Google Scholar] [CrossRef]
- Yang, H.; Hu, R.; Ruppert, H.; Noubactep, C. Modeling porosity loss in Fe0-based permeable reactive barriers with Faraday’s law. Sci. Rep. 2021, 11, 16998. [Google Scholar] [CrossRef]
- Li, L.; Benson, C.H.; Lawson, E.M. Modeling porosity reductions caused by mineral fouling in continuous-wall permeable reactive barriers. J. Contam. Hydrol. 2006, 83, 89–121. [Google Scholar] [CrossRef]
- Wilkin, R.T.; Puls, R.W. Capstone Report on the Application, Monitoring, and Performance of Permeable Reactive Barriers for Groundwater Remediation: Volume 1: Performance Evaluations at Two Sites; EPA/600-R-03-045a; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2003. [Google Scholar]
- Li, L.; Benson, C.H. Evaluation of Two Strategies to Enhance the Long-Term Hydraulic Performance of Permeable Reactive Barriers. In Proceedings of the GeoCongress: Geotechnics of Waste Management and Remediation, New Orleans, LA, USA, 9–12 March 2008. [Google Scholar]
- Li, L.; Benson, C.H. Evaluation of five strategies to limit the impact of fouling in permeable reactive barriers. J. Hazard. Mater. 2010, 181, 170–180. [Google Scholar] [CrossRef]
- Yeh, G.T. FEMWATER: A Finite-Element Model of Water Flow Through Saturated–Unsaturated Porous Media; Report No. 1370; Environmental Sciences Division, Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1980. [Google Scholar]
- Yeh, G.T. 3DFEMWATER: A Three-Dimensional Finite Element Model of Water Flow Through Saturated–Unsaturated Media; Report No. ORNL-6386; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1987. [Google Scholar]
- Yeh, G.T.; Tripathi, V.S. HYDROGEOCHEM: A Coupled Model of Hydrologic Transport and Geochemical Equilibria in Reactive Multicomponent Systems; Report No. ORNL-6371; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1990. [Google Scholar]
- Yeh, G.T.; Tripathi, V.S. A model for simulating transport of reactive multispecies components: Model development and demonstration. Water Resour. Res. 1991, 27, 3075–3094. [Google Scholar] [CrossRef]
- Sarr, D. Zero-Valent-Iron Permeable Reactive Barriers—How Long Will They Last? Remediation 2001, 11, 1–18. [Google Scholar]
- Lin, H.C.J.; Richards, D.R.; Talbot, C.A.; Yeh, G.T.; Cheng, J.R.; Cheng, H.P.; Jones, N.L. FEMWATER: A Three-Dimensional Finite Element Computer Model for Simulating Density-Dependent Flow and Transport in Variably Saturated Media; US Army Corps of Engineers, Waterways Experiment Station: Vicksburg, MS, USA, 1997. [Google Scholar]
- Yeh, G.T.; Cheng, J.R.; Lin, H.C. 3DFEMFAT: User’s Manual of a 3-Dimensional Finite Element Model of Density Dependent Flow and Transport Through Saturated-Unsaturated Media; U.S. Army Corps of Engineers, Waterway Experiment Station: Vicksburg, MS, USA, 1994. [Google Scholar]
- Yeh, G.T.; Chang, J.R.; Gwo, J.P.; Lin, H.C.; Richards, D.R. 3DSALT: A Three-Dimensional Finite Element Model of Density-Dependent Flow and Transport Through Saturated-Unsaturated Media; U.S. Army Corps of Engineers, Waterway Experiment Station: Vicksburg, MS, USA, 1994. [Google Scholar]
- Owczarek, J.A. Fundamentals of Gas Dynamics; International Textbook Company: New York, NY, USA, 1964. [Google Scholar]
- Allison, J.D.; Brown, D.S.; Novo-Gradac, K.J. MINTEQA2/PRODEFA2, A Geochemical Assessment Model for Environmental Systems: Version 3.0 User’s Manual; EPA-600/3-91-021; U.S. Environmental Protection Agency: Athens, GA, USA, 1991. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Hem, J.D. Study and Interpretation of the Chemical Characteristics of Natural Water, 3rd ed.; Water-Supply Paper 2254; U.S. Geological Survey: Alexandria, VA, USA, 1985. [Google Scholar]
- Langmuir, D. Aqueous Environmental Geochemistry; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Reardon, E.J. Anaerobic corrosion of granular iron: Measurement and interpretation of hydrogen evolution rates. Environ. Sci. Technol. 1995, 29, 2936–2945. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Watson, D.B.; Wu, L.Y.; Phillips, D.H.; White, D.C.; Zhou, J.Z. Microbiological characteristics in a zerovalent iron reactive barrier. Environ. Monit. Assess. 2002, 77, 293–309. [Google Scholar] [CrossRef]
- Gu, B.; Phelps, T.J.; Liang, L.; Dickey, M.J.; Roh, Y.; Kinsall, B.L.; Palumbo, A.V.; Jacobs, G.K. Biogeochemical dynamics in zero-valent iron columns: Implications for permeable reactive barriers. Environ. Sci. Technol. 1999, 33, 2170–2177. [Google Scholar] [CrossRef]
- Gandhi, S.; Oh, B.T.; Schnoor, J.L.; Alvarez, P.J. Degradation of TCE, Cr(VI), sulfate, and nitrate mixtures by granular iron in flow-through columns under different microbial conditions. Water Res. 2002, 36, 1973–1982. [Google Scholar] [CrossRef]
- Alowitz, M.J.; Scherer, M.M. Kinetics of nitrate, nitrite, and Cr(VI) reduction by iron metal. Environ. Sci. Technol. 2002, 36, 299–306. [Google Scholar] [CrossRef]
- Westerhoff, P. Reduction of nitrate, bromate, and chlorate by zero valent iron (Fe0). J. Environ. Eng. 2003, 129, 10–16. [Google Scholar] [CrossRef]
- Chen, J.L.; Al-Abed, S.R.; Ryan, J.A.; Li, Z. Effects of pH on dechlorination of trichloroethylene by zero-valent iron. J. Hazard. Mater. 2001, 83, 243–254. [Google Scholar] [CrossRef]
- Kober, R.; Schlicker, O.; Ebert, M.; Dahmke, A. Degradation of chlorinated ethylenes by Fe0: Inhibition processes and mineral precipitation. Environ. Geol. 2002, 41, 644–652. [Google Scholar]
- Hunter, K.; Wang, Y.; Van Cappellen, P. Kinetic modeling of microbially driven redox chemistry of subsurface environments: Coupling transport, microbial metabolism, and geochemistry. J. Hydrol. 1998, 209, 53–80. [Google Scholar] [CrossRef]
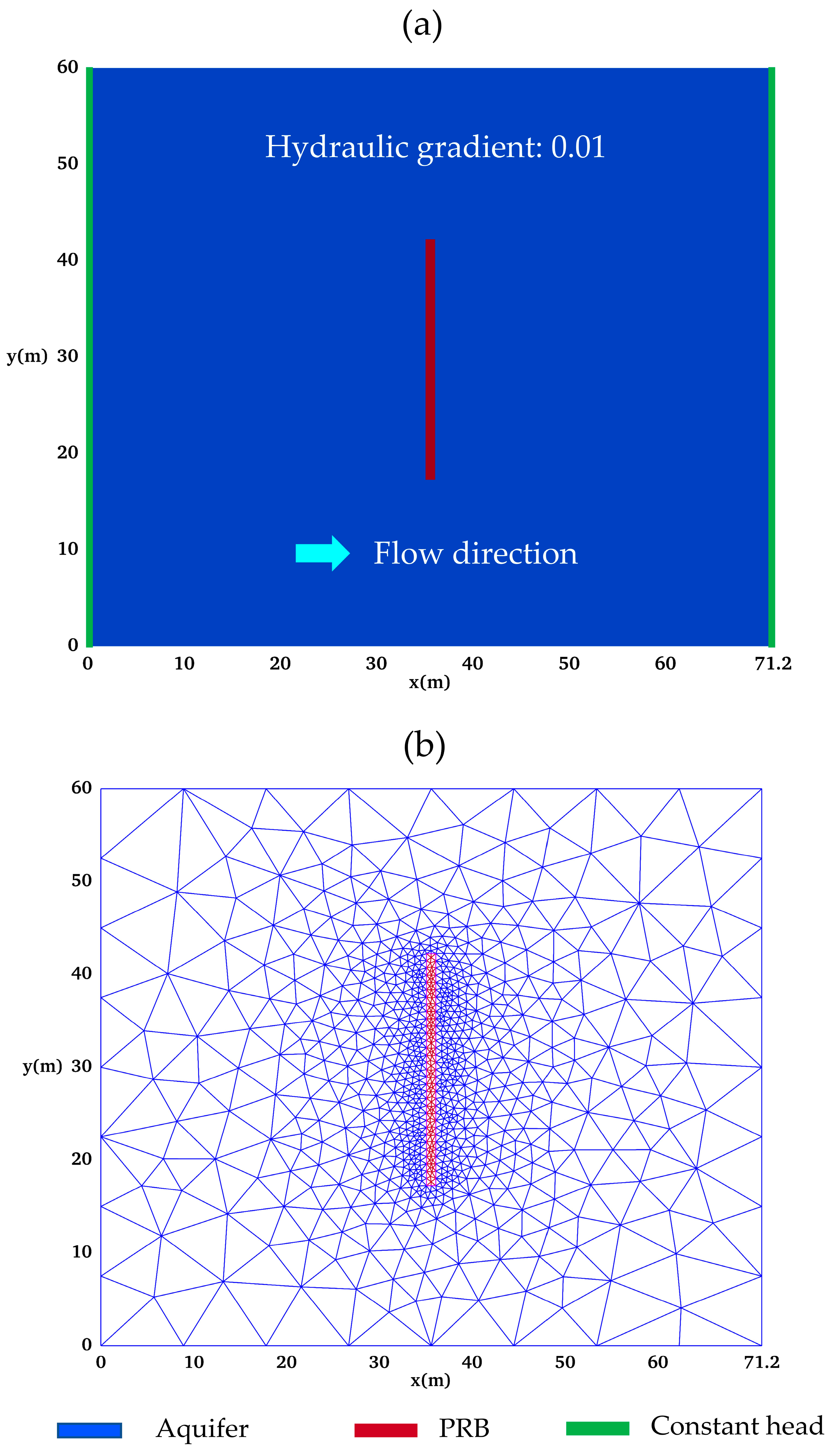
| Aquifer (Homogeneous) | PRB (Homogeneous) | |
|---|---|---|
| Domain (length × width) | 71.2 m × 60.0 m | 1.0 m × 25.0 m |
| Hydraulic conductivity (K) | 3.9 (m/day) | 216 (m/day) |
| Porosity initial (n0) | 0.3 | 0.6 |
| Boundary conditions | No flow: top, bottom Constant-head: upstream and downstream) | Upgradient: background groundwater concentrations |
| Reaction 1 | Mineral Formed | Solubility Constant log(Keq) 1 |
|---|---|---|
| Fe0 + H2O + 0.5O2 → Fe2+ + 2OH− | - | - |
| Fe0 + 2H2O → Fe2+ + H2 + 2OH− | - | - |
| 4Fe0 + 7H2O + NO3− → Fe2+ + 10OH− + NH4+ | - | - |
| SO42− + 4H2 → HS− + OH− + 3H2O | - | - |
| HCO3− ↔ H+ + CO32− | - | −10.07 |
| H2O ↔ H+ + OH− | - | −14.0 |
| CaCO3 ↔ Ca2+ + CO32− | Calcite/aragonite | −8.1 |
| CaMg(CO3)2 ↔ Ca2+ + Mg2+ + 2CO32− | Ca–Mg–carbonate | −17.7 |
| MgCO3 ↔ Mg2+ + CO32− | Magnesite | −7.2 |
| Mg(OH)2 ↔ Mg2+ + 2OH− | Brucite | −11.2 |
| MnCO3 ↔ Mn2+ + CO32− | Rhodochrosite | −9.3 |
| Mn(OH)2 ↔ Mn2+ + 2OH− | Pyrochroite | −12.9 |
| FeCO3 ↔ Fe2+ + CO32− | Siderite | −10.5 |
| Fe(OH)2 ↔ Fe2+ + 2OH− | Ferrous hydroxide | −15.2 |
| FeS + H2O ↔ Fe2+ + HS− + OH− | Ferrous sulfide | −18.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-T.-H.; Suk, H.; Liang, C.-P.; Chen, J.-S. Simulating the Porosity Reduction in a Permeable Reactive Barrier–Aquifer System Using THMC Software. Hydrology 2025, 12, 232. https://doi.org/10.3390/hydrology12090232
Nguyen T-T-H, Suk H, Liang C-P, Chen J-S. Simulating the Porosity Reduction in a Permeable Reactive Barrier–Aquifer System Using THMC Software. Hydrology. 2025; 12(9):232. https://doi.org/10.3390/hydrology12090232
Chicago/Turabian StyleNguyen, Thi-Tuyet-Han, Heejun Suk, Ching-Ping Liang, and Jui-Sheng Chen. 2025. "Simulating the Porosity Reduction in a Permeable Reactive Barrier–Aquifer System Using THMC Software" Hydrology 12, no. 9: 232. https://doi.org/10.3390/hydrology12090232
APA StyleNguyen, T.-T.-H., Suk, H., Liang, C.-P., & Chen, J.-S. (2025). Simulating the Porosity Reduction in a Permeable Reactive Barrier–Aquifer System Using THMC Software. Hydrology, 12(9), 232. https://doi.org/10.3390/hydrology12090232







