Improving Operational Ensemble Streamflow Forecasting with Conditional Bias-Penalized Post-Processing of Precipitation Forecast and Assimilation of Streamflow Data
Abstract
1. Introduction
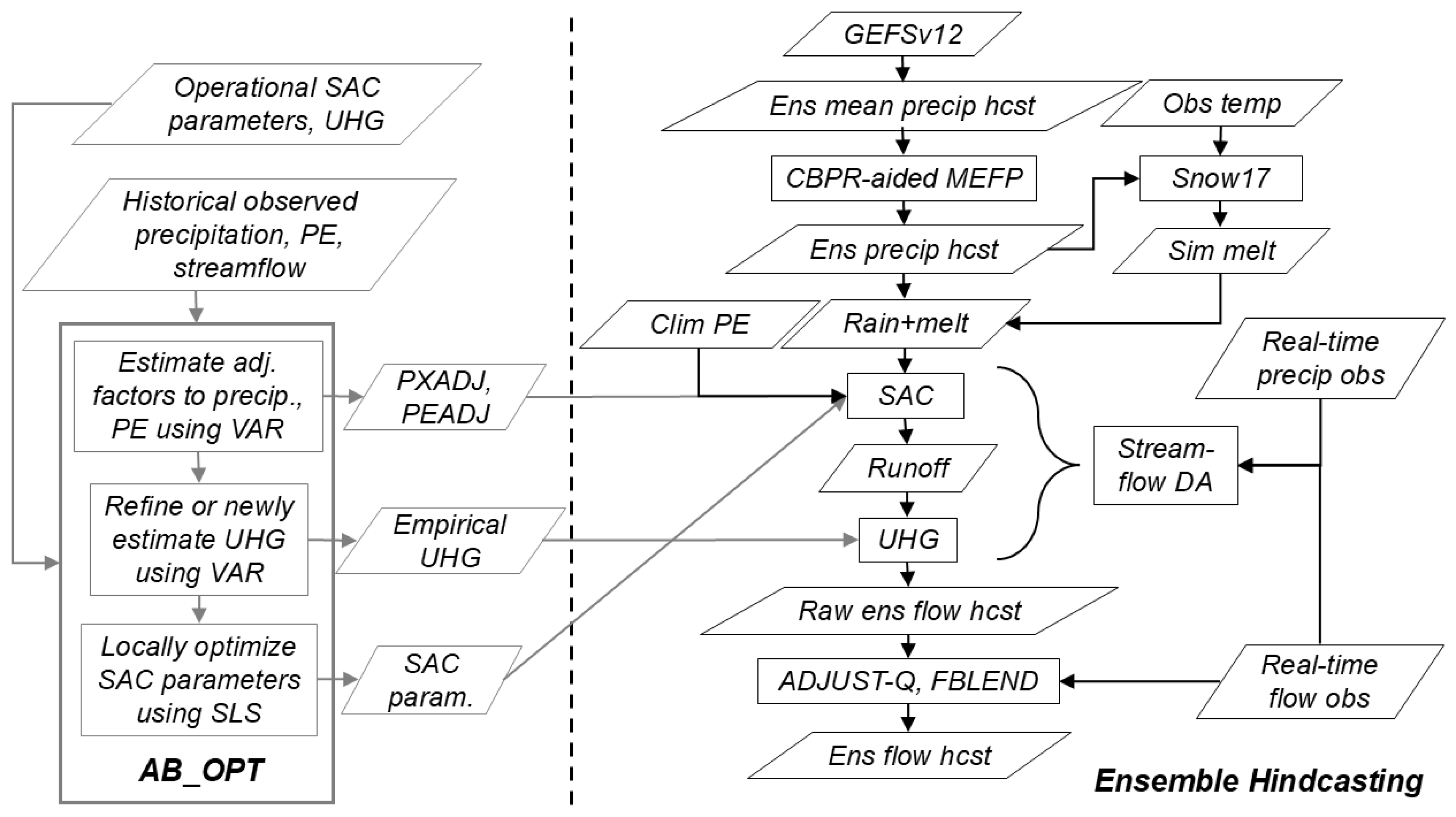
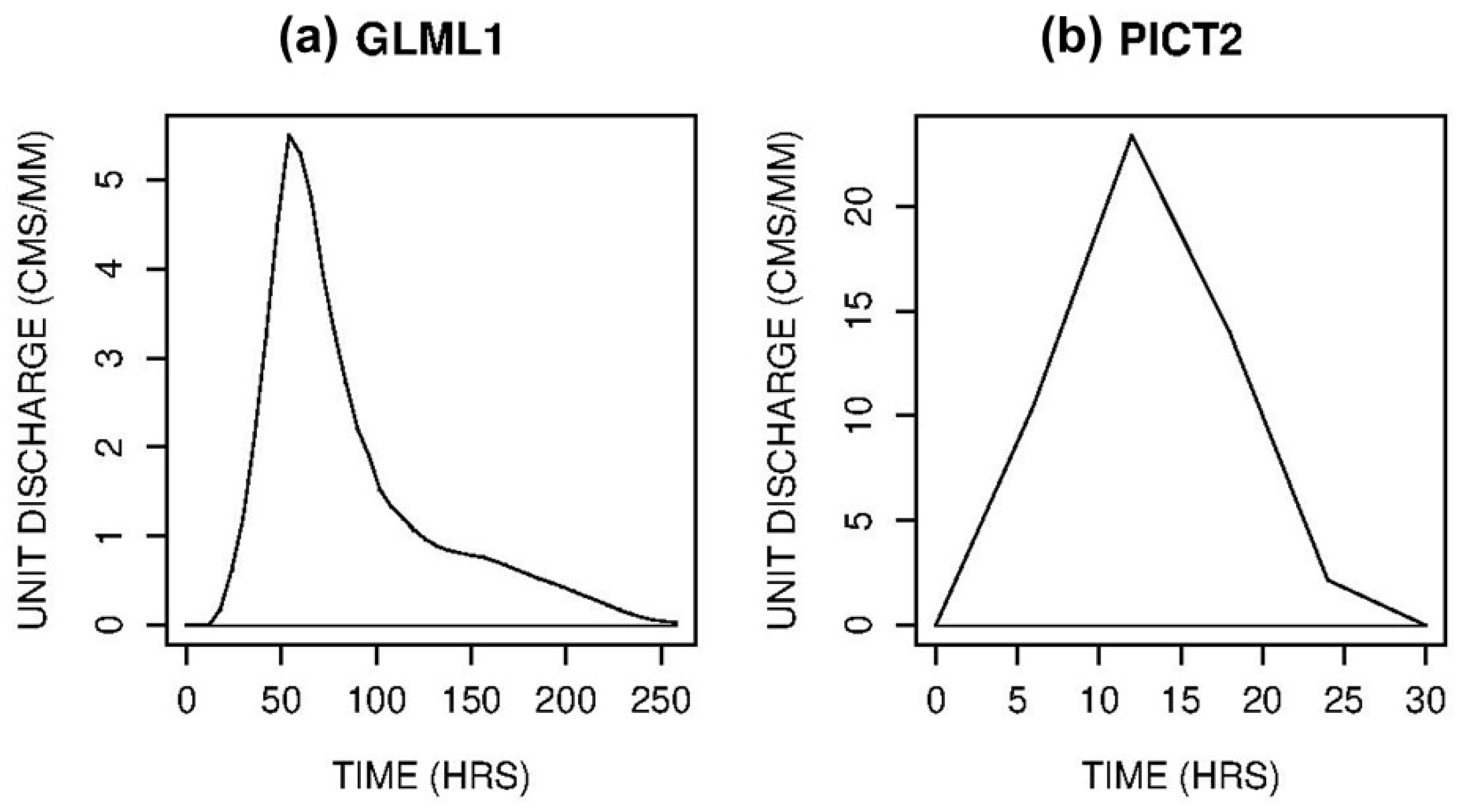
2. Experiment Design, Data, Models and Tools Used
3. Methods
3.1. Conditional Bias-Penalized Regression
3.2. Adaptive Conditional Bias-Penalized Kalman Filter
3.3. Comparative Evaluation
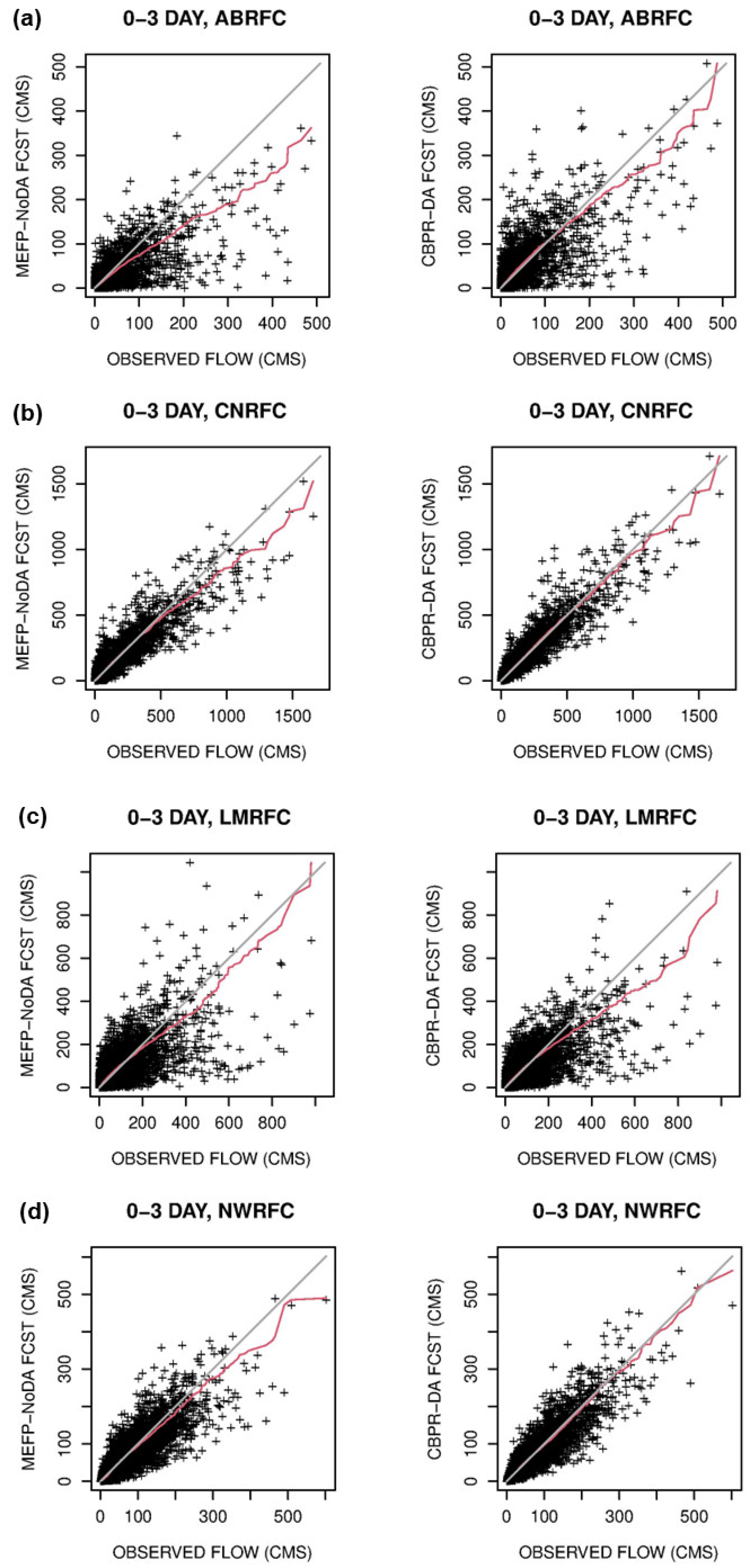
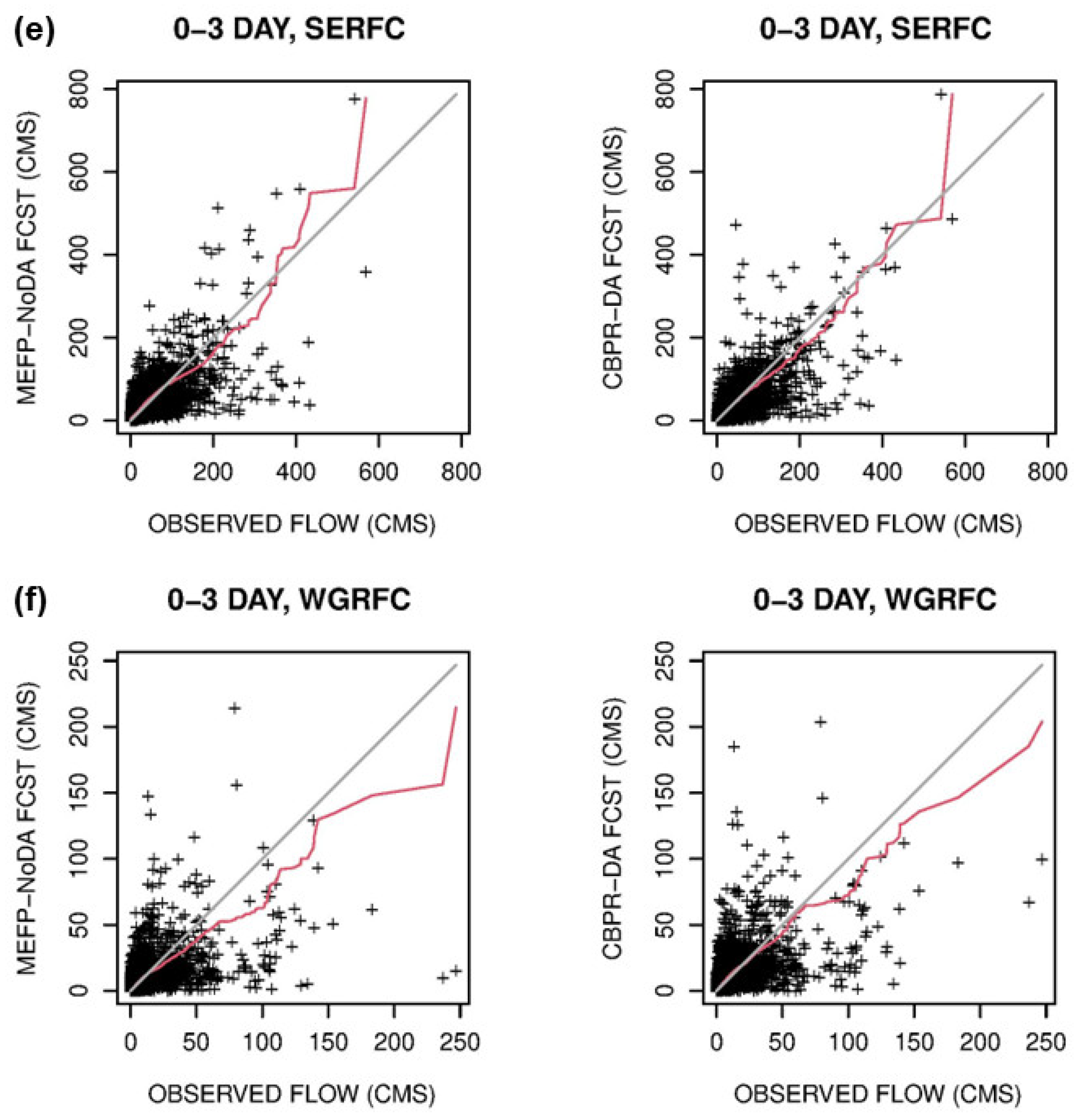
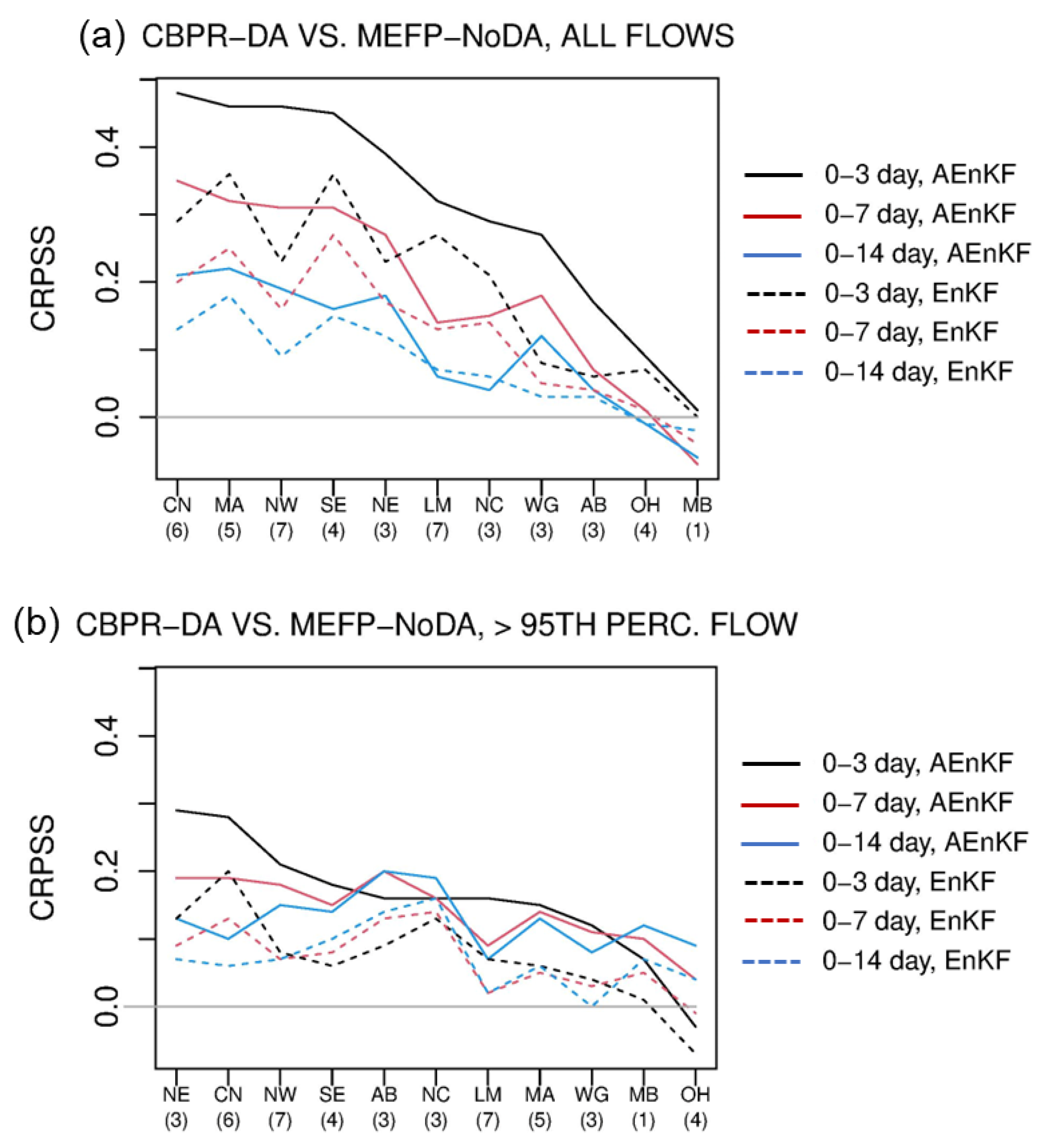
4. Results and Discussion
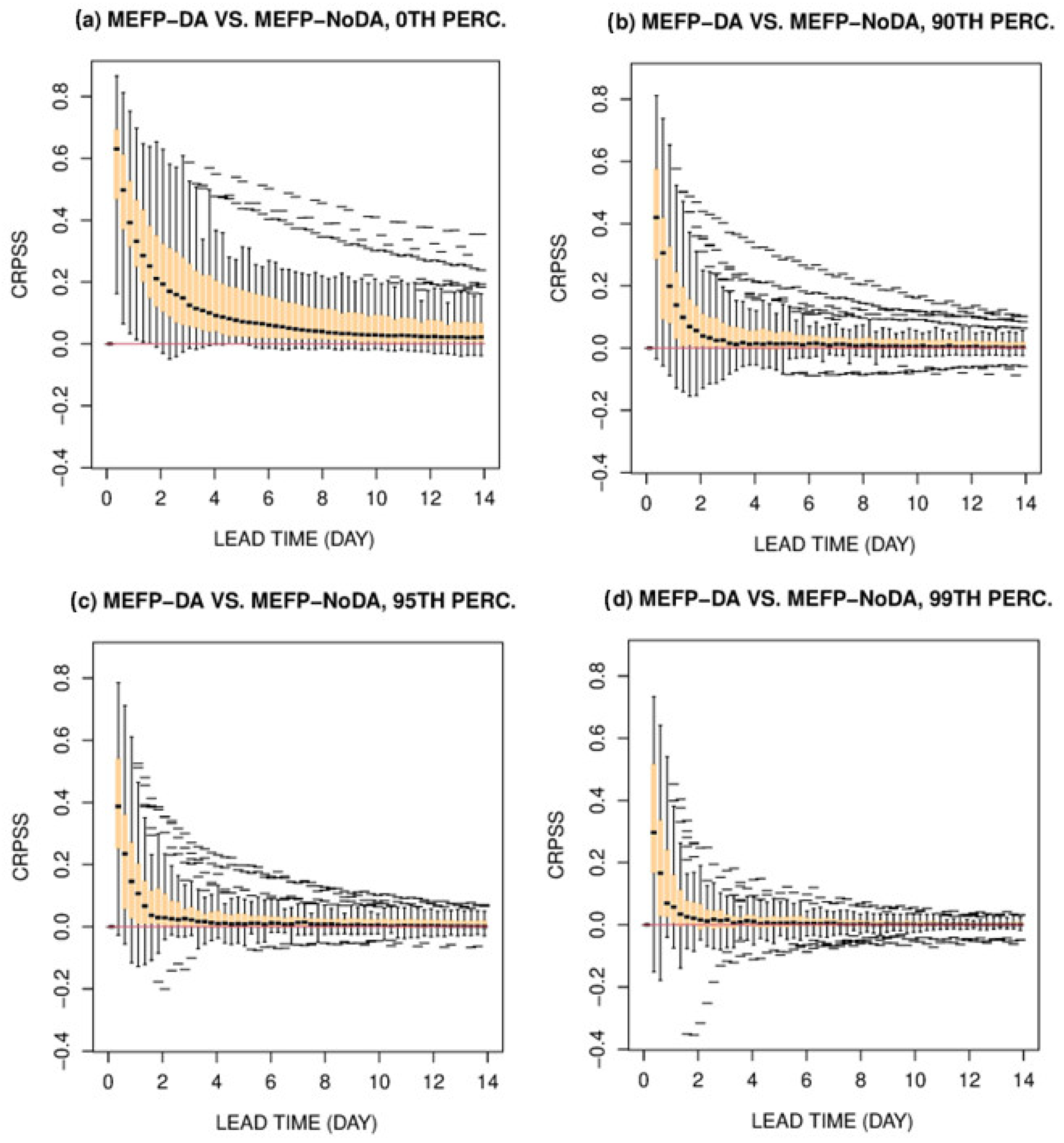
4.1. Impact of DA
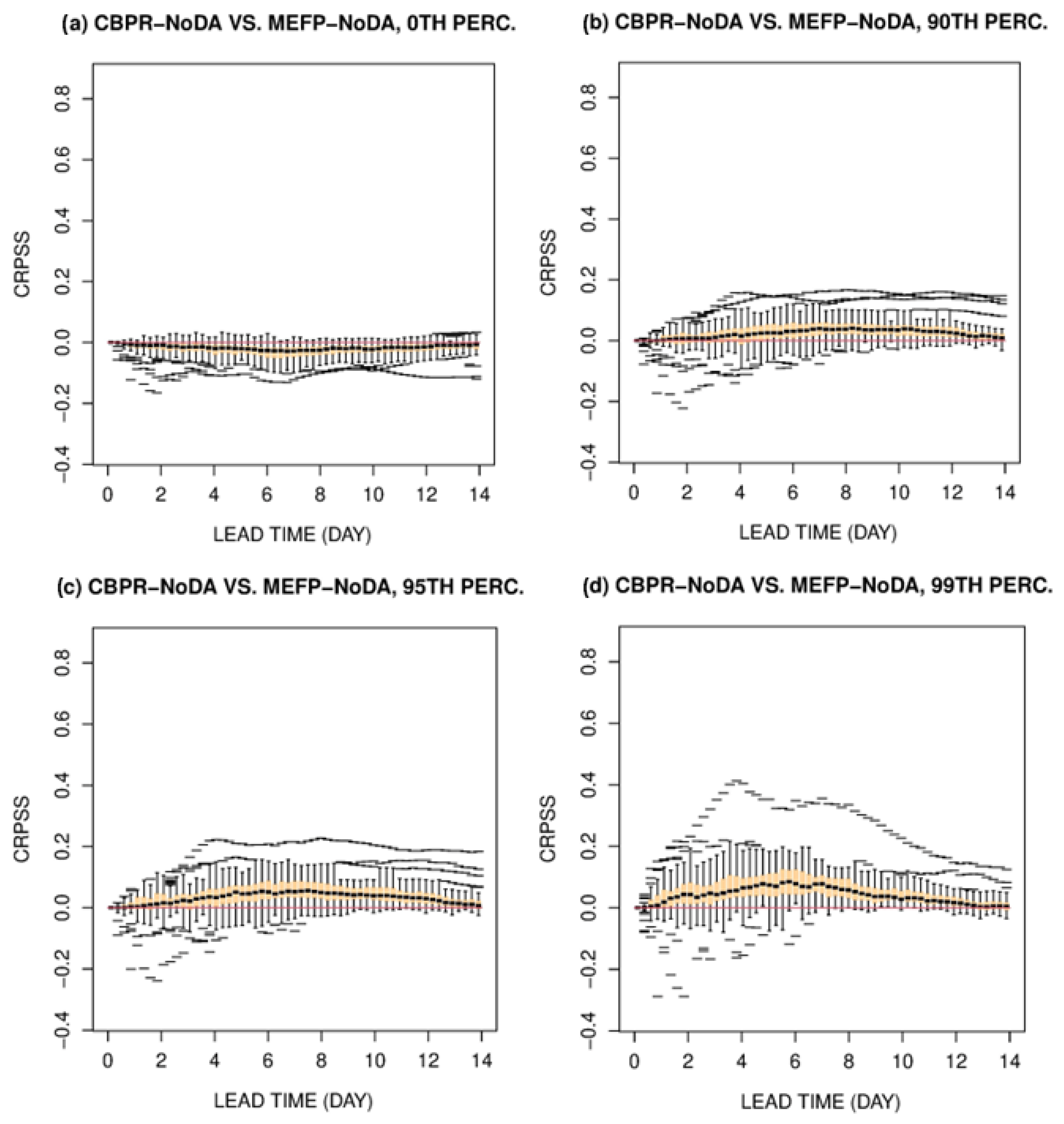
4.2. Impact of CBPR
4.3. Impact of CBPR and DA
4.4. Impact Without Post-Factum Reduction of Hydrologic Uncertainty in Model Calibration
4.5. Discussion
5. Conclusions and Future Research Recommendations
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A&F | AdjustQ and Fblend |
| AB_OPT | Adjoint-based optimizer |
| AEnKF | Adaptive conditional bias-penalized ensemble Kalman filter |
| AKF | Adaptive conditional bias-penalized Kalman filter |
| CB | Conditional bias |
| CBPR | Conditional bias-penalized regression |
| CHPS | Community Hydrologic Prediction System |
| CRPS | Continuous ranked probability score |
| CRPSS | Continuous ranked probability skill score |
| DA | Data assimilation |
| EnKF | Ensemble Kalman filter |
| GEFSv12 | Global Ensemble Forecast System version 12 |
| HEFS | Hydrologic Ensemble Forecast Service |
| IC | Initial condition |
| KF | Kalman filter |
| MAP | Mean areal precipitation |
| MAPE | Mean areal potential evapotranspiration |
| MAT | Mean areal temperature |
| MEFP | Meteorological Ensemble Forecast Processor |
| MOD | Run-time modification |
| NWP | Numerical weather prediction |
| NWS | National Weather Service |
| OLSR | Ordinary least-squares regression |
| RFC | River Forecast Center |
| RMSE | Root mean squared error |
| SAC | Sacramento soil moisture accounting model |
| SLS | Sequential line search |
| Snow17 | Snow17 snow ablation model |
| UHG | Unit hydrograph |
| VAR | Variational assimilation |
References
- Demargne, J.; Wu, L.; Regonda, S.; Brown, J.; Lee, H.; He, M.; Seo, D.-J.; Hartman, R.; Herr, H.; Fresch, M.; et al. The science of NOAA’s operational hydrologic ensemble forecast service. Bull. Am. Meteorol. Soc. 2014, 95, 79–98. [Google Scholar] [CrossRef]
- Troin, M.; Arsenault, R.; Wood, A.W.; Brissette, F.; Martel, J.-L. Generating ensemble streamflow forecasts: A review of methods and approaches over the past 40 years. Water Resour. Res. 2021, 57, e2020WR028392. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour. Res. 1999, 35, 2739–2750. [Google Scholar] [CrossRef]
- Seo, D.-J.; Herr, H.; Schaake, J. A statistical post-processor for accounting of hydrologic uncertainty in short-range ensemble streamflow prediction. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 1987–2035. [Google Scholar]
- Schaake, J.; Demargne, J.; Mullusky, M.; Welles, E.; Wu, L.; Herr, H.; Fan, X.; Seo, D.-J. Precipitation and temperature ensemble forecasts from single-value forecasts. Hydrol. Earth Syst. Sci. 2007, 4, 655–717. [Google Scholar]
- Wu, L.; Seo, D.-J.; Demargne, J.; Brown, J.D.; Cong, S.; Schaake, J. Generation of ensemble precipitation forecast from single-valued quantitative precipitation forecast for hydrologic ensemble prediction. J. Hydrol. 2011, 399, 281–298. [Google Scholar] [CrossRef]
- National Weather Service. MEFPPE Configuration Guide; NOAA/NWS/Office of Water Prediction: Silver Spring, MD, USA, 2022. Available online: https://vlab.noaa.gov/documents/207461/1893010/MEFPPEConfigurationGuide.pdf (accessed on 13 August 2025).
- National Weather Service. Meteorological Ensemble Forecast Processor (MEFP) User’s Manual; NOAA/NWS/Office of Water Prediction: Silver Spring, MD, USA, 2022. Available online: https://vlab.noaa.gov/documents/207461/1893026/MEFP_Users_Manual.pdf (accessed on 13 August 2025).
- Cui, B.; Toth, Z.; Zhu, Y.; Hou, D. Bias correction for global ensemble forecast. Weather Forecast. 2012, 27, 396–410. [Google Scholar] [CrossRef]
- Whitin, B.; He, K. MEFP Large Precipitation Event Analysis; California-Nevada River Forecast Center, NWS: Sacramento, CA, USA, 2015.
- Seo, D.-J.; Kim, S.; Alizadeh, B.; Limon, R.A.; Ghazvinian, M.; Lee, H. Improving Precipitation Ensembles for Heavy-to-Extreme Events and Streamflow Post-Processing for Short-to-Long Ranges; Department of Civil Engineering, University of Texas at Arlington: Arlington, TX, USA, 2019; 52p. [Google Scholar]
- Jozaghi, A.; Shen, H.; Ghazvinian, M.; Seo, D.-J.; Zhang, Y.; Welles, E.; Reed, S. Multi-model streamflow prediction using conditional bias-penalized multiple linear regression. Stoch. Environ. Res. Risk Assess. 2021, 35, 2355–2373. [Google Scholar] [CrossRef]
- Kim, S.; Jozaghi, A.; Seo, D.-J. Improving ensemble forecast quality for heavy-to-extreme precipitation for the Meteorological Ensemble Forecast Processor via conditional bias-penalized regression. J. Hydrol. 2025, 647, 132363. [Google Scholar] [CrossRef]
- Kim, S.; Seo, D.-J. Comparative evaluation of conditional bias-penalized regression-aided Meteorological Ensemble Forecast Processor for large-to-extreme precipitation events. Weather Forecast. 2025, 40, 959–975. [Google Scholar] [CrossRef]
- Alizadeh, B. Improving Post Processing of Ensemble Streamflow Forecast for Short-to-Long Ranges: A Multiscale Approach. Ph.D. Thesis, University of Texas at Arlington, Arlington, TX, USA, 2019; 125p. [Google Scholar]
- Alizadeh, B.; Limon, R.A.; Seo, D.; Lee, H.; Brown, J. Multiscale postprocessor for ensemble streamflow prediction for short to long ranges. J. Hydrometeorol. 2020, 21, 265–285. [Google Scholar] [CrossRef]
- Mendoza, P.; Wood, A.; Clark, E.; Nijssen, B.; Clark, M.; Ramos, M.-H.; Voisin, N. Improving medium-range ensemble streamflow forecasts through statistical post-processing. In Proceedings of the 2016 American Geophysical Union Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- National Weather Service. The Experimental Ensemble Forecast System (XEFS) Design and Gap Analysis; NOAA/NWS/Office of Hydrologic Development: Silver Spring, MD, USA, 2007; 50p.
- Hornberger, G.; Raffensperger, J.P.; Wiberg, P.L.; Eshleman, K.N. Elements of Physical Hydrology; Johns Hopkins University Press: Baltimore, MD, USA, 1998. [Google Scholar]
- Hersbach, H. Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather Forecast. 2000, 15, 559–570. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guidelines on the Verification of Hydrological Forecasts; WMO: Geneva, Switzerland, 2025; 197p. [Google Scholar]
- Lee, H.S.; Liu, Y.; Brown, J.; Ward, J.; Maestre, A.; Fresch, M.A.; Herr, H.; Wells, E. Validation of ensemble streamflow forecasts from the Hydrologic Ensemble Forecast Service (HEFS). In Proceedings of the American Geophysical Union 2018 Fall Meeting, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
- Lee, H.S.; Liu, Y.; Ward, J.; Kim, S.; Brown, J.; Maestre, A.; Fresch, M.A.; Herr, H.; Wells, E.; Camacho, F. On the improvements in precipitation, temperature and streamflow forecasts from the Hydrologic Ensemble Forecast Service after upgrading from the GEFSv10 to the GEFSv12. In Proceedings of the American Geophysical Union 2020 Fall Meeting, Virtual, 1–17 December 2020. [Google Scholar]
- Guan, H.; Zhu, Y.; Sinsky, E.; Fu, B.; Li, W.; Zhou, X.; Xue, X.; Hou, D.; Peng, J.; Nageswararao, M.M.; et al. GEFSv12 reforecast dataset for supporting subseasonal and hydrometeorological applications. Mon. Weather Rev. 2022, 150, 647–665. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Shlyaeva, A.; Bates, G.; Fredrick, S.; Pegion, P.; Sinsky, E.; Zhu, Y.; Tallapragada, V.; Guan, H.; et al. The Reanalysis for the Global Ensemble Forecast System, Version 12. Mon. Weather Rev. 2022, 150, 59–79. [Google Scholar] [CrossRef]
- Roe, J.; Dietz, C.; Restrepo, P.; Halquist, J.; Hartman, R.; Horwood, R.; Olsen, B.; Opitz, H.; Shedd, R.; Welles, E. NOAA’s Community Hydrologic Prediction System. In Proceedings of the Second Joint Federal Interagency Conference, Las Vegas, NV, USA, 27 June–1 July 2010; 12p. [Google Scholar]
- Burnash, R.J.C.; Ferral, R.L.; McGuire, R.A. A Generalized Streamflow Simulation System—Conceptual Modeling for Digital Computers. National Weather Service, NOAA, and the State of California Department of Water Resources Technical Report; Joint Federal-State River Forecast Center: Sacramento, CA, USA, 1973; 68p.
- Anderson, E.A. A Point Energy and Mass Balance Model of a Snow Cover. NOAA Technical Report; NWS: Silver Spring, MD, USA, 1976; Volume 19, 150p. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Seo, D.-J.; Cajina, L.; Corby, R.; Howieson, T. Automatic state updating for operational streamflow forecasting via variational data assimilation. J. Hydrol. 2009, 367, 255–275. [Google Scholar] [CrossRef]
- Bissell, V.C. When NWSRFS, SEUS and Snow Intersect. In Proceedings of the Western Snow Conference, Bend, OR, USA, 16–18 April 1996. [Google Scholar]
- Franz, K.; Hogue, T.; Barik, M.; He, M. Assessment of SWE data assimilation for ensemble streamflow predictions. J. Hydrol. 2014, 519 Pt D, 2737–2746. [Google Scholar] [CrossRef]
- Moser, C.L.; Kroczynski, S.; Hlywiak, K. Comparison of the SAC-SMA and API-CONT Hydrologic Models at Several Susquehanna River Headwater Basins. Eastern Region Technical Attachment No. 2013-01. 2013; 20p. Available online: https://www.weather.gov/media/erh/ta/ta2013-01.pdf (accessed on 13 August 2025).
- Kuzmin, V.; Seo, D.-J.; Koren, V. Fast and efficient optimization of hydrologic model parameters using a priori estimates and stepwise line search. J. Hydrol. 2008, 353, 109–128. [Google Scholar] [CrossRef]
- Seo, D.-J.; Shen, H.; Lee, H. Adaptive conditional bias-penalized Kalman filter with minimization of degrees of freedom for noise for superior state estimation and prediction of extremes. Comput. Geosci. 2022, 166, 105193. [Google Scholar] [CrossRef]
- Shen, H.; Lee, H.; Seo, D.-J. Adaptive conditional bias-penalized Kalman filter for improved estimation of extremes and its approximation for reduced computation. Hydrology 2022, 9, 35. [Google Scholar] [CrossRef]
- Shen, H.; Seo, D.-J.; Lee, H.; Liu, Y.; Noh, S. Improving flood forecasting using conditional bias-aware assimilation of streamflow observations and dynamic assessment of flow-dependent information content. J. Hydrol. 2022, 605, 127247. [Google Scholar] [CrossRef]
- Jozaghi, A.; Shen, H.; Seo, D.-J. Adaptive conditional bias-penalized kriging for improved spatial estimation of extremes. Stoch. Environ. Res. Risk Assess. 2024, 38, 193–209. [Google Scholar] [CrossRef]
- Seo, D.-J. Conditional bias-penalized kriging. Stoch. Environ. Res. Risk Assess. 2013, 27, 43–58. [Google Scholar] [CrossRef]
- Lee, H.; Noh, S.; Kim, S.; Shen, H.; Seo, D.-J.; Zhang, Y. Improving flood forecasting using conditional bias-penalized ensemble Kalman filter. J. Hydrol. 2019, 575, 596–611. [Google Scholar] [CrossRef]
- Schweppe, F.C. Uncertain Dynamic Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973; 563p. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Elsevier Academic Press: San Diego, CA, USA, 2006; 648p. [Google Scholar]
- Seo, D.-J.; Mohammad Saifuddin, M.; Lee, H. Conditional bias-penalized Kalman filter for improved estimation and prediction of extremes. Stoch. Environ. Res. Risk Assess. 2017, 32, 183–201. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 1994, 99, 143–162. [Google Scholar] [CrossRef]
- Lorentzen, R.J.; Naevdal, G. An iterative ensemble Kalman filter. IEEE Trans. Autom. Control 2011, 56, 1990–1995. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000. [Google Scholar] [CrossRef]
- Sorooshian, S.; Dracup, J.A. Stochastic parameter estimation procedures for hydrologic rainfall–runoff models: Correlated and heteroscedastic error cases. Water Resour. Res. 1980, 16, 430–442. [Google Scholar] [CrossRef]
- Carpenter, T.M.; Georgakakos, K.P. Impacts of parametric and radar rainfall uncertainty on the ensemble streamflow simulations of a distributed hydrologic model. J. Hydrol. 2004, 298, 202–221. [Google Scholar] [CrossRef]
- Weerts, A.H.; El Serafy, G.Y. Particle filtering and ensemble Kalman filtering for state updating with hydrological conceptual rainfall–runoff models. Water Resour. Res. 2006, 42, W09403. [Google Scholar] [CrossRef]
- Clark, M.P.; Rupp, D.E.; Woods, R.A.; Zheng, X.; Ibbitt, R.P.; Slater, A.G.; Schmidt, J.; Uddstorm, M.J. Hydrologic data assimilation with the ensemble Kalman filter: Use of streamflow observations to update states in a distributed hydrological model. Adv. Water Resour. 2008, 31, 1309–1324. [Google Scholar] [CrossRef]
- Rakovec, O.; Weerts, A.H.; Hazenberg, P.; Torfs, P.J.J.F.; Uijlenhoet, R. State updating of a distributed hydrological model with Ensemble Kalman Filtering: Effects of updating frequency and observation network density on forecast accuracy. Hydrol. Earth Syst. Sci. 2012, 16, 3435–3449. [Google Scholar] [CrossRef]
- National Weather Service. NWSRFS User Manual Documentation; Office of Water Prediction: Silver Spring, MD, USA, 2024.
- Bowler, N.E. Accounting for the effect of observation errors on verification of MOGREPS. Meteorol. Appl. 2008, 15, 199–205. [Google Scholar] [CrossRef]
- Bellier, J.; Zin, I.; Bontron, G. Sample stratification in verification of ensemble forecasts of continuous scalar variables: Potential benefits and pitfalls. Mon. Weather Rev. 2017, 145, 3529–3544. [Google Scholar] [CrossRef]
- Lerch, S.; Thorarinsdottir, T.L.; Ravazzolo, F.; Gneiting, T. Forecaster’s Dilemma: Extreme Events and Forecast Evaluation. Stat. Sci. 2017, 32, 106–127. [Google Scholar] [CrossRef]
- Moore, B.J. Flow dependence of medium-range precipitation forecast skill over California. Weather Forecast. 2023, 38, 699–720. [Google Scholar] [CrossRef]
- Noh, S.; Weerts, A.; Rakovec, O.; Lee, H.; Seo, D.-J. Assimilation of streamflow observations. In Handbook of Hydrometeorological Ensemble Forecasting; Duan, Q., Pappenberger, F., Thielen, J., Wood, A., Cloke, H.L., Schaake, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Smith, M.; Koren, V.; Zhang, Z.; Reed, S.; Seo, D.-J.; Moreda, F.; Kuzmin, V.; Cui, Z.; Anderson, R. NOAA NWS Distributed Hydrologic Modeling Research and Development. NOAA Technical Report; NWS: Silver Spring, MD, USA, 2004; Volume 51, 63p.
- van Velzen, N.; Altaf, M.U.; Verlaan, M. OpenDA-NEMO framework for ocean data assimilation. Ocean Dyn. 2016, 66, 691–702. [Google Scholar] [CrossRef][Green Version]
- Kim, S.; Shen, H.; Noh, S.; Seo, D.-J.; Welles, E.; Pelgrim, E.; Weerts, A.; Lyons, E.; Philips, B.; Smith, M.; et al. High-resolution modelling and prediction of urban floods using WRF-Hydro and data assimilation. J. Hydrol. 2020, 598, 126236. [Google Scholar] [CrossRef]
- Brown, J.D.; He, M.; Regonda, S.; Wu, L.; Lee, H.; Seo, D.-J. Verification of temperature, precipitation and streamflow forecasts from the NOAA/NWS Hydrologic Ensemble Forecast Service (HEFS): 2. Streamflow verification. J. Hydrol. 2014, 519 Pt D, 2847–2868. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Bari, M.A.; Kabir, A.; Hasan, M.M.; Woldemeskel, F.M.; Gamage, N.; Sunter, P.D.; Zhang, X.S.; Robertson, D.E.; Bennett, J.C.; et al. Development of a national 7-day ensemble streamflow forecasting service for Australia. Hydrol. Earth Syst. Sci. 2022, 26, 4801–4821. [Google Scholar] [CrossRef]
- Bari, M.A.; Hasan, M.M.; Amirthanathan, G.E.; Hapuarachchi, H.A.P.; Kabir, A.; Cornish, A.D.; Sunter, P.; Feikema, P.M. Performance Evaluation of a National Seven-Day Ensemble Streamflow Forecast Service for Australia. Water 2024, 16, 1438. [Google Scholar] [CrossRef]
- Kim, S.; Sadeghi, H.; Limon, R.A.; Seo, D.-J.; Philpott, A.; Bell, F.; Brown, J.; He, K. Ensemble streamflow forecasting using short- and medium-range precipitation forecasts for the Upper Trinity River Basin in North Texas via the Hydrologic Ensemble Forecast Service (HEFS). J. Hydrometeorol. 2018, 19, 1467–1483. [Google Scholar] [CrossRef]
- Zhang, J.; Li, W.; Duan, Q. Quantifying the contributions of hydrological pre-processor, post-processor, and data assimilator to ensemble streamflow prediction skill. J. Hydrol. 2025, 651, 132611. [Google Scholar] [CrossRef]



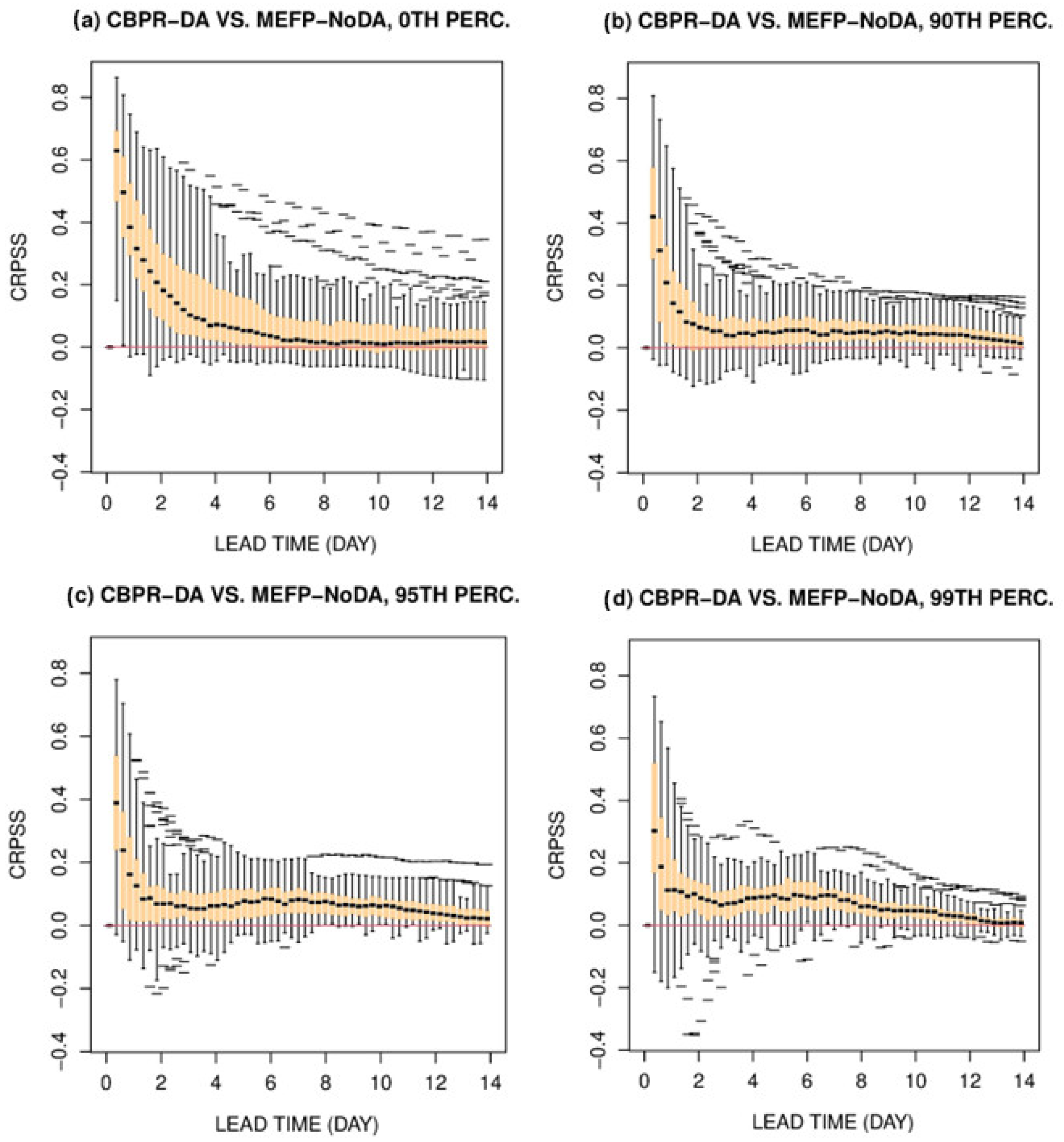
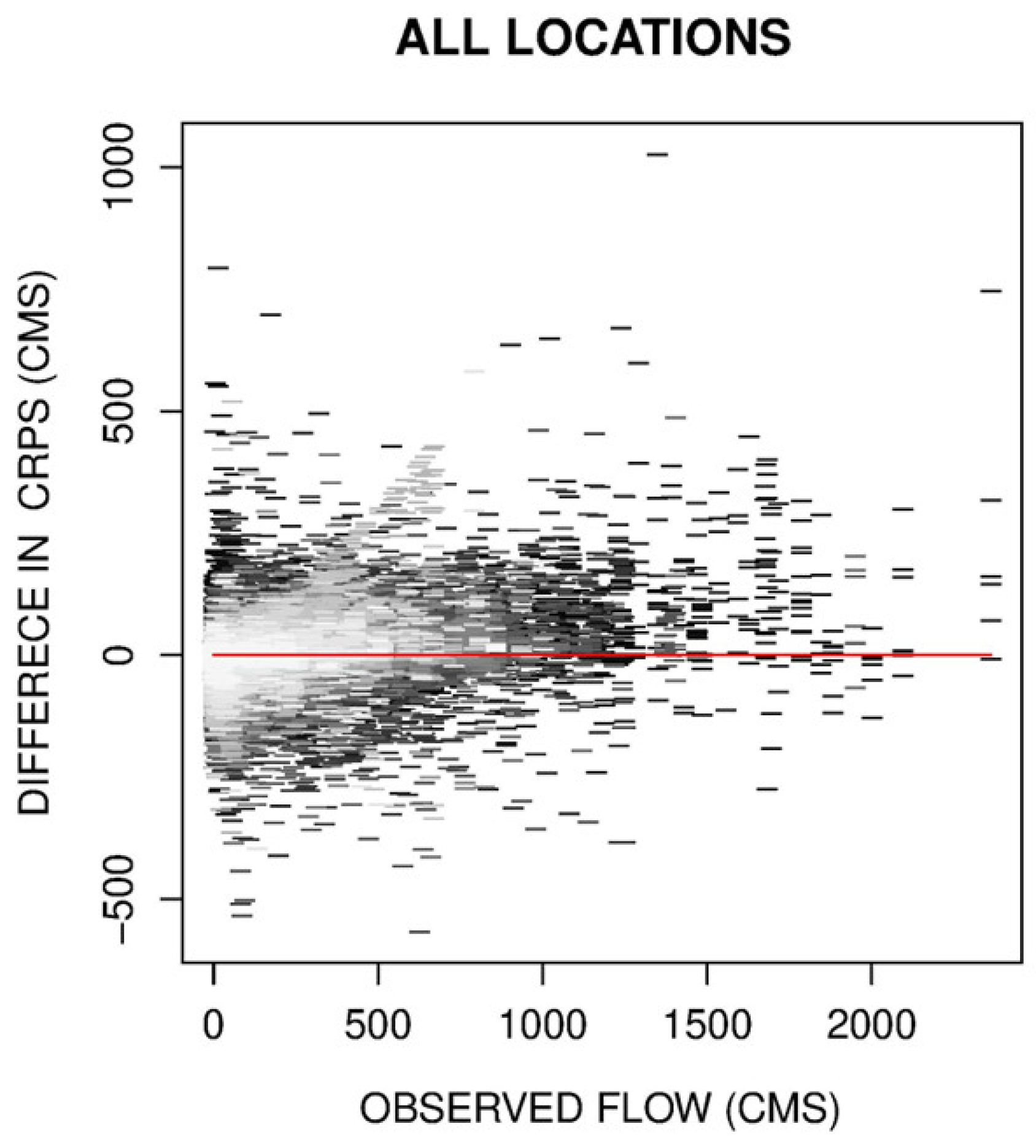
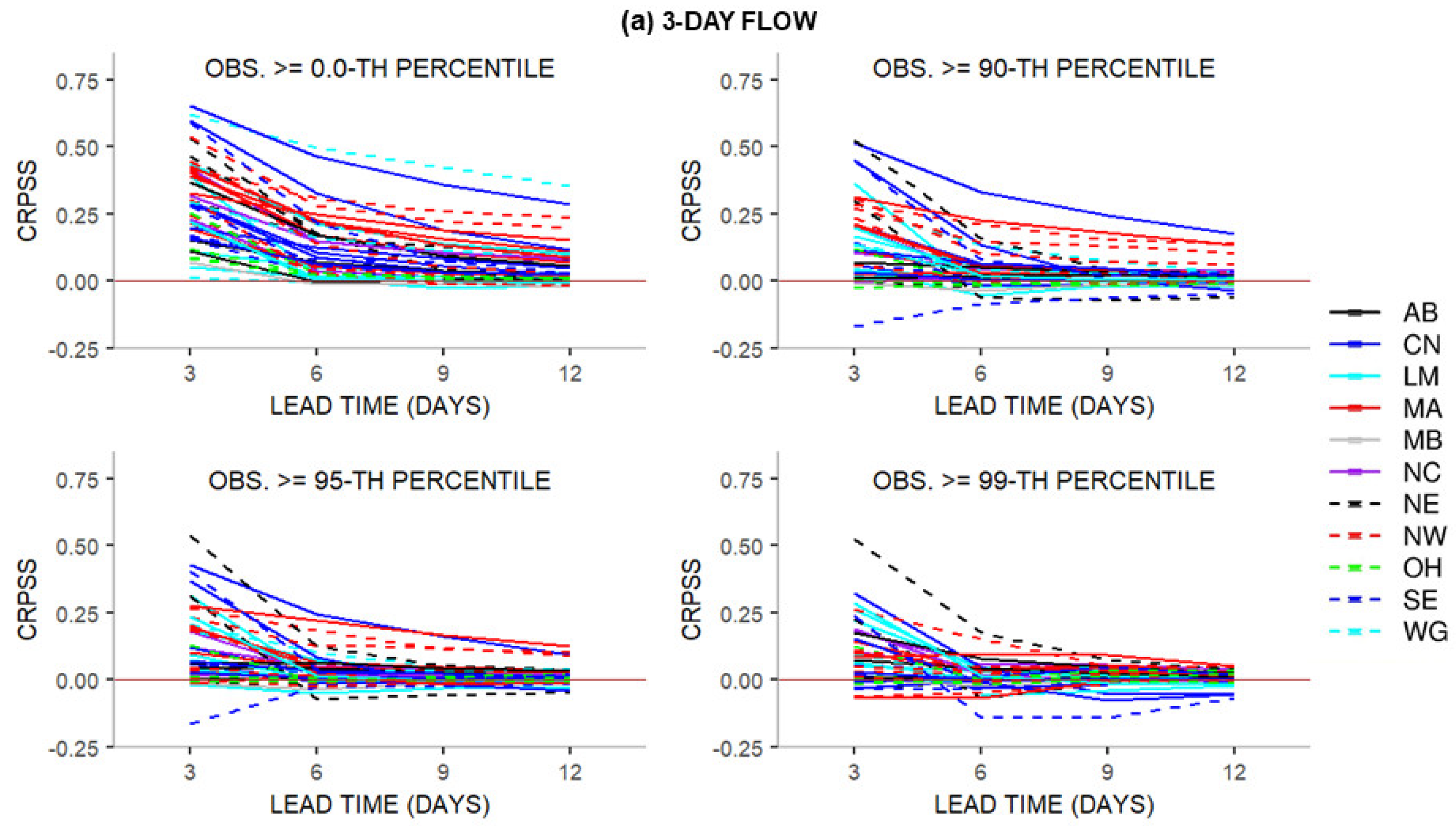
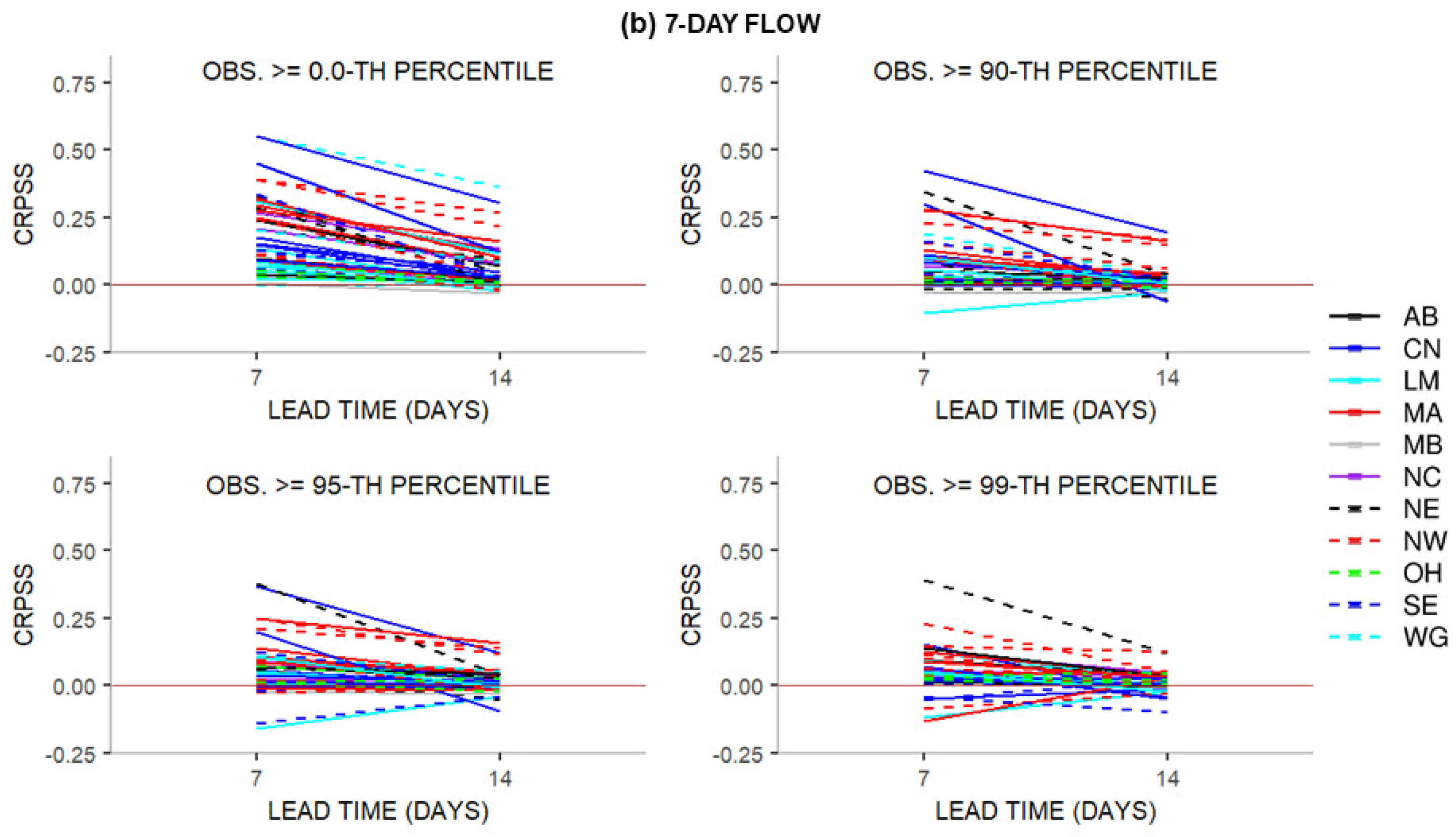
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Seo, D.-J. Improving Operational Ensemble Streamflow Forecasting with Conditional Bias-Penalized Post-Processing of Precipitation Forecast and Assimilation of Streamflow Data. Hydrology 2025, 12, 229. https://doi.org/10.3390/hydrology12090229
Kim S, Seo D-J. Improving Operational Ensemble Streamflow Forecasting with Conditional Bias-Penalized Post-Processing of Precipitation Forecast and Assimilation of Streamflow Data. Hydrology. 2025; 12(9):229. https://doi.org/10.3390/hydrology12090229
Chicago/Turabian StyleKim, Sunghee, and Dong-Jun Seo. 2025. "Improving Operational Ensemble Streamflow Forecasting with Conditional Bias-Penalized Post-Processing of Precipitation Forecast and Assimilation of Streamflow Data" Hydrology 12, no. 9: 229. https://doi.org/10.3390/hydrology12090229
APA StyleKim, S., & Seo, D.-J. (2025). Improving Operational Ensemble Streamflow Forecasting with Conditional Bias-Penalized Post-Processing of Precipitation Forecast and Assimilation of Streamflow Data. Hydrology, 12(9), 229. https://doi.org/10.3390/hydrology12090229




