Intelligent Decoupling of Hydrological Effects in Han River Cascade Dam System: Spatial Heterogeneity Mechanisms via an LSTM-Attention-SHAP Interpretable Framework
Abstract
1. Introduction
2. Materials and Methodology
2.1. Study Area
2.2. Multi-Period Data Collection
2.3. LSTM
2.4. Attention Mechanism
2.5. Data Processing
2.6. Model Architecture and Model Hyperparameter Settings
2.7. Interpretable Methods for Deep Learning Models
3. Results
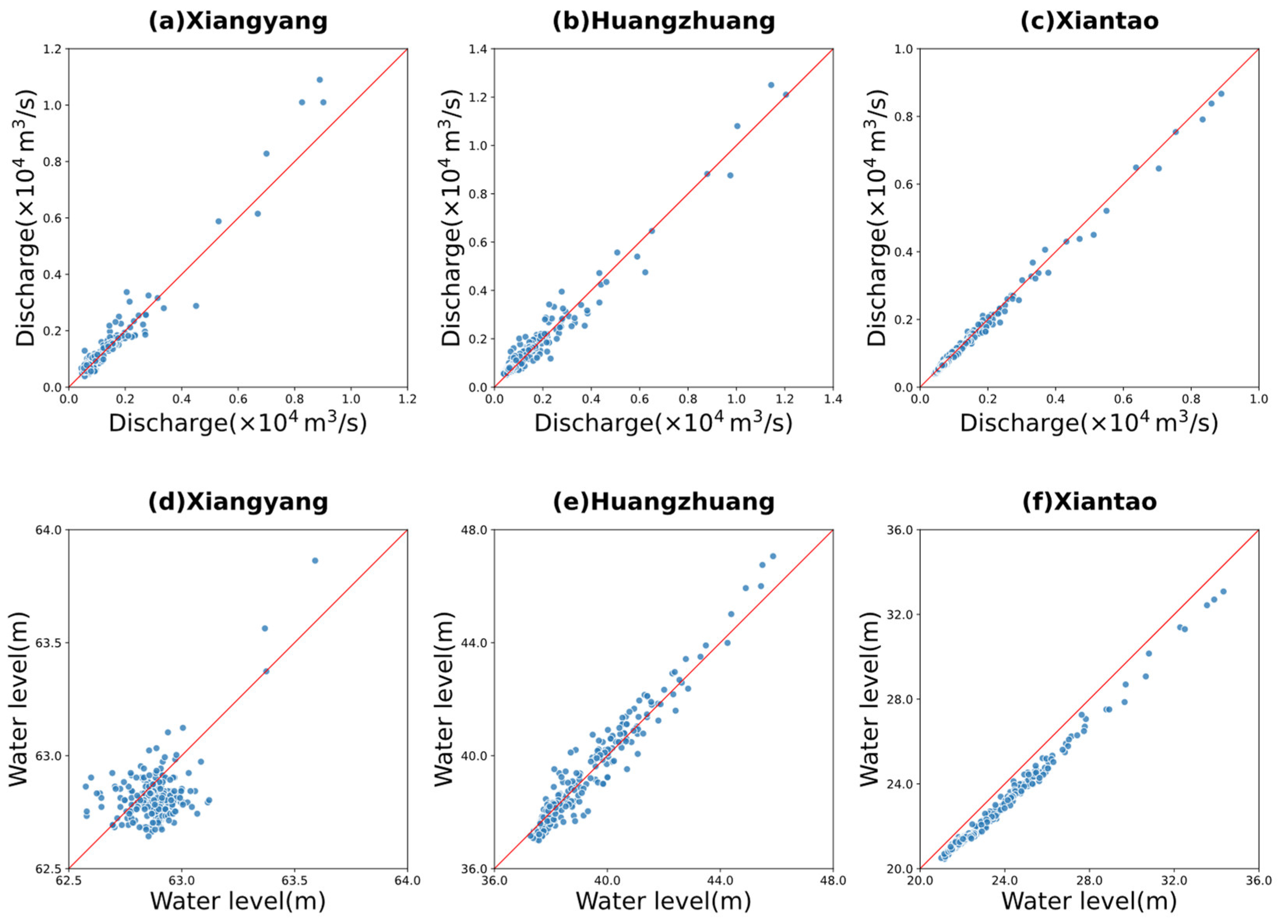
3.1. Prediction Performance of the LSTM Model
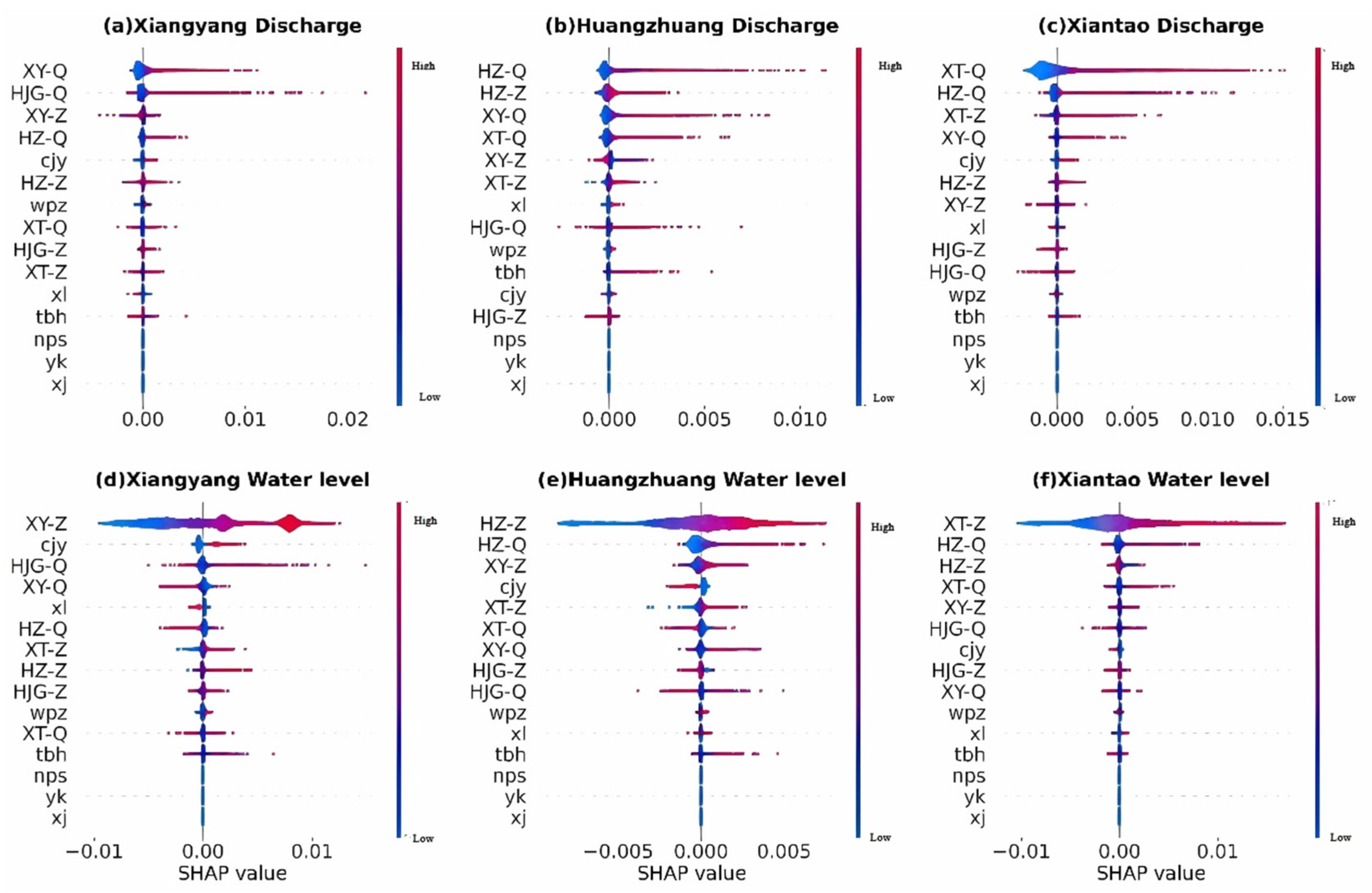
3.2. Contribution of Discharge Capacity
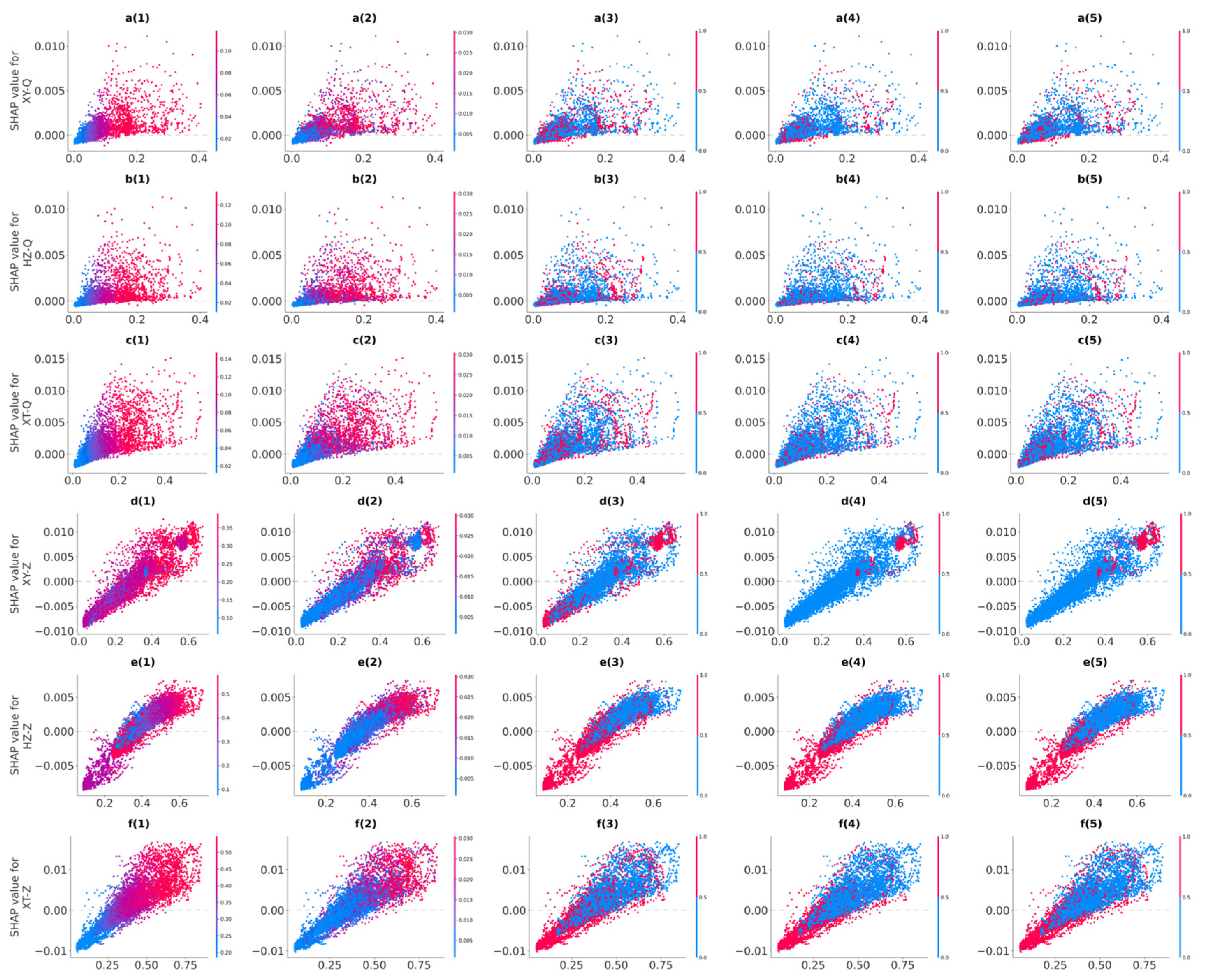
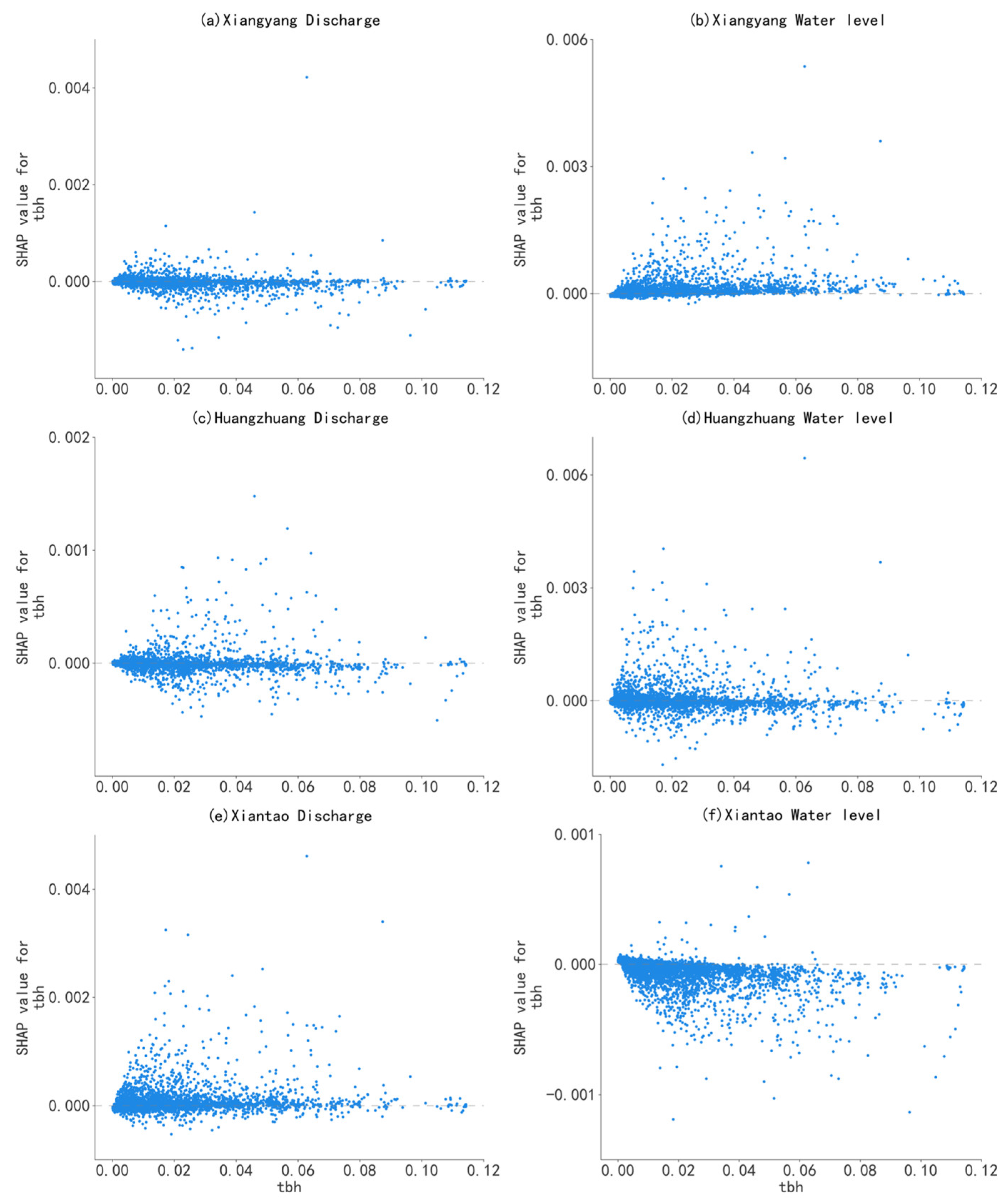
3.3. Spatial Heterogeneity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HJG-Q | Discharge at Huangjiagang Station |
| HJG-Z | Water level at Huangjiagang Station |
| XY-Q | Discharge at Xiangyang Station |
| XY-Z | Water level at Xiangyang Station |
| HZ-Q | Discharge at Huangzhuang Station |
| HZ-Z | Water level at Huangzhuang Station |
| XT-Q | Discharge at Xiantao Station |
| XT-Z | Water level at Xiantao Station |
| cjy | Cuijiaying Hydro Project |
| wpz | Wangfuzhou Hydro Project |
| xl | Xinglong Hydro Project |
| nps | Nianpanshan Hydro Project |
References
- Yang, X.; Hu, Y.; Sun, Z.; Li, Y.; Xiong, H.; Li, D. Human interventions alter morphodynamics of meandering channels: Insights from decadal to pre-industrial observations in the Yangtze River. J. Hydrol. 2024, 634, 131067. [Google Scholar] [CrossRef]
- Chang, C.-H.; Lee, H.; Do, S.; Du, T.; Markert, K.; Hossain, F.; Ahmad, S.; Piman, T.; Meechaiya, C.; Bui, D.; et al. Operational forecasting inundation extents using REOF analysis (FIER) over lower Mekong and its potential economic impact on agriculture. Environ. Model. Softw. 2023, 162, 105643. [Google Scholar] [CrossRef]
- Li, J.; Wu, G.; Zhang, Y.; Shi, W. Optimizing flood predictions by integrating LSTM and physical-based models with mixed historical and simulated data. Heliyon 2024, 10, e33669. [Google Scholar] [CrossRef]
- Stanley, D.J. Nile delta: Extreme case of sediment entrapment on a delta plain and consequent coastal land loss. Mar. Geol. 1996, 129, 189–195. [Google Scholar] [CrossRef]
- Ali, E.M.; El-Magd, I.A. Impact of human interventions and coastal processes along the Nile Delta coast, Egypt during the past twenty-five years. Egypt. J. Aquat. Res. 2016, 42, 1–10. [Google Scholar] [CrossRef]
- Kemper, J.T.; Rathburn, S.L.; Mueller, E.R.; Wohl, E.; Scamardo, J. Geomorphic response of low-gradient, meandering and braided alluvial river channels to increased sediment supply. Earth-Sci. Rev. 2023, 241, 104429. [Google Scholar] [CrossRef]
- Roccati, A.; Faccini, F.; Luino, F.; De Graff, J.V.; Turconi, L. Morphological changes and human impact in the Entella River floodplain (Northern Italy) from the 17th century. Catena 2019, 182, 104122. [Google Scholar] [CrossRef]
- Mahapatra, S.; Kumar Jha, M. Environmental flow estimation for regulated rivers under data-scarce condition. J. Hydrol. 2022, 614, 128569. [Google Scholar] [CrossRef]
- Zeiger, S.J.; Hubbart, J.A. Measuring and modeling event-based environmental flows: An assessment of HEC-RAS 2D rain-on-grid simulations. J. Environ. Manag. 2021, 285, 112125. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Liu, C.; Xu, Y.; Niu, C.; Li, R.; Li, M.; Hu, C.; Tian, L. An interpretable hybrid deep learning model for flood forecasting based on Transformer and LSTM. J. Hydrol. Reg. Stud. 2024, 54, 101873. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, Z.; Thé, J.V.G.; Yang, S.X.; Gharabaghi, B. The Discharge Forecasting of Multiple Monitoring Station for Humber River by Hybrid LSTM Models. Water 2022, 14, 1794. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, H.; Zhang, W.; Fenicia, F.; Peng, H.; Xu, G. Hydrologic impacts of cascading reservoirs in the middle and lower Hanjiang River basin under climate variability and land use change. J. Hydrol. Reg. Stud. 2022, 44, 101253. [Google Scholar] [CrossRef]
- Deng, P.; Xu, C.; Bing, J.; Wang, L.; Li, L. Refined analysis of flood-regional composition under changing environment in the middle reach of Hanjiang River. J. Hydro-Environ. Res. 2024, 53, 15–27. [Google Scholar] [CrossRef]
- Liu, H.; Lei, D.; Yuan, J.; Yuan, G.; Cui, C.; Wang, Y.; Xue, W. Ionospheric TEC Prediction in China Based on the Multiple-Attention LSTM Model. Atmosphere 2022, 13, 1939. [Google Scholar] [CrossRef]
- Chen, H.; Guo, S.; Xu, C.-y.; Singh, V.P. Historical temporal trends of hydro-climatic variables and runoff response to climate variability and their relevance in water resource management in the Hanjiang basin. J. Hydrol. 2007, 344, 171–184. [Google Scholar] [CrossRef]
- Hao, W.; Hao, Z.; Yuan, F.; Ju, Q.; Hao, J. Regional Frequency Analysis of Precipitation Extremes and Its Spatio-Temporal Patterns in the Hanjiang River Basin, China. Atmosphere 2019, 10, 130. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Wu, J. Assessing the impact of Danjiangkou reservoir on ecohydrological conditions in Hanjiang river, China. Ecol. Eng. 2015, 81, 41–52. [Google Scholar] [CrossRef]
- Sun, J.; Chen, W.; Hu, B.; Xu, Y.J.; Zhang, G.; Wu, Y.; Hu, B.; Song, Z. Roles of reservoirs in regulating basin flood and droughts risks under climate change: Historical assessment and future projection. J. Hydrol. Reg. Stud. 2023, 48, 101453. [Google Scholar] [CrossRef]
- Waqas, M.; Humphries, U.W. A critical review of RNN and LSTM variants in hydrological time series predictions. MethodsX 2024, 13, 102946. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Choi, Y.; Jeon, J.-J. Interpretable water level forecaster with spatiotemporal causal attention mechanisms. Int. J. Forecast. 2025, 41, 1037–1054. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Kim, M.K.; Fu, N.; Liu, J.; Wang, J.; Srebric, J. Investigating the impact of data normalization methods on predicting electricity consumption in a building using different artificial neural network models. Sustain. Cities Soc. 2025, 118, 105570. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.-P.; Yang, Z.; Wang, G.; Zhu, Q. Integration of a Parsimonious Hydrological Model with Recurrent Neural Networks for Improved Streamflow Forecasting. Water 2018, 10, 1655. [Google Scholar] [CrossRef]
- Kanji, S.; Das, S. Exploring the morpho-tectonic nature, hydrological and physical characteristics of a watershed and prioritizing sub-watersheds surface runoff potentialities by integrating MCDM and ensemble machine learning models. J. Environ. Manag. 2025, 386, 125772. [Google Scholar] [CrossRef]
- Haces-Garcia, F.; Ross, N.; Glennie, C.L.; Rifai, H.S.; Hoskere, V.; Ekhtari, N. Rapid 2D hydrodynamic flood modeling using deep learning surrogates. J. Hydrol. 2025, 651, 132561. [Google Scholar] [CrossRef]
- Kruk, M. SHAP-NET, a network based on Shapley values as a new tool to improve the explainability of the XGBoost-SHAP model for the problem of water quality. Environ. Model. Softw. 2025, 188, 106403. [Google Scholar] [CrossRef]
- Wang, S.; Peng, H. Multiple spatio-temporal scale runoff forecasting and driving mechanism exploration by K-means optimized XGBoost and SHAP. J. Hydrol. 2024, 630, 130650. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, Z.; Zhou, Q.; Zhu, Z.; Jiang, C. A direct two-way coupling of the hydrologic and 1D-2D hydrodynamic models for watershed flood simulation. J. Hydrol. 2024, 639, 131606. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Rubin, Z.K.; Minear, J.T. Dams on the Mekong: Cumulative sediment starvation. Water Resour. Res. 2014, 50, 5158–5169. [Google Scholar] [CrossRef]
- Arnaud, F.; Schmitt, L.; Johnstone, K.; Rollet, A.-J.; Piégay, H. Engineering impacts on the Upper Rhine channel and floodplain over two centuries. Geomorphology 2019, 330, 13–27. [Google Scholar] [CrossRef]
- Wang, Z.; Si, Y.; Chu, H. Daily Streamflow Prediction and Uncertainty Using a Long Short-Term Memory (LSTM) Network Coupled with Bootstrap. Water Resour. Manag. 2022, 36, 4575–4590. [Google Scholar] [CrossRef]
- Latrubesse, E.; Arima, E.; Dunne, T.; Park, E.; Baker, V.; d’Horta, F.; Wight, C.; Wittmann, F.; Zuanon, J.; Baker, P.; et al. Damming the rivers of the Amazon basin. Nature 2017, 546, 363–369. [Google Scholar] [CrossRef] [PubMed]
- Hecht, J.S.; Lacombe, G.; Arias, M.E.; Dang, T.D.; Piman, T. Hydropower dams of the Mekong River basin: A review of their hydrological impacts. J. Hydrol. 2019, 568, 285–300. [Google Scholar] [CrossRef]
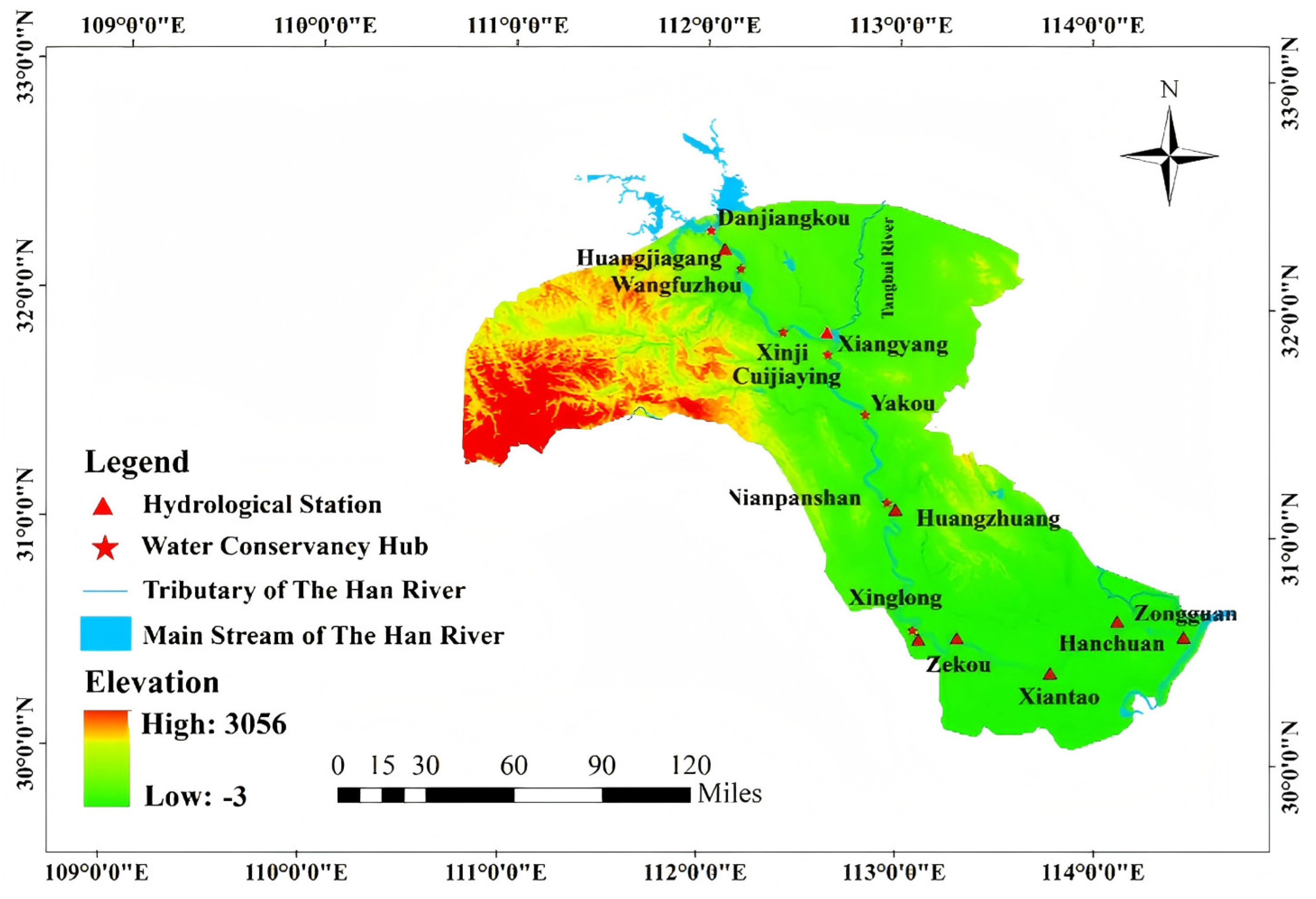
| Stations | Longitude | Latitude | Linking Hubs | Operation Time | Observed Items |
|---|---|---|---|---|---|
| Huangjiagang | 111°31′ E | 32°31′ N | Danjiangkou | 1973 | Water level, Discharge |
| Xiangyang | 112°10′ E | 32°02′ N | Wangfuzhou, Xinji | 1995, 2024 | |
| Huangzhuang | 112°30′ E | 31°13′ N | Yakou, Nianpanshan | 2022, 2023 | |
| Xiantao | 113°27′ E | 30°22′ N | Xinglong | 2013 |
| Hyperparameters | Search Space |
|---|---|
| lstm_units | [32, 64, 128] |
| num_heads | [4, 8] |
| learning_rate | [0.01, 0.001] |
| batch_size | [32, 64, 128] |
| dropout_rate | [0.2, 0.3, 0.5] |
| Gauging Stations | RMSE | MAE | R2 | NSE |
|---|---|---|---|---|
| Xiangyang | 247.488 | 10.134 | 0.938 | 0.938 |
| Huangzhuang | 230.292 | 9.733 | 0.879 | 0.879 |
| Xiantao | 107.847 | 6.772 | 0.988 | 0.988 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, S.; Xu, C.; Xu, W.; Zhou, M.; Zhang, J.; Zhang, G.; Pan, Z. Intelligent Decoupling of Hydrological Effects in Han River Cascade Dam System: Spatial Heterogeneity Mechanisms via an LSTM-Attention-SHAP Interpretable Framework. Hydrology 2025, 12, 217. https://doi.org/10.3390/hydrology12080217
Ouyang S, Xu C, Xu W, Zhou M, Zhang J, Zhang G, Pan Z. Intelligent Decoupling of Hydrological Effects in Han River Cascade Dam System: Spatial Heterogeneity Mechanisms via an LSTM-Attention-SHAP Interpretable Framework. Hydrology. 2025; 12(8):217. https://doi.org/10.3390/hydrology12080217
Chicago/Turabian StyleOuyang, Shuo, Changjiang Xu, Weifeng Xu, Mingyuan Zhou, Junhong Zhang, Guiying Zhang, and Zixuan Pan. 2025. "Intelligent Decoupling of Hydrological Effects in Han River Cascade Dam System: Spatial Heterogeneity Mechanisms via an LSTM-Attention-SHAP Interpretable Framework" Hydrology 12, no. 8: 217. https://doi.org/10.3390/hydrology12080217
APA StyleOuyang, S., Xu, C., Xu, W., Zhou, M., Zhang, J., Zhang, G., & Pan, Z. (2025). Intelligent Decoupling of Hydrological Effects in Han River Cascade Dam System: Spatial Heterogeneity Mechanisms via an LSTM-Attention-SHAP Interpretable Framework. Hydrology, 12(8), 217. https://doi.org/10.3390/hydrology12080217






